Предлагаемый способ управления может быть использован в космической технике при возвращении космического аппарата (КА) с окололунной орбиты к Земле.
Известен способ управления советской автоматической лунной станцией (АЛС) «Луна-16» при возврате от Луны к Земле [Левантовский В.И. Механика космического полета в элементарном изложении. М.: Наука, 1980. 512 с], выбранный в качестве аналога, включающий приложение управляющего импульса к АЛС для обеспечения возвращения к Земле. 21 сентября 1970 г. АЛС «Луна-16» находилась на поверхности Луны, затем с помощью собственной двигательной установки был выдан непрерывный импульс величиной ΔV~2700 м/с, позволяющий АЛС преодолеть притяжение Луны, выйти в окололунное пространство и после чего перейти на траекторию полета к Земле. Такой способ управления позволяет обеспечить выход на траекторию полета к Земле от Луны в любой момент времени за счет выбора азимута стрельбы.
Недостатком этого способа является значительная величина импульса для отлета к Земле, требующая больших затрат топлива.
Известен способ управления американским космическим кораблем (КК) «Апполон-8» при возврате к Земле с окололунной орбиты [Мировая пилотируемая космонавтика. История. Техника. Люди - под ред. Ю.Б. Батурина. М.: РТСофт.2005. 747 с], выбранный в качестве прототипа, включающий приложение к КК, находящемуся на окололунной орбите, управляющего импульса для схода с окололунной орбиты и перевода на траекторию возвращения к Земле. 25 декабря 1968 г. КК «Апполон-8» находился на околокруговой низкой окололунной орбите, после чего в определенный момент двигательной установкой КК выполнялся управляющий импульс величиной ΔV~1000 м/с.Момент выдачи ипараметры управляющего импульса КК «Апполон-8» выбирались исходя из условия преодоления лунного притяжения и обеспечения выхода на траекторию возвращения к Земле.
Недостатком этого способа управления является значительная величина импульса для отлета к Земле с окололунной орбиты, требующая больших затрат топлива. Также выполнение отлетного импульса такой величины возможно только в заданный временной промежуток, определяемый окном старта для отлета к Земле, появляющемся со скважностью половина лунного месяца.
Техническим результатом изобретения является снижение затрат суммарной характеристической скорости для отлета КА с окололунной орбиты к Земле, а также увеличение окон старта для отлета к Земле с оптимальными затратами характеристической скорости.
Технический результат достигается благодаря тому, что в способе управления КА при возврате к Земле с окололунной орбиты, включающем приложение управляющего импульса для схода с окололунной орбиты и перевода на траекторию возвращения к Земле, в отличие от известного, определяют, момент времени t1 с учетом соответствия аргумента широты u КА следующему неравенству (ϕ-90°<u<ϕ, где ϕ - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля, определяют величину управляющего импульса ΔV1, прикладываемого в указанный момент времени к КА для его перевода на промежуточную орбиту, а также определяют величину трансверсального управляющего импульса ΔV2 и момент времени его приложения t2, к которому плоскость промежуточной орбиты, за счет воздействия гравитационного поля Земли, развернется в положение, удовлетворяющее условию перелета к Земле за заданное время Т, после чего в момент времени t1 к космическому аппарату прикладывают управляющий импульс ΔV1, а затем в момент времени t2 прикладывают управляющий импульс ΔV2 для перевода на траекторию возвращения к Земле.
Сущность изобретения поясняется фиг. 1÷4, где:
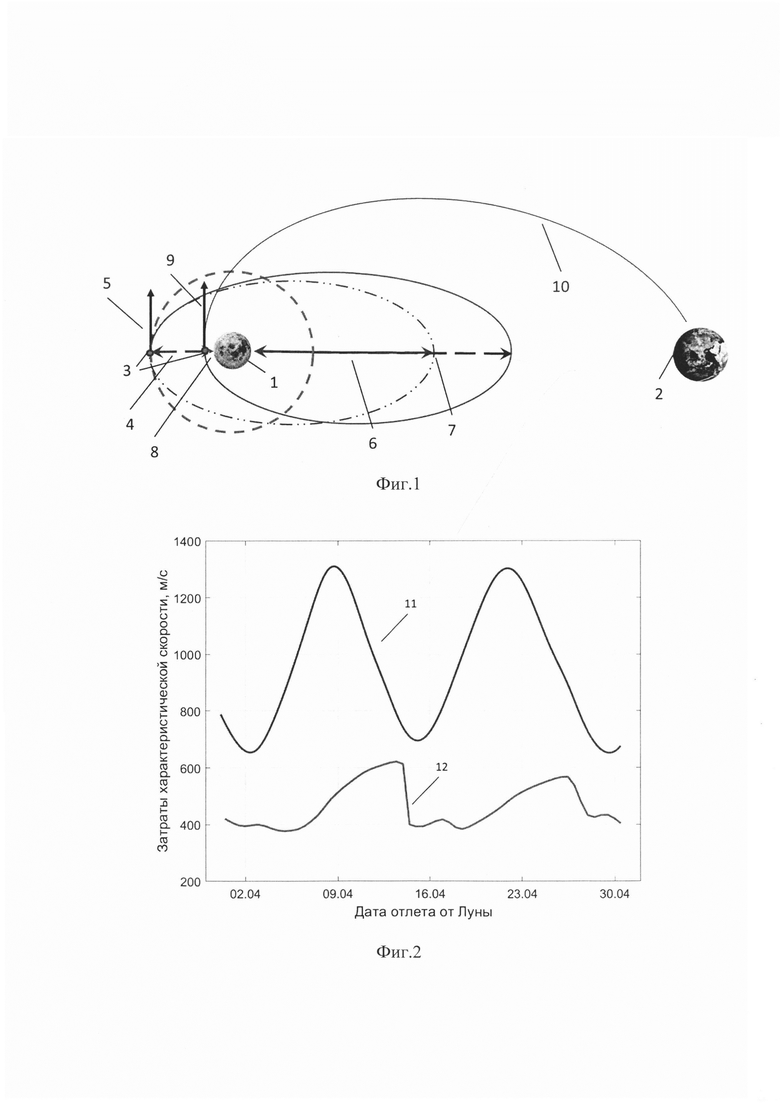
на фиг. 1 показа схема возвращения с окололунной орбиты к Земле предлагаемым способом управления по двухимпульсной схеме,
на фиг. 2 представлен график затрат суммарной характеристической скорости при возвращении с окололунной орбиты к Земле по одноимпульсной схеме, описанной в прототипе, и по предложенной двухимпульсной схеме в зависимости от даты отлета на интервале времени, соответствующем лунному месяцу,
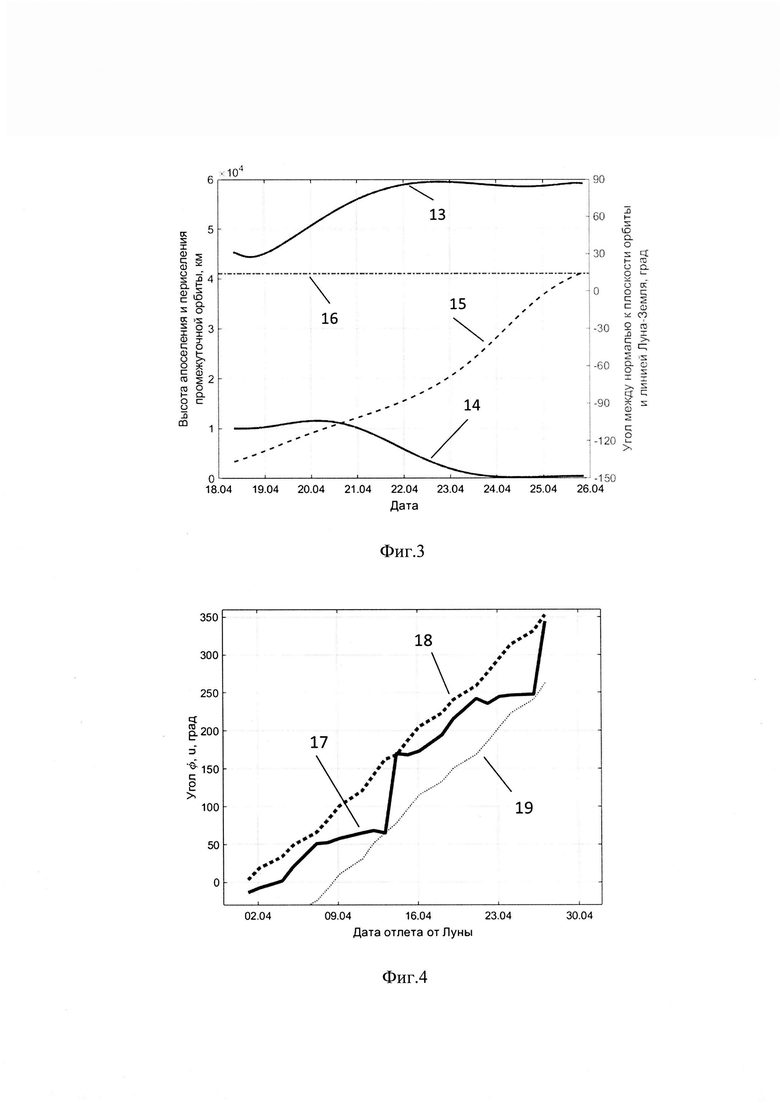
на фиг. 3 приведены графики высоты апоселения и периселения промежуточной орбиты, а также угла между нормалью к плоскости этой орбиты и линией Луна-Земля в сравнении с этим же углом для оптимального (трансверсального) одноимпульсного перелета,
на фиг. 4 представлены графики аргумента широты КА и угла между нормалью к плоскости окололунной орбиты и линией Луна-Земля в момент выдачи импульса V1 в зависимости от даты отлета на интервале времени, соответствующем лунному месяцу.
На этих фиг. отмечены следующие позиции:
1 - Луна, 2 - Земля, 3 - КА, 4 - окололунная орбита высотой Н, 5 - управляющий импульс ΔV1, 6 - высота апоселения Hα1 промежуточной орбиты, 7 - высота апоселения Нα2 промежуточной орбиты в момент времени t2, 8 - высота периселения Нπ2 промежуточной орбиты в момент времени t2, 9 - управляющий трансверсальный импульс ΔV2, 10 - траекторию перелета к Земле, 11 - кривая затрат суммарной характеристической скорости при прямой одноимпульсной схеме возвращения к Земле в зависимости от даты отлета, 12 - кривая затрат суммарной характеристической скорости при предлагаемой двухимпульсной схеме возвращения к Земле в зависимости от даты отлета, 13 - кривая высоты апоселения промежуточной орбиты для предлагаемого способа на дату отлета 18.04.2023 г., 14 - кривая высоты периселения промежуточной орбиты для предлагаемого способа на дату отлета 18.04.2023 г., 15 - угол между нормалью к плоскости промежуточной орбиты и линией Луна-Земля, 16 - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля для оптимального (трансверсального) одноимпульсного перелета, 17-аргумента широты КА в момент выдачи импульса ΔV1, 18 - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля в момент выдачи импульса ΔV1, 19 - кривая ϕ-90°.
На фиг. 1 показана схема возвращения с орбиты Луны (1) к Земле (2) по предлагаемому способу управления. К КА (3), находящемуся на окололунной орбите высотой Н (4), в момент времени t1 прикладывают управляющий импульс ΔV1 (5) для перевода на промежуточную орбиту с высотой апоселения Hα1 (6). Под действием гравитационных возмущений Земли за время движения КА по сформированной промежуточной орбите происходит непрерывная трансформация этой орбиты, приводящая на момент времени t2 к увеличению высоты апоселения Нα2 (7), снижению высоты периселения Нπ2 (8), а также к изменению положения плоскости промежуточной орбиты в пространстве. Варьированием высотой апоселения Hα1 регулируется положение плоскости промежуточной орбиты в пространстве, таким образом, чтобы на момент времени t2, при нахождении КА в окрестности периселении, обеспечивались условия перелета к Земле за заданное время Т при выполнении управляющего трансверсального импульса ΔV2 (9), необходимого для выхода КА на траекторию перелета к Земле (10). Увеличение высоты апоселения и уменьшение высоты периселения промежуточной орбиты за счет воздействия гравитационного поля Земли в итоге приводит к снижению затрат суммарной характеристической скорости для отлета КА с окололунной орбиты к Земле в сравнении с одноимпульсным перелетом, описанном в прототипе.
При полете КА по окололунной орбите воздействие гравитационного поля Земли можно представить в виде возмущающих ускорений [Эльясберг П.Е. Введение в теорию полета искусственных спутников Земли. М: Наука. 1965. 540 с. ]:
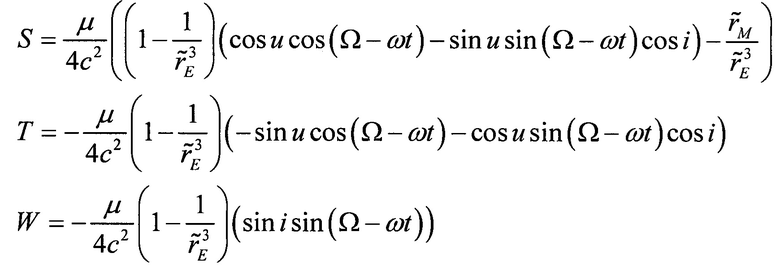
где S, Т, W - проекции возмущающих ускорений на оси орбитальной системы координат (S направлена по радиусу, Т - трансверсальная составляющая, W - перпендикулярна плоскости орбиты)
μ - гравитационная постоянная Луны
t - текущее время
ω - аргумент широты перицентра
Ω - долгота восходящего узла
i - наклонение орбиты
u - аргумент широты
2с=384400 км - расстояние от Земли до Луны

t - текущее время
р - параметр орбиты
rм - текущий радиус
ϑ - истинная аномалия.
Чем больше эксцентриситет окололунной орбиты и высота апоселения, тем больше величина этих возмущений и соответственно их воздействие на трансформацию орбиты [Лидов М.Л. Эволюция орбит искусственных спутников под воздействием гравитационных возмущений внешних тел //Искусственные спутники Земли. 1961. Т. 8. С. 5-45]. Предлагаемый способ основан на использовании этого эффекта.
Предлагаемый способ рассмотрим на примере перелета КА к Земле, находящегося на круговой окололунной орбите НЛОС=10 тыс.км наклонением 90°.
На фиг.2 представлен график затрат суммарной характеристической скорости для различных схем возвращения к Земле с окололунной орбиты высотой Н=10 тыс.км в зависимости от даты отлета на интервале времени, соответствующему лунному месяцу. Кривая 11 соответствует прямой одноимпульсной схеме возвращения к Земле, описанной в прототипе, а кривая 12 соответствует предлагаемой двухимпульсной схеме возвращения. Наименьшие затраты характеристической скорости прямого одноимпульсного перелета на рассмотренном интервале времени составляют ~650 м/с и превышают наибольшие затраты (~620 м/с) в предлагаемом способе. Если же рассматривать оптимальные даты перелета для предлагаемого способа, то его можно выполнить с затратами -380-420 м/с, что на 230-270 м/с меньше чем при прямом перелете в наилучшую дату. В целом же, при любой дате отлета предлагаемый способ значительно эффективнее прямого способа.
На фиг. 3 приведен график высоты апоселения (13) и периселения (14) промежуточной орбиты для предлагаемого способа на дату отлета 18.04.2023 г., а также угла между нормалью к плоскости этой орбиты и линией Луна-Земля (15) в сравнении с этим же углом для оптимального (трансверсального) одноимпульсного перелета (16). Графики представлены на интервале времени перелета по промежуточной орбите, начало которого соответствует выдачи первого импульса ΔV1, а конец - момент выдачи второго ΔV2. По графику видно, что за время перелета КА по промежуточной орбите высота апоселения растет со значения 45300 км до 59200 км. Высота периселения наоборот убывает с 10000 км начальной орбиты до 400 км. Угол между нормалью к плоскости этой орбиты и линией Луна-Земля (пунктирнаялиния) изменяется до значения 14°, что соответствует углу между нормалью к плоскости орбиты и линией Луна-Земля при одноимпульсном перелете в оптимальную дату (пунктирная линия с точкой).
На фиг. 4 приведен график и - аргумента широты КА (17) и ϕ - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля (18) в момент выдачи импульса ΔV1 в зависимости от даты отлета, а также приведен график кривой - ϕ-90° (19). График показывает, что в любую выбранную дату отлета на всем лунном месяце в момент выдачи импульса ΔV1 аргумент широты и КА соответствует следующему неравенству ϕ-90°<u<ϕ, что позволяет организовать быстрый численный поиск оптимального значения и u определить момент времени t1
Допустим первоначально КА находится на высокой круговой окололунной орбите высотой Н=10 тыс.км и долготой восходящего узла Ω=51°. Для возвращения к Земле с такой орбиты по одноимпульсной схеме необходимо приложить отлетный импульс 650-1300 м/с в зависимости от даты отлета (фиг. 2) на интервале в один лунный месяц - 30 суток, величина импульса характеризуется значением угла между нормалью к плоскости орбиты и линией Луна-Земля в момент отлета. Оптимальное значение характеристической скорости при такой схеме определяется окном старта для возвращения к Земле и кратно половине лунного месяца. При времени перелета по траектории возвращения к Земле 3,5 суток угол между плоскостью окололунной орбиты КА и линией Луна-Земля в момент выдачи отлетного импульса должен составлять 60°, что соответствует углу между нормалью к плоскости орбиты и линией Луна-Земля в 30° [Нариманов Г.С. Основы теории полета космических аппаратов. М.: Машиностроение, 1972. 612 с]. Так в рассматриваемом примере при использовании одноимпульсной схемы и времени перелета по траектории возвращения к Земле в 4,5 суток, где затраты характеристической скорости оптимальны и равны 650 м/с угол между нормалью к плоскости орбиты и линией Луна-Земля должен быть равен 14° (фиг. 3). Использование предлагаемого двухимпульсного способавозвращения к Земле (фиг. 1) за счет трансформации промежуточной орбиты позволяет сократить затраты характеристической скорости, определяемые суммой ΔV1+ΔV2. В зависимости от даты отлета, эта сумма будет находиться в диапазоне 380-620 м/с (фиг. 2).
Первоначально определяют момент времени t1 для приложения управляющего импульса ΔV1 с учетом соответствия аргумента широты u КА следующему неравенству ϕ-90°<u<ϕ, где ϕ - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля, который зависит от даты отлета на интервале в один лунный месяц (фиг. 4). Параметры импульса ΔV1 выбираются из условия перевода КА на промежуточную орбиту, во время движения по которой до окрестности переселения, за счет воздействия гравитационного возмущения от Земли, плоскость орбиты разворачивается до положения, удовлетворяющего условию перелета к Земле за заданное время Т при выполнении трансверсального импульса ΔV2, т.е. угол между нормалью к плоскости орбиты и линией Луна-Земля становится оптимальным для выполнения трансверсального импульса ΔV2 для выхода КА на траекторию полета по направлению к Земле.
Рассмотрим пример. КА находится на высокой круговой окололунной орбите высотой Н=10 тыс.км, наклонением 90° и долготой восходящего узла Ω=51°. 18.04.2023 г. в момент времени t1 выполняют импульс ΔV1=171 м/с для перевода КА на промежуточную высокоэллиптическую орбиту с высотой апоселения 45 тыс.км (фиг. 3). В момент t1 аргумент широты u=168,3°, а угол между нормалью к плоскости орбиты и линией Луна-Земля ϕ=187,3° (фиг. 4). За счет возмущений от гравитационного поля Земли промежуточная орбита трансформируется и к моменту времени t2 высота апоселения составит уже 59 тыс.км, высота периселения - 400 км и, при этом, плоскость орбиты развернется в пространстве таким образом, чтобы угол между нормалью к плоскости орбиты и линией Луна-Земля составил 14°, что соответствует условию перелета к Земле за 4.5 дня водноимпульсной схеме (фиг. 3). После чего выполняется импульс ΔV2=212 м/с для перевода на траекторию перелета к Земле за 4.5 дня.
Вышесказанное показывает, что влияние гравитационного поля Земли будет изменять форму промежуточной орбиты таким образом, что за время полета по такой орбите высота периселения уменьшится, а высота апоселения увеличится. Совокупное поднятие высоты апоселения и снижение высоты периселения за время полета КА в течение витка, а также выдача отлетного импульса ΔV2 в районе периселения позволяет уменьшить суммарные затраты характеристической скорости для возврата к Земле.
Изменение угла между плоскостью орбиты и линией Луна-Земля за время полета по промежуточной орбите (разворот плоскости орбиты) дает возможность совершить отлетный импульс к Земле ΔV2 при оптимальном угле, соответствующий трансверсальному импульсу и времени перелета к Земле Т.
Изобретение относится к космической технике, а именно к способам возвращения космического аппарата (КА) с окололунной орбиты к Земле. Для управления КА прикладывают управляющий импульс ΔV1 в момент времени t1 к КА, находящемуся на окололунной орбите. Момент времени t1 определяется с учетом соответствия аргумента широты u КА неравенству ϕ-90°<u<ϕ, где ϕ - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля. После приложения ΔV1 КА переходит на промежуточную орбиту. За время движения КА по сформированной промежуточной орбите плоскость орбиты, за счет воздействия гравитационного поля Земли, разворачивается до положения, удовлетворяющего условию перелета к Земле за заданное время Т при выполнении трансверсального импульса ΔV2. После чего в момент времени t2 прикладывают трансверсальный управляющий импульс ΔV2 для перевода КА на траекторию возвращения к Земле. Достигается снижение затрат суммарной характеристической скорости для отлета КА с окололунной орбиты к Земле, а также увеличение окон старта для отлета к Земле с оптимальными затратами характеристической скорости. 4 ил.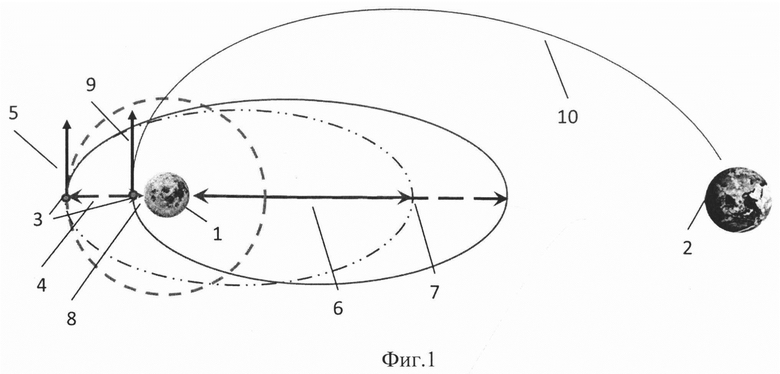
Способ управления космическим аппаратом при возврате к Земле с окололунной орбиты, включающий приложение управляющего импульса для схода с окололунной орбиты и перевода на траекторию возвращения к Земле, отличающийся тем, что определяют, момент времени t1 с учетом соответствия аргумента широты u космического аппарата следующему неравенству ϕ-90°<u<ϕ, где ϕ - угол между нормалью к плоскости окололунной орбиты и линией Луна-Земля, определяют величину управляющего импульса ΔV1, прикладываемого в указанный момент времени к космическому аппарату для его перевода на промежуточную орбиту, а также определяют величину трансверсального управляющего импульса ΔV2, и момент времени его приложения t2, к которому плоскость промежуточной орбиты, за счет воздействия гравитационного поля Земли, развернется в положение, удовлетворяющее условию перелета к Земле за заданное время Т, после чего в момент времени t1 к космическому аппарату прикладывают управляющий импульс ΔV1, а затем в момент времени t2 прикладывают управляющий импульс ΔV2 для перевода на траекторию возвращения к Земле.
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ АКТИВНОГО КОСМИЧЕСКОГО ОБЪЕКТА, СТЫКУЕМОГО С ПАССИВНЫМ КОСМИЧЕСКИМ ОБЪЕКТОМ | 2014 |
|
RU2562908C2 |
| Способ обслуживания космических объектов на орбитах различного наклонения и высокоорбитальная космическая инфраструктура для реализации способа | 2022 |
|
RU2775039C1 |
| Способ определения последовательности перелётов между объектами космического мусора в окрестности геостационарной орбиты | 2020 |
|
RU2759026C1 |
| CN 109606739 B, 27.10.2020 | |||
| US 8457810 B1, 04.06.2013. | |||
Авторы
Даты
2024-06-18—Публикация
2023-11-20—Подача