Предлагаемый способ управления может быть использован в космической технике при выведении космического объекта (КО), находящегося на околоземной орбите на заданную высокую окололунную орбиту.
Для перелета К Луне с орбиты Земли необходимо выполнить отлетный импульс, величина которого в зависимости от высоты околоземной орбиты варьируется от 3050 до 3200 м/с. По прилету к Луне траектория КО представляет селеноцентрическую гиперболическую орбиту. Для выхода на окололунную орбиту с заданными параметрами необходимо выполнить дополнительные операции.
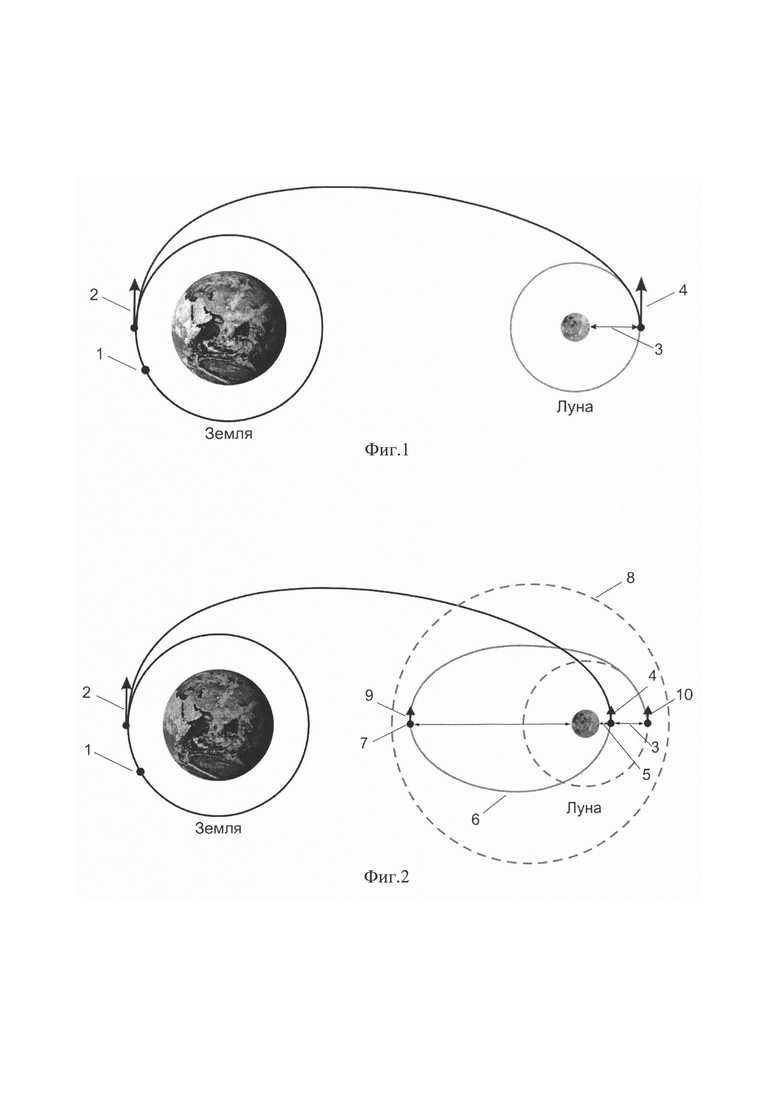
Известен способ управления, выбранный в качестве аналога (фиг. 1), в котором для выведения КО на заданную окололунную орбиту посредством отлетного импульса ΔV1 формируется траектория облета Луны на заданном расстоянии. Точка прохождения на заданном расстоянии от Луны является одновременно и точкой заданной орбиты. В окрестности этой точки выполняется тормозной импульс ΔV2 для перевода КО с траектории облета Луны на заданную орбиту вокруг Луны, [1. В.И. Левантовский, «Механика космического полета в элементарном изложении», Наука, 1980 г].
Несмотря на самый простой и быстрый переход на заданную орбиту, недостатком этого способа является значительная величина тормозного импульса ΔV1, требующая больших затрат топлива. В условиях дефицита топлива этот фактор может быть критическим. Определим величину импульса ΔV1 в терминах характеристической скорости для перевода КО на круговую окололунную орбиту высотой Н=10 тыс. км:
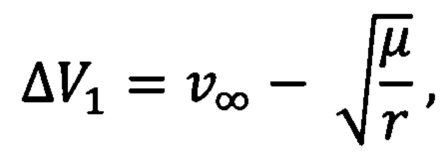
где μ - гравитационный параметр Луны, 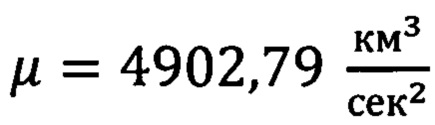 ,
,
r - радиус орбиты Луны и r=Н+rЛ, где rЛ=1737 км - радиус Луны [1],
ν∞ - скорость входа (скорость на бесконечности) в перицентре высотой H=10 тыс. км селеноцентрической гиперболической орбиты при перелете от Земли к Луне 4.5 суток составит  Таким образом, подставляя в формулу необходимые значения получим ΔVΣ1=ΔV1=667 м/с.
Таким образом, подставляя в формулу необходимые значения получим ΔVΣ1=ΔV1=667 м/с.
Известен способ управления движением КО при перелете с орбиты Земли на орбиту Луны (фиг. 2), выбранный в качестве прототипа [2. Гордиенко Е.С., Ивашкин В.В. «Использование трехимпульсного перехода для выведения космического аппарата на орбиты искусственного спутника Луны», «Космические исследования», 2017, том 55, №3, с. 207-217], включающий выполнение КО отлетного импульса для перелета от Земли к Луне по траектории с пролетом относительно Луны на заданной высоте, по достижению которой выполняют тормозной импульс для перевода КО на эллиптическую орбиту вокруг Луны. В отличие от аналога в этом способе используется три импульса для перевода КО на заданную орбиту. Первым тормозным импульсом КО переводится на переходную эллиптическую орбиту с высотой апоселения Hα1. Затем в апоселении выполняется второй импульс, уже разгонный, поднимающий высоту периселения до высоты периселения целевой орбиты Нπ2. И наконец, после прихода КО в периселений третьим тормозным импульсом осуществляется перевод КО на орбиту с высотой апоселения Нα2. В случае если целевая орбита круговая Нα2=Нπ2.
В зависимости от высоты апоселения Hα1 переходной эллиптической орбиты при использовании этого способа можно снизить затраты топлива для выведения на круговую окололунную орбиту высотой H=10 тыс. км на 100÷250 м/с. Согласно расчетам при высоте апоселения переходной эллиптической орбиты Нα1=50 тыс. км и дате прилета к Луне 01.12.27 значение ΔVΣ3 составит:

т.е. на 225 м/с меньше, чем при одноимпульсной схеме.
Для высот апоселения от 15 до 45 тыс. км ΔVΣ3 составит от 565 до 459 м/с, что по сравнению с одноимпульсной схемой меньше от 102 до 208 м/с.
Основным недостатком такого способа управления по-прежнему остается значительная суммарная величина импульса ΔVΣ3 для перевода КО на заданную орбиту.
Техническим результатом изобретения является дополнительное снижение затрат суммарной характеристической скорости для перевода КО на заданную орбиту.
Технический результат достигается благодаря тому, что в способе управления движением КО при перелете с орбиты Земли на орбиту Луны, включающем выполнение КО отлетного импульса для перелета от Земли к Луне по траектории с пролетом относительно Луны на заданной высоте, по достижению которой выполняют тормозной импульс для перевода КО на эллиптическую орбиту вокруг Луны, в отличие от известного, определяют эллиптическую орбиту с апоселением в окрестности грависферы Луны и высотой Нα в диапазоне 60÷75 тыс. км, у которой за счет гравитационных возмущений от Земли через виток изменится высота периселения до значения высоты периселения целевой орбиты Нπ, затем по значению высоты апоселения Нα корректируют тормозной импульс, который прикладывают к КО, а через виток, при прохождении периселения высотой Нπ, выполняют заключительный тормозной импульс для формирования целевой эллиптической орбиты вокруг Луны.
Предлагаемый способ рассмотрим на примере. Пусть в качестве околоземной орбиты КО рассматривается круговая орбита высотой 200 км. Рассмотрим задачу перелета КО на круговую орбиту вокруг Луны высотой 10 тыс. км. Схема перелета включает отлетный импульс ΔV1, формирующий пролет у Луны по гиперболе селеноцентрической орбиты на расстоянии около 100 км, тормозной импульс ΔV2 для перевода космического объекта на переходную высокоэллиптическую орбиту вокруг Луны. Затем, через виток полета по этой переходной орбите выполняется импульс ΔV3 для окончательного перехода КО на заданную орбиту вокруг Луны.
Технический результат в предлагаемом способе управления достигается за счет того, что апоселений переходной высокоэллиптической орбиты с высотой Нα, выбираемой в диапазоне 60÷75 тыс. км, находится в окрестности грависферы Луны (~66 тыс. км) [4. Е.В. Тарасов, «Космонавтика», Машиностроение, 1977]. После выполнения тормозного импульса ΔV2 КО с гиперболической пролетной орбиты переводится на переходную эллиптическую орбиту вокруг Луны. При правильно выбранной высоте апоселения Hα переходной орбиты, за счет гравитационного возмущения от Земли через виток высота периселения увеличивается до заданного значения (в нашем случае Нπ=10 тыс. км). Помимо увеличения высоты периселения наблюдается монотонное уменьшение высоты апоселения переходной орбиты, что, в свою очередь, снижает величину импульса ΔV3, который окончательно формирует орбиту вокруг Луны. Таким образом удается сократить число импульсов перехода с трех до двух и дополнительно снизить затраты характеристической скорости для перехода на окололунную орбиту. Снижение ΔVΣ2 по сравнению с биэллиптическим переходом происходит за счет:
- уменьшения тормозного импульса ΔV2, т.к. апоселений переходной орбиты увеличивается с 20÷50 тыс. км до 60÷75 тыс. км,
- исключения импульса в апоселении переходной орбиты, т.к. формирование перицентра заданной орбиты обеспечивается возмущающим влиянием гравитационного поля Земли,
- уменьшения тормозного импульса ΔV3, т.к. помимо высоты периселения, за счет возмущений от Земли уменьшается и высота апоселения переходной орбиты.
При оптимальной дате перелета от Земли к Луне, величина суммарного импульса ΔVΣ2 для перехода на круговую окололунную орбиту высотой 10 тыс. км может составить около 335 м/с, что по сравнению со способом, описанным в прототипе и при задании высоты апоселения переходной орбиты Hα1=50 тыс. км меньше на 107 м/с.
Сущность изобретения поясняется на фиг. 1÷6, где:
на фиг. 1 показана схема выведения аналога на круговую окололунную орбиту по одноимпульсной схеме;
на фиг. 2 показана схема выведения прототипа на круговую окололунную орбиту с биэллиптическим переходом по трехимпульсной схеме;
на фиг. 3 показана схема выведения на круговую окололунную орбиту по предлагаемому способу управления по двухимпульсной схеме;
на фиг. 4 представлены графики затрат суммарной характеристической скорости ΔVΣ3 и время выведения для биэллиптического перехода;
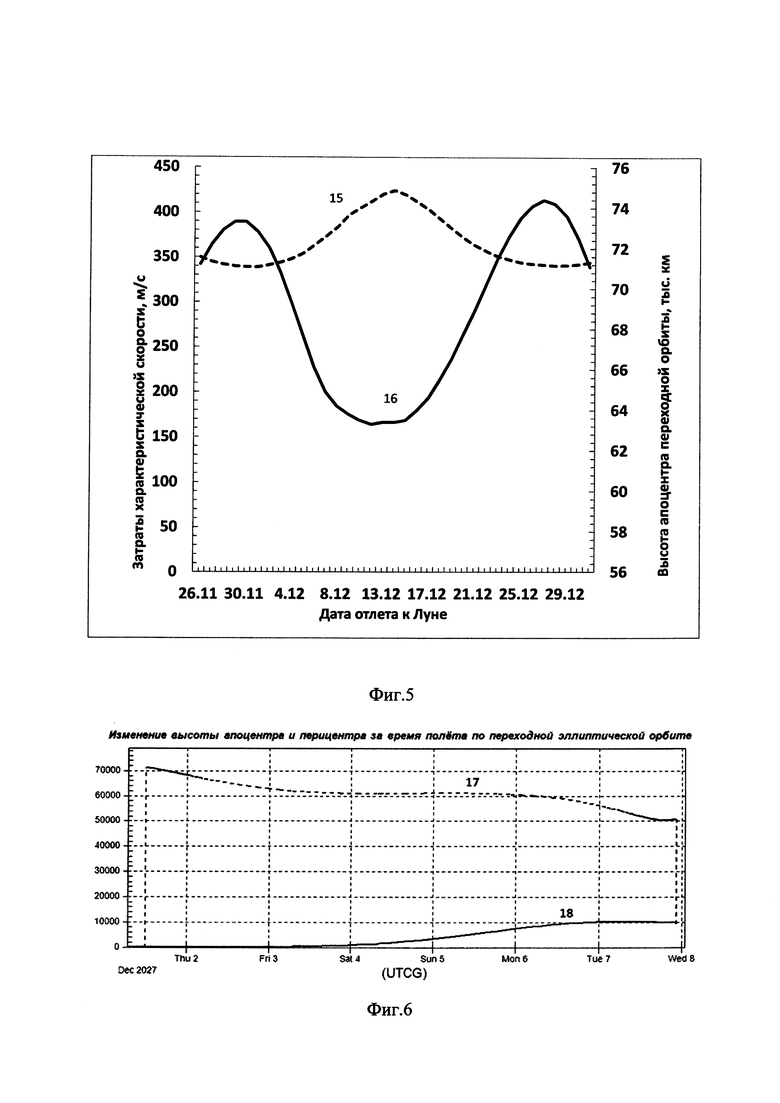
на фиг. 5 представлены графики затрат суммарной характеристической скорости ΔVΣ2 и высот апоселения Нα переходной орбиты для предлагаемой двухимпульсной схемы в зависимости от даты;
на фиг. 6 представлено изменение высоты периселения Нπ и апоселения Нα переходной эллиптической орбиты в течение витка за счет гравитационных возмущений от Земли.
На фиг. 1 показана схема выведения на круговую окололунную орбиту по одноимпульсной схеме. Вначале КО (1) отлетным импульсом ΔV1 (2) с околоземной орбиты переводится на траекторию полета к Луне с пролетом относительно Луны на расстоянии, соответствующем высоте Нπ2 (3) заданной круговой окололунной орбиты. После прилета на заданное расстояние КО выполняет тормозной импульс ΔV2 (4) для перехода на заданную круговую орбиту.
На фиг. 2 показана схема выведения на круговую окололунную орбиту по трехимпульсной схеме. Вначале КО (1) отлетным импульсом ΔV1 (2) с околоземной орбиты переводится на траекторию полета к Луне с пролетом относительно Луны на заданном минимальном расстоянии Нπ1 (5). После прилета на расстояние Нπ1 КО выполняет тормозной импульс ΔV2 (4) для перевода КО на переходную эллиптическую орбиту вокруг Луны (6) с апоселением (7) внутри грависферы Луны (8). Затем КО продолжает полет по этой орбите до прихода в апоселений (7), где выполняется разгонный импульс ΔV3 (9), формирующий орбиту с периселением на заданной высоте Нπ2 (3) круговой окололунной орбиты. После этого полет продолжается до прихода в периселений, где выполняется тормозной импульс ΔV4 (10), завершающий перевод КО на заданную круговую окололунную орбиту.
На фиг. 3 показана схема выведения на круговую окололунную орбиту по предлагаемому способу. Вначале КО (1) отлетным импульсом ΔV1 (2) с околоземной орбиты переводится на траекторию полета к Луне с пролетом относительно Луны на заданном минимальном расстоянии Нπ1 (5). После прилета на заданное расстояние КО выполняет тормозной импульс ΔV2 (4) для перевода на переходную эллиптическую орбиту вокруг Луны (6) с апоселением (7) в окрестности грависферы Луны (8) и высотой в диапазоне 60÷75 тыс. км. Затем КО продолжает полет по переходной орбите до следующего прихода в периселений. За счет гравитационных возмущений от Земли первоначальная переходная орбита (6) меняется и через виток принимает вид (11) с высотой периселения Нπ2 (3), соответствующей высоте периселения целевой орбиты. Затем в периселении высотой Нπ2 (3) выполняют тормозной импульс ΔV3 (10), завершающий переход КО на заданную круговую окололунную орбиту.
На фиг. 4 представлены график затрат характеристической скорости для биэллиптического перехода по трехимпульсной схеме (12) на полярную (наклонение орбиты 90°) окололунную круговую орбиту высотой H=10 тыс. км и график времени выведения (13) в зависимости от значения высоты апоселения переходной орбиты. Расчеты проводились при перелете к Луне за 4.5 суток после выдачи отлетного импульса с околоземной круговой орбиты высотой 200 км и наклонением 51.6°. Дата прилета к Луне на высоту Нπ1=100 км - 01.12.27. Также, для сравнения представлены затраты характеристической скорости, полученные на ту же дату при использовании одноимпульсной схемы (14). Из графиков видно, что одноимпульсная схема требует большей суммарной характеристической скорости.
На фиг. 5 представлены график затрат суммарной характеристической скорости ΔVΣ2 (15) для перехода на круговую окололунную орбиту высотой H=10 тыс. км по предлагаемому способу при старте от Земли с круговой орбиты высотой 200 км и наклонением 51.6° в зависимости от даты. Рассматривался диапазон дат отлета от Земли с 26.11.27 по 01.01.28, что заведомо превышает длительность лунного месяца (~27 дней). Также представлен график высот апоселения для каждой рассматриваемой даты (16). Из графика (15) видно, что значение ΔVΣ2 имеет циклический характер с периодом, соответствующим лунному месяцу и минимальное значение достигает 335 м/сек, что меньше минимального значения для биэллиптического перехода при Hα1=50 тыс. км на ~110 м/с. Из графика (16) видно, что начальная высота апоселения переходного эллипса в зависимости от даты варьируется от 63.5 до 74.5 тыс. км, т.е. находится в окрестности грависферы Луны.
На фиг. 6 представлены графики изменения высоты апоселения (17) (пунктирная линия) и периселения (18) (сплошная линия) переходной окололунной орбиты при полете по двухимпульсной схеме. График соответствует дате прилета к Луне 01.12.27 г. Как видно из графика (17) высота апоселения после первого тормозного импульса ΔV2 в периселении гиперболической орбиты скачком увеличивается до 71 тыс. км. Затем, в течение витка под действием гравитационных возмущений от Земли высота апоселения снижается на 20 тыс. км до 51 тыс. км. Из графика (18) видно, что за виток высота периселения переходной орбиты увеличивается до заданной высоты 10 тыс. км. В периселении выполняется тормозной импульс ΔV3, снижающий скачкообразно высоту апоселения до 10 тыс. км и, тем самым, завершается переход на круговую окололунную орбиту.
Рассмотрим пример. Допустим нам необходимо вывести КО на высокую круговую окололунную орбиту высотой 10 тыс. км. Наиболее просто это выполнить по одноимпульсной схеме, как показано на фиг. 1. Для этого значение высоты периселения пролетной гиперболической орбиты должна быть равной высоте конечной круговой орбиты, т.е. Нπ1=10 тыс. км. При прохождении периселения выполняется тормозной импульс величиной около 667 м/с, что приводит к формированию круговой орбиты высотой 10 тыс.км.
Можно уменьшить эти затраты используя биэллиптический переход для межорбитального перехода в центральном поле тяготения небесного тела [3. Р.Ф. Аппазов, О.С. Сытин, «Методы проектирования траекторий носителей и спутников Земли», Наука, 1987]. Согласно [3] при соотношении начального и конечного радиуса орбит 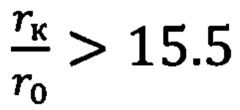 биэллиптический переход становится оптимальнее гомановского перехода. Так как радиус орбиты Луны 1737 км, то при высотах окололунных орбит свыше 30 тыс. км оптимальнее становится биэллиптический переход. Биэллиптический переход не с круговой, а гиперболической орбиты траектории пролета Луны, позволяет получить энергетический выигрыш и при меньшей высоте конечной круговой орбиты [2]. Как показано в [2], при переходе на круговую орбиту высотой около 4.5 тыс. км суммарные затраты на переход будут меньше, чем при одноимпульсной схеме на 200 м/с. Для круговой орбиты высотой 10 тыс. км, в зависимости от высоты апоселения переходной эллиптической орбиты, можно уменьшить суммарные затраты от 100 до 250 м/с, что и показано на фиг. 4. Естественно, что в этом случае увеличивается время выведения на заданную орбиту от 1.5 до 4-х суток.
биэллиптический переход становится оптимальнее гомановского перехода. Так как радиус орбиты Луны 1737 км, то при высотах окололунных орбит свыше 30 тыс. км оптимальнее становится биэллиптический переход. Биэллиптический переход не с круговой, а гиперболической орбиты траектории пролета Луны, позволяет получить энергетический выигрыш и при меньшей высоте конечной круговой орбиты [2]. Как показано в [2], при переходе на круговую орбиту высотой около 4.5 тыс. км суммарные затраты на переход будут меньше, чем при одноимпульсной схеме на 200 м/с. Для круговой орбиты высотой 10 тыс. км, в зависимости от высоты апоселения переходной эллиптической орбиты, можно уменьшить суммарные затраты от 100 до 250 м/с, что и показано на фиг. 4. Естественно, что в этом случае увеличивается время выведения на заданную орбиту от 1.5 до 4-х суток.
Если апоселений переходной эллиптической орбиты будет находиться в окрестности грависферы Луны, то влияние гравитационного поля Земли начнет возмущать эту орбиту таким образом, что через виток полета по такой орбите высота периселения увеличится, а высота апоселения уменьшится. При правильно подобранной высоте Hα1 переходной орбиты, как показано на фиг. 6, через виток высота периселения изменится с Нπ1 до Нπ2 и без выполнения разгонного импульса в апоселении орбиты, как предусмотрено трехимпульсной схемой. Таким образом, для выведения КО на заданную орбиту достаточно при повторном прохождении периселения выполнить импульс формирования заданной высоты апоселения Нα2.
Совокупное снижение высоты апоселения и поднятие высоты периселения за время полета КО в течение витка позволяет по сравнению с трехимпульсной схемой уменьшить суммарные затраты характеристической скорости для выведения на заданную окололунную орбиту. Так, представленные на фиг. 5 суммарные затраты характеристической скорости при выборе оптимальной даты для перелета показывают уменьшение более чем на 100 м/с.
Как и для трехимпульсной схемы, длительность двухимпульсного перехода увеличится до 6.5 суток за счет полета в течение витка по переходной эллиптической орбите с большой начальной высотой апоселения Hα1, но в случае полета беспилотного корабля этот фактор не является критичным.
Также необходимо отметить, что гравитационное возмущение от Земли, за время полета по переходной эллиптической орбите будет менять и наклонение заданной орбиты. В примере, в зависимости от даты это отклонение составляло от 15 до 25 градусов. Парировать это возмущение можно изменив начальное наклонение орбиты прилета к Луне на нужную величину (~15÷25 градусов).
Предлагаемый способ позволит уменьшить суммарную характеристическую скорость на выведение КО на высокую круговую окололунную орбиту. Так если за единицу измерения взять расход характеристической скорости на выведение по одноимпульсной схеме, то расход по способу прототипу составит от 66 до 85%, а по предлагаемому способу 50%. При доставке на высокую круговую окололунную орбиту КО массой 7тн дополнительное увеличение полезного груза по сравнению с трехимпульсной схемой может составить около 250 кг.
Предлагаемый способ может быть использован при доставке грузов на перспективную станцию, расположенную на высокой круговой окололунной орбите.

Изобретение относится к межпланетным перелётам, например при доставке космических объектов (КО) на станцию, расположенную на высокой окололунной орбите. Способ включает перелет от Земли к Луне по траектории с пролетом Луны на заданной высоте, где выполняют первый тормозной импульс для перевода КО на начальную окололунную орбиту. Апоселений этой орбиты находится в окрестности грависферы Луны (60-75 тыс. км). За счет гравитационных возмущений, главным образом от Земли, через виток высота периселения данной орбиты изменяется до значения высоты периселения целевой орбиты. В этом периселении выполняют второй тормозной импульс для формирования целевой эллиптической (или круговой) орбиты вокруг Луны. Техническим результатом изобретения является снижение суммарной характеристической скорости на выведение КО с пролётной траектории на целевую, преимущественно высокую окололунную орбиту. 6 ил.
Способ управления движением космического объекта при перелете с орбиты вокруг Земли на орбиту вокруг Луны, включающий выполнение космическим объектом отлетного импульса для перелета от Земли к Луне по траектории с пролетом относительно Луны на заданной высоте, по достижении которой выполняют тормозной импульс для перевода космического объекта на целевую эллиптическую орбиту вокруг Луны, отличающийся тем, что определяют эллиптическую орбиту с апоселением высотой Нα в диапазоне 60÷75 тыс. км в окрестности грависферы Луны, у которой за счет гравитационных возмущений от Земли через виток изменится высота периселения до значения высоты периселения целевой орбиты Нπ, затем по значению высоты апоселения Нα корректируют тормозной импульс, который прикладывают к космическому объекту, а через виток при прохождении периселения высотой Нπ выполняют заключительный тормозной импульс для формирования целевой эллиптической орбиты вокруг Луны.
| В.И | |||
| Левантовский | |||
| Механика космического полета в элементарном изложении | |||
| М., Наука, 1970, c.230-239, 243, 312-315 | |||
| Эдвард Белбруно | |||
| Динамика захвата и хаотические движения в небесной механике, с приложениями к конструированию малоэнергетических перелётов | |||
| М.-И., 2011, с.161-166 | |||
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ ДЛЯ ОБЛЁТА ЛУНЫ | 2015 |
|
RU2614464C2 |
| Приспособление для перекатки колесных пар по железнодорожному пути | 1918 |
|
SU2665A1 |
Авторы
Даты
2019-12-23—Публикация
2018-12-14—Подача