Группа изобретений относится к машиностроению и может быть использована в конструкциях, включающих гибкий ротор на электромагнитных подшипниках (ЭМП).
В механике, изучающей причины биений гибкого ротора на ЭМП, выделены понятия дисбаланса, заключающегося в смещениях центров распределенных масс рассматриваемого ротора относительно оси его вращения и компенсируемого в результате балансировки гибкого ротора, и остаточного дисбаланса - дисбаланса, сохраняемого после балансировки гибкого ротора и устраняемого при необходимости с помощью специальных мер повышения устойчивости гибкого ротора при его вращении в результате управления его работой.
Влияние остаточного дисбаланса проявляется при разгоне и выбеге гибкого ротора при прохождении критических частот (соответствующая критической частоте критическая угловая скорость - это критическая частота, умноженная на 2π); амплитуда колебаний гибкого ротора может при этом существенно возрасти и превысить допустимые значения.
Уровень техники в области конструкций, включающих гибкий ротор на ЭМП, в которых уменьшен остаточный дисбаланс, характеризуется известными патентами. Известен способ управления электромагнитным подвесом гибкого ротора, описанный в патенте US 6472787, F16C 32/04, 2002 г., технический результат которого заключается в обеспечении устойчивости системы гибкого ротора на собственных частотах колебаний этого ротора путем применения настраиваемого по частоте вращения указанного ротора режекторного фильтра, но данный способ не обеспечивает высокую степень устранения остаточного дисбаланса в связи с динамической сложностью поведения гибкого ротора при его вращении.
Известны также способы управления электромагнитным подвесом ротора (патенты US 6703735, H02K 7/09, 2004; US 5300842, H02K 7/09, 1994; US 20140077645, H02K 7/09, 2014; US 2003141772, H02K 7/09, 2003), но в этих изобретениях трудности устранения резонансных колебаний, связанных с остаточным дисбалансом, сохраняются.
Наиболее близкий способ управления работой гибкого ротора на ЭМП, выбранный заявителем в качестве прототипа (см. статью авторов В.В. Знышева, Е.В. Кирюшиной, М.Я. Николаева, В.Ф. Овчинникова и С.Ю. Литвинчук «Алгоритм формирования заданной силы электромагнитных подшипников в системе управления электромагнитного подвеса ротора». - Вестник Нижегородского университета им. Н.И. Лобачевского. 2010, №5 (1), с. 138-141), включающий измерение в дискретные моменты времени отклонений оси гибкого ротора в плоскости, перпендикулярной оси его вращения, в местах расположения радиальных ЭМП, вычисление производных по времени от указанных отклонений, определение двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора в каждом n-м радиальном ЭМП, в зависимости от указанных отклонений оси гибкого ротора и их производных, и последующее формирование указанных сил в каждом n-м радиальном ЭМП.
В качестве прототипа предлагаемой системы для осуществления заявляемого способа управления выбрана система для управления работой гибкого ротора, сведения о которой содержатся в указанной выше статье авторов В.В. Знышева и др.
Недостаток способа-прототипа, характерный также и для системы-прототипа, заключается в том, что сформированные в каждом радиальном ЭМП таким образом две ортогональные силы направлены на уменьшение остаточного дисбаланса, допускающее возможность возникновения резонансных колебаний в каждом радиальном ЭМП гибкого ротора на критических частотах. При этом амплитуда колебаний гибкого ротора на критических частотах может существенно увеличиваться.
Технический результат заявляемой группы изобретений - повышение надежности и ресурса работы гибкого ротора на ЭМП в результате увеличения степени компенсации остаточного дисбаланса за счет формирования в каждом радиальном ЭМП гибкого ротора двух дополнительных ортогональных управляющих сил, повышающих эффективность корректировки положения оси гибкого ротора в переходных режимах и определяемых с помощью предлагаемых системы и порядка управления работой гибкого ротора.
Для достижения указанного технического результата в способе управления работой гибкого ротора, включающем измерение в дискретные моменты времени отклонений оси гибкого ротора в плоскости, перпендикулярной оси его вращения, в местах расположения радиальных ЭМП, вычисление производных по времени от указанных отклонений, определение двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора в каждом n-м радиальном ЭМП, в зависимости от указанных отклонений оси гибкого ротора и их производных, и последующее формирование указанных сил в каждом n-м радиальном ЭМП, дополнительно измеряют в дискретные моменты времени угловую скорость вращения гибкого ротора Ω и угол его поворота Ф и для компенсации резонансных биений гибкого ротора в k-х интервалах указанной угловой скорости Ω, задаваемых граничными величинами 0,85Ωk и 1,30Ωk, где Ωk - k-я критическая угловая скорость гибкого ротора, определяют в каждом n-м радиальном ЭМП две дополнительные ортогональные управляющие силы F1(n) и F2(n) в соответствии с формулами
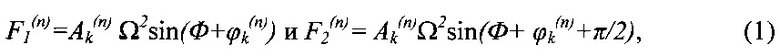
где Ak(n) и ϕk(n) - идентифицируемые величины n-го радиального ЭМП, соответственно параметра дисбаланса гибкого ротора на k-й критической угловой скорости и начального угла поворота гибкого ротора, компенсирующего дисбаланс на k-й критической угловой скорости, которые определяют программным методом идентификации распределения дисбаланса гибкого ротора, а затем формируют указанные дополнительные силы в каждом n-м радиальном ЭМП.
Для достижения технического результата (общего с техническим результатом от использования заявляемого способа), в системе для управления работой гибкого ротора в соответствии со способом по п. 1, состоящей из N каналов для создания двух ортогональных управляющих сил в радиальных ЭМП в каждом канале, содержащем блок измерения отклонений оси гибкого ротора в месте расположения радиального ЭМП в плоскости, перпендикулярной оси вращения гибкого ротора, соединенный своим выходом с входом блока вычисления производных по времени от указанных отклонений и программного определения величин двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора, подключенного в свою очередь к первому входу блока регулирования указанных управляющих сил в радиальном ЭМП, введен блок измерения угловой скорости вращения гибкого ротора и угла его поворота, а каждый канал системы снабжен блоком программного определения двух дополнительных ортогональных управляющих сил, подключенным своим выходом ко второму входу блока регулирования указанных управляющих сил в радиальном ЭМП, при этом блок измерения угловой скорости вращения гибкого ротора и угла его поворота своим многоканальным выходом соединен со входами указанных канальных блоков программного определения двух дополнительных ортогональных управляющих сил.
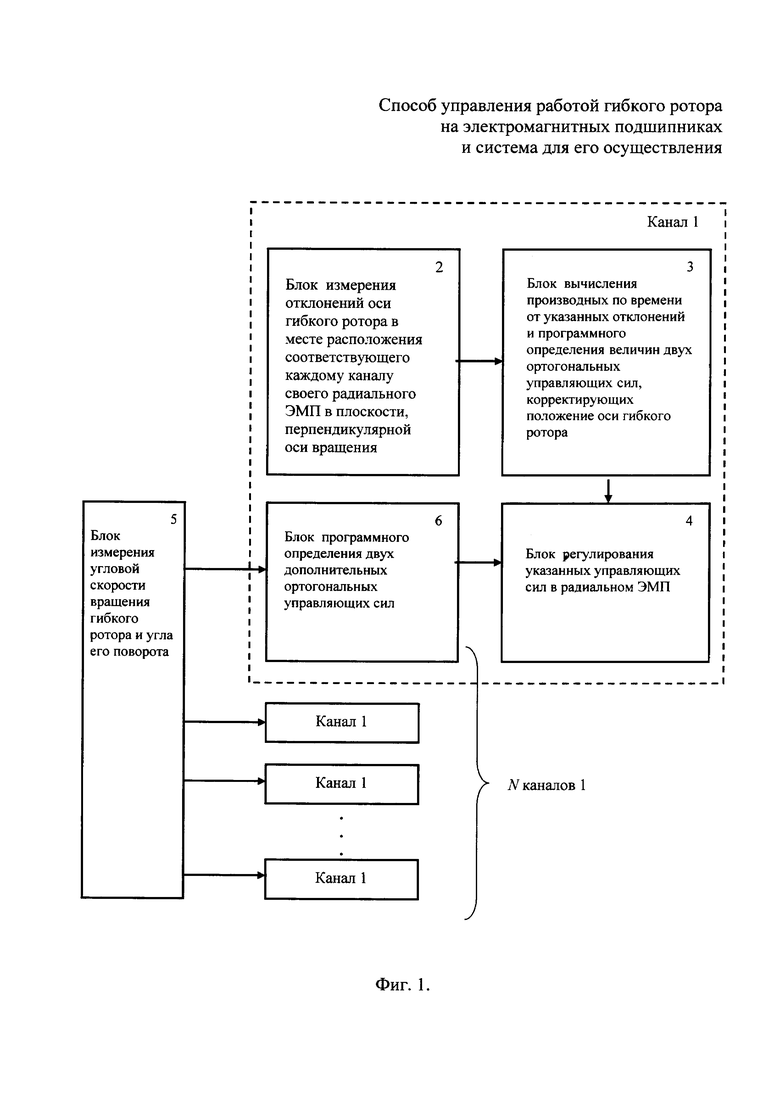
На фиг. 1 показана система для управления работой вертикального гибкого ротора в соответствии с предлагаемым способом; на фиг. 2 - первая и вторая формы собственных колебаний гибкого ротора; на фиг. 3 - третья и четвертая формы собственных колебаний гибкого ротора; на фиг. 4 - зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в двух ЭМП при разгоне этого ротора до рабочей частоты его вращения в условиях управления его работой в соответствии со способом-прототипом; на фиг. 5 - зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в двух ЭМП при останове этого ротора от рабочей частоты его вращения в условиях управления его работой в соответствии со способом-прототипом; на фиг. 6 - зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в двух ЭМП при разгоне этого ротора до рабочей частоты его вращения в условиях управления его работой в соответствии с предлагаемым способом; на фиг. 7 - зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в двух ЭМП при останове этого ротора от рабочей частоты его вращения в условиях управления его работой в соответствии с предлагаемым способом.
Предлагаемая система для управления работой гибкого ротора (см. фиг. 1) состоит из N каналов 1 для формирования в каждом радиальном ЭМП двух ортогональных управляющих сил.
Каждый канал 1 содержит блок 2 измерения отклонений оси гибкого ротора в месте расположения соответствующего каждому каналу своего радиального ЭМП в плоскости, перпендикулярной оси вращения гибкого ротора, соединенный своим выходом с входом блока 3 вычисления производных по времени от указанных отклонений и программного определения величин двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора, подключенного в свою очередь к первому входу блока 4 регулирования указанных управляющих сил в радиальном ЭМП.
В предлагаемую систему введен блок 5 измерения угловой скорости вращения гибкого ротора и угла его поворота, а каждый канал 1 системы снабжен блоком 6 программного определения двух дополнительных ортогональных управляющих сил, подключенным своим выходом ко второму входу блока 4 регулирования указанных управляющих сил в радиальном ЭМП. При этом блок 5 измерения угловой скорости вращения гибкого ротора и угла его поворота своим многоканальным выходом соединен со входами указанных канальных блоков 6 программного определения двух дополнительных ортогональных управляющих сил.
Предлагаемый способ управления работой гибкого ротора осуществляют в соответствии со следующим порядком функционирования системы для его осуществления, состоящей из N=2 каналов, в соответствии с приведенным ниже примером компьютерного моделирования динамики вертикального гибкого ротора, выполненного на двух радиальных ЭМП.
Демонстрация предложенного способа управления приводится на примере вертикального гибкого ротора генераторной части стенда масштабной модели ротора (ММР) (см. статью на англ. яз. авторов Drumov I.V., Kodochigov N.G., Belov S.E., Znamensky D.S., Baxi С.В., Telengator A., Razvi J. Studies of the ((Electromagnetic Suspension System for the GT-MHR Turbo Machine Rotor Model». - Proceedings of HTR. 2010. Prague, Czech Republic, October 18-20, 2010, №41, p. 1-7), длина которого составляет 5.4 м, а масса - 640 кг.
В каждом из соответствующих двум радиальным ЭМП канале 1 (фиг. 1) с номером n (n=1, 2) для создания двух ортогональных управляющих сил в соответствующем радиальном ЭМП в каждом канале, с помощью блока 2 измерения отклонений оси гибкого ротора (см. фиг. 1) производится измерение в дискретные моменты времени отклонений оси гибкого ротора в плоскости, перпендикулярной оси его вращения, в месте расположения соответствующего радиального ЭМП (U1(n), U2(n) - отклонения (перемещения) оси гибкого ротора в сечении расположения соответствующего радиального ЭМП), с помощью блока 3 осуществляется вычисление производных по времени от указанных отклонении - 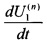 и
и 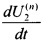 , и определение (в каждом соответствующем радиальном ЭМП в зависимости от указанных отклонений оси гибкого ротора и их производных) двух ортогональных управляющих сил -
, и определение (в каждом соответствующем радиальном ЭМП в зависимости от указанных отклонений оси гибкого ротора и их производных) двух ортогональных управляющих сил - 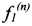 и
и 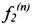 , корректирующих положение оси гибкого ротора в соответствии с выражениями:
, корректирующих положение оси гибкого ротора в соответствии с выражениями:
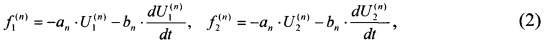
где индекс n - номер первого или второго канала 1 стенда ММР, n=1, 2;
an и bn - пропорциональный и дифференциальные коэффициенты, an=810000 Н/м, bn=6400 Н*с/м одинаковые во всех каналах управления.
В блоке 4 электромагнитами радиального ЭМП формируются управляющие силы 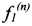 и
и 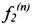 , воздействующие на гибкий ротор.
, воздействующие на гибкий ротор.
Изложенное выше функционирование предлагаемой системы совпадает с функционированием аналогичной системы-прототипа.
Затем в соответствии с предлагаемым способом дополнительно измеряют с помощью блока 5 в дискретные моменты времени угловую скорость вращения гибкого ротора Ω и угол его поворота Ф и для компенсации резонансных биений гибкого ротора в k-х интервалах указанной угловой скорости Ω, задаваемых граничными величинами 0,85Ωk и 1,30Ωk, где Ωk - k-я критическая угловая скорость гибкого ротора, определяют с помощью блока 6 в соответствующих первому и второму каналам 1 радиальных ЭМП две дополнительные ортогональные управляющие силы F1(n) и F2(n), в соответствии с формулами (1). Идентифицируемые величины Ak(n) - параметр дисбаланса гибкого ротора на k-й критической угловой скорости гибкого ротора и ϕk(n) - начальный угол поворота гибкого ротора, компенсирующие дисбаланс на k-й критической угловой скорости, относящиеся к соответствующим первому и второму каналам 1 радиальным ЭМП, определяют с помощью блока 6 программным методом идентификации распределения дисбаланса гибкого ротора по программе BALANS (см. статью авторов Ф.М. Митенкова, М.Я. Николаева, А.А. Кирюшина, В.Ф. Овчинникова, Е.В. Фадеевой и др. «Балансировка гибкого вертикального ротора на электромагнитном подвесе». - Вестник Нижегородского университета им. Н.И. Лобачевского Н. Новгород. Из-во ННГУ им. Н.И. Лобачевского, 2011 г. №4 (1), с. 134-139), а затем формируют с помощью блока 4 указанные дополнительные силы в каждом из двух радиальных ЭМП.
Идентифицируемые величины, необходимые для определения дополнительных ортогональных сил F1(n) и F2(n), представлены в таблице 1.
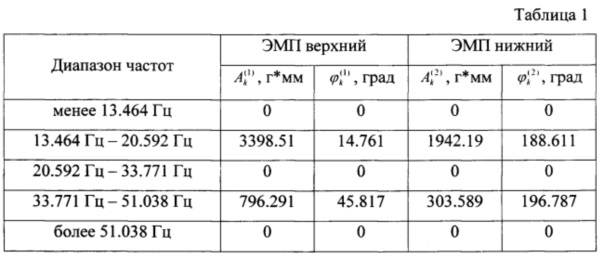
Так, например, на третьей критической частоте вращения гибкого ротора 15.84 Гц амплитуда дополнительных ортогональных сил F1(1) и F2(1) в ЭМП верхнем составляет 33.66 Н. Амплитуда дополнительных ортогональных сил F1(2) и F2(2) в ЭМП 2 - 19.24 Н. На четвертой критической частоте вращения гибкого ротора 39.26 Гц амплитуда дополнительной силы в ЭМП верхнем составляет 48.45 Н, а в ЭМП 2 - 18.47 Н.
Моделирование динамики рассматриваемого вертикального гибкого ротора на двух радиальных ЭМП проведено с помощью компьютерной модели, предназначенной для расчетного исследования динамики гибкого неоднородного ротора на ЭМП (см. статью авторов В.Ф. Овчинникова, М.Я. Николаева, Е.В. Кирюшиной, А.А. Кирюшина, В.Н. Литвинова, Е.В. Фадеевой, А.С. Чистова, Ф.М. Митенкова и Н.Г. Кодочигова «Модель динамики гибкого неоднородного ротора на электромагнитных подшипниках».-Вестник Нижегородского университета им. Н.И. Лобачевского, 2011 г. №4 (1), с. 134-139).
Первые (низшие) частоты собственных колебаний гибкого ротора ММР, или критические частоты, (соответствующая критической частоте критическая угловая скорость - это критическая частота, умноженная на 2π) составляют 7.48 Гц, 8.19 Гц, 15.84 Гц, 39.26 Гц, 77.45 Гц.
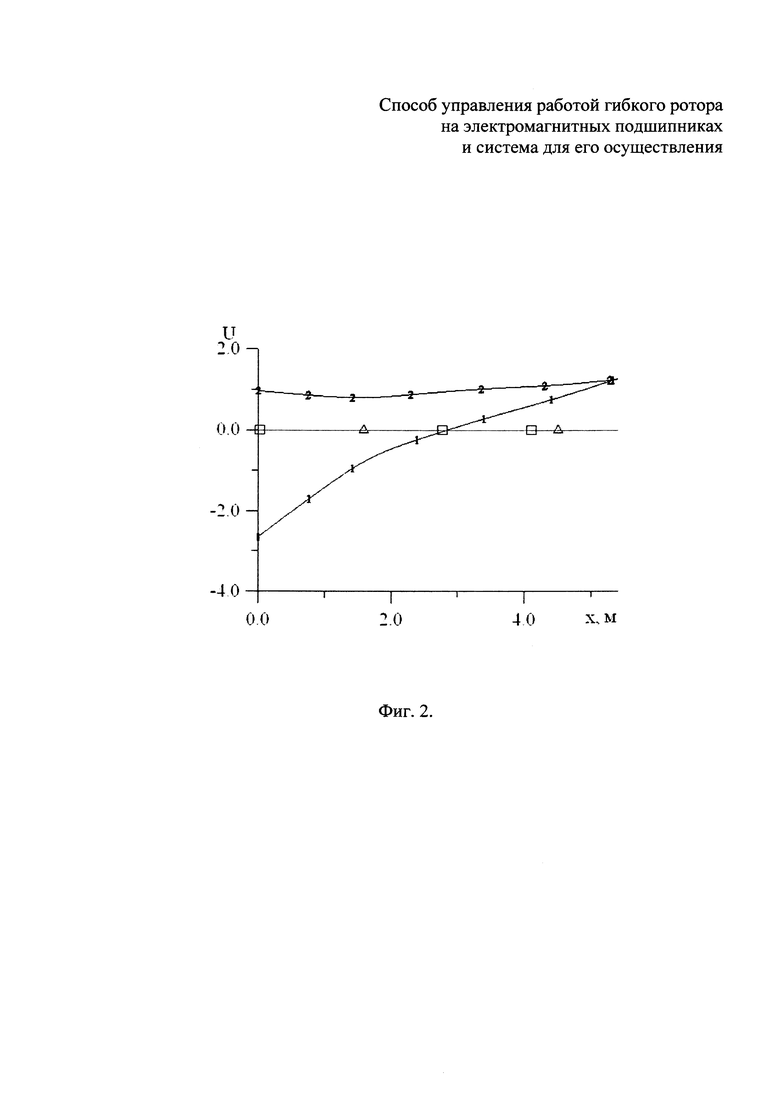
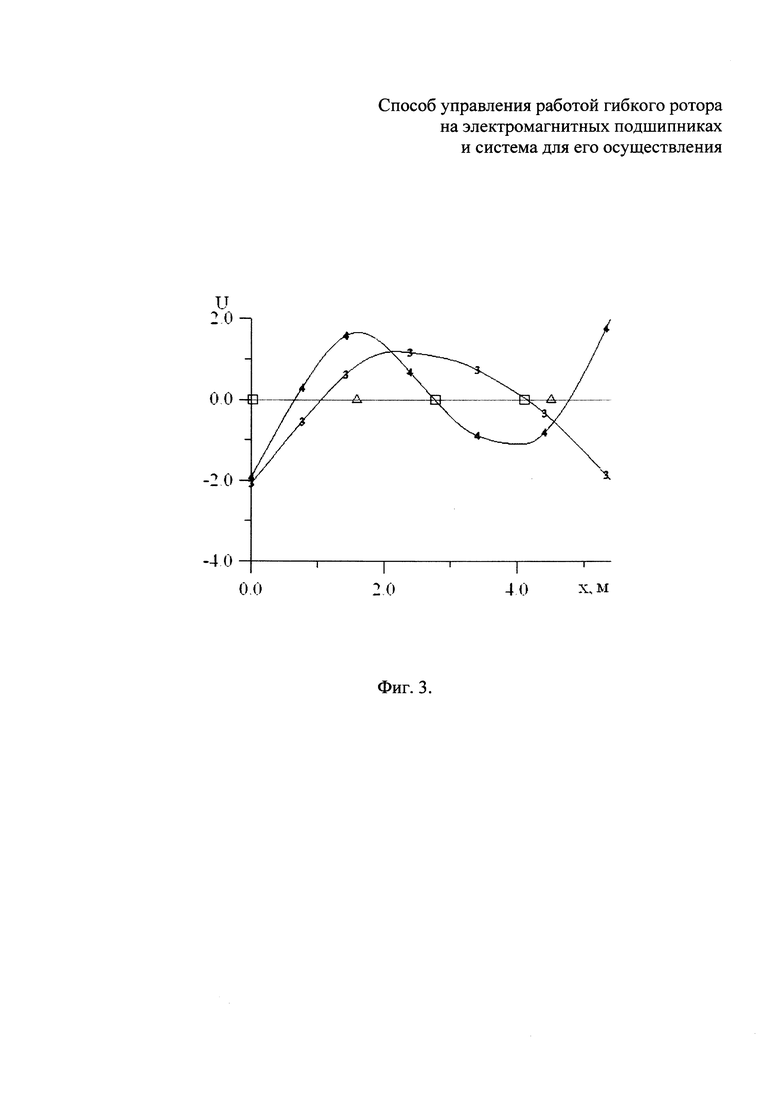
Формы собственных колебаний гибкого ротора генератора представлены на фиг. 2, 3
Треугольниками на фиг. 2, 3 отмечены места расположения радиальных ЭМП.
Рассмотрен вариант, когда остаточный дисбаланс гибкого ротора сосредоточен в трех сечениях:
- на расстоянии 20 мм от верхнего сечения гибкого ротора дисбаланс составляет 334 г⋅мм, угол дисбаланса равен 0.0°,
- на расстоянии 2770 мм от верхнего сечения гибкого ротора дисбаланс составляет 3579 г⋅мм, угол дисбаланса равен 150.0°,
- на расстоянии 4103 мм от верхнего сечения гибкого ротора дисбаланс составляет 2938 г⋅мм, угол дисбаланса равен 30.0°.
На фиг. 2, 3 места расположения дисбаланса отмечены квадратами.
Для гибкого ротора ММР рабочей является частота вращения 60 Гц.
На рабочей частоте вращения отклонения оси гибкого ротора находятся в пределах 0.05 мм, что на порядок меньше зазора в страховочных подшипниках.
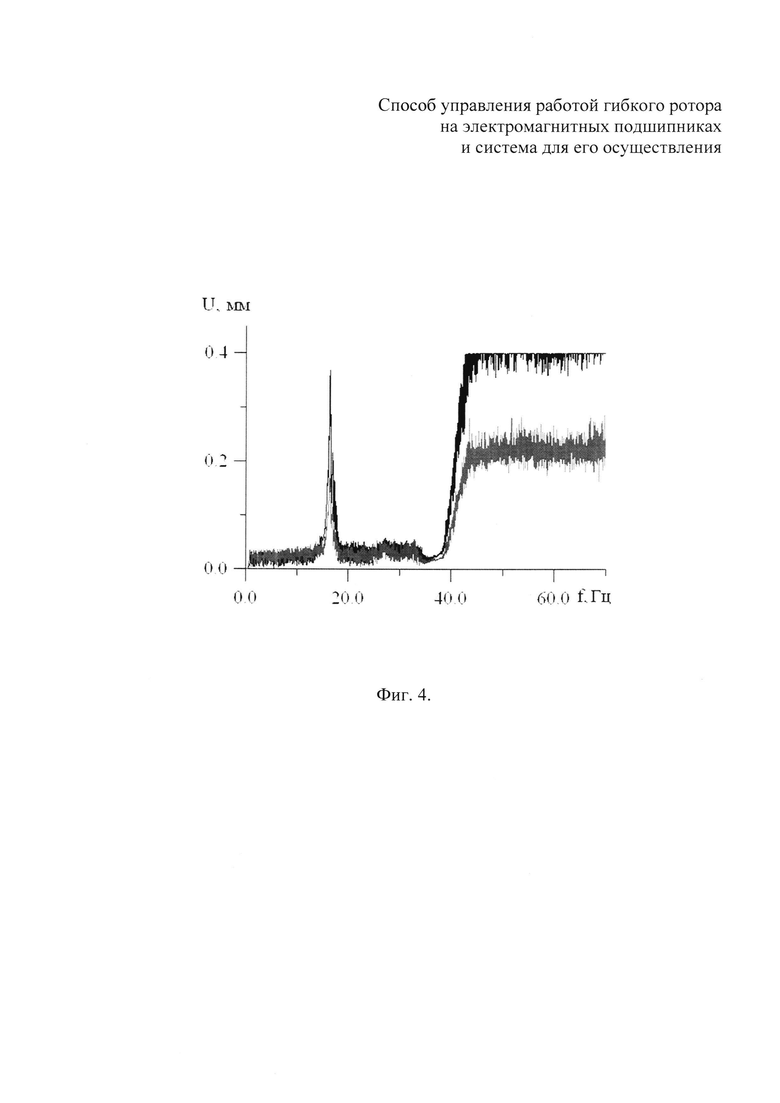
Проблемы возникают при разгоне гибкого ротора до рабочей частоты и при его останове. На фиг. 4 показаны зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в сечении ЭМП верхнего (черная кривая) и в сечении ЭМП нижнего (серая кривая) при разгоне гибкого ротора с ускорением 0.5 Гц в сек. Из представленных на фиг. 4 зависимостей следует, что прохождение третьей критической частоты вращения порядка 16 Гц, связанной с первой изгибной формой колебаний гибкого ротора, в сечении ЭМП верхнего, отклонения гибкого ротора практически достигают уровня зазора в страховочных подшипниках, что представляет серьезную опасность для эксплуатации такого ротора. При прохождении критической частоты вращения, связанной со второй изгибной формой колебаний гибкого ротора (частота порядка 40 Гц), в сечении ЭМП верхнего реализуется контакт гибкого ротора со страховочным подшипником, что является недопустимой ситуацией.
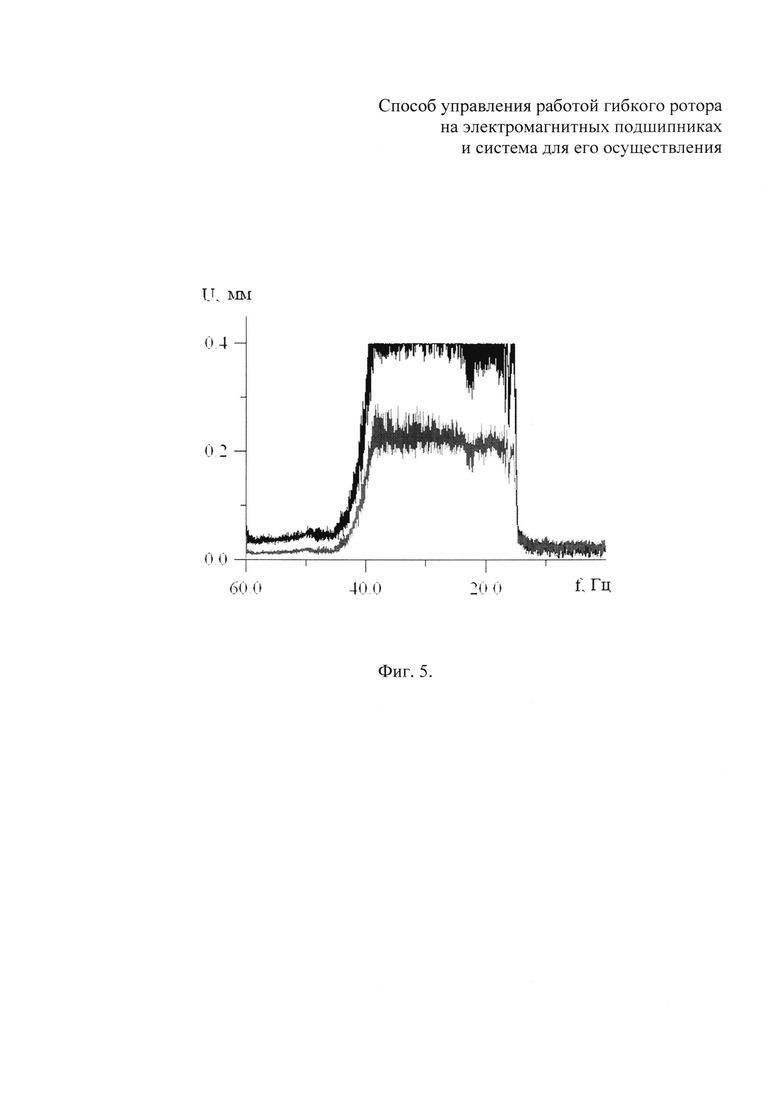
На фиг. 5 показаны зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в сечении ЭМП верхнего (черная кривая) и в сечении ЭМП нижнего (серая кривая), полученные при компьютерном моделировании останова гибкого ротора с ускорением - 0.5 Гц в секунду. Из представленных на фиг. 5 зависимостей следует, что прохождение диапазона критических частот вращения, границами которого являются критические частоты, связанные с первой и второй изгибными формой колебаний гибкого ротора (частоты порядка 16 Гц и 40 Гц), сопровождается постоянным контактом этого ротора с верхним страховочным подшипниках, что является недопустимой ситуацией.
Зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения, показанные на фиг. 4 и 5, получены в условиях управления его работой, совпадающих с условиями управления работой гибкого ротора в соответствии со способом управления - прототипом и свидетельствуют о недостаточности формирования (для компенсации резонансных колебаний, вызванных остаточным дисбалансом в переходных режимах работы гибкого ротора) с помощью блока 4 двух ортогональных сил 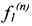 и
и 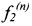 , определяемых блоком 3.
, определяемых блоком 3.
В результате компьютерного моделирования процесса разгона гибкого ротора при формировании сил F1(n) и F2(n), в соответствии с формулами (1) и параметрами в таблице 1 установлено, что прохождение диапазона критических частот вращения, связанных с первой и второй изгибными формами колебаний гибкого ротора (частоты порядка 16 Гц и 40 Гц), стало безопасным (см. фиг. 6 и 7).
На фиг. 6 показаны зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в сечении ЭМП верхнего (черная кривая) и в сечении ЭМП нижнего (серая кривая), полученные при компьютерном моделировании разгона гибкого ротора с ускорением 0.5 Гц в секунду.
Из представленных на фиг. 6 зависимостей следует, что отклонения оси гибкого ротора не превышают 0.12 мм, то есть прохождение всего частотного диапазона при разгоне этого ротора стало безопасным.
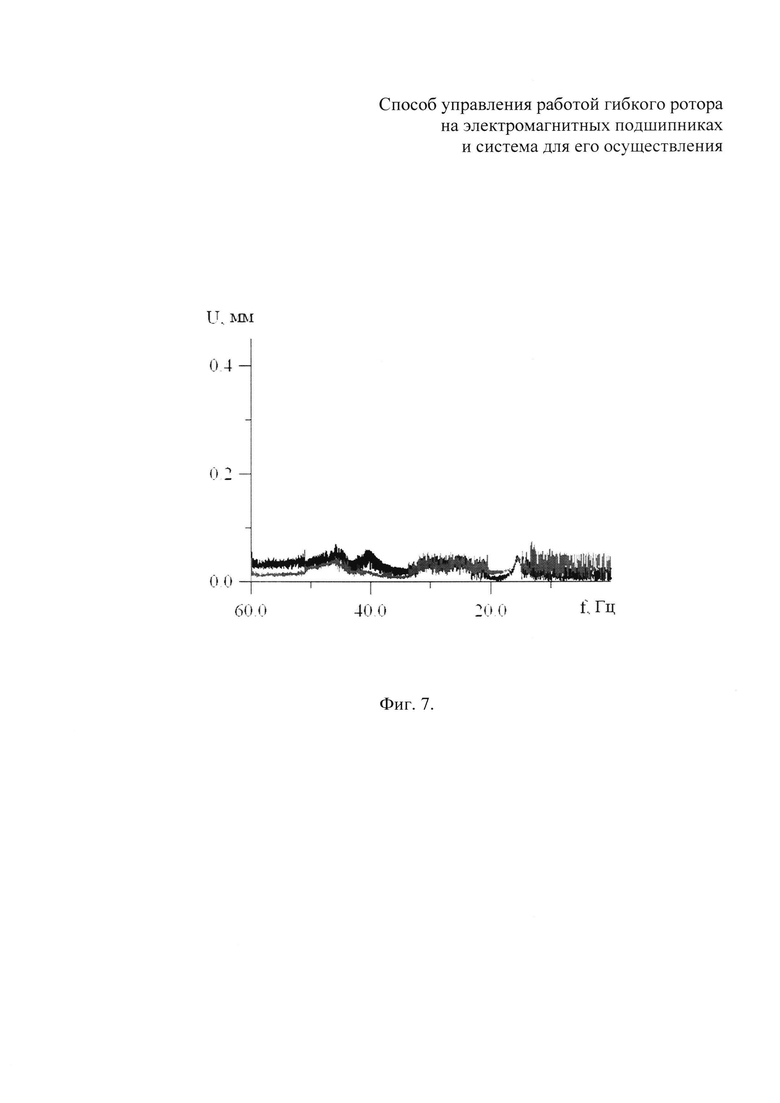
На фиг. 7 показаны зависимости амплитуды отклонений оси гибкого ротора от частоты его вращения в сечении ЭМП верхнего (черная кривая) и в сечении ЭМП нижнего (серая кривая), полученные при компьютерном моделировании останова гибкого ротора с ускорением -0.5 Гц в секунду.
Из представленных на фиг. 7 зависимостей следует, что отклонения оси гибкого ротора не превышают 0.08 мм, то есть прохождение частотного диапазона при останове гибкого ротора стало безопасным.
Сравнение графиков зависимостей амплитуды отклонений оси гибкого ротора при разгоне (фиг. 4 и 6) и при останове (фиг. 5 и 7) показывает высокую эффективность использования предлагаемого способа управления работой гибкого ротора при компенсации влияния остаточного дисбаланса на динамику гибкого ротора на ЭМП.
Обоснование вывода формул (1), используемых при осуществлении предлагаемого способа, раскрывается следующим образом.
Способ управления электромагнитным подвесом гибкого ротора базируется на наличии компьютерной модели динамики, отражающей основные свойства рассматриваемой конструкции (см. указанную выше статью авторов В.Ф. Овчинникова и др.). С использованием этой модели определяются критические скорости вращения гибкого ротора Ωk и вычисляются собственные моды φk(x), соответствующие критической скорости вращения, где индекс x - координата вдоль оси гибкого ротора, k - номер критической угловой скорости вращения и соответствующей собственной моды. Собственные моды удовлетворяют условию нормировки:

где μ(x) - масса на единицу длины гибкого ротора, L - длина гибкого ротора, М - масса гибкого ротора.
В режиме разгона гибкого ротора с помощью датчиков положения по каждому каналу управления (для каждого радиального ЭМП) измеряют отклонение гибкого ротора от центрального положения. При наличии остаточного дисбаланса при подходе к очередной критической частоте вращения гибкого ротора наблюдается увеличение амплитуды отклонений в местах расположения ЭМП (датчиков положений). Если эти амплитуды приближаются к границе допускаемого уровня (порядка 0.5 зазора в страховочных подшипниках), прекращается разгон гибкого ротора и реализуется его выбег до частот вращения с низким уровнем отклонений. В процессе выбега осуществляется запись угла поворота гибкого ротора, частоты вращения, показаний датчиков положения и датчиков тока в магнитах ЭМП. С использованием этой информации и имеющейся математической модели динамики гибкого ротора в соответствии с методикой идентификации дисбаланса гибкого ротора (см. статью авторов Ф.М. Митенкова, В.В. Знышева, Е.В. Кирюшиной, М.Я. Николаева и др. «Алгоритм определения дисбаланса ротора на электромагнитных опорах». - Проблемы машиностроения и надежности машин. 2007, №4, с. 9-14.) определяется еk - вектор приведенного эксцентриситета модального дисбаланса Qk гибкого ротора для k-ой критической угловой скорости вращения

где x - координата, отсчитываемая по оси гибкого ротора, вектор e(x) - эксцентриситет единичной массы, задаваемый в плоскости, перпендикулярной оси гибкого ротора в точке x, ek - вектор приведенного эксцентриситета модального дисбаланса, задаваемый в плоскости, перпендикулярной оси гибкого ротора. Векторы эксцентриситета и приведенного эксцентриситета модального дисбаланса задаются в системе координат, связанной с гибким ротором.
Если магниты радиальных ЭМП (xn - координата расположения n-го радиального ЭМП по оси гибкого ротора) будут формировать силы F(n) (n - номер канала 1 (см. фиг. 1) системы управления, совпадающий с номером радиального ЭМП; N - общее количество радиальных ЭМП), удовлетворяющие соотношению:

то эти силы будут компенсировать воздействие модального дисбаланса на динамику гибкого ротора в окрестности k-ой критической частоты.
Соотношение (5) представляет собой систему линейных алгебраических уравнений относительно неизвестных компонент сил F(n), причем число неизвестных превышает число уравнений. Поэтому для однозначного определения сил необходимы дополнительные условия, которые сформулируем так: F(n) должны обеспечивать минимум выражению

Решение задачи (5) при условии (6) задается выражениями:
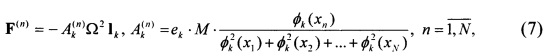
где ek - модуль вектора ek, Ik - единичный безразмерный вектор, совпадающий по направлению с ek.
Для каждого n-го канала системы управления, соответствующего своему радиальному ЭМП, проекции вектора силы F(n) на оси неподвижной системы координат в плоскости, перпендикулярной оси гибкого ротора, может быть записана в виде:
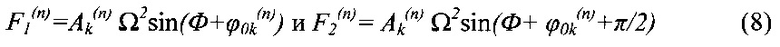
где Ak(n) - параметр дисбаланса, определяемый выражением (7), а ϕ0k(n) - угол, задающий вектор в связанной с гибким ротором полярной системе координат в плоскости, перпендикулярной оси гибкого ротора; Ω - угловая скорость гибкого ротора, Ф угол поворота гибкого ротора.
Система управления в процессе разгона или выбега гибкого ротора при подходе к критической частоте вращения создает дополнительные ортогональные управляющие силы, а после прохождении критической частоты эти силы отключаются.
При подходе к следующей критической частоте вся процедура определения дополнительных ортогональных управляющих сил и прохождения достигнутой критической частоты вращения повторяется.
Границы частотного интервала подключения указанных сил определяются из условия достижения отклонениями а гибкого ротора уровней a=±2,5а0, где a0 - стационарное значение, возникающее при самоцентрировании гибкого ротора. В окрестности критической частоты отклонения гибкого ротора, обусловленные действием дисбаланса, определяются зависимостью (без учета затухания) 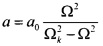 . Отсюда определяется нижняя и верхняя граница частотного диапазона подключения силы
. Отсюда определяется нижняя и верхняя граница частотного диапазона подключения силы

Полученное для компенсирующей дисбаланс силы выражение (8) не учитывает существующее в реальной системе запаздывание, обусловленное инерционностью электромагнитов, обмотки которых имеют индуктивности и активные сопротивления.
Входящий в (1) ϕk(n) - начальный угол поворота гибкого ротора, компенсирующий дисбаланс на k-й критической угловой скорости, определяется соотношением:

где Δϕk(n) - угол запаздывания, обусловленный инерционностью системы управления ЭМП.
Для оценки этого угла можно воспользоваться следующими соображениями.
Максимальный модуль силы F, компенсирующей дисбаланс, действующей в направлении одной из координат в радиальном ЭМП согласно (8) определяется соотношением

Эта сила создается электромагнитами радиального ЭМП и согласно книге на англ. яз. авторов Schweitzer, G. and Maslen, Е. «Magnetic Bearings: Theory, Design, and Application to Rotating Machinery)) Berlin: Springer. 2009, p. 535, в центральном положении гибкого ротора равна

где I0 - амплитудное значение тока, обеспечивающего максимальный модуль силы F, компенсирующей дисбаланс, L0 - индуктивность магнитов, создающих силу в одном из направлений в радиальном ЭМП при центральном положении гибкого ротора, S0 - номинальный магнитный зазор между гибким ротором и магнитами радиального ЭМП.
Из соотношений (11), (12) для амплитудного значения тока I0 получаем выражение

Согласно правилам Кирхгофа изменение тока I, протекающего в цепи магнитов, создающих силу в одном из направлений в радиальном ЭМП при центральном положении гибкого ротора, запишется в виде:

В этой записи R - активное сопротивление магнитов, создающих силу в одном из направлений в радиальном ЭМП, U0 - максимальное напряжение в цепи магнитов, создающих силу в одном из направлений радиального ЭМП. Решение дифференциального уравнения (14) при нулевых начальных условиях I(0)=0 имеет вид

Из этого выражения определяется время Т, необходимое для достижения током значения I0 и соответствующая нижняя оценка угла запаздывания 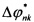 на критической угловой скорости вращения гибкого ротора Ωk
на критической угловой скорости вращения гибкого ротора Ωk
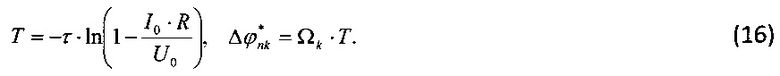
Принимая во внимание, что 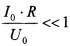 , можно записать
, можно записать

Выражение (17) дает нижнюю оценка угла запаздывания. Угол запаздывания Δϕk(n), входящий в выражение (10) для ϕk(n) начального угла поворота гибкого ротора, компенсирующего дисбаланс на k-й критической угловой скорости, определяется соотношением

Здесь kz=5 - эмпирический коэффициент. На основании выражений (10) и (18), начальный угол поворота гибкого ротора ϕk(n), запишется в виде:

Таким образом, в реальных условиях учета инерционности системы управления допустимо в выражении (8) использовать ϕk(n) вместо ϕ0k(n). В результате чего получаем для сил F1(n) и F2(n) формулы (1).
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОНТАЖА РОТОРА ГАЗОТУРБИННОГО ДВИГАТЕЛЯ | 2013 |
|
RU2528789C1 |
| Способ изготовления ротора электростатического гироскопа | 2024 |
|
RU2837483C1 |
| Способ определения динамического дисбаланса ротора авиационного газотурбинного двигателя | 2016 |
|
RU2627750C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОЙ БАЛАНСИРОВКИ РОТОРА | 2008 |
|
RU2426976C2 |
| Способ обеспечения автоматической балансировки статически неуравновешенного ротора | 2021 |
|
RU2766945C1 |
| Стиральная машина | 1989 |
|
SU1678934A2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ И ЭКСПЕРТНАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2175120C2 |
| Моментный электродвигатель постоянного тока с ограниченным углом поворота | 1990 |
|
SU1757038A1 |
| Способ управления магнитными опорами ротора | 1989 |
|
SU1712691A1 |
| ПОДАВЛЕНИЕ ПОПЕРЕЧНЫХ ВИБРАЦИЙ ЭЛЕКТРОЦЕНТРОБЕЖНОГО НАСОСА ПОСРЕДСТВОМ МОДУЛИРОВАНИЯ СКОРОСТИ ВРАЩЕНИЯ ДВИГАТЕЛЯ | 2008 |
|
RU2456481C2 |

Группа изобретений относится к машиностроению и может быть использована в конструкциях, включающих гибкий ротор на электромагнитных подшипниках (ЭМП). Технический результат - повышение надежности и ресурса работы гибкого ротора на ЭМП в результате увеличения степени компенсации остаточного дисбаланса за счет формирования в каждом радиальном ЭМП гибкого ротора двух дополнительных ортогональных управляющих сил, повышающих эффективность корректировки положения оси гибкого ротора в переходных режимах и определяемых с помощью предлагаемых системы и порядка управления работой гибкого ротора. Для достижения указанного технического результата в способе управления работой гибкого ротора, включающем измерение в дискретные моменты времени отклонений оси гибкого ротора дополнительно измеряют в дискретные моменты времени угловую скорость вращения гибкого ротора Ω и угол его поворота Ф и для компенсации резонансных биений гибкого ротора в k-х интервалах указанной угловой скорости Ω определяют в каждом n-м радиальном ЭМП две дополнительные ортогональные управляющие силы F1(n) и F2(n), а затем формируют указанные дополнительные силы в каждом n-м радиальном ЭМП. Для достижения технического результата в системе для управления работой гибкого ротора, состоящей из N каналов для создания двух ортогональных управляющих сил в радиальных ЭМП в каждом канале, содержащем блок измерения отклонений оси гибкого ротора в месте расположения радиального ЭМП, введен блок измерения угловой скорости вращения гибкого ротора и угла его поворота, а каждый канал системы снабжен блоком программного определения двух дополнительных ортогональных управляющих сил, подключенным своим выходом ко второму входу блока регулирования указанных управляющих сил в радиальном ЭМП, при этом блок измерения угловой скорости вращения гибкого ротора и угла его поворота своим многоканальным выходом соединен со входами указанных канальных блоков программного определения двух дополнительных ортогональных управляющих сил. 2 н.п. ф-лы, 7 ил., 1 табл.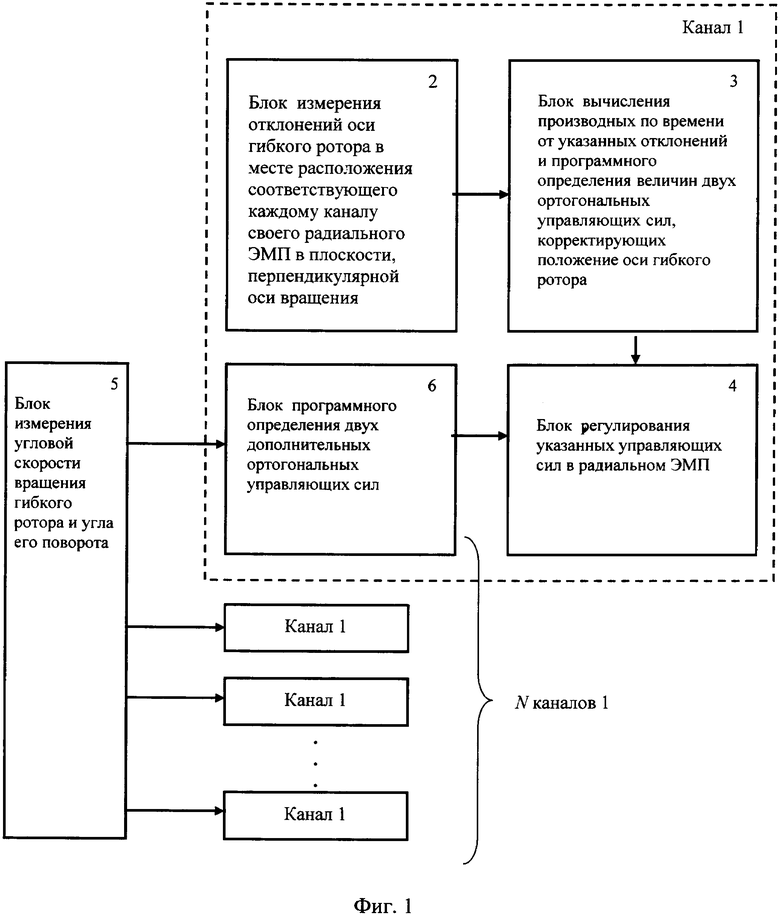
1. Способ управления работой гибкого ротора, включающий измерение в дискретные моменты времени отклонений оси гибкого ротора в плоскости, перпендикулярной оси его вращения, в местах расположения радиальных электромагнитных подшипников (ЭМП), вычисление производных по времени от указанных отклонений, определение двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора в каждом n-м радиальном ЭМП, в зависимости от указанных отклонений оси гибкого ротора и их производных, и последующее формирование указанных сил в каждом n-м радиальном ЭМП, отличающийся тем, что дополнительно измеряют в дискретные моменты времени угловую скорость вращения гибкого ротора Ω и угол его поворота Ф и для компенсации резонансных биений гибкого ротора в k-х интервалах указанной угловой скорости Ω, задаваемых граничными величинами 0,85Ωk и 1,30Ωk, где Ωk - k-я критическая угловая скорость гибкого ротора, определяют в каждом n-м радиальном ЭМП две дополнительные ортогональные управляющие силы 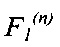 и
и 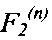 в соответствии с формулами
в соответствии с формулами
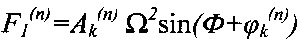 и
и 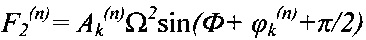 ,
,
где 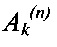 и
и 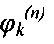 - идентифицируемые величины n-го радиального ЭМП соответственно параметра дисбаланса гибкого ротора на k-й критической угловой скорости и начального угла поворота гибкого ротора, компенсирующего дисбаланс на k-й критической угловой скорости, которые определяют программным методом идентификации распределения дисбаланса гибкого ротора, а затем формируют указанные дополнительные силы в каждом n-м радиальном ЭМП.
- идентифицируемые величины n-го радиального ЭМП соответственно параметра дисбаланса гибкого ротора на k-й критической угловой скорости и начального угла поворота гибкого ротора, компенсирующего дисбаланс на k-й критической угловой скорости, которые определяют программным методом идентификации распределения дисбаланса гибкого ротора, а затем формируют указанные дополнительные силы в каждом n-м радиальном ЭМП.
2. Система для управления работой гибкого ротора в соответствии со способом по п. 1, состоящая из N каналов для создания двух ортогональных управляющих сил в радиальных ЭМП в каждом канале, содержащем блок измерения отклонений оси гибкого ротора в месте расположения радиального ЭМП в плоскости, перпендикулярной оси вращения гибкого ротора, соединенный своим выходом с входом блока вычисления производных по времени от указанных отклонений и программного определения величин двух ортогональных управляющих сил, корректирующих положение оси гибкого ротора, подключенного в свою очередь к первому входу блока регулирования указанных управляющих сил в радиальном ЭМП, отличающаяся тем, что в предлагаемую систему введен блок измерения угловой скорости вращения гибкого ротора и угла его поворота, а каждый канал системы снабжен блоком программного определения двух дополнительных ортогональных управляющих сил, подключенным своим выходом ко второму входу блока регулирования указанных управляющих сил в радиальном ЭМП, при этом блок измерения угловой скорости вращения гибкого ротора и угла его поворота своим многоканальным выходом соединен со входами указанных канальных блоков программного определения двух дополнительных ортогональных управляющих сил.
| ГИБРИДНЫЙ МАГНИТНЫЙ ПОДШИПНИК С ОСЕВЫМ УПРАВЛЕНИЕМ | 2013 |
|
RU2540215C1 |
| МАГНИТНАЯ ОПОРА ДЛЯ АГРЕГАТА | 1997 |
|
RU2129228C1 |
| Способ управления магнитными опорами ротора | 1989 |
|
SU1712691A1 |
| УСТАНОВКА ДЛЯ ЦЕНТРОБЕЖНОЙ ЗАЛИВКИ ЛИТЕЙНЫХ ФОРМ | 1996 |
|
RU2109596C1 |
| JP 3916821 B2, 23.05.2007 | |||
| US 6365996 B2, 02.04.2002 | |||
| WO 2007066474 A1, 14.06.2007. | |||
Авторы
Даты
2017-05-05—Публикация
2015-12-09—Подача