Изобретение относится к области измерительных информационных систем и комплексов боевых самолетов и вертолетов, в котором рассматривается решение одной из частных задач общей задачи прицеливания, заключающейся в разработке математической процедуры определения текущего местоположения цели и параметров ее движения без включения лазерного дальномера.
Известен ряд способов решения указанной задачи, приведенных в учебнике Р.В. Мубаракшина, В.М. Балуева, Б.В. Воронова «Прицельные системы стрельбы», Часть 1, ВВИА им. Н.Е. Жуковского, 1973 г [1]:
- способ определения скорости и ускорения цели через ее координаты и их производные (стр. 43-46);
- способ определения скорости и ускорения путем измерения угловых скоростей и ускорений головки визирного устройства и производных дальности (стр. 46-49);
- способ определения скорости и ускорения цели через ее относительные координаты, измеряемые в различные моменты времени (стр. 49-51).
Перечисленные методы определения параметров движения цели представляются физически обоснованными. Но при этом уровень их инженерной проработки и прикладная значимость свидетельствуют о том, что при их разработке, очевидно, не стояла задача их эффективного промышленного использования, а преследовалась цель получения выражений для прямого расчета тех или иных параметров движения цели.
Представляется, что указанный подход далек от инженерного, поскольку, в соответствии с ним, для расчета параметров, типа дальности до цели и углов ее визирования, предполагается использование их первых и вторых производных, что непреемлемо при разработке точных математических процедур.
В учебном пособии В.Г. Гришутина «Лекции по авиационным прицельным системам стрельбы», КВВАИУ, Киев, 1980 г [2] представлен пример оптимального оценивания составляющих скорости цели, но для частного случая ее прямолинейного равномерного движения (стр. 164-167).
Дополнительно, но уже для общего случая движения цели, в [2], в подразделе «Способ прицеливания, основанный на последовательном уточнении данных о движении цели» (стр. 328) даются следующие полезные рекомендации относительно определения параметров ее движения:
«В маневренном бою, как правило, остро испытывается дефицит времени, поэтому при прицеливании по движущейся цели может оказаться нецелесообразным сразу оценивать все параметры ее движения.
На практике более предпочтительной может быть их оценка, выполненная последовательно несколько раз. В каждом новом цикле оценивания производится уточнение данных, полученных в предыдущем цикле.
С каждым таким циклом точность решения рассматриваемой задачи, а, следовательно, и точность прицеливания, закономерно должна увеличиваться и достигать некоторого предельного значения, определяемого, как динамикой системы оценивания, так и имеющими место случайными ошибками (шумами) измерения относительных координат текущего местоположения цели».
Указанные рекомендации, если их рассматривать в пределе, при достаточно малом цикле измерения относительных координат текущего местоположения цели, не превышающем 0,1 секунды, и таком же цикле их обработки и оптимального оценивания по ним искомых параметров движения цели, таких, как составляющие ее скорости и ускорения, следует расценивать не иначе, как осмысленную необходимость разработки рекуррентных, сходящихся и ассимптотически устойчивых оптимальных математических процедур оценивания, нашедших применение в некоторых из отечественных разработок.
Формализуя описание основанного на приведенных рекомендациях способа привязки к подвижной наземной цели, излагая его в характерных для него терминах и с акцентом на физическую суть выполняемых при его реализации операций, приведем его в следующем виде.
Способ оптимальной привязки к подвижной наземной цели, включающий непрерывное угловое сопровождение цели и дискретное измерение/определение текущей наклонной дальности до нее, по каждому из которых с использованием измеренной инерциальной навигационной системой (ИНС) информации и текущих углов визирования цели с теле-тепловизионной обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание текущих координат относительного местоположения цели и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью ее относительного движения, представленной в виде системы линейных уравнений 9-го порядка в проекциях на оси ПСК, для чего, по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК в проекциях на ее же оси, а компоненты абсолютной линейной скорости объекта в осях ПСК используют в качестве известного управления, по окончании активной фазы режима привязки, определяемой ограничением на время непрерывной работы лазерного дальномера (ЛД), полученные в результате оптимальной идентификации значения оценок параметров движения цели запоминают и используют в качестве начальных условий в рекуррентной процедуре их проноза, который реализуют в соответствии с уравнениями для расчета априорных оценок, для чего расчет оптимальных коэффициентов усиления останваливают, сами коэффициенты усиления и входные сигналы фильтра обнуляют и, также, как и в режиме привязки, используют рассчитанные по измеренной ИНС угловой и навигационной информации текущие значения компонент абсолютной угловой скорости вращения ПСК и составляющих абсолютной линейной скорости объекта в проекциях на оси ПСК, а по текущим значениям парметров движения объекта и цели формируют искомые поправки на стрельбу и в виде подвижной прицельной марки (ППМ) выдают их на коллиматорный прицел летчика, по которому, управлением объекта, осуществляют их отработку и прицельное применение выбранных неуправляемых средств поражения.
Учитывая, что предметом предлагаемого изобретения является синтез защищенного способа определения парметров относительного местоположения и движения цели, исключающего использование лазерного дальномера из состава обзорно-прицельной системы (ОПС), для измерения текущих значений наклонной дальности до подвижной, в общем случае, маневрирующей цели, представляется логичным основными недостатками прототипа считать:
- незащищенность объекта боевого применения в режиме привязки к подвижной наземной цели по причине использования дискретных измерений лазерного дальномера;
- неприемлемая точность режима программного сопровождения цели - прогноза параметров относительного местоположения и движения цели в случае ее маневрирования и, как следствие, низкая эффективность решения боевой задачи (БЗ).
Техническим результатом изобретения является:
- расширение функциональных возможностей оптико-электронных прицельно-навигационных комплексов (ОЭПрНК) объектов боевого назначения за счет разработки защищенного способа полноценной привязки к подвижной наземной цели, исключают использование лазерного дальномера;
- повышение точности и эффективности решения боевой задачи (БЗ) посредством реализации, унифицированной с режимом привязки процедуры оптимального оценивания на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчета наклонной дальности.
Указанный технический результат достигается за счет того, что в защищенном способе оптимальной привязки к подвижной наземной цели (ПНЦ), включающем непрерывное угловое сопровождение цели и дискретное определение текущей наклонной дальности до нее, по каждому из которых с использованием измеренной инерциальной навигационной системой (ИНС) пилотажной и навигационной информации и текущих углов визирования цели с теле-тепловизионной обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент относительной дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание текущих координат относительного местоположения ПНЦ и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью ее относительного движения, представленной системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего, по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК в проекциях на ее оси, а компоненты абсолютной линейной скорости объекта в осях ПСК используют в качестве известного управления, по оцененным в процессе оптимальной фильтрации и идентификации значениям параметров относительного местоположения и движения цели и текущей воздушно-скоростной информации объекта формируют искомые поправки на стрельбу и в виде подвижной прицельной марки (ППМ) выдают их на коллиматорный прицел летчика, по которому, управлением объекта, осуществляют их отработку и прицельное применение выбранных неуправляемых авиационных средств поражения (АСП), дополнительно для формирования сигналов измерения, входных сигналов оптимального фильтра-идентификатора, последовательно используют кинематический метод определения текущей наклонной дальности (КМОД) и модифицированный угломестный способ определения наклонной дальности (МУСОД) до ПНЦ, первый из которых, КМОД, используют для обеспечения информационной состоятельности второго, МУСОД, для чего, в 60-75-ти метрах по пути ожидаемого следования реальной ПНЦ, выбирают характерный для наблюдаемого рельефа земной поверхности (РЗП) неподвижный наземный ориентир (ННО), наводят на него неподвижное перекрестие (НИИ) ОПС и сопровождают в одном из режимов углового сопровождения в течение 3-3,5 секунд, предварительно уведомив БЦВМ комплекса подачей команды «КМОД» о начале углового сопровождения выбранного ННО, в процессе чего, с частотой от 2-х до 10-ти герц, в зависимости от скорости объекта, измеряют полный срез навигационной 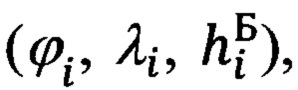 пилотажной (ψи i, υi, γi) и специальной (ϕy i, ϕz i) информации, и, обрабатывая (i-1)-ые текущие, i-ые измерения навигационных параметров последовательно формируют базовую дальность ΔDi-1 i между двумя соседними отсчетными точками и текущие значения азимута Ai-1 i и угла места θi-1 i ее пространственной ориентации относительно ГСТ ONHE, направление осей которого соответствует точке с координатами ϕi-1, λi-1, а используя (i-1)-ый и i-ый массивы пилотажной и специальной информации, последовательно определяют углы Ai-1, θi-1 и Ai, θi пространственной ориентации векторов
пилотажной (ψи i, υi, γi) и специальной (ϕy i, ϕz i) информации, и, обрабатывая (i-1)-ые текущие, i-ые измерения навигационных параметров последовательно формируют базовую дальность ΔDi-1 i между двумя соседними отсчетными точками и текущие значения азимута Ai-1 i и угла места θi-1 i ее пространственной ориентации относительно ГСТ ONHE, направление осей которого соответствует точке с координатами ϕi-1, λi-1, а используя (i-1)-ый и i-ый массивы пилотажной и специальной информации, последовательно определяют углы Ai-1, θi-1 и Ai, θi пространственной ориентации векторов 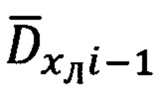 и
и 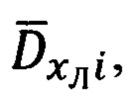 определяющих текущее направление на ННО, используя которые формируют пространственные углы βi-1 и βi между базовым вектором
определяющих текущее направление на ННО, используя которые формируют пространственные углы βi-1 и βi между базовым вектором 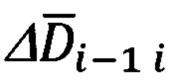 и векторами
и векторами 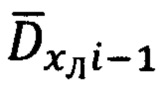 и
и 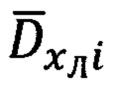 соответственно, знание которых обеспечивает корректное решение пространственного треугольника дальностей, в результате чего последовательно определяют текущее значение дальности Di до ННО и соответствующую ей геометрическую высоту hi объекта относительно ННО, сравнением которой с текущей бароинерциальной высотой
соответственно, знание которых обеспечивает корректное решение пространственного треугольника дальностей, в результате чего последовательно определяют текущее значение дальности Di до ННО и соответствующую ей геометрическую высоту hi объекта относительно ННО, сравнением которой с текущей бароинерциальной высотой 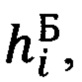 определяют высоту Δhi ННО и над уровнем моря и используют ее в рекуррентной процедуре нахождения среднего значения
определяют высоту Δhi ННО и над уровнем моря и используют ее в рекуррентной процедуре нахождения среднего значения 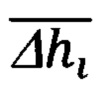 массива указанных высот, при этом, после каждого очередного определения текущих значений параметров Di,
массива указанных высот, при этом, после каждого очередного определения текущих значений параметров Di, 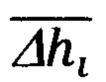 осуществляют операцию переприсваивания, принимая i-ый массив измеренных и рассчитанных
осуществляют операцию переприсваивания, принимая i-ый массив измеренных и рассчитанных 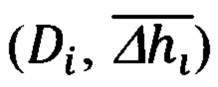 параметров за (i-1)-ый, а точку, на которую осуществляется полет - за i-ую, чем реализуют алгоритмический повтор приведенной процедуры КМОД, по окончании 1-го, вспомогательного этапа привязки к ПНЦ в БЦВМ комплекса формируют признак «КМОД ГОТОВ» и индицируют его на индикаторе оператора, по которому ОПС перенацеливают на реальную цель и нажимают кнопку «Привязка», по которой БЦВМ комплекса инициирует модифицированную угломестную процедуру расчета текущей наклонной дальности до ПНЦ, в которой сравнением текущей бароинерциальной высоты
параметров за (i-1)-ый, а точку, на которую осуществляется полет - за i-ую, чем реализуют алгоритмический повтор приведенной процедуры КМОД, по окончании 1-го, вспомогательного этапа привязки к ПНЦ в БЦВМ комплекса формируют признак «КМОД ГОТОВ» и индицируют его на индикаторе оператора, по которому ОПС перенацеливают на реальную цель и нажимают кнопку «Привязка», по которой БЦВМ комплекса инициирует модифицированную угломестную процедуру расчета текущей наклонной дальности до ПНЦ, в которой сравнением текущей бароинерциальной высоты 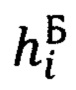 объекта со средним значением высоты
объекта со средним значением высоты 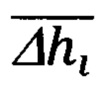 ПНЦ над уровнем моря определяют текущую геометрическую высоту hi объекта относительно цели, а используя текущее значение косинуса
ПНЦ над уровнем моря определяют текущую геометрическую высоту hi объекта относительно цели, а используя текущее значение косинуса 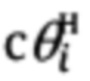 угла между географической вертикалью и направлением на цель, определяют текущее значение наклонной дальности Di до ПНЦ, на основе дискретной последовательности которых формируют массив входных сигналов оптимального фильтра-идентификатора параметров ПНЦ, последовательная обработка которых позволяет определить весь перечень параметров движения ПНЦ и обеспечить тем самым эффективное решение боевой задачи, при этом для обеспечения информационной состоятельности используемых в предлагаемом изобретении методов КМОД и МУСОД, формирование инерциальной информации реализуют в режиме инерциально-доплеровского оценивания и коррекции с расширением традиционной модели ошибок ИНС за счет включения в нее дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно доплеровского измерителя составляющих скорости (ДИСС) в проекциях на оси опорного трехгранника гироплатформы (ГП) ОТГП ИНС, чем обеспечивают корректное описание комплексной инерциально-доплеровской системы и повышенные характеристики наблюдаемости, точности и быстродействия оптимального оценивания ошибок ИНС, а синтез оптимального канала формирования бароинерциальной высоты и скорости ее изменения проводят параллельно с оптимальным комплексированием ИНС и ДИСС.
угла между географической вертикалью и направлением на цель, определяют текущее значение наклонной дальности Di до ПНЦ, на основе дискретной последовательности которых формируют массив входных сигналов оптимального фильтра-идентификатора параметров ПНЦ, последовательная обработка которых позволяет определить весь перечень параметров движения ПНЦ и обеспечить тем самым эффективное решение боевой задачи, при этом для обеспечения информационной состоятельности используемых в предлагаемом изобретении методов КМОД и МУСОД, формирование инерциальной информации реализуют в режиме инерциально-доплеровского оценивания и коррекции с расширением традиционной модели ошибок ИНС за счет включения в нее дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно доплеровского измерителя составляющих скорости (ДИСС) в проекциях на оси опорного трехгранника гироплатформы (ГП) ОТГП ИНС, чем обеспечивают корректное описание комплексной инерциально-доплеровской системы и повышенные характеристики наблюдаемости, точности и быстродействия оптимального оценивания ошибок ИНС, а синтез оптимального канала формирования бароинерциальной высоты и скорости ее изменения проводят параллельно с оптимальным комплексированием ИНС и ДИСС.
Приведем перечень и описание фигур, которые потребуются при осуществлении предлагаемого изобретения.
На фиг. 1 приведена ориентация инерциальной системы координат (ИСК) OXYZ, гринвической системы координат (ГСК) OX'Y'Z' и географического сопровождающего трехгранника (ГСТ) ONHE на земном эллипсоиде вращения.
ИСК OXYZ - это абсолютно неподвижная система координат, связанная со звездами.
ГСК OX'Y'Z' - это система координат, связанная с Землей, ось ОХ' которой параллельна оси вращения Земли, ось OY' - лежит в плоскости гринвического меридиана, а ось OZ' дополняет их до правого ортогонального трехгранника и направлена на Восток.
Рассогласование ГСК OX'Y'Z' и ИСК OXYZ определяется углом ut, где u - угловая скорость суточно-годового вращения Земли, t - текущее время. В начальный момент времени рассматриваемые системы координат совпадают.
На фиг. 2 приведена взаимная ориентация ГСК OX'Y'Z' и ГСТ ONHE.
Их рассогласование определяется углами географической долготы λ и широты ϕ.
Переход от осей ГСК OX'Y'Z' к осям ГСТ ONHE осуществляется посредством двух последовательных поворотов на угол λ и угол ϕ с угловыми скоростями 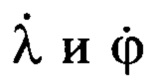 соответственно.
соответственно.
Приведенное на фиг. 2 направление отсчета углов λ и ϕ и угловых скоростей  является положительным.
является положительным.
На фиг. 3 приведена взаимная ориентация ГСТ ONHE и связанной с объектом (ССК) Oxyz.
Их рассогласование определяется углами истинного курса ψи тангажа υ и крена γ объекта.
Переход от осей ГСТ ONHE к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψи, υ и γ с угловыми скоростями 
Приведенное на фиг. 3 направление отсчета углов ψи, υ, γ и угловых скоростей 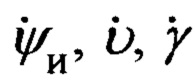 является положительным.
является положительным.
На фиг. 4 приведена взаимная ориентация ССК Oxyz и лучевой системы координат (ЛСК) OxЛyЛzЛ.
Их рассогласование определяется углами ϕy, ϕz визирования цели. Ось ОхЛ ЛСК направлена на цель, с указанной осью при угловом сопровождении цели совпадает вектор 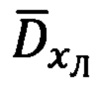 наклонной дальности до цели.
наклонной дальности до цели.
Переход от осей ССК Oxyz к осям ЛСК OxЛyЛzЛ осуществляется посредством двух последовательных поворотов на углы ϕy и ϕz с угловыми скоростями 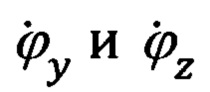 соответственно.
соответственно.
Приведенное на фиг. 4 направление отсчета углов ϕy, ϕz и угловых скоростей 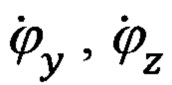 является положительным.
является положительным.
На фиг. 5 приведена взаимная ориентация ГСТ ONHE и ЛСК OxЛyЛzЛ.
Их рассогласование определяется углом азимута А и углом места θ направления на цель, а также углом лучевого крена γЛ.
Переход от осей ГСТ ONHE к осям ЛСК OxЛyЛzЛ осуществляется посредством трех последовательных поворотов на углы А, θ и γЛ с угловыми скоростями 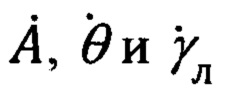 соответственно.
соответственно.
Приведенное на фиг. 5 направление отсчета углов A, θ и γЛ и угловых скоростей  является положительным.
является положительным.
На фиг. 6 приведена возможная схема относительного движения цели (Ц), для случая полета объекта (ЛА) над холмисто-гористой подстилающей поверхностью.
Под приведенными на указанной схеме обозначениями параметров движения объекта и цели следует понимать:
θi - угол между местной географической вертикалью и направлением на цель, косинус с θi угла которого сформирован по i-ым измерениям углов визирования цели и углов крена и тангажа объекта;
УМ - уровень моря, относительно которого осуществляется отсчет бароинерциальной высоты 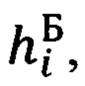 сформированной, как результат оптимального комплексирования измерений вертикального канала ИНС и баровысотомера из состава системы воздушных сигналов (СВС);
сформированной, как результат оптимального комплексирования измерений вертикального канала ИНС и баровысотомера из состава системы воздушных сигналов (СВС);
hi - расчетное значение текущей, i-ой высоты объекта относительно цели, или иначе, превышение объекта над целью, расчет hi осуществляют в соответствии с выражением 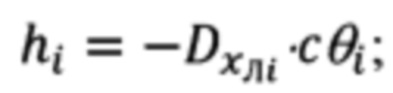
Δhi - текущее, i-oe значение высоты цели над уровнем моря, формируется сравнением бароинерциальной высоты 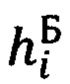 и расчетной высоты hi объекта:
и расчетной высоты hi объекта:
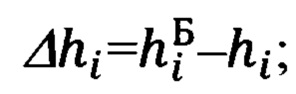
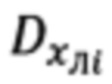 - текущее значение дальности до неподвижного ориентира, рассчитанное на основе кинематического метода определения дальности (КМОД);
- текущее значение дальности до неподвижного ориентира, рассчитанное на основе кинематического метода определения дальности (КМОД);
Di - текущее расчетное значение дальности до цели, рассчитываемое в соответствии с выражением Di=-hi/cθi;
На фиг. 7 приведен пространственный треугольник дальностей, на которой представлены:
- вектор 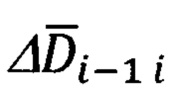 базовой дальности между двумя соседними отсчетными точками i-1 и i;
базовой дальности между двумя соседними отсчетными точками i-1 и i;
- векторы 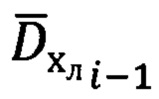 и
и 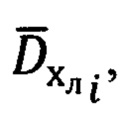 определяющие направление на цель (ориентир) из точек i-1 и i соответственно;
определяющие направление на цель (ориентир) из точек i-1 и i соответственно;
- углы βi-1, βi между базовым вектором 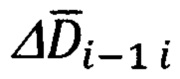 и векторами
и векторами 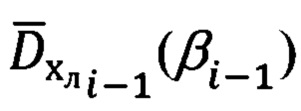 и
и 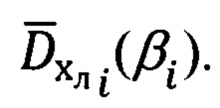
На фиг. 8 приведена взаимная ориентация ГСТ ONHE и ОТГП ИНС Oξηζ. Переход от осей ГСТ ONHE к осям ОТГП ИНС Oξηζ осуществляется посредством поворота на угол χ азимутальной ориентации ОТГП ИНС.
Приведенное на фиг. 8 направление отсчета угла χ и угловой скорости  является положительным.
является положительным.
На фиг. 9 приведена взаимная ориентация ОТГП ИНС Oξηζ и ССК Oxyz.
Их рассогласование определяется углами гироскопического курса ψг, тангажа и υ крена γ объекта.
Переход от осей ОТГП Oξηζ к осям ССК Oxyz осуществляется посредством трех последовательных поворотов на углы ψг, υ и γ с угловыми скоростями 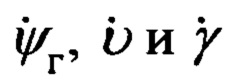 соответственно.
соответственно.
Приведенное на фиг. 9 направление отсчета углов ψг, υ, γ и угловых скоростей 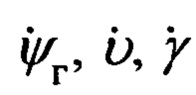 является положительным.
является положительным.
Процедура решения представленного треугольника дальностей приведена ниже, при описании кинематического метода определенич дальности.
С целью раскрытия физической сути предлагаемого способа привязки к подвижной наземной цели приведем подробное описание представленных выше систем координат, связывающих их матричных преобразований, дифференциальных уравнений относительного движения объекта и цели и входящих в них параметров, а также оптимальных математических процедур дискретной фильтрации Калмана.
В соответствии с фиг. 2, векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ГСТ ONHE по известным его компонентам в осях ГСК OX'Y'Z' и обратное ему выражение, имеют вид:

Матрица G преобразования (1), в соответствии с фиг. 2, равна:

При этом матрица GT обратного преобразования (2), являющаяся транспонированной по отношению к матрице G (3), будет равна:

В выражениях (3), (4) и далее под «s» следует понимать синус, а под «с» - косинус соответствующего угла.
Матричные преобразования произвольного вектора из ГСТ ONHE в ССК Oxyz и обратно имеют вид:

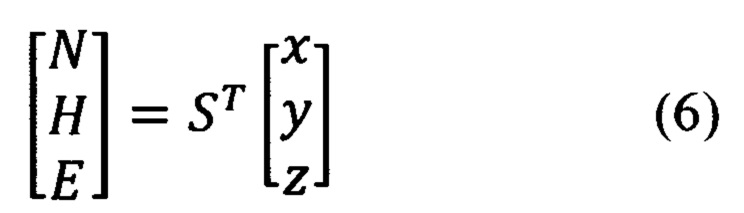
где матрица SГ и транспонированная ей матрица  , в соответствии с фиг. 3, равны:
, в соответствии с фиг. 3, равны:

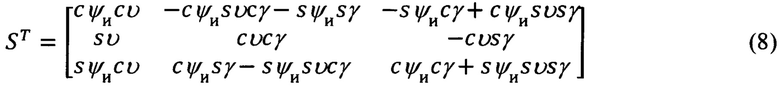
Матричные преобразования произвольного вектора из ССК Oxyz в ЛСК OxЛyЛzЛ и обратно имеют вид:
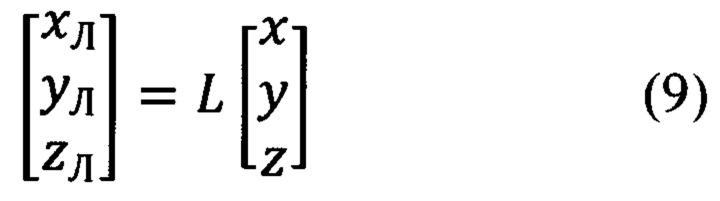
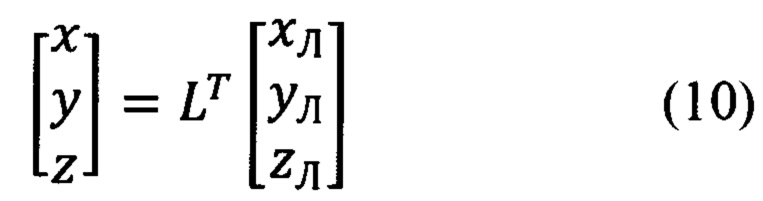
Входящие в (9) и (10) матрицы L и LT, в соответствии с фиг. 4, равны:

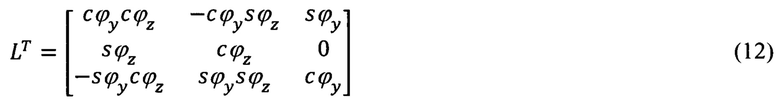
Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ЛСК OxЛyЛzЛ по известным его составляющим в осях ГСТ ONHE и обратное ему выражение, имеют вид (фиг. 5):
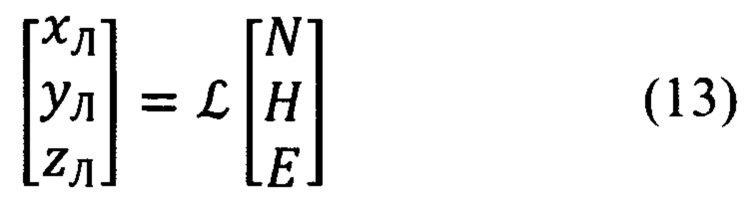
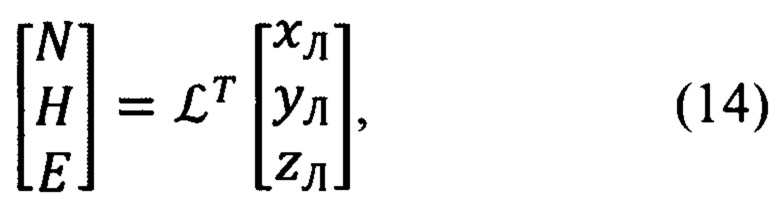
где матрица 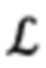 и транспонированная ей матрица
и транспонированная ей матрица 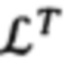 , в соответствии с фиг. 5, равны:
, в соответствии с фиг. 5, равны:
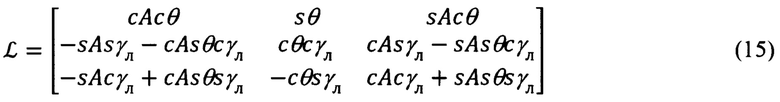
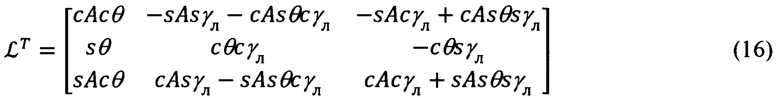
В соответствии с видом матрицы 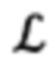 (15), выражения для расчета азимута А и угла места θ направления на цель (или ориентир), имеют вид:
(15), выражения для расчета азимута А и угла места θ направления на цель (или ориентир), имеют вид:

где  (i=1-3, j=1-3) - соответствующие элементы матрицы
(i=1-3, j=1-3) - соответствующие элементы матрицы 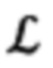 (15).
(15).
Последние матрицы (15), (16) и выражения (17) для расчета азимута А и угла места θ направления на цель являются вспомогательными.
Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ССК Oxyz по известным его составляющим в осях ОТГП ИНС Oξηζ обратное ему выражение имеют вид:
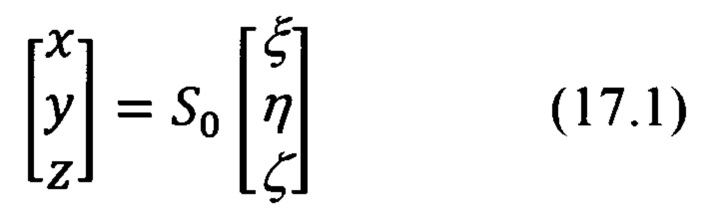
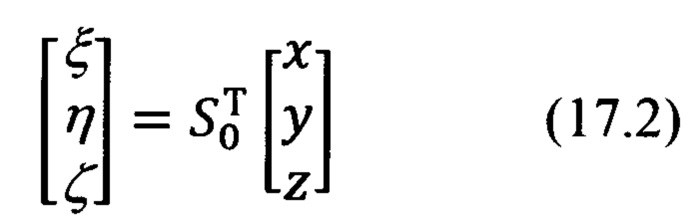
где матрица S0 и транспонированная ей матрица 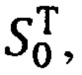 в соответствии с фиг. 8, будут равны:
в соответствии с фиг. 8, будут равны:
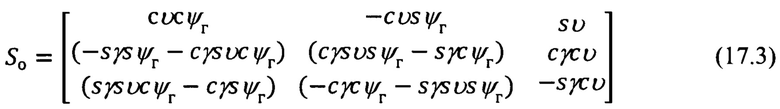
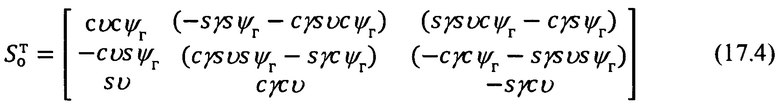
Векторно-матричное выражение для расчета компонент произвольного вектора в проекциях на оси ОТГП ИНС Oξηζ по известным его составляющим в проекциях на оси ГСТ ONHE и обратное ему выражение будут иметь вид:
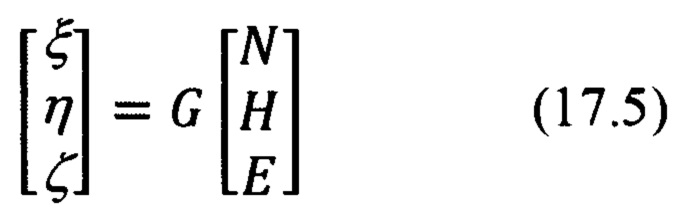
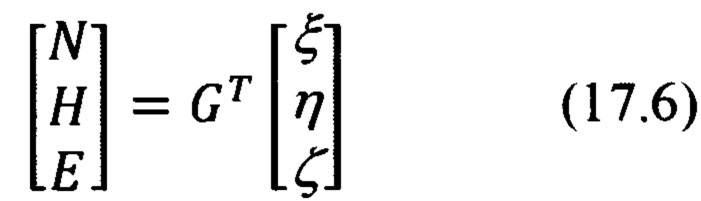
где матрица G и транспонированная ей матрица GT, в соответствии с фиг. 7, равны:
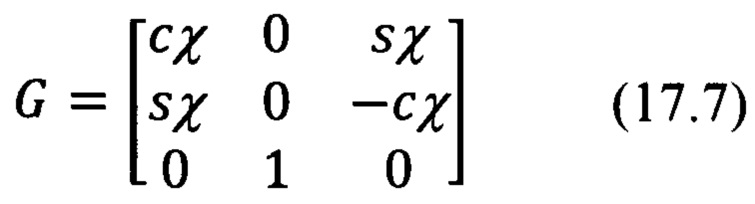
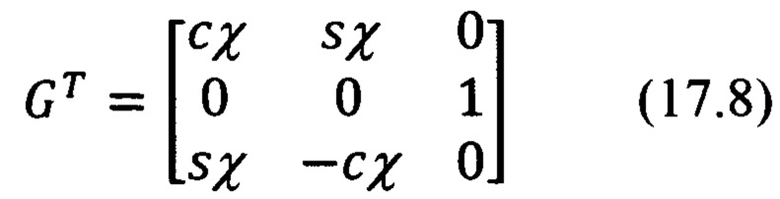
В процессе углового сопровождения цели возникнет необходимость постоянного вычисления текущей ориентации линии визирования ОПС относительно осей ГСТ ONHE на основе текущих измерений обзорно-прицельной системы (ϕy, ϕz) и углов ориентации объекта ψи, υ, γ.
Необходимые для этого векторно-матричные выражения можно получить,  подставляя выражение (5) в выражение (9) и выражение (10) в выражение (6).
подставляя выражение (5) в выражение (9) и выражение (10) в выражение (6).
Приведем их:
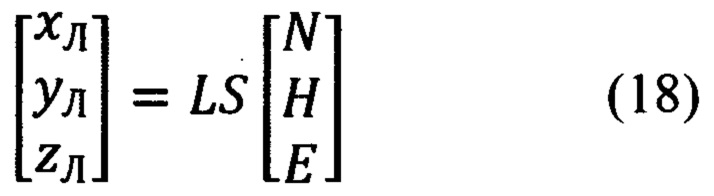
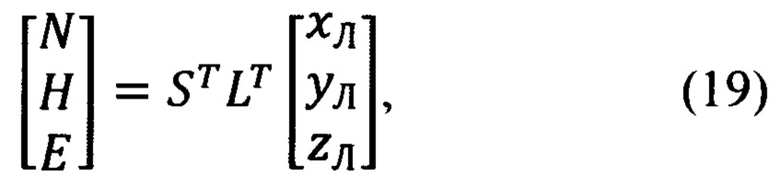
В соответствии с векторно-матричными выражениями (13), (18) и видом матрицы 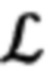 (15), ориентация ЛВ ОПС относительно ГСТ ONHE, будет определяться элементами первой строки матрицы
(15), ориентация ЛВ ОПС относительно ГСТ ONHE, будет определяться элементами первой строки матрицы 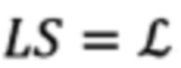 , а именно элементами
, а именно элементами 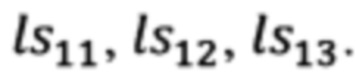 .
.
Выражения для них после нахождения произведения матриц LS, могут быть представлены в следующем виде:
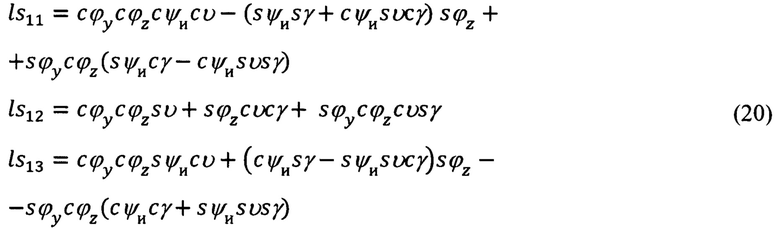
Подставляя в (17) полученные выше выражения для элементов 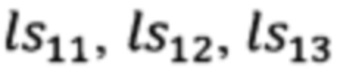 (20) получим искомые выражения для расчета углов текущего азимута А и угла места θ направления на сопровождаемую цель (ориентир).
(20) получим искомые выражения для расчета углов текущего азимута А и угла места θ направления на сопровождаемую цель (ориентир).
Расчет текущих значений элементов 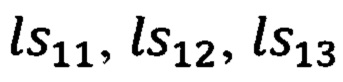 матрицы
матрицы 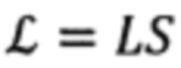 и углов А и θ визирования цели при реализации кинематического метода определения дальности (КМОД) до подвижной наземной цели должен осуществляться непрерывно с некоторой заранее установленной дискретностью.
и углов А и θ визирования цели при реализации кинематического метода определения дальности (КМОД) до подвижной наземной цели должен осуществляться непрерывно с некоторой заранее установленной дискретностью.
Для раскрытия физической сути КМОДа, а также с целью предания представленным выше материалам практической напрвленности, приведем один из возможных вариантов полета объекта относительно цели (ориентира), наклонная дальность до которой подлежит определению (фиг. 6).
В приведенном на фиг.6 варианте представлен полет объекта непосредственно на сопровождаемую цель (ориентир). Возможен и другой вариант полета, когда сопровождаемая цель (ориентир) находятся справа или слева от направления полета - это вариант облета цели без сближения с ней.
Для информационного обеспечения рассматриваемого метода определения дальности на пути следования объекта с заранее установленной дискретностью, принимаемой, в зависимости от скорости полета, равной 0,1-0,5 сек, производят измерение следующих параметров:
- географических координат текущего местоположения объекта ϕi, λi, hi, где hi - бароинерциальная высота;
- текущих углов ϕyi, ϕzi визирования цели (ориентира) совместно с текущими углами пространственной ориентации объекта ψиi, υi, γi.
В каждый текущий момент времени совместно обрабатывают текущий, i-ый, и предыдущий, (i-1)-ый массивы приведенной выше информации.
При этом реализуют следующие математические процедуры:
1. Расчет линейной дальности ΔDi-1 i между двумя отсчетными точками (i-1)-ой и i-ой и углов Ai-1,i, θi-1,i ее ориентации относительно ГСТ ONHE, соответствующего местоположению (i-1) точки.
2. Расчет значений азимута Ai-1 и угла места θi-1 вектора 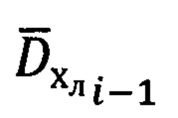 направления на цель (ориентир) в (i-1) момент времени.
направления на цель (ориентир) в (i-1) момент времени.
3. Расчет значений азимута Ai и угла места θi вектора 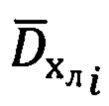 направления на цель (ориентир) в i-ый момент времени.
направления на цель (ориентир) в i-ый момент времени.
4. Расчет пространственных углов βi-1 и βi между векторами 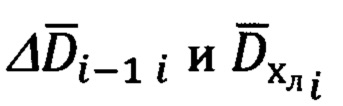 соответственно.
соответственно.
5. Решение пространственного треугольника дальностей и определение текущей дальности Di до цели (ориентира).
Приведем описание перечисленных выше математических процедур.
1. При расчете линейной дальности ΔDi-1 i между двумя отсчетными точками, (i-1)-ой и i-ой, целесообразно использовать аппарат линейных гринвичских координат, в соответствии с которым в каждой точке текущего местоположения объекта с координатами ϕ, λ, h может быть поставлена в соответствие тройка X', Y', Z' линейных гринвичских координат.
Зная географические координаты двух соседних отсчетных точек, (i-1)-ой и i-ой, определяют их гринвичские координаты, которые физически представляют из себя проекции точек с координатами ϕi-1, λi-1, hi-1 и ϕi, λi, hi на оси гринвичской системы координат OX'Y'Z'.
Для текущей, i-ой точки выражения для гринвичских координат X', Y', Z' будут иметь вид:
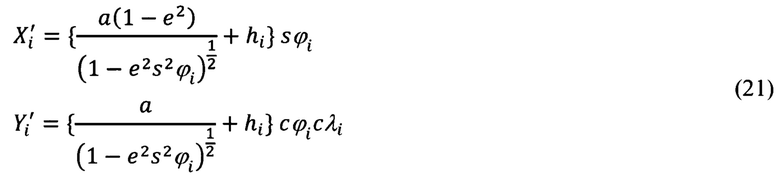
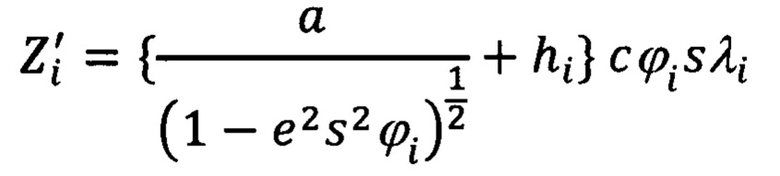
Аналогичные выражения для предыдущей, (i-1)-ой точки запишем в следующем виде:
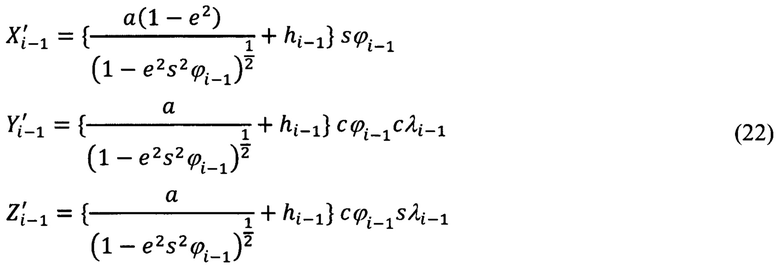
В приведенных выражениях (21), (22) под а следует понимать большую ось земного эллипсоида, а под е2 - квадрат первого эксцентриситета:

где b - малая ось земного эллипсоида вращения.
Приведенные параметры для эллипсоида Ф.Н. Красовского принимают равными:
a=6378245 м
a=6356863 м
е2=0,0066934
Очевидно, что разности между текущими (21) и предшествующими (22) компонентами гринвичских координат:

являются составляющими вектора дальности 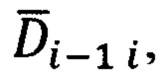 направленного от точки i-1 к точке i.
направленного от точки i-1 к точке i.
Соответственно, обратные им (24) компоненты:

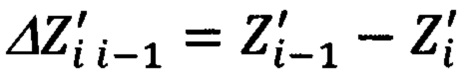
это составляющие вектора дальности 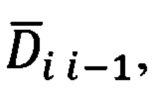 направленного от точки i к точке (i-1).
направленного от точки i к точке (i-1).
Приведем составляющие (24) прямого вектора дальности  к осям ГСТ ONHE соответствующей точке (i-1). Поэтому указанная операция должна быть выполнена с использованием географических координат ϕi-1, λi-1, соответствующих точке «ОТ» - от которой исходит вектор
к осям ГСТ ONHE соответствующей точке (i-1). Поэтому указанная операция должна быть выполнена с использованием географических координат ϕi-1, λi-1, соответствующих точке «ОТ» - от которой исходит вектор 
В соответствии с векторно-матричным выражением (1) и видом матрицы G (3), выражения для составляющих ΔNi-1 i, ΔHi-1 i, ΔEi-1 i вектора 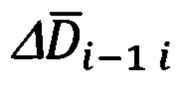 в проекциях на оси ГСТ ONHE, соответствующего точке с координатами ϕi-1, λi-1, будут иметь следующий вид:
в проекциях на оси ГСТ ONHE, соответствующего точке с координатами ϕi-1, λi-1, будут иметь следующий вид:
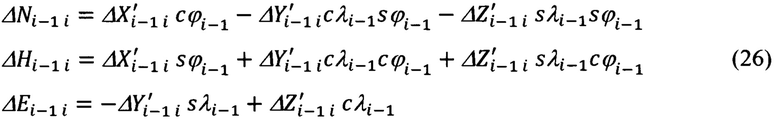
Модуль ΔDi-1 i вектора дальности 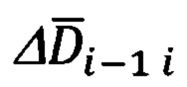 может быть определен с использованием любых приведенных выше составляющих (24), (25, (26). Целесообразно определять их с использованием компонент (26):
может быть определен с использованием любых приведенных выше составляющих (24), (25, (26). Целесообразно определять их с использованием компонент (26):
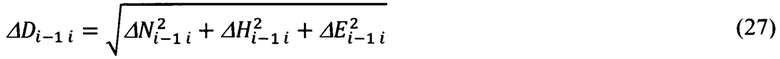
Ориентация вектора  относительно осей ГСТ ONHE будет определяться азимутом Ai-1 i и углом места θi-1 i.
относительно осей ГСТ ONHE будет определяться азимутом Ai-1 i и углом места θi-1 i.
В соответствии с принятым направлением отсчета указанных углов (фиг. 5), можно показать, что выражения для их расчета будут иметь следующий вид:
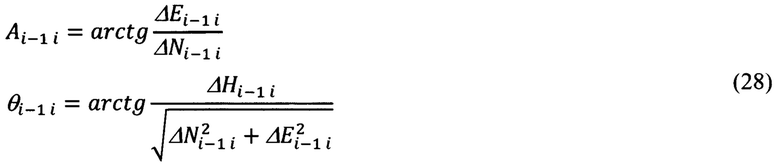
После того, как определена ориентация базового вектора  пространственного треугольника дальностей (фиг. 7), приведем достаточно полезное векторно-матричное выражение, которое будет использовано ниже, при решении упомянутого выше треугольника дальностей.
пространственного треугольника дальностей (фиг. 7), приведем достаточно полезное векторно-матричное выражение, которое будет использовано ниже, при решении упомянутого выше треугольника дальностей.
Для этого введем в рассмотрение некоторую систему координат 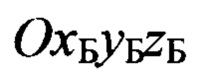 (символ «Б» означает «базовый») с осью ОхБ которой связан вектор
(символ «Б» означает «базовый») с осью ОхБ которой связан вектор 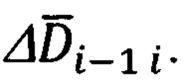 Тогда, очевидно, векторно-матричное выражение, связывающее компоненты вектора
Тогда, очевидно, векторно-матричное выражение, связывающее компоненты вектора 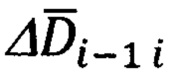 в проекциях на оси базовой системы координат (БСК) и ГСТ ONHE, будут иметь следующий вид:
в проекциях на оси базовой системы координат (БСК) и ГСТ ONHE, будут иметь следующий вид:

где матрица 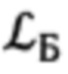 будет иметь вид, аналогичный матрице (15), но в функции углов Ai-1 i, θi-1 i (28) при γЛ=0. Значение γЛ принято равным нулю, поскольку связь между ΔDi-1 i и его компонентами ΔDN, ΔDH, ΔDE однозначно будет определяться поворотами на угол азимута Ai-1 i и угол места θi-1 i (см. фиг. 5).
будет иметь вид, аналогичный матрице (15), но в функции углов Ai-1 i, θi-1 i (28) при γЛ=0. Значение γЛ принято равным нулю, поскольку связь между ΔDi-1 i и его компонентами ΔDN, ΔDH, ΔDE однозначно будет определяться поворотами на угол азимута Ai-1 i и угол места θi-1 i (см. фиг. 5).
Следовательно, матрица  будет иметь вид:
будет иметь вид:
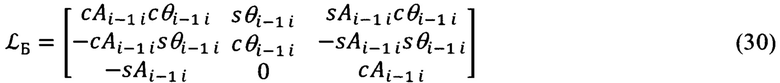
2. Для определения угловой ориентации вектора дальности связанного с направлением на цель (ориентир) в (i-1)-ой точке воспользуемся приведенными выше векторно-матричными выражениями (13), (18), видом матрицы
связанного с направлением на цель (ориентир) в (i-1)-ой точке воспользуемся приведенными выше векторно-матричными выражениями (13), (18), видом матрицы  (15), а также выражениями (20) для элементов
(15), а также выражениями (20) для элементов 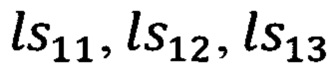 первой строки матрицы
первой строки матрицы 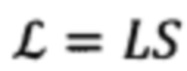 и выражениями для углов A и θ (17).
и выражениями для углов A и θ (17).
По произведенным в (i-1)-ой точке измерениям углов ϕy i-1, ϕz i-1 визирования цели (ориентира) и измеренным углам истинного курса ψи i-1 крена γi-1 и тангажа υi-1 объекта в соответствии с (20), рассчитывают текущие значения элементов первой строки матрицы 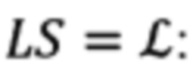
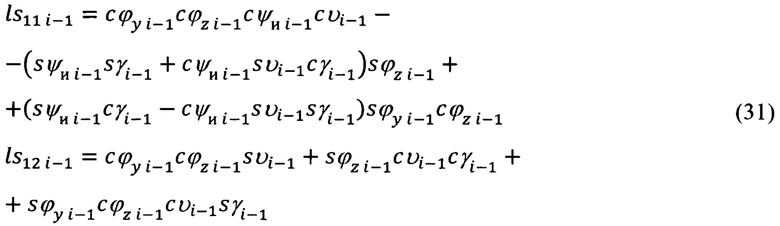
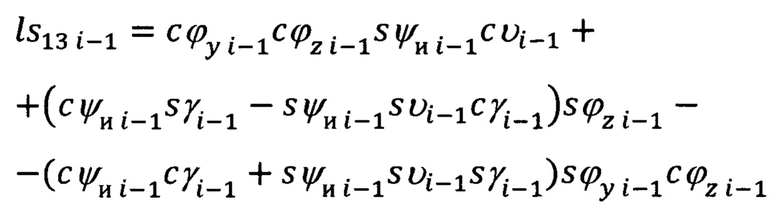
Расчет азимута Ai-1 и угла места θi-1, определяющих ориентацию вектора 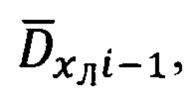 совпадающего с направлением на цель (ориентир) в (i-1)-ой отсчетной точке, осуществляют в соответствии с выражениями (17):
совпадающего с направлением на цель (ориентир) в (i-1)-ой отсчетной точке, осуществляют в соответствии с выражениями (17):
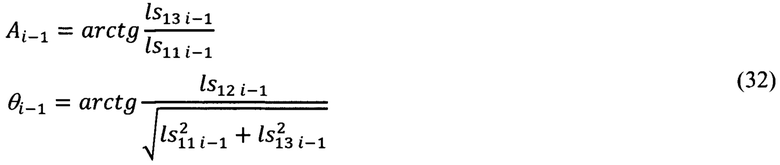
3. Расчет углов ориентации вектора 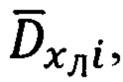 совпадающего с направлением на цель (ориентир) в i-ой точке, осуществляют по аналогии с п. 2.
совпадающего с направлением на цель (ориентир) в i-ой точке, осуществляют по аналогии с п. 2.
По произведенным измерениям углов ϕy i, ϕz i визирования цели (ориентира) и измеренным углам ψи i, υi, γi ориентации объекта рассчитывают текущие значения элементов 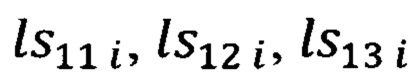 первой строки матрицы
первой строки матрицы 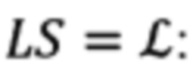
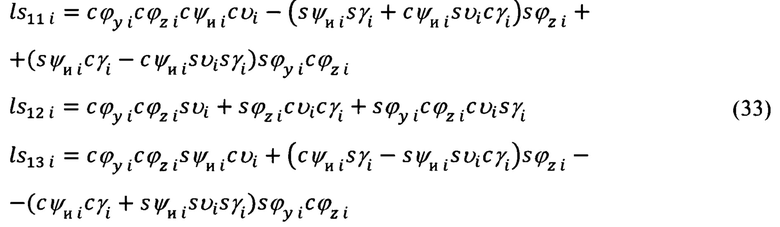
Расчет азимута Ai и угла места θi осуществляют в соответствии с выражениями (17):

4. Для расчета пространственных углов βi-1 и βi между вектором 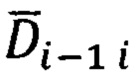 и векторами
и векторами 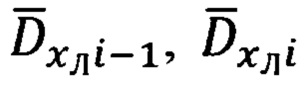 соответственно предварительно получим необходимые для этого векторно-матричные выражения, связывающие компоненты векторов
соответственно предварительно получим необходимые для этого векторно-матричные выражения, связывающие компоненты векторов 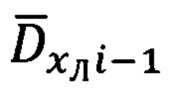 и
и 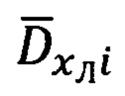 в проекциях на оси лучевой для указанных векторов системы координат и ГСТ ONHE.
в проекциях на оси лучевой для указанных векторов системы координат и ГСТ ONHE.
Для этого введем в рассмотрение две ЛСК OxЛi-1yЛi-1zЛi-1 и ОхЛiyЛizЛi, с осями OxЛi-1 и ОхЛi которых связаны векторы 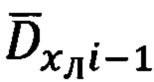 и
и 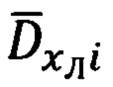 соответственно.
соответственно.
По аналогии с (29), для компонент рассматриваемых векторов в проекциях на оси ЛСК OxЛi-1yЛi-1zЛi-1 и ОхЛiyЛizЛi и ГСТ ONHE будут правомочны следующие векторно-матричные выражения:


Матрицы 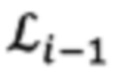 и
и 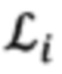 имеют вид, аналогичный матрице
имеют вид, аналогичный матрице 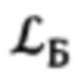 (30), но с использованием углов (32) и (34).
(30), но с использованием углов (32) и (34).
Запишем их:
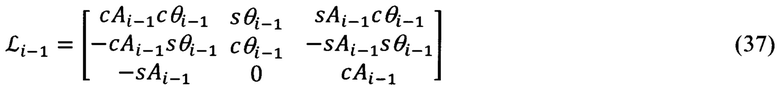

Умножая слева векторно-матричное выражение (35) на  а (36) - на
а (36) - на  получим следующие полезные выражения, которые являются обратными приведенным выше выражениям (35) и (36):
получим следующие полезные выражения, которые являются обратными приведенным выше выражениям (35) и (36):


Подставляя (39) и (40) в полученное ранее векторно-матричное выражение (29), получим следующие искомые выражения:


Входящие в (41), (42) матрицы  и
и 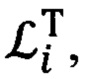 в соответствии с (37) и (38), равны:
в соответствии с (37) и (38), равны:
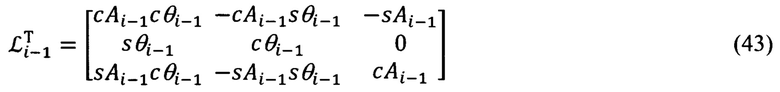

Из выражений (41) и (42) следует, что косинусы искомых углов, а именно, cβi-1 и cβi определяются элементами первой строки и первого столбца матриц 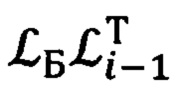 и
и 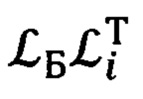 соответственно.
соответственно.
В соответствии с видом матриц 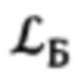 (30) и
(30) и  (43),
(43), 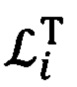 (44) искомые направляющие косинусы равны:
(44) искомые направляющие косинусы равны:
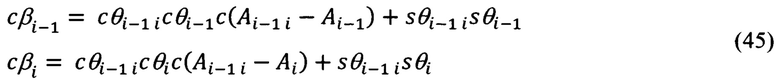
5. Решение пространственного треугольника скоростей i(i-1)Ц(ОР) (фиг. 7) и определение текущей, i-ой дальности Di до цели (ориентира).
Исходными данными для решения пространственного треугольника скоростей являются:
- базовая дальность ΔDi-1 i между двумя соседними отсчетными точками (27);
- косинусы cβi-1, cβi углов между вектором 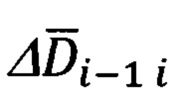 и векторами
и векторами 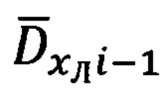 и
и 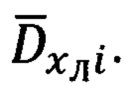
При известных cβi-1 и cβi достаточно просто определяются все три угла рассматриваемого треугольника.
Действительно, сами углы βi-1 и βi, учитывая, что они для рассматриваемого нами случая полета на цель (ориентир), являются острыми (<90°), могут быть рассчитаны в соответствии с выражениями:

Тогда внутренний угол при вершине Ц (ОР) будет равен:

а внутренний угол при вершине i: 180 - βi
Искомую текущую дальность Di до цели (ориентира), в соответствии с теоремой синусов, рассчитывают согласно выражению:

Далее приведенную в пп. 1-5 расчетную процедуру повторяют. Для этого, после каждого расчета текущей дальности Di (48) i-ая точка, а также весь измеренный для нее массив, принимается за (i-1)-ую, а точку, на которую осуществляется полет, принимают за i-ую и после измерения i-ого, текущего массива информации, повторяют описанную выше процедуру расчета. И так … до следующего этапа привязки. Такова физическая суть и математическое исполнение кинематического метода определения дальности (КМОД) до неподвижной наземной цели.
Преимущества указанного способа определения дальности по сравнению с традиционным угломестным неоспоримы, особенно, при его применении в горах и сильно пересеченной местности.
Применительно к предлагаемому способу привязки к подвижной наземной цели, приведенную выше процедуру КМОД используют для определения осредненного значения высоты 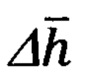 над уровнем моря того участка земной поверхности, по которой через 5-10 секунд после ее определения будет двигаться цель.
над уровнем моря того участка земной поверхности, по которой через 5-10 секунд после ее определения будет двигаться цель.
Физически это должно быть реализовано следующим образом.
Перед намеченной для атаки подвижной наземной целью, в пределах 60-75 м по направлению ее движения, выбирают ориентир, в виде характерной площадки рельефа земной поверхности (РЗП), наводят на него неподвижное прицельное перекрестие (НПП) ОПС и удерживают на нем в течении 2,5-3,0 секунд, реализуя при этом описанную выше кинематическую процедуру определения текущей наклонной дальности Di.
Дополнительно, в каждый i-ый момент времени определяют текущее значение косинуса угла между местной географической вертикалью ОН и направлением 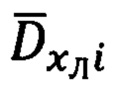 на выбранный ориентир (фиг. 6). Косинус
на выбранный ориентир (фиг. 6). Косинус 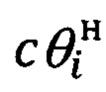 указанного угла используется при реализации угломестной процедуры определения дальности и равен:
указанного угла используется при реализации угломестной процедуры определения дальности и равен:
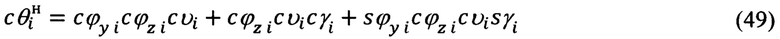
По известным текущим значениям Di (48) и 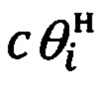 (49) определяют геометрическую высоту объекта относительно уровня выбранного ориентира, иначе, относительную высоту объекта:
(49) определяют геометрическую высоту объекта относительно уровня выбранного ориентира, иначе, относительную высоту объекта:

Сравнивая ее с текущим значением абсолютной бароинерциальной высоты 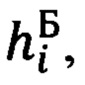 сформированной в результате оптимального комплексирования вертикального канала ИНС и баровысотомера, получают текущее значение высоты Δhi ориентира над уровнем моря:
сформированной в результате оптимального комплексирования вертикального канала ИНС и баровысотомера, получают текущее значение высоты Δhi ориентира над уровнем моря:

После применения к массиву Δhi рекуррентной процедуры нахождения среднего на упомянутом выше временном интервале 2,5-3,0 секунд:

получают необходимое для реализации модифицированной угломестной процедуры расчета дальности среднее значение высоты цели над уровнем моря:

где hц - некоторая константа, определяемая высотой цели, типа танк БМП, БТР, … может быть принята равной hц=1,5 м.
Далее, после перенацеливания ОПС на реальную цель и перехода к режиму ее углового сопровождения, реализуют полноценную оптимальную процедуру режима привязки к ней.
При этом расчет текущих значений дальности до цели ведут с частотой решения рассматриваемой задачи, которая составляет не менее 10 Гц.
Их расчет осуществляют следующим образом.
Зная текущее значение бароинерциальной высоты 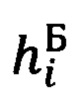 и высоты цели над уровнем моря
и высоты цели над уровнем моря 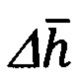 (53), определяют текущую высоту объекта относительно цели:
(53), определяют текущую высоту объекта относительно цели:

По известным текущим значениям относительной высоты hi (54) объекта и косинуса 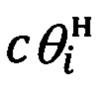 949) угла между местной географической вертикалью и направлением на цель определяют текущее значение наклонной дальности до подвижной наземной цели:
949) угла между местной географической вертикалью и направлением на цель определяют текущее значение наклонной дальности до подвижной наземной цели:

Наличие текущих значений наклонной дальности Di (55), углов ϕу, ϕz визирования цели и традиционной для объекта боевого назначения навигационной и пилотажной информации позволяет реализовать полноценную оптимальную процедуру привязки к подвижной, в общем случае, маневрирующей наземной цели.
А то обстоятельство, что при осуществлении предлагаемого способа нет никакой необходимости в реализации процедуры прогноза параметров относительного движения цели, позволяет ожидать от его использования высокой эффективности боевого применения всей номенклатуры неуправляемых АСП. При этом, под эффективностью следует понимать, в первую очередь, точность.
При разработке оптимальной процедуры привязки к подвижной цели необходимо определиться с системой координат, в проекциях на оси которой представляют дифференциальные уравнения относительного движения цели, поскольку от ее выбора существенным образом зависит как структура получаемых при этом дифференциальных уравнений, так и синтезируемая процедура оценивания и обслуживающие ее вспомогательные алгоритмы.
Действительно, на основании векторного дифференциального уравнения относительного движения цели:

где 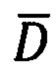 - вектор дальности между объектом и целью;
- вектор дальности между объектом и целью; 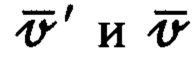 - векторы абсолютной линейной скорости цели и объекта соответственно;
- векторы абсолютной линейной скорости цели и объекта соответственно; 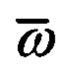 - вектор абсолютной скорости подвижной системы координат;
- вектор абсолютной скорости подвижной системы координат; 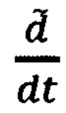 - символ локальной производной,
- символ локальной производной,
можно показать, что его скалярное представление в проекциях на оси некотрой подвижной системы координат Oxyz имеет вид:

Приведенной системой дифференциальных уравнений описывается относительное движение объекта и цели в самом общем случае.
Указанную структуру имеют дифференциальные уравнения в проекциях на оси связанной с объектом системы координат ССК Oxyz, географического сопровождающего трехгранника ГСТ ONHE и опорного трехгранника гироплатформы ОТГП Oξηζ ИНС.
Из этого ряда выпадают дифференциальные уравнения в проекциях на оси ЛСК OxЛyЛzЛ, ГСК OX'Y'Z' и ИСК OXYZ.
В частности, в проекциях на оси ГСК OX'Y'Z', учитывая, что составляющие ее абсолютной угловой скорости равны ωX'=u, ωY'=ωZ'=0, где u - угловая скорость суточно-годового вращения Земли (фиг. 1), указанные уравнения имеют вид:

Особое место в этом ряду занимает случай, когда в качестве подвижной принимается инерциальная система отсчета ИСК OXYZ (фиг. 1).
Ее принципиальное отличие от всех предыдущих является то, что в рассматриваемом случае абсолютная угловая скорость подвижной (инерциальной) системы координат относительно неподвижной (инерциальной) системы координат будет равна нулю, т.е. ωX=ωY=ωZ=0, что приводит к закономерному упрощению представленной выше системы дифференциальных уравнений (57), которая в рассматриваемом случае примет вид:

Впервые на указанное свойство ИСК OXYZ применительно к модели относительного движения цели обратили внимание в [1] (стр. 49, 5-9 строки сверху), но по каким-то причинам не довели его до инженерного применения.
Из приведенной системы дифференциальных уравнений (59) следует, что для рассматриваемого случая взаимосвязанная система уравнений (57) трансформируется в систему трех независимо интегрируемых уравнений первого порядка, что не только упрощает процедуру их численного интегрирования, но и позволяет на их основе синтезировать простые поканально декомпозированные, достаточно эффективные и математически корректные процедуры оптимального оценивания.
Учитывая, что ряд особенностей, связанных с выбором подвижной системы координат ПСК и имеющих принципиальное значение для синтеза и программной реализации оптимальных процедур оценивания параметров движения цели, исследован ранее и в виде законченных инженерных решений направлен на экспертизу в соответствующую федеральную службу, представляется целесообразным в предлагаемом изобретении не раскрывать физическую суть ИСК, а рассматривать процедуру оценивания для общего случая математического представления уравнений относительного движения объекта и подвижной наземной цели.
При этом синтез структуры оптимального фильтра-идентификатора будем проводить в соответствии с традиционной линейной процедурой оптимальной фильтрации Калмана.
Сводка ее основных соотношений приведена в Э. Сейдж, Дж. Меле «Теория оценивания и ее применение в связи и управлении», «Связь», Москва, 1976 [3] (стр. 269).
Приведем ее:
1. Исходная модель сообщения:

2. Модель наблюдения:

3. Априорные данные, используемые при синтезе:
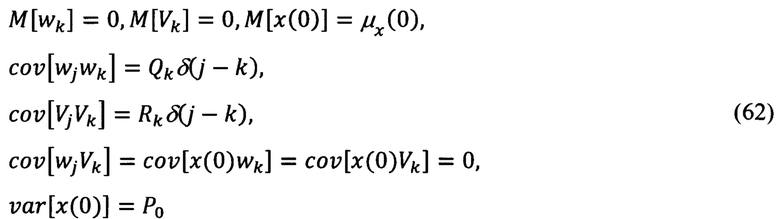
4. Структура оптимального фильтра:
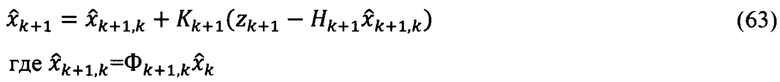
5. Вычисление матрицы априорных ошибок оценивания:
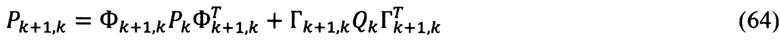
6. Вычисление оптимальных коэффициентов усиления:
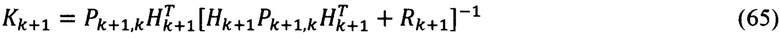
7. Вычисление матрицы апостериорных ошибок оценивания:

В приведенных выше соотношениях приняты следующие условные обозначения:
xk - вектор параметров состояния системы;
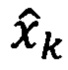 - вектор оптимальных апостериорных оценок параметров состояния;
- вектор оптимальных апостериорных оценок параметров состояния;
wk - вектор случайных возмущений модели сообщения;
Vk - вектор случайных шумов измерения;
Фk+1,k - фундаментальная матрица системы (модели сообщения);
Гk+1,k - матрица передачи случайных возмущений системы;
Hk - матрица измерения;
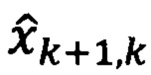 - вектор априорных оценок параметров состояния системы;
- вектор априорных оценок параметров состояния системы;
Pk+1,k - априорная корреляционная матрица ошибок оценивания;
Pk+1 - апостериорная корреляционная матрица ошибок оценивания;
Qk - корреляционная матрица случайных шумов системы;
Rk - корреляционная матрица случайных шумов измерения;
zk - вектор сигналов измерения;
Kk+1 - матрица оптимальных коэффициентов усиления.
Учитывая, что предлагаемый способ привязки к ПНЦ предполагает использование высокоточной навигационной и пилотажной информации представляется целесообразным все описанные выше математические процедуры осуществлять на основе параллельно реализованной процедуры оптимального инерциально-доплеровкого оценивания и коррекции счисляемой и измеряемой ИНС информации.
Кроме того, корректный синтез высокоточного бароинерциального канала формирования абсолютной высоты и вертикальной скорости также невозможен без использования оцениваемых в процессе инерциально-доплеровской коррекции параметров, таких как 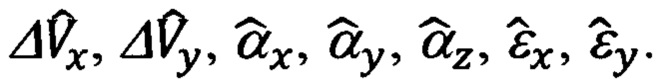
Поэтому, учитывая, что инженерная разработка бароинерциального канала по своей физической сути и математическому содержанию может вполне стать предметом отдельного рассмотрения, представляется целесообразным описание предлагаемого изобретения завершить подробным рассмотрением инерциально-доплеровской процедуры оптимального оценивания и коррекции.
При этом, при синтезе комплексной инерциально-доплеровской системы необходимо использовать следующие новые инженерно-целесообразные и достаточно эффективные приемы и математические процедуры.
Один из основных приемов синтеза эффективной по точности и быстродействию оптимальной процедуры инерциально-доплеровского оценивания и коррекции продиктован необходимостью алгоритмического учета относительного размещения задействованных в этом режиме информационных систем ИНС и ДИСС.
Неучет координат размещения ИНС относительно ДИСС при выполнении объектом высокодинамичных маневров, типа «змейки», координированного или боевого разворотов приводит к появлению в сигналах измерения математически неописанных составляющих кинематической скорости, которые, будучи алгоритмически неучтенными, вместо методически обоснованного и ожидаемого оценивания всех параметров состояния, включая и слабонаблюдаемые, приводит к совершенно обратному результату, а именно, к расходимости процедуры оценивания.
Для реализации алгоритмического учета относительного размещения ИНС и ДИСС достаточно расширить традиционную для ИНС модель ошибок, включив в нее систему из трех дифференциальных уравнений первого порядка, описывающих характер изменения относительных координат Δξ, Δη, Δζ размещения на объекте указанных информационных систем в проекциях на оси опорного трехгранника гироплатформы ИНС.
Из простых физических соображений можно показать, что указанные уравнения будут иметь следующий вид:

где 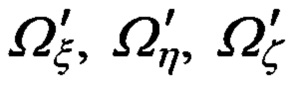 - составляющие угловой скорости вращения объекта относительно опорного трехгранника гироплатформы ИНС Oξηζ;
- составляющие угловой скорости вращения объекта относительно опорного трехгранника гироплатформы ИНС Oξηζ; 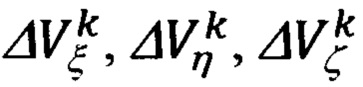 - кинематические составляющие скорости перемещения ИНС относительно ДИСС.
- кинематические составляющие скорости перемещения ИНС относительно ДИСС.
Включение приведенных выше дифференциальных уравнений (66.1) в проекциях на оси ОТГП ИНС Oξηζ в состав традиционной для инерциально-допплеровского режима коррекции модели ошибок ИНС позволяет получить ее расширенную модель, которая описывает не только традиционные для ИНС параметры и их связи, но и те кинематические составляющие сигналов измерения, которые ранее не учитывались.
Расширение модели ошибок ИНС позволяет устранить основную причину алгоритмической несостоятельности известных алгоритмов коррекции, заключающуюся в некорректном математическом описании исходной системы, и обеспечить тем самым гарантированную наблюдаемость и устойчивую сходимость всех и, в первую очередь, слабонаблюдаемых параметров состояния ИНС, таких, как угол αz азимутального ухода гироплатформы и дрейф εу продольного канала ИНС.
Более того, только в этом случае достаточно просто и эффективно может быть обеспечен алгоритмический учет и устранение всех нежелательных последствий, к которым приводят математически не описанные кинематические составляющие скорости, имеющие место при маневре объекта и обусловленные геометрией относительного размещения задействованных в рассматриваемом режиме информационных систем.
Важное практическое значение имеет и математически строгая, структурно замкнутая, унифицированная процедура алгоритмического учета текущих ошибок счисления/ измерения навигационной информации и ее эффективной коррекции по результатам оптимального оценивания или прогноза.
Использование указанной процедуры в режиме инерциально-доплеровского оценивания и коррекции осуществляется всякий раз, при формировании сигналов измерения оптимального фильтра-идентификатора.
При их формировании необходимо знать математическое описание как выходных сигналов ИНС, так и аналогичных сигналов, сформированных по измерениям ДИСС с использованием при этом дополнительных измерений ряда навигационных и пилотажных параметров с ИНС.
Следует отметить, что при разработке (выводе) модели ошибок ИНС важное значение имеет форма аналитического представления ее выходных сигналов по скорости, которая не только определяет вид матрицы наблюдения (измерения), но от нее существенным образом зависит и сама модель ошибок ИНС.
Не приводя и не анализируя возможные формы указанного представления, отметим, что наиболее распространенным, проработанным и приемлемым для решения рассматриваемой задачи является представление вида:

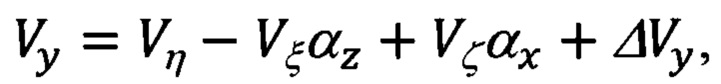
где Vξ, Vη, Vζ - составляющие абсолютной линейной скорости объекта в проекциях на оси ОТГП ИНС; αх, αу, αz - углы рассогласования реального и опорного трехгранников ГП; ΔVx, ΔVy - погрешности измерения/расчета горизонтальных составляющих абсолютной скорости, входящие, наряду с малыми углами αх, αу, αz рассогласования, в перечень параметров состояния ИНС.
Составляющие (66.2) по своей физической сути являются чисто инерциальными и в явном виде не включают в себя компоненты скорости кинематического характера (66.1).
Кинематические составляющие скорости будут представлены при сравнении составляющих скорости (66.2) и аналогичных составляющих, сформированных по текущим измерениям ДИСС.
Прежде, чем переходить к рассмотрению этих вопросов, целесообразно отметить, что при этом, впервые в практике разработки подобных алгоритмов, будут использованы известные кинематические соотношения, связывающие погрешности Δϕ, Δλ, Δχ автономного инерциального счисления основных навигационных параметров, а именно, географической широты ϕ, долготы λ и угла χ азимутальной ориентации опорного трехгранника гироплатформы ИНС, и погрешности Δυ, Δγ, Δψг измерения основной тройки пилотажных углов тангажа υ, крена γ и гироскопического курса ψг с малыми ошибками αх, αу выдерживания вертикали ИНС углом αz азимутального ухода ее гироплатформы ГП.
Указанные соотношения имеют следующий вид:


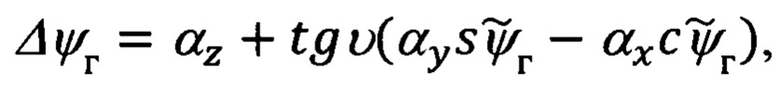
При формировании горизонтальных составляющих абсолютной линейной скорости объекта по измерениям ДИСС с использованием счисленных ИНС текущих значений географической широты и угла азимутальной ориентации опорного трехгранника ее гироплатформы должны быть выполнены следующие математические операции:
- приведение измеренных ДИСС составляющих 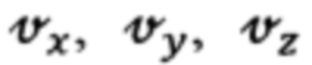 путевой скорости в проекциях на оси связанной с объектом системы координат к осям опорного трехгранника гироплатформы ИНС;
путевой скорости в проекциях на оси связанной с объектом системы координат к осям опорного трехгранника гироплатформы ИНС;
- расчет горизонтальных составляющих 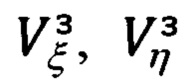 абсолютной линейной скорости, обусловленной суточно-годовым вращением Земли.
абсолютной линейной скорости, обусловленной суточно-годовым вращением Земли.
Первая операция достаточно просто может быть реализована в соответствии с векторно-матричным выражением (17.1).
Итак, в соответствии с (17.1) и видом матрицы 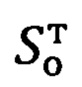 (17.2), выражения для расчета составляющих
(17.2), выражения для расчета составляющих 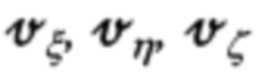 будут иметь следующий вид:
будут иметь следующий вид:
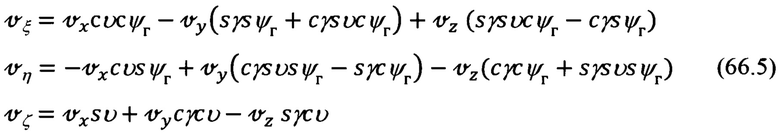
Приведенные выражения для расчета составляющих 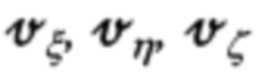 путевой скорости объекта по измерениям ее компонент
путевой скорости объекта по измерениям ее компонент 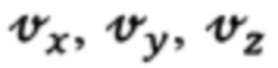 в проекциях на оси ССК Oxyz предполагают использование точных углов ψг, υ, γ эволюции объекта.
в проекциях на оси ССК Oxyz предполагают использование точных углов ψг, υ, γ эволюции объекта.
Не располагая указанными углами, подставим в выражения (66.5) вместо ψг, υ, γ их значения, определяемые соотношениями:

в которых 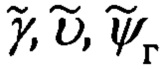 - измеренные значения углов эволюции объекта; Δγ, Δυ, Δψг - погрешности их измерения.
- измеренные значения углов эволюции объекта; Δγ, Δυ, Δψг - погрешности их измерения.
Можно показать, что подстановка (66.6) в выражения для 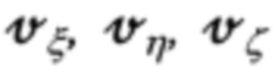 (66.5), приведет к их следующему представлению:
(66.5), приведет к их следующему представлению:

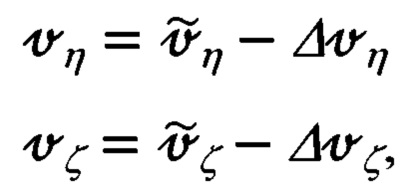
где приняты следующие обозначения для ошибочно рассчитанных составляющих 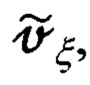
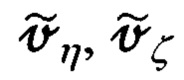 путевой скорости и ошибок
путевой скорости и ошибок 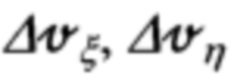 их расчета:
их расчета:
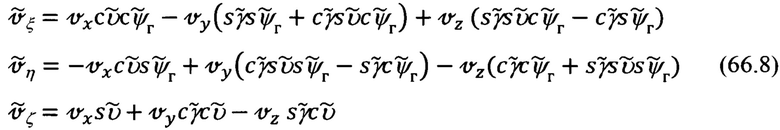
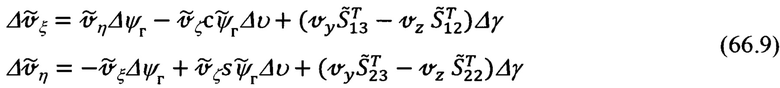
Подставляя в (66.9) вместо ψг, Δυ, Δγ значения в функции малых углов αх, αy, αz рассогласования реального и опорного трехгранников ГП ИНС (66.4), получим их следующее представление:

в котором приняты следующие обозначения:
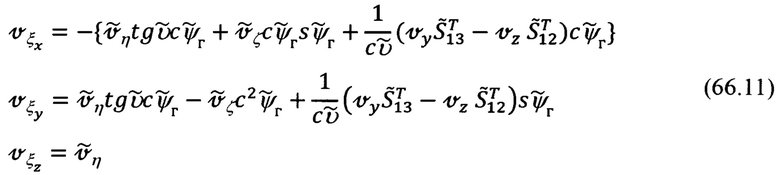
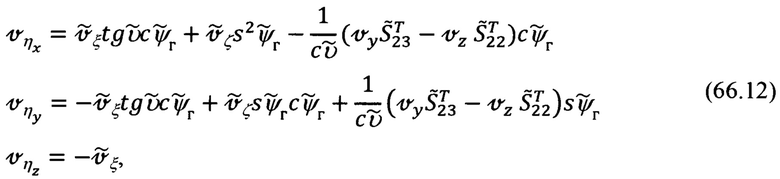
В приведенных выражениях (66.9), (66.11) под 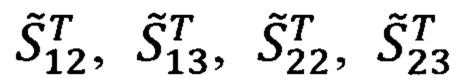 следует понимать соответствующие элементы матрицы
следует понимать соответствующие элементы матрицы 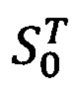 (17.2), но в функции измеренных углов эволюции объекта
(17.2), но в функции измеренных углов эволюции объекта 
Все последующие операции будут исполнены на основе использования инерциальной информации и кинематических соотношений (66.3), связывающих ошибки счисления основных навигационных параметров Δϕ, Δλ, Δχ с малыми углами αх, αу, αz рассогласования реального и опорного трехгранников ГП ИНС.
Учитывая, что эти операции приводятся впервые, представим их без сокращений.
Запишем выражение для идеальной восточной составляющей  линейной скорости, обусловленной суточным вращением Земли:
линейной скорости, обусловленной суточным вращением Земли:

где ϕ - идеальное значение географической широты.
Учитывая, что идеальная широта, в общем случае, не известна, представим ее в виде:

где: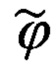 - счисленное значение широты, а Δϕ - погрешность ее счисления.
- счисленное значение широты, а Δϕ - погрешность ее счисления.
Подставляя (66.14) в (66.13), с учетом соотношения для Δϕ (66.3) получим следующее выражение для 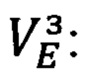
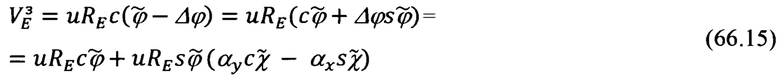
Входящий в (66.15) главный радиус RE земного эллипсоида вращения, определяемый выражением вида:

запишем в следующем, более целесообразном для дальнейшего рассмотрения виде:

В выражениях (66.16) и (66.17) под е2 следует понимать квадрат первого эксцентриситета эллипсоида вращения Земли, который для измерений, произведенных Ф.Н. Красовским, равен е2=0,0066934; h - бароинерциальная высота объекта.
Подставим в (66.17) соотношение (66.14). В результате, с точностью до величин первого порядка малости относительно Δϕ, получим:

где 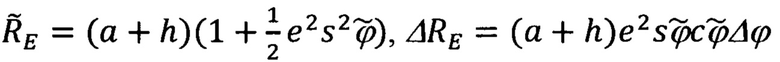
Подставляя (66.18) в выражение для 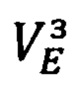 (66.15) получим следующее выражение для восточной составляющей линейной скорости, обусловленной суточно-годовым вращением Земли:
(66.15) получим следующее выражение для восточной составляющей линейной скорости, обусловленной суточно-годовым вращением Земли:
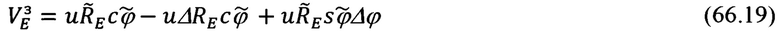
С учетом обозначений, принятых для 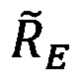 и ΔRE (66.18), выражение (66.19) примет вид:
и ΔRE (66.18), выражение (66.19) примет вид:
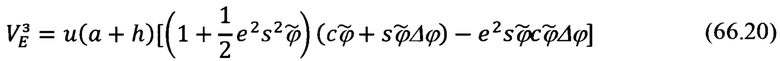
Запишем последнее выражение в более приемлемом для дальнейшего рассмотрения виде:
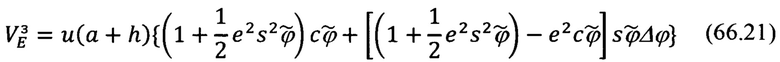
Выражение для проекций  на оси опорного трехгранника гироплатформы ИНС будут равны:
на оси опорного трехгранника гироплатформы ИНС будут равны:

С учетом того, что идеальное значение угла азимутальной ориентации опорного трехгранника гироплатформы ИНС равно:

выражения для горизонтальных составляющих  (66.22) примут вид:
(66.22) примут вид:

Подставим в (66.24) выражение для 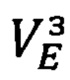 (66.21). В результате, с точностью до величин первого порядка малости относительно Δϕ и Δχ, получим следующие выражения для составляющих
(66.21). В результате, с точностью до величин первого порядка малости относительно Δϕ и Δχ, получим следующие выражения для составляющих 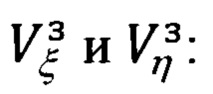

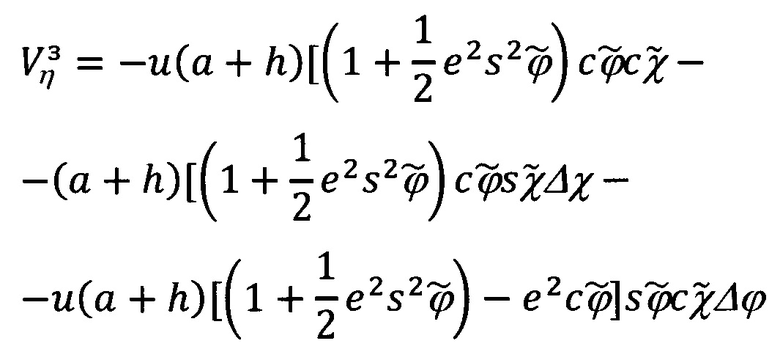
Если к составляющим (66.25) прибавить соответствующие компоненты путевой скорости (66.7), то, с точностью, определяемой величинами первого порядка малости относительно малых величин вида Δϕ и Δχ, будут получены горизонтальные составляющие абсолютной линейной скорости объекта. Приведем их:

В дальнейшем, несмотря на то, что при формировании (66.26) использовалась не только информация, измеренная ДИСС, указанные составляющие абсолютной линейной скорости будем трактовать, как скорости, сформированные по измерениям ДИСС.
Входящие в (66.26) составляющие скорости 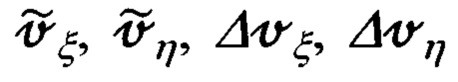 описываются представленными выше выражениями (66.8) и (66.10).
описываются представленными выше выражениями (66.8) и (66.10).
Полученные выше идеальные составляющие 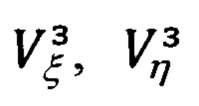 (66.25) абсолютной линейной скорости, обусловленные вращением Земли, целесообразно представить в следующем виде:
(66.25) абсолютной линейной скорости, обусловленные вращением Земли, целесообразно представить в следующем виде:

В приведенных выражениях, в соответствии с (66.25), приняты следующие обозначения:
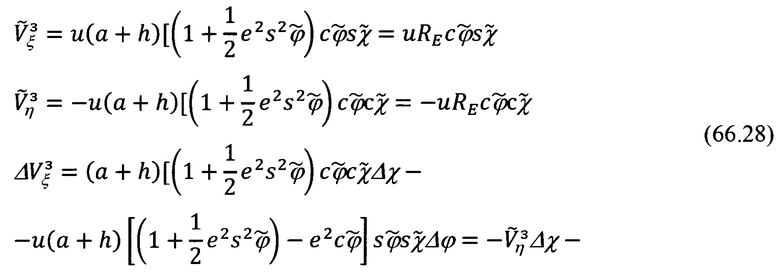
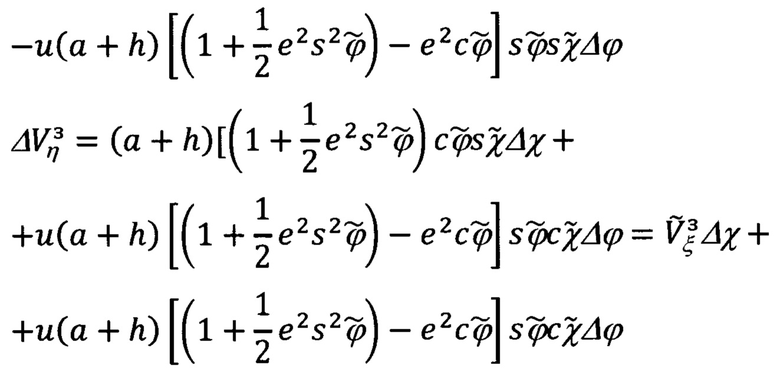
С учетом (66.27), выражения (66.26) примут вид:

Представляется целесообразным выражения (66.29) записать в следующем виде:

Сравнивая соответствующие выражения (66.2) и (66.30), вычитая из левых частей выражений (66.2) левые части выражений (66.30) и аналогично, для правых частей указанных выражений, учитывая при этом кинематические составляющие 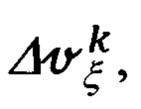
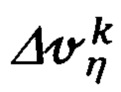 скорости (66.1), имеющие место при маневренном полете объекта и обусловленные координатами относительного размещения рассматриваемых информационных систем (ИНС, ДИСС), получим следующие уравнения связи:
скорости (66.1), имеющие место при маневренном полете объекта и обусловленные координатами относительного размещения рассматриваемых информационных систем (ИНС, ДИСС), получим следующие уравнения связи:

Обозначим левые части приведенных уравнений связи через z1 и z2, понимая под ними сигналы измерения, наблюдаемые на фоне некоррелированных шумов измерения V1 и V2 с известными интенсивностями:

Подставляя в (66.32) выражения (66.28) для 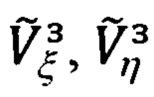 и (66.8) для
и (66.8) для 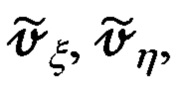 получим развернутое представление для сигналов измерения z1 и z2:
получим развернутое представление для сигналов измерения z1 и z2:
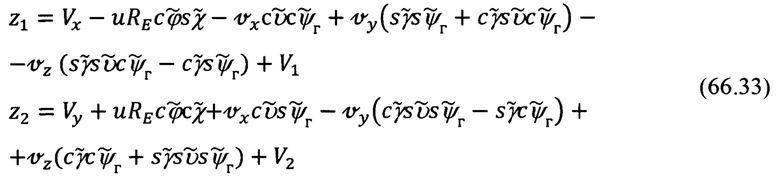
Приведенные выражения в дальнейшем будем рассматривать, как выражения для расчета сигналов измерения оптимального фильтра-идентификатора параметров комплексной инерциально-доплеровской системы.
В правые части полученных уравнений связи (66.31) вместо 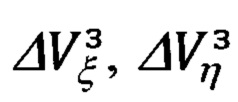 и
и 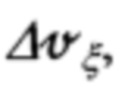 ,
, 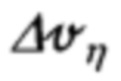 подставим соответствующие выражения (66.28) и (66.10). В результате получим следующее развернутое представление матричного выражения вида:
подставим соответствующие выражения (66.28) и (66.10). В результате получим следующее развернутое представление матричного выражения вида:
z=Hx+W,
где х - вектор параметров состояния рассматриваемой системы, Н - матрица наблюдения.
Но прежде, чем выполнить упомянутые выше подстановки, целесообразно выражения для 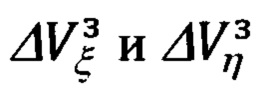 (66.28) представить в функции инерциально-доплеровской системы параметров состояния. Для этого вместо Δϕ и Δχ необходимо подставить в них соответствующие соотношения системы (66.3).
(66.28) представить в функции инерциально-доплеровской системы параметров состояния. Для этого вместо Δϕ и Δχ необходимо подставить в них соответствующие соотношения системы (66.3).
В результате получим:
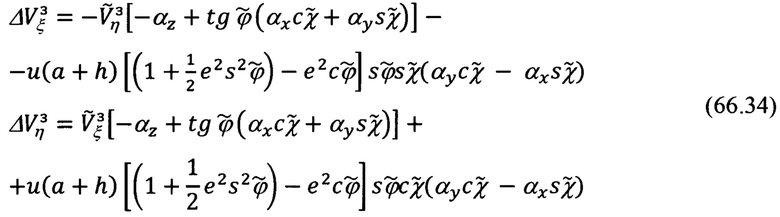
Группируя в приведенных выражениях члены по параметрам состояния αх, αу, αz, получим их следующее представление:
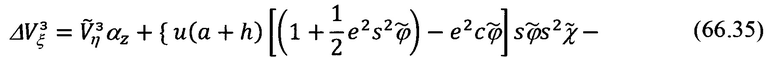
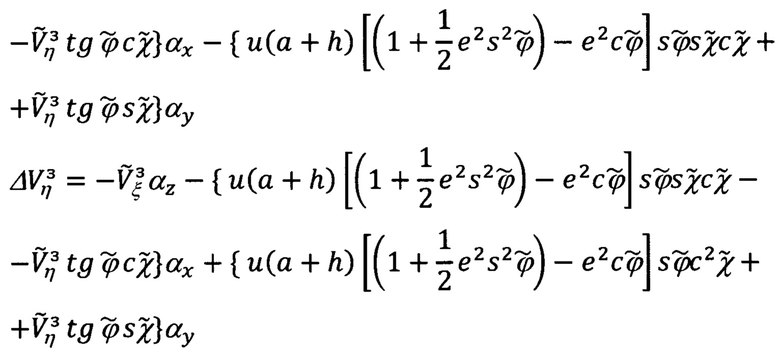
Приведем компактное представление полученных выражений:

где приняты следующие обозначения:
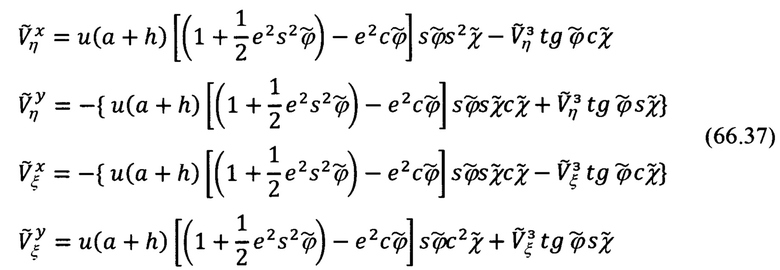
После приведения выражений для 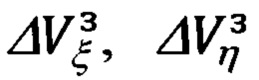 (66.28) к алгоритмически целесообразному виду (66.36) могут быть реализованы упомянутые выше операции по приведению правой части уравнений связи (66.31) к виду, удобному для формирования элементов матрицы наблюдения.
(66.28) к алгоритмически целесообразному виду (66.36) могут быть реализованы упомянутые выше операции по приведению правой части уравнений связи (66.31) к виду, удобному для формирования элементов матрицы наблюдения.
Для этого подставим (66.36) и (66.10) в (66.31). В результате получим следующее представление для сигналов измерения:
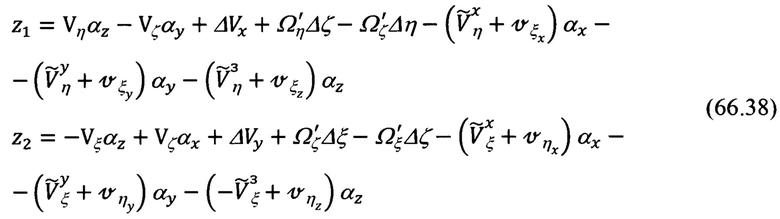
После приведения подобных членов в выражениях для z1 и z2 (66.38) они примут следующий вид:
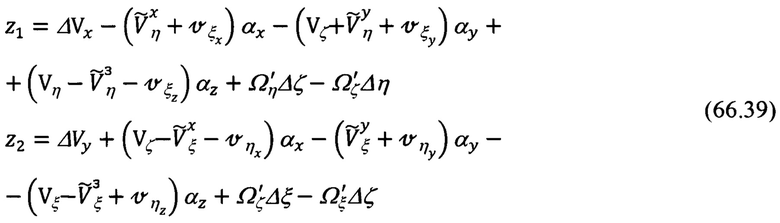
Для формирования матрицы наблюдения необходимо знать порядок следования параметров состояния рассматриваемой системы в векторе оцениваемых параметров. Приведем его:
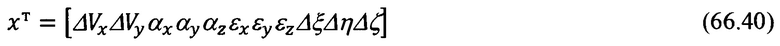
В соответствии с (66.39) и (66.40) матрица наблюдения будет иметь следующий вид:

Из полученной матрицы наблюдения следует, что в рассматриваемом режиме инерциально-доплеровской коррекции практически все параметры состояния, кроме нескомпенсированных дрейфов εx, εy, εz, имеют прямую непосредственную связь и, как следствие, влияние на выходные - измеряемые сигналы ИНС, что свидетельствует о потенциальной наблюдаемости указанных параметров.
Способность параметров состояния рассматриваемой системы напрямую влиять на характер изменения выходных сигналов ИНС следует расценивать, как необходимое условие их наблюдаемости.
И главное при этом - это активизировать эти потенциально существующие связи между конкретными параметрами и измеряемыми выходными сигналами. Основным инструментом управления указанными связями является движение объекта, а конкретно, различные виды выполняемых им маневров. И это важно, прежде всего, для управления процедурой устойчивого оценивания всех параметров состояния рассматриваемой системы и, прежде всего, слабонаблюдаемых.
Отличительной особенностью предлагаемого способа коррекции ИНС по измерениям ДИСС, выделяющей его из всего многообразия существующих алгоритмов, является то, что для реализации эффективной процедуры оптимального оценивания и коррекции, включая и коррекцию автономно счисленных координат местоположения объекта, впервые в практике разработки подобных алгоритмов, помимо алгоритмического учета геометрии относительного пространственного размещения комплесируемых систем, при формировании сигналов и матрицы измерения используются кинематические соотношения связи погрешностей счисления основной тройки навигационных параметров Δϕ, Δλ, Δχ и ошибок измерения углов эволюции объекта Δυ, Δγ, Δψг с малыми углами αх, αу, αz рассогласования реального и опорного трехгранников гироплатформы ИНС.
И при этом преследуется, прежде всего, цель обеспечения максимально корректного и математически строгого описания исходной системы, которая работает, исключительно, на достижение заявленной выше основной цели предлагаемого способа коррекции, а именно, на повышение его точности и быстродействия.
Именно указанный подход, при отсутствии точных навигационных и пилотажных параметров позволяет, с точностью до величин первого порядка малости относительно таких параметров, как малые углы αх, αу, αz рассогласования реального и опорного трехгранников гироплатформы ИНС, получить искомые математически строгие и информационно обеспеченные выражения для определения сигналов измерения оптимального идентификатора ошибок ИНС и элементов его матрицы наблюдения.
Наличие точных оценок 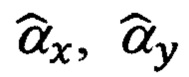 погрешностей выдерживания вертикали и оценки
погрешностей выдерживания вертикали и оценки 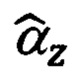 угла азимутального ухода гироплатформы позволяет не только откорректировать составляющие абсолютной линейной скорости Vx, Vy, но и сформировать оценки ошибок
угла азимутального ухода гироплатформы позволяет не только откорректировать составляющие абсолютной линейной скорости Vx, Vy, но и сформировать оценки ошибок 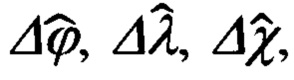 а также
а также 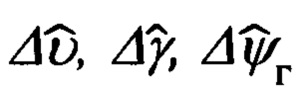 и откорректировать счисленные ИНС навигационные параметры и измеренные углы эволюции объекта.
и откорректировать счисленные ИНС навигационные параметры и измеренные углы эволюции объекта.
Для оценивания всех ошибок ИНС, математическое описание которых представлено в виде расширенной системы взаимосвязанных дифференциальных уравнений первого порядка с вектором параметров состояния вида (66.40), необходимо предусмотреть два участка полета.
На первом горизонтальном участке прямолинейного полета без ускорений осуществляется так называемое «горизонтирование» гироплатформы с оцениванием хорошо наблюдаемых параметров горизонтальных каналов ИНС, таких как ΔVx, ΔVy, αх, αу, εх и согласованное (не раздельное) оценивание слабонаблюдаемых параметров, типа αz, εy. Длительность этого участка коррекции составляет не более 4,5 - 5-ти минут, по окончании которого, с целью точного оценивания слабонаблюдаемых параметров, выполняется маневр, типа «змейки», координированного или боевого разворотов.
Длительность маневра, как правило, не превышает 30-40 сек.
В результате его выполнения осуществляется точное оценивание таких параметров состояния, как αz, εy, Δξ, Δη, Δζ, а также доуточнение оценки дрейфа εz азимутального гироскопа.
Точное оценивание координат Δξ, Δη, Δζ местоположения ИНС относительно ДИСС является показателем качества оптимального оценивания в целом.
По окончании маневра завершается активная фаза оптимального оценивания ошибок автономного инерциального счисления, основанная на рекуррентной процедуре обработки, фильтрации и идентификации постоянно обновляющейся входной последовательности сигналов, формируемых по измерениям ИНС и ДИСС.
После чего фильтр-идентификатор переводят в режим долгосрочного - до следующего сеанса коррекции, прогноза полученных оценок, по результатам которого, также, как и в процессе оптимального оценивания осуществляют коррекцию всех счисленных и измеренных ИНС параметров.
Саму процедуру коррекции навигационных 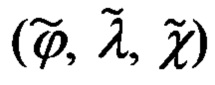 и пилотажных
и пилотажных 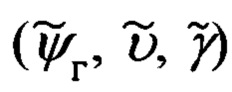 параметров, включая и истинный курс
параметров, включая и истинный курс 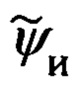 объекта, осуществляют в соответствии с кинематическими соотношениями (66.3) и (66.4) и с учетом таких удивительных свойств инерциальных систем, построенных на основе принципа невозмущенного измерения ускорений, которые заключаются в их способности опосредованно «запоминать» и «хранить» информацию о текущих значениях ошибок автономного инерциального счисления.
объекта, осуществляют в соответствии с кинематическими соотношениями (66.3) и (66.4) и с учетом таких удивительных свойств инерциальных систем, построенных на основе принципа невозмущенного измерения ускорений, которые заключаются в их способности опосредованно «запоминать» и «хранить» информацию о текущих значениях ошибок автономного инерциального счисления.
Формализованно, эти свойства как раз и представлены приведенными выше соотношениями.
И физический смысл их заключается в том, что текущие значения ошибок Δχ, Δλ, Δϕ (66.3) счисления основной тройки навигационных параметров χ, λ, ϕ и ошибок Δψг, Δγ, Δυ (66.4) измерения текущих углов ψг, γ, и эволюции объекта могут быть определены по результатам оптимального оценивания таких параметров состояния ИНС, как входящие в (66.3) и (66.4) малые углы αх, αу, αz ухода реальной ГП ИНС (виртуальной ГП для БИНС) относительно ее опорного трехгранника.
Таким образом, располагая текущими значениями оценок 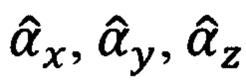 малых углов αх, αу, αz ухода реальной/виртуальной ГП ИНС/БИНС относительно ее опорного трехгранника, полученными в процессе инерциально-доплеровского оценивания, и счисленными/измеренными значениями навигационных ϕ, λ, χ и пилотажных параметров ψг, γ, υ достаточно просто могут быть сформированы оценки
малых углов αх, αу, αz ухода реальной/виртуальной ГП ИНС/БИНС относительно ее опорного трехгранника, полученными в процессе инерциально-доплеровского оценивания, и счисленными/измеренными значениями навигационных ϕ, λ, χ и пилотажных параметров ψг, γ, υ достаточно просто могут быть сформированы оценки 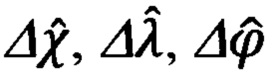 ошибок счисления навигационных параметров и оценки
ошибок счисления навигационных параметров и оценки 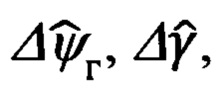
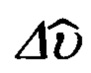 ошибок измерения углов эволюции объекта, и откорректированы все ошибочно счисленные/измеренные параметры ИНС, включая и истинный курс.
ошибок измерения углов эволюции объекта, и откорректированы все ошибочно счисленные/измеренные параметры ИНС, включая и истинный курс.
При этом коррекцию истинного курса ψи объекта осуществляют по той же схеме, что и представленные выше навигационные и пилотажные параметры.
В соответствии с (66.3) и (66.4) можно показать, что текущее значение оценки 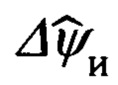 ошибки определения истинного курса объекта будет равно:
ошибки определения истинного курса объекта будет равно:
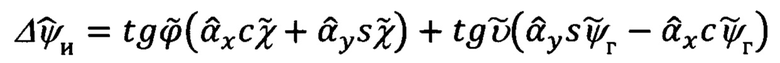
Следовательно, откорректированное значение истинного курса 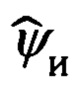 может быть определено в соответствии с выражением:
может быть определено в соответствии с выражением:
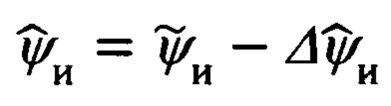
Систематизируя приведенное выше описание предлагаемого способа привязки к подвижной наземной цели (ПНЦ), полагая, что оптимальное оценивания параметров ее движения осуществляется посредством оптимальной фильтрации и идентификации сформированных в режиме углового сопровождения цели компонент модифицированной угломестной дальности и в полном соответствии с кинематической моделью ее относительного движения, представленной в проекциях на оси подвижной системы координат ПСК, приведем последовательное изложение процедуры его алгоритмической реализации.
Итак, заявляемый способ привязки к подвижной наземной цели реализуется следующим образом.
1. Для информационного обеспечения предлагаемого способа привязки реализуют:
- полноценный режим инерциально-доплеровского оптимального оценивания ошибок ИНС с коррекцией ее навигационных и пилотажных параметров;
- режим формирования бароинерциальной высоты и вертикальной скорости на основе оптимального комплексирования вертикального канала ИНС и баровысотомера из состава СВС.
2. Методически рассматриваемый способ привязки к подвижной наземной цели основан на последовательном использовании:
- кинематического метода определения дальности КМОД до неподвижного наземного ориентира;
- модифицированного угломестного способа формирования текущей наклонной дальности до подвижной наземной цели.
3. В предлагаемом способе привязки к ПНЦ КМОД используют для определения среднего значения высоты над уровнем моря (УМ) некоторой характерной площадки рельефа земной поверхности (РЗП), расположенной в 50-60 м по пути следования реальной цели.
Для этого неподвижное прицельное перекрестие НПП ОПС наводят на эту площадку и сопровождают ее в течение 3÷3,5 секунд, уведомив о начале ее углового сопровождения БЦВМ комплекса подачей соответствующей разовой команды (РК) «КМОД».
4. В момент получения указанной команды БЦВМ комплекса инициирует работу программного модуля (ПМ) КМОД с использованием текущих значений сформированных им дальностей Di для расчета соответствующих значений относительной высоты hi объекта над сопровождаемым ориентиром и высоты ОР Δhi над уровнем моря.
Для чего, БЦВМ комплекса на всем интервале работы ПМ КМОД, с частотой, изменяющейся в зависимости от скорости полета объекта, от 2-х до 10-ти герц, осуществляет измерение следующего среза навигационной, пилотажной и специальной информации:
- текущих географических координат ϕi, λi местоположения объекта и бароинерциальной высоты 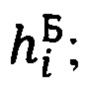
- текущих углов истинного курса ψи i, тангажа υi и крена γi объекта;
- текущих углов ϕy i, ϕz i визирования ориентира.
5. В каждый текущий момент времени совместно обрабатывают текущий i-ый и предыдущий (i-1)-ый массивы представленной выше информации (фиг. 7) и на их основе реализуют следующие математические процедуры:
- расчет линейной дальности ΔDi-1,i между (i-1)-ой и i-ой отсчетными точками и азимута ΔAi-1,i и угла места θi-1,i ее ориентации относительно ГСТ ONHE, соответствующего местоположению (i-1)-ой точки с координатами ϕi-1, λi-1;
- расчет значений азимута Ai-1 и угла места θi-1 вектора 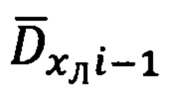 направления на ориентир в (i-1)-ой точке;
направления на ориентир в (i-1)-ой точке;
- расчет значений азимута Ai и угла места θi вектора 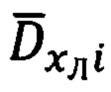 направления на ориентир в i-ый момент времени (i-ой точке);
направления на ориентир в i-ый момент времени (i-ой точке);
- расчет пространственных углов βi-1 и βi между векторами и ΔDi-1,i и 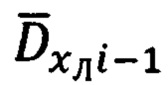 и ΔDi-1,i и
и ΔDi-1,i и 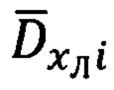 соответственно;
соответственно;
- решение пространственного треугольника дальностей и определение текущей наклонной дальности Di до ориентира.
6. Расчет базовой дальности ΔDi-1,i между соседними отсчетными точками осуществляют в соответствии с выражением (27), в котором используют компоненты дальности (26), полученные в результате выполнения расчетной цепочки, представленной выражениями (21), (22), (24).
Расчет углов Ai-1 и θi-1 пространственной ориентации базовой дальности ΔDi-1,i относительно ГСТ ONHE, соответствующего координатам ϕi-1, λi-1, осуществляют в соответствии с выражениями (28).
Векторно-матричное выражение, связывающее компоненты вектора 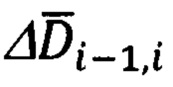 в проекциях на оси базовой системы координат OxБyБzБ, по оси ОхБ которой ориентирован вектор
в проекциях на оси базовой системы координат OxБyБzБ, по оси ОхБ которой ориентирован вектор 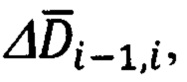 и ГСТ ONHE имеет вид (29), где входящая в него матрица
и ГСТ ONHE имеет вид (29), где входящая в него матрица 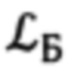 представлена выражением (30).
представлена выражением (30).
7. Расчет углов пространственной ориентации вектора дальности 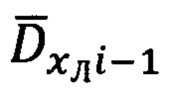 осуществляют в соответствии с выражениями (32), в которых используют направляющие косинусы (31). Выражения для расчета аналогичных углов пространственной ориентации вектора дальности
осуществляют в соответствии с выражениями (32), в которых используют направляющие косинусы (31). Выражения для расчета аналогичных углов пространственной ориентации вектора дальности 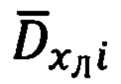 имеют вид (34), а выражения для используемых при этом направляющих косинусов
имеют вид (34), а выражения для используемых при этом направляющих косинусов 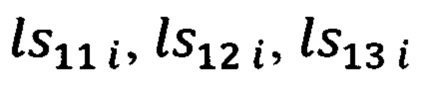 - (33).
- (33).
По аналогии с (29), векторно-матричные выражения для компонент векторов 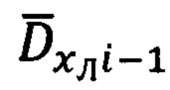 и
и 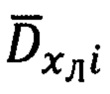 в проекциях на оси систем координат OxЛiyЛizЛi, по осям OxЛi-1 и ОхЛi ориентированы векторы
в проекциях на оси систем координат OxЛiyЛizЛi, по осям OxЛi-1 и ОхЛi ориентированы векторы 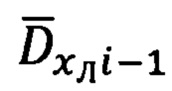 и
и 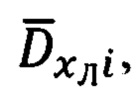 и ГСТ ONHE, имеют вид (35), (36), а используемые в них матрицы
и ГСТ ONHE, имеют вид (35), (36), а используемые в них матрицы 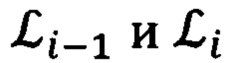 - (37), (38).
- (37), (38).
8. Для определения углов βi-1 и βi между вектором 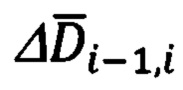 и векторами
и векторами 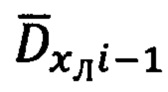 и
и 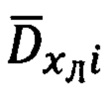 предварительно получают векторно-матричные выражения (41) и (42). Связывающие компоненты произвольного вектора в проекциях на оси базовой системы координат OxБyБzБ и систем координат OxЛi-1yЛi-1zЛi-1, OxЛiyЛizЛi, из которых получают простые выражения для расчета косинусов cβi-1 и cβi пространственных углов (45) (фиг. 7).
предварительно получают векторно-матричные выражения (41) и (42). Связывающие компоненты произвольного вектора в проекциях на оси базовой системы координат OxБyБzБ и систем координат OxЛi-1yЛi-1zЛi-1, OxЛiyЛizЛi, из которых получают простые выражения для расчета косинусов cβi-1 и cβi пространственных углов (45) (фиг. 7).
9. При решении пространственного треугольника дальностей (фиг. 7), в соответствии с (46), определяют углы βi-1 и βi, а в соответствии с (47) угол Δβ, после чего, в соответствии с теоремой синусов рассчитывают текущую наклонную дальность Di до неподвижного наземного ориентира.
Дополнительно, в каждый текущий, i-ый, момент времени, в соответствии с (49), рассчитывают косинус угла между местной географической вертикалью и направлением 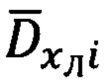 на выбранный ориентир (фиг. 6), используя который определяют текущие значения геометрической высоты hi (50) объекта и высоты Δhi (51) ориентира над уровнем моря.
на выбранный ориентир (фиг. 6), используя который определяют текущие значения геометрической высоты hi (50) объекта и высоты Δhi (51) ориентира над уровнем моря.
Каждое, вновь поступившее значение Δhi, используют в рекуррентной процедуре осреденения (52).
После проведения расчета текущих значений дальности Di (48), геометрической высоты hi (50) и высоты Δhi (51) ориентира над уровнем моря, i-ую точку, а также весь измеренный для нее массив информации, принимают за (i-1)-ую, а точку, на которую осуществляется полет, считают i-ой, текущего массива информации, процедуру КМОД повторяют.
10. Реализуемый на основе кинематического метода определения дальности кратковременный этап привязки к неподвижному наземному ориентиру является вспомогательным, поскольку он обеспечивает информационную самостоятельность основного этапа предлагаемого способа привязки, основанного на модифицированной угломестной процедуре расчета текущей наклонной дальности до ПНЦ.
Длительность указанного этапа составляет не менее 10-ти секунд и определяется по ситуации, поскольку программный сброс режима привязки в предлагаемом способе целесообразно осуществлять по сбросу боевой задачи (БЗ). Тем более, учитывая, что объективных показаний к ограничению временных рамок указанного режима нет никаких.
По окончании первого, краткосрочного и вспомогательного этапа привязки к ПНЦ, БЦВМ комплекса формирует РК «КМОД ГОТОВ», которая индицируется на индикаторе летчика-оператора. По указанной команде оператор перенацеливает ОПС на реальную цель и по факту перехода на ее угловое сопровождение нажимает кнопку «Привязка», по которой БЦВМ переходит к выполнению этапа привязки к подвижной наземной цели, основанный на модифицированной угломестной процедуре способа определения наклонной дальности (МУСОД) до ПНЦ.
11. На указанном этапе привязки реализуют полноценную оптимальную процедуру привязки к ПНЦ с определением текущих параметров ее движения и относительного местоположения.
Входными сигналами фильтра-идентификатора являются текущие значения компонент дальности до ПНЦ в проекции на оси одной из ПСК, наблюдаемые на фоне случайных шумов измерения. При их формировании используют текущую навигационную и пилотажную информацию, измеренную ИНС в режиме ее коррекции по измерениям доплеровского измерителя составляющих скорости (ДИСС), углы визирования цели и текущие значения наклонной дальности, формируемые на основе модифицированного угломестного способа их определения.
Процедура их формирования включает три основные операции:
- расчет текущего значения косинуса cθi угла между местной, географической вертикалью и направлением на ПНЦ (49);
- расчет текущего значения относительной высоты объекта над ПНЦ hi (54), (53);
- расчет текущего значения наклонной дальности Di (55).
12. Синтез структуры оптимального фильтра-идентификатора осуществляют в соответствии с дискретной процедурой оптимального рекуррентного оценивания, представленной матричными выражениями вида (60)-(66).
Основой для ее синтеза является модель относительного движения цели в виде системы линейных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК (57), дополненная дифференциальными уравнениями, описывающими характер изменения соответствующих составляющих скорости и ускорения цели:
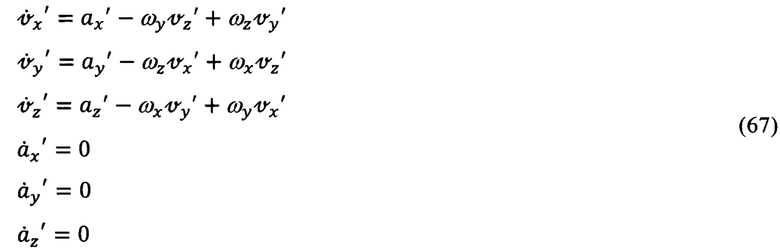
Из проведенного описания защищенного способа привязки к подвижной наземной цели следует, что суть предлагаемого инженерного решения раскрыта, а то обстоятельство, что оно позволяет синтезировать абсолютно защищенный способ привязки к ПНЦ, для реализации которого не требуется использование лазерного дальномера и организации процедуры программного сопровождения (прогноза) параметров движения цели, чем устраняют один из основных источников ошибок рассматриваемого режима, свидетельствует о том, что технический результат изобретения достигнут.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ И ЕЁ КОРРЕКЦИИ ПО НЕПОДВИЖНОМУ НАЗЕМНОМУ ОРИЕНТИРУ С ИЗВЕСТНЫМИ ГЕОГРАФИЧЕСКИМИ КООРДИНАТАМИ | 2019 |
|
RU2713582C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ МОДИФИЦИРОВАННОЙ, ИНВАРИАНТНОЙ К РЕЛЬЕФУ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ УГЛОМЕСТНОЙ ПРОЦЕДУРЫ РАСЧЁТА ДАЛЬНОСТИ | 2016 |
|
RU2617373C1 |
| СПОСОБ ФОРМИРОВАНИЯ БАРОИНЕРЦИАЛЬНОЙ ВЫСОТЫ И ВЕРТИКАЛЬНОЙ СКОРОСТИ | 2019 |
|
RU2713583C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ СУБОПТИМАЛЬНОЙ ПРОЦЕДУРЫ УГЛОВОГО СОПРОВОЖДЕНИЯ | 2016 |
|
RU2621374C1 |
| СПОСОБ ФОРМИРОВАНИЯ ВОЗДУШНО-СКОРОСТНЫХ ПАРАМЕТРОВ МАНЕВРЕННОГО ОБЪЕКТА | 2019 |
|
RU2713585C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ СПУТНИКОВОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2015 |
|
RU2617565C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ПРИЦЕЛИВАНИЯ ПО ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2016 |
|
RU2629130C1 |
| СПОСОБ КОРРЕКЦИИ КОМПЛЕКСНОЙ ИНС ПО АНОМАЛИИ ГРАВИТАЦИОННОГО ПОЛЯ ЗЕМЛИ | 1985 |
|
SU1840368A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОНТРОЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ПРОСТРАНСТВЕННО-УГЛОВОЙ ОРИЕНТАЦИИ САМОЛЁТА НА ТРАССАХ И ПРИАЭРОДРОМНЫХ ЗОНАХ ПРИ ЛЁТНЫХ ИСПЫТАНИЯХ ПИЛОТАЖНО-НАВИГАЦИОННОГО ОБОРУДОВАНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2584368C1 |
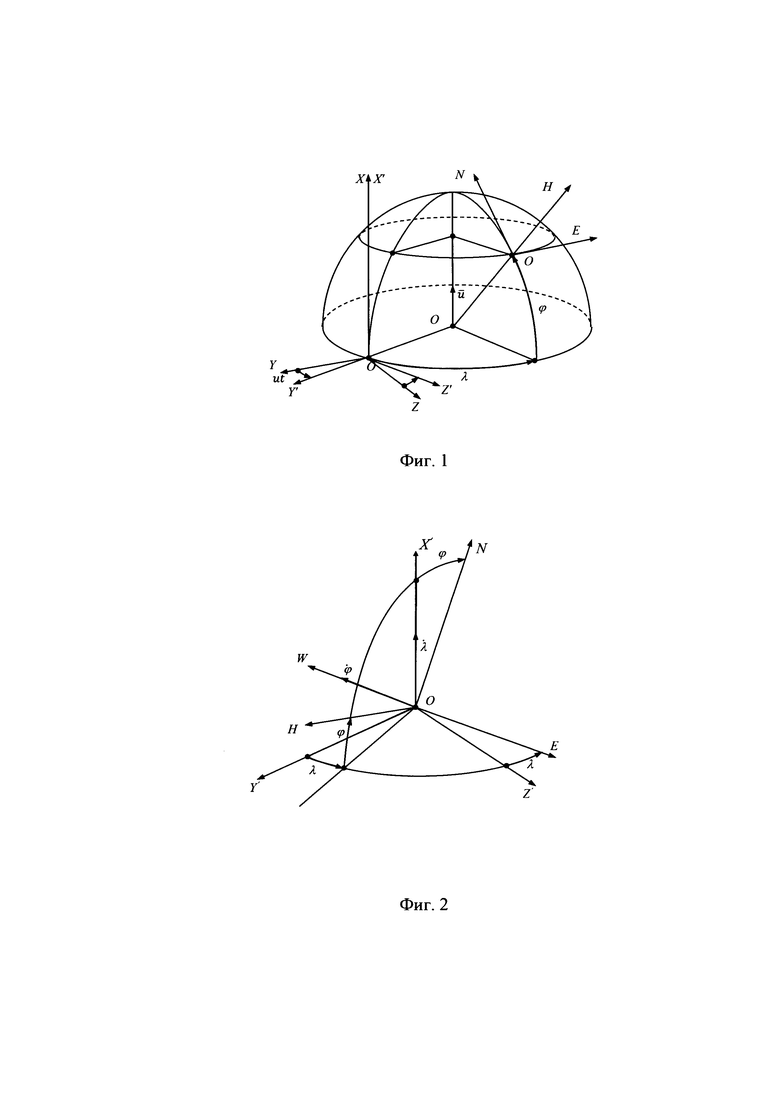
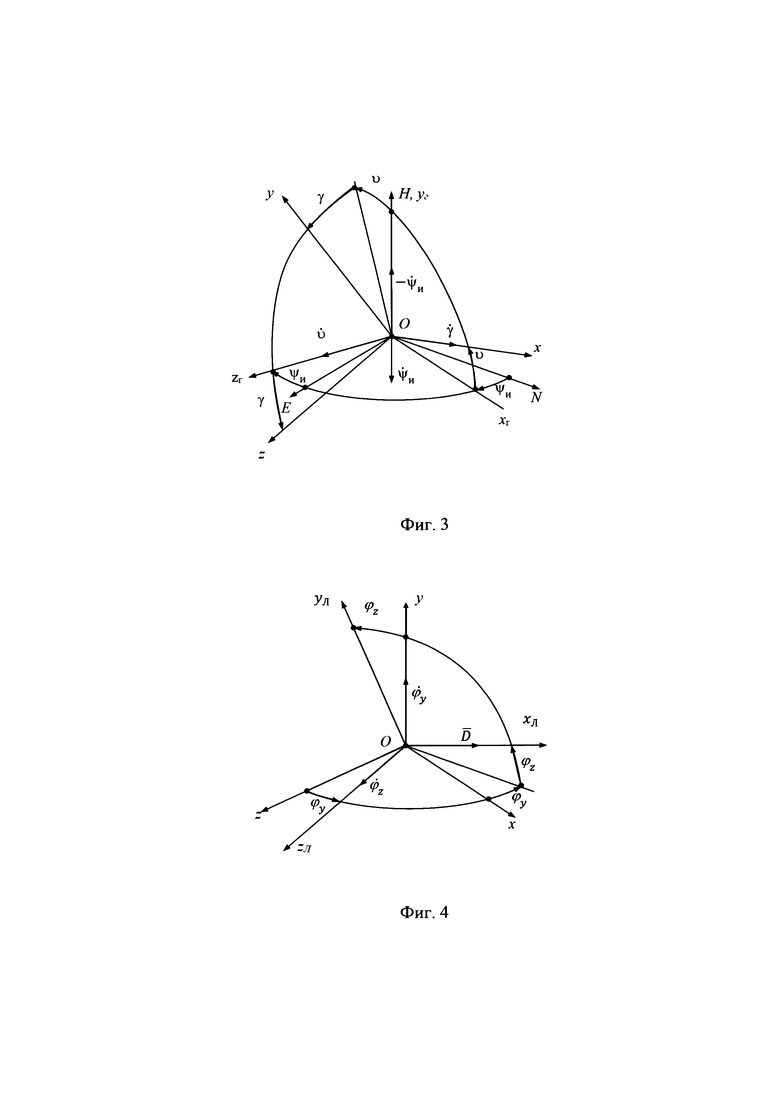
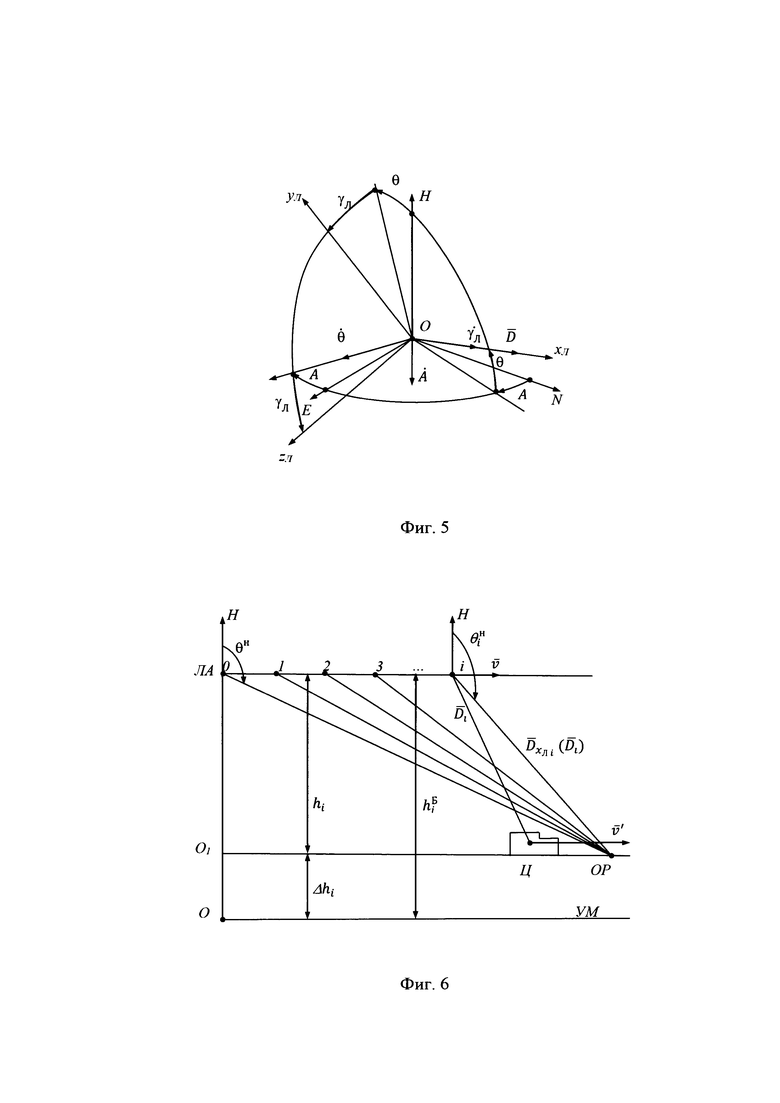

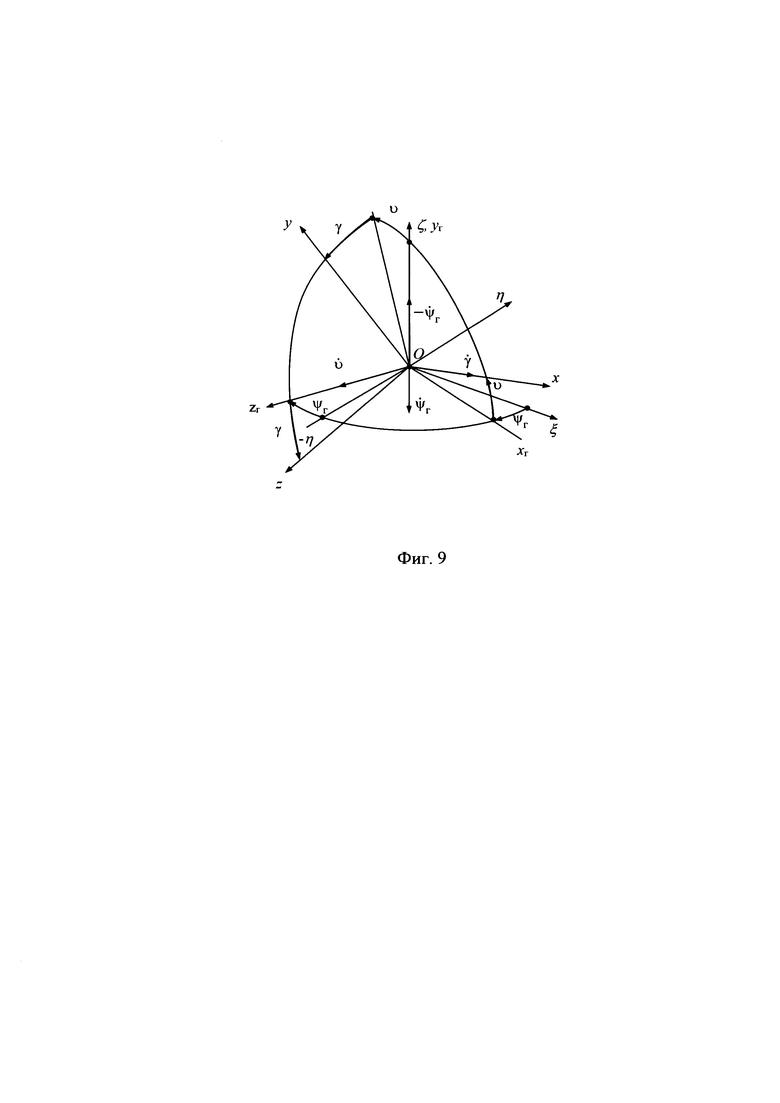
Изобретение относится к области измерительных информационных систем и комплексов боевых летательных аппаратов ЛА. Предлагаемый защищенный способ привязки к подвижной наземной цели основан на комбинации кинематического метода определения наклонной дальности (КМОД) и модифицированного угломестного способа определения текущей дальности до подвижной наземной цели (МУСОД) и предполагает реализацию оптимальной процедуры инерциально-доплеровского оценивания и коррекции, а также синтез бароинерциального канала формирования абсолютной высоты и вертикальной скорости. Техническим результатом изобретения является расширение функциональных возможностей оптико-электронных прицельно-навигационных комплексов (ОЭПрНК) объектов боевого назначения за счет разработки дополнительного, защищенного способа привязки к подвижной наземной цели, а также повышение точности и эффективности решения боевой задачи (БЗ) за счет разработки альтернативной прогнозу параметров движения цели, унифицированной с режимом привязки процедуры оптимального оценивания на основе модифицированной, инвариантной к рельефу подстилающей поверхности угломестной процедуры расчета наклонной дальности. 9 ил.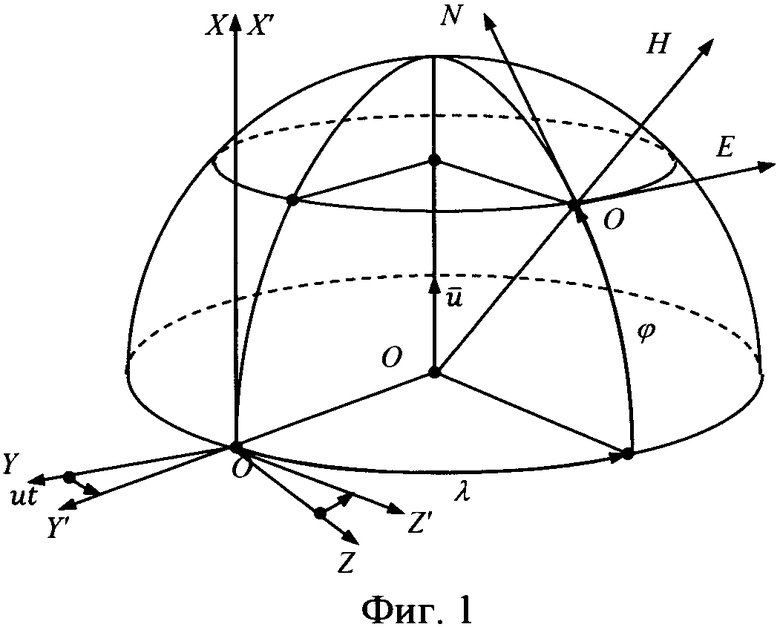
Способ защищенной оптимальной привязки к подвижной наземной цели (ПНЦ), включающий непрерывное угловое сопровождение цели и дискретное определение текущей наклонной дальности до нее, по каждому из которых с использованием измеренной инерциальной навигационной системой (ИНС) пилотажной и навигационной информации и текущих углов визирования цели с теле-тепловизионной обзорно-прицельной системы (ОПС) формируют входные сигналы оптимального фильтра-идентификатора в виде наблюдаемых на фоне случайных шумов измерения компонент относительной дальности до цели в проекциях на оси подвижной системы координат (ПСК), при этом оценивание текущих координат относительного местоположения ПНЦ и компонент ее абсолютной линейной скорости и ускорения осуществляют в соответствии с кинематической моделью ее относительного движения, представленной системой линейных взаимосвязанных дифференциальных уравнений 9-го порядка в проекциях на оси ПСК, для чего по измеренной ИНС информации осуществляют расчет составляющих абсолютной угловой скорости ПСК в проекциях на ее оси, а компоненты абсолютной линейной скорости объекта в осях ПСК используют в качестве известного управления, по оцененным в процессе оптимальной фильтрации и идентификации значениям параметров относительного местоположения и движения цели и текущей воздушно-скоростной информации объекта формируют искомые поправки на стрельбу и в виде подвижной прицельной марки (ППМ) выдают их на коллиматорный прицел летчика, по которому управлением объекта осуществляют их отработку и прицельное применение выбранных неуправляемых авиационных средств поражения (АСП), отличающийся тем, что для формирования сигналов измерения входных сигналов оптимального фильтра-идентификатора, последовательно используют кинематический метод определения текущей наклонной дальности (КМОД) и модифицированный угломестный способ определения наклонной дальности (МУСОД) до ПНЦ, первый из которых, КМОД, используют для обеспечения информационной состоятельности второго, МУСОД, для чего в 60-75-ти метрах по пути ожидаемого следования реальной ПНЦ выбирают характерный для наблюдаемого рельефа земной поверхности (РЗП) неподвижный наземный ориентир (ННО), наводят на него неподвижное перекрестие (НПП) ОПС и сопровождают в одном из режимов углового сопровождения в течение 3-3,5 секунд, предварительно уведомив БЦВМ комплекса подачей команды «КМОД» о начале углового сопровождения выбранного ННО, в процессе чего, с частотой от 2-х до 10-ти герц, в зависимости от скорости объекта, измеряют полный срез навигационной 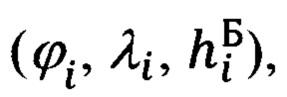 пилотажной (ψи i, υi, γi) и специальной (ϕy i, ϕz i) информации, и, обрабатывая (i-1)-ые текущие, i-ые измерения навигационных параметров, последовательно формируют базовую дальность ΔDi-1 i между двумя соседними отсчетными точками и текущие значения азимута Ai-1 i и угла места θi-1 i ее пространственной ориентации относительно ГСТ ONHE, направление осей которого соответствует точке с координатами ϕi-1, λi-1, а используя (i-1)-ый и i-ый массивы пилотажной и специальной информации, последовательно определяют углы Ai-1, и θi-1 и Ai, θi пространственной ориентации векторов
пилотажной (ψи i, υi, γi) и специальной (ϕy i, ϕz i) информации, и, обрабатывая (i-1)-ые текущие, i-ые измерения навигационных параметров, последовательно формируют базовую дальность ΔDi-1 i между двумя соседними отсчетными точками и текущие значения азимута Ai-1 i и угла места θi-1 i ее пространственной ориентации относительно ГСТ ONHE, направление осей которого соответствует точке с координатами ϕi-1, λi-1, а используя (i-1)-ый и i-ый массивы пилотажной и специальной информации, последовательно определяют углы Ai-1, и θi-1 и Ai, θi пространственной ориентации векторов 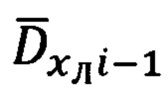 и
и 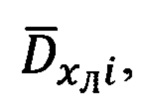 определяющих текущее направление на ННО, используя которые формируют пространственные углы βi-1 и βi между базовым вектором
определяющих текущее направление на ННО, используя которые формируют пространственные углы βi-1 и βi между базовым вектором 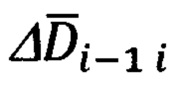 и векторами
и векторами 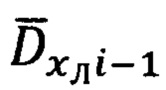 и
и 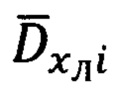 соответственно, знание которых обеспечивает корректное решение пространственного треугольника дальностей, в результате чего последовательно определяют текущее значение дальности Di до ННО и соответствующую ей геометрическую высоту hi объекта относительно ННО, сравнением которой с текущей бароинерциальной высотой
соответственно, знание которых обеспечивает корректное решение пространственного треугольника дальностей, в результате чего последовательно определяют текущее значение дальности Di до ННО и соответствующую ей геометрическую высоту hi объекта относительно ННО, сравнением которой с текущей бароинерциальной высотой 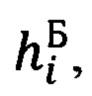 определяют высоту Δhi ННО и над уровнем моря и используют ее в рекуррентной процедуре нахождения среднего значения
определяют высоту Δhi ННО и над уровнем моря и используют ее в рекуррентной процедуре нахождения среднего значения 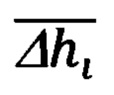 массива указанных высот, при этом после каждого очередного определения текущих значений параметров Di,
массива указанных высот, при этом после каждого очередного определения текущих значений параметров Di,  осуществляют операцию переприсваивания, принимая i-ый массив измеренных и рассчитанных
осуществляют операцию переприсваивания, принимая i-ый массив измеренных и рассчитанных 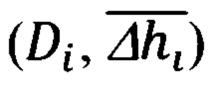 параметров за (i-1)-ый, а точку, на которую осуществляется полет - за i-ую, чем реализуют алгоритмический повтор приведенной процедуры КМОД, по окончании 1-го, вспомогательного этапа привязки к ПНЦ в БЦВМ комплекса формируют признак «КМОД ГОТОВ» и индицируют его на индикаторе оператора, по которому ОПС перенацеливают на реальную цель и нажимают кнопку «Привязка», по которой БЦВМ комплекса инициирует модифицированную угломестную процедуру расчета текущей наклонной дальности до ПНЦ, в которой сравнением текущей бароинерциальной высоты
параметров за (i-1)-ый, а точку, на которую осуществляется полет - за i-ую, чем реализуют алгоритмический повтор приведенной процедуры КМОД, по окончании 1-го, вспомогательного этапа привязки к ПНЦ в БЦВМ комплекса формируют признак «КМОД ГОТОВ» и индицируют его на индикаторе оператора, по которому ОПС перенацеливают на реальную цель и нажимают кнопку «Привязка», по которой БЦВМ комплекса инициирует модифицированную угломестную процедуру расчета текущей наклонной дальности до ПНЦ, в которой сравнением текущей бароинерциальной высоты 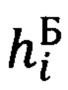 объекта со средним значением высоты
объекта со средним значением высоты 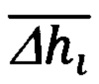 ПНЦ над уровнем моря определяют текущую геометрическую высоту hi объекта относительно цели, а используя текущее значение косинуса с
ПНЦ над уровнем моря определяют текущую геометрическую высоту hi объекта относительно цели, а используя текущее значение косинуса с 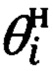 угла между географической вертикалью и направлением на цель, определяют текущее значение наклонной дальности Di до ПНЦ, на основе дискретной последовательности которых формируют массив входных сигналов оптимального фильтра-идентификатора параметров ПНЦ, последовательная обработка которых позволяет определить весь перечень параметров движения ПНЦ и обеспечить тем самым эффективное решение боевой задачи, при этом для обеспечения информационной состоятельности используемых в предлагаемом изобретении методов КМОД и МУСОД, формирование инерциальной информации реализуют в режиме инерциально-доплеровского оценивания и коррекции с расширением традиционной модели ошибок ИНС за счет включения в нее дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно доплеровского измерителя составляющих скорости (ДИСС) в проекциях на оси опорного трехгранника гироплатформы (ГП) ОТГП ИНС, чем обеспечивают корректное описание комплексной инерциально-доплеровской системы и повышенные характеристики наблюдаемости, точности и быстродействия оптимального оценивания ошибок ИНС, а синтез оптимального канала формирования бароинерциальной высоты и скорости ее изменения проводят параллельно с оптимальным комплексированием ИНС и ДИСС.
угла между географической вертикалью и направлением на цель, определяют текущее значение наклонной дальности Di до ПНЦ, на основе дискретной последовательности которых формируют массив входных сигналов оптимального фильтра-идентификатора параметров ПНЦ, последовательная обработка которых позволяет определить весь перечень параметров движения ПНЦ и обеспечить тем самым эффективное решение боевой задачи, при этом для обеспечения информационной состоятельности используемых в предлагаемом изобретении методов КМОД и МУСОД, формирование инерциальной информации реализуют в режиме инерциально-доплеровского оценивания и коррекции с расширением традиционной модели ошибок ИНС за счет включения в нее дифференциальных уравнений, описывающих характер изменения координат местоположения ИНС относительно доплеровского измерителя составляющих скорости (ДИСС) в проекциях на оси опорного трехгранника гироплатформы (ГП) ОТГП ИНС, чем обеспечивают корректное описание комплексной инерциально-доплеровской системы и повышенные характеристики наблюдаемости, точности и быстродействия оптимального оценивания ошибок ИНС, а синтез оптимального канала формирования бароинерциальной высоты и скорости ее изменения проводят параллельно с оптимальным комплексированием ИНС и ДИСС.
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ СУБОПТИМАЛЬНОЙ ПРОЦЕДУРЫ УГЛОВОГО СОПРОВОЖДЕНИЯ | 2016 |
|
RU2621374C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ПРИЦЕЛИВАНИЯ ПО ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2016 |
|
RU2629130C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ОПРЕДЕЛЕНИЯ НАВИГАЦИОННО-ТОПОГЕОДЕЗИЧЕСКИХ ПАРАМЕТРОВ | 2010 |
|
RU2431803C1 |
| СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ И ПРОГНОЗА ЕЁ ПАРАМЕТРОВ НА ОСНОВЕ МОДИФИЦИРОВАННОЙ, ИНВАРИАНТНОЙ К РЕЛЬЕФУ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТИ УГЛОМЕСТНОЙ ПРОЦЕДУРЫ РАСЧЁТА ДАЛЬНОСТИ | 2016 |
|
RU2617373C1 |
| US 7962285 B2, 14.06.2011. | |||
Авторы
Даты
2020-02-05—Публикация
2019-01-29—Подача