Настоящее изобретение относится к области анализа данных, в частности к задаче обработки и анализа многомерных пространственных траекторий движущихся объектов, у которых есть общие цели, и которые близки по конечным координатам. Настоящее изобретение может быть использовано при обнаружении скрытых целей движущихся объектов для идентификации установившихся потоков движения при решении задачи секторизации воздушного пространства расширенной зоны аэропорта в трехмерном случае. Также настоящее изобретение может быть использовано при создании автоматических (беспилотных) систем захода ЛА на посадку (в том числе при посадке в условиях сложного географического ландшафта, плохой видимости, на палубу корабля) и при определении оптимальных (нормальных) траекторий движения объектов в пространстве на основании данных радара.
В настоящий момент в связи с постоянно увеличивающимся объемом данных важной задачей является создание методов и алгоритмов, которые позволяют обрабатывать большие объемы данных быстро и в автоматическом режиме. Для анализа больших наборов данных требуются новые методы, которые позволяют распознавать скрытые паттерны движения и идентифицировать движущиеся объекты со сходными характеристиками движения и/или одной и той же конечной целью.
Наибольший интерес представляют задачи, связанные с анализом многомерных пространственных траекторий движения. В частности, эти задачи приобретают все большее значение в авиации в связи постоянным увеличением воздушного трафика, необходимостью оптимизации загруженности взлетно-посадочных полос (ВПП) и совершенствования существующих систем управления воздушным движением (СУВД).
Траектории самолета представляются четырехмерным описанием состояний самолета во времени, где под состояниями могут пониматься как положение центра масс или иных характеристик движения таких, как скорость, высота или вес. В общем случае пространственная траектория представляет собой многомерное описание пути движущегося объекта.
Согласно данным Федерального агентства воздушного транспорта Российской Федерации (Росавиация) и Международной организации гражданской авиации (ИКАО) значительное число авиационных происшествий связано с организацией воздушного движения в непосредственной близости аэропортов. В связи с этим для обеспечения безопасности полетов в условиях постоянно увеличивающейся загруженности аэропортов и поддержания высокого уровня безопасности полетов необходима модернизация и оптимизация работы существующих СУВД.
Из патента US 6393358 В1 известна автоматическая радиолокационная система TRACON (Terminal Radar Approach Control), использование которой направлено на упрощение работы диспетчерских служб, обеспечение безопасности полетов и более эффективной загруженности воздушного пространства в расширенной зоне вокруг аэропорта. Подобные системы позволяют обеспечивать безопасность движения в воздушном пространстве и улучшать пропускную способность аэропорта. С помощью радара TRACON фиксируются метаданные, содержащие информацию о пространственных координатах положения центра масс ЛА, на основании которых вычисляются траектории их движения.
Особенность задачи управления воздушным движением состоит в том, что в связи с разделительными ограничениями (separation constraints) различные по весу самолеты не могут следовать в караване к одной ВПП. Из заявки US 20140019033 А1 известен способ планирования воздушного движения, включающий определение сети, состоящей из узловых точек и основных направлений посадки (an arrival network of nodes and legs), который применяется для оптимизации расписания прибывающих самолетов.
Для оптимизации движения в расширенной зоне аэропорта могут применяться методы анализа данных (data mining). В частности, с помощью методов анализа данных решается задача секторизации воздушного пространства расширенной зоны аэропорта, т.е. разделения пространства на сектора или зоны ответственности диспетчерских служб. Причем, секторизация воздушного пространства должна выполняться с учетом установившегося разделения полетов по маршрутам посредством выделения характерных потоков движения в наборе траекторий самолетов, регистрируемых радаром.
Важно заметить, что сложность решаемой задачи связана с особенностями пространственной геометрии траекторий движения (их потенциальными пересечениями, кривизной и кручением) (см. Фиг. 1а) и возможными пространственными пересечениями пучков многомерных траекторий между собой.
Таким образом, при разработке методов анализа траекторных данных желательно использовать такую меру близости, которая позволяла бы разделять траектории сходной формы, даже если они пересекаются в пространстве. Используемая мера близости должна отражать подобие (или различие) формы траекторий в трехмерном пространстве.
Решение задачи секторизации в настоящее время находится на начальной стадии и связана с решением задачи выделения пучков траекторий, то есть групп траекторий движения, имеющих сходные характеристики и общие цели. (В случае посадочных траекторий необходимо также дополнительно учесть направление подлета и заданную взлетно-посадочную полосу).
Если объекты движутся к общим (определенным, заданным) целям, их конечные координаты близки. Таким образом, траектории объектов формируют сходящиеся пучки многомерных пространственных траекторий движения как, например, в случае посадочных траекторий самолетов, приземляющихся на заданную ВПП (см. Фиг. 1б). В общем случае траектории в таких пучках имеют множественные пересечения. Схождение пучка определяется параметром порога. Параметр порога для пучка траекторий не превышает ширины ВПП.
Анализ безопасности полетов гражданской авиации РФ, проведенный Федеральным Агентством Воздушного Транспорта (управление инспекции по безопасности полетов) показывает, что случаи невыдерживания безопасной траектории снижения на конечном этапе захода на посадку, маневрирование на этапе посадки (повышенная скорость, отклонения от глиссады) и выкатывание за пределы ВПП представляют наибольшую угрозу для безопасности полетов, поскольку даже незначительное отклонение от безопасного маршрута может приводить к крушению самолета, особенно, если аэропорт находится в зоне сложного географического ландшафта.
В настоящем изобретении предлагается способ секторизации воздушного пространства в трехмерном случае, который позволяет определить опорную траекторию посадки ЛА (так называемую, усредненную траекторию или центроид) и выбросы - траектории пучка, наиболее удаленные от центральной, движение по которым потенциально находится в зоне риска.
Анализ траекторий движения самолетов часто используется в системах управления и безопасности воздушного трафика (airtraffic management). В частности, на основании анализа данных об успешных посадках однотипных самолетов выводятся дальнейшие траектории движения (см. US 9020662) и определяются траектории, наиболее оптимальные в данных метеорологических условиях (см. US 8977484).
Однако упомянутые методы обладают рядом недостатков, связанных, в первую очередь, с существенным сокращением размерности анализируемых данных, а также с использованием в качестве меры близости траекторий самолетов Евклидовой меры. Евклидова мера близости не учитывает эти особенности и не позволяет разделять пересекающиеся, но различные по геометрии траектории движения. Алгоритмы кластеризации [1], используемые для решения задачи секторизации в настоящее время, не могут быть применены на практике, т.к. не позволяют получить устойчивых результатов.
В настоящем изобретении предлагается новый способ [2, 3] обработки многомерных траекторий движущихся объектов с общими целями и близкими конечными координатами с целью выделения объектов с общими целями. Настоящее изобретение позволяет при применении ЭВМ к данным о зарегистрированных характеристиках движения объекта (например, летательного аппарата (ЛА)) выделять асимптотически сходящиеся пучки траекторий многомерных пространственных траекторий движения - посадки ЛА на заданные ВПП. Способ основан на определении геометрической асимптоты, касательной выделяемому пучку траекторий, в пространстве меньшей размерности. Пучок траекторий (после определения касательной к нему в пространстве меньшей размерности) выделяется в результате обратного перехода в пространство исходной размерности. Таким образом, не происходит потери размерности данных. Такой подход при его применении к реальным данным (например, данным радара) позволяет получать устойчивые результаты и решать задачу секторизации воздушного пространства зоны аэропорта в трехмерном случае.
Принципиальным отличием настоящего изобретения от известных аналогов является использование в качестве меры близости пространственных траекторий экспериментальной меры сходства траекторий движения - меры косинуса как на этапе определения касательной к пучку траекторий, так и при выделении пучка траекторий, центральной траектории пучка.
Использование меры косинуса позволяет учитывать особенности пространственной геометрии многомерных траекторий и разделять пересекающиеся, но различные по геометрии траектории движения и, таким образом, точно выделять пучки траекторий (решать задачу секторизации воздушного пространства в трехмерном случае) и определять в выделенных пучках траекторий усредненные траектории (центральные траектории или центроиды).
Под усредненной траекторией (центральной траекторией, центроидом) следует понимать возможную траекторию движения ЛА, связанную с асимптотическим поведением траекторий сходящегося пучка многомерных траекторий движения при заданном значении параметра порога, которая представляет собой пространственное усреднение всех траекторий в выделенном пучке.
Под выбросами следует понимать траектории асимптотически сходящихся пучков многомерных траекторий, наиболее удаленные от соответствующих центроидов по мере косинуса. В контексте решения задач обеспечения безопасности можно говорить, что выделяемая таким образом траектория асимптотически сходящегося пучка многомерных траекторий является граничной (минимально допустимой), т.е. потенциально опасной траекторией.
Задача, решаемая в рамках настоящего изобретения, связана с дальнейшим совершенствованием методов управления и контроля движения объектов в заданных направлениях (например, в случае захода летательных аппаратов (ЛА) на посадку). Технический результат, достигаемый при решении такой задачи, заключается в определении числа целей движения объектов и выделении областей пространства, соответствующих траекториям движения объектов к таким целям. Практический аспект такого результата может быть связан с повышением безопасности движения объектов (в частности, полетов ЛА), например, предотвращением конфликтных ситуаций при задании траекторий движения объектов в ограниченной области пространства и снижением числа внештатных (аварийных) ситуаций.
Поставленный результат в общем виде достигается заявленным способом последовательного определения усредненных траекторий движения материальных объектов в трехмерном пространстве в выделенных направлениях, включающим последовательность следующих этапов:
(1) регистрацию объектов с набором параметров движения, включающих, по меньшей мере, пространственные координаты и скорость движения в последовательные моменты времени, выделение из зарегистрированного набора тех объектов, параметры движения которых характеризуются снижением скорости движения, свидетельствующим об окончании движения, формирование выборки траекторий движения выделенных объектов на основании набора параметров их движения, определение необходимости выравнивания траекторий выборки во времени и, при необходимости - выравнивание;
(2) представление траекторий сформированной выборки в виде набора точек, составлявших каждую траекторию, формирование двумерной ортогональной проекции набора точек;
(3) по меньшей мере, однократное упорядочение точек сформированной проекции в направлении возрастания или убывания значения одной из координат, анализ для упорядоченных точек сформированной проекции наиболее правдоподобной модели ортогональной линейной регрессии с определением геометрической асимптоты при заданном параметре порога и выделение в сформированной выборке асимптотически сходящегося с параметром порога пучка траекторий движения материальных объектов в трехмерном пространстве на основании меры близости траекторий выборки к определенной выше геометрической асимптоте, при этом мера близости определяется по мере косинуса при заданном параметре порога и вычисляется в диапазоне значений от 0 до +1, а выделенный пучок содержит, по меньшей мере, две траектории движения материальных объектов в трехмерном пространстве;
(4) определение в выделенном пучке усредненной траектории движения материального объекта в трехмерном пространстве из условия того, что сумма квадратов расстояний от такой траектории до всех траекторий пучка, вычисленных по мере косинуса, минимальна;
(5) удаление выделенного пучка из сформированной выборки траекторий и повторение этапов (3)÷(5).
Варианты реализации способа предполагают, что материальным объектом является летательный аппарат (ЛА), а выделенным направлением - посадочная траектория такого аппарата, при этом параметр порога определяется шириной взлетно-посадочной полосы.
Изобретение иллюстрируется принципиальной блок-схемой, отображающей этапы реализации способа (фиг. 1), и фиг. 2-5, иллюстрирующими практическую осуществимость заявленного способа. В частности, на фиг. 2а показан общий вид пучков многомерных пространственных траекторий посадки самолетов на полосы аэродрома, на фиг. 2б - пучки посадочных траекторий, соответствующие различным взлетно-посадочным полосам (ВПП). Трехмерное представление посадочных траекторий, регистрируемых радаром, представлено на фиг. 3а, на фиг. 3б - разбиение этих траекторий на пять кластеров, выполняемое по методу полиномиальных регрессий [4, 5]. Далее траектории каждого кластера считаются выборкой траекторий, в которой возможно выделение пучков. На фиг. 4 рассматриваются проекции на координатные оси траекторий выборки, соответствующей розовому кластеру на фиг. 3б. Фиг. 5 иллюстрирует последовательные этапы выделения пучков многомерных пространственных траекторий в выборке, представленной на фиг. 4.
Раскрывая возможность реализации заявленного назначения и практической осуществимости заявленного решения, в настоящем описании устанавливается, что траектории движения материальных объектов в трехмерном пространстве в выделенных направлениях или многомерные траектории движения объектов (например, летательных аппаратов (ЛА), подводных судов и т.п.), представляемые многомерными векторами, вычисляются на основании регистрируемых в соответствующие моменты времени метаданных, содержащих, в частности, пространственные координаты (например, координаты положения центра масс, скорость, высота полета и т.п.). Последовательность регистрируемых метаданных определяет многомерные пространственные траектории движения объекта (которые далее кратко называются траекториями движения). Многомерность определяется длинной траектории и числом используемых параметров метаданных.
Необходимо отметить, что настоящее изобретение применяется при анализе данных о движении объектов к определенным (одинаковым, заданным) целям. Примером такого движения являются посадки ЛА на заданные взлетно-посадочные полосы (ВПП). В общем случае, если объекты движутся к общей цели, то траектории их движения образуют пучок многомерных пространственных траекторий движения (который далее кратко называется пучок траекторий), при этом в пучке траектории движения могут пересекаться. Для целей раскрытия осуществимости настоящего изобретения устанавливается, что пучок траекторий считается сходящимся (и кратко называется сходящимся пучком траекторий), если траектории движения в пучке имеют общую цель и близки по конечным координатам (например, при анализе посадочных траекторий ЛА - на плоскости посадки), при этом схождение пучка траекторий определяется параметром порога. При анализе траекторий посадок ЛА в зоне аэропорта (см. фиг. 2а) возможно выделение сходящихся пучков траекторий - посадок на заданные ВПП (см. фиг. 2б), при этом в общем случае параметр порога не превышает ширины ВПП.
Достижение поставленного результата связано с вышеупомянутыми особенностями анализируемых данных и обусловлено последовательным определением геометрических асимптот соответствующих пучков траекторий посредством определения наиболее правдоподобных ортогональных линейных регрессий, которое, в свою очередь, выполняется при переходе к рассмотрению двумерной проекции точек траекторий движения. В результате такого перехода происходит существенное сокращение размерности исходных данных. Следует отметить, что такое сокращение размерности данных не приводит к потере информации, поскольку после определения геометрической асимптоты происходит обратный переход в исходное пространство, где при ограничении параметра порога и в соответствии с мерой косинуса между траекториями выборки и определенной в пространстве меньшей размерности геометрической асимптотой выделяется соответствующий ей пучок траекторий.
Оценка асимптоты пучка траекторий
Формально пучок траекторий 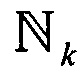 ,
, 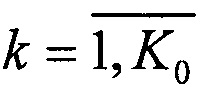 (K0 - эмпирический параметр) считается асимптотически сходящимся с параметром порога, если для векторов
(K0 - эмпирический параметр) считается асимптотически сходящимся с параметром порога, если для векторов 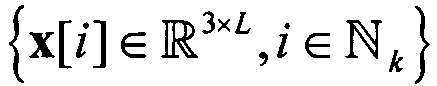 , представляющих пучок траекторий
, представляющих пучок траекторий 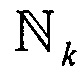 ,
, 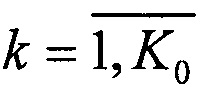 , выполняется условие асимптотического схождения пучка
, выполняется условие асимптотического схождения пучка
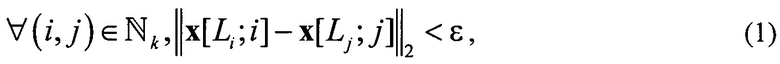
где 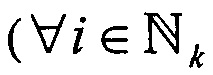 ,
, 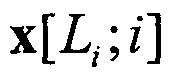 - координаты точек траекторий, которые почти совпадают, т.е. параметры Li,
- координаты точек траекторий, которые почти совпадают, т.е. параметры Li, 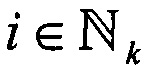 подлежат определению,
подлежат определению, 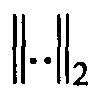 - евклидова мера расстояния в трехмерном пространстве
- евклидова мера расстояния в трехмерном пространстве  , ε - порог (который при рассмотрении сходящихся пучков, образуемых траекториями посадки ЛА, не превосходит ширины ВПП).
, ε - порог (который при рассмотрении сходящихся пучков, образуемых траекториями посадки ЛА, не превосходит ширины ВПП).
Рассматривая заявленный подход к определению числа сходящихся пучков многомерных траекторий, первоначально следует принять во внимание, что траектории в асимптотически сходящихся пучках имеют типичную форму (профиль) и характерную геометрическую асимптоту в области сходимости траекторий (1) [6]. Геометрической асимптотой сходящегося пучка многомерных посадочных траекторий самолетов является линия в  (трехмерное пространство координат), удовлетворяющая условию (1). Траектории в асимптотически сходящихся пучках имеют касательную в окрестности конечных точек
(трехмерное пространство координат), удовлетворяющая условию (1). Траектории в асимптотически сходящихся пучках имеют касательную в окрестности конечных точек 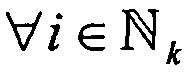 , x[Li;i] всех траекторий пучка с порогом ε (1)) [6], так что асимптотически сходящиеся пучки траекторий могут быть идентифицированы посредством определения касательных им геометрических асимптот в точках их фокусов.
, x[Li;i] всех траекторий пучка с порогом ε (1)) [6], так что асимптотически сходящиеся пучки траекторий могут быть идентифицированы посредством определения касательных им геометрических асимптот в точках их фокусов.
Поскольку дискретные точки траекторий пучка плотно лежат в окрестности асимптоты, основа предлагаемого способа определения числа пучков сходящихся многомерных пространственных траекторий движения объектов состоит в том, что набор векторов выборки многомерных траекторий 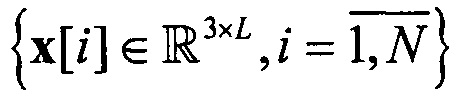 рассеивается во множество точек этих траекторий
рассеивается во множество точек этих траекторий
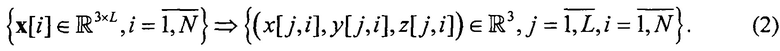
Множество точек (2) должно быть упорядочено по значениям одной из координат (в направлении возрастания - ascend или убывания - descend). При этом происходит упорядочение по остальным координатам всех точек, представляющих сходящийся пучок траекторий по определенному профилю. После этого для рассеянных трехмерных данных 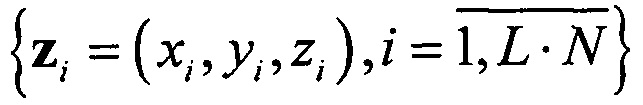 (2), например, с помощью алгоритма RANSAC (Random Sample and Consensus - случайная выборка и консенсус) [7, 8], анализируются модели ортогональной линейной регрессии
(2), например, с помощью алгоритма RANSAC (Random Sample and Consensus - случайная выборка и консенсус) [7, 8], анализируются модели ортогональной линейной регрессии
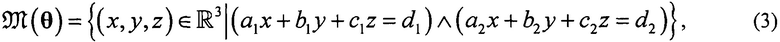
где ∧ - конъюнкция, θ={а1,b1, с1, d1, а2, b2, с2, d2} - вектор параметров этих моделей при заданном пороге евклидового расстояния 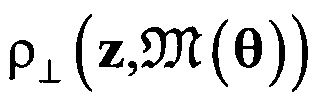 , вычисляемого по ортогональной проекции точки z=(x,y,z) из (2) на линию
, вычисляемого по ортогональной проекции точки z=(x,y,z) из (2) на линию 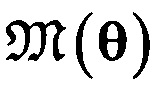 . Таким образом, модель (3) симметрична относительно координат x,y,z. Для выдвижения гипотезы относительно модели ортогональной линейной регрессии (3) достаточно любой пары точек из (2). Окончательная модель (3) подтверждается наибольшим относительным количеством (процентом) рассеянных данных
. Таким образом, модель (3) симметрична относительно координат x,y,z. Для выдвижения гипотезы относительно модели ортогональной линейной регрессии (3) достаточно любой пары точек из (2). Окончательная модель (3) подтверждается наибольшим относительным количеством (процентом) рассеянных данных 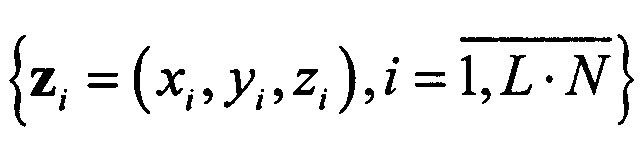 (2). Для данных целей может быть использован алгоритм MLESAC (Maximum Likelihood Estimation Sample Consensus - консенсус выборок с оценкой по максимуму правдоподобия) [9, 10] - вероятностная версия алгоритма RANSAC. Этот алгоритм оценивает правдоподобие модели (3), представляя распределение расстояния рассеянных данных
(2). Для данных целей может быть использован алгоритм MLESAC (Maximum Likelihood Estimation Sample Consensus - консенсус выборок с оценкой по максимуму правдоподобия) [9, 10] - вероятностная версия алгоритма RANSAC. Этот алгоритм оценивает правдоподобие модели (3), представляя распределение расстояния рассеянных данных 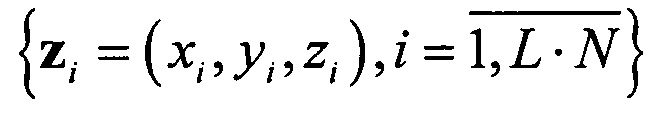 от модели
от модели 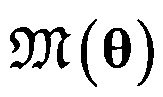 (3) как смесь распределения данных, подтверждающих модель (3) (inliers), и распределения данных, отклоняющих эту модель (outliers). Считая, что рассеянные данные
(3) как смесь распределения данных, подтверждающих модель (3) (inliers), и распределения данных, отклоняющих эту модель (outliers). Считая, что рассеянные данные 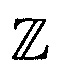 (2) независимые, получаем выражение для логарифма правдоподобия в виде
(2) независимые, получаем выражение для логарифма правдоподобия в виде
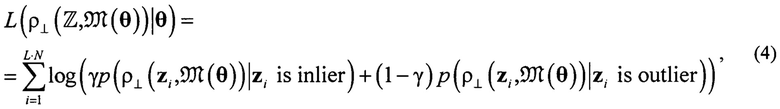
где γ - параметр смешивания. Распределение расстояний до данных, подтверждающих модель (3), представляется гауссовым распределением
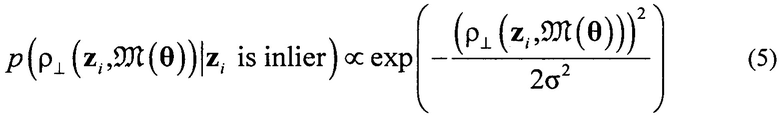
где σ - стандартное отклонение. Распределения расстояний до данных, отклоняющих модель (3), описывается равномерным распределением
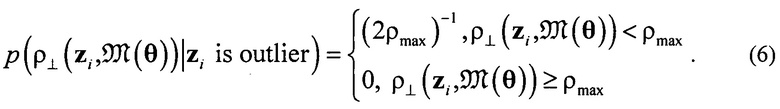
где ρmax - наибольшее расстояние до данных (определяется контекстом). Минимизация логарифма правдоподобия (4) позволяет оценить вектор параметров θ и параметр смешивания γ, что обеспечивается итерациями алгоритма ожидания-максимизации правдоподобия.
Для специалиста очевидно, что при определении геометрической асимптоты 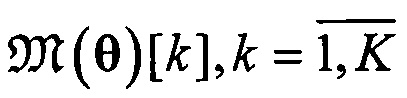 (3) одного из пучков при условии (1) помимо рассматриваемых в настоящей заявке алгоритмов могут быть использованы и другие методы.
(3) одного из пучков при условии (1) помимо рассматриваемых в настоящей заявке алгоритмов могут быть использованы и другие методы.
Наиболее правдоподобная линейная регрессия рассеянных данных выборки траекторий определяет геометрическую асимптоту 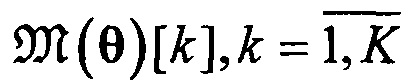 (3) одного из его пучков при условии (1). Полученная таким образом геометрическая асимптота удовлетворяет условию
(3) одного из его пучков при условии (1). Полученная таким образом геометрическая асимптота удовлетворяет условию
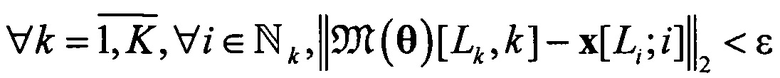 .
.
Выделение пучка траекторий
Касательный выделенной геометрической асимптоте пучок траекторий определяется в результате нахождения минимума целевой функции
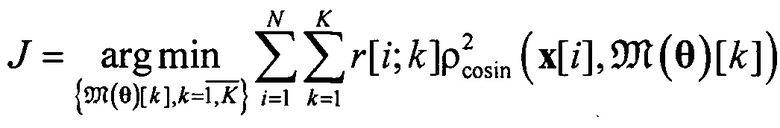 ,
,
где 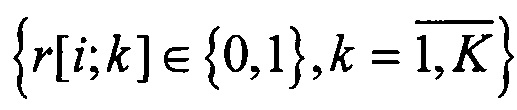 ,
,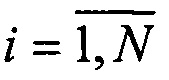 - набор бинарных индикаторных переменных (т.е. если вектор x[i] назначен пучку k, то r[i;k]=1 и r[i;k]=0 в противном случае). Расстояние между геометрической асимптотой и траекториями выборки вычисляется по мере косинуса
- набор бинарных индикаторных переменных (т.е. если вектор x[i] назначен пучку k, то r[i;k]=1 и r[i;k]=0 в противном случае). Расстояние между геометрической асимптотой и траекториями выборки вычисляется по мере косинуса
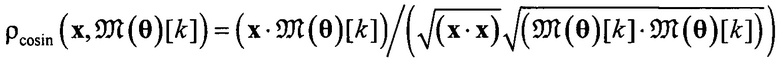 .
.
После удаления из рассеянных данных (2) тех точек, которые представляют траектории выделенного пучка, процедура определения геометрической асимптоты повторяется и выделяется следующий пучок траекторий. Поскольку определение модели (3) должно быть симметричным относительно координат x,y,z, при формировании рассеянных данных оставшихся траекторий в (2) производится сортировка по очередной пространственной координате по сравнению с использованной в (2) при определении предыдущей асимптоты (3). Возможная зависимость результата (3) от направления координат устраняется изменением направления сортировки в (2) с возрастания на убывание или наоборот. Анализ траекторий кластера завершается определением всех пучков в кластере.
В общем случае описанный выше подход к определению числа асимптотически сходящихся пучков многомерных пространственных траекторий движения состоит из двух этапов. Существенное уменьшение размерности данных на первом этапе упрощает обнаружение в данных характерных особенностей. При рассмотрении двумерных проекций рассеянных точек трехмерных траекторий определяется наиболее правдоподобная ортогональная линейная регрессия рассеянных данных, которая соответствует геометрической асимптоте одного из пучков в анализируемом наборе траекторий. На втором этапе выполняется обратный переход в пространство исходной размерности данных. При этом пучок траекторий выделяется из анализируемой выборки траекторий в соответствии с его близостью к выделенной асимптоте по мере косинуса. Таким образом, при таком подходе не происходит потери информации об исходных данных.
Определение усредненной траектории (центроида) для пучка траекторий
Центроид 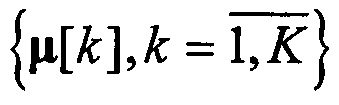 для пучка траекторий
для пучка траекторий 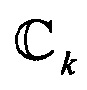 определяется на основе однократного применения формулы
определяется на основе однократного применения формулы
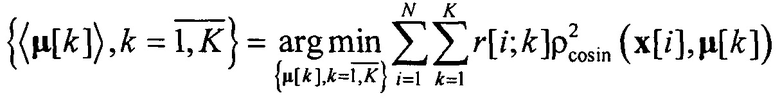
при условии
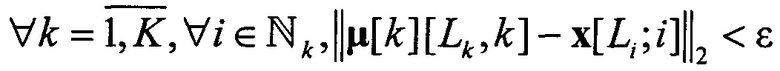
с использованием квадрата меры косинуса

Такая оценка эффективна при представлении векторов 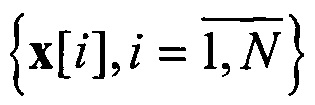 и
и 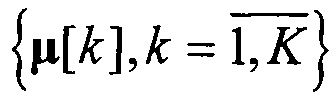 в исходном пространстве состояний.
в исходном пространстве состояний.
Именно использование меры косинуса в качестве меры близости между многомерными пространственными траекториями (например, посадочных траекторий ЛА) позволяет разделять пересекающиеся, но различные по геометрии многомерные траектории движения и обеспечивает точное определение центроидов для асимптотически сходящихся (потенциально пересекающихся) пучков многомерных траекторий при решении условной задачи оптимизации, при которой среднеквадратичное отклонение центроида от всех траекторий в пучке минимально по мере косинуса.
Помимо этого благодаря использованию меры косинуса в качестве меры близости между многомерными траекториями в пучке возможно определение так называемых выбросов, т.е. траекторий пучка, наиболее удаленных от центроида по мере косинуса.
Возможность практической реализации заявленного способа рассматривается на примере анализа данных 116 посадочных траекторий ЛА, зарегистрированных радаром TRACON 1 января 2006 г. над заливом Сан-Франциско (находятся в свободном доступе https://c3.nasa.gov/dashlink/resources/132/). Начало координат совпадает с положением радара, интервал времени между точками регистрации составляет порядка 5 с. В работе учитываются только 160 последних точек каждой траектории, что исключает случайные маневры самолетов перед заходом на посадку.
На фиг. 3а представлено исходное трехмерное представление анализируемых данных. Далее эти данные разбиваются на кластеры (см. фиг. 3б) по методу полиномиальных регрессий [4, 5] в соответствии со сходством формы и скоростных режимов. Распределение траекторий по кластерам следующее: 16 траекторий в розовом кластере, 13 - в зеленом, в синем, черном и красном кластерах - 3, 37 и 38 соответственно. Траектории каждого кластера соответствуют определенной выборке траекторий, в которой возможно выделение пучков траекторий, соответствующих определенным профилям посадки.
В качестве примера определим пучки траекторий выборки, определяемой розовым кластером (см. фиг. 4). Следует отметить, что пучки траекторий анализируемой выборки существенно пересекаются. Другой их особенностью является присутствие практически линейных участков в их хвостах вдали от фокуса. Поскольку все траектории в выборке имеют одинаковое направление времени, то при анализе этих траекторий используются рассеянные данные сокращенных траекторий с частью точек quotum ≈ 0.4, считая от фокусов пучков.
На фиг. 5а показаны выравненные во времени рассеянные данные двумерных проекций сокращенных траекторий выборки. На фиг. 5б - результат их линейной регрессии с использованием алгоритма MLESAC. На фиг. 5в определена асимптота первого пучка (голубая линия). Следует отметить, что в этом случае результаты ортогональной линейной регрессии рассеянных данных сокращенных и полных траекторий совпадают. Траектории первого (голубого) пучка (см. фиг. 5г) удаляются из выборки на основании близости траекторий к голубой асимптоте (рис. 5в) по мере косинуса. После удаления из выборки траекторий первого выделенного пучка в оставшейся части выборки аналогично определяется следующая асимптота (см. фиг. 5д-з) и соответствующий ей пучок траекторий. Далее траектории второго (зеленого) пучка удаляются из рассматриваемой выборки на основе близости траекторий движения к зеленой асимптоте по мере косинуса. На фиг. 5з представлены выделенные в рассматриваемой выборке в результате последовательных итераций три пучка траекторий движения (голубой, зеленый и синий). Толстая красная линия в центре каждого пучка соответствует центральной траектории в пучке.
Литература
1. Mcfadyen A. et al. Aircraft trajectory clustering techniques using circular statistics. IEEE Aerospace Conference (IEEE, Big Sky, MT, 2016) - 2016.
2. Solntseva-Chaley, M., New data mining technique for multidimensional aircraft trajectories analysis / Proceedings of International Conference on Big Data and its Applications (ICBDA 2016). September 2016, Moscow. V. 8. P. 1-7. http://dx.doi.org/10.1051/itmconf/20160801001
3. Кухаренко Б.Г., Солнцева-Чалей M.O. Моделирование центроидов для пучков многомерных траекторий // Информационные технологии. 2016 г. Т. 22. №2.
4. Gaffney S., Smyth P. Joint probabilistic curve clustering and alignment / Saul L., Weiss Y., Bottou L., eds. Proceedings of Neural Information Processing Systems (NIPS 2004). December 13-18, 2004, Vancouver, British Columbia, Canada. Advances in Neural Information Processing Systems. V. 17. Cambridge, MA: MIT Press. 2005. P. 473-480.
5. Кухаренко Б.Г., Солнцева M.O. Кластеризация управляемых объектов на основе сходства их многомерных траекторий // Информационные технологии. 2014. №5. С. 3-7.
6. Погорелов А.И. Дифференциальная геометрия. 6-е изд. М.: Наука. 1974.
7. Fischler М.A., Bolles R.С. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography // Communications of the ACM. - 1981. - T. 24. - №.6. - C. 381-395.
8. Zuliani M. RANSAC for Dummies // Vision Research Lab, University of California, Santa Barbara. - 2009.
9. Torr P.H.S., Zisserman A. MLESAC: A new robust estimator with application to estimating image geometry // Journal of Computer Vision and Image Understanding. 2000. V. 78, No. 1. P. 138-156.
10. Кухаренко Б.Г. Алгоритмы анализа изображений для определения локальных особенностей и распознавания объектов и панорам. Информационные технологии. 2011. №7. Приложение. С. 1-32.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОСАДОЧНЫХ ТРАЕКТОРИЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ, СООТВЕТСТВУЮЩИХ ОДНОЙ ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЕ | 2015 |
|
RU2616106C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОСАДОЧНОЙ ТРАЕКТОРИИ ЛЕТАТЕЛЬНОГО АППАРАТА НА ОСНОВАНИИ ДАННЫХ О ЗАРЕГИСТРИРОВАННЫХ ТРАЕКТОРИЯХ С ПРИМЕНЕНИЕМ В КАЧЕСТВЕ МЕРЫ СХОДСТВА ТРАЕКТОРИЙ МЕРЫ КОСИНУСА (ВАРИАНТЫ) | 2015 |
|
RU2616107C9 |
| Способ определения географических координат источников радиоизлучения в многоцелевой обстановке | 2021 |
|
RU2773307C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
| СПОСОБ ЗАЩИТЫ ОТ ПОДДЕЛКИ ЦЕННОГО ДОКУМЕНТА, ЦЕННЫЙ ДОКУМЕНТ, ЗАЩИЩЕННЫЙ ОТ ПОДДЕЛКИ, СПОСОБ ИДЕНТИФИКАЦИИ ЕГО ПОДЛИННОСТИ И УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ПОДЛИННОСТИ ЦЕННОГО ДОКУМЕНТА | 2010 |
|
RU2425757C1 |
| СПОСОБ БЕСКОНТАКТНЫХ ИЗМЕРЕНИЙ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБЪЕКТА В ПРОСТРАНСТВЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2551396C1 |
| Способ контроля пространственного положения участников спортивного события на игровом поле | 2016 |
|
RU2616152C1 |
| СПОСОБ РЕКОНСТРУКЦИИ ТРЕХМЕРНОГО ОБРАЗА ФИЗИЧЕСКОГО СОСТОЯНИЯ ОБЪЕКТА МОНИТОРИНГА В ИЗМЕРИТЕЛЬНОЙ ТОЧКЕ | 2010 |
|
RU2542589C2 |
| ИНТЕГРАЛЬНЫЙ ПИЛОТАЖНО-НАВИГАЦИОННЫЙ ДИСПЛЕЙ | 1991 |
|
RU2014250C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И УГЛОВ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА ОТНОСИТЕЛЬНО ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2378664C1 |
Изобретение относится к способу определения траекторий движения материальных объектов в трехмерном пространстве в выделенных направлениях. Для осуществления способа регистрируют объекты с определенным набором параметров движения, на основании которых формируют выборку траекторий, производят выравнивание траекторий при необходимости, формируют двумерную ортогональную проекцию набора точек, с помощью которого представляют сформированную выборку траекторий, производят упорядочивание точек сформированной проекции определенным образом, определяют усредненную траекторию в выделенном пучке. Обеспечивается выделение областей пространства, соответствующих траекториям движения объектов к выделенным целям их движения. 2 з.п. ф-лы, 5 ил. 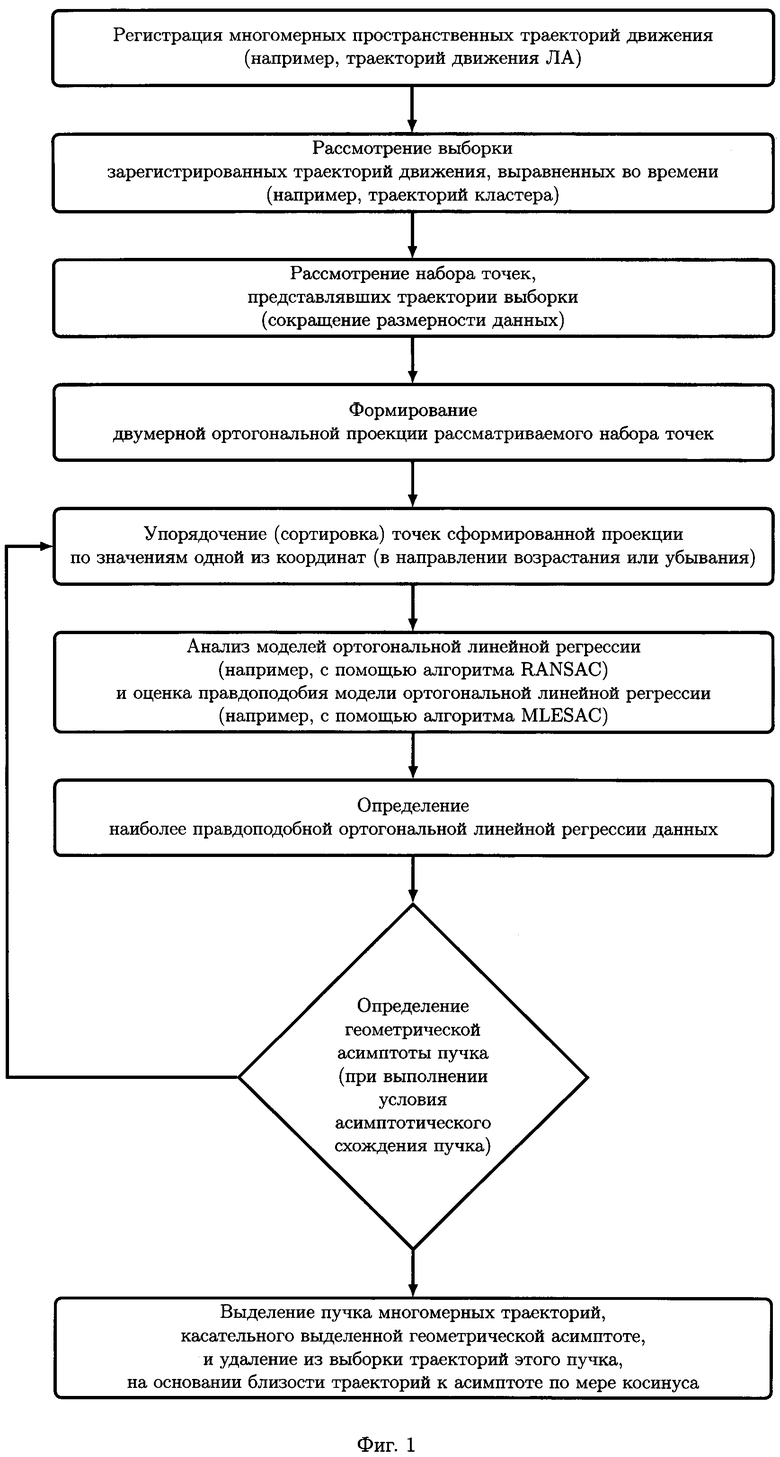
1. Способ последовательного определения усредненных траекторий движения материальных объектов в трехмерном пространстве в выделенных направлениях, включающий последовательность следующих этапов:
(1) регистрацию объектов с набором параметров движения, включающих, по меньшей мере, пространственные координаты и скорость движения в последовательные моменты времени, выделение из зарегистрированного набора тех объектов, параметры движения которых характеризуются снижением скорости движения, свидетельствующим об окончании движения, формирование выборки траекторий движения выделенных объектов на основании набора параметров их движения, определение необходимости выравнивания траекторий выборки во времени и, при необходимости - выравнивание;
(2) представление траекторий сформированной выборки в виде набора точек, составлявших каждую траекторию, формирование двумерной ортогональной проекции набора точек;
(3) по меньшей мере, однократное упорядочение точек сформированной проекции в направлении возрастания или убывания значения одной из координат, анализ для упорядоченных точек сформированной проекции наиболее правдоподобной модели ортогональной линейной регрессии с определением геометрической асимптоты при заданном параметре порога и выделение в сформированной выборке асимптотически сходящегося с параметром порога пучка траекторий движения материальных объектов в трехмерном пространстве на основании меры близости траекторий выборки к определенной выше геометрической асимптоте, при этом мера близости определяется по мере косинуса при заданном параметре порога и вычисляется в диапазоне значений от 0 до +1, а выделенный пучок содержит, по меньшей мере, две траектории движения материальных объектов в трехмерном пространстве;
(4) определение в выделенном пучке усредненной траектории движения материального объекта в трехмерном пространстве из условия того, что сумма квадратов расстояний от такой траектории до всех траекторий пучка, вычисленных по мере косинуса, минимальна;
(5) удаление выделенного пучка из сформированной выборки траекторий и повторение этапов (3)÷(5).
2. Способ по п. 1, в котором материальным объектом является летательный аппарат, а выделенным направлением - посадочная траектория такого аппарата.
3. Способ по п. 2, в котором параметр порога определяется шириной взлетно-посадочной полосы.
| US 20140019033, 16.01.2014 | |||
| Способ получения 4-аминомасляной кислоты или ее производных | 1979 |
|
SU902662A3 |
| US 2014188378, 03.07.2014 | |||
| US 8290696 B1, 16.10.2012 | |||
| СПОСОБ ФОРМИРОВАНИЯ МАНЕВРОВ ПРОИЗВОЛЬНОЙ КОНФИГУРАЦИИ НА КОНЕЧНОМ УЧАСТКЕ ТРАЕКТОРИИ ПЛАНИРУЮЩЕГО БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2013 |
|
RU2554568C2 |
Авторы
Даты
2018-04-19—Публикация
2017-01-16—Подача