Изобретение относится к области анализа данных, в частности, многомерных траекторий движения воздушных судов, регистрируемых радаром в зоне аэропорта, и может быть использовано для секторизации воздушного пространства, проектирования воздушных коридоров, моделирования и определения оптимальных (нормальных) траекторий захода на посадку воздушных судов, проектирования автоматических (беспилотных) систем захода на посадку (в частности, в условиях сложного географического ландшафта, а также в случае отсутствия глиссады планирования) и при решении задач выявления и предотвращения потенциальных конфликтов.
В связи с растущей загруженностью аэропортов, для оптимизации работы диспетчерских служб актуальна задача разделения воздушного пространства аэропорта на сектора и проектирование воздушных коридоров для полетов со сходными траекториями. Для этого необходимо учитывать установившееся разделение воздушного пространства по маршрутам и динамику воздушного движения.
Статистические данные Международной Организации Гражданской Авиации (ИКАО) показывают, что заход на посадку и посадка являются наиболее критическими этапами полета воздушного судна. Большинство авиационных происшествий с крупными воздушными судами происходит после выхода воздушного судна на направление взлетно-посадочной полосы (ВПП) и в пределах 19 км от нее. Анализ безопасности полетов гражданской авиации РФ, проведенный Федеральным Агентством Воздушного Транспорта (управление инспекции по безопасности полетов) показывает, что случаи невыдерживания безопасной траектории снижения на конечном этапе захода на посадку, маневрирование на этапе посадки (повышенная скорость, отклонения от глиссады) и выкатывание за пределы ВПП представляют наибольшую угрозу для безопасности полетов, поскольку даже незначительное отклонение от безопасного маршрута может приводить к крушению самолета, особенно, если аэропорт находится в зоне сложного географического ландшафта.
В настоящее время активно разрабатываются подходы, методы и системы, упрощающие пилотирование самолетов на конечном этапе посадки. Для этого применяются как системы управления полетами (flight management system), так и приборы автоматического выбора маршрута посадки (см. US 8489261). На заключительном этапе полета экипаж может задать бортовой системе один из вариантов захода на посадку. В этом случае бортовая система автоматически определяет координаты следования выбранной траектории.
Анализ траекторий движения самолетов используется в системах управления и безопасности воздушного траффика (airtraffic management). В частности, на основании анализа данных об успешных посадках однотипных самолетов выводятся дальнейшие траектории движения (см. US 9020662) и определяются траектории, наиболее оптимальные в данных метеорологических условиях (см. US 8977484).
Задачи анализа, классификации и кластеризации траекторий движения летательных аппаратов (ЛА) становятся все более актуальными для исследований, организации и оптимизации движения в зоне аэропорта. Неотъемлемой частью этих задач является группировка сходных траекторий в кластеры, сопровождаемая измерением расстояния между траекториями. Однако следует отметить, что на практике задачи объединения сходных траекторий решаются либо с помощью непосредственного анализа сходства текущей траектории с траекториям из базы данных, либо на основе кластеризации траекторий с использованием геометрических моделей близости траекторий, использующих, в частности, Евклидово расстояния в качестве меры близости.
В кластерах, полученных в результате разбиения воздушного пространства на сектора или группировки сходных траекторий, возможно выделение пучков траекторий (например, траекторий, соответствующих посадкам на заданную ВПП), в которых моделируются центральные траектории, называемые далее центроидами. Определение центроидов для пучков многомерных траекторий может выполняться различными способами.
В настоящее время для разделения воздушного пространства в зоне аэропорта, для группировки сходных траекторий и определения центроидов для пучков многомерных траекторий применяются, в частности, методы, основанные на диаграммах Вороного (Voronoi diagram [1]) и K-means кластеризации.
Первый из упомянутых методов предполагает, что пространство (например, воздушное пространство в зоне аэропорта или пространство векторов, представляющих траектории движения) разбивается на заданное число секторов или ячеек. Если пучки Nk, 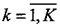 определяются кластерами Ck,
определяются кластерами Ck, 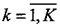 , полученными в результате геометрического разбиения пространства векторов
, полученными в результате геометрического разбиения пространства векторов 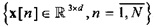 , d>>1 на ячейки «в стиле диаграмм Воронова», то центроиды пучков, полученных таким образом, определяются алгоритмом разбиения на заданное число кластеров (K-means algorithm) [2].
, d>>1 на ячейки «в стиле диаграмм Воронова», то центроиды пучков, полученных таким образом, определяются алгоритмом разбиения на заданное число кластеров (K-means algorithm) [2].
Метод кластеризации K-means предполагает, что для многомерных векторов 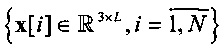 , представляющих многомерные траектории движения (L>>1 - длина траектории), при Евклидовой мере расстояния решается задача идентификации центроидов
, представляющих многомерные траектории движения (L>>1 - длина траектории), при Евклидовой мере расстояния решается задача идентификации центроидов 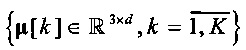 пучков многомерных траекторий, ассоциируемых с кластерами Ck,
пучков многомерных траекторий, ассоциируемых с кластерами Ck, 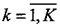 . В этом случае для набора центроидов сумма квадратов Евклидовых расстояний до векторов в соответствующих кластерах Ck,
. В этом случае для набора центроидов сумма квадратов Евклидовых расстояний до векторов в соответствующих кластерах Ck, 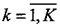 является минимальной. Для решения этой задачи в результате итеративного процесса минимизируется целевая функция алгоритма K-means, которая имеет вид:
является минимальной. Для решения этой задачи в результате итеративного процесса минимизируется целевая функция алгоритма K-means, которая имеет вид:
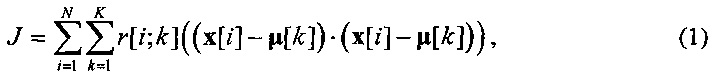
где «⋅» обозначает скалярное произведение векторов в пространстве состояний R3×L и 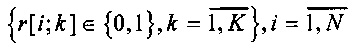 - набор бинарных индикаторных переменных принадлежности траектории кластеру. Если вектор x[i] назначен кластеру k, то r[i;k]=1, в противном случае r[i;k]=0, что также может быть записано в виде
- набор бинарных индикаторных переменных принадлежности траектории кластеру. Если вектор x[i] назначен кластеру k, то r[i;k]=1, в противном случае r[i;k]=0, что также может быть записано в виде 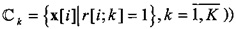 .
.
В алгоритме K-means для инициализации центроидов 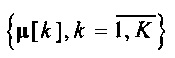 используются векторы
используются векторы 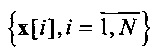 . Минимизация J (1) осуществляется последовательными итерациями, состоящими из двух шагов: оценки
. Минимизация J (1) осуществляется последовательными итерациями, состоящими из двух шагов: оценки 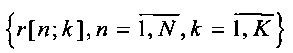 при фиксированных
при фиксированных 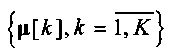 в замкнутой форме
в замкнутой форме
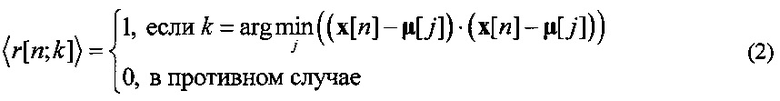
и оценки 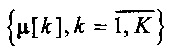 при фиксированных
при фиксированных 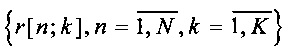
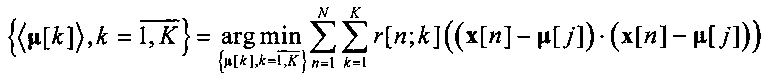
в замкнутой форме
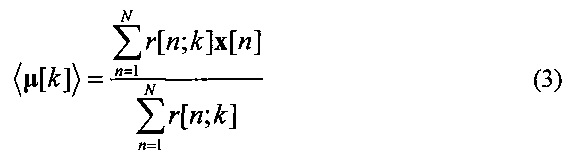
до достижения сходимости.
Применительно к задачам определения центроидов для пучков посадочных траекторий самолетов (т.е. при рассмотрении воздушного пространства зоны аэропорта) ограничения и недостатки указанных методов состоят в том, что:
выделяемые области пространства состояния R3×d имеют различное число граней, поэтому представление о геометрическом разбиении пространства векторов 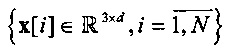 , d>>1 на ячейки в стиле диаграмм Воронова не отражает характер пучков траекторий (например, пучков посадочных траекторий самолетов);
, d>>1 на ячейки в стиле диаграмм Воронова не отражает характер пучков траекторий (например, пучков посадочных траекторий самолетов);
Евклидова мера расстояния между траекториями (в целом) в пространстве состояний R3×d плохо отображает сходство (различие) формы (профилей) траекторий в 3-мерном пространстве. Она велика для разнесенных в пространстве, но сходных траекторий и не разделяет пересекающиеся, но различные по геометрии траектории;
на практике, в R3 пучки траекторий пересекаются. При использовании Евклидовой меры расстояния особенности пространственной геометрии (например, возможные пересечения в пространстве, кривизна и кручение) многомерных траекторий не учитываются. К тому же, непосредственная реализация алгоритма K-means относительно медленная, поскольку на каждом шаге определения r[i;k], 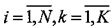 (2) вычисляется Евклидово расстояние между каждым вектором μ[k],
(2) вычисляется Евклидово расстояние между каждым вектором μ[k], 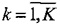 и каждым вектором x[i],
и каждым вектором x[i], 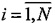 .
.
В целом, использование Евклидовой метрики в качестве меры близости между многомерными пространственными траекториями движения является общим существенным недостатком упомянутых выше и других известных подходов к анализу многомерных траекторий движения.
Таким образом, задача, решаемая при создании настоящего изобретения, направлена на дальнейшее совершенствование методов разделения воздушного пространства в зоне аэропорта на сектора с учетом установившихся потоков движения, систем автоматического (беспилотного) захода на посадку и проектирования воздушных коридоров для полетов со сходными посадочными траекториями, в частности, в повышении точности вывода (нацеливания) самолета на посадку, при этом технический результат, достигаемый при решении такой задачи, состоит в повышении безопасности полетов и снижении количества внештатных (аварийных) ситуаций применительно к случаям захода на посадку и посадки самолета.
Поставленный результат в первом из заявленных вариантов достигается предлагаемым способом определения оптимальных посадочных траекторий летательного аппарата (ЛА) для асимптотически сходящихся с параметром порога пучков многомерных пространственных посадочных траекторий с использованием меры косинуса, включающем сбор и регистрацию данных о характеристиках движения ЛА в единицу времени, вычисление на основании зарегистрированных характеристик многомерных пространственных посадочных траекторий движения ЛА, определение, по меньшей мере, одного, асимптотически сходящегося с параметром порога, пучка многомерных пространственных посадочных траекторий по мере косинуса, содержащего, по меньшей мере, две многомерные пространственные посадочные траектории и определение оптимальной, при котором оптимальной траекторией (центроидом) является траектория, сумма квадратов расстояний от которой до всех траекторий пучка, вычисленных по мере косинуса, минимальна, а параметр порога при асимптотическом схождении пучка не превышает ширины взлетно-посадочной полосы (ВПП).
Поставленный результат во втором из заявленных вариантов достигается предлагаемым способом определения минимально допустимых посадочных траекторий летательного аппарата (ЛА) для асимптотически сходящихся с параметром порога пучков многомерных пространственных посадочных траекторий с использованием меры косинуса, включающем сбор и регистрацию данных о характеристиках движения ЛА в единицу времени, вычисление на основании зарегистрированных характеристик многомерных пространственных посадочных траекторий движения ЛА, и определение, по меньшей мере, одного асимптотически сходящегося с параметром порога пучка многомерных пространственных посадочных траекторий по мере косинуса, при этом одна из траекторий в пучке является оптимальной (центроидом), при котором минимально допустимой (выбросом) является траектория в пучке, наиболее удаленная по мере косинуса от оптимальной, а разброс конечной точки такой потенциально опасной траектории относительно конечной точки оптимальной не превышает параметра порога, равного ширине взлетно-посадочной полосы.
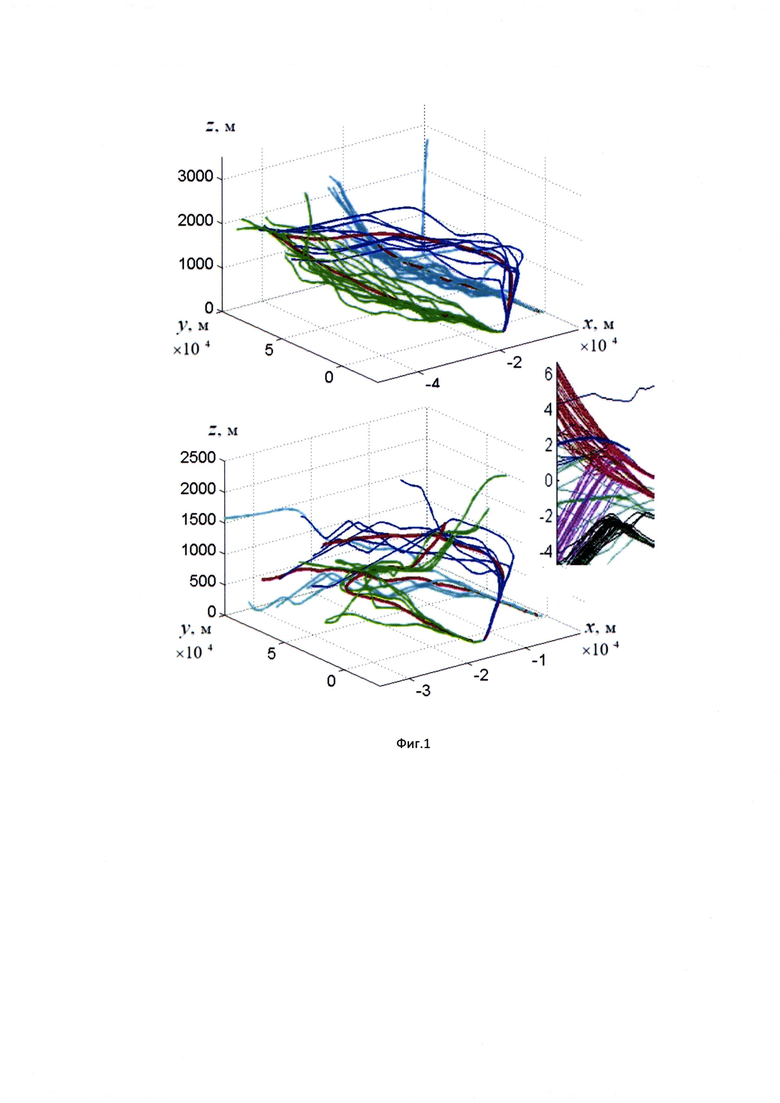
Изобретение иллюстрируется примером практического определения центроидов пучков траекторий посадки самолетов на полосы аэродрома (фиг. 1), а также блок-схемой, отображающей этапы выполнения вариантов способа (фиг. 2).
Возможность достижения заявленного результата обусловлена использованием меры косинуса как экспериментальной меры сходства многомерных пространственных посадочных траекторий движения ЛА (например, самолетов) для оценки асимптотически сходящихся пучков многомерных траекторий движения, их центроидов и выбросов (значение терминов будет пояснено ниже). Выбросами можно считать траектории пучка многомерных траекторий, наиболее удаленные от соответствующих центроидов по мере косинуса при решении условной задачи оптимизации оценки центроидов асимптотически сходящихся пучков многомерных посадочных траекторий. Другими словами, мера косинуса используется для оценки близости возможно пересекающихся пространственных траекторий движения в потенциально пересекающихся пучках многомерных траекторий.
В отличие от Евклидовой меры расстояния, мера косинуса, применяемая в качестве экспериментальной меры сходства многомерных пространственных траекторий (например, посадочных траекторий ЛА), учитывает особенности пространственной геометрии многомерных траекторий (их потенциальные пространственные пересечения, кривизну и кручение) и позволяет разделять пересекающиеся, но различные по геометрии многомерные траектории движения.
Раскрывая возможность реализации заявленного назначения и практической осуществимости решения, в настоящем описании устанавливается, что многомерные посадочные траектории движения ЛА, представляемые многомерными векторами, вычисляются на основании регистрируемых в соответствующие моменты времени метаданных, содержащих, в частности, пространственные координаты ЛА (например, координаты положения центра масс) и скорость движения ЛА. Последовательность мета-данных, регистрируемых радаром в зоне аэропорта, определяет многомерные траектории движения ЛА (которые далее кратко называются многомерными траекториями). Многомерность определяется длинной траектории и числом используемых параметров мета-данных (например, пространственные координаты ЛА, скорость в соответствующие моменты времени и др.).
Траектории движения ЛА, в частности, в зоне аэропорта, подразделяются на траектории взлета и посадки, которые в свою очередь образуют пучки многомерных траекторий. Многомерные траектории посадки на полосы аэродрома образуют пучки многомерных посадочных траекторий. При этом траектории в пучках могут пересекаться в пространстве. Пучок многомерных траекторий движения считается сходящимся, если многомерные траектории в пучке имеют общую цель и близки по конечным координатам (например, на плоскости посадки). В частности, наборы трехмерных пространственных траекторий самолетов при заходе на заданные взлетно-посадочные полосы являются примером сходящихся пучков многомерных траекторий. Схождение пучка многомерных траекторий определяется параметром порога, который не превышает ширины взлетно-посадочной полосы.
Под центроидом или оптимальной (нормальной, опорной) траекторией следует понимать возможную траекторию движения ЛА, связанную с асимптотическим поведением траекторий сходящегося пучка многомерных траекторий движения при заданном значении параметра порога.
Под выбросами следует понимать траектории асимптотически сходящихся пучков многомерных траекторий, наиболее удаленные от соответствующих центроидов по мере косинуса. В контексте решения задач обеспечения безопасности можно говорить, что выделяемая таким образом траектория асимптотически сходящегося пучка многомерных траекторий является граничной (минимально допустимой), т.е. потенциально опасной траекторией.
Пучок многомерных траекторий считается асимптотически сходящимся с параметром порога, если для векторов 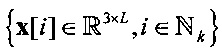 , представляющих пучок многомерных траекторий Nk,
, представляющих пучок многомерных траекторий Nk, 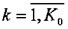 (K0 - эмпирический параметр), выполняется условие асимптотического схождения пучка
(K0 - эмпирический параметр), выполняется условие асимптотического схождения пучка
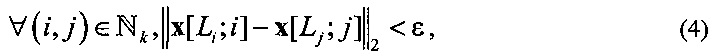
где (∀i ∈ Nk, x[Li;i] - координаты точек траекторий, которые почти совпадают, т.е. параметры Li, i∈Nk подлежат определению, 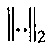 - евклидова мера расстояния в трехмерном пространстве R3, ε - порог, не превосходит ширины взлетно-посадочной полосы в случае настоящего изобретения.
- евклидова мера расстояния в трехмерном пространстве R3, ε - порог, не превосходит ширины взлетно-посадочной полосы в случае настоящего изобретения.
Траектории в асимптотически сходящихся пучках имеют типичную форму (профиль) и характерную геометрическую асимптоту в области сходимости траекторий (4) [3].
Геометрической асимптотой сходящегося пучка многомерных посадочных траекторий самолетов является линия в R3 (трехмерное пространство координат), удовлетворяющая условию (4).
Траектории в асимптотически сходящихся пучках имеют касательную в окрестности конечных точек ∀i ∈ Nk, x[Li;i] всех траекторий пучка с порогом ε (4)) [3].
Центроиды 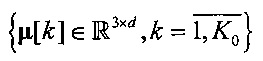 асимптотически сходящихся пучков также удовлетворяют условию типа (4) в виде
асимптотически сходящихся пучков также удовлетворяют условию типа (4) в виде
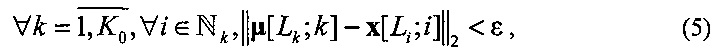
где параметры Li, i∈Nk и Lk, 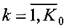 подлежат определению.
подлежат определению.
Следует отметить, что в настоящее время при определении центроидов для сходящихся пучков многомерных траекторий существует жесткая взаимозависимость между определением центроидов и соответствующих им асимптотически сходящихся пучков многомерных траекторий. Как было упомянуто выше, известны двухшаговые методы независимого определения сходящихся пучков и последующего определения центроидов для уже определенных пучков многомерных траекторий движения. Например, определение центроидов и пучков многомерных траекторий с помощью алгоритма K-means. Однако этот метод обладает существенным недостатком: определение центроидов для асимптотически сходящихся пучков многомерных траекторий оказывается неустойчивым к случайным отклонениям (outliers). Также недостатки этого метода связаны с возможной неудачной инициализацией, в результате которой алгоритм может сходится не к глобальному, а к локальному минимуму, и с относительно медленной реализацией алгоритма K-средних, связанной с вычислением Евклидова расстояние между каждым вектором μ[k], 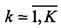 и каждым вектором x[i],
и каждым вектором x[i], 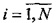 .
.
Необходимо отметить, что для точного определения центроидов и пучков многомерных посадочных траекторий, при решении задачи определения кластеров, представляющих пучки траекторий, минимизация целевой функции (1) должна производиться с учетов условия (5) в виде
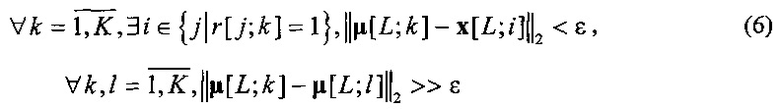
где 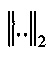 - евклидова мера расстояния в трехмерном пространстве R3.
- евклидова мера расстояния в трехмерном пространстве R3.
Существуют способы адаптации условной задачи оптимизации (1), (6) к анализу пучков пространственных траекторий. Возможно использование для центроидов 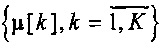 модели полиномиальной регрессии [4-5] или представление векторов
модели полиномиальной регрессии [4-5] или представление векторов 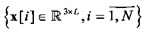 , L>>1 в пространствах абстрактных характеристик
, L>>1 в пространствах абстрактных характеристик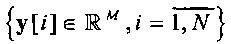 с евклидовой мерой расстояния [6-8]. При этом, вектора, представляющие пучки многомерных траекторий, которые геометрически неразделимы в исходном пространстве состояний R3×L, в пространствах абстрактных характеристик становятся разделимыми, поэтому в этих пространствах используется евклидова мера расстояния [9-10]. При отображении в исходное пространство состояний эта метрика становится неевклидовой.
с евклидовой мерой расстояния [6-8]. При этом, вектора, представляющие пучки многомерных траекторий, которые геометрически неразделимы в исходном пространстве состояний R3×L, в пространствах абстрактных характеристик становятся разделимыми, поэтому в этих пространствах используется евклидова мера расстояния [9-10]. При отображении в исходное пространство состояний эта метрика становится неевклидовой.
Примером неевклидовой меры расстояния для векторов траекторий в пространстве состояний, является, например, мера косинуса:
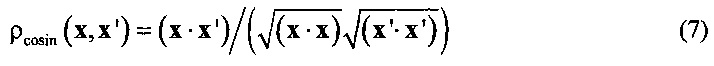
Указанная мера наиболее адекватно отражает близость векторов 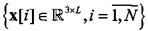 , L>>1 в пространстве состояний, представляющих пучки траекторий определенного профиля [11]. Поэтому, можно модифицировать задачу оптимизации (1), (6), заменив в (1) скалярное произведение на общую меру расстояния.
, L>>1 в пространстве состояний, представляющих пучки траекторий определенного профиля [11]. Поэтому, можно модифицировать задачу оптимизации (1), (6), заменив в (1) скалярное произведение на общую меру расстояния.
Таким образом, целевая функция обобщается введением общей меры расстояния ρ(x,x') между двумя векторами x, x'∈R3×L и минимизацией целевой функции
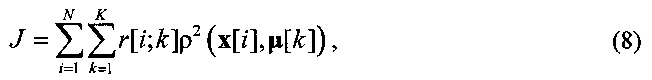
(K-medoids algorithm) [12].
При заданных центроидах 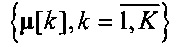 шаг оценки
шаг оценки 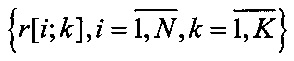 включает назначение каждого вектора x[i],
включает назначение каждого вектора x[i], 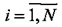 кластеру Ck,
кластеру Ck, 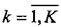 , для которого расстояние ρ(x[i],μ[k]) с соответствующим центроидом минимально
, для которого расстояние ρ(x[i],μ[k]) с соответствующим центроидом минимально
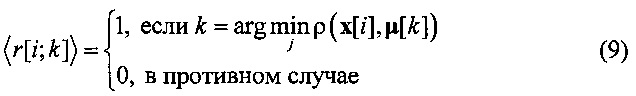
с оценкой вычислительной сложности O(K⋅N). Однако шаг оценки 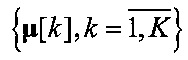 является потенциально более сложным.
является потенциально более сложным.
При стандартном ограничении, где каждый центроид является одним из векторов, назначенных соответствующему кластеру, условие (6) выполняется автоматически, что позволяет реализовать алгоритм для любого выбора меры расстояния ρ(x[i],μ[k:]), которая непосредственно вычисляется.
Шаг определения 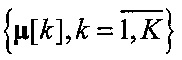 включает дискретный поиск по всем Nk векторам, назначенным этому кластеру Ck,
включает дискретный поиск по всем Nk векторам, назначенным этому кластеру Ck, 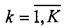 , и требует O(Nk2) оценок меры расстояния ρ(x[i],μ[k]).
, и требует O(Nk2) оценок меры расстояния ρ(x[i],μ[k]).
Отметим, что взаимосвязь центроидов и кластеров 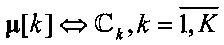 навязана логикой алгоритма K-средних и его обобщениями и, в принципе, центроиды
навязана логикой алгоритма K-средних и его обобщениями и, в принципе, центроиды 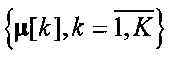 и кластеры Ck,
и кластеры Ck, 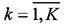 , представляющие пучки траекторий Nk,
, представляющие пучки траекторий Nk, 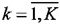 , могут определяться независимо.
, могут определяться независимо.
В качестве независимых методов оценки центроидов 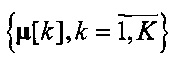 используются скрытые компоненты линейных и нелинейных динамических моделей (см. [13-14]), и скрытые последовательности Марковских моделей (см. [15-16]) при условии (6), затем пучки траекторий определяются по схеме
используются скрытые компоненты линейных и нелинейных динамических моделей (см. [13-14]), и скрытые последовательности Марковских моделей (см. [15-16]) при условии (6), затем пучки траекторий определяются по схеме 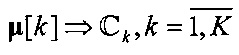 на основе однократного применения формулы (9) с мерой косинуса (7).
на основе однократного применения формулы (9) с мерой косинуса (7).
Оптимизация целевой функции алгоритма K-means с условием асимптотического схождения пучка позволяет определить центроиды для пучков пространственных траекторий. Для оценки пучков траекторий могут использоваться геометрические методы триангуляции, например [17, 18], затем центроиды 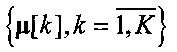 определяются по схеме
определяются по схеме 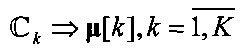 на основе однократного применения формулы
на основе однократного применения формулы
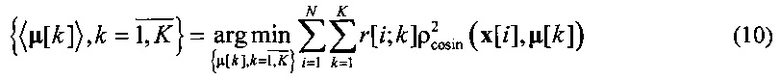
при условии (6) с использованием квадрата меры косинуса (7).
Оценка (10) эффективна при представлении векторов 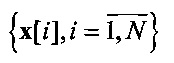 и
и 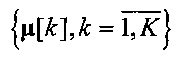 в исходном пространстве состояний.
в исходном пространстве состояний.
В качестве примера, с использованием заявленного способа определены центроиды пучков траекторий посадки самолетов на полосы аэродрома, представленные на фигуре. Показаны пучки многомерных посадочных траекторий самолетов, полученные с использованием меры косинусов в качестве меры близости траекторий на основании анализа данных (выборки) траекторий самолетов, идущих на посадку в международном аэропорту г. Сан-Франциско (США). Начало координат совпадает с положением радара, интервал времени между точками регистрации составляет порядка 5 с. Для целей исключения случайных маневров воздушных судов перед заходом на посадку, рассматривались траектории длинной 160 точек. Для выделенных пучков (голубой, зеленый и синий цвета), их центроиды показаны толстыми красными линиями. Видно, что траектории в пучках существенно пересекаются и закручены.
Таким образом, использование меры косинуса в качестве меры близости между многомерными пространственными траекториями (например, посадочных траекторий ЛА) позволяет разделять пересекающиеся, но различные по геометрии многомерные траектории движения и обеспечивает точное определение центроидов для асимптотически сходящихся (потенциально пересекающихся) пучков многомерных траекторий при решении условной задачи оптимизации, при которой среднеквадратичное отклонение центроида от всех траекторий в пучке минимально по мере косинуса.
Помимо этого, благодаря использованию меры косинуса в качестве меры близости между многомерными траекториями в пучке возможно определение, так называемых выбросов, т.е. траекторий пучка, наиболее удаленных от центроида по мере косинуса.
Литература
1. de Berg M., Cheong О., van Kreveld M., Overmars M. Computational Geometry. Algorithms and Applications. Third Edition. Berlin, Heidelberg: Springer-Verlag. 2008.
2. MacQueen J. Some methods for classification and analysis of multivariate observations / LeCam L.M., Neyman J., eds. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. University of California Press. 1967. V. 1. P. 281-297.
3. Погорелов А.И. Дифференциальная геометрия. 6-е изд. М.: Наука. 1974.
4. Gaffney S., Smyth P. Joint probabilistic curve clustering and alignment / Saul L., Weiss Y., Bottou L., eds. Proceedings of Neural Information Processing Systems (NIPS 2004). December 13-18, 2004, Vancouver, British Columbia, Canada. Advances in Neural Information Processing Systems. V. 17. Cambridge, MA: MIT Press. 2005. P. 473-480.
5. Кухаренко Б.Г., Солнцева-Чалей M.O. Кластеризация управляемых объектов на основе сходства их многомерных траекторий // Информационные технологии. 2014. №5. С. 3-7.
6. Anjum N., Cavallaro A. Trajectory clustering for scene context learning and outlier detection / Schonfeld D., Shan C, Tao D., Wang L., eds. Video Search and Mining. Berlin. Studies in Computational Intelligence. V. 287. Heidelberg: Springer. 2010. P. 33-51.
7. Кухаренко Б.Г., Солнцева M.O. Покомпонентный дискриминантный анализ результатов кластеризации многомерных траекторий. Информационные технологии. 2014. №11. С. 3-7.
8. Кухаренко Б.Г., Солнцева М.О. Итеративная кластеризация траекторий управляемых объектов в многомерном пространстве характеристик. Информационные технологии. 2014. №8. С. 11-16.
9. Chen G., Lerman G. Spectral curvature clustering (SCC) // International Journal on Computer Vision. 2009. V. 81, No. 3. P. 317-330.
10. Кухаренко Б.Г., Солнцева-Чалей M.O. Спектральный метод с использованием полярной кривизны для анализа результатов кластеризации многомерных траекторий. Информационные технологии. 2015. Т. 21. №11.
11. Listgarten J., Neal R.M., Roweis S.T., Emili A. Multiple alignment of continuous time series / Saul L.K., Weiss Y., Bottou L., eds. Proceedings of Neural Information Processing Systems (NIPS 2004). December 13-18, 2004, Vancouver, British Columbia, Canada. Advances in Neural Information Processing Systems. V. 17. Cambridge, MA: MIT Press. 2005. P. 5-13.
12. Hodgson M.E. Reducing computational requirements of the minimum-distance classifier // Remote Sensing of Environments. 1998. V. 25. P. 117-128.
13. Кухаренко Б.Г., Солнцева-Чалей M.O. Применение моделей непрерывного профиля для анализа результатов кластеризации многомерных траекторий. Информационные технологии. 2015. Т. 21. №8. С. 585-590.
14. Галанин М.П., Щеглов И.А. Разработка и реализация алгоритмов трехмерной триангуляции сложных пространственных областей: прямые методы. Препринт. М.: Институт прикладной математики им. М.В. Келдыша РАН. 2006.
15. Torr P.H.S., Zisserman A. MLESAC: A new robust estimator with application to estimating image geometry // Journal of Computer Vision and Image Understanding. 2000. V. 78, No. 1. P. 138-156.
16. Кухаренко Б.Г. Алгоритмы анализа изображений для определения локальных особенностей и распознавания объектов и панорам. Информационные технологии. 2011. №7. Приложение. С. 1-32.
17. Moore A.W. The anchors hierarch: using the triangle inequality to survive high dimensional data / Proceedings of the Twelfth Conference on Uncertainty in Artificial Intelligence. 2000. P. 397-405.
18. Dempster A., Laird N.M., Rubin D.B. Maximum likelihood from incomplete data via the EM algorithm // Journal of the Royal Statistical Society B. 1977. V. 39, No 1. P. 1-38.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОСАДОЧНЫХ ТРАЕКТОРИЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ, СООТВЕТСТВУЮЩИХ ОДНОЙ ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЕ | 2015 |
|
RU2616106C2 |
| СПОСОБ ПОСЛЕДОВАТЕЛЬНОГО ОПРЕДЕЛЕНИЯ УСРЕДНЕННЫХ ТРАЕКТОРИЙ ДВИЖЕНИЯ МАТЕРИАЛЬНЫХ ОБЪЕКТОВ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ | 2017 |
|
RU2651342C1 |
| СПОСОБ ПИЛОТИРОВАНИЯ ЛА ПО ЗАДАВАЕМОЙ ТРАЕКТОРИИ С ЗАДАВАЕМОЙ СКОРОСТЬЮ | 1997 |
|
RU2129699C1 |
| ПРЕЦИЗИОННАЯ СИСТЕМА ПОСАДКИ ДЛЯ НАВЕДЕНИЯ САМОЛЕТА ВДОЛЬ ЗАДАННОЙ ПОСАДОЧНОЙ ТРАЕКТОРИИ В ПРЕДЕЛАХ РАДИУСА ДЕЙСТВИЯ НАЗЕМНОГО ЗАПРОСЧИКА (ВАРИАНТЫ) | 1992 |
|
RU2100820C1 |
| СПОСОБ ЗАЩИТЫ ОТ ПОДДЕЛКИ ЦЕННОГО ДОКУМЕНТА, ЦЕННЫЙ ДОКУМЕНТ, ЗАЩИЩЕННЫЙ ОТ ПОДДЕЛКИ, СПОСОБ ИДЕНТИФИКАЦИИ ЕГО ПОДЛИННОСТИ И УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ПОДЛИННОСТИ ЦЕННОГО ДОКУМЕНТА | 2010 |
|
RU2425757C1 |
| УСТРОЙСТВО ДЛЯ ПРЕДОТВРАЩЕНИЯ СТОЛКНОВЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 1995 |
|
RU2153195C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И УГЛОВ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА ОТНОСИТЕЛЬНО ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ | 2014 |
|
RU2548366C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И УГЛОВ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНОГО АППАРАТА ОТНОСИТЕЛЬНО ВЗЛЕТНО-ПОСАДОЧНОЙ ПОЛОСЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2378664C1 |
| Способ формирования полетной траектории летательного аппарата | 2015 |
|
RU2611453C1 |
| ИНТЕГРАЛЬНЫЙ ПИЛОТАЖНО-НАВИГАЦИОННЫЙ ДИСПЛЕЙ | 1991 |
|
RU2014250C1 |
Группа изобретений относится к способам определения посадочных траекторий летательного аппарата (ЛА). Для определения оптимальной посадочной траектории ЛА регистрируют в соответствующие моменты времени пространственные координаты движения ЛА в единицу времени, вычисляют на основании зарегистрированных характеристик многомерные пространственные посадочные траектории движения ЛА, определяют асимптотически сходящийся с параметром порога пучок многомерных пространственных посадочных траекторий по мере косинуса, определяют посадочную оптимальную посадочную траекторию ЛА определенным образом. Для определения минимально допустимой траектории ЛА дополнительно к вышеперечисленным действиям определяют минимально допустимую посадочную траекторию в пучке (выброс) из следующих условий: минимально допустимая посадочная траектория наиболее удалена от оптимальной по мере косинуса и на плоскости посадки расстояние от конечной точки оптимальной посадочной траектории ЛА до конечной точки минимально допустимой посадочной траектории ЛА не превышает ширину ВПП. Обеспечивается повышение безопасности полетов и снижение количества аварийных ситуаций при посадке самолета. 2 н.п. ф-лы, 2 ил.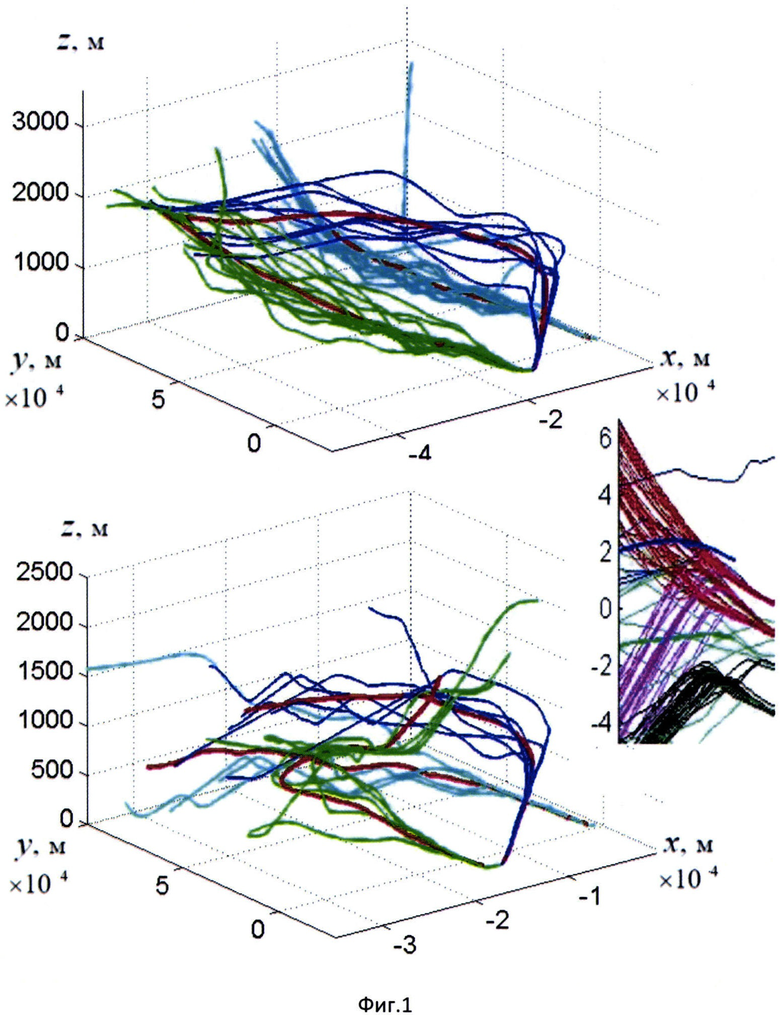
1. Способ определения оптимальной посадочной траектории летательного аппарата (ЛА), при котором регистрируют в соответствующие моменты времени пространственные координаты движения ЛА в единицу времени, вычисляют на основании зарегистрированных характеристик многомерные пространственные посадочные траектории движения ЛА, определяют по меньшей мере один, асимптотически сходящийся с параметром порога, пучок многомерных пространственных посадочных траекторий по мере косинуса, содержащий по меньшей мере две многомерные пространственные посадочные траектории, и определяют оптимальную посадочную траекторию летательного аппарата (центроида) из условия, при котором центроидом является траектория, сумма квадратов расстояний от которой до всех траекторий пучка, вычисленных по мере косинуса, минимальна, а параметр порога при асимптотическом схождении пучка не превышает ширины взлетно-посадочной полосы (ВПП).
2. Способ определения минимально допустимой траектории летательного аппарата (ЛА), при котором регистрируют в соответствующие моменты времени пространственные координаты движения ЛА в единицу времени, вычисляют на основании зарегистрированных характеристик многомерные пространственные посадочные траектории движения ЛА, выделяют по меньшей мере один асимптотически сходящийся с параметром порога пучок многомерных пространственных посадочных траекторий по мере косинуса, содержащий по меньшей мере две многомерные пространственные посадочные траектории,
определяют по мере косинуса в выделенном пучке оптимальную посадочную траекторию (центроид) движения ЛА,
определяют минимально допустимую посадочную траекторию в пучке (выброс) из следующих условий: минимально допустимая посадочная траектория наиболее удалена от оптимальной по мере косинуса;
на плоскости посадки расстояние от конечной точки оптимальной посадочной траектории ЛА до конечной точки минимально допустимой посадочной траектории ЛА не превышает параметра порога, равного ширине ВПП.
| US 8977484 B1, 10.03.2015 | |||
| US 9020662 B2, 28.04.2015 | |||
| РАДИОНАВИГАЦИОННАЯ СИСТЕМА ДЛЯ КОНТРОЛЯ ПОЛЕТА И ПОСАДКИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ "БАГИС-С" | 1995 |
|
RU2108613C1 |
| US 20140188378 A1, 03.07.2014 | |||
| US 8290696 B1, 16.10.2012. | |||
Авторы
Даты
2017-04-12—Публикация
2015-07-17—Подача