Изобретение относится к вычислительной технике и предназначено для выполнения операции умножения чисел, представленных в модулярно-позиционном формате с плавающей точкой на универсальных многоядерных процессорах.
Известен итерационный способ умножения чисел, представленных в одном из позиционных двоичных форматов с плавающей точкой, определенных стандартом IEEE-754. В этом способе умножение состоит из последовательности сложений с накоплением мантисс сомножителей, которые выполняются последовательно, сложения порядков и сложения по модулю два знаков сомножителей. Последовательность сложений с накоплением мантисс сомножителей выполняется следующим образом. При сдвигах мантиссы множителя освободившиеся разряды заполняются нулями. Если первый бит t-разрядной позиционной мантиссы множителя равен единице, то первое слагаемое является мантиссой множимого, иначе первое слагаемое равно нулю. Если второй бит мантиссы множителя равен единице, то второе слагаемое является мантиссой множимого, сдвинутой на один разряд влево, иначе второе слагаемое равно нулю. К сумме первого и второго слагаемого прибавляется мантисса множимого, сдвинутая на два разряда влево, если второй бит мантиссы множителя равен единице, иначе прибавляется нуль. Затем к полученной сумме прибавляется мантисса множимого, сдвинутая на три разряда влево, если третий бит мантиссы множителя равен единице, иначе прибавляется нуль. И так далее до t-го разряда мантиссы множителя, к накопленной сумме прибавляется мантисса множимого, сдвинутая на v разрядов влево, если t-ый бит мантиссы множителя равен единице, иначе прибавляется нуль. В итоге накопленная сумма является искомым произведением мантисс сомножителей. Далее выполняется сложение смещенных позиционных порядков сомножителей, тем самым получается порядок результата. Знак результата определяется сложением по модулю два знаков сомножителей.
Недостаток итерационного способа умножения позиционных двоичных чисел с плавающей точкой состоит в том, что, во-первых, при умножении мантисс выполняется t-1 операций суммирования t-разрядных операндов. Если принять, что операция суммирования t-разрядных операндов выполняется за t тактов процессора, то общее время выполнения операции умножения мантисс позиционных операндов с плавающей точкой составит t·(t-1) тактов. Во-вторых, процесс формирования суммы является последовательным процессом.
Техническим результатом применения способа организации выполнения операции умножения двух чисел в модулярно-позиционном формате представления с плавающей точкой на универсальных многоядерных процессорах является повышение скорости вычисления за счет замены операции умножения t-разрядных позиционных мантисс сомножителей n параллельно выполняемыми операциями умножения q-разрядных знакопозиций чисел в системе счисления в остаточных классах, причем q≈t/n. Если принять за время суммирования пары t-разрядных чисел t тактов работы процессора, а за время суммирования пары q-разрядных чисел q тактов работы процессора, то, при условии, что число вычислительных ядер универсального многоядерного процессора не меньше n, а операция умножения q-разрядных чисел может быть выполнена посредством q-1 операции сложения q-разрядных чисел, то предельное ускорение вычислений S составляет: 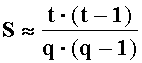
Описание способа организации выполнения операции умножения двух чисел в модулярно-позиционном формате представления с плавающей точкой на универсальных многоядерных процессорах: реализация способа осуществляется посредством подачи набора электрических, нейронных либо других сигналов на устройства управления каждого вычислительного ядра многоядерного процессора универсального назначения, которые, в соответствии с данными сигналами, формируют управляющие команды для операционных устройств соответствующих вычислительных ядер.
В позиционных двоичных форматах с плавающей точкой стандарта IEEE-754 любое вещественное число представляется трехэлементным набором:
где М- рациональная мантисса, е - порядок числа, еmin=2-2w-1 и еmax=2w-1-1, s - знак числа.
Величина чисел, записанных в таком формате, выражается формулой -1s·М·2е. Машинными представлениями чисел вида (1) являются (w+t+1) - разрядные двоичные векторы 〈srw…r2r1dt…d2d1〉, где разряды c d1 по dt отводятся под представление рациональных двоичных мантисс М=dt·dt-1…d2d1, разряды с r1, по rw отводятся под представление целочисленных двоичных порядков е, записанных в форме с избытком Е=rwrw-1…r2r1=е+еmax, разряд s выражает знак числа.
Определим целочисленную мантиссу М'=dtdt-1…d2d1 как t-разрядное неотрицательное целое двоичное число, такое что М=М'·21-t. Определим перемещенный порядок λ как целое двоичное число со знаком, такое, что λ=е-t+1, где е-w-разрядный порядок числа, представленного в двоичном формате (1).
Зададим n целочисленных положительных q-разрядных оснований системы остаточных классов Р1,Р2,…,Рn таких, что ∀i1,i2∈{l,2,…,n},i1≠i2:gcd(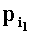
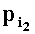
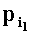
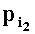
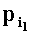
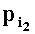
Целочисленную мантиссу М'=dtdt-1…d2d1 преобразуем в систему остаточных
классов с заданными основаниями р1,р2,…,рn, получая тем самым модулярную мантиссу 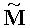
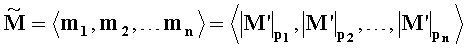
где mi∈[0,pi-1], i=1,2,…,n - q-разрядные цифры (модулярные разряды) модулярной мантиссы 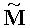
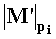
Таким образом, число с плавающей точкой вида (1) можно преобразовать к следующему модулярно-позиционному формату:
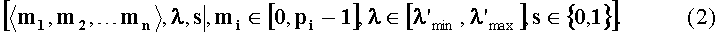
где (m1,m2,…,mn) - набор знакопозиций (модулярных разрядов) модулярной мантиссы 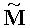
Диапазон допустимых значений модулярных мантисс 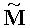
Примеры преобразования позиционных чисел с плавающей точкой в модулярно-позиционный формат: пусть числа представлены в 10-разрядном двоичном формате вида (1), в котором под смещенный порядок Е отводится четыре бита (максимальный порядок еmax=24-1-1=7, соответственно е=Е-7), под дробную часть мантиссы - пять бит (т.е. t=6, причем целая часть d6 рациональной мантиссы М в явном виде не записана) и под знак числа - один бит. Пусть для представления модулярных мантисс в модулярно-позиционном формате [〈m1,m2,…,mn〉,λ,s] используется три основания: p1=3=22-1, p2=7=23-1, p3=31=25-l.
Пример 1: необходимо перевести число Х=[1.5,-1,0]=-1°·1.5·2-1, представленное в двоичном формате [М,е,s], в модулярно-позиционный формат [〈m1,m2,…,mn〉,λ,s].
С учетом принятых характеристик двоичного формата [М,е,s], число Х будет записано в памяти ЭВМ в виде двоичного вектора 〈0011010000〉. Для его преобразования в модулярно-позиционный формат (2) необходимо выполнить следующие действия:
1. Выделить составные части числа X: знак числа s=0, дробная часть рациональной мантиссы d5…d2d1=100002, смещенный (избыточный) порядок Е=01102=6.
2. Восстановить целую часть d6 мантиссы M=d6.d5…d2d1: d6=1, т.к. Е>0, следовательно М=1.100002.
3. Определить порядок е: е=Е-еmax=6-7=-1, т.к. Е>0.
4. Определить перемещенный позиционный порядок λ и целочисленную мантиссу M':λ=e-t+1=-1-6+1=-6,M'=d6d5…d2d1=1100002=48.
5. Найти модулярную мантиссу 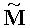
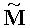
В результате получается число X, представленное в модулярно-позиционном формате с плавающей точкой: X=[〈0,6,17〉,-6,0]=-10·〈0,6,17〉·2-6.
Пример 2: необходимо перевести число X=[0.625-6,1]=-11·0.625·2-6 из двоичного формата [М,е,s] в модулярно-позиционный формат [〈m1,m2,…,mn〉,λ,s].
С учетом принятых характеристик двоичного формата [М,е,s], число Х будет записано в памяти ЭВМ в виде двоичного вектора 〈1000010100〉. Для его преобразования в модулярно-позиционный формат (2) необходимо выполнить следующие действия:
1. Выделить составные части числа X: знак числа s=1, дробная часть d5…d2d1=101002, смещенный порядок Е=00002=0.
2. Восстановить целую часть d6 мантиссы M=d6·d5…d2d1: d6=0, т.к. Е=0, следовательно М=0.101002.
3. Определить порядок е: е=еmin=2-24-1=-6, т.к. Е=0.
4. Определить перемещенный порядок λ и целочисленную мантиссу М': λ=e-t+1=-6-6+1=-11, M'=d6d5…d2d1=0101002=20.
5. Найти модулярную мантиссу 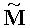
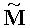
Пусть A=[〈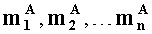
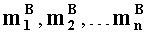

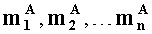

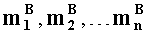
1. Множитель A=[〈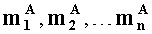
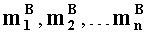
1.1. Если число g вычислительных ядер процессора превышает число n оснований р1,р2,…,рn системы остаточных классов, используемых для представления модулярных мантисс 
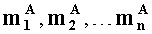

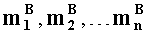
- в первое ядро универсального многоядерного процессора загружают q-разрядные двоичные представления первых знакопозиций 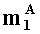
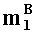

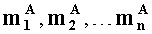

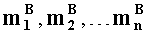
основание системы остаточных классов pi, разрядность q которого не превышает размер k разрядной сетки процессора;
- параллельно с этим, во второе ядро универсального многоядерного процессора загружают q-разрядные двоичные представления вторых знакопозиций 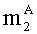
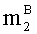


- параллельно с этим, в n-ое ядро универсального многоядерного процессора загружают q-разрядные двоичные представления n-ых знакопозиций 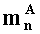
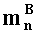


- параллельно с этим, в (n+1)-ое ядро универсального многоядерного процессора загружают k-разрядные двоичные порядки λA и λB, а также знаки sA и sB чисел А и В соответственно.
1.2. Если число n оснований p1, p2,…,pn системы остаточных классов используемых для представления модулярных мантисс 
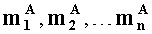

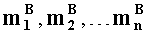
- q-разрядные двоичные представления первых знакопозиций 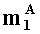
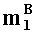


- параллельно с этим, q-разрядные двоичные представления вторых знакопозиций 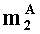
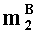


- параллельно с этим, q-разрядные двоичные представления (g-1)-ыx знакопозиций 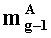
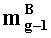


- q-разрядные двоичные представления g-ых знакопозиций 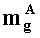
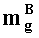


- q-разрядные двоичные представления (g+1)-ыx знакопозиций 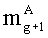
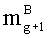


- и т.д., пока не будут загружены n-ые знакопозиций 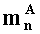
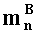

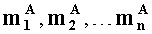

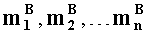
- параллельно с этим, k-разрядные двоичные порядки λА и λB, а также знаки sA и sB чисел А и В соответственно загружают в g-oe ядро универсального многоядерного процессора.
2. После того как множитель A=[〈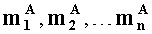
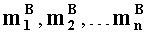
2.1. Если число g вычислительных ядер процессора превышает число n оснований p1,p2,…;pn системы остаточных классов, используемых для представления модулярных мантисс 
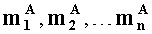

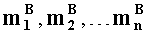
- в первом вычислительном ядре процессора выполняется операция целочисленного умножения 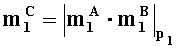
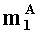
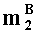

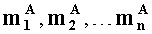

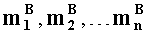
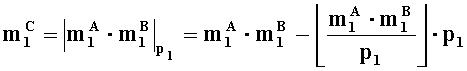
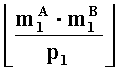
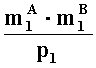
- параллельно с этим, во втором вычислительном ядре процессора выполняется 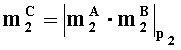
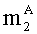
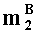


- параллельно с этим, в n-ом вычислительном ядре процессора выполняется операция умножения 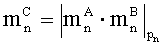
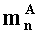
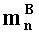


- параллельно с этим, в (n+1)-м вычислительном ядре процессора выполняется сложение двоичных порядков λA и λB, а также сложение по модулю два sC=|sA+sB|2 знаков sA и SB чисел А и В соответственно.
2.2. Если число n оснований р1,p2,…,pn системы остаточных классов используемых для представления модулярных мантисс 
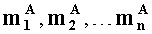

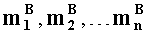
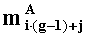
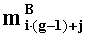
- в первом вычислительном ядре процессора последовательно выполняются операции умножения 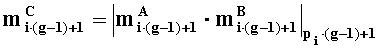
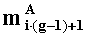
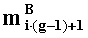

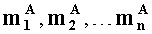

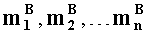
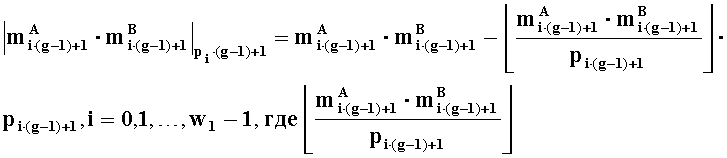
- наибольшее целое, не превышающее 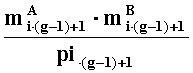
- параллельно с этим, во втором вычислительном ядре процессора последовательно выполняются
операции умножения
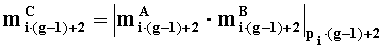
по модулям рi·(g-1)+2, i=0,1,…,w2-1, q-разрядных двоичных представлений всех w2 загруженных в него знакопозиций 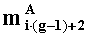
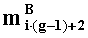


- параллельно с этим, в (g-l)-M вычислительном ядре процессора последовательно выполняются операции умножения 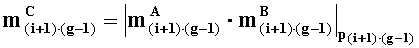
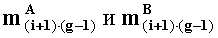


- параллельно с этим, в g-м вычислительном ядре процессора выполняется сложение двоичных порядков λA и λB, а также сложение по модулю два sC=|sA+sB|2 знаков sA и sB чисел А и В соответственно.
В результате выполнения данных операций получается произведение
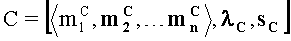
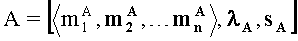
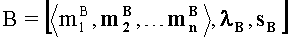
Пример: необходимо выполнить операцию умножения С=А·В в модулярно-позиционном формате с плавающей точкой на универсальном процессоре, содержащем четыре 5-разрядных вычислительных ядра. Для представления мантисс операндов заданы следующие 5-разрядные основания системы остаточных классов: р1=3=22-1, p2=7=23-1, р3,=31=25 -1, P=p1·p2·p3=65l - произведение оснований (верхний предел допустимого диапазона представления модулярных мантисс). Сомножители заданы в модулярно-позиционном формате следующим образом: А=[〈2,4,11〉,-4,1], B=[〈2,3,17〉,2,0].
1. Множитель А=[〈2,4,11〉,-4,1] и множимое В=[〈2,3,17〉,2,0] загружаем в универсальный 5-разрядный процессор, содержащий четыре вычислительных ядра, следующим образом:
- в первое ядро загружаем первые знакопозиции 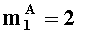
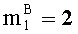


- параллельно с этим, во второе ядро загружаем вторые знакопозиции 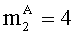
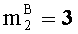


- параллельно с этим, в третье ядро загружаем третьи знакопозиции 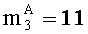
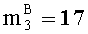


- параллельно с этим, в четвертое ядро универсального многоядерного процессора загружаем 5-разрядные двоичные порядки λA=-4 и λB=2, а также знаки sA=1 и sB =0.
2. Так как число вычислительных ядер процессора превышает число оснований p1,р2,…,pn системы остаточных классов, используемых для представления модулярных
мантисс 

- в первом вычислительном ядре процессора выполняем операцию
целочисленного умножения по модулю p1: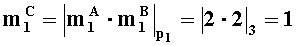
- параллельно с этим, во втором вычислительном ядре процессора выполняем операцию целочисленного умножения по модулю p2: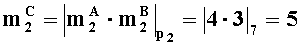
- параллельно с этим, в третьем вычислительном ядре процессора выполняем операцию целочисленного умножения по модулю p3: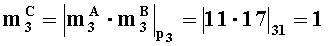
- параллельно с этим, в четвертом вычислительном ядре процессора выполняем сложение двоичных порядков λA и λB, а также сложение по модулю два sC=|sA+sB|2 знаков sA и sB чисел А и В соответственно: λC=λA+λB=-4+2=-2, sC=|sA+sB|2=|1+0|2=1.
В результате получен результат С=[〈1,5,1〉, -2,1] в модулярно-позиционном формате с плавающей точкой, соответствующий позиционному числу -11·187·2-2.
Если принять за время сложения пары q-разрядных остатков q тактов работы универсального процессора, содержащего g k-разрядных вычислительных ядер, причем q≤k, то время вычисления произведения t-разрядных мантисс чисел с плавающей точкой А и В, при t≈q·n в предельном случае (когда 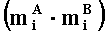
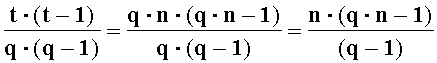
Изобретение относится к вычислительной технике и может быть использовано для выполнения операции умножения чисел, представленных в модулярно-позиционном формате с плавающей точкой на универсальных многоядерных процессорах. Техническим результатом является повышение скорости вычисления за счет замены операции умножения t-разрядных позиционных мантисс сомножителей n параллельно выполняемыми операциями умножения q-разрядных знакопозиций чисел в системе счисления в остаточных классах. Способ реализуется на универсальном многоядерном вычислителе, содержащем g k-разрядных вычислительных ядер, каждое из которых обеспечивает выполнение системы из f операций, в состав которых входят операции алгебраического умножения и алгебраического сложения над числами, представленными в позиционных целочисленных форматах данных. При организации выполнения операций умножения каждое число, множитель и множимое, представляется в модулярно-позиционном формате с плавающей точкой в виде (1+k+q·n) - элементного вектора.
Способ организации выполнения операции умножения двух чисел в модулярно-позиционном формате представления с плавающей точкой на универсальных многоядерных процессорах, заключающийся в том, что:
универсальный многоядерный вычислитель содержит g k-разрядных вычислительных ядер, каждое из которых обеспечивает выполнение системы из f операций, в состав которых входят операции алгебраического умножения и алгебраического сложения над числами, представленными в позиционных целочисленных форматах данных;
при организации выполнения операций умножения каждое число, множитель и множимое, представляется в модулярно-позиционном формате с плавающей точкой в виде (1+k+q·n) - элементного вектора, где:
первый слева разряд s является старшим разрядом в формате числа и отводится под значение знака числа, причем если s=0, то число считается положительным, а если s=1, то число считается отрицательным;
следующие за первым разрядом s числа k разрядов отводятся под хранение позиционного порядка числа, представляющего собой целое двоичное число λ со знаком sλ, изменяющееся для конечных чисел с плавающей точкой в диапазоне λmin≤λ≤λmax и получаемое в результате преобразования числа из позиционного формата с плавающей точкой посредством вычисления выражения λ=е-t+1, где е определяет величину числа в двоичном позиционном формате с плавающей точкой в выражении (-1s·М·2е) при 0≤М<2, являющейся рациональной t-разрядной мантиссой числа в двоичном позиционном формате с плавающей точкой, λmin=2-2k-1, λmax=2k-1-2, при sλ=0 порядок λ считается положительным, а при sλ=1 порядок λ считается отрицательным;
следующие за (k+1) разрядами q·n разрядов, причем q≤k, отводятся для представления мантиссы числа 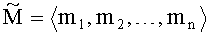
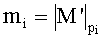
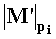
диапазон изменения модулярной мантиссы 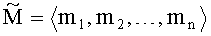
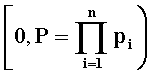
значения порядка λ и мантиссы 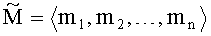
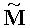
значения порядка λ и мантиссы 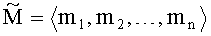
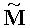
значение положительной бесконечности представляется в модулярно-позиционном формате следующим образом: s=0, λ=λmax+1=2k-1-1, 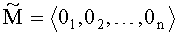
значение отрицательной бесконечности представляется в модулярно-позиционном формате следующим образом: s=1, λ=λmax+1=2k-1-1, 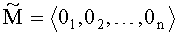
для положительных нечисловых величин (NaN) в модулярно-позиционном формате [s,λ,〈m1,m2,…,mn〉], при s=0, значение позиционного порядка λ определяется выражением λ=λmax+1=2k-1-1, а значения мантиссы 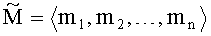
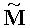
для отрицательных нечисловых величин (NaN) в модулярно-позиционном формате, при s=1, значение позиционного порядка λ определяется выражением λ=λmax+1=2k-1-1, а значения мантиссы 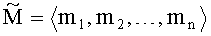
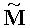
величины в модулярно-позиционном формате, имеющие значение позиционного порядка λ=λmin-1=1-2k-1, при изменении значений модулярной мантиссы в диапазоне 〈11,12,…,1n〉 ≤ 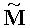
по сигналу процессора, множитель 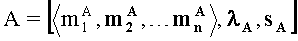
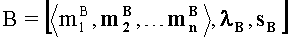
при условии, что g≥n+1, т.е. если число вычислительных ядер процессора превышает число оснований системы остаточных классов, используемых для представления модулярных мантисс 
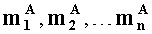

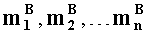
в первое ядро универсального многоядерного процессора загружают q-разрядные двоичные представления первых знакопозиций 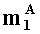
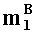

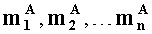

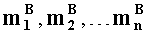
параллельно с этим, во второе ядро универсального многоядерного процессора загружают q-разрядные двоичные представления вторых знакопозиций 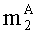
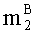


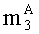
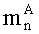
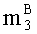
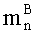


параллельно с этим в (n+1)-ое ядро универсального многоядерного процессора загружают k-разрядные двоичные порядки λA и λB, а также знаки sA и sB чисел А и В соответственно;
при условии, что g<n+1, т.е. если число оснований системы остаточных классов используемых для представления модулярных мантисс 
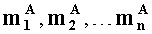

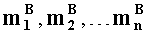
q-разрядные двоичные представления первых знакопозиций 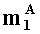
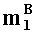


параллельно с этим, q-разрядные двоичные представления вторых знакопозиций 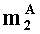
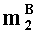


параллельно с этим аналогичным образом загружают q-разрядные двоичные представления третьих ÷(q-1)-ых знакопозиций 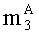
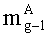
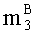
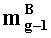


q-разрядные двоичные представления g-ых знакопозиций 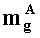
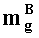


аналогичным образом q-разрядные двоичные представления (g+1)-ых знакопозиций 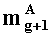
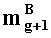


процесс циклической загрузки продолжается пока не будут загружены n-ые знакопозиции 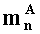
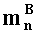

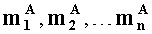

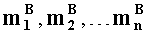
параллельно с этим, k-разрядные двоичные порядки λA и λB, а также знаки sA и sB чисел А и В соответственно загружают в g-oe ядро универсального многоядерного процессора;
после того как множитель 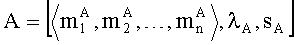
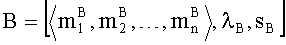
плавающей точкой, загружены в универсальный k-разрядный процессор, содержащий g-вычислительных ядер, операция их умножения выполняется следующим образом:
при условии, что g≥n+1, т.е. если число вычислительных ядер процессора превышает число оснований системы остаточных классов, используемых для представления модулярных мантисс 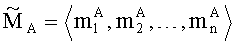
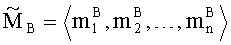
в первом вычислительном ядре процессора выполняется операция целочисленного умножения 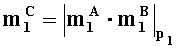
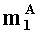
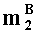
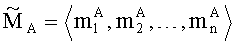
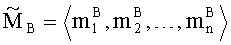
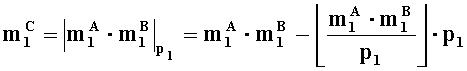
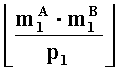
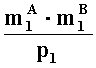
параллельно с этим, во втором вычислительном ядре процессора аналогичным образом выполняется операция умножения 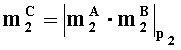
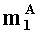
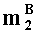


параллельно с этим, в третьем ÷ n-ом вычислительном ядре процессора аналогичным образом выполняется операция умножения 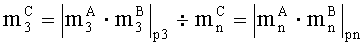
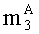
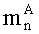
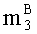
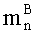


параллельно с этим, в (n+1)-м вычислительном ядре процессора выполняется сложение двоичных порядков λA и λB, а также сложение по модулю два sC=|sA+sB|2 знаков sA и sB чисел А и В соответственно;
при условии, что g<n+1, т.е. если число оснований системы остаточных классов используемых для представления модулярных мантисс 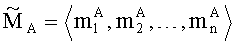
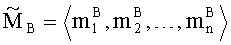
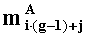
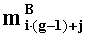
в первом вычислительном ядре процессора для всех i=0,1,…,w1-1 последовательно выполняются операции умножения 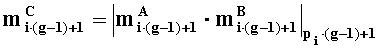
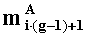
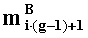
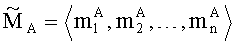
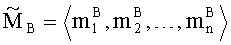
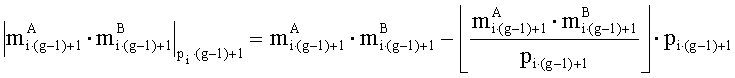
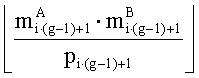
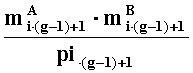
параллельно с этим, во втором вычислительном ядре процессора аналогичным образом для всех i=0,1,…,w2-1 последовательно выполняются операции умножения 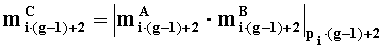
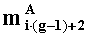
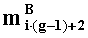


параллельно с этим в третьем ÷(g-1)-M вычислительном ядре процессора аналогичным образом последовательно для всех i=0,1,…,w3-1÷i=0,1,…,wg-1-1 выполняются операции умножения 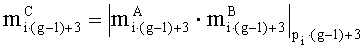
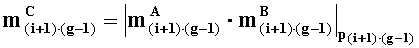
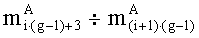
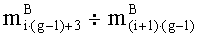


параллельно с этим в g-м вычислительном ядре процессора выполняется сложение двоичных порядков λA и λB, а также сложение по модулю два sC=|sA+sB|2 знаков sA и sB чисел А и В соответственно;
в результате выполнения данных операций получается произведение 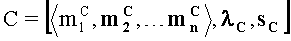
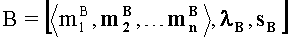
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ S-ИЧНЫХ ЦИФР В ПОЗИЦИОННО-ОСТАТОЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 1991 |
|
RU2006919C1 |
| Устройство для умножения чисел с плавающей запятой | 1985 |
|
SU1280624A1 |
| Устройство для умножения чисел в модулярной системе счисления | 1986 |
|
SU1352483A1 |
| US 2011231465 A1, 22.09.2011 | |||
| US 2002120658 A1, 29.08.2002 | |||
| US 2006184600 A1, 17.08.2006. | |||
Авторы
Даты
2014-03-10—Публикация
2012-07-27—Подача