Изобретение относится к области приборостроения, а именно к области приборов и систем ориентации, и может быть применено в системах управления подвижных объектов.
Известен способ определения параметров ориентации подвижных объектов, основанный на обработке информации инерциального измерительного модуля, в состав которого входят трехкомпонентные гироскопический измеритель угловой скорости (ТГИУС), измеритель кажущегося ускорения (ТИКУ) и магнитометр трехкомпонентный (МТ). Параметры ориентации вычисляются в бортовом компьютере (БК) по информации ТГИУС при решении кинематических уравнений в углах Эйлера-Крылова, направляющих косинусах, параметрах Родрига-Гамильтона или кватернионах. При этом, информация ТИКУ и МТ используется для определения начальных условий (начальная выставка) (Основы построения бесплатформенных инерциальных навигационных систем // В.В. Матвеев, В.Я. Распопов / Под общ. ред. д.т.н. В.Я. Распопов. - СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009).
Недостатком этого способа: является низкая точность вычисления параметров ориентации и высокий уровень шума в автономном режиме работы при отсутствии поправок от других навигационных датчиков. В этом случае, решения кинематических уравнений дают приемлемую точность в течение короткого промежутка времени и результаты вычислений устойчивы не асимптотически. При переходе к дискретным моделям имеет место расходимость их решения.
Известен способ определения ориентации на основе ТГИУС и решении кинематических дифференциальных уравнений Эйлера-Крылова с введением членов позиционной и интегральной, коррекции по информации ТИКУ. В уравнениях Эйлера-Крылова члены позиционной и интегральной коррекции вводятся вместо составляющих переносной абсолютной угловой скорости географического сопровождающего трехгранника. Введение позиционной и интегральной коррекции позволяет добиться асимптотической устойчивости вычисленных оценок двух углов ориентации (тангаж и крен), а при наличии только интегральной коррекции - настроить динамическую систему на период Шулера для компенсации баллистических погрешностей. (Плотников П.К., Элементы теории работы одной разновидности бесплатформенных инерциальных систем ориентации / П.К. Плотников // Гироскопия и навигация. - 1999 - №3. с. 23-35).
Недостатком этого способа является низкая точность определения углов ориентации, связанная с неасимптотической устойчивостью оценок угла курса при интегрально-позиционной коррекции и неасимптотической устойчивостью оценок углов, курса, крена и тангажа при настройке на период Шулера системы с интегральной коррекцией. Кроме того, точность снижается из-за ухудшения соотношения сигнал/шум в оценках углов ориентации при введении интегральной обратной связи.
Известен способ определения ориентации, при котором осуществляется обработка сигналов ТГИУС, ТИКУ и МТ. (В.Л. Волков. Обработка информации в системе ориентации на основе МЭМС / В.Л. Волков, Н.В. Жидкова // Труды Нижегородского государственного технического университета им. Р.Е. Алексеева №3(110) ст. 279-286, 2015). В способе осуществляется вычисление углов ориентации на основе кинематических уравнений Пуассона для параметров Родрига-Гамильтона. Корректирующие углы курса, крена и тангажа вычисляются по информации ТИКУ и МТ. Для компенсации ошибок применяется схема на основе ПИ-регулятора, позволяющая определять и компенсировать ошибки дрейфа ТГИУС.
Недостатками этого способа являются возможность коррекции углов курса, крена и тангажа только во время прямолинейного равномерного движения подвижного объекта, наличие виражных погрешностей при маневрировании объекта, высокий уровень шума в сигналах вычисляемых параметров ориентации.
Наиболее близким к заявленному способу является способ определения ориентации по информации ТГИУС на основе решения многоступенчатых кинематических уравнений Пуассона в параметрах Родрига-Гамильтона с добавление членов горизонтальной радиальной позиционно-интегральной коррекции от ТИКУ. (Плотников П.К. Построение и анализ кватернионых дифференциальных уравнений задачи определения ориентации твердого тела с помощью бесплатформенной инерциальной навигационной системы / П.К. Плотников // Механика твердого тела, - 1999, - №2, - С. 3-14). Кинематические уравнения в параметрах Родрига-Гамильтона первой ступени устойчивы асимптотически по части компонентов кватерниона ориентации за счет добавления членов коррекции, по остальным - устойчивы неасимптотически.
Недостатком этого способа является то, что настойка на частоту Шулера и снижение баллистической погрешности возможны только при построении уравнений второй ступени с интегральной коррекцией, а также большой объем вычислений, обусловленный многоступенчатым алгоритмом. В сигналах вычисляемых параметров ориентации высокий уровень шума, обусловленный шумами в выходных сигналах ТГИУС, ТИКУ и МТ.
Технической проблемой заявляемого изобретения является необходимость повышения точности автономного определения параметров ориентации подвижных объектов. Поставленная проблема решается следующим образом.
В способе автономного определения параметров ориентации, основанном на измерении проекций абсолютной угловой скорости и кажущегося ускорения, вектора напряженности магнитного поля трехосным инерциальным измерительным модулем, в состав которого входят ТГИУС, ТИКУ и МТ, при вычислении углов ориентации применяются кинематические уравнения Пуассона с позиционной коррекцией, дополнительно вводят сигналы с перекрестными членами в каждом канале, коэффициенты которых задаются исходя из необходимых динамических свойств системы. При этом собственные коэффициенты коррекции не равны коэффициентам перекрестной коррекции, а один из перекрестных коэффициентов коррекции имеет противоположный по отношению к остальным знак. Это позволяет добиться асимптотической устойчивости и необходимых динамических свойств системы. Например, настроить систему на период Шулера для снижения баллистических погрешностей и на фильтр нижних частот (ФНЧ) с заданной полосой пропускания для снижения дисперсии шумов в выходных сигналах оценок параметров ориентации.
Совокупность отличительных признаков заявляемого изобретения обеспечивает выполнение поставленной технической проблемы.
Из изученной научно-технической и патентной информации авторам не известен способ с указанными в формуле изобретения отличительными признаками. Это дает основание сделать вывод о соответствии заявляемого способа критериям изобретения.
Заявленное изобретение поясняется фигурой 1, отображающей особенности обработки информации ТГИУС, ТИКУ и МТ инерциального измерительного модуля. С датчиков инерциального измерительного модуля поступают сигналы угловой скорости (ωх, ωy, ωz), формируемые ТГИУС (1), линейных ускорения (ах, ау, az), формируемые ТИКУ (2), и напряженности магнитного поля (hx, hy, hz), формируемые МТ (3). На основе сигналов ТГИУС в блоке 4 осуществляется вычисление правых частей кинематических уравнений Пуассона в соответствии с выражениями (3). Из блока 4 сигналы поступают в вычитающее устройство 7, на вторые входы которого поступают корректирующие поправки k1…k9 из блока 8. Эти корректирующие поправки формируются на основе сигналов ТИКУ (2) и МТ (3). В блоке 5 по сигналам ТИКУ и МТ определяются величины корректирующих углов ориентации (курса ψk, крена γk и тангажа ϑk) в соответствии с выражениями (7). В блоке 6 формируется матрица направляющих косинусов коррекции c11к…с33к (6) вида (2). В блоке 8 формируются сигналы коррекции k1…k9 в соответствии с выражениями (18), которые поступают на вычитающее устройство 7. Далее сигналы поступают в интегрирующее устройство 9, на выходе которого получается матрица направляющих косинусов c11…с33. Эта матрица с11…с33 поступает в блок 10, в котором осуществляется вычисление углов курса, крена и тангажа в соответствии с выражениями (4) и, по линиям обратных связей, в блоки 4 и 8.
Работа блока 8 поясняется фигурой 2.
На фигуре 2 приведена структурная схема блока обработки сигналов коррекции. Рассмотрим работу формирователя сигналов коррекции на примере первой тройки из девяти уравнений Пуассона. Формирование сигнала коррекции k1 осуществляется в соответствии с первым выражением из (18). Из разности направляющего косинуса с11 и корректирующего направляющего косинуса c11k, умноженной на коэффициент позиционной коррекции k11, вычитаются сигналы перекрестных связей, которые формируются на основе разностей c13k и c13, умноженных на перекрестный коэффициент усиления позиционной коррекции k13p, а также разностей элементов c12k и c12, умноженных на перекрестный коэффициент k12p. Аналогично формируются сигналы коррекции k2 и k3, в соответствии со вторым и третьим выражениями из (18). При этом собственные коэффициенты коррекции (k11 k12 и k13) не равны коэффициентам перекрестной коррекции (k11p, k12p и k13p), а один из коэффициентов коррекции (k11p) имеет противоположный по отношению к остальным знак. Аналогично задаются значения коэффициентов коррекции в двух других тройках уравнений Пуассона.
В дальнейшем показано, что такое формирование сигналов коррекции позволяет добиться асимптотической устойчивости и нужных динамических свойств системы. Например, настроить систему на период Шулера для снижения баллистических погрешностей и на фильтр нижних частот с заданной полосой пропускания для снижения уровня шумов в выходных сигналах оценок углов ориентации.
Поясним достижение этих эффектов при использовании способа более подробно.
Рассмотрим кинематическое уравнение Пуассона в направляющих косинусах:

где С - матрица преобразования координат при переходе от связанной с объектом системы координат к географическому сопровождающему трехграннику, ω - проекции вектора абсолютной угловой скорости на оси связанной с объектом системы координат.
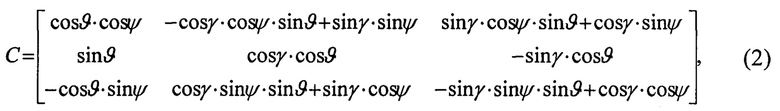
Представим матрицу преобразования координат С и проекции вектора абсолютной угловой скорости ω в виде:

В результате получим матричное уравнение Пуассона в направляющих косинусах в виде:

На основе матричного уравнения составим скалярные дифференциальные уравнения:

Решения системы уравнений (3) на основе информации ТГИУС позволяют определить углы курса, тангажа и крена

Недостатком такого способа определения ориентации является низкая точность, обусловленная неасимптотической устойчивостью системы (3).
Добавим в кинематические уравнения (1) члены позиционной коррекции:

где: Ck - матрица направляющих косинусов коррекции, k - матрица коэффициентов коррекции.
Матрицу направляющих косинусов коррекции запишем в виде:

Ее элементы вычисляются по показаниям акселерометров ax, ay, az и магнитометров hx, hy, hz в соответствии с выражениями

и видом матрицы (2).
В (7) g - вектор ускорения силы тяжести, ax, ау, az - составляющие линейного ускорения, измеряемые ТИКУ, hx, hy, hz - проекции вектора напряженности магнитного поля, измеряемые МТ.
Запишем уравнение (5) в скалярном виде для первой тройки уравнений в соответствии с прототипом, для второй и третьей тройки уравнения составляются аналогично:
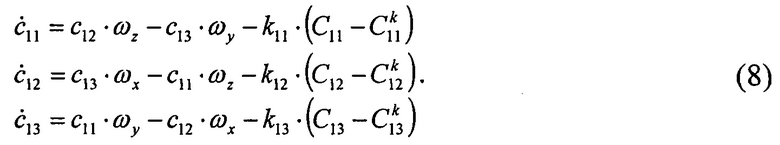
Выбором коэффициентов κij можно обеспечить асимптотическую устойчивость решений систем вида (8).
На основе скалярных уравнений (8) составим собственную матрицу системы:

Положим угловые скорости ωx=0, ωу=0, ω=0 равными нулю и примем, что коэффициенты позиционной коррекции равны между собой k11=k12=k13=k, в результате преобразуем собственную матрицу системы к виду:

Для составления характеристического уравнения воспользуемся матричным уравнением:

где Е - единичная матрица, р - оператор Лапласа, А - собственная матрица динамической системы.
После подстановки получим характеристическое уравнение:

Корни характеристического уравнения (11) приведены далее:

Из корней (12) видно, что система асимптотически устойчива. В то же время, так как все корни действительные отрицательные, система не может быть настроена на период Шулера и фильтры нижних частот 2-го или более высоких порядков.
Добавим к сигналам коррекции перекрестные сигналы.

Структура сигналов коррекции k4…k9 в двух других тройках уравнений Пуассона должна быть аналогична.
Запишем уравнение (5) в скалярном виде с учетом перекрестных связей для первой тройки уравнений:

На основе скалярных уравнений (14) составим собственную матрицу системы:

Положим угловые скорости ωх=0, ωу=0, ωz=0 равными нулю, в результате получим собственную матрицу системы в виде:

Положим коэффициенты позиционной коррекции равными между собой k11=k12=k13=k, а коэффициенты перекрестных связей  , в результате характеристическое уравнение (9) примет вид:
, в результате характеристическое уравнение (9) примет вид:


Корни характеристического уравнения (16):

Так как корни действительные и при определенных значениях могут быть отрицательными, при kp<k система асимптотически устойчива. В то же время, система не может быть настроена на период Шулера.
Поменяем знак у перекрестного коэффициента 

Система уравнений (14) примет вид:

При ωx=0, ωу=0, ωz=0


Если 

Вычисляя определитель (22), получим характеристическое уравнение:

Корни характеристического уравнения:

Система имеет один действительный и два комплексно-сопряженных корня, значит, при kp<k она асимптотически устойчива и может быть настроена на период Шулера и фильтр нижних частот 2-го порядка.
Аналогичные результаты получаются, если поменять знаки отдельно у коэффициентов 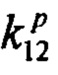 или
или 
Частотные характеристики углов ориентации по отношению к выходным сигналам ТГИУС, ТИКУ и МТ в этом случае имеют вид фиг. 3, где L(f) - логарифмическая амплитудно-частотная характеристика, ω(f) - фазо-частотная характеристика. Они подтверждают настройку системы как ФНЧ для снижения уровня шумов в оценках углов ориентации по отношению к шумам в выходных сигналах датчиков.
Аналогичные выкладки можно привести для случая использования в системе ориентации уравнений Пуассона в параметрах Родрига-Гамильтона (кватернионах).
Данный способ, по сравнению с прототипом, позволяет повысить точность решения задачи автономной ориентации подвижных объектов за счет асимптотической устойчивости системы по всем трем углам ориентации, возможности настройки системы на период Шулера для компенсации баллистических погрешностей без введения интегральной коррекции, возможности настройки системы как фильтр нижних частот по всем входам и выходам, включая сигналы ТГИУС.
Использование изобретения позволяет решать задачи автономной ориентации и навигации подвижных объектов в условиях отсутствия возможности применения спутниковых навигационных систем, что повышает безопасность и эффективность эксплуатации образцов авиационной, морской и наземной техники.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ оценки пространственного и углового положения объекта | 2024 |
|
RU2831368C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОРРЕКТИРУЮЩИХ ПОПРАВОК В БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЕ | 2017 |
|
RU2654964C1 |
| Способ автономной ориентации объектов в околоземном пространстве | 2022 |
|
RU2787971C1 |
| СПОСОБ АВТОНОМНОЙ ИНЕРЦИАЛЬНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2800846C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
| КОМБИНИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ АСТРОИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2017 |
|
RU2654965C1 |
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| СПОСОБ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ И ЕЁ КОРРЕКЦИИ ПО НЕПОДВИЖНОМУ НАЗЕМНОМУ ОРИЕНТИРУ С ИЗВЕСТНЫМИ ГЕОГРАФИЧЕСКИМИ КООРДИНАТАМИ | 2019 |
|
RU2713582C1 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК АВТОНОМНОЙ, БЕСПЛАТФОРМЕННОЙ ГИРОВЕРТИКАЛИ С ИНТЕГРАЛЬНОЙ КОРРЕКЦИЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2021 |
|
RU2801620C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОШИБОК БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ПО ВНЕШНЕЙ ПОЗИЦИОННОЙ И СКОРОСТНОЙ ИНФОРМАЦИИ | 2017 |
|
RU2668658C1 |



Изобретение относится к области приборостроения, а именно к области приборов и систем ориентации, и может быть применено в системах управления подвижных объектов. Сущность изобретения состоит в том, что в известном способе определения ориентации объекта с помощью инерциального измерительного модуля, состоящем в том, что измеряют проекции векторов напряженности магнитного поля трехосным блоком магнитометров, кажущегося ускорения объекта трехосным блоком акселерометров и абсолютной угловой скорости вращения объекта трехосным блоком гироскопов, входящих в инерциальный измерительный модуль, вычисляют корректирующие сигналы позиционной коррекции и решают кинематические уравнения для вычисления оценок углов ориентации, к корректирующим сигналам позиционной коррекции добавляют перекрестные сигналы коррекции в каждом канале. Коэффициенты перекрестных сигналов должны иметь определенные знаки и удовлетворять определенным соотношениям. Этим достигается снижение погрешностей ориентации за счет асимптотической устойчивости, настройки на период Шулера, снижения уровня шумов в сигналах оценок углов ориентации. 3 ил.
Способ автономной ориентации подвижного объекта с помощью инерциального измерительного модуля, состоящий в измерении проекций векторов напряженности магнитного поля трехосным блоком магнитометров, кажущегося ускорения объекта трехосным блоком акселерометров и абсолютной угловой скорости вращения объекта трехосным блоком гироскопов, входящих в инерциальный измерительный модуль, вычислении корректирующих сигналов позиционной коррекции и решении кинематических уравнений для вычисления оценок углов ориентации, отличающийся тем, что к корректирующим сигналам позиционной коррекции добавляют перекрестные сигналы коррекции в каждом канале, коэффициенты которых задаются исходя из необходимых динамических свойств системы, при этом собственные коэффициенты коррекции в кинематических уравнениях не равны коэффициентам перекрестной коррекции, а один из перекрестных коэффициентов коррекции имеет противоположный по отношению к остальным знак.
| СПОСОБ АВТОНОМНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2017 |
|
RU2653967C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНЫХ ОБЪЕКТОВ И КОМПЛЕКСИРОВАННАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2395061C1 |
| RU 2191351 C1, 20.10.2002 | |||
| CN 109765938 A, 17.05.2019. | |||
Авторы
Даты
2020-12-11—Публикация
2019-12-30—Подача