Изобретение относится к измерительной технике, предназначено для измерения гравитационного ускорения на борту космических аппаратов и может быть использовано, в частности, в геологии для глобального поиска и определения запасов полезных ископаемых, в геодезии для уточнения глобальной и локальной моделей гравитационного поля Земли (ГПЗ) и других планет, для мониторинга временных вариаций гравитационного поля, а также в навигации по ГПЗ для подготовки глобальных навигационных гравиметрических карт.
Известен способ измерения гравитационного ускорения на борту космического аппарата (КА), который может быть реализован с помощью космической геодезической системы PRARE [1]. Название PRARE является акронимом от Precise Range And Range-Rate Equipment - аппаратура для точного измерения расстояний и скорости изменения расстояний. Это компактная космическая бортовая запросная двухчастотная дальномерно-доплеровская микроволновая измерительная система. Система участвует в бортовых спутниковых геодезических измерениях, начиная со спутника ERS-2, запущенного в мае 1995 г. Принцип действия системы состоит в следующем: с борта КА на землю посылается запросный сигнал известной структуры и частоты, который наземной станцией ретранслируется обратно на спутник. На борту спутника ретранслированный сигнал принимается и сравнивается по времени и по частоте с сигналом, излученным на Землю. В результате определяется запаздывание и доплеровское смещение частоты принятого сигнала, по которым определяется дальность и радиальная скорость КА относительно наземного ретранслятора. Данные измерений используются для уточнения геодезических координат наземных ретрансляторов. Система содержит около 29 наземных ретрансляторов, равномерно распределенных по поверхности суши.
Система может использоваться для уточнения текущего гравитационного ускорения КА, которое соответствует ускорению свободного падения в подспутниковой точке.
Способ измерения на основе системы PRARE состоит в использовании доплеровского смещения частоты запросного сигнала, излучаемого со спутника, и включает следующие операции:
1. С борта спутника на Землю излучают запросный сигнал известной частоты.
2. На наземном ответчике сигнал принимают и ретранслируют обратно на спутник.
3. На борту спутника сигнал принимают и измеряют удвоенное доплеровское смещение его частоты относительно частоты излученного сигнала.
4. По разности доплеровских смещений, измеренных в двух точках траектории спутника и отнесенных к интервалу времени между этими измерениями, определяют радиальное (лучевое) ускорение КА относительно наземного ретранслятора. По величине этого ускорения определяют текущее гравитационное ускорение КА на середину интервала времени между измерениями доплеровского смещения частоты.
Недостатки этого способа измерений заключаются в следующем:
- ограниченная точность измерений гравитационного ускорения вследствие ограниченной точности измерения разностного доплеровского смещения;
- недостаточная дискретность (детальность, плотность) измерений ускорения на единицу длины орбиты вследствие большого интервала времени между необходимыми измерениями доплеровского смещения.
Прототип предлагаемого способа основан на использовании геодезической доплеровской системы DORIS [2].
Название DORIS расшифровывается как Doppler Orbitography and Radiopositioning Integrated by Satellite. Система DORIS включает сеть наземных излучающих маяков и бортовое спутниковое приемное оборудование. Она предназначена для уточнения орбит спутников и положений наземных источников сигналов (маяков) по доплеровским измерениям, выполняемым на спутнике. Система разработана во Франции с целью высокоточного решения геодезических задач с погрешностью до единиц сантиметров. Создана Международная Служба International Doris Service (IDS).
В основу принципа действия системы DORIS заложено точное измерение доплеровского сдвига радиочастоты сигналов, излучаемых наземными маяками и принимаемых на борту космического аппарата. Частоты излучений наземных маяков составляют 2.03625 ГГц и 401.25 МГц (вторая частота - для коррекции ионосферной задержки при распространении сигналов).
Оборудование системы DORIS располагается на борту целого ряда геодезических спутников (например, TOPEX/POSEIDON, Jason-1,2,3, ENVISAT и др.), а также на борту спутников для дистанционного зондирования SPOT-2, SPOT-3, SPOT-4 и SPOT-5 и др. Наземная сеть системы содержит более 50 маяков-излучателей.
Бортовое оборудование системы включает:
- всенаправленную двухчастотную приемную антенну, ориентированную в «надир»;
- двухчастотный радиоприемник;
- высокостабильный кварцевый генератор с кратковременной нестабильностью частоты не более 10-13 за время прохождения спутника зоны приема сигнала от наземного маяка (15-20 мин);
- измеритель доплеровского смещения принимаемого сигнала и соответствующей радиальной скорости.
Погрешность доплеровских измерений радиальной скорости спутника относительно наземного излучателя в реальном времени составляет 2,5 мм/с, в постобработке - 0,3 мм/с.
С использованием спутникового оборудования системы DORIS может быть реализован способ-прототип измерения гравитационного ускорения спутника, по которому рассчитывается величина ускорения свободного падения гравитационного поля Земли в подспутниковой точке.
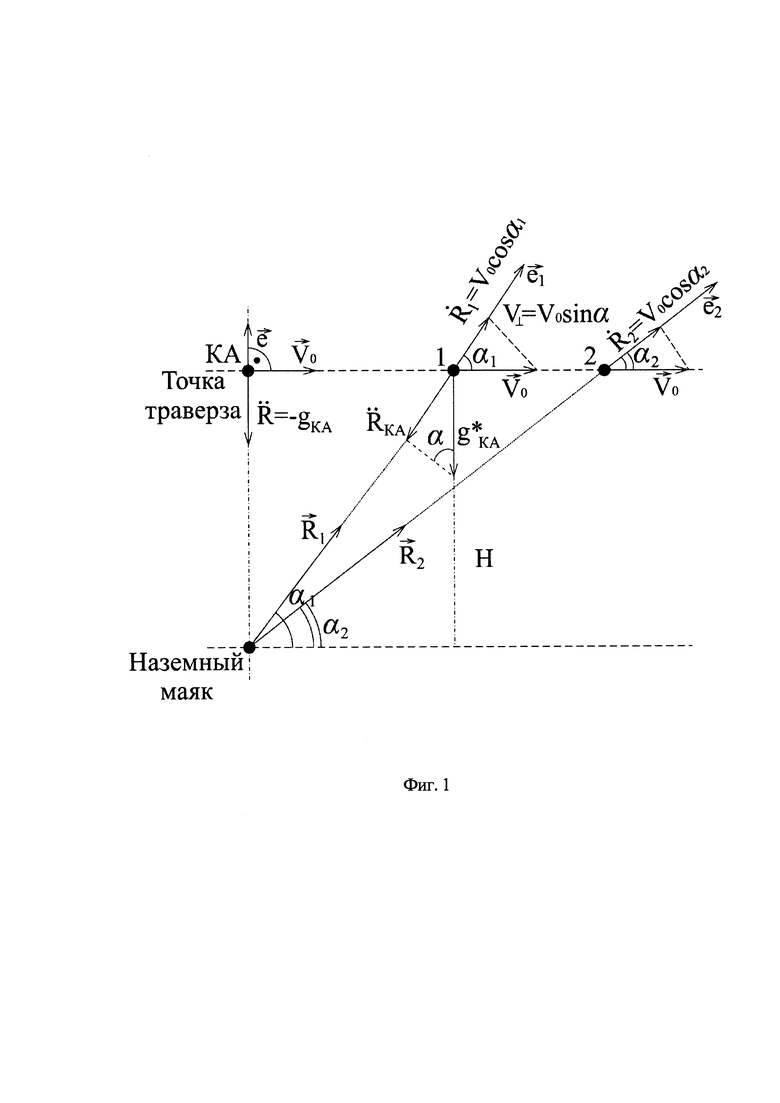
Способ-прототип измерения гравитационного ускорения на основе системы DORIS, поясняется рисунком на фиг. 1, на котором изображен случай движения КА, когда плоскость его орбиты проходит через наземный маяк. Способ-прототип включает следующие операции:
1. С наземного маяка системы DORIS в верхнюю полусферу околоземного пространства излучают непрерывный сигнал с частотой 2.03625 ГГц (длина волны λ≈15 см).
2. На борту КА, движущегося по низкой орбите, принимают этот сигнал и измеряют доплеровское смещение его частоты, которое разделяют текущей радиальной скоростью спутника 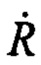 относительно наземного маяка:
относительно наземного маяка:
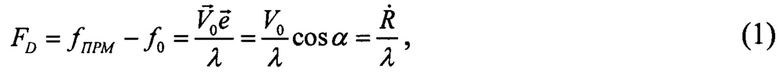
где ƒПPM, ƒ0 - соответственно, частота принимаемого сигнала и частота бортового стандарта частоты; α - угол между вектором орбитальной скорости КА V0 и единичным вектором в направлении распространения волны 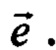 Согласно рисунку на фиг. 1, для круговой орбиты этот угол является текущим углом места КА.
Согласно рисунку на фиг. 1, для круговой орбиты этот угол является текущим углом места КА.
Отсюда следует выражение для погрешности измерения доплеровского смещения в системе:

где 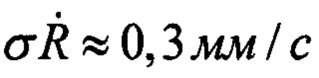 - случайная погрешность измерения радиальной скорости, заявленная в системе.
- случайная погрешность измерения радиальной скорости, заявленная в системе.
3. По результатам текущих измерений доплеровского смещения частоты на спутнике вычисляют его приращение (изменение) ΔFD при перемещении спутника вдоль орбиты из точки 1 в точку 2:
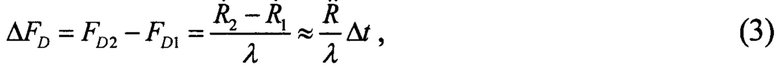
где 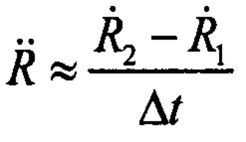 - радиальное (лучевое) ускорение спутника относительно мажа; Δt - интервал времени, на котором определялось приращение ΔFD и радиальное ускорение.
- радиальное (лучевое) ускорение спутника относительно мажа; Δt - интервал времени, на котором определялось приращение ΔFD и радиальное ускорение.
4. Ускорение 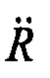 определяется относительно наземной точки размещения маяка и определяется расстоянием R до него, которое в свою очередь определяется высотой ΚΑ Η=Rsinα. Искомое гравитационное ускорение КА gKA не зависит от этого расстояния и определяется только геоцентрической высотой ρКА. Для приведения этих ускорений к единой высоте Η введем в рассмотрение приведенное к высоте спутника гравитационное ускорение
определяется относительно наземной точки размещения маяка и определяется расстоянием R до него, которое в свою очередь определяется высотой ΚΑ Η=Rsinα. Искомое гравитационное ускорение КА gKA не зависит от этого расстояния и определяется только геоцентрической высотой ρКА. Для приведения этих ускорений к единой высоте Η введем в рассмотрение приведенное к высоте спутника гравитационное ускорение 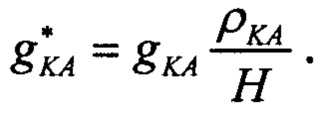 Отсюда, согласно рисунку на фиг. 1, имеем:
Отсюда, согласно рисунку на фиг. 1, имеем:

На основании этого соотношения из формулы (3) вычисляют искомое гравитационное ускорение спутника:

Отсюда, с учетом (2), следует формула для оценки случайной погрешности определения искомого ускорения в зависимости от заявленной в системе DORIS погрешности измерения радиальной скорости по доплеровскому смещению 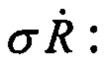

Оценку точности проведем для орбиты спутника высотой Η=1000 км, ρКА ≈ (R3+Η)=7,4⋅106 м, которая проходит через точку размещения наземного маяка. В этом случае угол α есть угол места КА. Вблизи точки траверза спутника, где угол места КА α=90°, приемлемая для практики погрешность измерения гравитационного ускорения 1 мГал (10-5 м/с2) достигается при достижимой в системе погрешности измерений 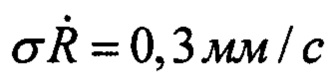 на интервале времени между двумя соседними измерениями доплеровского смещения Δt ≈ 5,6 с. Такая дискретность измерений гравитационного ускорения соответствует длине измерительного участка орбиты L=V0-Δt=41 км, что примерно в 2 раза превышает длину самой короткой волны в разложении потенциала ГПЗ, принятой в наиболее совершенной модели ГПЗ EGM2008 [3]. При углах места, отличных от 90°, необходимая длина измерительного участка возрастает. Так, при α=30° она превысит 80 км. При меньших углах эта длина еще больше. Такая длина измерительного участка и дискретность измерений для практики гравиметрии малопригодны.
на интервале времени между двумя соседними измерениями доплеровского смещения Δt ≈ 5,6 с. Такая дискретность измерений гравитационного ускорения соответствует длине измерительного участка орбиты L=V0-Δt=41 км, что примерно в 2 раза превышает длину самой короткой волны в разложении потенциала ГПЗ, принятой в наиболее совершенной модели ГПЗ EGM2008 [3]. При углах места, отличных от 90°, необходимая длина измерительного участка возрастает. Так, при α=30° она превысит 80 км. При меньших углах эта длина еще больше. Такая длина измерительного участка и дискретность измерений для практики гравиметрии малопригодны.
С другой стороны, если принять длину мерного участка равную расстоянию между спутниками геодезической системы GRACE 200 км (Δt ≈ 27 с) [4], то, согласно (5), при α=30° погрешность измерений гравитационного ускорения таким способом составит 3,1 мГал. Такая большая ошибка неприемлема для практической гравиметрии.
Недостатками способа-прототипа на основе системы DORIS являются:
- малая дискретность (плотность, детальность) получения данных о значениях гравитационного ускорения ГПЗ приемлемой точности;
- недостаточная точность измерений гравитационного ускорения.
Техническим результатом, получаемым от внедрения изобретения, является повышение точности и дискретности (детальности) измерения гравитационного ускорения на борту КА.
Предлагаемый способ измерения текущего гравитационного ускорения спутника с повышенной пространственной дискретностью и повышенной точностью основан на использовании следующих новых операций:
- во-первых, на прямом выделении в бортовой аппаратуре с помощью цифровой линии задержки малого разностного доплеровского смещения (до 50 Гц) частоты принимаемого сигнала, соответствующего двум близко расположенным точкам орбиты КА;
- во-вторых - в высокоточном измерении этой малого частотного смещения с помощью цифрового периодомера на основе использования высокостабильной последовательности счетных импульсов, формируемых бортовым высокостабильным стандартом частоты.
Предлагаемый способ реализуется с помощью следующих операций:
1. С наземного маяка системы DORIS в верхнюю полусферу околоземного пространства излучают непрерывный сигнал с частотой ƒ0=2,03625 ГГц (длина волны λ ≈ 15 см).
2. Планируют последовательность измерений доплеровского смещения для заданной трассы полета на борту КА перед входом в зону приема сигнала. Задача планирования - определить моменты времени и интервалы (продолжительность) измерений доплеровского смещения заданной величины вдоль трассы, исходя из необходимости определения радиального (лучевого) ускорения КА по приращениям радиальной скорости. В результате планирования при заданной величине доплеровского сдвига вычисляется величина требуемого интервала времени между измерениями и соответствующего мерного участка орбиты для различных точек положения КА на этой орбите.
3. С помощью аналогово-цифрового преобразователя (АЦП) с высокой тактовой частотой преобразуют в цифровую форму доплеровское смещение частоты принимаемого сигнала, определяемое на момент t1.
4. Доплеровский сигнал с частотой на момент t1 в цифровой форме подают на переменную цифровую линию задержки (регистр сдвига), где его задерживают на интервал времени задержки Δt3, равный заранее вычисленному времени перемещения КА из точки 1 в точку 2 орбиты, т.е. Δt3=Δt.
5. Доплеровское смещение частоты принимаемого сигнала, определяемое на момент t2, с помощью аналогово-цифрового преобразователя (АЦП) с высокой тактовой частотой также преобразуют в цифровую форму.
6. Два цифровых сигнала - задержанный доплеровский сигнал с частотой на момент t1 и сигнал в реальном времени с частотой на момент t2 подают на входы цифрового смесителя и выделяют разностную частоту.
7. Измеряют между двумя сигналами малую разностную частоту, величина которой составляет десятки герц, с помощью периодомера на основе использования высокочастотных высокостабильных по частоте счетных импульсов.
8. По результатам измерений разностного доплеровского смещения принимаемой частоты на борту КА вычисляют искомое гравитационное ускорение КА.
Обоснование принципа измерений в предлагаемом способе
Условимся, что в общем случае плоскость орбиты КА, находящегося на круговой орбите, проходит через точку размещения наземного маяка (фиг. 1). Высота орбиты КА над плоскостью местного горизонта равна H, вектор его орбитальной скорости равен V0 и параллелен этой плоскости. Направление распространения радиолуча от наземного маяка в сторону КА характеризуется вектором радиолуча 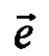 , а также углом места α (углом между вектором
, а также углом места α (углом между вектором 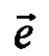 и плоскостью местного горизонта). Положение и относительное движение КА относительно наземного маяка характеризуется текущей дальностью R и радиальной скоростью
и плоскостью местного горизонта). Положение и относительное движение КА относительно наземного маяка характеризуется текущей дальностью R и радиальной скоростью 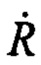 , которые определяются в соответствии с фиг. 1 соотношениями:
, которые определяются в соответствии с фиг. 1 соотношениями:


Принцип измерений определим следующими операциями способа:
Операция 1. С наземного маяка системы DORIS в верхнюю полусферу околоземного пространства излучают непрерывный сигнал с частотой ƒ0=2,03625 ГГц (длина волны λ ≈ 15 см).
Операция 2. Далее планируют последовательность измерений доплеровского смещения для заданной трассы полета на борту КА перед входом в зону приема сигнала. Задача планирования - определить моменты времени и интервалы (продолжительность) измерений доплеровского смещения вдоль трассы, исходя из необходимости определения радиального (лучевого) ускорения КА по приращениям радиальной скорости и, как результат, - текущего гравитационного ускорения КА вдоль трассы.
Для этого предварительно вычисляют ожидаемые доплеровские смещения FD1 и FD1 принимаемого сигнала вдоль трассы полета КА для моментов времени t1, t2, разнесенных на промежуток времени Δt вдоль трассы, а также разность этих доплеровских смещений.
Как известно, частота сигнала, принимаемого на борту низкоорбитального КА, определяется текущей радиальной скоростью спутника 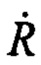 относительно наземного маяка:
относительно наземного маяка:

Поэтому, в соответствии с рисунком на фиг. 1 для моментов t1, t2 имеем:

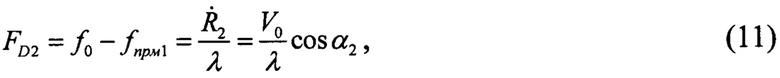
где индексами «1, 2» помечены значения текущих параметров на момент t1, t2.
Величина и знак доплеровских смещений (10) и (11) зависит от орбитальной скорости КА, а также от значений угла места α. Для геодезического КА с высотой орбиты Η=1000 км; V0=7,35⋅103 м/с (т.е. для КА типа «ΓΈΟ-ИК») в ситуации, когда плоскость орбиты проходит через точку размещения наземного маяка при α ≈ 10° (cos10° ≈ 0,98) доплеровские смещения 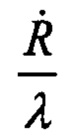 на краях зоны приема сигнала максимальны и имеют разные знаки: FD1= ±4,8 кГц.
на краях зоны приема сигнала максимальны и имеют разные знаки: FD1= ±4,8 кГц.
На основе выражений (10) и (11) получаем выражение для ожидаемого приращения доплеровского смещения частоты на интервале Δt=t2 - t1:
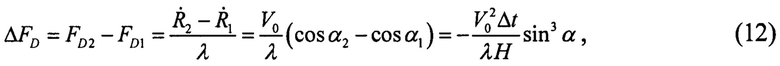
где использовано разложение в ряд по малому параметру 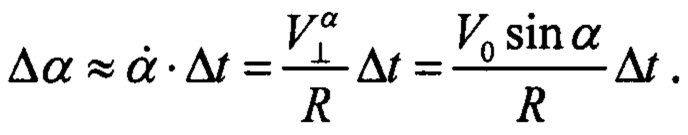 Здесь
Здесь 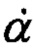 - угловая скорость КА относительно наземного маяка по углу α;
- угловая скорость КА относительно наземного маяка по углу α; 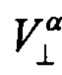 - поперечная составляющая скорости КА.
- поперечная составляющая скорости КА.
Если установить примерно постоянную величину разностного смещения ΔFD, то из соотношения (12) по параметрам орбиты находится планируемый текущий интервал времени Δt, обеспечивающий примерно постоянное смещение ΔFD вдоль всей трассы полета от момента входа до момента выхода из зоны приема сигнала наземного маяка (знак для простоты не учитываем):

В качестве примера, для круговой орбиты КА с высотой и орбитальной скоростью, соответственно, Η=1000 км; V0=7,35⋅103 м/с при ΔFD ≈ 50 Гц по этой формуле вычислим величину требуемого интервала Δt и соответствующего мерного участка орбиты L=V0⋅Δt для различных точек положения КА на этой орбите.
При этом, согласно фиг. 1, рассмотрим следующие варианты:
- α1=20° (КА на краю зоны видимости) имеем: Δt=3,48 с; L=25,5 км;
- α2=30° имеем: Δt=1,1 с; L=8,17 км;
- α2=45° имеем: Δt=0,39 с; L=2,9 км;
- α3=90° (КА находится в зените): Δt=0,139 с; L=1,0 км..
Таким образом, планирование полета КА показало, что при заданном доплеровском смещении около 50 Гц пространственная дискретность (плотность) измерений может быть существенно выше, чем в прототипе. В зените требуемая продолжительность мерного интервала составляет доли секунды, а длина мерного участка не превышает 1 км.
Операция 3. Преобразуют в цифровую форму доплеровское смещение частоты принимаемого сигнала FD1, определяемое соотношением (10) на момент t1, с помощью аналогово-цифрового преобразователя (АЦП) с тактовой частотой ƒT. Тактовая частота создается на основе высокостабильной частоты бортового стандарта частоты. Относительная погрешность дискретизации при ƒT=20 ГГц (что вполне достижимо для современной цифровой техники) и FD1 ≤5 кГц не превысит величины FD1/ƒТ=2,5⋅10-7.
Операция 4. Доплеровский сигнал с частотой FD1 в цифровой форме подают на переменную цифровую линию задержки (регистр сдвига), где его задерживают на интервал времени задержки Δt3, равный заранее вычисленному интервалу времени перемещения КА из точки 1 в точку 2 орбиты (13), т.е. Δt3=Δt.
Операция 5. Доплеровское смещение частоты принимаемого сигнала FD2, определяемое соотношением (11) на момент t2, с помощью аналогово-цифрового преобразователя (АЦП) с тактовой частотой ƒT также преобразуют в цифровую форму. Относительная погрешность дискретизации - аналогичная частоте FD1.
Операция 6. Два цифровых сигнала - задержанный сигнал с частотой FD1 и сигнал в реальном времени с частотой FD2 подают на входа цифрового смесителя и выделяют разностную частоту, которая определяется соотношением (12) при условии Δt=Δt3:
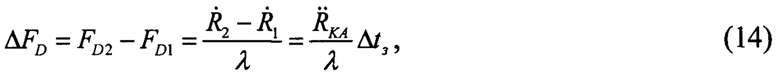
где  - радиальное (лучевое) ускорение КА относительно наземного маяка, которое необходимо выразить через искомое гравитационное ускорение gKA.
- радиальное (лучевое) ускорение КА относительно наземного маяка, которое необходимо выразить через искомое гравитационное ускорение gKA.
Если пренебречь малым ускорением КА, вызванным влиянием сопротивления остаточной атмосферы, ускорение 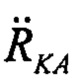 определяется относительно наземной точки размещения маяка и определяется расстоянием R до него, которое в свою очередь определяется высотой ΚΑ Η=Rsinα. Искомое гравитационное ускорение КА gKA не зависит от этого расстояния и определяется только геоцентрической высотой ρКА. Для приведения этих ускорений к единой высоте H введем в рассмотрение приведенное к высоте спутника гравитационное ускорение
определяется относительно наземной точки размещения маяка и определяется расстоянием R до него, которое в свою очередь определяется высотой ΚΑ Η=Rsinα. Искомое гравитационное ускорение КА gKA не зависит от этого расстояния и определяется только геоцентрической высотой ρКА. Для приведения этих ускорений к единой высоте H введем в рассмотрение приведенное к высоте спутника гравитационное ускорение 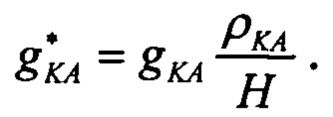 Если пренебречь для простоты малым ускорением КА, вызванным влиянием сопротивления остаточной атмосферы, отсюда, согласно рисунка на фиг. 1, имеем:
Если пренебречь для простоты малым ускорением КА, вызванным влиянием сопротивления остаточной атмосферы, отсюда, согласно рисунка на фиг. 1, имеем:

Подставляя это выражение в формулу (14), получаем:

откуда следует рабочая формула для вычисления искомого гравитационного ускорения:

Операция 7. Измеряют малую разностную частоту ΔFD, величина которой составляет около 50 Гц, с помощью периодомера на основе использования высокочастотных высокостабильных по частоте счетных импульсов.
Период колебания, соответствующий доплеровскому смещению ΔFD ≈ 50 Гц составляет около  Поэтому с помощью счетных импульсов, поступающих от источника высокостабильных импульсов с частотой Fсч=1010 Гц и соответствующим периодом следования δTсч=10-10 с заданные интервалы можно измерить с относительной погрешностью 0,5⋅10-8. С погрешностью такого же порядка определяется искомая разностная частота (16): δTсч/TD=δFD/FD ≈ 10-8.
Поэтому с помощью счетных импульсов, поступающих от источника высокостабильных импульсов с частотой Fсч=1010 Гц и соответствующим периодом следования δTсч=10-10 с заданные интервалы можно измерить с относительной погрешностью 0,5⋅10-8. С погрешностью такого же порядка определяется искомая разностная частота (16): δTсч/TD=δFD/FD ≈ 10-8.
Операция 8. По результатам измерений разностного доплеровского смещения принимаемой частоты на борту КА вычисляют искомое гравитационное ускорение КА по формуле (17).
Оценка погрешности определения гравитационного ускорения предлагаемым способом
Оценку погрешности определения гравитационного ускорения проведем на основе формулы (17).
Путем дифференцирования этой формулы находим полную относительную среднеквадратическую погрешность определения искомого ускорения:
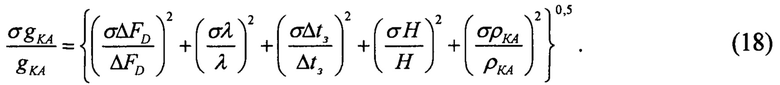
Среднеквадратические относительные ошибки всех входящих в эту формулу величин для геодезических спутников не превышают 10-7-10-8. Поэтому абсолютная погрешность определения гравитационного ускорения КА на высоте 1000 км в зените (при α=90°) составляет: 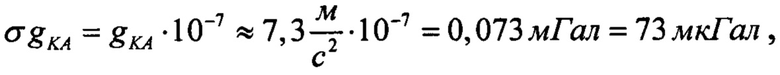 что существенно меньше, чем в прототипе (1 мГал).
что существенно меньше, чем в прототипе (1 мГал).
Таким образом, заявленный технический результат от внедрения изобретения, состоящий в повышении точности измерения гравитационного ускорения на борту КА, достигнут. Погрешность измерений снижена более, чем в 13 раз.
Заявленный технический результат от внедрения изобретения, состоящий в повышении дискретности (детальности) измерения гравитационного ускорения на борту КА, также достигнут. Дискретность (детальность) измерений вблизи точки траверза в предлагаемом способе составляет 1 км. В прототипе эта величина составляет 41 км, т.е. выигрыш в предлагаемом способе составляет более, чем в 40 раз. При угле места КА α=30° дискретность (детальность) измерений составляет 8,17 км, в прототипе она превышает 80 км. Выигрыш в дискретности (плотности) измерений в предлагаемом способе составляет почти 10 раз. При других углах также достигается многократный выигрыш.
Способ работоспособен и при излучении задающего сигнала с известной частотой с борта КА. В этом случае операции приема сигнала, выделения сигналов с доплеровским смещением, а также операция выделения разностной частоты с помощью линии задержки выполняются на наземной приемной станции. Все проведенные расчеты дискретности и точности справедливы и для этого случая.
Источники информации
1. W.Lechner, Ch. Reigber. The PRARE/GPS Experiment - A Contribution to Geodesy, Geodynamics and Navigation.
2. M. Dorrer. Le systeme DORIS Toulouse, March 1989, CNES.
3. Pavlis, N. & Holmes, S.A. & Kenyon, S.C. & Schmidt, D. & Trimmer, R.. (2005). A Preliminary Gravitational Model to Degree 2160.10.1007/3-540-26932-0_4.
4. Tapley, B.D. et al, "GRACE Mission Proposal to the ESSP Program", 1997.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ автономного измерения параметров гравитационного поля на борту космического аппарата | 2022 |
|
RU2784481C1 |
| РАЗНОСТНО-ДАЛЬНОМЕРНЫЙ СПОСОБ И НАЗЕМНО-КОСМИЧЕСКАЯ СИСТЕМА ИЗМЕРЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ЛЕТАТЕЛЬНЫХ АППАРАТОВ ПО СИГНАЛАМ РАДИОИЗЛУЧЕНИЯ ИХ БОРТОВОГО РАДИОЭЛЕКТРОННОГО ОБОРУДОВАНИЯ | 2015 |
|
RU2599984C1 |
| Лазерный космический гравитационный градиентометр | 2021 |
|
RU2754098C1 |
| ПРОСТРАНСТВЕННО-ВРЕМЕННАЯ СИСТЕМА РЕАЛЬНОГО ВРЕМЕНИ | 2005 |
|
RU2274953C1 |
| ГЛОБАЛЬНАЯ КОСМИЧЕСКАЯ СИСТЕМА ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И РАДИОНАВИГАЦИИ, РАДИОМАЯК И ПРИЕМНИК, ИСПОЛЬЗУЕМЫЕ В ДАННОЙ СИСТЕМЕ | 1996 |
|
RU2182341C2 |
| СПОСОБ ВЫСОКОТОЧНЫХ ИЗМЕРЕНИЙ ТРАЕКТОРНЫХ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА В ЛЕТНЫХ ИССЛЕДОВАНИЯХ НА ТРАССАХ БОЛЬШОЙ ПРОТЯЖЕННОСТИ | 2008 |
|
RU2393430C1 |
| СПОСОБ КОРРЕКЦИИ ТРАЕКТОРИИ ПОЛЕТА КОСМИЧЕСКОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2013 |
|
RU2537818C1 |
| КОМПЛЕКС БОРТОВЫХ ТРАЕКТОРНЫХ ИЗМЕРЕНИЙ | 1995 |
|
RU2116666C1 |
| СПОСОБ АВТОНОМНОГО СНИЖЕНИЯ ПОРОГОВ ОБНАРУЖЕНИЯ И ОТСЛЕЖИВАНИЯ НЕСУЩИХ СИГНАЛОВ, ПРИНИМАЕМЫХ НА ОРБИТЕ | 1997 |
|
RU2187127C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ | 2019 |
|
RU2734108C1 |
Изобретение относится к области радиолокации и может быть использовано для измерения гравитационного ускорения космического аппарата (КА). Сущность: излучают задающий сигнал известной частоты с наземного передатчика и измеряют на борту КА доплеровское смещение этой частоты. Вычисляют разность доплеровских частот задающего сигнала на известном интервале времени. При этом до начала приема сигнала наземного передатчика вычисляют необходимый интервал задержки доплеровского сигнала вдоль всей трассы движения КА в зоне приема сигнала наземного передатчика. Выделенный сигнал доплеровской частоты в цифровой форме последовательно вдоль трассы движения КА задерживают на вычисленные интервалы времени задержки с помощью переменной цифровой линии задержки. Выделяют разность доплеровских частот прямого и задержанного доплеровских сигналов для каждого интервала задержки. Измеряют текущие малые разности доплеровских частот вдоль орбиты с помощью цифрового периодомера. Вычисляют текущее гравитационное ускорение КА вдоль орбиты для каждого текущего интервала задержки. Технический результат: повышение точности и дискретности измерений гравитационного ускорения на борту КА. 1 ил.
Способ измерения гравитационного ускорения космического аппарата (КА), основанный на излучении задающего сигнала известной частоты с наземного передатчика и измерении на борту КА доплеровского смещения этой частоты, а также вычислении разности доплеровских частот задающего сигнала на известном интервале времени, отличающийся тем, что до начала приема сигнала наземного передатчика на борту КА, руководствуясь условием малой разности частот доплеровского сигнала на интервале задержки, вычисляют необходимый интервал задержки доплеровского сигнала вдоль всей трассы движения КА в зоне приема сигнала наземного передатчика, выделенный сигнал доплеровской частоты в цифровой форме последовательно вдоль трассы движения КА задерживают на вычисленные интервалы времени задержки с помощью переменной цифровой линии задержки, далее выделяют разность доплеровских частот прямого и задержанного доплеровских сигналов для каждого интервала задержки, измеряют текущие малые разности доплеровских частот вдоль орбиты с помощью цифрового периодомера и вычисляют текущее гравитационное ускорение КА вдоль орбиты для каждого текущего интервала задержки.
| CN 111483619 A, 04.08.2020 | |||
| В.Ф.Фатеев, Р.А.Давлатов | |||
| Многоспутниковый кластер для определения параметров гравитационного поля Земли / Известия вузов | |||
| Приборостроение, 2019, т.62, N5, стр.470-476 | |||
| Способ определения скорости объекта в доплеровской радиолокации | 2016 |
|
RU2709626C1 |
Авторы
Даты
2022-03-24—Публикация
2021-03-23—Подача