Изобретение относится к измерительной технике и может быть использовано для морских, воздушных и наземных объектов. Задачей изобретения является повышение точности бесплатформенной инерциальной навигационной системы (БИНС) и уменьшение требуемых вычислительных затрат путем создания способа непрерывной коррекции углов пространственной ориентации от спутниковой навигационной системы (СНС) с одним приемником.
В распространенном способе комплексирования при помощи статистического фильтра оцениваются погрешности навигационных параметров и инструментальных погрешностей инерциальных датчиков. По результатам оценок по уравнениям динамики косвенным образом оценивают ошибки текущих измерений углов пространственной ориентации ЛА и корректируют текущие углы ориентации. Для обеспечения заданной точности при этом необходимо оценивать свыше двадцати параметров, что требует больших вычислительных мощностей. Определение углов пространственной ориентации спутниковыми навигационными системами путем измерения фазового сдвига принятых сигналов от каждого космического аппарата требует установки на ЛА нескольких антенн и линий приема и обработки сигналов, что на малогабаритных ЛА не всегда возможно.
Известен способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем Патент №2379700, Российская Федерация. Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем. МПК G01S 5/02. Опубл. 20.01.2010, бюл. №2.
В приведенном выше способе сигналы принимают от навигационных спутников двумя или более разнесенными антеннами, измеряют фазовые сдвиги между принятыми сигналами от каждого космического аппарата, осуществляют m измерений фазовых сдвигов между парами антенно-приемных устройств, осуществляют подбор значений целочисленных неоднозначностей в измерениях фазовых сдвигов для минимального созвездия из n спутников, по которым определяют возможные значения углов ориентации ЛА.
Недостатком этого изобретения является то, что для его реализации необходимо иметь несколько антенн и линий приема и обработки сигналов. Требуется предварительная коррекция измеренных фазовых сдвигов на величину составляющей систематической погрешности, вызванной неодинаковыми значениями группового времени запаздывания (ГВЗ) сигналов в антенно-приемных устройствах (далее антенно-приемные каналы), являющихся составной частью устройства определения угловой ориентации, размещаемого на объекте. При неодинаковых значениях ГВЗ в антенно-приемных каналах, разность значений ГВЗ в них будет отличаться от нуля. Если в расчетах принять указанную разность значений ГВЗ равной нулю, то это приведет к снижению точности оценки угловой ориентации объекта. Кроме того на малоразмерных ЛА размещение нескольких приемных антенн проблематично.
Существует патент на изобретение №2646954, Российская Федерация. Способ коррекции бесплатформенной инерциальной навигационной системы. МПК G01C 21/06. Опубл. 12.03.2018, бюл. №8. Принят нами за прототип.
Способ включает в себя комплексирование сигналов, соответствующих угловой скорости и линейной скорости объекта, с сигналами, соответствующими линейным ускорениям, преобразованными, с учетом параметров полета объекта. Адаптивную оценку крена и тангажа получают при помощи фильтра Калмана, в котором коэффициент усиления изменяется в зависимости от текущих значений модулей перегрузки, линейной скорости, а также угловых скоростей. Используют сигнал, соответствующий истинной воздушной скорости объекта, полученный от системы воздушных сигналов (СВС) в виде функции от динамического давления, и сигнал, соответствующий продольному ускорению, полученный путем дифференцирования с последующим сглаживанием сигнала скорости от СВС.
Недостатком известного способа является то, что в приведенном изобретении не предусмотрено измерение курса. Кроме того в условиях непрерывного маневрирования ЛА этот способ обладает недостаточной точностью. Это может привести к возникновению значительных погрешностей в результате постоянного маневрирования высокоманевренных ЛА.
Цель работы - повышение точности коррекции БИНС по углам крена, тангажа и обеспечение коррекции курса по сигналам одноантенного приемника СНС во всем диапазоне параметров полета при уменьшении вычислительных затрат БЦВМ.
Поставленная цель достигается за счет того, что согласно способу коррекции углов ориентации бесплатформенной инерциальной навигационной системы (БИНС) на скользящем интервале, при котором по сигналам датчиков угловых скоростей (ДУС) определяют углы крена и тангажа летательного аппарата (ЛА) и осуществляют коррекцию углов крена и тангажа БИНС путем совместной обработки угловых скоростей, линейных ускорений ЛА, дополнительно, корректируют текущий курс ЛА, используя полученные от одного приемника СНС проекции путевых скоростей (спутниковых скоростей), для этого осуществляют совместное использование множества измерений на скользящем интервале наблюдений, составляют одинаковой размерности (m) три массива спутниковых скоростей VN (ti), VH (ti), VE(ti), три массива угловых скоростей ωx (ti), ωу (ti), ωz (ti), и три массива линейных ускорений nx (ti), ny (ti), nz (ti), определяют наличие угловых скоростей вращения ЛА и их изменчивости на рассматриваемом интервале и вводят два признака:
Pr1=1, если 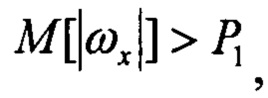
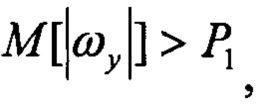
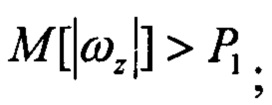
Pr2=1, если Pr1=1 и 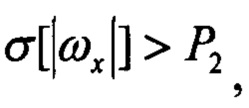
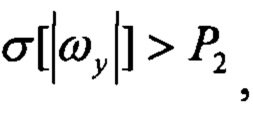
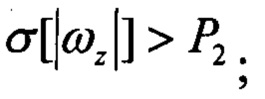
здесь 
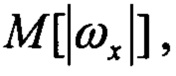
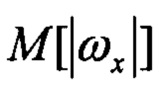 - средние значения модулей угловых скоростей;
- средние значения модулей угловых скоростей;
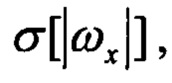
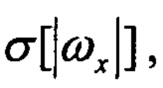
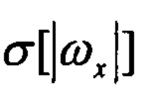 - СКО угловых скоростей; Р1, Р2 - пороговые значения; при невыполнении указанных условий признаки Pr1, Pr2 равны нулю;
- СКО угловых скоростей; Р1, Р2 - пороговые значения; при невыполнении указанных условий признаки Pr1, Pr2 равны нулю;
если Pr1=0 вращение ЛА отсутствует и выполняется переход на конец алгоритма;
при помощи преобразования Хартли в низкочастотной области формируют вектор дискретных финитных изображений спутниковых скоростей, назовем это преобразование - решением Хартли: по начальным значениям кватерниона ориентации задают текущие значения углов ориентации и выполняют интегрирование кватерниона ориентации с отрицательным шагом и вычисляют матрицу поворота A(t), вычисляют оценки углов ориентации по матрице поворота, выполняют интегрирование уравнений оценок скоростей в связанной системе координат (связанных скоростей) с отрицательным шагом, выполняют интегрирование кватерниона ориентации с отрицательным шагом, по оценкам связанных скоростей, используя матрицу поворота, определяют оценки проекций связанных скоростей на текущую плановую систему координат (плановых скоростей), определяют вектор дискретных финитных изображений 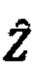 оценок спутниковых скоростей по Хартли
оценок спутниковых скоростей по Хартли 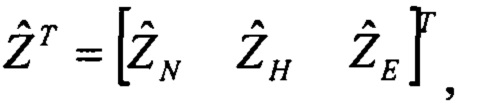
далее определяют вектор рассогласований изображений спутниковых скоростей и изображений их оценок 
выполняют решение Хартли с малым приращением δϑ начального условия тангажа и определяют оценки изображений плановых скоростей
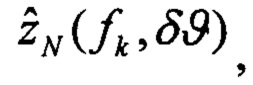
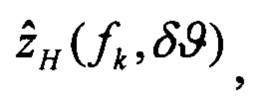
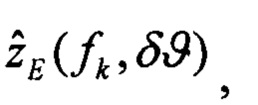
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариациям начального условия по тангажу:
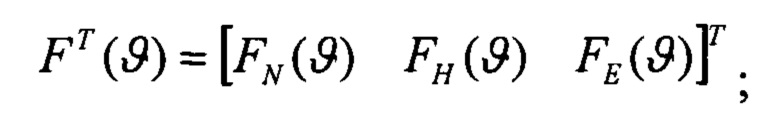
выполняют решение Хартли с малым приращением δγ начального условия крена, определяют оценки изображений плановых скоростей
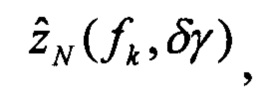
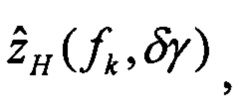
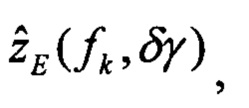
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариациям начального условия по крену:
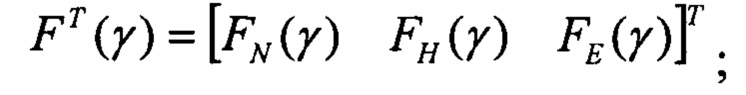
выполняют решение Хартли с малым приращением δψ начального условия курса, определяют оценки изображений плановых скоростей
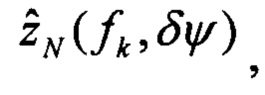
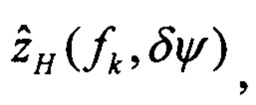
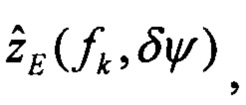
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариациям начального условия по курсу:
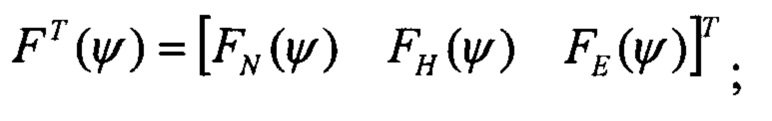
далее на основании линеаризации вектора изображений измерений спутниковых скоростей 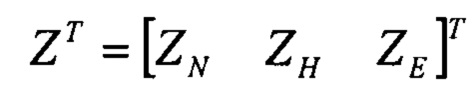 относительно искомого вектора ориентации
относительно искомого вектора ориентации 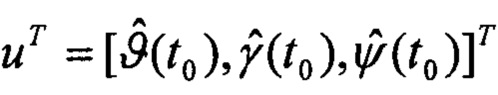 составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения:
составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения: 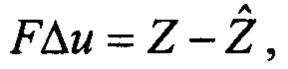
систему уравнений решают методом наименьших квадратов, результирующие оценки углов ориентации содержатся в векторе 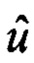 :
:
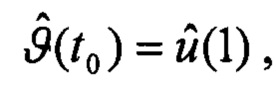
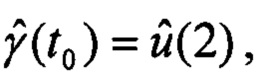
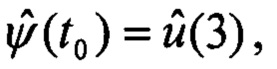 вычисляется очередное приближение вектора ориентации:
вычисляется очередное приближение вектора ориентации: 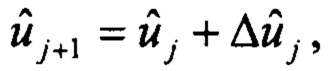 точность оценивания контролируют по среднему модулю погрешностей оценок спутниковых скоростей, сходимость итераций контролируют по модулю вектора приращений Δu, сравнивая с заданной малой величиной, выполняют расчет кватерниона БИНС по скорректированным углам;
точность оценивания контролируют по среднему модулю погрешностей оценок спутниковых скоростей, сходимость итераций контролируют по модулю вектора приращений Δu, сравнивая с заданной малой величиной, выполняют расчет кватерниона БИНС по скорректированным углам;
следующая итерация начинается с выполнения проверки вводимых двух признаков вращения ЛА, по выполненным признакам устанавливают весовые коэффициенты коррекции:
условие Pr1=1 означает нижний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят показания БИНС, а результаты идентификации ориентации по СНС учитываются в меньшей степени,
условие Pr1=1, Pr2=1 означает верхний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят результаты идентификации ориентации по СНС, а показания БИНС учитываются в меньшей степени, При невыполнении указанных условий признаки Pr1, Pr2 равны нулю;
если Pr1=1, принимается решение, что вращение ЛА отсутствует и выполняется, переход на конец алгоритма,
если Pr1=1, выполняется следующая итерация.
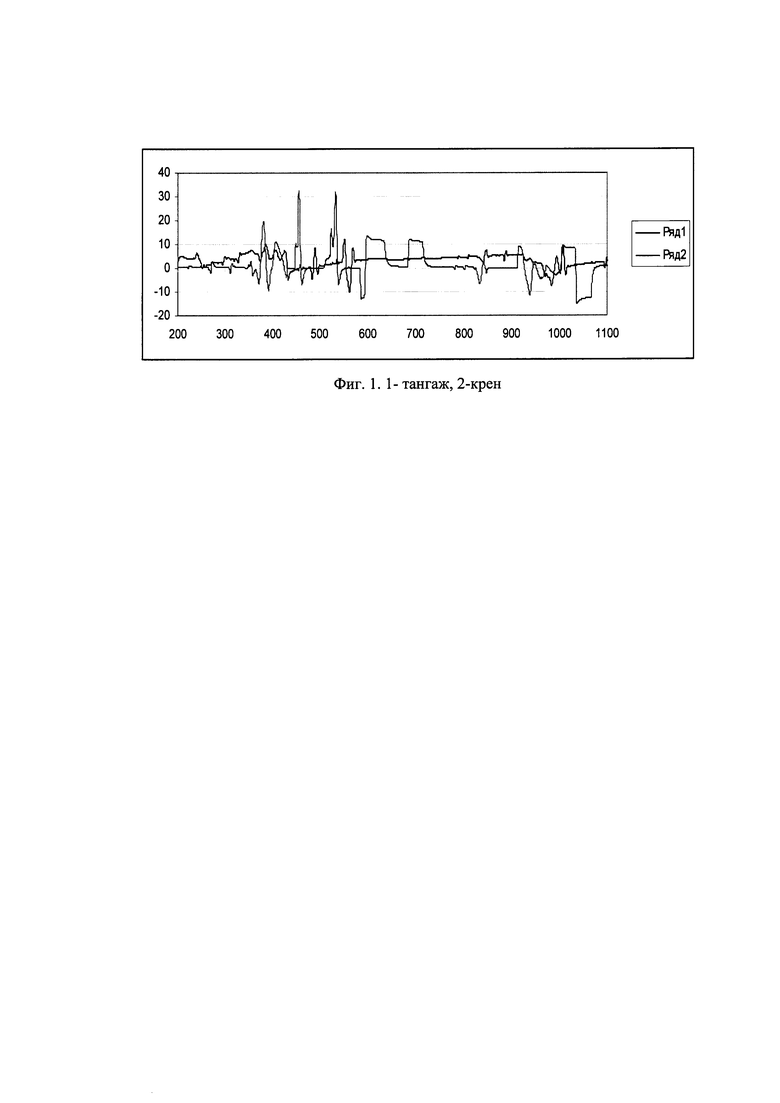
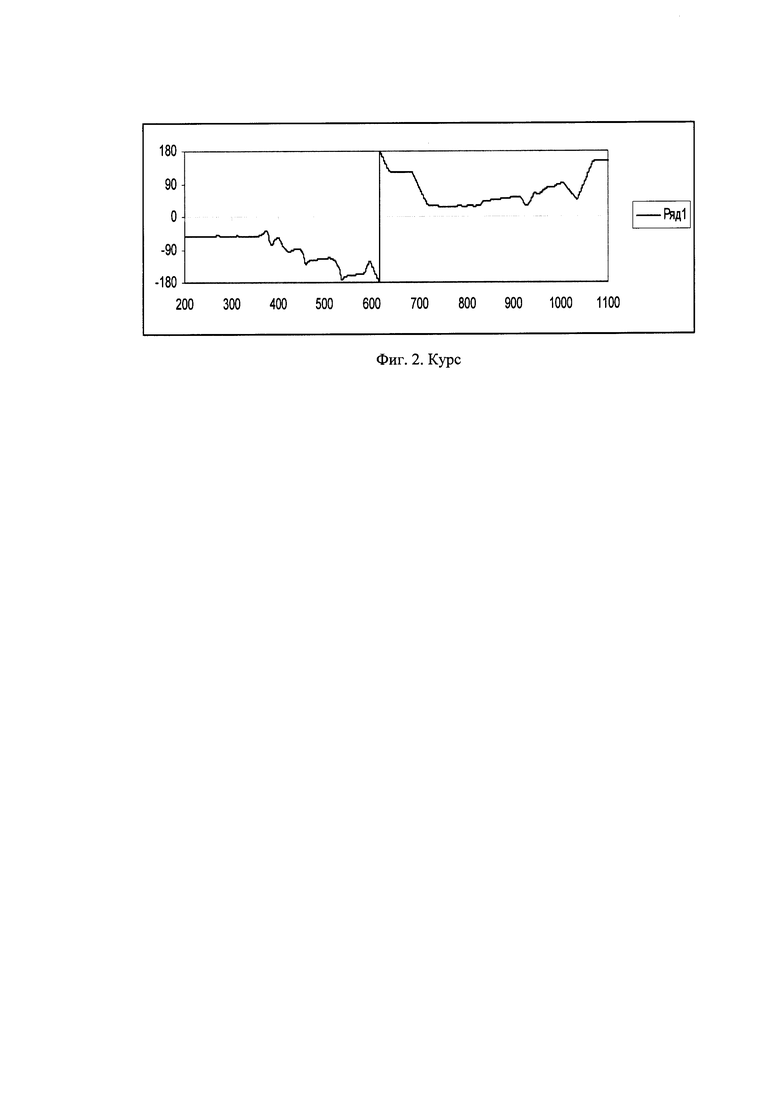
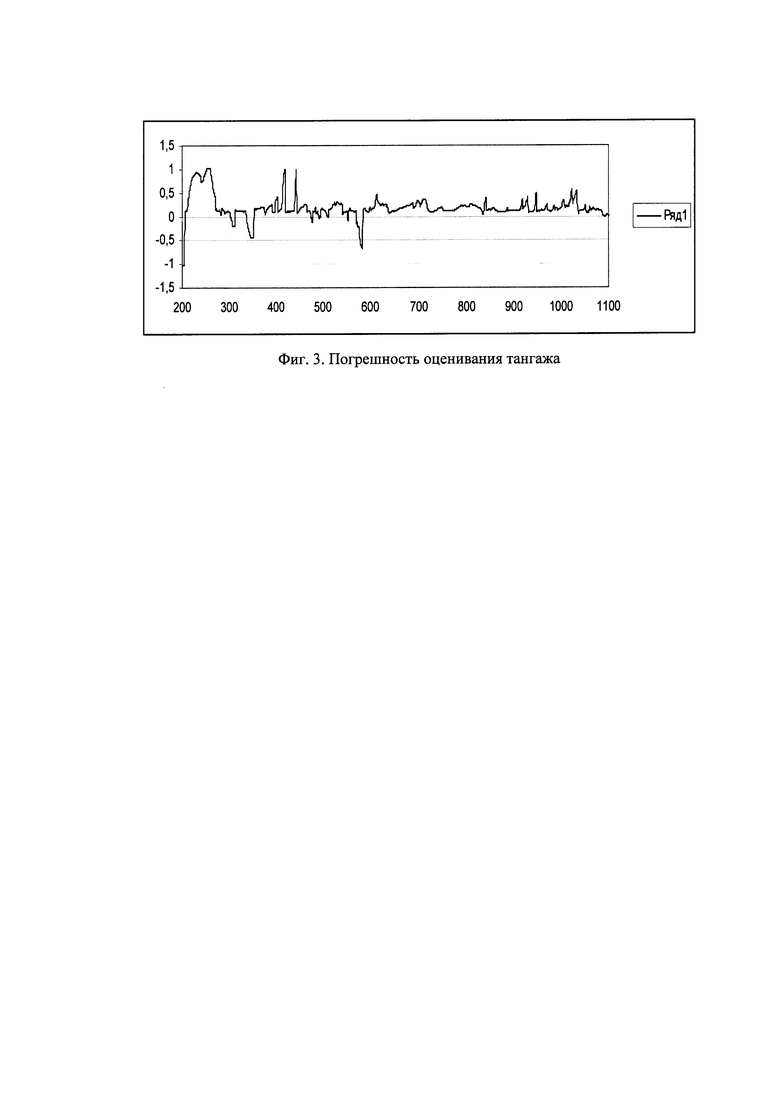
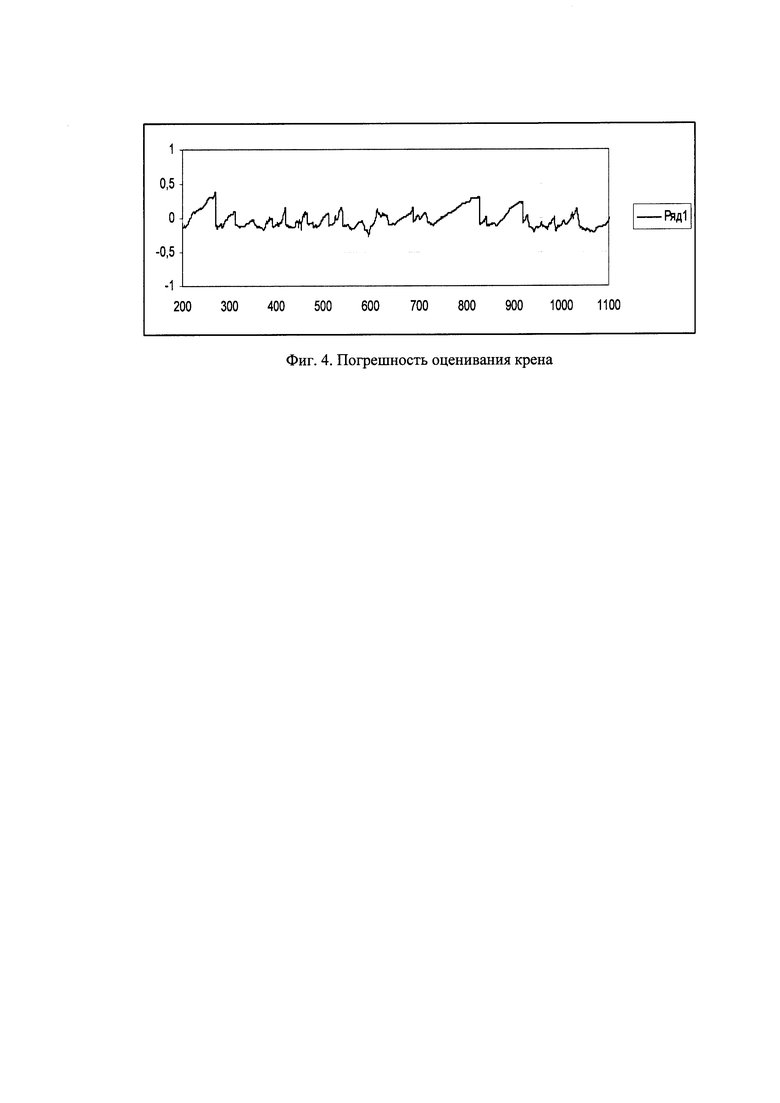
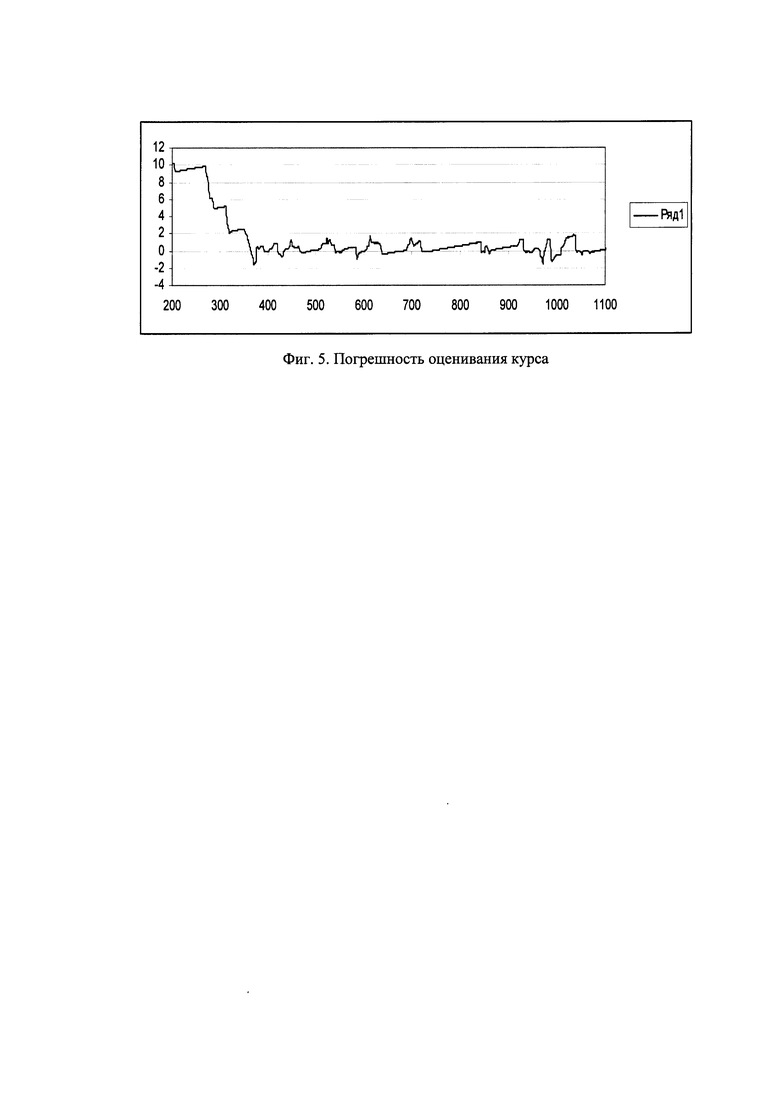
На фиг. 1. представлены текущие значения: 1 - тангаж, 2 - крен. На фиг. 2. представлены текущие значения курса. На фиг. 3, 4, 5 представлены погрешности оценивания тангажа, крена и курса в течение всего полета.
Описание работы способа представлено ниже.
На каждом малом шаге Δt регистрации измерений инерциальных датчиков выполняется накопление текущих измерений инерциальных датчиков и спутниковых скоростей в буферные регистры (массивы), при этом прошлые измерения сдвигаются и сохраняются в пределах длины интервала наблюдения.
Способ коррекции работает параллельно с алгоритмом БИНС, а его выполнение начинается по заполнении буферных регистров. Задача решается с частотой поступления измерений спутниковых скоростей от СНС (10 Гц), но использует информацию, накопленную в буферных регистрах с частотой измерений инерциальных датчиков (100 Гц).
Входными данными являются три массива спутниковых скоростей, три массива угловых скоростей и три массива линейных ускорений:
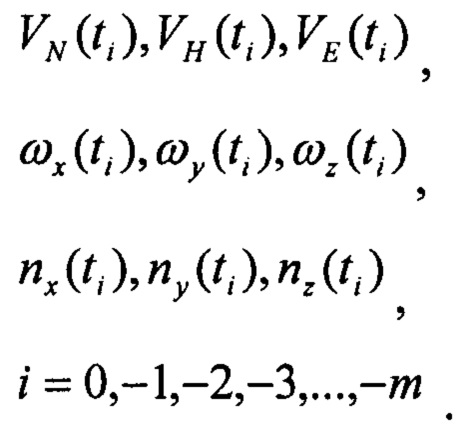
Здесь m - размерность буферных регистров, t0 - текущий момент реального времени, 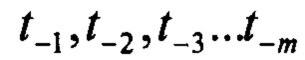 - прошлые моменты времени, отстоящие, друг от друга на шаг дискретизации Δt.
- прошлые моменты времени, отстоящие, друг от друга на шаг дискретизации Δt.
Выходными данными являются оценки углов ориентации для текущего момента времени t0: 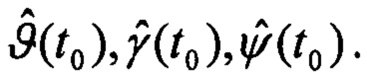
Задача определения корректирующих углов является итерационной. В ней используются не сами измерения спутниковых скоростей, а их изображения в частотной области, формируемые с помощью преобразования Хартли. При этом учитывается набор низкочастотных гармоник:
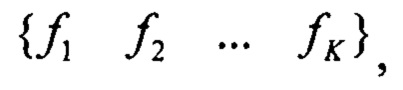
fk=(k-1)Δƒ, Δƒ=1/{{m-1)Δt), k=1,2…К
где К - число учитываемых гармоник, Δƒ - разрешающая способность преобразования.
Рассмотрим вычисления, которые выполняются для одного положения интервала наблюдений.
Шаг 1.
Начало алгоритма.
Выполняют сдвиг информации в буферных регистрах и запоминание последних по времени измерений СНС и инерциальных датчиков.
Шаг 2.
Определяют наличие угловых скоростей вращения ЛА и их изменчивости на рассматриваемом интервале. Вводят два признака:
Pr1=1 при 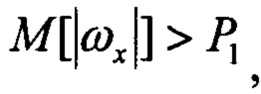

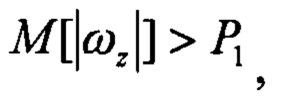
Pr2=1 при Pr1=1 и 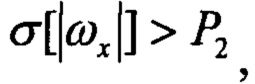

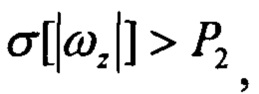
Здесь 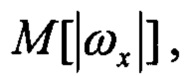
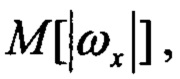
 - средние значения модулей угловых скоростей;
- средние значения модулей угловых скоростей;
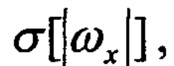
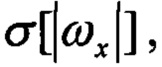
 - СКО угловых скоростей; Р1, Р2 - пороговые значения.
- СКО угловых скоростей; Р1, Р2 - пороговые значения.
При невыполнении указанных условий признаки Pr1, Pr2 равны нулю.
При Pr1=0 вращение ЛА отсутствует и выполняется, переход на конец алгоритма.
При Pr1=1 выполняется переход на следующий шаг 3.
Шаг 3.
По измерениям спутниковых скоростей, накопленным в буферных регистрах, формируют вектор их изображений Z, который имеет вид:

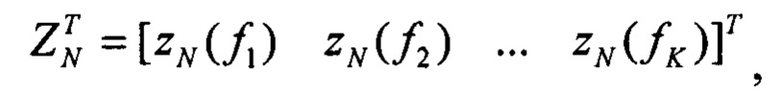
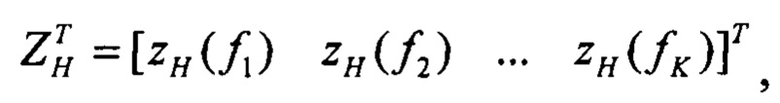
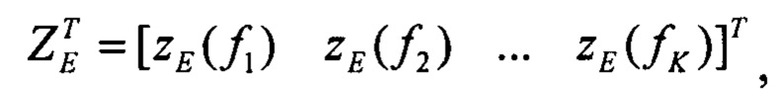
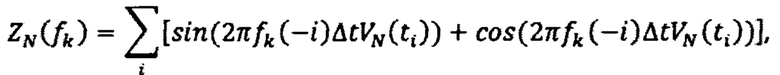
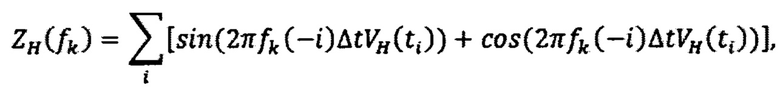
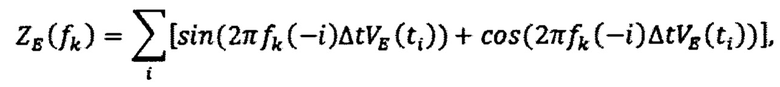
k=1,2…К
Число учитываемых гармоник не менее трех. В приведенном ниже примере учитывалось шесть гармоник. Дальнейшее увеличение числа гармоник не повышает точность коррекции, но увеличивает объем вычислений.
Заметим, что использование низкочастотных изображений спутниковых скоростей оправдано инерционностью угловых движений ЛА. При этом снижается размерность задачи, а также уменьшаются погрешности, обусловленные более медленным и ступенчатым изменением низкочастотных измерений СНС относительно измерений инерциальных датчиков БИНС.
Шаг 4.
Начало итераций
Шаг 4.1.
Задают текущие приближения искомых углов:

На первой итерации они принимаются в виде:
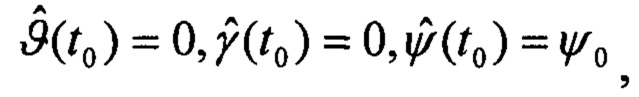
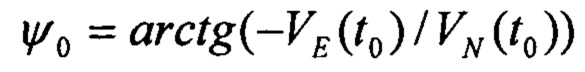 - начальное приближение курса, за которое принимается путевой угол.
- начальное приближение курса, за которое принимается путевой угол.
Определяют начальное значение кватерниона ориентации q:
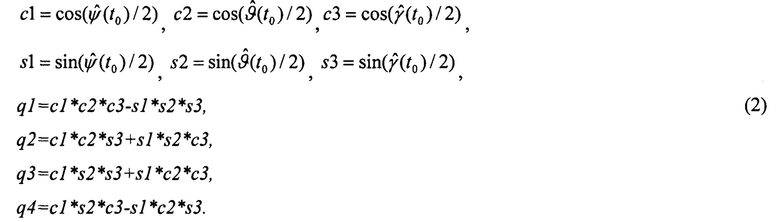
Выполняют интегрирование кватерниона ориентации в обратном времени с отрицательным шагом «-Δt» для получения оценок углов и координат в прошлые моменты времени 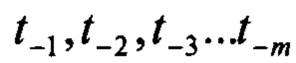 .
.

где 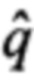 - оценка кватерниона ориентации для текущих приближений углов ориентации в момент времени t0; qω - кватернион угловых скоростей, запомненных в буферных регистрах:
- оценка кватерниона ориентации для текущих приближений углов ориентации в момент времени t0; qω - кватернион угловых скоростей, запомненных в буферных регистрах: 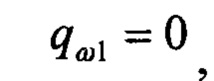
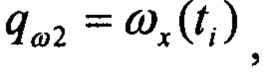
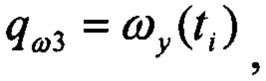
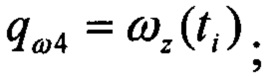
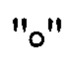 - операция умножения кватернионов.
- операция умножения кватернионов.
Определяют матрицу поворота Δ(t) для моментов времени 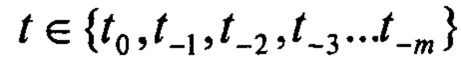 по кватерниону ориентации:
по кватерниону ориентации:
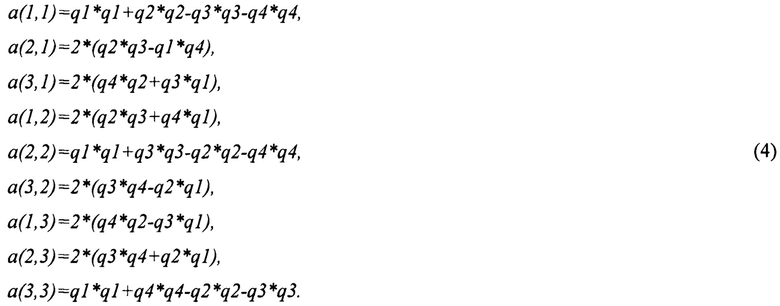
Определяют оценки углов ориентации по матрице поворота:
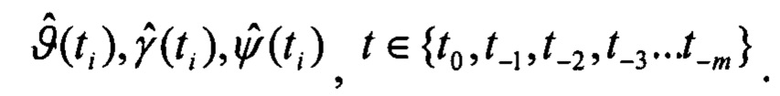
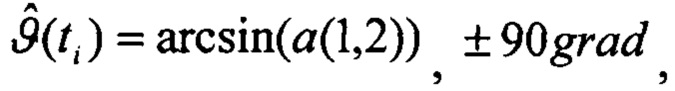
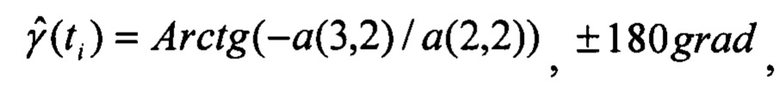
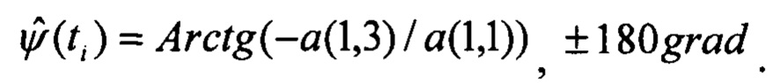
Выполняют интегрирование уравнений оценок составляющих вектора скорости в связанных с ЛА осях (связанных скоростей) в обратном времени:
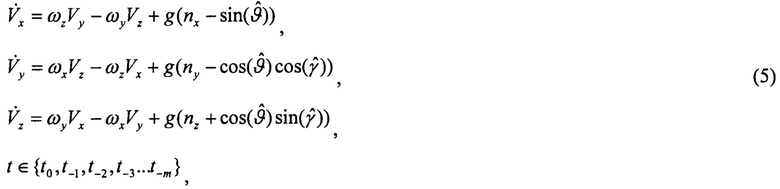
с начальными условиями:

Определяют оценки плановых скоростей по оценкам связанных скоростей и оценкам матрицы поворота:
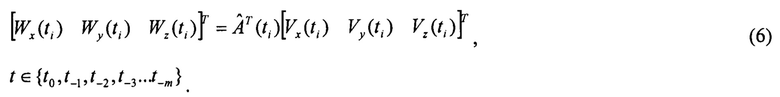
Определяют вектор дискретных финитных изображений оценок спутниковых скоростей по Хартли:
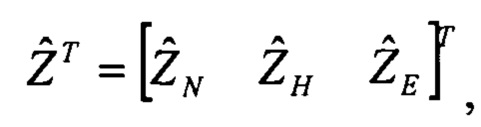
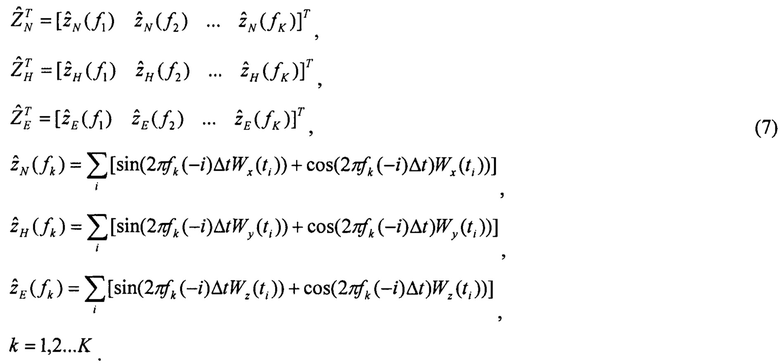
Определяют вектор рассогласований изображений спутниковых скоростей и изображений их оценок:
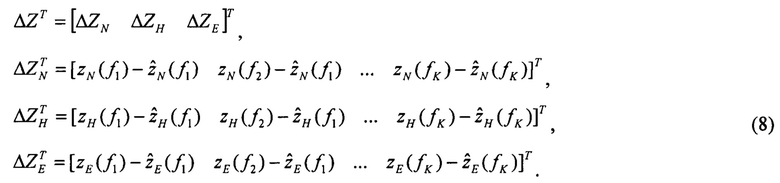
Шаг 4.2.
Выполняют решение выражений (2)-(7) с малым приращением δϑ начального условия тангажа:

При этом определяются оценки изображений плановых скоростей:
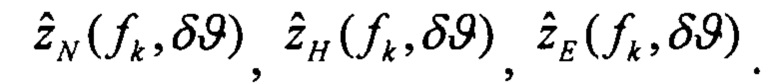
Определят вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по тангажу:
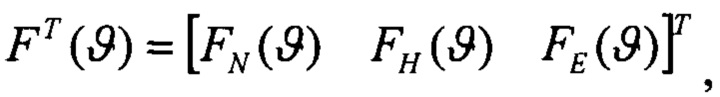

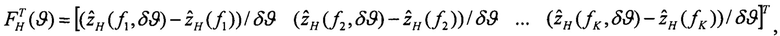

Шаг 4.3.
Выполняют решение выражений (2)-(7) с малым приращением δγ начального условия крена:

При этом определяют оценки изображений плановых скоростей:
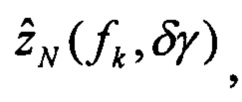
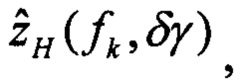
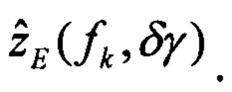
Определяют вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по крену:
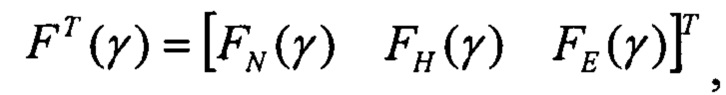
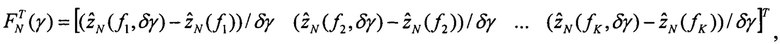
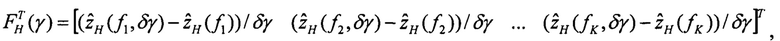
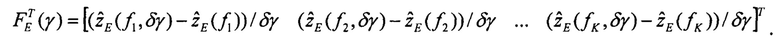
Шаг 4.4.
Выполняют решение выражений (2)-(7) с малым приращением δψ начального условия курса:

При этом определяют оценки изображений плановых скоростей:
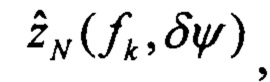
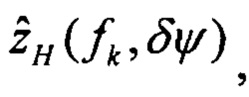

Определяют вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по курсу:
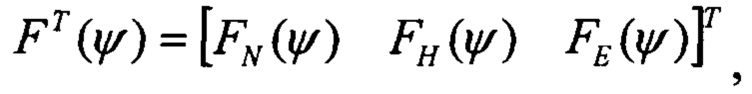
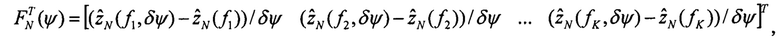
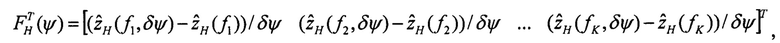
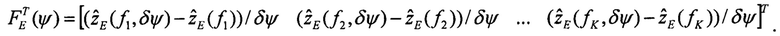
Шаг 5.
На основании линеаризации вектора изображений измерений спутниковых скоростей  относительно искомого вектора ориентации
относительно искомого вектора ориентации  составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения:
составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения:

где векторы Z,  определены на шагах 3 и 4.1
определены на шагах 3 и 4.1
F - матрица функций чувствительности, размерностью (К,3), столбцы которой определены на шагах 4.2, 4.3, 4.4:
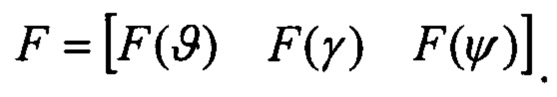
Систему уравнений (12) решают методом наименьших квадратов:

где j - номер итерации.
Определяют очередное приближение вектора ориентации для текущего момента времени t0:

Если заданное число итераций не выполнено, переход на шаг 4.1.
Шаг 6.
Конец итераций.
Результирующие оценки углов ориентации для текущего момента времени t0 содержатся в векторе  :
:

Проверяют качество итераций.
Сходимость итераций контролируют по модулю вектора приращений Δu, который должен стремиться к нулю. Если на последней итерации он больше заданной малой величины Δu>eps1, переход на конец алгоритма.
Точность оценивания контролируют по среднему модулю погрешностей оценок спутниковых скоростей:
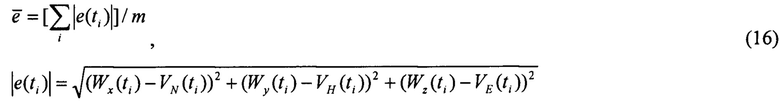
Если он больше заданной величины  , переход на конец алгоритма.
, переход на конец алгоритма.
Шаг 7.
Выполняют проверку признаков вращения ЛА, сформированных на шаге 2, и осуществляют коррекцию показаний БИНС:
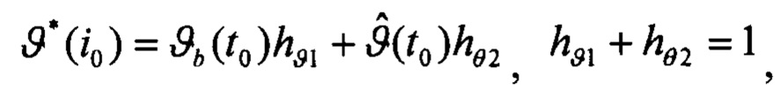
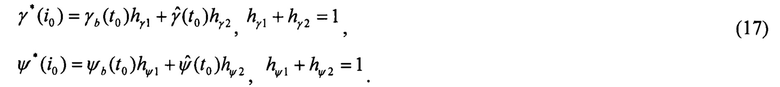
Здесь: 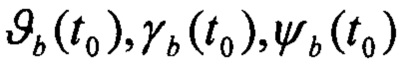 - тангаж, крен и курс, полученные от БИНС;
- тангаж, крен и курс, полученные от БИНС;
 - скорректированные тангаж, крен и курс;
- скорректированные тангаж, крен и курс;
 - весовые коэффициенты коррекции.
- весовые коэффициенты коррекции.
При выполнении (17), в зависимости от значений признаков, устанавливают весовые коэффициенты коррекции.
Выполнение условия Pr1=1 означает нижний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят показания БИНС, а результаты идентификации ориентации по СНС учитываются в меньшей степени.

Выполнение условий Pr1=1, Pr2=1 означает верхний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят результаты идентификации ориентации по СНС, а показания БИНС учитываются в меньшей степени.
hϑl≤hθ2, hγ1<hγ2, hψ1<hψ2.
Выполняют расчет кватерниона БИНС по скорректированным углам: ϑ*, γ*, ψ*.
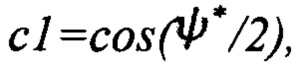

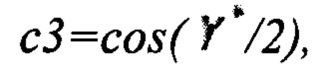
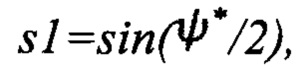
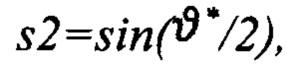
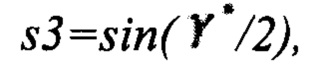
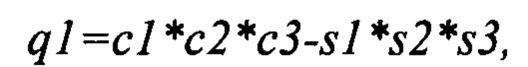
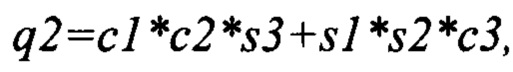
Конец алгоритма.
Таким образом, для коррекции ориентации по СНС достаточно наличия угловых скоростей, а также их некоторого изменения на интервале наблюдения.
Эти требования не являются чрезмерными, так как удовлетворяются даже при небольших угловых движениях ЛА. Так пороговое значение Рх для среднего модуля угловых скоростей принималось 0.1 град/с, а пороговое значение Р2 для СКО модуля угловых скоростей принималось 0.25 град/с. При увеличении уровня шумов измерений пороги следует увеличить.
Результаты моделирования.
Алгоритм решался по данным имитации полета легкого самолета на авиасимуляторе. Полет включал в себя участки прямолинейного горизонтального движения и участки вращения с разными по амплитуде угловыми скоростями.
Начальное значение курса было задано с погрешностью +10 градусов.
На фиг. 1, 2 представлены процессы изменения тангажа, крена и курса.
На фиг. 3, 4, 5 представлены погрешности оценивания тангажа, крена и курса в течение всего полета.
Данный способ претендует на универсальность в смысле отсутствия зависимости от вида объекта, на котором установлена БИНС, и особенностей его движения.
Техническим результатом использования изобретения является повышение точности при уменьшении вычислительных затрат, обеспечение непрерывной коррекции углов тангажа, крена и курса в условиях незначительного маневрирования в полете и с использованием одноантенного приемника СНС, а также универсальность применения способа на объектах различных видов. Способ позволяет использовать датчики ДУС и ДЛУ средней и низкой точности, в том числе микромеханического типа.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| Адаптивный корректор углов ориентации для БИНС | 2020 |
|
RU2749152C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| Малогабаритный навигационный комплекс | 2016 |
|
RU2644632C1 |
| Комплексный способ навигации летательных аппаратов | 2016 |
|
RU2646957C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| Малогабаритная адаптивная курсовертикаль | 2016 |
|
RU2714144C2 |
| КОМПЛЕКСИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА НАВИГАЦИИ НА "ГРУБЫХ" ЧУВСТВИТЕЛЬНЫХ ЭЛЕМЕНТАХ | 2008 |
|
RU2380656C1 |
| МАЛОГАБАРИТНАЯ БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА СРЕДНЕЙ ТОЧНОСТИ, КОРРЕКТИРУЕМАЯ ОТ СИСТЕМЫ ВОЗДУШНЫХ СИГНАЛОВ | 2012 |
|
RU2502049C1 |
Изобретение относится к измерительной технике и может быть использовано для морских, воздушных и наземных объектов. Задачей изобретения является повышение точности бесплатформенной инерциальной навигационной системы (БИНС) путем создания способа непрерывной коррекции углов ориентации от спутниковой навигационной системы (СНС) с одним приемником, обеспечение универсальности его использования для любого ЛА. Способ коррекции углов ориентации БИНС на скользящем интервале, при котором по сигналам датчиков угловых скоростей (ДУС) определяют углы крена и тангажа ЛА и осуществляют коррекцию углов крена и тангажа БИНС путем совместной обработки угловых скоростей, линейных ускорений ЛА. При этом дополнительно корректируют текущий курс ЛА, используя полученные от одного приемника СНС проекции путевых скоростей, для этого осуществляют совместное использование множества измерений на скользящем интервале наблюдений, составляют одинаковой размерности три массива спутниковых скоростей, три массива угловых скоростей и три массива линейных ускорений. Далее определяют наличие угловых скоростей вращения ЛА и их изменчивость на рассматриваемом интервале. При этом предлагаются алгоритмы совместного оценивания крена, тангажа и курса ЛА по измерениям трехкомпонентных датчиков ДУС, ДЛУ и одного приемника СНС итерационным алгоритмом по методу Хартли. Данный алгоритм удобен для практического применения, так как может быть реализован при относительно небольших вычислительных затратах. Для применения рассматриваемого алгоритма предварительная настройка его на процессах, характерных для конкретного вида ЛА не требуется. Технический результат – повышение точности и обеспечение непрерывной коррекции углов тангажа, крена и курса в условиях маневрирования в полете. 5 ил.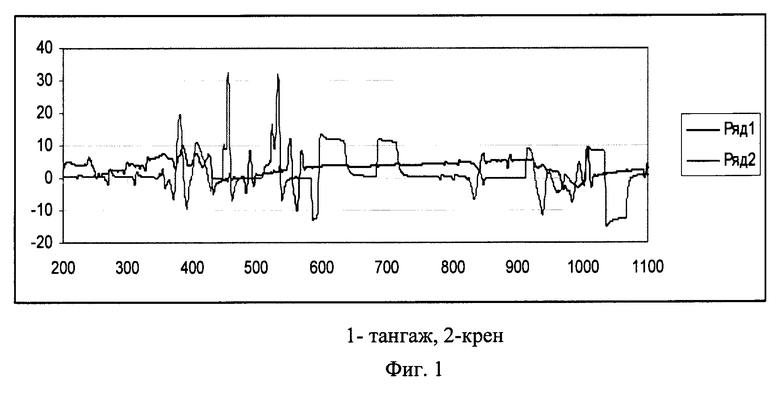
Способ коррекции углов ориентации бесплатформенной инерциальной навигационной системы (БИНС) на скользящем интервале, при котором по сигналам датчиков угловых скоростей (ДУС) определяют углы крена и тангажа летательного аппарата (ЛА) и осуществляют коррекцию углов крена и тангажа БИНС путем совместной обработки угловых скоростей, линейных ускорений ЛА, отличающийся тем, что дополнительно корректируют текущий курс ЛА, используя полученные от одного приемника СНС проекции путевых скоростей - спутниковых скоростей, для этого осуществляют совместное использование множества измерений на скользящем интервале наблюдений, составляют одинаковой размерности (m) три массива спутниковых скоростей, VN(ti), VH(ti), VE(ti), три массива угловых скоростей ωx (ti), ωу (ti), ωz (ti), и три массива линейных ускорений nx (ti), ny (ti), nz (ti), определяют наличие угловых скоростей вращения ЛА и их изменчивость на рассматриваемом интервале и для этого вводят два признака:
Pr1=1, если 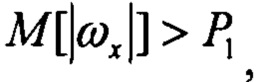
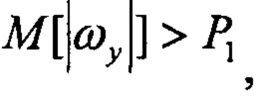
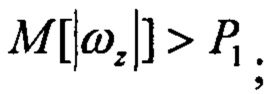
Pr2=1, если Pr1=1 и 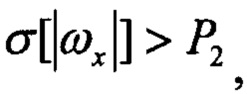
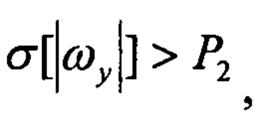
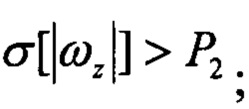
здесь 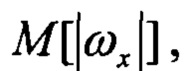

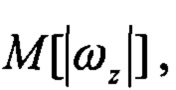 - средние значения модулей угловых скоростей;
- средние значения модулей угловых скоростей;
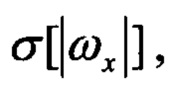
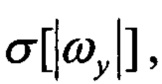
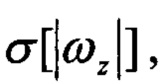 - СКО угловых скоростей; Р1, Р2 - пороговые значения,
- СКО угловых скоростей; Р1, Р2 - пороговые значения,
при невыполнении указанных условий признаки Pr1, Pr2 равны нулю,
если Pr1=0, вращение ЛА отсутствует и выполняется переход на конец алгоритма, при помощи преобразования Хартли в низкочастотной области формируют вектор дискретных финитных изображений спутниковых скоростей, назовем это преобразование - решением Хартли: по начальным значениями кватерниона ориентации задают текущие значения углов ориентации и выполняют интегрирование кватерниона ориентации с отрицательным шагом, вычисляют матрицу поворота A(t), вычисляют оценки углов ориентации по матрице поворота, выполняют интегрирование уравнений оценок скоростей в связанной системе координат - связанных скоростей с отрицательным шагом, выполняют интегрирование кватерниона ориентации с отрицательным шагом, по оценкам связанных скоростей используя матрицу поворота определяют оценки проекции связанных скоростей на текущую плановую систему координат – плановых скоростей, определяют вектор дискретных финитных изображений 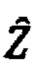 оценок спутниковых скоростей по Хартли
оценок спутниковых скоростей по Хартли 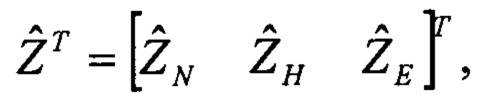 далее определяют вектор рассогласований изображений спутниковых скоростей и изображений их оценок
далее определяют вектор рассогласований изображений спутниковых скоростей и изображений их оценок
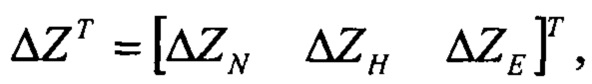
выполняют решение Хартли с малым приращением δϑ начального условия тангажа и определяют оценки изображений плановых скоростей,
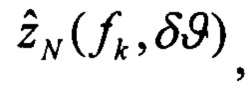
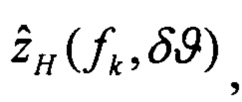
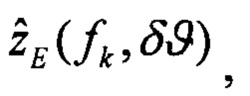
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по тангажу:
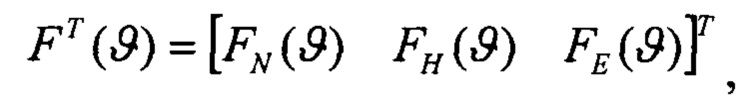
выполняют решение Хартли с малым приращением δγ начального условия крена, определяют оценки изображений плановых скоростей
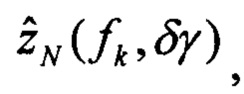
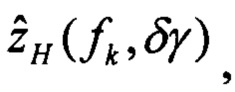
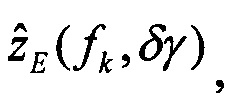
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по крену:
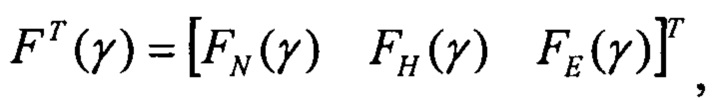
выполняют решение Хартли с малым приращением δψ начального условия курса, определяют оценки изображений плановых скоростей
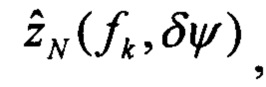
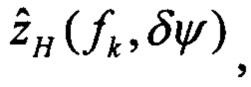
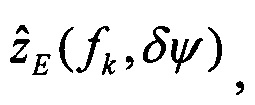
определяют вектор функций чувствительности изображений оценок плановых скоростей к вариации начального условия по курсу:
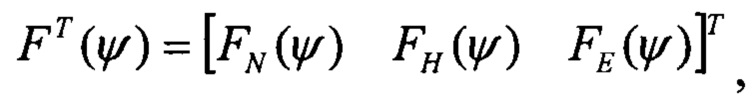
далее на основании линеаризации вектора изображений измерений спутниковых скоростей
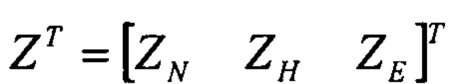 относительно искомого вектора ориентации
относительно искомого вектора ориентации 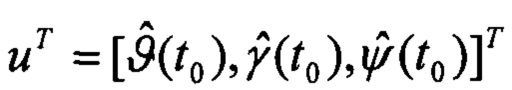 составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения:
составляют систему линейных алгебраических уравнений для приращения Δu относительно текущего приближения: 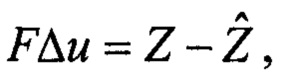
систему уравнений решают методом наименьших квадратов, результирующие оценки углов ориентации содержатся в векторе 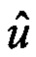 :
:

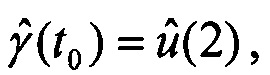
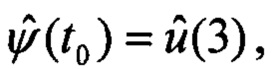 вычисляется очередное приближение вектора ориентации:
вычисляется очередное приближение вектора ориентации: 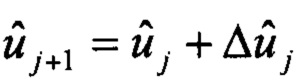 , точность оценивания контролируют по среднему модулю погрешностей оценок спутниковых скоростей, сходимость итераций контролируют по модулю вектора приращений Δu, сравнивая с заданной малой величиной, выполняют расчет кватерниона БИНС по скорректированным углам;
, точность оценивания контролируют по среднему модулю погрешностей оценок спутниковых скоростей, сходимость итераций контролируют по модулю вектора приращений Δu, сравнивая с заданной малой величиной, выполняют расчет кватерниона БИНС по скорректированным углам;
следующая итерация начинается с выполнения проверки вводимых двух признаков вращения ЛА, по выполненным признакам устанавливают весовые коэффициенты коррекции: условие Pr1=1 означает нижний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят показания БИНС, а результаты идентификации ориентации по СНС учитываются в меньшей степени,
условие Pr1=1, Pr2=1 означает верхний уровень коррекции, то есть больший вклад в результирующие оценки углов ориентации вносят результаты идентификации ориентации по СНС, а показания БИНС учитываются в меньшей степени, при невыполнении указанных условий признаки Pr1, Pr2 равны нулю,
если Pr1=0, принимается решение, что вращение ЛА отсутствует и выполняется, переход на конец алгоритма,
если Pr1=1, выполняется следующая итерация.
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2646954C2 |
| Способ определения углов ориентации ЛА на вертикальных траекториях полета | 2017 |
|
RU2671291C1 |
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы беспилотного летательного аппарата малой дальности с использованием интеллектуальной системы геопространственной информации | 2019 |
|
RU2722599C1 |
| US 6415223 B1, 02.07.2002. | |||
Авторы
Даты
2023-02-14—Публикация
2022-01-27—Подача