ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к области робототехники, а именно к способам калибровки промышленных роботов.
ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ
Из уровня техники известен, в частности, способ повышения точности перемещений промышленного робота в процессе инкрементального формообразования (см. RU 2762693C1, опубл. 06.07.2020)(1). Для повышения точности позиционирования промышленного робота в процессе инкрементального формообразования проводится оценка по результатам измерения с помощью лазерного трекера положения инструмента относительно базовой поверхности, которая задается с помощью 4 сферических отражателей. При проведении измерений положения инструментального центра робота-манипулятора рядом с ним установлен сферический отражатель, положение которого относительно базовой плоскости определяется по результатам измерений с помощью лазерного трекера, имеющего частоту сканирования, соответствующую тактовой частоте робота-манипулятора. В точке, соответствующей начальному положению пуансона, проводится измерение координат инструментального центра робота-манипулятора для оценки погрешности измерений и калибровки робота, а оценка рассогласования заданной и реальной траектории перемещения робота осуществляется путем сравнения текущих и реальных координат инструментального центра робота в заданных точках на каждом шаге углубления пуансона, при пошаговом перемещении инструмента, или витке, при спиральном перемещении инструмента, с формированием корректирующего сигнала в случае превышения допустимой величины, определяемой заданной точностью обработки.
Хотя цель заявленного способа и аналога (1) близка, средства, которыми она достигается неоднородны. При применении предварительной калибровки точность перемещения выше, чем без неё.
Наиболее близким аналогом заявленного способа, по мнению заявителя, является способ повышения точности позиционирования промышленного робота (см. RU2671787C1, опубл. 06.11.2018) Для калибровки некинематических параметров измеряют координаты точки на запястье робота в заданных координатах расположения робота с рабочей нагрузкой при вращении наиболее длинных звеньев А и Б с заданным шагом. Вычисляют функцию удельной ошибки угла поворота звена Б от угла звена Б к горизонту и набор функций удельной ошибки угла поворота звена А от заданного угла звена А к горизонту для всех измеренных углов звена Б. Вносят изменения в кинематическую модель робота, при этом угловая поправка для звеньев А и Б вычисляется интегрированием функции удельной ошибки угла поворота соответствующего звена на участке между максимумом функции и заданным значением угла поворота звена к горизонту.
В предложенном аналоге (2), также как и в заявленном способе применяется предварительная калибровка. Поиск оптимальных конфигураций робота (2) осуществляется в основном с помощью решения задачи оптимизации, что является крайне вычислительно сложным процессом. Для робота с шестью звеньями пространство поиска будет представлять собой все возможные конфигурации в пространстве состояний и шестимерные векторы усилий, прилагаемых к роботу. На практике, планирование эксперимента для 12 таких конфигураций может занимать до 100 часов, используя методы градиентного спуска из множества начальных значений. Это обстоятельство определенно затрудняет использование планирования эксперимента в реальных индустриальных задачах. однако степень точности применяемой калибровки значительно ниже.
КРАТКОЕ ИЗЛОЖЕНИЕ ИЗОБРЕТЕНИЯ
Техническим результатом изобретения является повышение точности калибровки промышленного робота.
Технический результат достигается посредством создания способа калибровки промышленного робота, основанном на эластостатической калибровке, для которой была выбрана система, описывающая манипулятор как жесткую модель, состоящий из неподвижного основания и последовательной цепи податливых звеньев, ряда податливых приводимых в движение шарниров и рабочего органа, который контактирует с обрабатываемой деталью, на котором установлены маркеры для измерений и система подвеса груза, включающий построение модели жесткости для эластостатической калибровки, которая описывает эластостатические свойства манипулятора и отклонения рабочего органа при внешней нагрузке, выбор оптимальных конфигураций для измерения и соответствующих внешних сил, вызывающих эластостатические отклонения, проведение калибровочных экспериментов с использованием полученных конфигураций, вычисление желаемых эластостатических параметров с использованием измеренных отклонений и сил, компенсацию эластостатических ошибок путем настройки входной программы контроллера, описывающей траекторию цели с использованием идентифицированных параметров.
Заявленный способ калибровки характеризуется тем, что для построения модели жесткости робота, моделируют жесткость каждого звена с помощью пружины с шестью степенями свободы, три из которых соответствуют перемещению, а три - ориентации и жесткость шарнира с помощью пружины с одной степенью свободы, расположенной вдоль ось вращения, в результате чего получается матрица жесткости манипулятора, которую обрабатывают методами численных алгоритмов оптимизации обеспечивая итоговую точность для целевой траектории движения рабочего органа робота.
В предпочтительном варианте выполнения в качестве ограничений для конфигурации робота использованы физические лимиты поворота каждого сустава, накладываемые барьером безопасности робота или клеткой.
В предпочтительном варианте выполнения целевой функцией для численной оптимизации служил один из подходов на основе критерия оптимальной конфигурации.
В предпочтительном варианте выполнения выбор оптимальных конфигураций для измерения и соответствующих внешних сил, вызывающих эластостатические отклонения опирается на соответствующий показатель эффективности, учитывающий особенности технологического процесса, геометрические и физические ограничения рабочей ячейки для обеспечения желаемой точности позиционирования с использованием минимального количества калибровочных экспериментов при заданных статистических свойствах шума измерений.
В предпочтительном варианте выполнения при проведение калибровочных экспериментов с использованием полученных конфигураций положение рабочего органа измеряют дважды для каждой конфигурации робота: до и после приложения нагрузки, требуемые перемещения рабочего органа вычисляют как их разность, при этом приложенные нагрузки измеряют при помощью датчика силы, в результате получают набор отклонений рабочего органа и соответствующих нагрузок и оценивает точность идентификации параметров модели, а также ожидаемую точность позиционирования
КРАТКОЕ ОПИСАНИЕ РИСУНКОВ
Сущность изобретения поясняется чертежами, на которых:
Фиг.1 –промышленный робот FANUC R-2000iC/165F для операции механической;
Фиг.2 – пример тестовой конфигурации промышленного робота для измерений.
Позиции на фиг.1,2 обозначают следующее:
1- основание робота;
2- рабочий инструмент робота;
3- барьер безопасности;
4- маркеры для измерений;
5- система подвеса груза;
Эти чертежи не охватывают и, кроме того, не ограничивают весь объем вариантов реализации данного технического решения, а представляют собой только иллюстративный материал частного случая его реализации.
ВАРИАНТ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
В заявленном способе калибровки промышленного робота для повышения эффективности выбора оптимальной позы для измерения, предлагается использовать методы основанные на искусственном интеллекте. Для получения оптимальных конфигураций и усилий для калибровки будет проводиться поиск на основе эволюционного программирования других эвристических подходов. Использование методов искусственного интеллекта позволит сделать ещё один шаг в этом направлении и расширить зону поиска и количество параметров модели.
В способе калибровки промышленного робота основной целью является достижение желаемой точности позиционирования робота при минимальном количестве экспериментов. По сравнению с классическими процедурами калибровки робота, предлагается ввести дополнительный этап – планирование эксперимента, которое выполняется перед измерениями и направлено на получение набора поз робота для измерений, обеспечивающих хорошие результаты калибровки (точность робота после компенсации). Это позволяет повысить эффективность компенсации ошибок и оценить точность робота, что весьма важно для промышленного применения.
Предлагаемая эластостатическая калибровка промышленного робота состоит из нескольких этапов:
Этап 1: Моделирование. Данный этап направлен на разработку подходящей (т.е. пол- ной и не избыточной) модели жесткости для эластостатической калибровки, которая должным образом описывает эластостатические свойства манипулятора и отклонения рабочего органа при внешней нагрузке.
Этап 2: Планирование эксперимента. Второй этап направлен на выбор оптимальных конфигураций для измерения и соответствующих внешних сил, вызывающих эластостатические отклонения. Данный процесс должен опираться на соответствующий показатель эффективности, учитывающий особенности технологического процесса, геометрические и физические ограничения рабочей ячейки. Первостепенной задачей здесь является достижение желаемой точности позиционирования с использованием минимального количества калибровочных экспериментов (при заданных статистических свойствах шума измерений).
Этап 3: Измерение. Третий этап касается проведения калибровочных экспериментов с использованием полученных конфигураций. В отличие от геометрической калибровки, здесь положение рабочего органа следует измерять дважды для каждой конфигурации робота: до и после приложения нагрузки. Требуемые перемещения рабочего органа вычисляются как их разность. Кроме того, приложенные нагрузки следует измерять с помощью датчика силы. Результатом этого шага является набор отклонений рабочего органа и соответствующих нагрузок.
Этап 4: Идентификация параметров. На четвертом этапе желаемые эластостатические параметры вычисляются с использованием расширенной эластостатической модели, измеренных отклонений и сил. На этом этапе также оценивается точность идентификации параметров модели, а также ожидаемая точность позиционирования.
Этап 5: Компенсация. На последнем этапе эластостатические ошибки компенсируются путем настройки входной программы контроллера (описывающей траекторию цели) с использованием идентифицированных параметров. Здесь стратегия оперативной компенсации вряд ли применима, так как обычно невозможно интегрировать эластостатическую модель манипулятора в контроллер промышленного робота.
Критерии для выбора оптимальных конфигураций
В робототехнике, как и в других областях, для достижения хорошей точности требуется адекватная модель и точные параметры для этой модели. Хотя на практике структура модели обычно хорошо известна, идентификация параметров модели требует существенной экспериментальной работы, а точность результатов калибровки сильно зависит от конфигурации манипулятора. По этой причине планирование экспериментов является важной проблемой и эффективным инструментом, позволяющим повысить точность идентификации параметров за счет правильного выбора конфигураций измерений. Следует отметить, что первоначально эта идея пришла из анализа линейной регрессии.
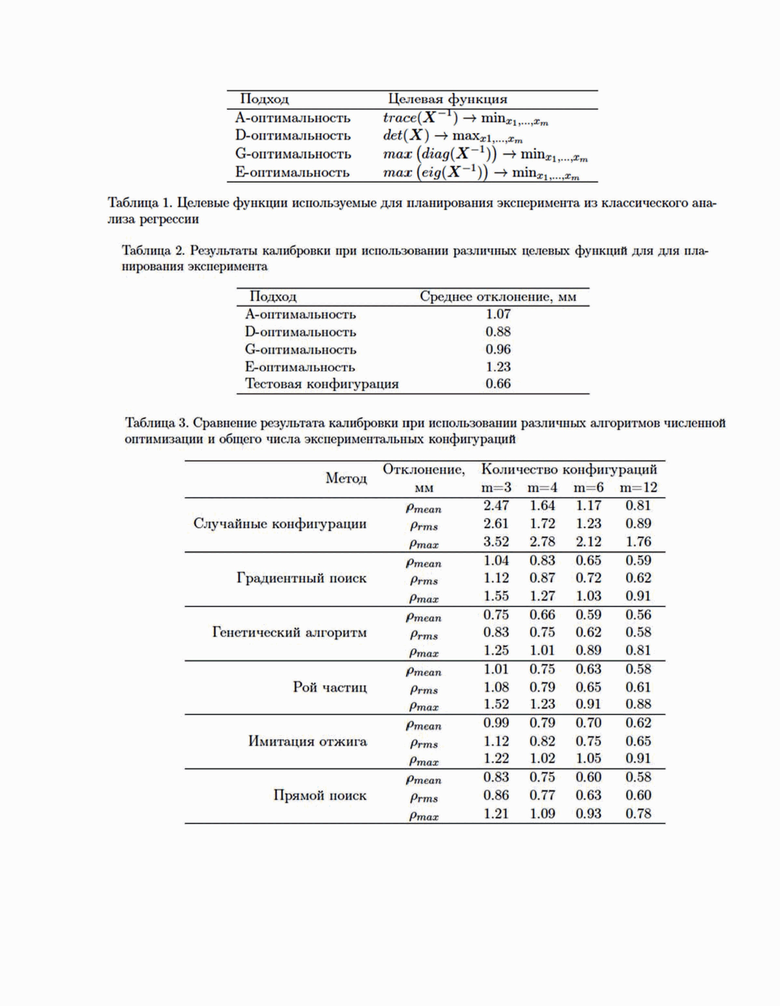
Очевидно, что задача выбора критерия оптимальности конфигураций нетривиальна и для сравнения решений требуются некоторые численные критерии. С их помощью разработаны так называемые принципы А-, Т-, D-, G-, E-оптимальности, представленные в
А- и Т-оптимальность оперируют следом матрицы ковариации и информационной матрицы соответственно. Эти два подхода имеют почти схожие цели, направленные на минимизацию средней дисперсии оцениваемых параметров, однако результаты оптимизации могут различаться. В общем, принцип Т-оптимальности проще в применении, поскольку он имеет дело с информационной матрицей (где обращение матрицы не требуется). Однако, такой подход ненадежен, поскольку недиагональные элементы информационной матрицы не включаются в целевую функцию. Кроме того, оба этих критерия трудно применимы, если параметры имеют разные единицы измерения (в этом случае конечные результаты сильно зависят от их нормировки).
D-оптимальность нацелена на максимизацию определителя информационной матрицы. Данный критерий имеет тенденцию придавать чрезвычайно важное значение параметру, к которому модель наиболее чувствительна. Одна из потенциальных проблем здесь заключается в том, что объем доверительной области может быть уменьшен благодаря уменьшению дисперсии конкретного параметра. Однако, погрешности по всем остальным параметрам могут оставаться очень большими.
G-оптимальность стремится минимизировать максимальные диагональные элементы в ковариационной матрице.
E-оптимальность предназначена для минимизации максимального собственного значения ковариационной матрицы Целью этого подхода является минимизация максимальной дисперсии всех возможных нормированных линейных комбинаций оценок параметров. Данная функция часто используется для уменьшения корреляции параметров.
Линейный регрессионный анализ является хорошо изученной областью, и методы планирования экспериментов для соответствующих регрессионных моделей были должным образом рассмотрены и описаны. По этой причине их применение в робототехнике на первый взгляд кажется многообещающим для задачи повышения точности идентификации параметров.
Все критерии оптимизации, которые представлены в Таблице 1, не оценивают напрямую влияние ошибки измерения на точность робота. Промышленные роботы обычно работают с ограниченным набором конфигураций, и задача калибровки - обеспечить наилучшую точность для этих конкретных состояний робота.
Также стоит отметить, что данный показатель может быть легко адаптирован для различных приложений, в которых точность позиционирования является критически важной. Например, для операции захвата и перемещения, когда робот выполняет свою задачу только в двух целевых положениях, использование этих двух тестовых положений достаточно для достижения наилучшей точности после компенсации эластостатической ошибки. Аналогично, для механической обработки и инкрементальной формовки крупногабаритных заготовок можно ввести несколько опорных точек, соответствующих разным участкам желаемой траектории.
Для получения требуемых параметров модели жесткости из экспериментальных данных следует использовать процедуру идентификации. Основная цель здесь - найти неизвестные параметры жесткости на основе измерений крутящего момента и смещения. Уравнение (9) устанавливает взаимосвязь между смещением рабочего органа и приложенной силой через матрицу жесткости и позволяет нам сформулировать задачу идентификации параметров.
Основная трудность эластостатической калибровки заключается в том, что прямое применение метода на основе виртуальных пружин (МВП) дает чрезмерное количество параметров, влияние которых на точность позиционирования робота существенно различается (в основном из-за их величины). Более того, прямое применение этой техники дает избыточную модель, не подходящую для калибровки. В частности, весь набор эластостатических параметров для манипулятора с 6 степенями свободы включает 258 значений и приводят к сбою числовых процедур, используемых при калибровке, что вызвано сингулярностью соответствующей матрицы наблюдения. Для получения нередуцируемой или несокращаемой модели были разработаны соответствующие алгебраические инструменты в виде набора правил. Кроме того, при эластостатической калибровке дополнительную трудность вызывает существенное различие значений параметров. Как следует из нашего опыта, соответствующие результаты идентификации могут нарушать фундаментальные физические свойства матриц жесткости.
Таким образом можно сделать следующие выводы:
• полная эластостатическая модель манипулятора включает в себя огромное количество параметров (258 для обычного серийного робота с 6 степенями свободы), одновременная идентификация которых при наличии шума измерения затруднена или даже невозможна;
• перед применением метода идентификации по методу наименьших квадратов эластостатическая модель манипулятора должна быть уменьшена и избыточные параметры должны быть устранены, чтобы гарантировать обратимость информационной матрицы; этот этап может быть выполнен с использованием методов, аналогичных тем, которые разработаны для геометрической калибровки;
• среди оставшихся не избыточных параметров есть ряд несущественных, абсолютные значения которых относительно невелики, точность идентификации довольно низкая и влияние на податливость всего манипулятора практически ничтожно; эти параметры можно рассматривать как «практически не идентифицируемые», и их также следует исключить из модели;
• при разработке соответствующих методов, позволяющих обнаруживать «практически идентифицируемые» параметры, разумно учитывать некоторые специфические свойства матриц податливости, такие как симметрия матрицы податливости, наличие строго нулевых элементов (разреженность матрицы), положительной определенности и т. д.
Следовательно, для получения надежной модели жесткости, подходящей для калибровки, содержащей только значимые и практически идентифицируемые параметры при достаточно хорошем описании эластостатических свойств манипулятора, необходимо раз- работать специальные методы для сокращения модели и соответствующие правила, позволяющие минимизировать количество параметров, которые необходимо оценить и реконструировать исходную модель на основе метода виртуальных пружин по этим данным с учетом математических соотношений между параметрами модели, обусловленных их физическим смыслом.
Непосредственный подход к моделированию жесткости манипулятора приводит к выявлению полного, но избыточного числа параметров. Например, каждое звено описывается матрицей 6х6, включающей 36 параметров, которые рассматриваются как независимые. Однако, как следует из физики, число чисто физических и независимых параметров существенно ниже. Следовательно, между этими 36 параметрами существует сильная взаимосвязь, но этот факт обычно игнорируется при эластостатической калибровке. Кроме того, в силу фундаментальных свойств консервативной системы искомые матрицы соответствия должны быть строго симметричными и положительно определенными. Кроме того, для типичных звеньев манипулятора матрицы податливости разрежены из-за симметрии формы относительно некоторой оси, но это свойство также не принимается во внимание при идентификации эластостатических параметров. Чтобы воспользоваться преимуществами свойств матрицы соответствия и повысить точность идентификации, можно применить три простых метода, которые позволяют сократить количество параметров, которые необходимо вычислить в процедуре идентификации. Их можно рассматривать как методы редукции моделей, основанные на физике, и формализовать их следующим образом.
Для идентификации всех матриц податливости возможно заменить пару симметричных параметров с помощью одного.
Для всех матриц податливости из набора неизвестных исключаются параметры, соответствующие нулям в шаблоне матрицы жесткости, полученном аналитически для звена манипулятора аналогичной формы. Для получения желаемой матрицы шаблона удобно использовать любое реалистичное приближение формы звена.
Все податливости шарниров не могут быть идентифицированы по отдельности и должны быть включены в матрицу податливости предыдущего звена путем модификации соответствующих диагональных элементов. Эти изменения касаются идентифицированных значений и исключения соответствующих столбцов в матрице наблюдения.
Исключим из набора параметров модели те, которые соответствуют податливости шарниров, перед которыми имеется соответствующее звено. С точки зрения идентифицируемости параметров податливость таких шарниров неотделима от звеньев.
Обобщая эти методы, следует отметить, что представленные выше методы существенно сокращают количество идентифицируемых параметров, но не нарушают полноту, то есть способность описывать любой прогиб, вызванный нагрузкой. Однако сокращенная модель все же может иметь некоторую избыточность в структуре всего манипулятора.
Из геометрической калибровки известно, что несмотря на то, что избыточная модель подходит для прямых и обратных вычислений, ее нельзя использовать при идентификации, поскольку матрица наблюдения не имеет достаточного ранга. Аналогичная проблема возникает при эластостатической калибровке, когда некоторые коэффициенты жесткости соседних звеньев не могут быть идентифицированы отдельно.
Строгие методы сокращения, основанные на физических и математических свойствах матрицы податливости, довольно ограничены, если шум измерения достаточно велик. Это дает нам основания для разработки некоторых эвристических правил, учитывающих влияние шума измерения на точность идентификации. Понятно, что крайне низкая точность недопустима, но часто соответствующие параметры настолько малы, что их влияние на прогибы рабочего органа практически незначительны. Это поддерживает идею эвристической редукции малых параметров модели, но оставляет открытой проблему их дальнейшего восстановления в МВП-модели с использованием некоторых эмпирических или полуэмпирических соотношений, индуцированных математическими соотношениями между элементами матрицы жесткости.
Таким образом, представленный подход обладает двумя крайне полезными функциями: (i) удаление малых (но теоретически отличных от нуля) параметров и (ii) обнаружение элементов, соответствующих нулям в шаблоне матрицы, если последнее было определено достаточно тщательно. Использование этого метода позволяет идентифицировать эластостатические параметры манипулятора даже с учетом их избыточности.
Применяя метод планирование эксперимента к эластостатической калибровке, можно найти оптимальный набор конфигураций измерений, обеспечивающий наилучшую точность позиционирования рабочего органа манипулятора после калибровки. Очевидно, что аналитические решения соответствующих оптимизационных задач вряд ли могут быть получены (например, при очень большом количестве идентифицируемых параметров аналитические вычисления обращения матриц в этих выражениях вряд ли возможны). Таким образом, применение метода численной оптимизации является единственным разумным способом, однако, ключевыми вопросами становятся скорость сходимости, общее время вычислений и возможность достижения глобального минимума. По этой причине ниже представлены несколько традиционных методов оптимизации, а также несколько методов, основанных на мета-эвристике или искусственном интеллекте. Также представлено сравнительное исследование этих методов и критериев оптимизации.
Самый простой способ решить задачу оптимизации для выбора конфигурации робота и приложенной силы измерения состоит в применении обычных методов оптимизации, включенных в коммерческое математическое программное обеспечение. Понятно, что простой поиск с регулярной сеткой неприемлем из-за высокой сложности и огромного количества сравниваемых решений. По этой причине были исследованы два традиционных алгоритма: (i) случайный поиск, (ii) градиентный поиск. Также были исследованы четыре алгоритма на основе мета-эвристики и различных эволюционных методиках: (iii) генетический алгоритм, (iv) алгоритм на основе роя частиц, (v) алгоритм имитирующий отжиг, и (vi) на базе прямого поиска или поиска по шаблону. Их сравнительное исследование представлено ниже и сведено в Таблицу 3 и Таблицу 4, где использовались два критерия: время вычислений и возможность найти оптимальное решение (оценивается через точность манипулятора после калибровки). Вычислительные эксперименты проводились с использованием инструментария оптимизации Matlab, который был запущен на компьютере с процессором с 8 ядрами, частотой 3,3 ГГц и 40 Гб ОЗУ. Для всех вычислительных экспериментов предполагалось, что погрешности измерений составляет 0,05 мм (что соответствует точности лазерного измерителя FARO).
Контрольный пример касается планирования калибровочных экспериментов для промышленного манипулятора с шестью степенями свободы FANUC R-2000 i C/165F (фиг. 1), выполняющий операцию механической обработки. Этот робот состоит из неподвижного основания, последовательной цепи звеньев с податливостью, ряда податливых приводимых в движение шарниров и рабочего органа, который контактирует с обрабатываемой деталью. Внешняя сила w применяется к рабочему органу робота в результате технологического процесса. Чтобы построить модель полной жесткости робота, МВП предлагает моделировать жесткость каждого звена с помощью пружины с шестью степенями свободы (три из которых соответствуют перемещению, а три - ориентации) и жесткость шарнира с помощью пружины с одной степенью свободы, расположенной вдоль ось вращения, в результате чего получается полная матрица жесткости манипулятора Kf R42×42. Для использования этой модели необходимо знать более 250 параметров, которая в идеале может быть получена из CAD-модели робота.
Целевой функцией для численной оптимизации служил один из подходов описанных в Таблице 1. В качестве ограничений для конфигурации робота использованы физические лимиты поворота каждого сустава робота qlow < qi < qhi из документации робота, ограничения накладываемые барьером безопасности робота или клеткой (см рис. 1). Для проверки последнего оценивалась дальность элементов робота относительно стенок барьера, где положение узлов робота рассчитывалось из прямой кинематики робота как p = f (qi). Ограничением для приложенной силы wi = [wF wM ]T служили допустимая нагрузка ро- бота из документации и способ получения внешней силы в реальном эксперименте: сила wF и момент wM на фланце робота создаются грузом, подвешенным через плечо, как по- казано на фиг. 2. В качестве целевой траектории движения конечного инструмента робота была выбрана фигура "квадрат" с длиной каждой стороны в 50 см. В качестве тестовой конфигурации выбран центр этого квадрата.
Прежде чем перейти к сравнению численных алгоритмов оптимизации, важно выбрать целевую функцию. Для этого в Таблице 2 представлено сравнение итоговой точности системы после калибровки, при этом на этапе планирования эксперимента были использованы целевые функции из Таблицы 1 и подход тестовой конфигурации, описанный выше. В качестве численного метода оптимизации был использован генетический алгоритм, общее количество конфигураций m = 4. Очевидно, что подход, основанный на тестовой конфигурации, позволяет достичь лучшей итоговой точности для целевой траектории движения рабочего органа робота. Таким образом, для сравнительного анализа численных методов оптимизации в рамках планирования эксперимента целесообразно
Первый из рассмотренных алгоритмов (i) основан на прямом выборе наилучшего решения из множества сгенерированных случайным образом. Для этого исследования было получено 10 000 решений для различного количества конфигураций измерения m = 3, 4, 6, 12. Как следует из результатов, этот алгоритм очень быстр и требует от 1 до 10 минут для нахождения наилучшего решения. Однако оптимальное решение, полученное этим методом, существенно хуже решений, полученных с помощью других алгоритмов (на 15-30%).
Второй алгоритм (ii) использует градиентный поиск со встроенной численной оценкой производных, доступной в Matlab. Начальные точки были сгенерированы случайным образом и, чтобы избежать сходимости к локальным минимумам, оптимизационный поиск был повторен 5000 раз (начиная с разных точек). В этом случае был получен наилучший результат с точки зрения искомой цели, но вычислительные затраты были очень высокими (могут достигать нескольких суток). Таким образом, эта методика вряд ли применима на практике. Следует отметить, что уменьшение количества итераций здесь довольно опасно, так как существует ряд локальных минимумов, к которым алгоритм может сходиться.
Третий из рассмотренных методов (iii) применяет генетический алгоритм, основанный на адаптивном эвристическом поиске. Генетические алгоритмы — это адаптивные эвристические алгоритмы поиска, которые относятся к большей части эволюционных алгоритмов. Используемый размер популяции равен 200 индивидуумов. Алгоритм позволяет получить высокую итоговую точность после калибровки, особенно для среднего значения ошибки позиционирования и сходиться достаточно быстро. Увеличение числа конфигураций в 4 раза увеличило время поиска всего в 2 раза, что позволяет быстро найти множество конфигураций для случаев, когда необходима большая точность. Однако, следует отметить, что алгоритм достаточно чувствителен к начальным значениям популяции, и при малом размере популяции иногда остается в локальном минимуме. Для решения этой проблемы можно увеличивать размер популяции, что, несомненно, увеличит время расчета, либо запускать генетически алгоритм несколько раз с разными начальными популяциями.
Четвертый алгоритм на основе роя частиц (iv). Алгоритм роя частиц — это мощный мета-эвристический алгоритм оптимизации, вдохновленный поведением роя, наблюдаемым в природе, например стайкой рыб и птиц. Является простым и эффективным алгоритмом оптимизации. Он отличается от других алгоритмов оптимизации тем, что нужна только целевая функция, и она не зависит от градиента или какой-либо дифферен- циальной формы задачи. Используемое количество частиц равно 400. В данном анализе, результаты работы алгоритма близки к генетическому, но генетический алгоритм чуть бо- лее точный, когда как алгоритм на основе роя показывает более быструю сходимость (на 10-15%).
Пятый алгоритм на основе имитации отжига (v). Алгоритм имитации отжига основан на физическом отжиге в реальной жизни. Физический отжиг — это процесс нагревания материала до тех пор, пока он не достигнет температуры отжига, а затем он будет медленно охлаждаться, чтобы изменить материал до желаемой структуры. Когда материал горячий, молекулярная структура слабее и более восприимчива к изменениям. Когда материал остывает, молекулярная структура становится тверже и менее подвержена изменениям. Имитация отжига имитирует процесс физического отжига, но используется для оптимизации параметров модели. Этот процесс очень полезен в ситуациях, когда существует множество локальных минимумов, на которых такие алгоритмы, как градиентный спуск, застревают. Полученная точность близка к той, что была получена обычным градиентным спуском, хотя время необходимое на поиск оптимальных значений в 3-5 раз меньше.
Шестой алгоритм с использованием прямого поиска (vi). Алгоритм адаптивного прямого поиска разработан для задач оптимизации для условно неизвестной функции, для которой цель и ограничения обычно являются выходными данными моделирования. Это метод оптимизации без производных, разработанный для непрерывных переменных и поддерживаемый анализом сходимости, основанным на исчислении Кларка. В рамках проведенного сравнения, алгоритм показал отличную точность, но время поиска сильно зависит от количества переменных.
Таким образом, можно сделать следующие выводы основываясь на представленном сравнении численных методов оптимизации для этапа планирования эксперимента калиб- ровки. Случайный поиск (i) достаточно быстрый, но неэффективный, так как может привести к неприемлемым решениям. Следующий метод, градиентный поиск (ii) может найти глобальный минимум при условии, что он повторяется много раз с разными начальными точками (что очень затратно с вычислительной точки зрения). С точки зрения итоговой точности и времени поиска рекомендуется использовать генетический алгоритм (iii) или алгоритм на основе роя частиц (iv), оба подхода позволяют уменьшить время поиска оптимального значения в десятки раз (20-30 раз) по сравнению с классическим градиентным спуском при равном или лучшем уровне точности. Также следует отметить алгоритм прямого поиска (vi), который хоть и требует относительно большего времени для нахождения оптимального значения, но показывает хорошую точность для малых значений количества искомых конфигураций (m = 3, 4).
Анализ полученных результатов с точки зрения времени необходимого для получения конфигураций, оптимального значения, а также итоговой точности после применения калибровки показал преимущество рассматриваемых техник оптимизации на основе искусственного интеллекта над классическими методами поиска оптимального значения. Использование метода планирования эксперимента в целом позволило добиться увеличения точности в несколько раз по сравнению со случайными конфигурациями при равном количестве измерений, что очевидно позволит уменьшить время, требуемое на калибровку робота при реальном промышленном применении.
ПРОМЫШЛЕННОЕ ПРИМЕНЕНИЕ
Предложенный способ предназначен для ряда применений, включающих применение для калибровки промышленного робота, используемых в различных областях техники, в частности позволяет увеличить точность позиционирования рабочего органа робота после калибровки для контактных операций с высокими нагрузками, например таких как механическая обработка и инкрементальная формовка.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и система для определения по меньшей мере одного свойства манипулятора | 2014 |
|
RU2672654C2 |
| Способ калибровки кинематических параметров многостепенных манипуляторов | 2019 |
|
RU2719207C1 |
| СПОСОБ ОДНОВРЕМЕННОГО ПЛАНИРОВАНИЯ ТРАЕКТОРИИ И ПОСЛЕДОВАТЕЛЬНОСТИ ДЕФОРМАЦИЙ ДЛЯ ТЕНСЕГРИТИ ДРОНА | 2022 |
|
RU2795629C1 |
| Система и способ калибровки кинематических параметров роботизированного манипулятора | 2022 |
|
RU2810082C1 |
| Робот-ассистированный комплекс минимально инвазивной абдоминальной хирургии для автоматизированного выполнения операций методами локальной деструкции новообразований печени | 2023 |
|
RU2841089C1 |
| ЭКСПЕРТНАЯ СИСТЕМА НА БАЗЕ МЕДИЦИНСКОГО МАНИПУЛЯЦИОННОГО РОБОТА ДЛЯ ТРАНСПЕДИКУЛЯРНОЙ ФИКСАЦИИ ПОЗВОНОЧНИКА | 2023 |
|
RU2833780C1 |
| ОПТИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНЫХ КОМБИНАТОРНЫХ ПРОЦЕССОВ | 2004 |
|
RU2352984C2 |
| СПОСОБ И СИСТЕМА ЗАХВАТА ОБЪЕКТОВ С ПОМОЩЬЮ РОБОТИЗИРОВАННОГО УСТРОЙСТВА | 2020 |
|
RU2745380C1 |
| Способ и система определения по меньшей мере одной характеристики сочленения | 2013 |
|
RU2667938C2 |
| Промышленный робот-манипулятор с системой двойных энкодеров и способ его позиционирования | 2018 |
|
RU2696508C1 |

Изобретение относится к области робототехники, а именно к способам калибровки промышленных роботов. Способ калибровки промышленного робота основан на эластостатической калибровке, для которой была выбрана система, описывающая манипулятор как жесткую модель, состоящий из неподвижного основания и последовательной цепи податливых звеньев, ряда податливых приводимых в движение шарниров и рабочего органа, который контактирует с обрабатываемой деталью, на котором установлены маркеры для измерений и система подвеса груза. Для построения модели жесткости робота, моделируют жесткость каждого звена с помощью пружины с шестью степенями свободы, три из которых соответствуют перемещению, а три – ориентации, и жесткость шарнира с помощью пружины с одной степенью свободы, расположенной вдоль ось вращения, в результате чего получается матрица жесткости манипулятора, которую обрабатывают методами численных алгоритмов оптимизации для обеспечения итоговой точности для целевой траектории движения рабочего органа робота. 4 з.п. ф-лы, 2 ил., 3 табл.
1. Cпособ калибровки промышленного робота, основанный на эластостатической калибровке, для которой была выбрана система, описывающая манипулятор как жесткую модель, состоящий из неподвижного основания и последовательной цепи податливых звеньев, ряда податливых приводимых в движение шарниров и рабочего органа, который контактирует с обрабатываемой деталью, на котором установлены маркеры для измерений и система подвеса груза, включающий построение модели жесткости для эластостатической калибровки, которая описывает эластостатические свойства манипулятора и отклонения рабочего органа при внешней нагрузке, выбор оптимальных конфигураций для измерения и соответствующих внешних сил, вызывающих эластостатические отклонения, проведение калибровочных экспериментов с использованием полученных конфигураций, вычисление желаемых эластостатических параметров с использованием измеренных отклонений и сил, компенсацию эластостатических ошибок путем настройки входной программы контроллера, описывающей траекторию цели с использованием идентифицированных параметров, отличающийся тем, что для построения модели жесткости робота моделируют жесткость каждого звена с помощью пружины с шестью степенями свободы, три из которых соответствуют перемещению, а три – ориентации, и жесткость шарнира с помощью пружины с одной степенью свободы, расположенной вдоль ось вращения, в результате чего получается матрица жесткости манипулятора, которую обрабатывают методами численных алгоритмов оптимизации, обеспечивая итоговую точность для целевой траектории движения рабочего органа робота.
2. Cпособ по п.1, отличающийся тем, что в качестве ограничений для конфигурации робота использованы физические лимиты поворота каждого сустава, накладываемые барьером безопасности робота или клеткой.
3. Cпособ по п.1, отличающийся тем, что целевой функцией для численной оптимизации служил один из подходов на основе критерия оптимальной конфигурации.
4. Cпособ по п.1, отличающийся тем, что выбор оптимальных конфигураций для измерения и соответствующих внешних сил, вызывающих эластостатические отклонения опирается на соответствующий показатель эффективности, учитывающий особенности технологического процесса, геометрические и физические ограничения рабочей ячейки для обеспечения желаемой точности позиционирования с использованием минимального количества калибровочных экспериментов при заданных статистических свойствах шума измерений.
5. Cпособ по п.1, отличающийся тем, что при проведении калибровочных экспериментов с использованием полученных конфигураций положение рабочего органа измеряют дважды для каждой конфигурации робота: до и после приложения нагрузки, требуемые перемещения рабочего органа вычисляют как их разность, при этом приложенные нагрузки измеряют при помощью датчика силы, в результате получают набор отклонений рабочего органа и соответствующих нагрузок и оценивает точность идентификации параметров модели, а также ожидаемую точность позиционирования.
| Способ повышения точности позиционирования промышленного робота | 2017 |
|
RU2671787C1 |
| Способ повышения точности перемещений промышленного робота в процессе инкрементального формообразования | 2020 |
|
RU2762693C1 |
| Способ калибровки кинематических параметров многостепенных манипуляторов | 2019 |
|
RU2719207C1 |
| СПОСОБ КОНТРОЛЯ ТОЧНОСТИ КОНТУРНЫХ ПЕРЕМЕЩЕНИЙ ПРОМЫШЛЕННЫХ РОБОТОВ | 2011 |
|
RU2466858C1 |
| US 20110022216 A1, 27.01.2011. | |||
Авторы
Даты
2024-11-05—Публикация
2023-11-24—Подача