Предлагаемое изобретение относится к развитию способов определения местоположения неподвижного источника излучения (ИИ) с борта летательного аппарата пеленгационными методами.
Известен способ местоопределения ИИ с борта летательного аппарата кинематическим методом [Ю.П. Мельников, С.В. Попов. Радиотехническая разведка. Методы оценки эффективности местоопределения источников излучения. М.: Радиотехника, 2008. 432 с.: ил., стр. 158-163. Защита радиолокационных систем от помех. Под ред. Канащенкова А.И. и Меркулова В.И. М.: Радиотехника, 2003. 416 с.: ил., стр. 319-322]. Способ заключается в последовательном выполнении летательным аппаратом маневров с отворотом от ИИ и нахождении дальности до него как отношения тангенциальной скорости пеленгатора к угловой скорости линии визирования ИИ, определяемой путем обработки результатов нескольких измерений пеленгов. Недостатком способа является то, что для достижения приемлемых точностей определения дальности до ИИ летательный аппарат, на котором установлен пеленгатор, должен в течение длительного времени выполнять интенсивное маневрирование в несколько этапов (например, движение по «змейке») и при этом отклоняться от направления на ИИ [Ю.П. Мельников, С.В. Попов. Радиотехническая разведка. Методы оценки эффективности местоопределения источников излучения. М.: Радиотехника, 2008. 432 с.: ил., стр. 163].
Наиболее близким по сущности и достигаемому эффекту (прототипом) является способ местоопределения ИИ при двукратной пеленгации (триангуляционный метод) [Ю.П. Мельников, С.В. Попов. Радиотехническая разведка. Методы оценки эффективности местоопределения источников излучения. М.: Радиотехника, 2008. 432 с.: ил., стр. 11-25. Защита радиолокационных систем от помех. Под ред. Канащенкова А.И. и Меркулова В.И. М.: Радиотехника, 2003. 416 с.: ил., стр. 315-318]. Способ заключается в том, что с борта летательного аппарата, осуществляющего прямолинейный полет, последовательно выполняется пеленгация ИИ в азимутальной плоскости (например, фазовым методом). Фиксируются две точки на линии полета, в которых курсовые углы (пеленги) на ИИ составляют α1=54,75° и α2=125,25°, определяется измерительная база d как расстояние между первой и второй точками пеленгации и оценивается местоположение источника излучения по двум углам пеленга и измерительной базе. При этом треугольник, образованный точками пеленгации и местоположения ИИ, является равнобедренным, а сумма курсовых углов на ИИ (пеленгов) равна развернутому углу 180°. Такая геометрия обеспечивает минимальную погрешность определения местоположения ИИ, нормированную к дальности до ИИ по линии траверза, по двум углам α1, α2 и базе d. [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с. С. 149-151]. Недостатком данного способа является то, что в нем учитывается влияние на точность определения местоположения ИИ только ошибок пеленгации ИИ из двух точек и предполагается, что измерительная база известна точно [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с. С. 150]. Таким образом, составляющая ошибки определения местоположения ИИ, связанная с неточным знанием измерительной базы, приводит к повышению реальной погрешности определения местоположения ИИ в 2…3 и более раза по сравнению с ожидаемой и, соответственно, к снижению точности местоопределения ИИ.
Техническим результатом изобретения является повышение точности местоопределения ИИ триангуляционным методом при неточном знании измерительной базы.
Указанный результат достигается тем, что в известном способе местоопределения ИИ триангуляционным методом с борта летательного аппарата, состоящем в последовательной пеленгации ИИ при прямолинейном полете летательного аппарата, фиксации первой и второй точек пеленгации, в которых углы пеленга достигают заданных значений, составляющих в сумме развернутый угол, определении измерительной базы как расстояния между первой и второй точками пеленгации и оценке местоположения ИИ по двум углам пеленга и измерительной базе,
согласно изобретению по достижении второй точки пеленгации нормируют известное значение среднеквадратической ошибки измерительной базы к рассчитанной по оцененному местоположению ИИ дальности до него по линии траверза,
с использованием нормированной ошибки базы и угловых ошибок пеленгации определяют оптимальные по критерию минимума ошибки местоопределения ИИ значения углов пеленга на него,
продолжают прямолинейный полет,
определяют оптимальную измерительную базу как расстояние между точками на линии базы, в которых углы пеленга равны вычисленным оптимальным значениям,
и уточняют местоположение ИИ по оптимальным двум углам пеленга и измерительной базе.
Сущность изобретения заключается в том, что в интересах повышения точности местоопределения ИИ дополнительно, после оценки местоположения ИИ и определения его дальности по линии траверза Z, как это делалось в способе-прототипе, нормируют известную среднеквадратическую ошибку знания измерительной базы к этой дальности (σd/Z) и, с учетом полученной нормированной ошибки и известной среднеквадратической ошибки пеленгации ИИ (σа), определяют новые (оптимальные) значения углов пеленга ИИ α1opt, α2opt, при которых среднеквадратическая ошибка местоопределения ИИ (σr/Z) будет минимальной. Путем измерения пройденного пути между точками на линии базы, в которых углы пеленга равны вычисленным оптимальным значениям α1opt, α2opt, определяют новое (оптимальное) значение измерительной базы dopt и уточняют местоположение ИИ.
В [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с. С. 149-151] показано, что оценка местоположения ИИ при двукратной пеленгации при точном знании базы, то есть без учета ошибки σd, будет иметь минимальную относительную ошибку (σr/Z) тогда, когда треугольник с вершинами в точках первой и второй пеленгации и в точке нахождения ИИ является равнобедренным (расстояние до ИИ от точки первой пеленгации равно расстоянию до ИИ от точки второй пеленгации), а значения курсовых углов в точках пеленгации равны α1=54,75°, α2=125,25°; угол между двумя пеленгами соответственно равен γ=α2-α1=70,5°.
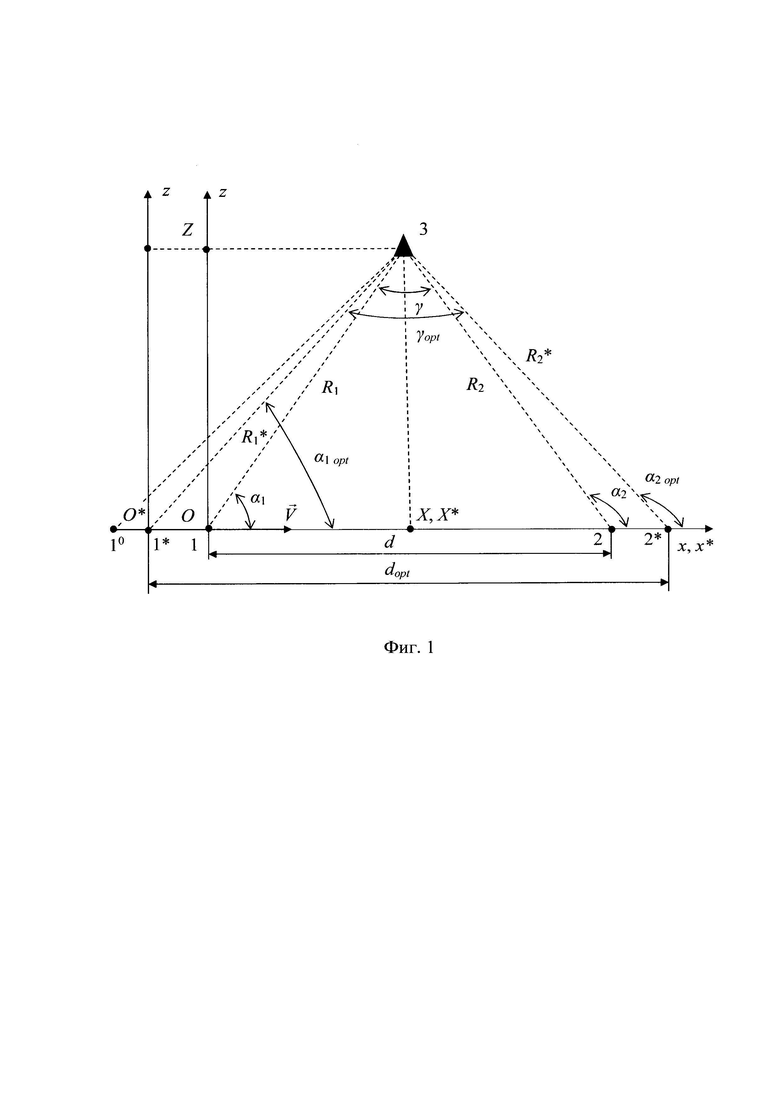
На фиг. 1 представлена геометрия взаимного расположения летательного аппарата и ИИ в плоскости. На фиг. 1 обозначены: Oxz (O*x*z) - декартова система координат для способа-прототипа (предлагаемого способа); 10 - точка начала пеленгации ИИ и счисления пройденного вдоль линии базы пути; 1, 2, α1, α2, R1, R2 (1*, 2*, α1opt, α2opt, R1*, R2*) - точки пеленгации ИИ и соответствующие им курсовые углы (пеленги) на ИИ и расстояния до ИИ для способа-прототипа (предлагаемого способа); 3, X, Z (3, X*, Z) - точка расположения ИИ и его координаты для способа-прототипа (предлагаемого способа); γ, γopt - угол между двумя пеленгами для способа-прототипа (предлагаемого способа); d, dopt - расстояние между точками пеленгации-измерительная база для способа-прототипа (предлагаемого способа); 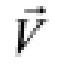 - вектор скорости летательного аппарата-носителя пеленгатора.
- вектор скорости летательного аппарата-носителя пеленгатора.
Утверждение, что нормированная среднеквадратическая ошибка определения местоположения ИИ σr/Z при двукратной пеленгации достигает минимального значения, когда R1 и R2 равны между собой, то есть треугольник с вершинами (1, 3, 2) на фиг. 1 равнобедренный, а углы принимают значения α1=54,75°, γ=70,5°, α2=125,25 [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с. С. 149-151], справедливо лишь тогда, когда с неточностью знания измерительной базы можно не считаться, то есть когда среднеквадратическая ошибка знания базы σd существенно меньше ошибки определения местоположения ИИ σr. Однако отсутствие систем точной навигации, их подавление или нахождение в нерабочем состоянии может привести к достаточно большим ошибкам знания базы σd, игнорирование которых повлечет к повышению среднеквадратической ошибки σr. Так, например, системы дальней навигации обеспечивают определение координат летательного аппарата с погрешностью от 0,46 км (Лоран-С) до 3,7-7,4 км (Омега) [Сосновский А.А., Хаймович И.А., Лутин Э.А. и др. Авиационная радионавигация: Справочник / Под ред. А.А. Сосновского. - М.: Транспорт, 1990. - 264 с. С. 44]. При таких погрешностях ошибка знания базы σd составит от 0,65 км до 5,2-10,46 км.
Оценим зависимость ошибки определения местоположения ИИ σr/Z от ошибки знания измерительной базы σd.
Пусть местоположение ИИ (см. фиг. 1) определяется ее координатами X и Z в системе координат Oxz, начало которой О совмещено с первой позицией пеленгации (точка 1), а ось Ох направлена вдоль линии базы. В соответствии с [Дрогалин В.В., Ефимов В.А., Канащенков А.И. и др. Способы оценивания точности определения местоположения источников радиоизлучения пассивной угломерной двухпозиционной бортовой радиолокационной системой // Успехи современной радиоэлектроники. - 2003. - №5. - С. 22-39] координаты Х и Z определяются следующими выражениями:
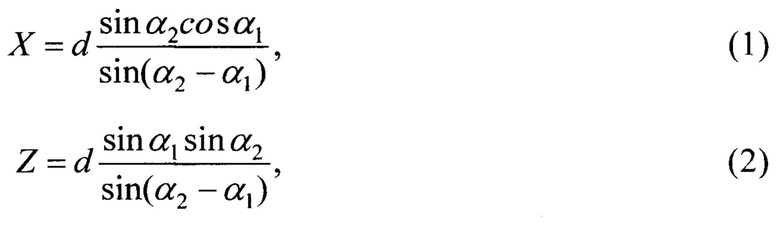
Местоположение ИИ определяется также дальностью до него от начала системы координат (от точки первой пеленгации):

Мерой погрешности определения местоположения ИИ служат дисперсии 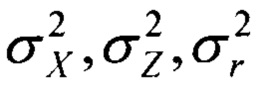 величин (1), (2), (3), определяемые следующими соотношениями [Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964. - 564 с.]:
величин (1), (2), (3), определяемые следующими соотношениями [Вентцель Е.С. Теория вероятностей. - М.: Наука, 1964. - 564 с.]:
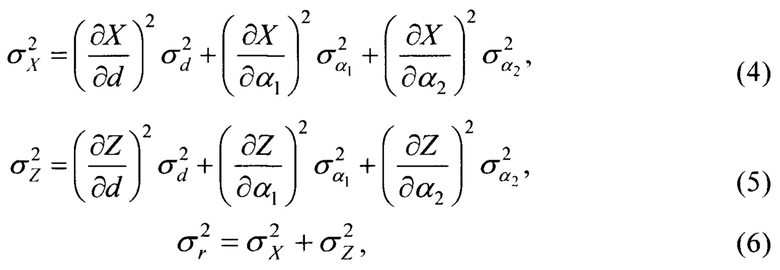
где 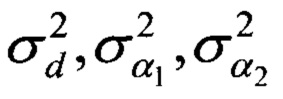 - дисперсии ошибок знания размеров базы и ошибок пеленгации.
- дисперсии ошибок знания размеров базы и ошибок пеленгации.
Определим дисперсию 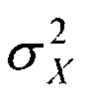 в соответствии с выражением (4):
в соответствии с выражением (4):
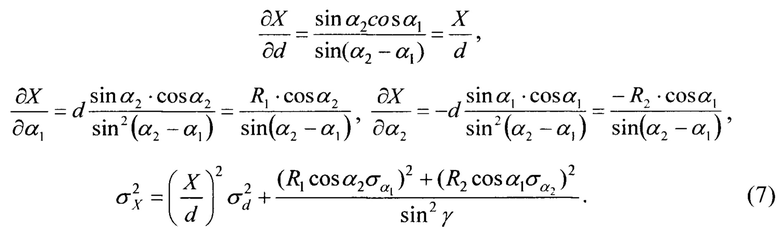
Аналогично определим дисперсию 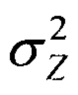 в соответствии с (5):
в соответствии с (5):
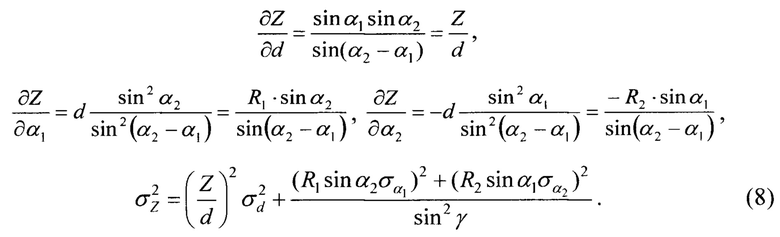
Подставляя (7) и (8) в (6), получим выражение для радиальной дисперсии:
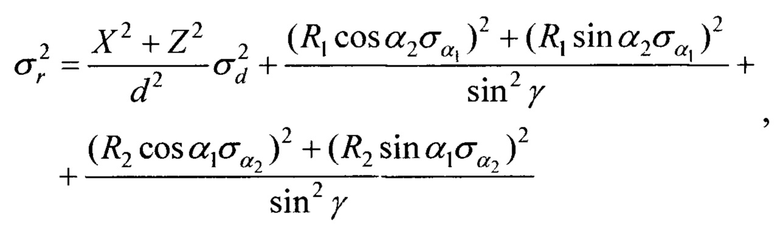
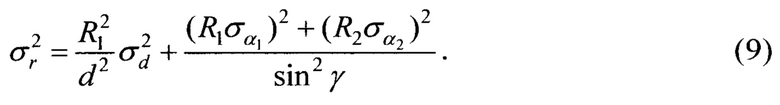
При 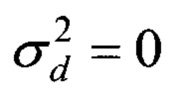 выражение (9) сводится к известному результату, приведенному в [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с.].
выражение (9) сводится к известному результату, приведенному в [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с.].
В симметричном случае, когда треугольник с вершинами в точках пеленгации и в точке расположения ИИ является равнобедренным, справедливы соотношения R1=R2=R, α2=180° - α1, с учетом которых, полагая 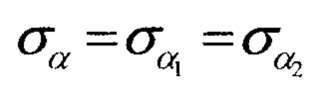 и используя известные тригонометрические соотношения [Бронштейн И.Н. и Семендяев К.А. Справочник по математике. - М.: Наука, 1964, 608 с, с. 183-185], приведем выражение (9) к виду:
и используя известные тригонометрические соотношения [Бронштейн И.Н. и Семендяев К.А. Справочник по математике. - М.: Наука, 1964, 608 с, с. 183-185], приведем выражение (9) к виду:
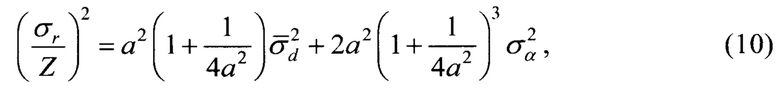
где 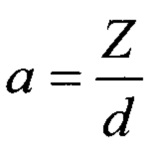 - нормированная к базе дальность до ИИ по траверзу;
- нормированная к базе дальность до ИИ по траверзу;
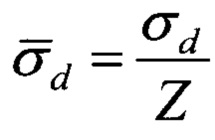 - нормированная к дальности до ИИ по линии траверза среднеквадратическая ошибка знания размеров базы.
- нормированная к дальности до ИИ по линии траверза среднеквадратическая ошибка знания размеров базы.
Определим оптимальное значение параметра а, при котором относительная ошибка σr/Z минимальна. Для этого найдем производную правой части выражения (10) по а и приравняем ее к нулю:
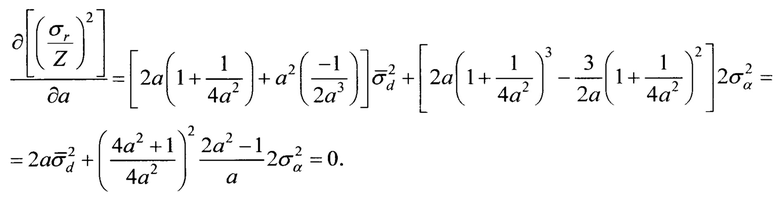
Решение данного уравнения [Бронштейн И.Н. и Семендяев К.А. Справочник по математике. - М.: Наука, 1964, 608 с., с. 137-144] дает окончательное выражение для оптимального значения параметра а:
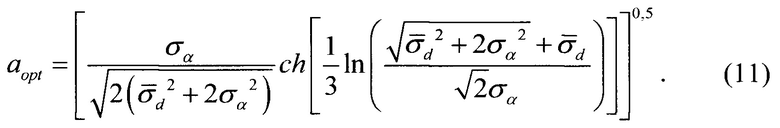
При точном знании размера базы, то есть при 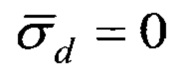 , выражение (11) сводится к известному результату
, выражение (11) сводится к известному результату 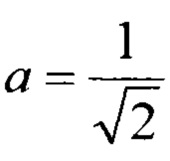 , приведенному в [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с., с. 149-150].
, приведенному в [Мельников Ю.П. Воздушная радиотехническая разведка (методы оценки эффективности). - М.: Радиотехника, 2005. - 304 с., с. 149-150].
Оптимальное значение параметра aopt однозначно определяет оптимальные углы γopt, α1opt, α2opt, при которых ошибка определения местоположения ИИ σr/Z минимальна:
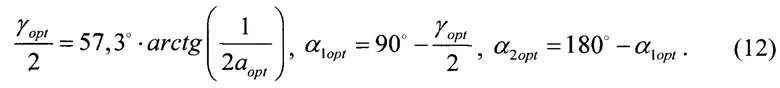
Техническая реализация предлагаемого способа в целом не отличается от технической реализации способа-прототипа. То есть может быть реализована с использованием известных устройств: пеленгатора источника излучения и бортового вычислителя с запоминающим устройством.
Способ может быть реализован следующим образом.
1) Выполняют прямолинейный полет на летательном аппарате с размещенным на его борту пеленгатором, непрерывное измерение курсового угла на ИИ и счисление пройденного вдоль линии базы пути.
2) Фиксируют моменты достижения точки на линии базы, в которой курсовые углы равны α1=54,75° и α2=125,25°.
3) Определяют расстояние между точками пеленгации, то есть измерительную базу d для способа-прототипа.
4) По полученным данным α1, α2 и d в первом приближении оценивают дальность до ИИ по линии траверза Z (без учета ошибки знания базы σd).
5) Нормируют известную ошибку знания базы σd к рассчитанной дальности Z и c учетом угловой ошибки пеленгации σа по формулам (11), (12) вычисляют оптимальные значения углов γopt, α1opt, α2opt.
6) Продолжают прямолинейный полет и счисление пройденного вдоль линии базы пути до момента достижения точки на линии базы, в которой курсовой угол на ИИ равен α2opt.
7) Определяют значение измерительной базы dopt как расстояние от точки маршрута полета летательного аппарата, в которой курсовой угол на ИИ был равен α1opt, до точки, в которой курсовой угол на ИИ стал равен α2opt.
8) Знание α1opt, α2opt и dopt позволяет по известным формулам (1), (2), (3) уточнить местоположение ИИ (X*, Z, R1*) с учетом ошибки знания базы σd.
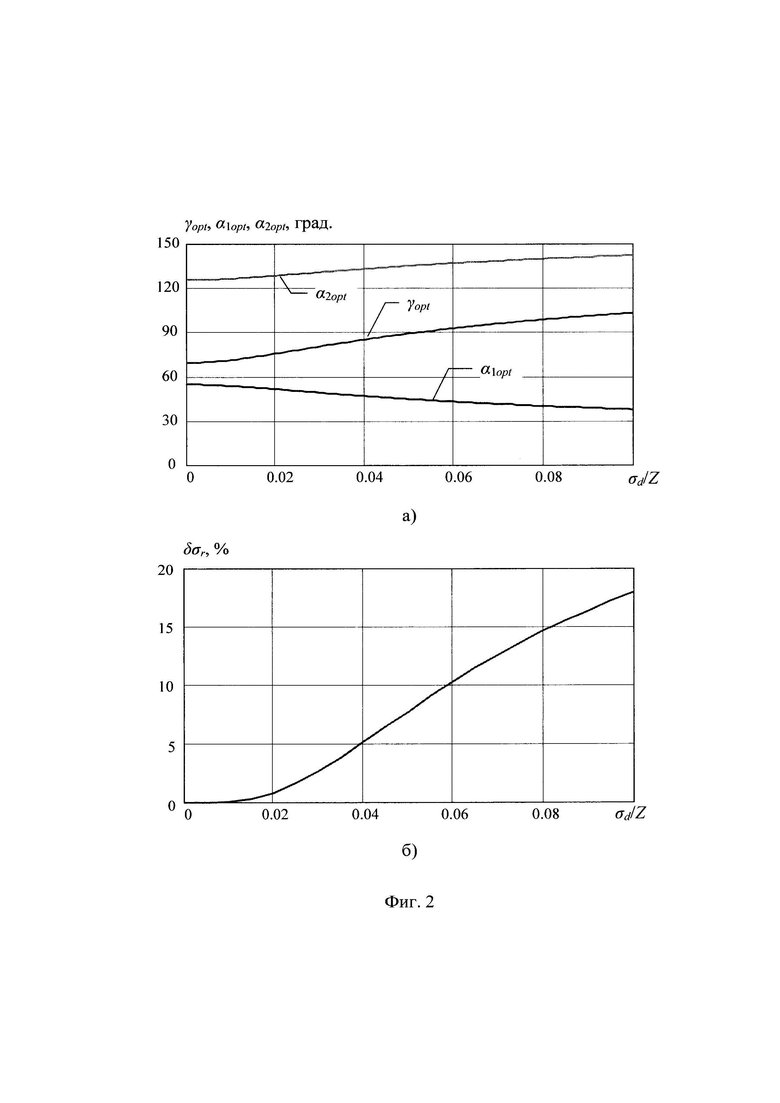
В интересах оценки выигрыша в точности местоопределения ИИ предложенным способом по сравнению со способом-прототипом было осуществлено моделирование для случая, когда значение угловой ошибки составляло σa=1°. На фиг. 2 а) представлены зависимости углов γopt, α1opt, α2opt от значения нормированной ошибки 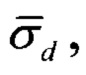 а на фиг. 2 б) относительное повышение точности местоопределения ИИ предложенным способом по сравнению со способом-прототипом от значения нормированной ошибки
а на фиг. 2 б) относительное повышение точности местоопределения ИИ предложенным способом по сравнению со способом-прототипом от значения нормированной ошибки 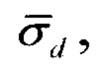 Относительное повышение точности определялось по формуле:
Относительное повышение точности определялось по формуле:
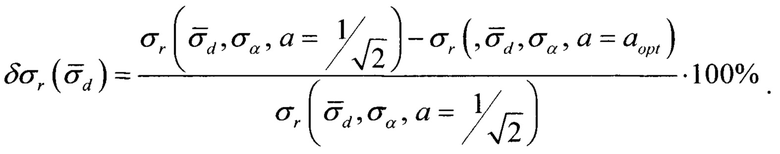
Из фиг. 2 видно, что при значении нормированной ошибки знания базы σd/Z=0,1 ошибка определения координат ИИ будет минимальна при углах: γopt=104,4°, α1opt=37,8°, α2opt=142,2°. При этом точность определения координат ИИ, по сравнению со способом-прототипом, повысится на 18,0%.
Таким образом, заявленный способ обеспечивает повышение точности местоопределения источника излучения триангуляционным методом при неточном знании измерительной базы.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ИСТОЧНИКА ИЗЛУЧЕНИЯ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА | 2021 |
|
RU2760975C1 |
| Способ определения дальности до неподвижного источника излучения движущимся пеленгатором | 2016 |
|
RU2617447C1 |
| Способ определения расстояния до неподвижного источника излучения движущимся пеленгатором | 2016 |
|
RU2617210C1 |
| КИНЕМАТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ИСТОЧНИКА ИЗЛУЧЕНИЯ | 2023 |
|
RU2825200C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ИСТОЧНИКА ИЗЛУЧЕНИЯ С БОРТА САМОЛЕТА | 2021 |
|
RU2777147C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО НАЗЕМНОГО ИСТОЧНИКА ИЗЛУЧЕНИЯ С САМОЛЕТА, ОСНАЩЕННОГО АЗИМУТАЛЬНЫМ ФАЗОВЫМ ПЕЛЕНГАТОРОМ | 2022 |
|
RU2796121C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ НЕПОДВИЖНЫХ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ ПРИ ОДНОКООРДИНАТНОЙ ПЕЛЕНГАЦИИ В СВЯЗАННОЙ СИСТЕМЕ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА | 2024 |
|
RU2834277C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ ПРИ АМПЛИТУДНО-ФАЗОВОЙ ПЕЛЕНГАЦИИ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2432580C1 |
| АДАПТИВНЫЙ СПОСОБ ПРОСТРАНСТВЕННОГО ОТОЖДЕСТВЛЕНИЯ ПЕЛЕНГОВ С НАЗЕМНЫМИ ИСТОЧНИКАМИ РАДИОИЗЛУЧЕНИЯ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2018 |
|
RU2686481C1 |
| СПОСОБ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ ПО КУРСУ В УГЛОМЕРНОЙ ДВУХПОЗИЦИОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЕ | 2006 |
|
RU2308093C1 |
Изобретение относится к способам определения местоположения неподвижного источника излучения с борта летательного аппарата пеленгационными методами. Техническим результатом является повышение точности местоопределения источника излучения с борта летательного аппарата триангуляционным методом при неточном знании измерительной базы. Заявленный способ заключается в последовательной пеленгации источника излучения при прямолинейном полете летательного аппарата, фиксации первой и второй точек пеленгации, в которых углы пеленга достигают заданных значений, составляющих в сумме развернутый угол, определении измерительной базы как расстояния между первой и второй точками пеленгации и оценке местоположения источника излучения по двум углам пеленга и измерительной базе. При этом дополнительно по достижении второй точки пеленгации нормируют известное значение среднеквадратической ошибки измерительной базы к рассчитанной по оцененному местоположению источника излучения дальности до него по линии траверза, с использованием которой и угловых ошибок пеленгации определяют оптимальные по критерию минимума ошибки местоопределения источника излучения значения углов пеленга на него. Продолжают прямолинейный полет, определяют оптимальную измерительную базу как расстояние между точками на линии базы, в которых углы пеленга равны вычисленным оптимальным значениям, и уточняют местоположение источника излучения по двум оптимальным углам пеленга и измерительной базе. 2 ил.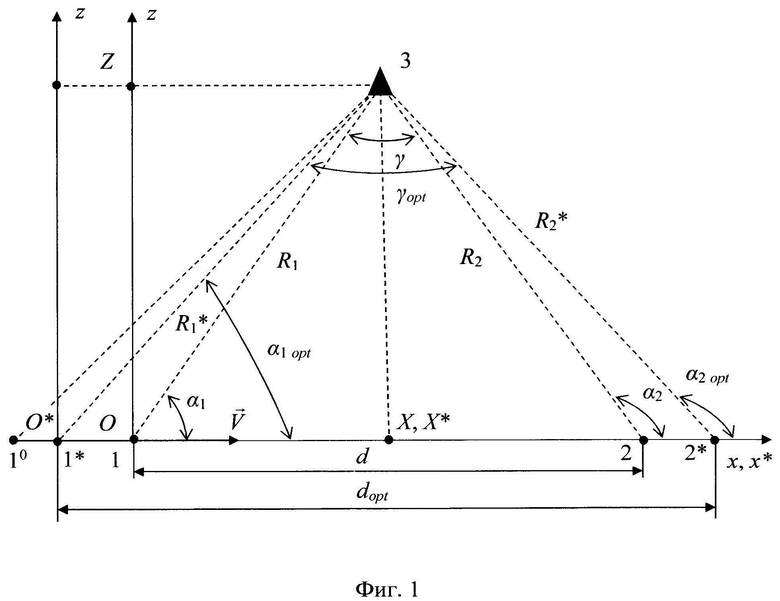
Способ местоопределения источника излучения триангуляционным методом с борта летательного аппарата, состоящий в последовательной пеленгации источника излучения при прямолинейном полете летательного аппарата, фиксации первой и второй точек пеленгации, в которых углы пеленга достигают заданных значений, составляющих в сумме развернутый угол, определении измерительной базы как расстояния между первой и второй точками пеленгации и оценке местоположения источника излучения по двум углам пеленга и измерительной базе, отличающийся тем, что по достижении второй точки пеленгации нормируют известное значение среднеквадратической ошибки измерительной базы к рассчитанной по оцененному местоположению источника излучения дальности до него по линии траверза, с использованием нормированной ошибки базы и угловых ошибок пеленгации определяют оптимальные по критерию минимума ошибки местоопределения источника излучения значения углов пеленга на него, продолжают прямолинейный полет, определяют оптимальную измерительную базу как расстояние между точками на линии базы, в которых углы пеленга равны вычисленным оптимальным значениям, и уточняют местоположение источника излучения по оптимальным двум углам пеленга и измерительной базе.
| СПОСОБ ФОРМИРОВАНИЯ МАРШРУТА НОСИТЕЛЯ ПЕЛЕНГАТОРА, ОПРЕДЕЛЯЮЩЕГО МЕСТОПОЛОЖЕНИЕ ИЗЛУЧАТЕЛЯ МЕТОДОМ ТРИАНГУЛЯЦИИ | 2005 |
|
RU2303794C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ИСТОЧНИКА ИЗЛУЧЕНИЯ С БОРТА САМОЛЕТА | 2021 |
|
RU2777147C1 |
| СПОСОБ ФОРМИРОВАНИЯ МАРШРУТА НОСИТЕЛЯ ПЕЛЕНГАТОРА, ОПРЕДЕЛЯЮЩЕГО МЕСТОПОЛОЖЕНИЕ НЕПОДВИЖНОГО ИЗЛУЧАТЕЛЯ | 2008 |
|
RU2373549C1 |
| АДАПТИВНЫЙ СПОСОБ ПРОСТРАНСТВЕННОГО ОТОЖДЕСТВЛЕНИЯ ПЕЛЕНГОВ С НАЗЕМНЫМИ ИСТОЧНИКАМИ РАДИОИЗЛУЧЕНИЯ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2018 |
|
RU2686481C1 |
| Угломерно-корреляционный способ определения местоположения наземных источников радиоизлучения | 2021 |
|
RU2764149C1 |
| МЕЛЬНИКОВ Ю.П., ПОПОВ С.В | |||
| Радиотехническая разведка | |||
| Методы оценки эффективности местоопределения источников излучения | |||
| М.: Радиотехника, 2008 | |||
| ПЛУГ С ВРАЩАЮЩИМИСЯ РАБОЧИМИ ПОВЕРХНОСТЯМИ | 1925 |
|
SU432A1 |
| С | |||
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| US 2004207553 A1, 21.10.2004 | |||
| US 8588998 B2, | |||
Авторы
Даты
2025-02-19—Публикация
2024-05-24—Подача