Робастный стохастический фильтр Российский патент 2021 года по МПК H03H19/00 G06F17/18 

Изобретение относится к области информационно-измерительных систем и может быть использовано для робастной фильтрации стохастических сигналов и параметров состояния стохастических систем в условиях неопределенности вероятностных характеристик помех измерения.

Известен фильтр стохастических сигналов и параметров состояния стохастических систем, обеспечивающий оптимальную по среднеквадратическому критерию оценку измеряемого сигнала или вектора состояния, - фильтр Калмана [Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 2004. - 304с.; Синицын И.Н. Фильтры Калмана и Пугачева. - М.: Логос, 2006. - 640с.]. Недостатком данного фильтра является необходимость точного априорного задания вероятностных характеристик помех измерения оцениваемого сигнала, т.к. для реальных информационно-измерительных систем, функционирующих в условиях различных возмущений, параметры помех измерения или меняются случайным образом во времени, или известны приближенно [A.Ferrero, R.Ferrero, W.Jiang, S.Salicone. The Kalman Filter Uncertainty Concept in the Possibility Domain, IEEE Trans. Instrum. Meas. 68 (2019), Р.4335-4347].

Известны фильтры, использующие для обеспечения устойчивости процесса фильтрации при априорной неопределенности интенсивности помех измерения введение эмпирических масштабных коэффициентов при вычислении апостериорной ковариационной матрицы или дисперсионной матрицы помех измерения [E.P. Herrera, H. Kaufmann. Adaptive methods of Kalman filtering for personal positioning systems, in: 23rd Int. Tech. Meet. Satell. Div. Inst. Navig. 2010, ION GNSS 2010; Патент № 1639377. Модифицированный нелинейный фильтр Калмана, СССР, Н03Н 21/00; Патент № 1651355. Регуляризованный фильтр Калмана, СССР, Н03Н 21/00; Патент № 1800588. Адаптивный фильтр Калмана, СССР, Н03Н 21/00; Патент № 2160496. Модифицированный фильтр Калмана, РФ, Н03Н 21/00]. Недостатком этих способов является отсутствие строгих критериев выбора масштабных коэффициентов и процедуры их вычисления, а также обоснования повышения точности фильтрации, что не позволяет обеспечить требуемую точность и устойчивость процесса фильтрации при отсутствии априорного задания вероятностных характеристик помех измерения оцениваемого сигнала. Известен также фильтр, использующий для обеспечения устойчивости калмановской фильтрации расширение размерности вектора состояния [D.Wang, H.Ly, J.Wu. Augmented Cubature Kalman filter for nonlinear RTK/MIMU integrated navigation with non-additive noise, Measurement. 97, 2017, р.р.111-125.]. Недостатком данного способа являются существенные вычислительные затраты на его реализацию. Наиболее близким к предлагаемому фильтру является фильтр, обеспечивающий робастную оценку измеряемого сигнала на основе минимизации на текущем интервале времени нелинейного функционала, ядро которого определяется наиболее неблагоприятным классом распределения помехи измерения [Huber P.J., Ronchetti E.M. Robust statistics. New Jersey: John Wiley Sons, 2009. 371 с.; Цыпкин Я.З., Поляк Б.Т. Огрубленный метод максимального правдоподобия // Динамика систем. Математические методы теории колебаний. Горький. 1977. № 12.; Хьюбер П. Дж. Робастность в статистике / Пер. с англ. под ред. Я.З.Цыпкина. - М.: Мир, 1984. 304 с.].

Недостатком данного фильтра является невозможность робастного оценивания в реальном времени динамических процессов в силу большого объема вычислительных затрат, связанных с поиском глобального минимума многомерной нелинейной случайной функции в реальном времени. Технический результат изобретения заключается в повышении быстродействия и точности робастной фильтрации динамических процессов, а также сокращении вычислительных затрат за счет реализации робастного фильтра измеряемого сигнала в дифференциальной форме.

Поставленная задача возникает в управляющих и информационно-измерительных системах, функционирующих в условиях неопределенных возмущений наблюдаемого объекта и помех измерителя.

Технический результат достигается тем, что в устройство введены три блока векторного функционального преобразования, два блока матричного функционального преобразования, блок вычитания векторов, блок умножения матриц, блок умножения матрицы на вектор, блок суммирования векторов и блок интегрирования вектора, входом устройства является вход уменьшаемого блока вычитания векторов, вход вычитаемого которого соединен с выходом второго блока векторного функционального преобразования, а выход подключен ко входу третьего блока векторного функционального преобразования, выход которого подключен к К-размерному входу блока умножения матрицы на вектор, N*К- размерный вход которого соединен с выходом блока умножения матрицы на матрицу, N*N - размерный вход которого соединен с выходом первого блока матричного функционального преобразования, а N*К - размерный вход соединен с выходом второго блока матричного функционального преобразования, выход блока умножения матрицы на вектор подключен к первому входу блока суммирования векторов, второй вход которого соединен с выходом первого блока векторного функционального преобразования, а выход подключен ко входу блока интегрирования вектора, выход которого подключен ко входам первого и второго блоков векторного функционального преобразования, первого и второго блоков матричного функционального преобразования, а также является выходом устройства.

В основу работы устройства положены следующие теоретические результаты.

Динамический объект, вектор состояния которого х подлежит оцениванию, описывается стохастическим дифференциальным уравнением вида:

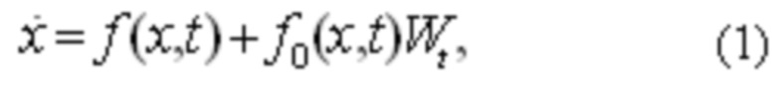
где 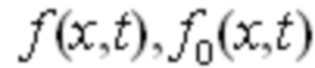известные векторная и матричная функции размерности, соответственно, N и N*M,

вектор-шум объекта размерности M с функцией распределения, принадлежащей классу распределений с ограниченными средними квадратами [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.],

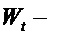
и измеряется нелинейным наблюдателем

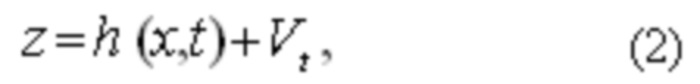
где z - вектор измерений размерности К,

известная вектор-функция размерности К,

вектор помехи измерения размерности К с функцией распределения, определенной в некотором известном классе распределений.

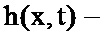
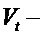
В практических приложениях в качестве основных классов распределений рассматриваются, как правило, распределения:

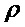
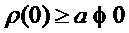
- с плотностью, непрерывной в нуле (),

- распределения с ограниченными средними квадратами (),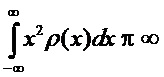

- «засоренные» распределения (),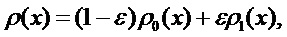

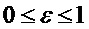
- существующие на ограниченном интервале аргумента (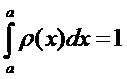) и некоторые др. [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.].

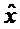
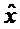
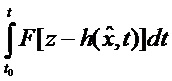
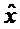
Т.к. в рассматриваемом случае для помехи измерения известен только класс распределения, но не его вид, то оценкувектора состояния х будем искать как оценку, гарантирующую наилучшую точность оценивания в минимаксном смысле (т.е. минимальные ошибки в наиболее неблагоприятной ситуации, определяемой заданным классом распределения). В традиционной постановке [Huber P.J., Ronchetti E.M. Robust statistics. New Jersey: John Wiley Sons, 2009. 371 с.; Цыпкин Я.З., Поляк Б.Т. Огрубленный метод максимального правдоподобия // Динамика систем. Математические методы теории колебаний. Горький. 1977. № 12.; Хьюбер П. Дж. Робастность в статистике / Пер. с англ. под ред. Я.З.Цыпкина. - М.: Мир, 1984. 304с.] данная задача решается как задача определения оценкииз условия минимизации функционала , где функция F определяется выбранным наиболее неблагоприятным классом распределения помехи измерения. При подобной оптимизации приведенного функционала по вектору, не учитывающей apriori известную стохастическую динамику вектора состояния х, возникают существенные вычислительные сложности, связанные с поиском глобального минимума многомерной нелинейной случайной функции в реальном времени. Очевидно, что такой подход, несмотря на его «классическую» робастность и универсальность применения, при практической реализации в реальных системах может существенно проигрывать по вычислительным затратам и точности алгоритмам робастной фильтрации, реализуемым в дифференциальной (или рекуррентной) форме. В связи с этим возникает задача разработки такого подхода к синтезу алгоритмов робастной оценки, который обеспечивал бы как универсальность его использования для всех известных классов неблагоприятных распределений помех измерения, так и практически доступный уровень вычислительных затрат за счет реализации алгоритмов в дифференциальной форме. Рассмотрим далее решение данной задачи.

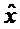
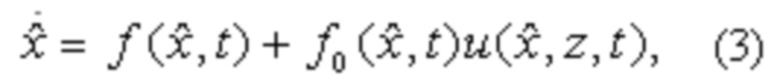
Исходя из вида уравнения (1), описывающего динамику стохастического вектора состояния х, искомую оценкувектора х будем искать в следующей дифференциальной форме:

где 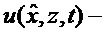вектор-функция, определяемая из условия обеспечения робастности оценки (3), т.е. минимальности ошибок оценивания при наиболее неблагоприятном классе распределения помехи измерения.

В качестве исходной формы минимизируемого функционала, гарантирующего наилучшую точность оценивания в минимаксном смысле, предварительно рассмотрим классический функционал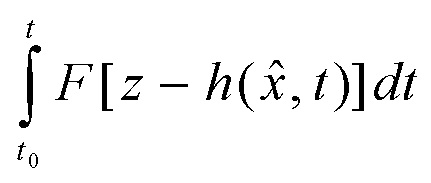. Анализ всех известных видов его подынтегральной функции F показывает [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.; Huber P.J., Ronchetti E.M. Robust statistics. New Jersey: John Wiley Sons, 2009. 371 с.], что данная функция является неотрицательно определенной для всей области определения аргумента. 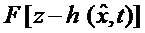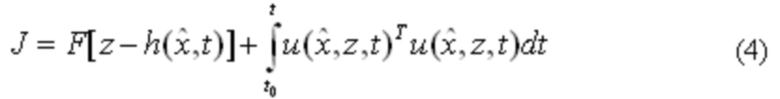Это обстоятельство позволяет перейти от минимизации данного функционала к минимизации функции и с учетом принадлежности функции распределения шума объекта классу распределений с ограниченными средними квадратами, для которого функция F является квадратичной [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.], окончательно сформировать минимаксный критерий оптимальности J в виде:

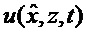
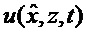
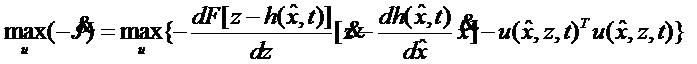
Для последующего определения искомой функции используем тот известный факт, что при неотрицательно определенной критериальной функции для обеспечения ее минимального значения в каждый момент времени достаточно, чтобы производная ее по времени, взятая с обратным знаком, имела максимум [Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975]. Это позволяет для рассматриваемого случая получить исходное условие для определения вектора :

С учетом уравнения оценки (3) данное условие трансформируется к виду:

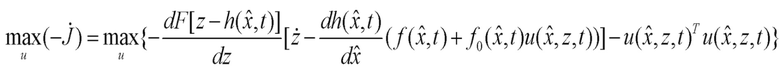
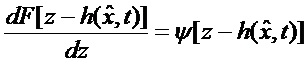
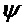
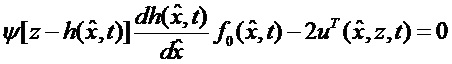
Вводя, следуя [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.], обозначение (где виды функций для основных классов распределений приведены там же), из последнего условия имеем уравнение

,

позволяющее сразу определить искомую вектор-функцию :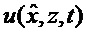

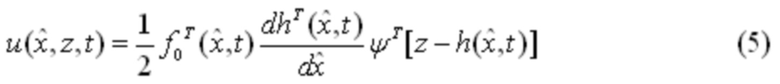
С учетом (5) уравнение робастной оценки (3) окончательно принимает вид:

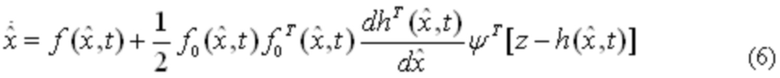
При этом, выбор начальных условий оценивания, следуя описанному минимаксному подходу, целесообразно осуществлять из условия минимизации функции F₀, соответствующей наиболее неблагоприятному предположению о распределении начальных условий вектора состояния х, т.е. из условия .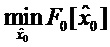

Функциональная схема робастного стохастического фильтра (далее - устройства) приведена на фиг.1.

Устройство содержит:

- первый блок 1 векторного функционального преобразования 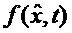размерности N,

- первый блок 2 матричного функционального преобразования 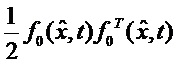размерности N*N,

- второй блок 3 матричного функционального преобразования 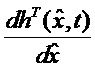размерности N*К,

- второй блок 4 векторного функционального преобразования 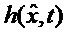размерности К,

- блок 5 вычитания векторов размерности К,

- третий блок 6 векторного функционального преобразования 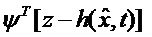размерности К,

- блок 7 умножения матрицы размерности N*N на матрицу размерности N* К,

- блок 8 умножения матрицы размерности N* К на вектор размерности К,

- блок 9 суммирования векторов размерности N,

- блок 10 интегрирования вектора размерности N.

Входом устройства является вход уменьшаемого блока вычитания векторов 5. Вход вычитаемого блока вычитания векторов 5 соединен с выходом второго блока векторного функционального преобразования 4, а выход подключен к входу третьего блока векторного функционального преобразования 6. Выход третьего блока векторного функционального преобразования 6 подключен к К-размерному входу блока умножения матрицы на вектор 8, N*К- размерный вход которого соединен с выходом блока умножения матрицы на матрицу 7. N*N - размерный вход блока умножения матрицы на матрицу 7 соединен с выходом первого блока матричного функционального преобразования 2, а его N* К - размерный вход соединен с выходом второго блока матричного функционального преобразования 3. Выход блока умножения матрицы на вектор 8 подключен к первому входу блока суммирования векторов 9, второй вход которого соединен с выходом первого блока векторного функционального преобразования 1, а выход подключен к входу блока интегрирования вектора 10. Выход блока интегрирования вектора 10 подключен к входам первого 1 и второго 4 блоков векторного функционального преобразования, первого 2 и второго 3 блоков матричного функционального преобразования, а также является выходом устройства.

Устройство работает следующим образом.

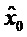
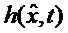
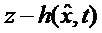
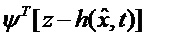
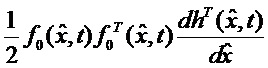
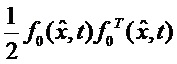
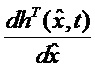
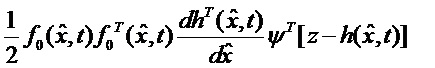
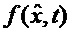
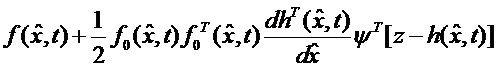
В начальный момент времени с выхода блока интегрирования вектора 10 вводится начальное значение вектора оценки, которое поступает на входы первого 1 и второго 4 блоков векторного функционального преобразования и первого 2 и второго 3 блоков матричного функционального преобразования. Одновременно с входа устройства на вход уменьшаемого блока вычитания векторов 5 поступает сигнал измерения z. Т.к. на вход вычитаемого блока вычитания векторов 5 с выхода второго блока векторного функционального преобразования 4 поступает векторный сигнал , то с выхода блока вычитания векторов 5 векторный сигнал невязки поступает на вход третьего блока векторного функционального преобразования 6, с выхода которого векторный сигнал поступает на К-размерный вход блока умножения матрицы на вектор 8. На N*К-размерный вход блока умножения матрицы на вектор 8 поступает матричный сигнал с выхода блока умножения матрицы на матрицу 7, на N*N - размерный вход которого, в свою очередь, поступает матричный сигнал с выхода первого блока матричного функционального преобразования 2, а на N*К - размерный вход - матричный сигнал с выхода второго блока матричного функционального преобразования 3. С выхода блока умножения матрицы на вектор 8 векторный сигнал поступает на первый вход блока суммирования векторов 9, на второй вход которого поступает векторный сигнал с выхода первого блока векторного функционального преобразования 1. Суммарный векторный сигнал , равный , с выхода блока суммирования векторов 9 поступает на вход блока интегрирования вектора10, с выхода которого снимается векторный сигнал текущей робастной оценки , который поступает далее на входы первого 1 и второго 4 блоков векторного функционального преобразования и первого 2 и второго 3 блоков матричного функционального преобразования, а также на выход устройства.

Предложенный робастный стохастический фильтр повышает быстродействие процесса оценивания, обеспечивая формирование оценки наблюдаемого вектора состояния в реальном времени, точность фильтрации за счет устойчивости к неопределенным возмущениям вектора состояния и помехам измерения, а также обеспечивает сокращение вычислительных затрат за счет простой конструктивной реализации фильтра.

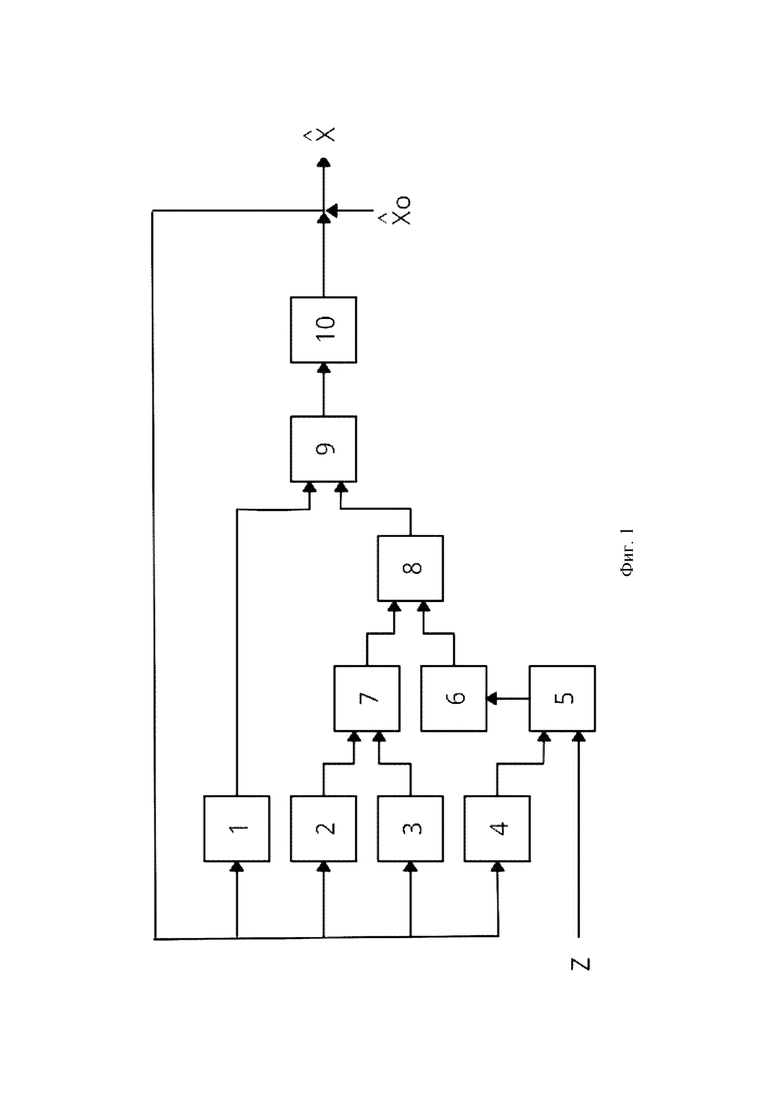
Изобретение относится к области информационно-измерительных систем и может быть использовано для робастной фильтрации стохастических сигналов и параметров состояния стохастических систем в условиях неопределенности вероятностных характеристик помех измерения. Технический результат заключается в повышении быстродействия и точности робастной фильтрации динамических процессов, а также сокращении вычислительных затрат за счет реализации робастного фильтра измеряемого сигнала в дифференциальной форме. Согласно изобретению фильтр содержит первый блок 1 векторного функционального преобразования размерности N, первый блок 2 матричного функционального преобразования размерности N*N, второй блок 3 матричного функционального преобразования размерности N*К, второй блок 4 векторного функционального преобразования размерности К, блок 5 вычитания векторов размерности К, третий блок 6 векторного функционального преобразования размерности К, блок 7 умножения матрицы размерности N*N на матрицу размерности N* К, блок 8 умножения матрицы размерности N* К на вектор размерности К, блок 9 суммирования векторов размерности N, блок 10 интегрирования вектора размерности N. 1 ил.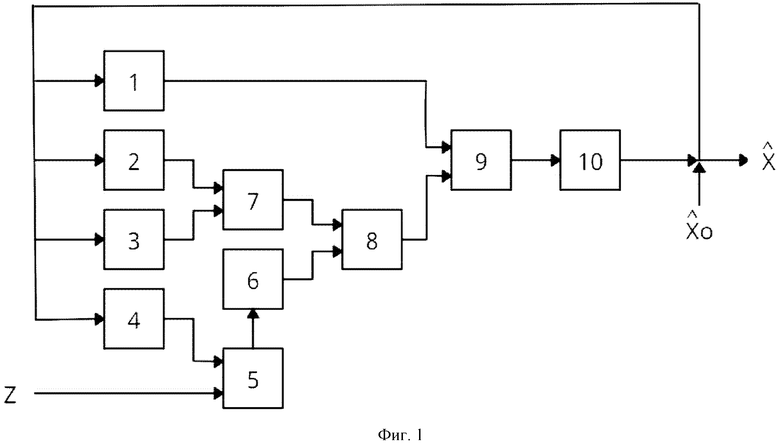

Робастный стохастический фильтр, отличающийся тем, что в него введены три блока векторного функционального преобразования, два блока матричного функционального преобразования, блок вычитания векторов, блок умножения матриц, блок умножения матрицы на вектор, блок суммирования векторов и блок интегрирования вектора, входом устройства является вход уменьшаемого блока вычитания векторов, вход вычитаемого которого соединен с выходом второго блока векторного функционального преобразования, а выход подключен к входу третьего блока векторного функционального преобразования, выход которого подключен к К-размерному входу блока умножения матрицы на вектор, N*К-размерный вход которого соединен с выходом блока умножения матрицы на матрицу, N*N - размерный вход которого соединен с выходом первого блока матричного функционального преобразования, а N*К-размерный вход соединен с выходом второго блока матричного функционального преобразования, выход блока умножения матрицы на вектор подключен к первому входу блока суммирования векторов, второй вход которого соединен с выходом первого блока векторного функционального преобразования, а выход подключен к входу блока интегрирования вектора, выход которого подключен к входам первого и второго блоков векторного функционального преобразования, первого и второго блоков матричного функционального преобразования, а также является выходом устройства.