Область техники
Изобретение относится к области инерциальных навигационных систем.
В частности, оно относится к способу оценки навигационного состояния подвижного носителя с использованием расширенного фильтра Калмана (обычно обозначаемого в литературе сокращением EKF), а также к инерциальной системе, выполненной с возможностью осуществления такого способа.
Уровень техники
Навигационная инерциальная система является прибором, предназначенным для выдачи данных в реальном времени о состоянии носителя: его положении, его скорости, его ориентации и т.д. Эти данные можно использовать для управления носителем.
Известное решение, применяемое для их оценки, состоит в применении в инерциальной системе расширенного фильтра Калмана, который выдает оценочное состояние носителя, объединяя данные инерциальных датчиков (акселерометров, гироскопов) и не инерциальных датчиков, адаптированных к типу носителя (одометр, барометрический альтиметр, радар Доплера, приемник GPS и т.д.). Инерциальные данные выполняют роль команд, а не инерциальные данные - роль наблюдений.
Фильтр Калмана представляет собой алгоритм, как правило, содержащий повторяемые во времени этап предсказания и этап обновления: на этапе предсказания вычисляют текущее состояние на основании предыдущего состояния и входных команд; этап обновления уточняет текущее состояние при помощи наблюдений. Вычисления предсказания основаны на уравнении распространения, моделирующем динамику состояния в зависимости от состояния и от команды. Вычисления обновления основаны на уравнении наблюдения, моделирующем наблюдение в зависимости от состояния.
В фильтре Калмана уравнения распространения и наблюдения являются линейными и принимают форму матриц, не зависящих от оценочного состояния.
В расширенном фильтре Калмана по меньшей мере одна из этих функций является нелинейной. Объединение данных производят путем линеаризации этих функций на этапах распространения и обновления. Следовательно, вычисления осуществляют, используя матрицы, которые зависят от оценочного состояния.
При этом расширенный фильтр Калмана можно рассматривать как алгоритм, осуществляющий, с одной стороны, нелинейные вычисления и, с другой стороны, линейные вычисления, осуществляемые в фильтре Калмана внутри расширенного фильтра Калмана. В дальнейшем состояние, предсказанное нелинейным уравнением распространения будет называться «общим состоянием». Состояние, оцененное фильтром Калмана, будет называться «линеаризованным состоянием». Общее состояние можно скорректировать при помощи данных, содержащихся в состоянии, линеаризованном во время этапов коррекции.
Кроме того, фильтр Калмана (расширенный или не расширенный) вычисляет предел погрешности, соответствующий оценке состояния с учетом оценки статистический погрешности, связанной с многими факторами, такими как первоначальные погрешности и шумы используемых инерциальных датчиков. Статистическую погрешность в данный момент можно отобразить в виде облака точек в пространстве состояния, при этом каждая точка соответствует возможной реализации. Чтобы оценить этот предел погрешности инерциальная система имеет гауссову статистическую модель погрешности, характеризуемую в каждый момент нулевой средней величиной, и ковариантную матрицу. Последняя определяет огибающую эллипсоидного объема с центром на нулевой погрешности, содержащую 99,97% оценочных погрешностей в каждом направлении пространства состояния. В дальнейшем эта огибающая будет называться «огибающей 3 сигма»
Реальная статистическая закономерность погрешностей неизвестна и характеризуется другой огибающей 3 сигма. Как правило, эта огибающая не центрована на нуле, и ее форма не является эллипсоидной.
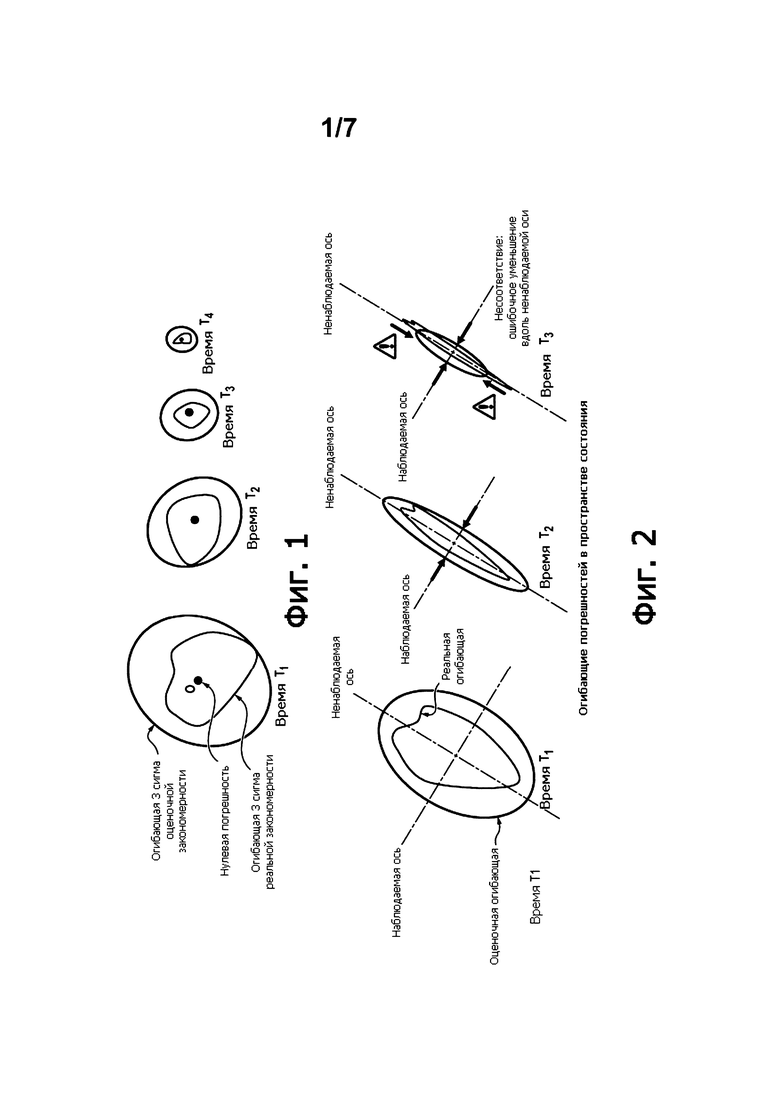
На фиг. 1 показано изменение оценочной огибающей 3 сигма и реальной огибающей 3 сигма на разных итерациях фильтра Калмана. Реальная огибающая 3 сигма должна содержаться в оценочной огибающей 3 сигма. Это является критерием когерентности, который необходимо соблюдать в любой момент и для всех реализаций случайных переменных системы.
Как правило, при помощи наблюдений фильтр Калмана улучшает свою оценку во времени, и огибающие 3 сигма стремятся к уплощению вдоль некоторых осей пространства состояния, называемых «наблюдаемыми», как показано на фиг. 2. Оси, которые являются ортогональными по отношению к последним, называются «ненаблюдаемыми». При этом оценочная огибающая 3 сигма принимает удлиненную форму вдоль ненаблюдаемых осей, что создает корреляции между оценочными погрешностями.
Хотя несовершенство модели, используемой фильтром, может иметь большое значение, было отмечено, что нелинейности и шумы системы часто мешают соблюдению вышеупомянутого критерия когерентности, когда используют расширенный фильтр Калмана (например, в момент Т3 на фиг. 2 становится невозможно локализовать реальную огибающую 3 сигма внутри оценочной огибающей 3 сигма вдоль ненаблюдаемой оси).
Со временем эти несоответствия могут стать значительными и распространиться на другие оси векторного пространства оцениваемого состояния.
Как правило, эти несоответствия появляются только в конкретных условиях, зависящих, например, от траектории носителя и от первоначальных условий. Эти условия характерны для наблюдения, и их может быть трудно предусмотреть. Они являются тем более значительными, так как наблюдение является нелинейным.
Причина несоответствий известна: этап линеаризации, присущий расширенному фильтру Калмана, подвержен влиянию шумов от погрешностей оценки. Действительно, эту линеаризацию осуществляют по последней оценке, произведенной фильтром, которая по определению является неточными данными. Изменения второго порядка, производимые этим шумом оценки на линеаризованных функциях, изменяют наблюдения и являются причиной несоответствий.
В первом случае наблюдаемую переменную фильтр может принять за ненаблюдаемую, но этот случай является маловероятным; во втором случае фильтр может посчитать ненаблюдаемую переменную как наблюдаемую. Это уменьшает оценочную огибающую 3 сигма вдоль ненаблюдаемых осей, тогда как она должна сохранять свое первоначальное значение. Вместе с тем, это не уменьшает реальное облако погрешности вдоль этих осей, поскольку последние действительно являются ненаблюдаемыми. При этом все более значительная часть облака погрешности рискует не оказаться внутри оценочной огибающей 3 сигма, как только она начинает уменьшаться. Последствия этого несоответствия могут быть серьезными и зависят от первоначальной огибающей вдоль таких ненаблюдаемых осей.
Известное решение, позволяющее в большинстве случаев компенсировать уменьшение оценочной огибающей 3 сигма, состоит в применении шума модели. Действительно, алгоритм EKF включает в себя операцию, во время которой увеличивают ковариацию в фазе предсказания при помощи матрицы шумов модели, чтобы учитывать переменные и их динамику, которые не были моделированы в фильтре. При этой проблеме когерентности матрица шума отходит от своей функции, так как уменьшение оценочной огибающей связано не с проблемой моделирования, а с проблемой наблюдаемости. Кроме того, из соображений архитектуры и цифровой точности вычисления шумы часто применяют по диагонали матрицы шумов модели: как и в случае ковариационной матрицы, диагональ этой матрицы соответствует составляющим линеаризованного состояния, отслеживаемым фильтром. Следовательно, шум не применяют только в направлении ненаблюдаемых осей. Отсюда следует, что проблема когерентности может быть решена не полностью и, кроме всего прочего, это снижает точность оценок.
Действительно, применяемый шум содержит проекцию на ненаблюдаемые оси и проекцию на наблюдаемые оси, причем эти проекции могут изменяться в течение времени в соответствии с изменением ненаблюдаемых осей. Чем больше проекция на наблюдаемые оси и чем больше асимптотическое значение погрешности в этих направлениях, тем ниже точность оценок.
Что касается значения применяемого шума, то оно не известно. Выбирают эмпирическое и, как правило, достаточно большое значение, чтобы учитывать все известные случаи, создающие проблему. Это еще больше усложняет проблему точности.
С другой стороны, поскольку шум модели не применяют в надлежащем направлении, оценочная огибающая удлиняется в направлении удаления от реальной ненаблюдаемой оси. Следовательно, эта эллипсоидная огибающая, которая, естественно, становится больше вдоль своих главных осей, может не перекрывать облако реальных погрешностей. Следовательно, несоответствие может сохраняться.
Таким образом, в предшествующем уровне техники к проблеме наблюдаемости подходили при помощи решения, которое не решало полностью проблему и, кроме того, отрицательно сказывалось на точности оценок.
Раскрытие изобретения
Задачей изобретения является оценка общего состояния мобильного носителя, управляемого нелинейной моделью, с одновременной минимизацией появления несоответствий, определенных во вступительной части.
В связи с этим, изобретением предложен способ оценки навигационного состояния с несколькими переменными мобильного носителя в соответствии с методом расширенного фильтра Калмана, содержащий следующие этапы:
- считывание измерений по меньшей мере одной из переменных,
- обработку при помощи расширенного фильтра Калмана, выдающего текущее оценочное состояние и ковариационную матрицу, ограничивающую в пространстве навигационного состояния область погрешностей, на основании предыдущего оценочного состояния, матрицы наблюдения, переходной матрицы и считанных измерений,
при этом способ отличается тем, что содержит этап коррекции переходной матрицы и матрицы наблюдения до их использования в расширенной фильтрации Калмана таким образом, чтобы скорректированные матрицы отвечали условию наблюдаемости, которое зависит по меньшей мере от одной из переменных состояния носителя, при этом условие наблюдаемости адаптируют таким образом, чтобы помешать фильтру Калмана уменьшать размер области по меньшей мере вдоль одной ненаблюдаемой оси пространства состояния, в котором условие наблюдаемости, проверяемое скорректированными переходной матрицей и матрицей наблюдения, является обращением в нуль ядра связанной с ними матрицы наблюдаемости, и
в котором коррекция содержит следующие этапы:
- вычисление по меньшей мере одного первичного базиса ненаблюдаемых векторов на основании предыдущего оценочного состояния,
- для каждой корректируемой матрицы - вычисление по меньшей мере одного матричного отклонения, связанного с матрицей, на основании первичного базиса векторов,
- смещение каждой корректируемой матрицы на связанное с ней матричное отклонение, чтобы проверить условие наблюдаемости.
Заявленный способ позволяет не только улучшить когерентность оценок, но также повысить точность оценок, так как можно исключить участие шумов модели, предлагаемое в известных решениях, в решении проблем наблюдаемости.
Кроме того, этот способ меняет лишь в незначительной степени программную архитектуру фильтра EKF и может применяться в виде незначительного программного обновления на уже работающем оборудовании. Это обновление состоит в добавлении функции коррекции двух матриц и в уменьшении регулировок шумов модели.
Изобретение можно дополнить следующими признаками, которые можно рассматривать отдельно или в технически возможных комбинациях.
Этап расширенной фильтрации Калмана может содержать следующие подэтапы:
- распространение предыдущего оценочного состояния на предсказанное состояние при помощи скорректированной переходной матрицы,
- линеаризация предсказанного состояния нелинейной модели для получения матрицы наблюдения до коррекции,
- коррекция матрицы наблюдения, полученной посредством линеаризации.
Применение линеаризации после этапа распространения позволяет осуществлять эту линеаризацию в более вероятной точке векторного пространства: в предсказанном состоянии, полученном на этапе распространения. При этом коррекция матрицы наблюдения учитывает это распространение и выдает более точные результаты, чем когда линеаризацию осуществляют до этапа распространения в предыдущем оценочном состоянии.
Кроме того, коррекция может включать в себя этап ортогонализации первичного базиса для получения вторичного базиса векторов, который сохраняют в памяти от одного цикла к другому, и матричное отклонение, соответствующее матрице наблюдения, вычисляют на основании вторичного базиса векторов.
Матричное отклонение, связанное с матрицей наблюдения, может быть суммой нескольких независимых матричных отклонений, при этом каждое матричное отклонение вычисляют на основании вектора соответствующего вторичного базиса.
Этапы способа можно повторять в последовательных циклах. Данный цикл, называемый текущим циклом, может при этом содержать следующие этапы:
- сохранение в памяти вторичного базиса векторов и коэффициентов ортогонализации, тоже полученных на этапе ортогонализации, и
- преобразование первичного базиса векторов в третичный базис векторов при помощи коэффициентов ортогонализации, сохраненных в ходе предыдущего цикла,
- при этом матричное отклонение, связанное с переходной матрицей, применяют на основании вторичного базиса, сохраненного в памяти в ходе предыдущего цикла, и третичного базиса, вычисленного в ходе текущего цикла.
Кроме того, матричное отклонение, связанное с переходной матрицей, может быть суммой нескольких независимых элементарных матричных отклонений, при этом каждое матричное отклонение вычисляют на основании вторичного вектора вторичного базиса, сохраненного в памяти в ходе предыдущего цикла, и третичного вектора третичного базиса, вычисленного в ходе текущего цикла, при этом вторичный и третичный векторы являются специфическими для элементарного матричного отклонения.
Кроме того, по меньшей мере для одной корректируемой матрицы можно вычислить:
- множество матричных отклонений-кандидатов, при этом каждое матричное отклонение-кандидат вычисляют на основании соответствующего первичного базиса ненаблюдаемых векторов, и
- множество метрик, при этом каждая метрика отображает амплитуду коррекции, заданную соответствующим матричным отклонением-кандидатом,
при этом осуществляют этап смещения корректируемой матрицы на матричное отклонение, выбираемое среди матричных отклонений-кандидатов в зависимости от вычисленных метрик.
Выбранное матричное отклонение может быть матричным отклонением-кандидатом, связанным с метрикой, отображающей наименьшую амплитуду коррекции.
Смещение можно применять, только если метрика выбранного матричного отклонения меньше заранее определенного порога.
Еще одним объектом изобретения является инерциальная система, содержащая множество датчиков и модуль оценки, выполненный с возможностью оценивать навигационное состояние инерциальной системы с несколькими переменными посредством осуществления заявленного способа.
Краткое описание чертежей
Другие признаки, задачи и преимущества изобретения будут более очевидны из нижеследующего описания, представленного исключительно в качестве не ограничительного примера, со ссылками на прилагаемые чертежи, на которых:
Фиг. 1 и 2 (уже описаны) иллюстрируют два изменения огибающий 3 сигма в течение времени во время применения расширенного фильтра Калмана.
Фиг. 3 - схема носителя, содержащего инерциальную систему согласно варианту выполнения изобретения.
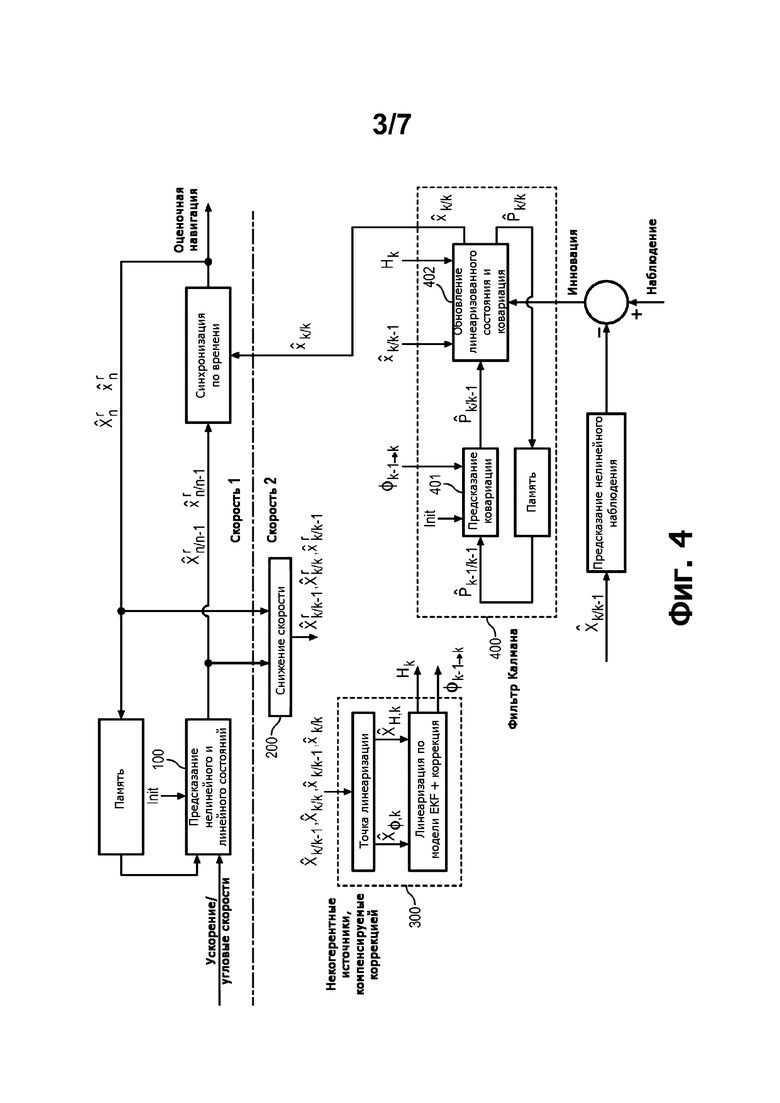
Фиг. 4 - функциональная схема эстиматора согласно варианту выполнения.
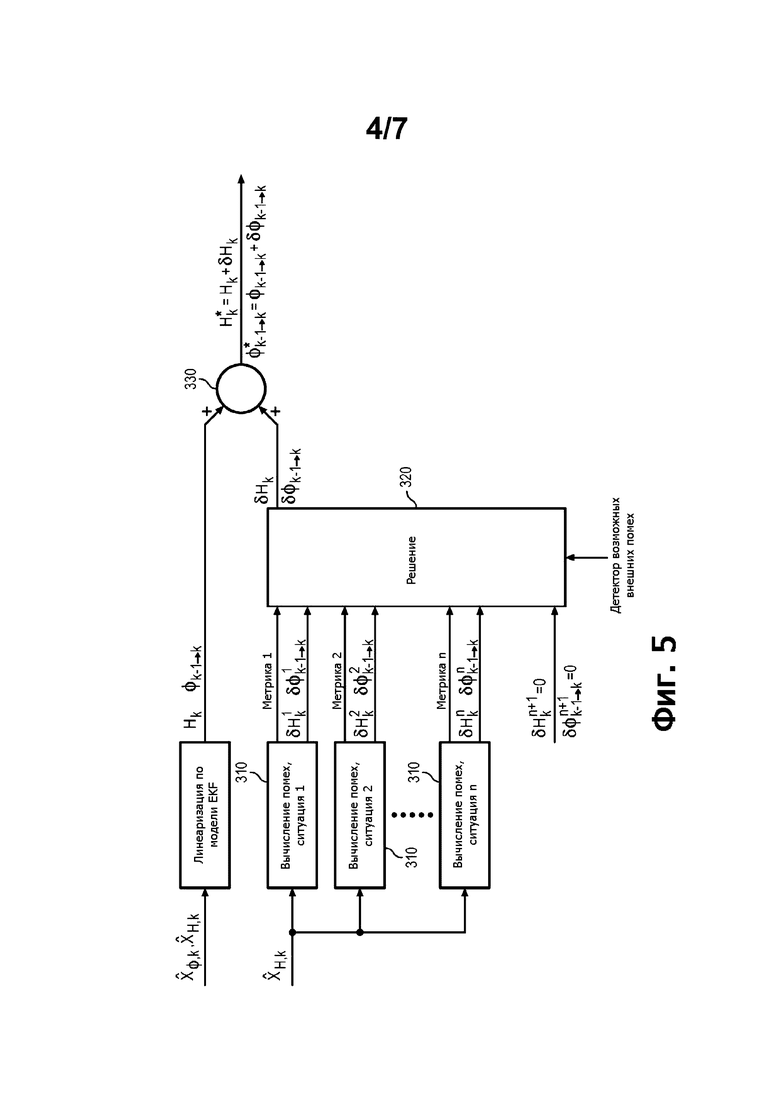
Фиг. 5 - функциональная схема блока линеаризации и коррекции, входящего в состав эстиматора, показанного на фиг. 2.
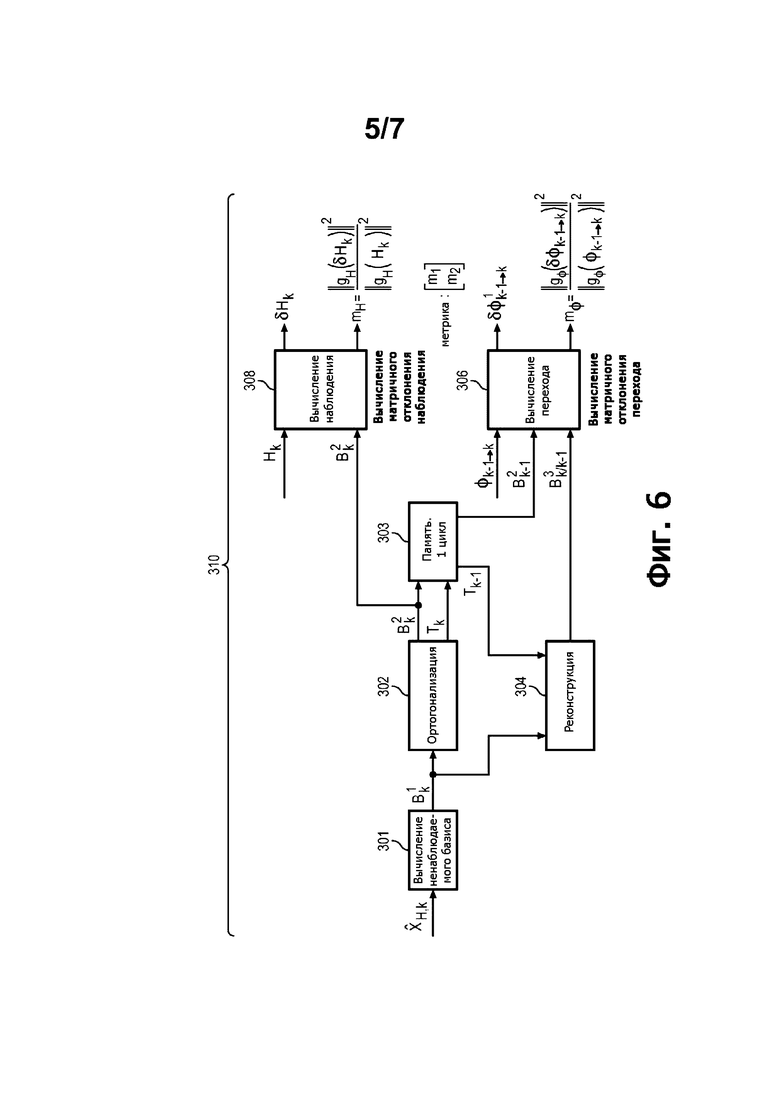
Фиг. 6 - функциональная схема подблока, показанного на фиг. 5.
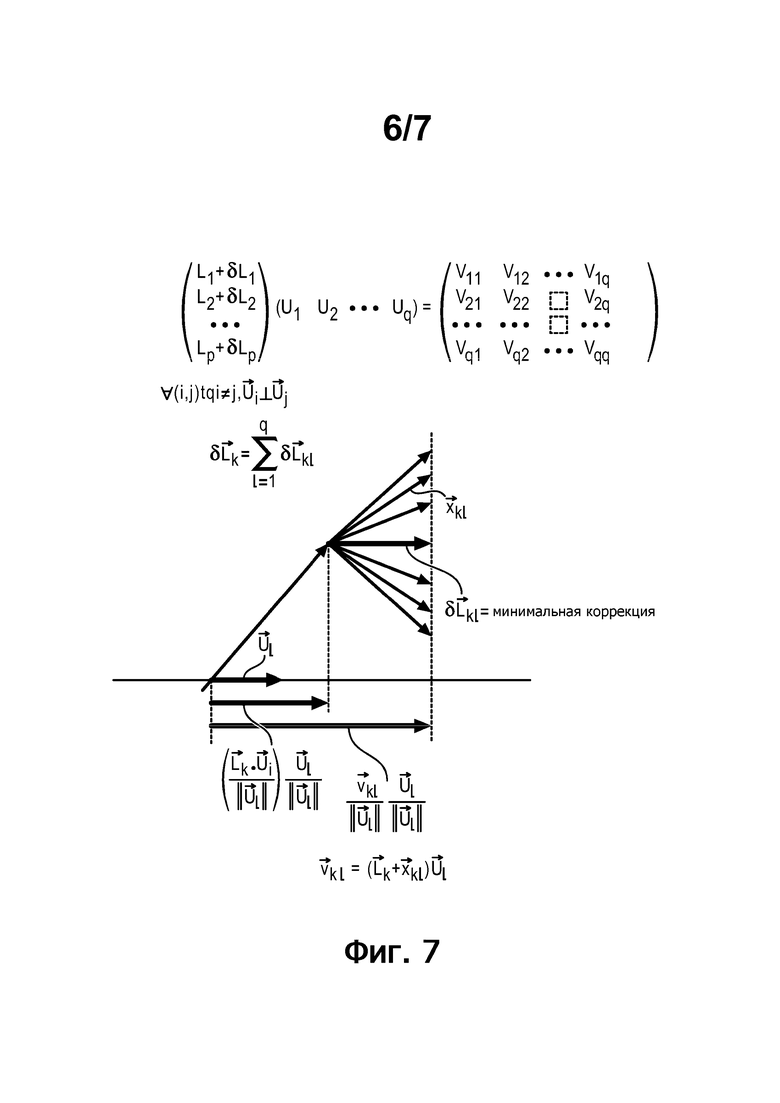
Фиг. 7 - геометрическое обоснование коррекции матриц, используемых фильтром Калмана.
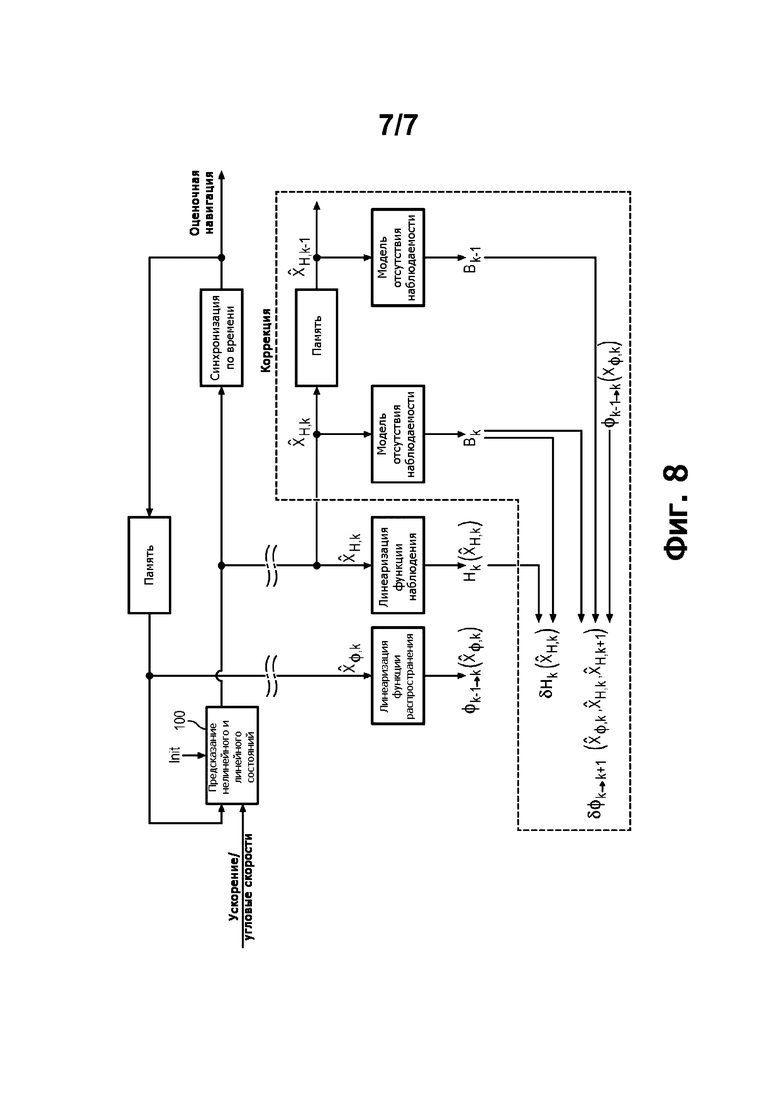
Фиг. 8 - поток данных, соответствующий осуществлению этапов, представленных на фиг. 3.
На всех фигурах аналогичные элементы имеют одинаковые обозначения.
Осуществление изобретения
Показанная на фиг. 3 инерциальная система IN установлена на мобильном носителе Р, таком как наземное транспортное средство, вертолет, самолет и т.д.
Инерциальная система IN содержит несколько частей: инерциальные датчики CI, дополнительные датчики СС и средства Е для осуществления вычислений оценки. Эти части могут быть физически отделены друг от друга.
Как правило, инерциальные датчики CI являются акселерометрами и/или гироскопами, измеряющими соответственно специфические силы и скорости вращения, воздействию которых подвергается носитель в инерциальной системе отсчета. Специфическая сила соответствует первоначальному негравитационному ускорению. Если датчики являются неподвижными относительно носителя, систему называют “strap down”.
Дополнительные датчики СС могут быть самыми разными в зависимости от типа носителя, от его динамики и от предусмотренного назначения. Как правило, в инерциальных системах используют приемник GNSS (например, GPS). Для наземного транспортного средства речь идет также об одном или нескольких одометрах. Для судна речь может идти о «лаге», определяющем скорость судна относительно скорости воды или относительно морского дна. Другим примером датчиков являются камеры.
Навигационные средства оценки Е в дальнейшем будут обозначены термином «эстиматор». Средства Е обычно содержат один или более процессоров.
Выходные данные эстиматора Е представляют собой состояние навигации носителя и, возможно, внутренние состояния инерциальной системы.
В частности, эстиматор содержит расширенный фильтр Калмана EKF, выполненный с возможностью объединения данных, выдаваемых дополнительными датчиками и инерциальными датчиками, чтобы получить оптимальную оценку навигационных данных.
Объединение осуществляют в соответствии с непрерывной динамической системой, служащей моделью для предсказания состояния в каждый момент при помощи нелинейной функции f распространения, а также чтобы наблюдать его при помощи функции h наблюдения, которая тоже может быть нелинейной (в этой связи можно обратиться к Приложению 5, где указаны несколько принципов на динамических системах), причем эта функция зависит от типа используемого датчика СС:
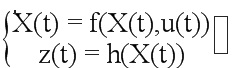
где  является входной командой, содержащей указание специфической силы и угловой скорости. Эти две величины измеряют при помощи датчиков дискретно во времени в соответствии с периодом
является входной командой, содержащей указание специфической силы и угловой скорости. Эти две величины измеряют при помощи датчиков дискретно во времени в соответствии с периодом 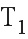 .
.
Кроме всего прочего, общее состояние 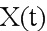 содержит другие координаты положения, скорости, а также ориентацию носителя в виде одного или нескольких вращений, каждое из которых представлено, например, матрицей или кватернионом высоты над уровнем моря.
содержит другие координаты положения, скорости, а также ориентацию носителя в виде одного или нескольких вращений, каждое из которых представлено, например, матрицей или кватернионом высоты над уровнем моря.
Эстиматор Е использует дискретную версию этих уравнений с непрерывным времени в соответствии с известными правилами:
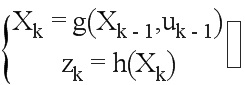
Фильтр EKF работает итеративно в соответствии с этапом предсказания, учитывая измерения датчиков CI, и с этапом обновления, учитывая измерения датчиков СС:
Этап предсказания включает в себя предсказание оценочного общего состояния и предсказания соответствующей ковариации.
Предсказание оценочного общего состояния: 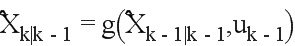
Предсказание соответствующей ковариации: 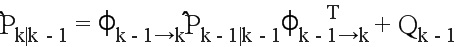 ,
,
где 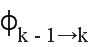 соответствует переходной матрице, зависящей от функции f распространения, и Q является матрицей шумов модели.
соответствует переходной матрице, зависящей от функции f распространения, и Q является матрицей шумов модели.
На этапе обновления используют следующие переменные:
Инновация: 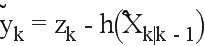
Ковариация инновации: 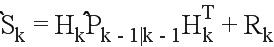
где 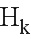 соответствует матрице наблюдения.
соответствует матрице наблюдения.
Коэффициент усиления Калмана: 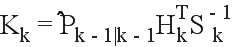
Обновление осуществляют следующим образом:
Обновление оценочного общего состояния: 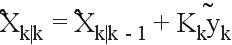
Обновление соответствующей ковариации: 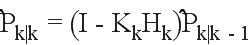
Теоретическая переходная матрица: 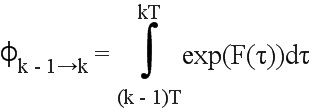
где: 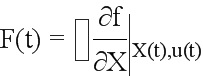
Матрица наблюдения: 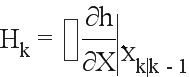
Хотя эстиматор Е и близок к этому алгоритму, он все же слегка от него отличается. Обновление общего состояния можно осуществлять не полностью аддитивно, в частности, чтобы сохранить свойства матриц поворота, а также чтобы учитывать быстрый ритм измерений датчиков CI. При этом предсказание оценочного общего состояния можно производить в более быстром ритме, чем другие операции. Отличие ритма может зависеть от динамики носителя. Возможны и другие отличия. Например, аппроксимацию можно осуществлять на переходной матрице.
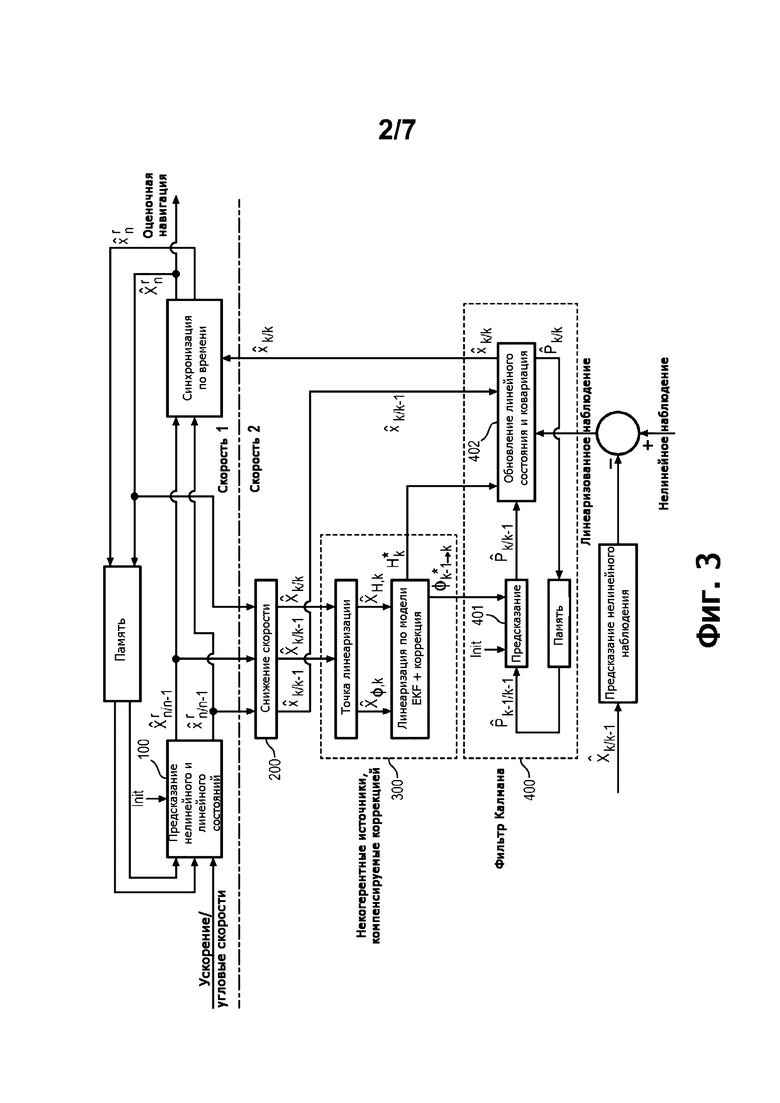
На фиг. 4 показан эстиматор Е согласно варианту выполнения, содержащий различные функциональные блоки, соответствующие этапам его применения.
Оценку можно производить путем последовательным итераций, при этом каждая итерация обозначена индексом k.
Предсказание оценочного общего состояния со скоростью 1 осуществляют на этапе 100.
Память в 1 цикле, а также этап синхронизации по времени работают в одном и том же ритме. Этот этап синхронизации по времени учитывает данные, обновленные с более медленной скоростью 2.
Все другие виды обработки работают на скорости 2. На этапе 200 состояния скорости 1 конвертируют в состояния скорости 2. На скорости 2 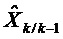
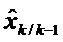
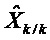
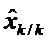
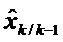
Вычисление переходных матриц и матриц наблюдения производят на этапе 300 линеаризации. К нему добавляют подэтап коррекции в соответствии с изобретением, который будет подробно описан ниже.
Инновацию вычисляют по предсказанному общему состоянию и по наблюдению датчиков СС, что показано внизу на фиг. 4.
Другие этапы EKF сгруппированы на этапе 400, на котором производят оценки при помощи матриц и который применяет фильтр Калмана, причем эти оценки относятся к линеаризованным состояниям и к ковариациям. Особенностью является то, что этап 400 не содержит предсказания линеаризованного состояния, которое можно включить в этап 100 со скоростью 1.
Этап 401 содержит предсказание ковариации, соответствующей предсказанному общему состоянию, и использует переходную матрицу. Этап 402 содержит вычисление ковариации инновации, коэффициентов усиления Калмана, обновления ковариации общего состояния и обновления линеаризованного состояния. На этом этапе используют матрицу наблюдения.
На этапе 300 точки линеаризации можно вычислять в зависимости от 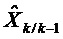
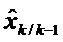
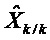
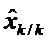
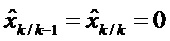
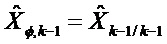
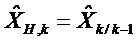
Первая точка линеаризации 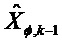
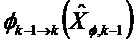
Вторая точка линеаризации 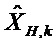
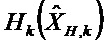
Чтобы упростить обозначения, в дальнейшем переходная матрица 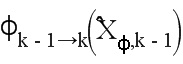 будет обозначена как
будет обозначена как 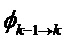
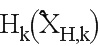 будет обозначена как
будет обозначена как 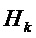
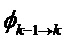
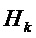
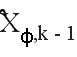 и
и  .
.
Как было указано выше, этапы повторяют рекурсивно при следующей итерации в момент k+1 на скорости 2, которая является скоростью фильтра Калмана.
Коррекция переходной матрицы и матрицы наблюдения
Этап линеаризации, осуществляемый на каждом цикле Калмана, является слабой точкой эстиматора Е.
Поэтому на этапе 300 способ оценки включает в себя дополнительный этап коррекции в зависимости от условия наблюдаемости, на котором корректируют матрицы, созданные на этом этапе линеаризации, перед их использованием для фильтра Калмана: с одной стороны, переходную матрицу, служащую для распространения ковариационной матрицы, и, с другой стороны, матрицу наблюдения.
Условие наблюдаемости представляет собой условие, задаваемое ядру матрицы наблюдаемости (определение этой матрицы представлено в приложении 6) посредством коррекции переходной матрицы и матрицы наблюдения таким образом, чтобы включить в ядро заранее определенную модель ненаблюдаемого векторного подпространства. Эта модель ненаблюдаемости представляет собой уравнение в пространстве состояния векторного подпространства, представленного базисом, в зависимости от общего состояния, причем это векторное подпространство обновляют в каждом цикле Калмана. Включение этого подпространства в ядро матрицы наблюдаемости делает его ненаблюдаемым и снижает риск несоответствия, если модель является надлежащей.
Общее состояние, на основании которого вычисляют это ставшее ненаблюдаемым векторное подпространство, соответствует точке линеаризации функции наблюдения (см. приложение 6). Действительно, ненаблюдаемый вектор имеет нулевое изображение через матрицу наблюдения, и этот вектор соответствует линеаризованному состоянию вблизи общего состояния, соответствующего точке линеаризации функции наблюдения.
В ходе этапа коррекции для каждой из обеих переходной матрицы и матрицы наблюдения вычисляют соответствующее матричное отклонение.
Условно далее будут использованы обозначения со звездочками, чтобы обозначить переходную матрицу и матрицу наблюдения, полученные в результате коррекции.
Поток данных, необходимых для вычисления коррекции, схематично представлен на фиг. 8, где наглядно показано, что коррекция матрицы наблюдения зависит от точки линеаризации функции наблюдения в текущем цикле Калмана и что коррекция переходной матрицы зависит от точки линеаризации функции наблюдения в текущем цикле и в предыдущем цикле.
Следовательно, необходимо использовать базис 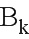 , генерирующий ненаблюдаемое векторное подпространство в цикле k, а также базис
, генерирующий ненаблюдаемое векторное подпространство в цикле k, а также базис 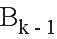 , генерирующий ненаблюдаемое векторное подпространство в цикле k-1.
, генерирующий ненаблюдаемое векторное подпространство в цикле k-1.
При этом в цикле Калмана можно сохранить в памяти точку линеаризации и генерировать 2 раза за цикл ненаблюдаемый базис, как показано на фиг. 8. Точно так же в цикле Калмана можно сохранить в памяти ненаблюдаемый базис, чтобы генерировать его только один раз за цикл. Этот второй вариант соответствует принципиальной схеме, показанной на фиг. 6. Здесь детально показаны функции коррекции, описанные со ссылками на фиг. 5.
На фиг. 6 показаны вычисления, позволяющие получить два матричных отклонения, относящихся к переходной матрице и к матрице наблюдения, в цикле Калмана в момент k.
Переходную матрицу цикла Калмана k-1 в цикле k и матрицу наблюдения в цикле k корректируют в соответствии с моделью ненаблюдаемости с использованием векторов общих состояний 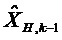
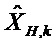
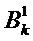
Два примера рисковых ситуаций, которые можно обрабатывать при помощи заявленного способа, описаны в приложении 1. Модель ненаблюдаемого базиса, характерная для статического выравнивания, представлена в Приложении 2.
Чтобы выработать эту модель во время фазы разработки, необходимо сделать два упрощающих предположения, так как никакое уравнение, содержащее ограниченное число переменных, не может отобразить реальную действительность. Так, реальное облако погрешности может медленно уменьшаться во всех направлениях пространства состояния, но при этом, учитывая нелинейность и шумы оценки, фильтр EKF оценивает более быстрое уменьшение вдоль некоторых осей, что создает несоответствие. В этом случае можно моделировать медленное уменьшение вдоль определенной оси по нулевому уменьшению во времени и рассматривать эту ненаблюдаемую ось, чтобы задавать для нее условие. Это упрощение слегка снижает точность, но гарантирует когерентность оценок. Поскольку отпадает необходимость в использовании шумов модели для предупреждения уменьшения оценочной огибающей 3 сигма вдоль ненаблюдаемых осей, в конечном итоге все равно получают выигрыш в точности.
Статическое выравнивание, описанное в приложении 1, является примером ситуации, в которой модель не учитывает слабые неощутимые движения, которые в краткосрочном плане не имеют влияния, но которые можно наблюдать за длительное время, что приводит к медленному уменьшению реальной огибающей 3 сигма на некоторых осях. Для упрощения модели было предложено не принимать его во внимание и моделировать ненаблюдаемый базис, считая, что эти слабые движения являются нулевыми, что и является примером упрощения. Во втором примере из приложения 1 по этой же причине можно пренебречь волнообразным движением при моделировании ненаблюдаемого базиса.
Если базис 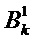
На этапе 302 ортогонализации первичный базис 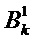
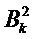
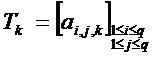
Обозначим число векторов ненаблюдаемого первичного базиса как q. Получаем:
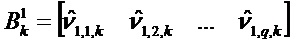
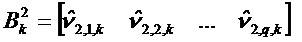
В цикле k на этапе ортогонализации можно применить следующее вычисление:
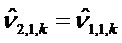
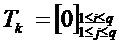
Затем: 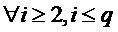

При
Этот базис 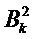
На этапе 308 базис 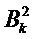
Матричное отклонение δHk, относящееся к матрице наблюдения Hk, можно разложить на q элементарных матричных отклонений:
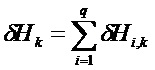
Это разложение позволяет осуществлять параллельно вычисление каждого элементарного матричного отклонения и, следовательно, сократить время вычисления на этапе 308.
Согласно приложению 3, каждое элементарное матричное отклонение можно вычислить следующим образом: при i, составляющем от 1 до q,
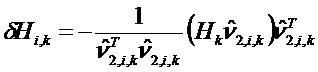
Кроме того, в цикле k базис 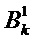
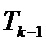
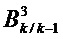
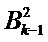
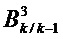
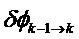

В цикле k на этапе 304 реконструкции можно применить следующее вычисление:
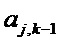
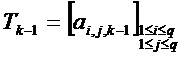
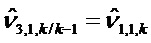
Затем: 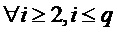
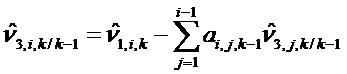
На этапе 306 вычисляют матричное отклонение, относящееся к переходной матрице.
Матричное отклонение 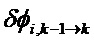
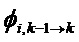
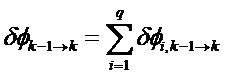
Согласно приложению 3, каждое элементарное матричное отклонение можно вычислить следующим образом:
При i, составляющем от 1 до q,
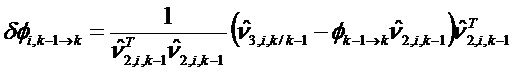
Это разложение позволяет осуществлять параллельно вычисление каждого элементарного матричного отклонения и, следовательно, сократить время вычисления на этапе 306.
Чтобы уменьшить занимаемый объем памяти и вычисления, можно рассматривать только подматрицу переходной матрицы, то есть подматрицу, согласующуюся с не нулевыми значениями ненаблюдаемых векторов.
Оба полученных матричных отклонения позволяют проверить важное условие наблюдаемости, описанное в Приложении 7.
Кроме того, Приложение 3 поясняет происхождение метода вычисления, а Приложение 8 дает математическую демонстрацию.
Кроме того, на этапе 306 вычисления получают метрику, характеризующую амплитуду коррекции, задаваемую матричным отклонением, относящимся к переходной матрице.
На этапе 308 вычисления получают также метрику, характеризующую амплитуду коррекции, задаваемую матричным отклонением, относящимся к матрице наблюдения.
Для переходной матрицы и для матрицы наблюдения можно применять один и тот же тип вычисления. Например, для переходной матрицы отдельно вычисляют квадрат нормы матричного отклонения и квадрат нормы переходной матрицы. При этом метрика соответствует соотношению этих двух величин или квадратному корню соотношения этих двух величин.
В случае необходимости, норма использует весовые коэффициенты для нормализации величин, участвующих в векторе состояния. Например, погрешность положения может составлять порядка нескольких метров, тогда как погрешность ориентации может составлять порядка нескольких миллирадиан. Норма матрицы может соответствовать норме вектора, который получили бы, придав всем членам матрицы форму вектора столбца (норма Фробениуса).
В Приложении 4 пояснено, как использовать весовые коэффициенты при вычислении метрик.
При вычислении метрик можно применить функции взвешивания 
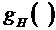
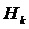
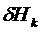
Возвращаясь к фиг. 5, на этапе смещения 330 переходную матрицу суммируют с соответствующим матричным отклонением, чтобы получить скорректированную переходную матрицу; и матрицу наблюдения суммируют с соответствующим матричным отклонением, чтобы получить скорректированную матрицу наблюдения.
Весь цикл 310, показанный на фиг. 6, дающий пару матричных отклонений и пару метрик, можно осуществлять параллельно n раз.
Предположим, что для n заранее определенных ситуаций в непрерывной области известна модель ненаблюдаемого базиса. Эту модель получают путем решения системы уравнений, характеризующих соответствующий тип наблюдения и, возможно, соответствующую траекторию вектора состояния; метод этого решения представлен в Приложении 6.
На этапе 320 принятия решения выбирают одну из n пар матричных отклонений (например, пару получают посредством коррекции, соответствующей ситуации i) и этап смещения осуществляют только с этой парой матриц, чтобы получить скорректированные метрики.
На этапе 320 принятия решения осуществляют тест на правдоподобие для каждой пары матричных отклонений, контролируя значение соответствующих метрик. Этот тест позволяет принять решение для распознавания такой или иной ситуации.
Выбранное матричное отклонение является матричным отклонением-кандидатом, связанным с метрикой, отображающей наименьшую амплитуду коррекции. Таким образом, коррекцию производят с наиболее «правдоподобными» матричными отклонениями. Критерий правдоподобности может касаться коррекции переходной матрицы и/или матрицы наблюдения.
Кроме того, смещение производят, только если метрика выбранного матричного отклонения меньше заранее определенного порога: действительно, лучше не производить смещение переходной матрицы и матрицы наблюдения, если это смещение считается недостаточно надежным и приводит к дополнительному шуму в системе вместо ее коррекции.
Описанный выше способ оценки можно осуществлять при помощи компьютерной программы, исполняемой средствами вычисления инерциальной системы IN. Кроме того, карта 1 идентификации содержит программный компьютерный продукт, содержащий командные коды программы для осуществления этапов описанного способа, когда эту программу исполняет карта 1 идентификации.
ПРИЛОЖЕНИЕ 1: Примеры рисковых ситуаций инерциальной навигационной системы, использующей фильтр EKF
Первый пример относится к инерциальной навигационной системе в фазе статического выравнивания на земле. В этой фазе локальную вертикаль оценивают, измеряя вектор силы тяжести при помощи акселерометров, и ориентацию системы оценивают, измеряя вектор угловой скорости вращения Земли при помощи гироскопов. Как правило, в качестве наблюдения в этой фазе обычно применяют ZUPT (Zero velocity Update), которое является наблюдением виртуального датчика, показывающим, что скорости носитель является нулевой по отношению к Земле. Погрешность измерения моделируют при помощи белого шума. Однако иногда инерциальные датчики регистрируют неслучайные слабые движения, связанные, например, с ветром или с эффектами расширения от тепла. Это соответствует определенной погрешности измерения, не учитываемой в модели не инерциального датчика, производящего наблюдение ZUPT. При этом возникает несоответствие между реальной динамической системой и моделированной динамической системой. Если продолжительность статического выравнивания является короткой, несоответствием можно пренебречь. С другой стороны, существуют многие варианты применения, требующие выравнивания в течение нескольких часов или нескольких дней, недель или месяцев. В этом случае несоответствие может стать определяющим.
Второй пример касается инерциальной навигационной системы, установленной на надводном судне, использующей наблюдение скорости в проекции в системе координат судна. Как правило, это не инерциальное измерение осуществляют при помощи датчика типа «лаг», и, кроме того, речь идет об измерении относительно воды. Осуществление измерения в проекции в системе координат судна создает зависимость измерения относительно ориентации судна. В этом случае, если предположить, что используют только это наблюдение, может появиться несоответствие между оценками фильтра EKF и реальной действительностью, и это несоответствие может привести к значительным погрешностям по истечении нескольких часов, если судно идет с постоянным курсом.
ПРИЛОЖЕНИЕ 2: Модель ненаблюдаемых осей при статическом выравнивании
В этом приложении представлено моделирование ненаблюдаемого базиса, позволяющего решить проблему несоответствия из первого примера приложения 1 при помощи предложенного способа.
Предположения: фильтр Калмана использует модель погрешностей в PHI, и механизация работает по свободному азимуту.
Используют следующие обозначения:
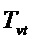
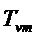
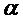
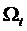
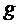
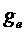
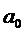
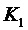
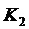
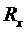
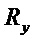
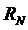
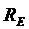
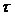

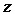
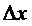
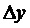
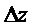
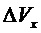
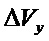
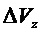


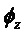
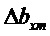

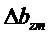
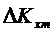
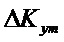


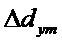
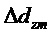
Составляющие состояний, участвующие в уравнениях, представлены в произвольном порядке:
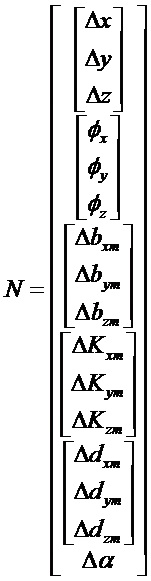
Другие нулевые составляющие: 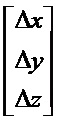
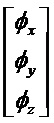
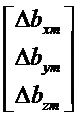
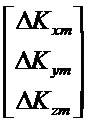
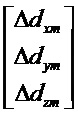
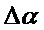
Считываемыми измерениями являются скорости. Предполагается, что носитель является идеально неподвижным как в поступательном движении, так и во вращении. Предполагается также, что погрешности датчиков являются постоянными во времени.
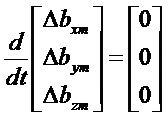

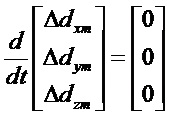
Эти уравнения образуют стационарную систему следующего вида:

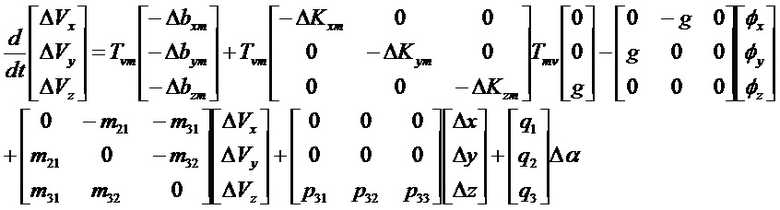
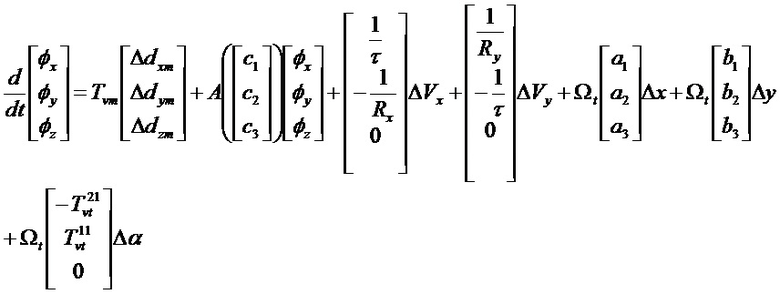
Метод выявления ненаблюдаемых векторов:
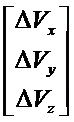
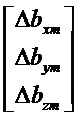


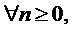
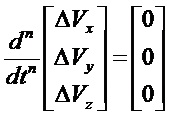
Ненаблюдаемыми осями являются:
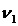
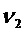
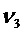
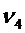





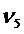
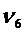
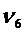

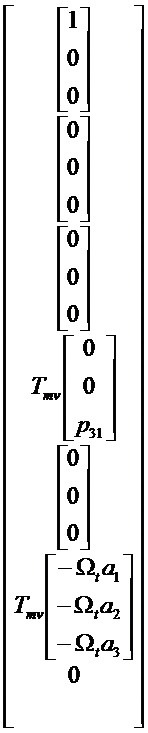
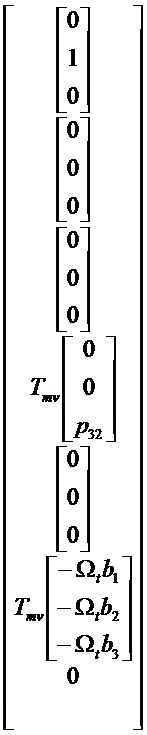

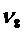
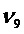
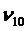



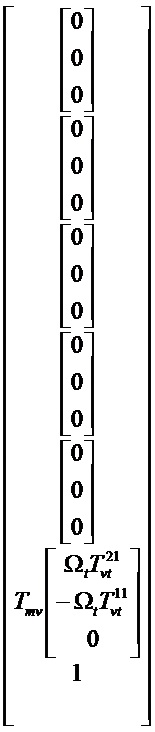
ПРИЛОЖЕНИЕ 3: ограничение фильтра
Матричные отклонения применяют к переходной матрице и к матрице наблюдения в каждом цикле Калмана в соответствии с моделью q ненаблюдаемых осей 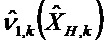
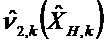
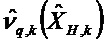
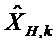
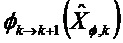
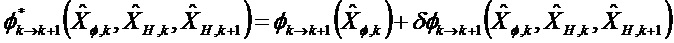
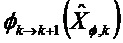
Уравнение 1: 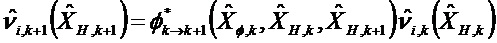
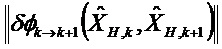
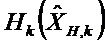
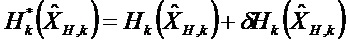
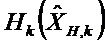
Уравнение 2: 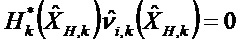
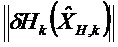
Рассматриваемая нома матрицы является нормой Фробениуса.
Матрицы 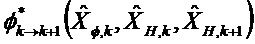

Далее используют следующие обозначения:
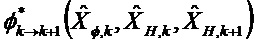
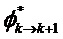
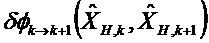
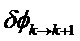
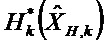
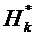
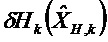
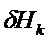
Решение уравнений 1 и 2 в случае, когда моделированные ненаблюдаемые векторы 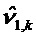
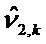
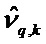
Общее матричное отклонение переходной матрицы соответствует сумме q независимых матричных отклонений. Это же относится и к матричному отклонению матрицы наблюдения.
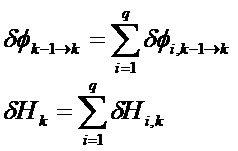
и для i, составляющего от 1 до q:
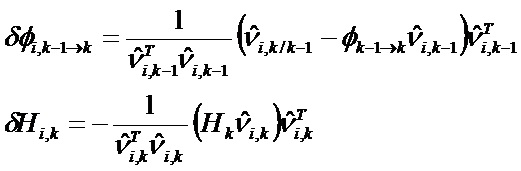
Демонстрация этих отношений представлена в приложении 8 в соответствии с геометрическим методом.
Решение уравнений 1 и 2 для не ортогонального базиса и при любом q:
Этот базис определяет модель ненаблюдаемого векторного пространства: любая линейная комбинация базисных векторов является ненаблюдаемой.
Таким образом, отображение любой линейной комбинации этих векторов скорректированной матрицей наблюдения является нулевым. Следовательно, можно произвести ортогонализацию базиса, затем применить предыдущий метод для вычисления матричного отклонения матрицы наблюдения.
С другой стороны, отображение линейной комбинации ненаблюдаемых векторов скорректированной переходной матрицей соответствует этой же линейной комбинации, применяемой к отображениям этой же переходной матрицей каждого из исходных ненаблюдаемых векторов. Следовательно, можно определить линейную комбинацию, позволяющую произвести ортогонализацию базиса ненаблюдаемых векторов в цикле k-1 и использовать эту же комбинацию для преобразования модели ненаблюдаемого базиса в цикле k. Это позволяет применить предыдущий метод для вычисления матричного отклонения переходной матрицы
ПРИЛОЖЕНИЕ 4: Взвешенные метрики
Скаляры 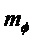
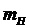
Можно применять разные методы для сравнения 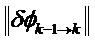
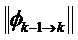
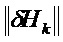
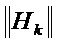
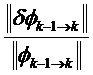
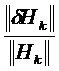
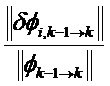
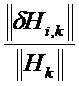
Ниже приведены примеры:
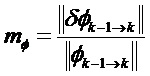
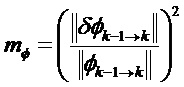
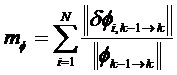

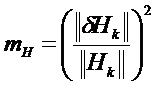
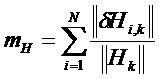
Возможны варианты с применением функций взвешивания gφ и gH для уравновешивания веса различных составляющий при вычислении матричных норм. Можно обратиться к предыдущим примерам, в которых можно учесть эти функции.
Например: 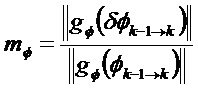
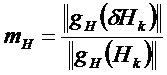
Возможный вариант получения этих функций взвешивания состоит прежде всего в построении функции взвешивания f вектора состояния, затем на ее основании определяют gφ и gH.
Таким образом, при помощи этого метода с вектором 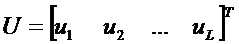
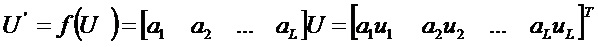
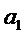
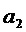
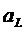
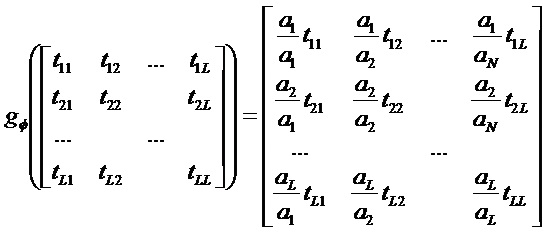
Это связано с тем, что, если 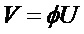
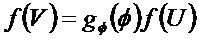
Действительно, предположив, что 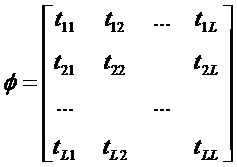
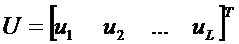

получаем 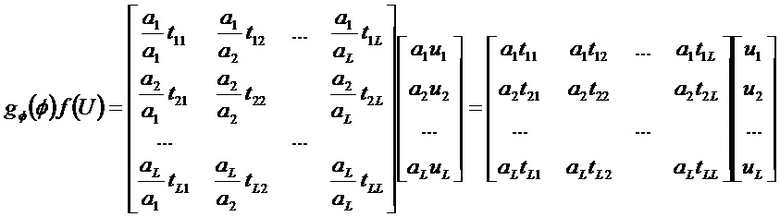
То есть 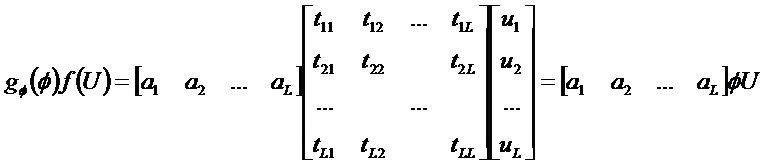
Следовательно, 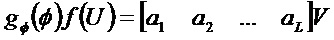
Следовательно, 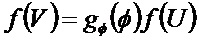
Аналогично 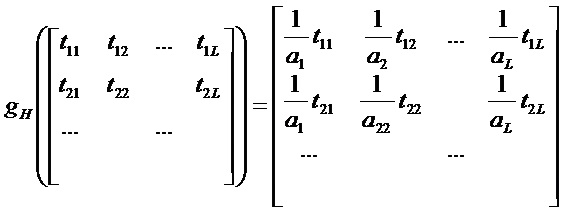
ПРИЛОЖЕНИЕ 5: Понятие динамической системы и применение для навигации
Речь идет о детерминистской системе, содержащей уравнение изменения и уравнение наблюдения. Уравнение изменения описывает вектор состояния в зависимости от его предыдущего состояния и от команды. Уравнение наблюдения позволяет получить скаляр или вектор, зависящий от вектора состояния. Эти уравнения могут быть нелинейными. Существуют системы с непрерывным временем и с дискретным временем.
Система с непрерывным временем: 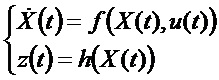
Система с дискретным временем: 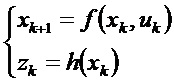
где 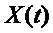
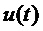
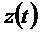
Уравнения классической механики Ньютона позволяют описать состояние подвижного ориентира в зависимости от его ускорения и от его угловой скорости в любой момент. Эти уравнения представляют собой пример непрерывной функции изменения, при этом вектор состояния объединяет данные положения, скорости и ориентации подвижного ориентира, и вектор команды представляет собой ускорение и угловую скорость.
В известной инерциальной навигационной системе вычисления можно производить только дискретно. В результате эту непрерывную функцию изменения моделируют в виде дискретной функции изменения. Различные известные методы позволяют преобразовать непрерывные уравнения изменения в дискретные уравнения изменения.
Моделированная функция наблюдения в динамической системе с дискретным временим инерциальной системы описывает измерения, производимые конкретным не инерциальным датчиком. При этом можно применять несколько функций наблюдения последовательно во времени в зависимости от используемых датчиков.
Таким образом, динамическая система с дискретным временем, используемая в инерциальной навигационной системе, является наиболее надежной возможной моделью другой динамической системы с непрерывным временем, соответствующей реальной действительности. Следовательно, эти две системы имеют разные свойства наблюдаемости.
Свойства наблюдаемости динамической системы характеризуют данные о состоянии системы в данный момент, которые могут быть получены с учетом производимых в дальнейшем наблюдений и функций изменения и наблюдения. В частности, эти свойства зависят от команды, то есть от движений носителя в случае инерциальной навигационной системы.
ПРИЛОЖЕНИЕ 6: Наблюдаемость системы с непрерывным временем
Рассмотрим нелинейную непрерывную динамическую систему, которая в момент 0 находится в состоянии Х(0). В дальнейшем функция распространения, а также входная команда переводят систему в состояния X(t), определяя таким образом конкретную траекторию в пространстве состояния.
Поскольку эта траектория является непрерывной, предположим, что первоначальное состояние отклонилось от Х(0) на небольшое значение 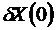
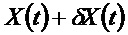
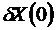
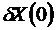
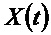
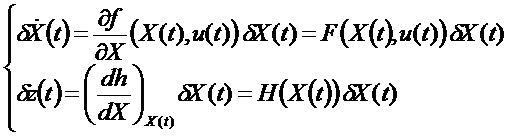
При этом ненаблюдаемое пространство состоит из линеаризованных состояний 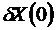
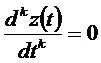
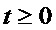
Решения формируют векторное пространство линеаризованных состояний. При этом существует базис В(0) этого пространства, образующий ненаблюдаемые векторы 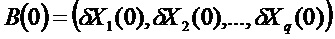
ПРИЛОЖЕНИЕ 7: Наблюдаемость системы с дискретным временем
Рассмотрим нелинейную дискретную динамическую систему, которая в момент 0 находится в состоянии Х0. В разные последовательные дискретные моменты функция распространения, а также входная команда переводят систему в состояния Х1, Х2,… . Зная эти последовательные состояния, предположим, что первоначальное состояние отклоняется от Х0 на небольшое значение 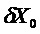


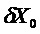
Ненаблюдаемое пространство в момент 0, характеризующееся состоянием Х0, можно определить, рассматривая динамическую систему линеаризованных состояний 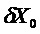
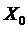
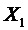
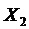
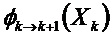
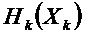
Первое наблюдение отклонения 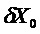
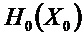
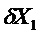
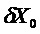
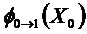
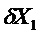
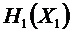
При этом известно, что ненаблюдаемое пространство системы, описывающее помеху, является ядром матрицы:
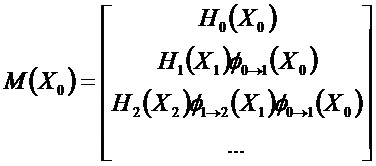
Таким образом, ненаблюдаемое пространство и наблюдаемое пространство зависят от первоначального контрольного состояния Х0, от входной команды (инерциальные данные в случае инерциальных систем) и от функций изменения и наблюдения.
Предположим, что вектор 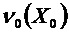
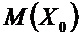
Положим, что: 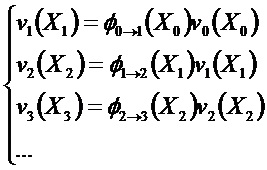
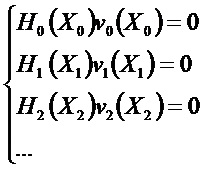
В данный момент условие наблюдаемости получают для ненаблюдаемого направления при помощи системы уравнений:
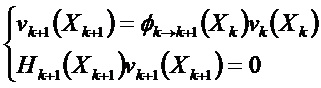
где 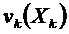
Это условие применяют в каждый момент, и оно связано с траекторией 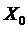
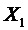
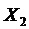
В фильтре ЕKF эта траектория зашумлена погрешностями оценки. Этот шум стремится уменьшить ядро матрицы наблюдаемости и, следовательно, уменьшить размер ненаблюдаемого пространства.
Кроме того, переходная функция и функция наблюдения не линеаризованы в одной и той же точке. Последовательность 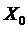
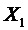
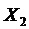
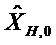
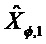
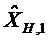
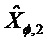
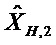
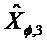
и: 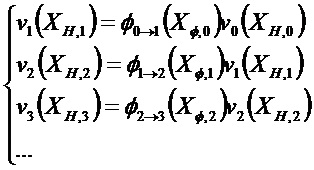
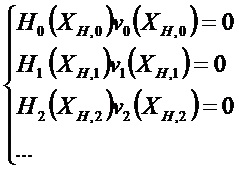
Условие наблюдаемости имеет вид:
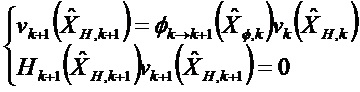
ПРИЛОЖЕНИЕ 8: Демонстрация формулы коррекции матрицы для ортогонального базиса векторов
Предположение: р матриц столбца Ui, при которых 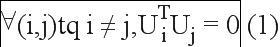
Пусть р матриц столбца Vi имеют тот же размер, что и Ui.
Рассмотрим матрицу А.
Задача: ставится целью выявление матрицы δА минимальной нормы, при которой:
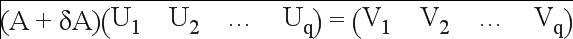
Матрица А + δА может принять вид р матриц строка-столбец, а векторы Vk - вид q скаляров в столбце:
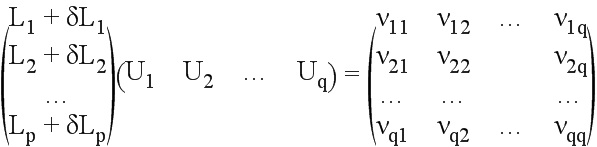
Таким образом, выявляют значения δLk минимальной нормы, при которых:
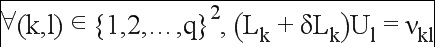 (2)
(2)
Геометрическая интерпретация задачи: Матрицы строка-столбец связаны с векторами в векторном пространстве размером, превышающим q. Сохраняют те же обозначения, добавляя стрелку над переменными.
Условие (1) выражается как: 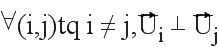
Условие (2) выражается следующим скалярным произведением
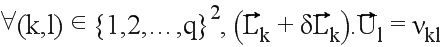
Проекция вектора  на ориентированной оси, определенной унитарным вектором
на ориентированной оси, определенной унитарным вектором 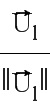 , имеет абсциссу
, имеет абсциссу 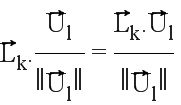 на этой оси. Это является направляющим косинусом of
на этой оси. Это является направляющим косинусом of по этой оси.
по этой оси.
Ставится задача выявления 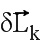 , при котором проекция
, при котором проекция 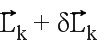 на эту ось является
на эту ось является 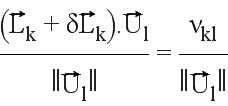 .
.
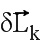 можно разложить по векторам Ui, которые генерируют векторное пространство размером q, и по остаточной составляющей
можно разложить по векторам Ui, которые генерируют векторное пространство размером q, и по остаточной составляющей 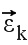 , ортогональной к этой пространству:
, ортогональной к этой пространству:
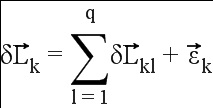
Следовательно, 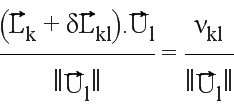 .
.
На фиг. 7 видно, что существует бесконечное число решений 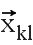 . Минимальное решение соответствует вектору
. Минимальное решение соответствует вектору 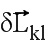 , коллинеарному с
, коллинеарному с 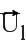 .
.
В соответствии с фигурой получаем:

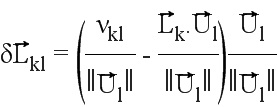
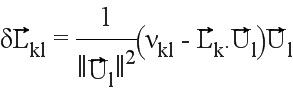
Следовательно, получаем 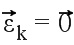 , и:
, и:
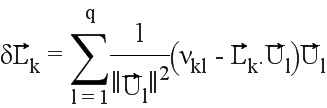
В матричном обозначении получаем:
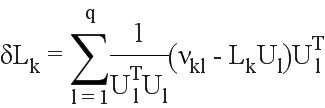
Преобразуя матрицы 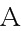 и
и 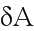 , после нескольких преобразований получаем:
, после нескольких преобразований получаем:
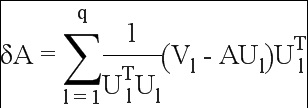
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ восстановления векторной информации в информационно-измерительных системах | 2020 |
|
RU2757828C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
| НАВИГАЦИОННЫЙ КОМПЛЕКС | 2014 |
|
RU2565345C2 |
| Способ калибровки погрешностей электростатических гироскопов бескарданной инерциальной системы ориентации в условиях орбитального космического аппарата | 2018 |
|
RU2678959C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
| СПОСОБ И СИСТЕМА ОЦЕНКИ РАСХОДА ТЕКУЧЕЙ СРЕДЫ | 2015 |
|
RU2690080C2 |
| СЕЛЕКТИВНЫЙ НАВИГАЦИОННЫЙ КОМПЛЕКС | 2014 |
|
RU2561252C1 |
| СПОСОБ КОМБИНИРОВАННОЙ КАЛИБРОВКИ БЛОКА АКСЕЛЕРОМЕТРОВ | 2020 |
|
RU2758891C1 |
| СПОСОБ АВТОНОМНОЙ ИНЕРЦИАЛЬНОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2022 |
|
RU2800846C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ОБЪЕКТА И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2017 |
|
RU2661446C1 |
Изобретение относится к области навигационного приборостроения и может найти применение в системах оценки подвижных транспортных систем. Технический результат – повышение точности. Для этого способ оценки навигационного состояния с несколькими переменными мобильного носителя в соответствии с методом расширенного фильтра Калмана содержит следующие этапы: считывание измерений по меньшей мере одной из переменных, обработку (400) при помощи расширенного фильтра Калмана, выдающего текущее оценочное состояние и ковариационную матрицу, ограничивающую в пространстве навигационного состояния область погрешностей, на основании предыдущего оценочного состояния, матрицы наблюдения, переходной матрицы и считанных измерений, при этом способ отличается тем, что содержит этап (310, 330) коррекции переходной матрицы и матрицы наблюдения до их использования в расширенной фильтрации Калмана таким образом, чтобы скорректированные матрицы отвечали условию наблюдаемости, которое зависит по меньшей мере от одной из переменных состояния носителя, при этом условие наблюдаемости адаптируют таким образом, чтобы помешать фильтру Калмана уменьшать размер области по меньшей мере вдоль одной ненаблюдаемой оси пространства состояния, в котором условие наблюдаемости, проверяемое скорректированными переходной матрицей и матрицей наблюдения, является обращением в нуль ядра связанной с ними матрицы наблюдаемости, и в котором коррекция содержит следующие этапы: вычисление (301) по меньшей мере одного первичного базиса ненаблюдаемых векторов на основании предыдущего оценочного состояния, для каждой корректируемой матрицы - вычисление (306, 308) по меньшей мере одного матричного отклонения, связанного с матрицей, на основании первичного базиса векторов, смещение (330) каждой корректируемой матрицы на связанное с ней матричное отклонение, чтобы проверить условие наблюдаемости. 2 н. и 5 з.п. ф-лы, 8 ил. 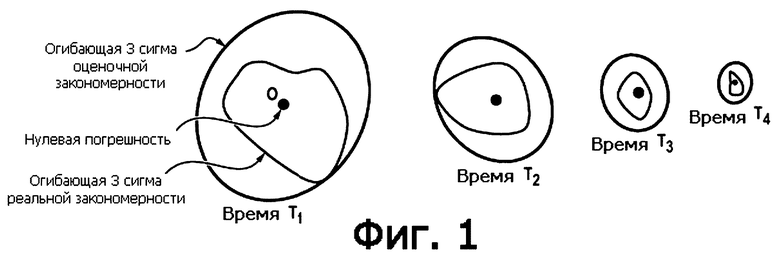
1. Способ оценки навигационного состояния с несколькими переменными мобильного носителя в соответствии с методом расширенного фильтра Калмана, содержащий следующие этапы:
- считывание измерений по меньшей мере одной из переменных,
- обработку (400) при помощи расширенного фильтра Калмана, выдающего текущее оценочное состояние и ковариационную матрицу, ограничивающую в пространстве навигационного состояния область погрешностей, на основании предыдущего оценочного состояния, матрицы наблюдения, переходной матрицы и считанных измерений,
отличающийся тем, что выполняет коррекцию (310, 330) переходной матрицы и матрицы наблюдения до их использования в расширенной фильтрации Калмана таким образом, чтобы скорректированные матрицы отвечали условию наблюдаемости, которое зависит по меньшей мере от одной из переменных состояния носителя, при этом условие наблюдаемости адаптируют таким образом, чтобы помешать фильтру Калмана уменьшать размер области по меньшей мере вдоль одной ненаблюдаемой оси указанного пространства состояния,
при этом условием наблюдаемости, проверяемым указанными скорректированными переходной матрицей и матрицей наблюдения, является обращением в нуль ядра связанной матрицы наблюдаемости, связанной с указанными матрицами, и
при указанной коррекции переходной матрицы и матрицы наблюдения:
- вычисляют (301) по меньшей мере один первичный базис ненаблюдаемых векторов на основании предыдущего оценочного состояния,
- для каждой корректируемой матрицы вычисляют (306, 308) по меньшей мере одно матричное отклонение, связанное с указанной матрицей, на основании указанного первичного базиса векторов,
- смещают (330) каждую корректируемую матрицу на связанное с ней указанное матричное отклонение с тем, чтобы проверить условие наблюдаемости.
2. Способ по п. 1, в котором при указанной обработке при помощи расширенного фильтра Калмана:
- распространяют предыдущее оценочное состояние на предсказанное состояние при помощи указанной скорректированной переходной матрицы,
- линеаризуют в предсказанном состоянии нелинейную модель для получения указанной матрицы наблюдения до выполнения указанной коррекции,
- корректируют матрицу наблюдения, полученную посредством линеаризации.
3. Способ оценки по п. 1 или 2, в котором дополнительно выполняют ортогонализацию (302) первичного базиса для получения вторичного базиса векторов, при этом матричное отклонение, соответствующее матрице наблюдения, вычисляют на основании вторичного базиса векторов.
4. Способ оценки по любому из пп. 1-3, в котором матричное отклонение, связанное с матрицей наблюдения, является суммой нескольких элементарных матричных отклонений, при этом каждое элементарное матричное отклонение вычисляют на основании вектора указанного вторичного базиса, связанного с указанным элементарным матричным отклонением.
5. Способ оценки по любому из пп. 1-4, в котором указанные операции повторяют в виде последовательных циклов, при этом заданный цикл, называемый текущим циклом, содержит этапы, на которых:
- сохраняют в памяти (303) вторичный базис векторов и коэффициентов ортогонализации, также полученных на указанном этапе ортогонализации, и
- преобразуют (304) первичный базис векторов в третичный базис векторов при помощи коэффициентов ортогонализации, сохраненных в ходе предыдущего цикла,
при этом вычисление (306) указанного матричного отклонения, связанного с переходной матрицей, осуществляют на основании вторичного базиса, сохраненного в памяти в ходе предыдущего цикла, и указанного третичного базиса, вычисленного в ходе текущего цикла.
6. Способ оценки по п. 5, в котором матричное отклонение, связанное с переходной матрицей, является суммой нескольких элементарных матричных отклонений, при этом каждое элементарное матричное отклонение вычисляют на основании вектора вторичного базиса, сохраненного в памяти в ходе предыдущего цикла и характерного для указанного элементарного матричного отклонения, и на основании вектора третичного базиса, вычисленного в ходе текущего цикла и характерного для указанного элементарного матричного отклонения.
7. Инерциальная система (IN), содержащая множество датчиков (CI, CC) и средство (E) для оценки навигационного состояния инерциальной системы посредством осуществления способа оценки по любому из пп. 1-6.
| WO 2014130854 A1, 28.08.2014 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| СПОСОБ АВТОНОМНОЙ НАВИГАЦИИ И ОРИЕНТАЦИИ КОСМИЧЕСКИХ АППАРАТОВ | 2006 |
|
RU2318188C1 |
| US 5054719 A1, 08.10.1991 | |||
| DE 3417661 A1, 15.11.1984 | |||
| СПОСОБ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1988 |
|
RU2012034C1 |
Авторы
Даты
2019-09-25—Публикация
2015-10-23—Подача