Изобретение относится к области информационно-измерительных систем и может быть использовано для робастной фильтрации стохастических сигналов и параметров состояния стохастических систем в условиях неопределенности вероятностных характеристик помех измерения.
Известен фильтр стохастических сигналов и параметров состояния стохастических систем, обеспечивающий оптимальную по среднеквадратическому критерию оценку измеряемого сигнала или вектора состояния, - фильтр Калмана [Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 2004. – 304 с.; Синицын И.Н. Фильтры Калмана и Пугачева. - М.: Логос, 2006. – 640 с.]. Недостатком данного фильтра является необходимость точного априорного задания вероятностных характеристик помех измерения оцениваемого сигнала, т.к. для реальных информационно-измерительных систем, функционирующих в условиях различных возмущений, параметры помех измерения или меняются случайным образом во времени, или известны приближенно [A. Ferrero, R. Ferrero, W. Jiang, S. Salicone. The Kalman Filter Uncertainty Concept in the Possibility Domain, IEEE Trans. Instrum. Meas. 68 (2019), Р.4335-4347].
Известны фильтры, использующие для обеспечения устойчивости процесса фильтрации при априорной неопределенности интенсивности помех измерения введение эмпирических масштабных коэффициентов при вычислении апостериорной ковариационной матрицы или дисперсионной матрицы помех измерения [E.P. Herrera, H. Kaufmann. Adaptive methods of Kalman filtering for personal positioning systems, in: 23rd Int. Tech. Meet. Satell. Div. Inst. Navig. 2010, ION GNSS 2010; Патент № 1639377. Модифицированный нелинейный фильтр Калмана, СССР, Н03Н 21/00; Патент № 1800588. Адаптивный фильтр Калмана, СССР, Н03Н 21/00; Патент № 2160496. Модифицированный фильтр Калмана, РФ, Н03Н 21/00]. Недостатком этих способов является отсутствие строгих критериев выбора масштабных коэффициентов и процедуры их вычисления, а также обоснования повышения точности фильтрации, что не позволяет обеспечить требуемую точность и устойчивость процесса фильтрации при отсутствии априорного задания вероятностных характеристик помех измерения оцениваемого сигнала.
Известен также фильтр, использующий для обеспечения устойчивости калмановской фильтрации расширение размерности вектора состояния [D. Wang, H. Ly, J. Wu. Augmented Cubature Kalman filter for nonlinear RTK/MIMU integrated navigation with non-additive noise, Measurement. 97, 2017, р.р.111-125.]. Недостатком данного способа являются существенные вычислительные затраты на его реализацию.
Известен фильтр, обеспечивающий робастную оценку измеряемого сигнала на основе минимизации на текущем интервале времени нелинейного функционала, ядро которого определяется наиболее неблагоприятным классом распределения помехи измерения [Huber P.J., Ronchetti E.M. Robust statistics. New Jersey: John Wiley Sons, 2009. 371 с.; Цыпкин Я.З., Поляк Б.Т. Огрубленный метод максимального правдоподобия // Динамика систем. Математические методы теории колебаний. Горький. 1977. № 12.; Хьюбер П.Дж. Робастность в статистике / Пер. с англ. под ред. Я.З. Цыпкина. - М.: Мир, 1984. 304 с.].
Недостатком данного фильтра является невозможность робастного оценивания в реальном времени динамических процессов в силу большого объема вычислительных затрат, связанных с поиском глобального минимума многомерной нелинейной случайной функции в реальном времени.
Наиболее близким к предлагаемому фильтру является регуляризованный фильтр Калмана [Патент №1651355, СССР, Н03Н 21/00, 1991 г.], содержащий сумматор, блок вычитания, интегратор, умножитель и др. Недостатками данного фильтра являются его сложность, невозможность оценки нелинейных динамических процессов, а также низкая точность оценивания при наличии шумов наблюдаемого объекта и помех измерения с неизвестными вероятностными распределениями.
Технический результат изобретения заключается в упрощении устройства и повышении точности фильтрации нелинейных динамических процессов при наличии шумов наблюдаемого объекта и помех измерения с неизвестными вероятностными распределениями.
Поставленная задача возникает в управляющих и информационно-измерительных системах, функционирующих в условиях неопределенных шумов наблюдаемого объекта и помех измерителя.
Технический результат достигается тем, что в устройство введены четыре блока функционального преобразования, входом устройства является вход уменьшаемого блока вычитания, вход вычитаемого которого соединен с выходом третьего блока функционального преобразования, а выход подключен к входу четвертого блока функционального преобразования, выход которого подключен к первому входу умножителя, второй вход которого соединен с выходом второго блока функционального преобразования, а выход подключен к первому входу сумматора, второй вход которого соединен с выходом первого блока функционального преобразования, а выход подключен к входу интегратора, выход которого подключен к входам первого, второго и третьего блоков функционального преобразования, а также является выходом устройства.
В основу работы устройства положены следующие теоретические выводы.
Динамический нелинейный объект задан следующим дифференциальным уравнением:
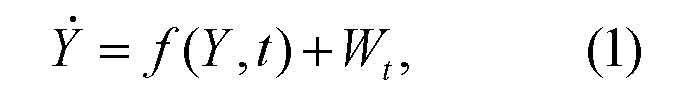
где f(Y,t) - известная нелинейная функция,
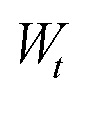 - случайный шум с неизвестной плотностью вероятности из класса плотностей с конечными вторыми моментами [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.],
- случайный шум с неизвестной плотностью вероятности из класса плотностей с конечными вторыми моментами [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.],
и наблюдается нелинейным измерителем:
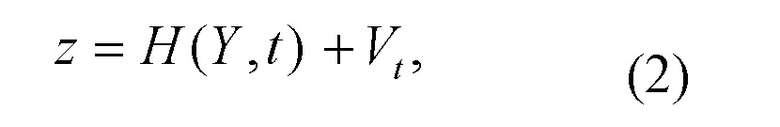
где z - выходной сигнал наблюдателя,
H(Y,t) - известная нелинейная функция,
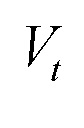 - помеха измерения с неизвестной плотностью вероятности из априори определенного класса [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.].
- помеха измерения с неизвестной плотностью вероятности из априори определенного класса [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.].
Традиционная дифференциальная схема оценивания, учитывающая динамику наблюдаемой переменной (1) и лежащая в основе практически всех алгоритмов фильтрации [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.], имеет вид:
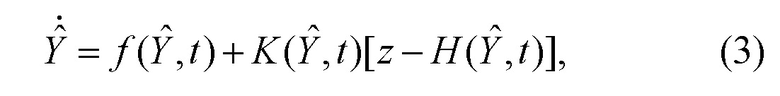
где 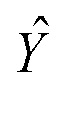 - оценка переменной Y,
- оценка переменной Y,
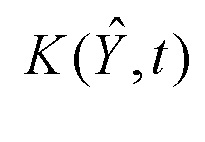 - нелинейная функция, определяемая тем или иным типом используемого фильтра.
- нелинейная функция, определяемая тем или иным типом используемого фильтра.
Т.к. в рассматриваемом случае для помехи наблюдения определен только класс распределения, оценку 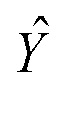 переменной Y следует искать как гарантирующую минимальную ошибку в наиболее неблагоприятной ситуации, определяемой заданным классом вероятностного распределения. Исходя из этого, определение функции
переменной Y следует искать как гарантирующую минимальную ошибку в наиболее неблагоприятной ситуации, определяемой заданным классом вероятностного распределения. Исходя из этого, определение функции 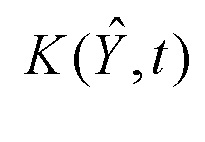 будем осуществлять из условия обеспечения робастности оценки
будем осуществлять из условия обеспечения робастности оценки 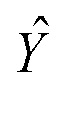 , т.е. минимизации ошибок оценивания при заданном наиболее неблагоприятном классе вероятностного распределения помехи измерения.
, т.е. минимизации ошибок оценивания при заданном наиболее неблагоприятном классе вероятностного распределения помехи измерения.
В качестве исходной формы оптимизируемого функционала рассмотрим традиционный функционал 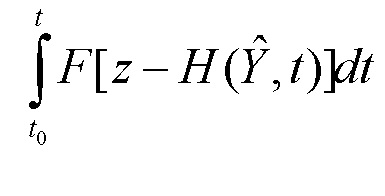 , гарантирующий максимальную точность оценивания при наиболее неблагоприятном распределении помехи.
, гарантирующий максимальную точность оценивания при наиболее неблагоприятном распределении помехи.
Выбор функции F в данном функционале определяется видом наиболее неблагоприятного вероятностного распределения помехи измерения. Анализ всех известных видов подынтегральной функции F показывает [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.], что данная функция является неотрицательно определенной для всей области определения аргумента. Это обстоятельство обеспечивает возможность перехода от минимизации традиционного функционала к минимизации функции 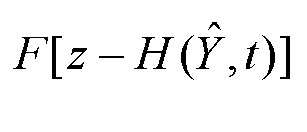 и с учетом принадлежности плотности вероятности шума Wt классу плотностей распределений с ограниченными средними квадратами, позволяет окончательно сформировать минимаксный критерий оптимальности J в виде:
и с учетом принадлежности плотности вероятности шума Wt классу плотностей распределений с ограниченными средними квадратами, позволяет окончательно сформировать минимаксный критерий оптимальности J в виде:
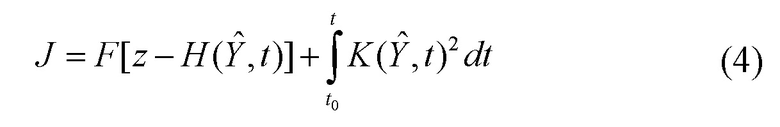
Для дальнейшего определения функции 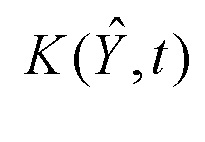 используем тот известный факт, что при неотрицательно определенной критериальной функции для обеспечения ее минимального значения в каждый момент времени достаточно, чтобы производная ее по времени, взятая с обратным знаком, имела максимум [Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975. 432 с.]. В рассматриваемом случае это позволяет получить следующее условие для определения функции
используем тот известный факт, что при неотрицательно определенной критериальной функции для обеспечения ее минимального значения в каждый момент времени достаточно, чтобы производная ее по времени, взятая с обратным знаком, имела максимум [Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975. 432 с.]. В рассматриваемом случае это позволяет получить следующее условие для определения функции 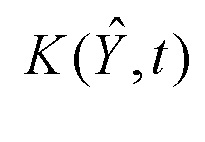 :
:
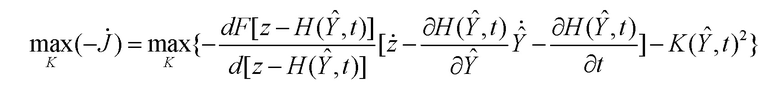
Данное условие с учетом уравнения оценки (3) приводится к виду:
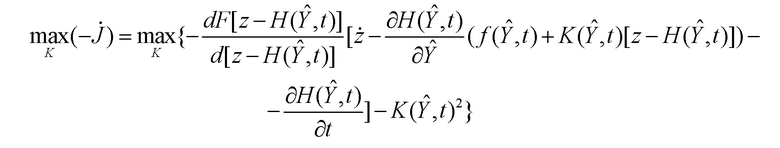
Вводя для сокращения записи, следуя [Справочник по теории автоматического управления / Под ред. Красовского А.А. М.: Наука. Гл. ред. физ. -мат. лит. 1987. 712 с.], обозначение 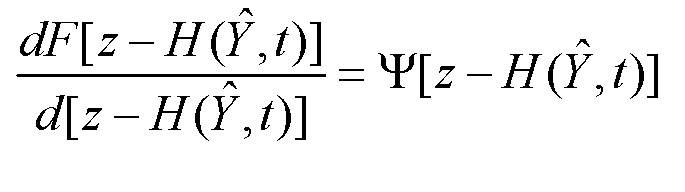 , из последнего условия имеем уравнение:
, из последнего условия имеем уравнение:
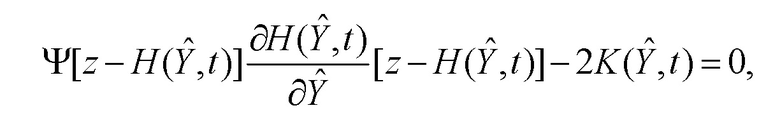
позволяющее сразу определить искомую функцию 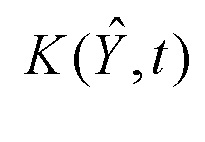 :
:
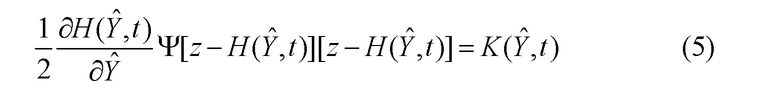
С учетом (5) уравнение робастной оценки (3) принимает вид:
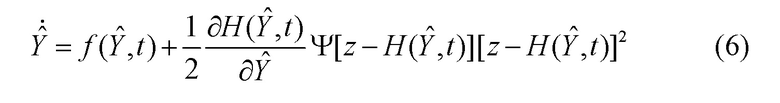
Объединяя функциональные преобразования 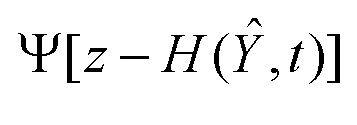 и
и 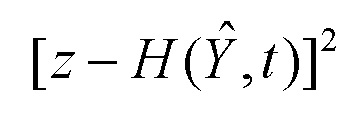 в единое функциональное преобразование
в единое функциональное преобразование 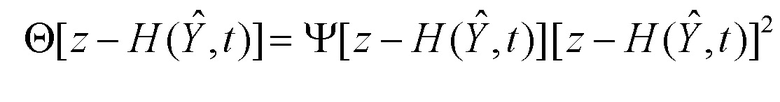 , окончательно имеем:
, окончательно имеем:
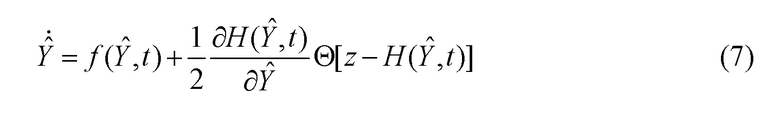
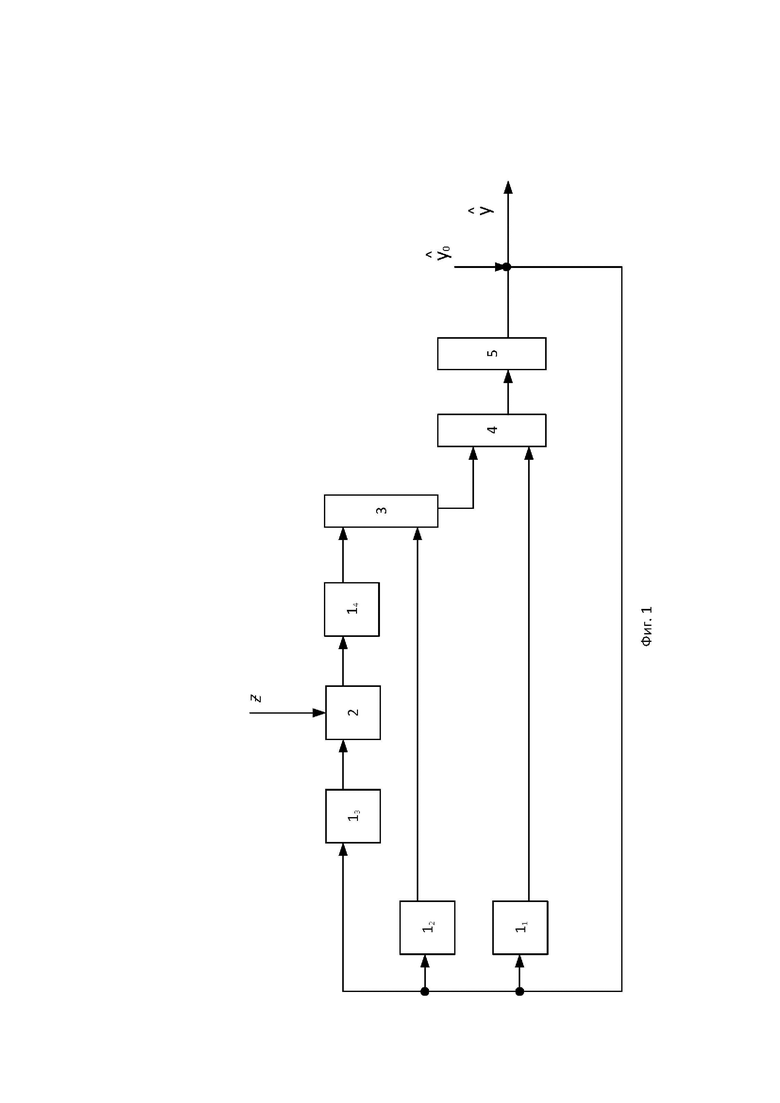
Функциональная схема робастного стохастического фильтра (далее - устройства) приведена на фиг.1.
Устройство содержит:
- первый 11 блок функционального преобразования 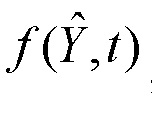 ,
,
- второй 12 блок функционального преобразования 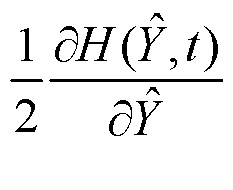 ,
,
- третий 13 блок функционального преобразования 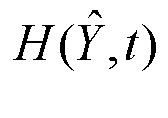 ,
,
- четвертый 14 блок функционального преобразования 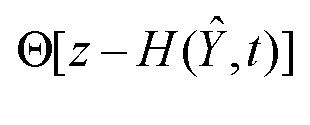 ,
,
- блок вычитания 2,
- умножитель 3,
- сумматор 4,
- интегратор 5.
Входом устройства является вход уменьшаемого блока вычитания 2. Вход вычитаемого блока вычитания 2 соединен с выходом третьего блока функционального преобразования 13, а выход подключен к входу четвертого блока функционального преобразования 14. Выход четвертого блока функционального преобразования 14 подключен к первому входу умножителя 3, второй вход которого соединен с выходом второго блока функционального преобразования 12, а выход подключен к первому входу сумматора 4. Второй вход сумматора 4 соединен с выходом первого блока функционального преобразования 11, а выход подключен к входу интегратора 5. Выход интегратора 5 подключен к входам первого 11, второго 12 и третьего 13 блоков функционального преобразования, а также является выходом устройства.
Устройство работает следующим образом.
В начальный момент времени с выхода интегратора 5 вводится начальное значение оценки 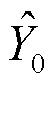 , которое поступает на входы первого 11, второго 12 и третьего 13 блоков функционального преобразования. Одновременно с входа устройства на вход уменьшаемого блока вычитания векторов 2 поступает сигнал измерения z. Т.к. на вход вычитаемого блока вычитания 2 с выхода третьего блока функционального преобразования 13 поступает сигнал
, которое поступает на входы первого 11, второго 12 и третьего 13 блоков функционального преобразования. Одновременно с входа устройства на вход уменьшаемого блока вычитания векторов 2 поступает сигнал измерения z. Т.к. на вход вычитаемого блока вычитания 2 с выхода третьего блока функционального преобразования 13 поступает сигнал 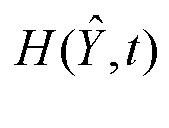 , то с выхода блока вычитания 2 сигнал невязки
, то с выхода блока вычитания 2 сигнал невязки 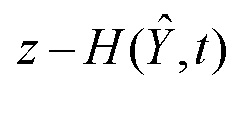 поступает на вход четвертого блока функционального преобразования 14, с выхода которого сигнал
поступает на вход четвертого блока функционального преобразования 14, с выхода которого сигнал 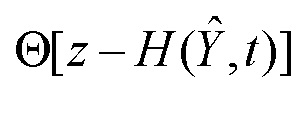 поступает на первый вход умножителя 3. На второй вход умножителя 3 поступает сигнал
поступает на первый вход умножителя 3. На второй вход умножителя 3 поступает сигнал 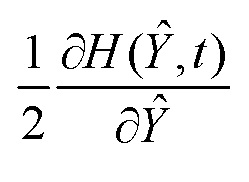 с выхода второго блока функционального преобразования 12. На выходе умножителя 3 формируется сигнал
с выхода второго блока функционального преобразования 12. На выходе умножителя 3 формируется сигнал 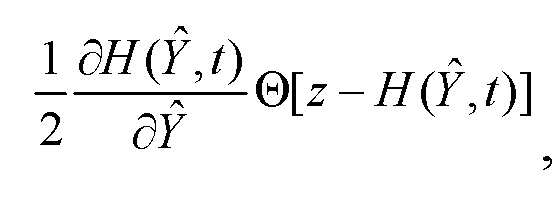 который поступает на первый вход сумматора 4, на второй вход которого поступает сигнал
который поступает на первый вход сумматора 4, на второй вход которого поступает сигнал 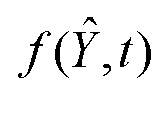 с выхода первого блока функционального преобразования 11. С выхода сумматора 4 сигнал
с выхода первого блока функционального преобразования 11. С выхода сумматора 4 сигнал 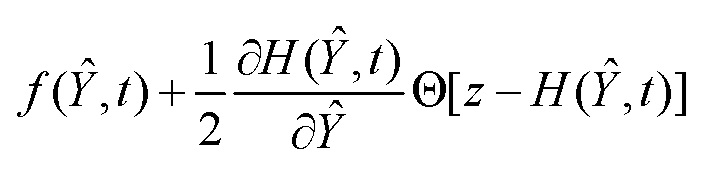 поступает на вход интегратора 5, с выхода которого снимается сигнал текущей робастной оценки
поступает на вход интегратора 5, с выхода которого снимается сигнал текущей робастной оценки 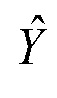 , который поступает далее на входы первого 11, второго 12 и третьего 13 блоков функционального преобразования, а также на выход устройства.
, который поступает далее на входы первого 11, второго 12 и третьего 13 блоков функционального преобразования, а также на выход устройства.
Предложенный робастный стохастический фильтр повышает точность фильтрации за счет устойчивости к неопределенным возмущениям наблюдаемого объекта и помехам измерения, а также обеспечивает сокращение аппаратных затрат за счет простой конструктивной реализации фильтра.
| название | год | авторы | номер документа |
|---|---|---|---|
| Робастный стохастический фильтр | 2021 |
|
RU2755677C1 |
| Робастный дискретный стохастический фильтр | 2023 |
|
RU2804256C1 |
| РОБАСТНЫЙ ДИСКРЕТНЫЙ СТОХАСТИЧЕСКИЙ ФИЛЬТР | 2024 |
|
RU2830681C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
| Способ позиционирования подвижного транспортного объекта | 2023 |
|
RU2811665C1 |
| Фильтр Калмана | 1987 |
|
SU1385265A1 |
| АДАПТИВНЫЙ ФИЛЬТР ДЛЯ ОЦЕНИВАНИЯ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ | 1993 |
|
RU2110883C1 |
| Субоптимальный фильтр для оценки параметра случайного процесса | 1989 |
|
SU1619307A1 |
| Адаптивное фильтрующее устройство | 1987 |
|
SU1436271A1 |
| Стохастический фильтр | 1989 |
|
SU1675905A1 |
Изобретение относится к области вычислительной техники. Технический результат заключается в повышении точности фильтрации нелинейных динамических процессов при наличии шумов наблюдаемого объекта и помех измерения с неизвестными вероятностными распределениями. Технический результат достигается за счет робастного стохастического фильтра, содержащего сумматор, блок вычитания, интегратор, умножитель и четыре блока функционального преобразования. 1 ил.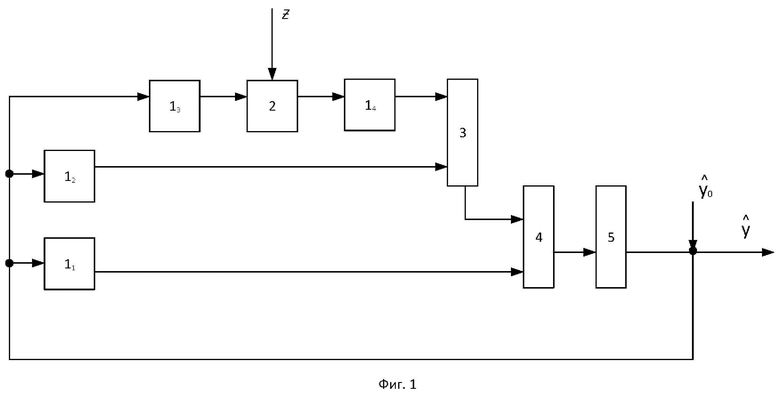
Робастный стохастический фильтр, содержащий сумматор, блок вычитания, интегратор, умножитель, отличающийся тем, что в него введены четыре блока функционального преобразования, входом устройства является вход уменьшаемого блока вычитания, вход вычитаемого которого соединен с выходом третьего блока функционального преобразования, а выход подключен к входу четвертого блока функционального преобразования, выход которого подключен к первому входу умножителя, второй вход которого соединен с выходом второго блока функционального преобразования, а выход подключен к первому входу сумматора, второй вход которого соединен с выходом первого блока функционального преобразования, а выход подключен к входу интегратора, выход которого подключен к входам первого, второго и третьего блоков функционального преобразования, а также является выходом устройства.
| Робастный дискретный стохастический фильтр | 2023 |
|
RU2804256C1 |
| Робастный стохастический фильтр | 2021 |
|
RU2755677C1 |
| СТОХАСТИЧЕСКИЙ ФИЛЬТР | 1992 |
|
RU2050590C1 |
| Способ адаптивной фильтрации | 2022 |
|
RU2782955C1 |
| Изложница с суживающимся книзу сечением и с вертикально перемещающимся днищем | 1924 |
|
SU2012A1 |
Авторы
Даты
2024-09-18—Публикация
2024-04-06—Подача