Изобретение относится к системам автоматического регулирования и управления, предназначено для высококачественного вьщеления полезного сигнала из аддитивной смеси сигнала и помехи.
Известен оптимальный дискретный фильтр, позволяющий повысить качество систем автоматического управт ления при воздействии на них аддитивной смеси сигнала и шума lj .
Наиболее близким к предлагаемому является дискретньА фильтр, содержащий первый корректирующий блок и последовательно соединенные блок задержки, блок экстраполяции, блок - обратной связи и первый элемент сравнения 2j .
Недостатком известного фильтра является то, что будучи синтезирован из условий оптимальности, он не обеспечивает высококачественного воспроизведения полезного сигнала при наложенных на него ошибках в случае отсутствия возмущающего шума
Цель изобретения - повьшение точности воспроизведения полезного сигнала при наложенных на него ошибках измерение в случае отсутствия возмущающего Шума.
Поставл енная цель достигается тем, что в дискретный фильтр введены компенсационный фильтр, второй элемент сравнения, первый и второй сумматоры и второй корректирующий блок,вход которого соединен с выходом первого корректирующего блока и первым входом первого сумматора, вторым входом соединенного с выходом блока экстраполяции и первым входом второго сумматора, второй вход которого соединен с выходом второго корректир5гющего блока, вход компенсационного фильтра подклк чен к второму входу первого элемента сравнения, а выход - к первому входу второго элемента сравнения, вторым входом подключенного к выходу первого элемента сравнения, выходом - к входу Первого блока коррекции, а выход первого сумматора соединен с входом блока задержки.
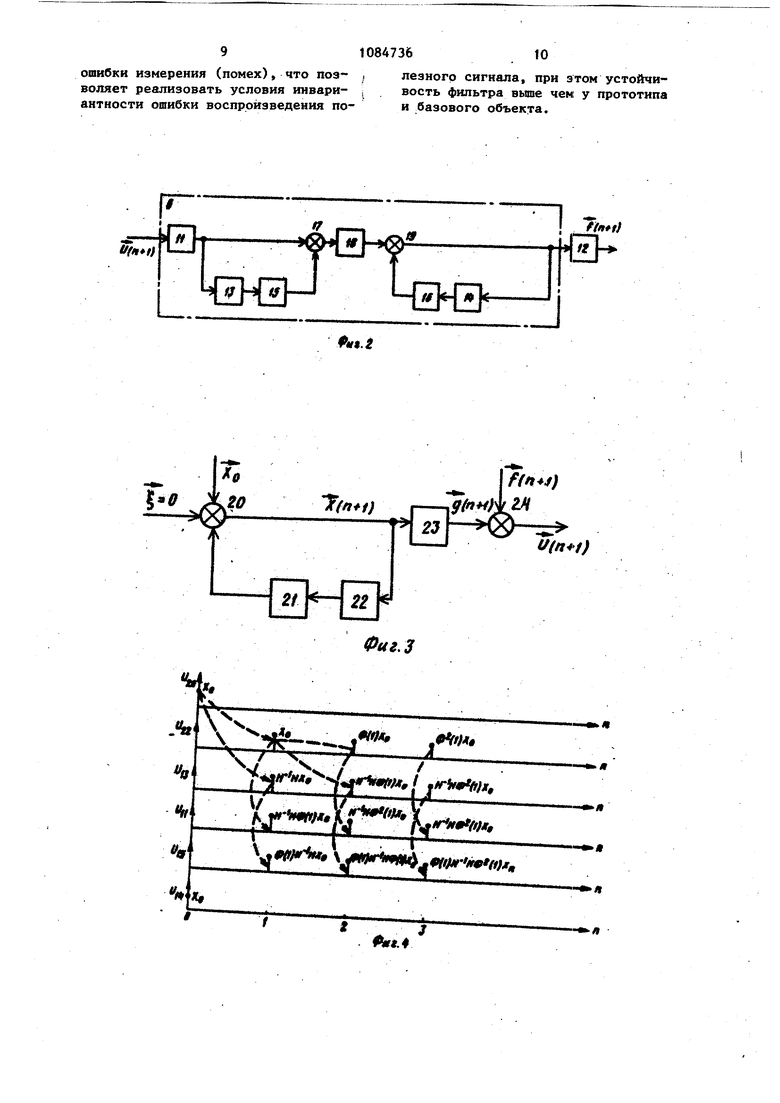
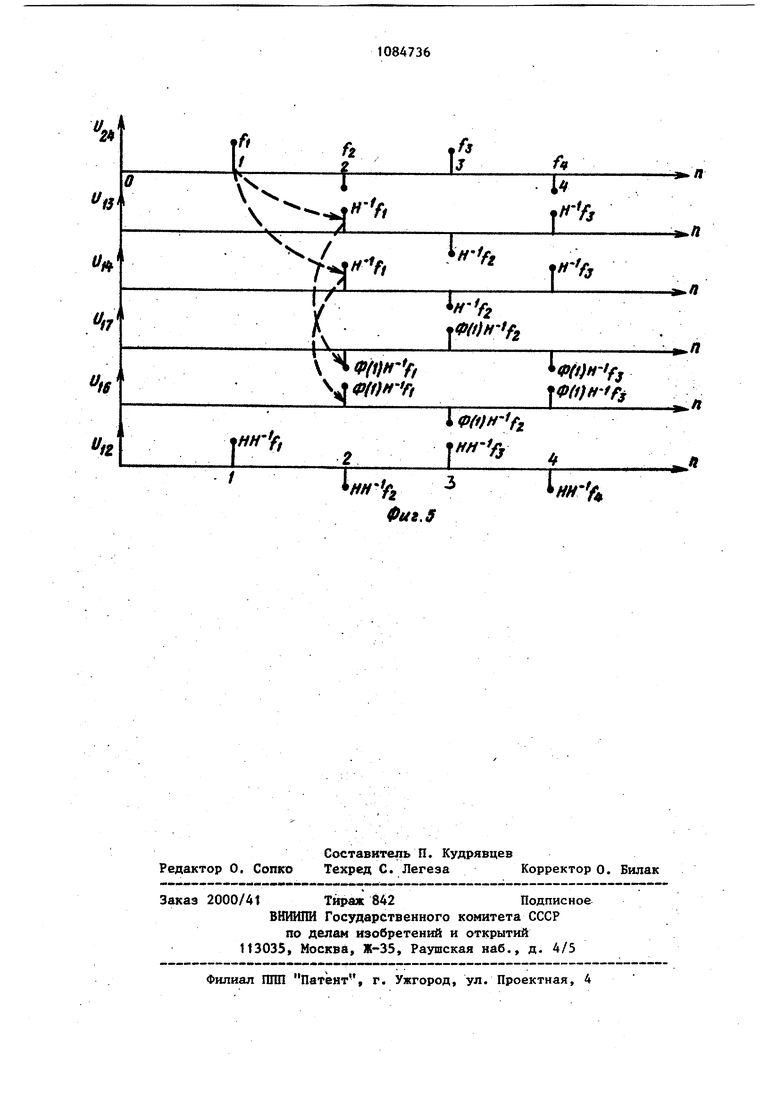
На фиг. 1 изображена структурная схема предлагаемого дискретного фильтраJ йа фиг. 2 - структурная схема компенсационного фильтраi на фиг. 3 - структурная схема модели входного воздействия; на фиг. 4 графики прохождения полезного сигнала на фиг. 5 - графики прохождения помехи (ошибок измерения).
Дискретный фильтр содержит первый (сорректируклций блок 1, блок 2 задержки, блок 3 экстраполяции, блок 4 обратной связи, первый элемент 5 сравнения, компенсационный фильтр 6, второй элемент 7 сравнения, первый 8 и второй 9 сумматоры, второй корректирующий блок 10. Блоки 1,3,4, 10 описьгаа отся матрицами передачи К, К, К, соответственно, а блок 2 - оператором задержки Е
На фиг. 2 изображена матричная структурная схема компенсационного фильтра, синтезированная на основе X свойства симметрии по отношению к
модели входного воздействия, изображенной на фиг. 3. Здесь - вектор возмущающего шума (ои полагается равным нулю), Хд, х ,g ,-i ,3 .векторы начального состояния, сос тояния, полезного воздействия, ошибок Измерения и входного воздействия фильтра соответственно. Компенсационный фильтр 6 тшеет следующие I блоки: блоки 11 и 12 наблюдения с матрицами И и Н соответственно, блоки 13 и 14 задержки, блоки 15 и 16 экстраполяции с матрицей передачи Ф(1), элемент 17 сравнения, блок 18 передачи с коэффициентом
К« 0
в момент времени п 0 и
Ч8
в моменты п О, сумматор 19, сумматор 20, блок 21 экстраполяции с матрицей передачи Ф(1), блок 22 задержки, блок 23 наблюдения с матрицей И, сумматор 24.
Из сравнения схем фиг. 2 и фиг.З следует, что блоки 11, 13, 15 и 17 компенсационного фильтра симметричны (относительно точки п{жложения вектора ошибок измеренияi (n+l) соответствующим блокам 23, 22, 21 и 2 модели входного воздействия. Кроме того, имеет место обращение математических операций в блоках компенсационного фильтра по отношению к соответствующим блокам математической модели входного воздействия (суммирование в блоке 20 и вычитание в элементе 17, прямое Н преобразование в блоке 23 и обратное ему преобразование блоке 11).
На фиг. 4 представлены графики полезных сигналов на выходах блоков модели и компенсационного фильтра. из которьрс видно, что полезный сигнал на выходе элемента 17 сравнения всюду равен нулю, кроме начального момента времени Л 0, Это объясняется тем, что экстраполятор блока 1 точно такой же как и экстраполятор блока 21, а матрицы блоков 23 и 11 взаимно обратны. На фиг. 5 показаны графики ошибок измерения (помехи) на выходах блоков компенсационного фильтра, иллюстрирующие порядок прохождения ошибок измерения , 2 ,. через блоки компенсационного фильтра. Устройство работает следующим об разом. . Входной сигнал фильтра U (n+l), представлякшрШ собой аддитивную смесь полезного сигнала(и+1) и ошибок измерения (п+1), поступает на элемент 5 сравнения и компенсационный фильтр 6. Сигнал невязки AuCn- l) с выхода элемента 5 сравнения и выходной сигнал компенсационного фильтра 6, представляющий собой вектор ошибок измерения (n+ вычитаются в элементе 7 сравнения, выходной сигнал которого, пропорци ональный полезному сигналу через корректирующий блок 1 поступает на сумматор 8 и второй корректирующий блок 10. С выхода сумматора 8 сигнал через последовательно соединенные блок 2 задержки и блок 3 экстраполяции поступает на второй вход этого сумматора, а также на сумматор 9 и через блок 4 обратной связи на элемент 5 сравнения. Выходной сигнал фильтра снимается с су№1атЬра 9, на второй вход которого поступает сигнал с выхода бло ка 10. Покажем, что в предлагаемом дис кретном фильтре действительно обес печивается высококачественное воспроизведение полезного сигнала при наложенных на него ошибках измерен в случае отсутствия возмущающего шума и что устойчивость данного фильтрд , чем у прототипа. Учитывая, что полезное воздействие и ошибки измерения связаны аддитивным оператором, можно подой ти к задаче построения эффективног дискретного фильтра с других позиций. На основе свойства симметрии при известной модели полезного сиг нала можно синтезировать компенсационный фильтр для ослабления вектора ошибок измерения. Тогда становится возможным синтез д полннтельного корректирующего устройства из условия инвариантности ошибки от полезного сигнала. В момент П О коэффициент блока 18 равен О и запись полезного сигнала х в блок 14 задержки не производится. В момент времени производится запись помехи -1 в блок 13 и в блок 14 (так как коэффициент блока 18 уже равен 1) и, кроме Toroi- эта помеха проходит на вы- . ход компенсационного фильтра без изменений (так как - единичная матрица). В следую1ф1й момент времени происходит компенсация за счет изменения полярности помехи в элементе 17 сравнения, при этом помеха in проходит на щыход фильтра без изменений и т.д. В результате работы компенсационного фильтра на его выходе, начиная с момента времени ri -I, будет только ошибка измерения (помеха) , а полезный сигнал отсутствует. Включение компенсационного фильтра 6 в схему дискретного фильтра (фиг.) позволяет полностью устранить, наличие помех в сигнале невязки &U что дает возможность произвести расчет второго корректирующего блока 10 из (УСЛОВИЙ инвариантности. С этой целью из структурной схемы (фиг. 1) найдем сигнал Х(и+1). Х,(«40-КвХ,(п+1)Е-Ч|С,нх{п44))Г1..(1) Откуда X,tnt).,K4K3E-7XHxUM). (2) Вводя обозначение ,1С4цг -..:у Il- 3 получим следующие вьфажения для сигнала Х- (п+1) ).НЁ-Х(пи);(3) Найдем сигнал X(ifj +1) i ХДп4)К,,«лЛи 1И г ,HX(miVk4kirV,(. Kq Н, то с учетом (2) Так как получим ХэМ-,оК,К4 1-КгЕЧ- н1х П4-дУ (4) 51 Складывая выражения (3) и (4) име емследующее выражение для оценки полезного сигнала, снимаемого с сумматора 9, Х(г иУ-Х2(пмНХ1, К,о):Л4-К оКлК41 зЕ - н х(иИ). Из (5) следует, что выходной сигнал фильтра Й(п+1) будет равен входному полезному сигналу Х(п+1) в том случае, если выражение в фигурных скобках будет равно 1.. Это произойдет в том случае, если матрица корректирующего блока 10 будет иметь ви 10 , 6) В отличие от оптимального фильтра Калмана здесь не существует жестких ограничений на выбор элементов матрицы Кд. Поэтому корректирующий блок 1 на фиг. 1 может быть выбран из условий устойчивости замкнутого контура управления, образованного блоками 1-8. Существующие алгоритмы настройки корректирующего блока 1 (т.е. устройства с переменными параметрами) рассчитываются из условий оптимальности фильтра, а поэтому не обеспечивают его устойчивости, вслед ствие чего реальные процессы, протекающие в системах обработки радиоэлектронной информации, имеют тенденцию к расходимости. Эффективность предлагаемого дискретного фи-ттьтра перед известным, в качестве которого выбран дискретный фильтр с постоянными параметрами (памятью) (1), покажем на конкретном примере. Пусть полезное воздействие X(t) в дискретном времени (t ц) описывается полиномом первой степени )((nHUxU- T, где Т - период дискретности Х(п-1) - скорость изменения полезного воздействия . Вводя переменные состояния х/п)- (п), ) х(г)) получим cлeдyющ ie уравнения экстраполяции дискретного фильтра Х(И,Х, (п-1) f ) Т, XjCn) X(n-l). Откуда матрица экстраполяции при мет вид 1 т 10 lj Полагая, что измеряется (наблюдается) одно состояние Х.(п), получим матрицу наблюдения И l о (8) И поэтому весовая матрица К дискретного фильтра вид -ш где ОС и Д - постоянные параметры. Покажем, что на выходе компенсационного фильтра 6 (фиг. 1) будет вьщеляться помеха i . На фиг. 5 для момента времени И 1 имеем U«-HH-4,,-,, .v,.«-.,.,, ibiol o ii -™...f,. Так как значение помехи на выходе блоков 16 и 17 одинаковы и противоположны по знаку, то их сумма равна нулю, и в момент времени Ц 2 на выходе компенсационного фильтра значение помехи равна i. Таким образом, компенсационный фильтр 6 производит вьщеление помехи i () при И 1, 2, С другой стороны, согласно графиков фиг. 4 полезный сигнал 5( на выходах блоков 11 и 15 в момент времени ц 1 соответственно примет ид - . ,, где XQ и Х02 величины полезного воздействия и его скорости в начальньй момент времени. Отсюда видно, что недокомпенсация полезного сигнала на выходе элемента 17 сравнения равна вектору IX Т1 0,2 . Нетрудно убедиться, что веО J личина недокомпенсации остается той же самой и при п 1. Пройдя блоки И9, 16, 14 и 12 эта недокомпенсация становится скалярной величиной где п 1,,... равной virXo2 Так как в элементе 7 сравнения происходит ее вьтитание из сигнала невязки ли , то с целью сохранения и формации о полезном сигнале (полезной информации на выходе элемента 7 ,сравнения) необходимо матрицу блока 4 выбрать равной 4 , где П 1,2,... . Тогда по цепи компенсирующей обратной связи на элемент 5 сравнения будут поступать дополнительные сигналы, равные пТХ, что приведет к устранению недокомпенсации. . Следовательно, сигнал невязки ЛU .на выходе элемента 7 сравнения будет очищен от помех,,т.е. iiU - X,- -5 , где Xj - истинное значение полезного сигнала; - экстраполированное значе ние полезного сигнала, (значение сигнала на выходе блока 4 без дополни тельного сигнала ТХ02) J 6g ошибка экстраполяции. Согласно условия (6) элементы матрицы К должны быть обратны элементам матрицы . Поэтому с н которым приближением выберем Ilk о 1 о 1((JУчитывая (9) и (10), найдем сиг нал Х на выходе блока 1, имеем .«С iUl Г ot, ЕэТ р/т J С учетом (11) получим сигнал X, на выходе блока 10 й{об аПГо еэ Г еэ о Из схемы фиг. 1 получим вектор оцениваемых параметров X как сумму векторов Х2иХ2,т.ё. .е,. - - - Xx-l Заменяя Е на ( согласно (10 получим (14 ,,Т Г х,-х,э 1 -.Гх. LXzJ ZjU23J4l|TCX,-X,,)j Хл X,,M|T(X,-X,,)J. (.15) Из выражения (15) видно, что оценка Х полезного сигнала равна истинному значению Х самого полезного сигнала. Рассмотрим оценку J, скорости измерения полезного воздей ствия. Из (15) инее/ 2 Х„ДСХ,-Х,). (16) Анализ выражения (16) произвеем для момента оценивания И 1, поагая известными начальное значение Q полезного воздействия и Х.у скорости его изменения. Тогда .1..;.., Т . S °-i т Так .как оценка полезного сигнала равна истинному значению самого полезного сигнала, т.е. Х Х(0) ,то. XK,,i.X,W. (.7, Из (17) видно, что оценка Х2 скорости изменения полезного сигнала равна истинному значению Х2 скороети полезного сигнала. Запаздьтание во времени на период дискретности Т при оценке скорости объйсняется не полной наблюдаемостью всех компонент полезного сигнала X(i) и присуще как прототипу, так и базовому объекту. Следовательно, ошибка в воспроизведении полезного сигнала и его скорости изменения в предлагаемом дискретном фильтре равна нулю (т.е. Х Х, л, тогда как в прототипе эти ошибки не равны нулю и определяются диагональными элементами матрицы ошибок фильтрации. Преимущество предлагае юго дискретного фильтра перед известными раскрывается при анализе ошибок оценивания для условий рассмотренного примера. Таким образом, в предлагаемом дискретном фильтре в отсутствии возмущающего шума ( 0, фиг. 3) обеспечивается полная компенсация ошибки измерения (помех), что поз , воляет реализовать условия инвари- , антиости ошибки воспроизведения полезного сигнала, при этом устойчивость фильтра выше чем у прототипа и базового объекта.



| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АДАПТИВНОГО СОПРОВОЖДЕНИЯ РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2018 |
|
RU2679598C1 |
| АДАПТИВНЫЙ СЛЕДЯЩИЙ ИЗМЕРИТЕЛЬ | 2012 |
|
RU2492506C1 |
| Устройство для экстраполяции | 1974 |
|
SU570901A1 |
| ДИСКРЕТНАЯ СИСТЕМА ОЦЕНИВАНИЯ | 2007 |
|
RU2398258C2 |
| ИНЕРЦИАЛЬНО-РАДИОНАВИГАЦИОННАЯ СИСТЕМА | 2013 |
|
RU2539846C1 |
| Дискретная система оценивания | 1989 |
|
SU1727110A1 |
| ЦИФРОВАЯ СЛЕДЯЩАЯ СИСТЕМА | 2010 |
|
RU2444038C1 |
| Режекторный фильтр | 1978 |
|
SU803104A1 |
| СПОСОБ ОЦЕНКИ ПАРАМЕТРОВ ТРАЕКТОРИИ ОБЪЕКТА | 2016 |
|
RU2610831C1 |
| Линейный корректор коррелированного сигнала | 1984 |
|
SU1243136A1 |

ДИСКРЕТНЫЙ ФИЛЬТР, содержащий первый корректирующий блок и последовательно соединенные блок saf держки, блок экстраполяции, блок обратной связи и первый элемент Сравнения, отличающийся тем, что, с целью повышения точности воспроизведения полезного сигнала при наложенных на него ошибках измерения в случае отсутствия возмущающего шума, в него введены компенсационный фильтр, второй элемент сравнения, первый и второй сумматоры и второй корректирующий блок, вход которого соединен с выходом первого корректирующего блока и с первым входом первого сумматора, вторым входом соединенного с выходом блока экстраполяции и первым входом второго сумматора, второй вход которого соединен с выходом второго корректирующего блока, вход компен.сационного фильтра подключен к второму входу первого элемента сравнения, а выход - к первому входу второго элемента сравнения, вторым (Л входом подключенного к выходу первого элемеита сравнения, выходом к входу первого корректирующего блока, а выход первого сумматора соединен с входом блока задержки. X) 4 а
f(n4t}
Jfn)±i
ff()
Фаг.З ftHft)
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Кузьмин С.З | |||
| Основы теории цифровой обработки радиолокационной информации | |||
| М., Советское радио | |||
| ПРИБОР ДЛЯ ЗАПИСИ И ВОСПРОИЗВЕДЕНИЯ ЗВУКОВ | 1923 |
|
SU1974A1 |
| Передвижная комнатная печь | 1922 |
|
SU383A1 |
| Прибор для нанесения на чертеж точек при вычерчивании углов и треугольников | 1922 |
|
SU392A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Медич Дж | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Гидравлическая или пневматическая передача | 0 |
|
SU208A1 |
Авторы
Даты
1984-04-07—Публикация
1982-07-05—Подача