VI
ю VI




| название | год | авторы | номер документа |
|---|---|---|---|
| ДИСКРЕТНАЯ СИСТЕМА ОЦЕНИВАНИЯ | 2007 |
|
RU2398258C2 |
| Экстраполятор | 1990 |
|
SU1837317A1 |
| СИСТЕМА ПАССИВНОЙ ЛОКАЦИИ ДВИЖУЩЕГОСЯ ОБЪЕКТА | 1991 |
|
RU2050557C1 |
| ТЕЛЕВИЗИОННЫЙ КООРДИНАТОР | 1987 |
|
SU1521242A1 |
| СПОСОБ АДАПТИВНОГО СОПРОВОЖДЕНИЯ РАДИОЛОКАЦИОННЫХ ЦЕЛЕЙ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2018 |
|
RU2679598C1 |
| ТЕЛЕВИЗИОННЫЙ АДАПТИВНЫЙ ИЗМЕРИТЕЛЬ КООРДИНАТ | 1988 |
|
SU1623536A1 |
| Устройство для экстраполяции | 1983 |
|
SU1107137A1 |
| Устройство обнаружения и определения координат объекта на изображении | 1990 |
|
SU1737755A1 |
| Генератор дискретных ортогональных полиномов Кравчука | 1988 |
|
SU1621018A1 |
| Устройство для прогнозирования длительности производственных операций | 1990 |
|
SU1781685A1 |
Изобретение относится к радиотехнике и автоматике и может быть использовано в радиолокации для оптимальной линейной оценки параметров движения летательных аппаратов. Цель изобретения - повышение динамической точности системы. Дискретная система оценивания содержит первый вычитатель 1, блок 2 коррекции, сумматор 3, первый блок 4 задержки, блок 5 экстраполяции, второй 6 и третий 7 вычитатели, второй блок 8 задержки, усилитель 9, счетчик 10, двухканальный мультиплексор 11, компаратор 12; умножитель 13, сумматор 14, элементы 15-17 памяти коэффициентов. Цель изобретения достигается за счет введения элементов и блоков 6-17. 3 ил.
Т Т т cp.i
о
Изобретение относится к радиотехнике и автоматике, в частности может использоваться в радиолокации для оптимальной линейной оценки параметров движения летательных объектов.
Известны дискретные системы оценивания, предназначенные для оценивания параметров движения объектов.
Недостатком систем является отсутствие возможности качественно управлять динамической точностью в переходном режиме.
Известна также дискретная система оценивания, содержащая последовательно соединенные элемент сравнения, блок коррекции, сумматор, блок задержки, блок экстраполяции, блок обратной связи, Данная система имеет возможность оптимально оценивать параметры движения объектов в установившемся режиме. Недостатком данной системы является невысокая динамическая точность в переходном режиме.
Наиболее близкой к предлагаемой является дискретная система оценивания, которая имеет возможность оптимальным образом оценивать параметры движения обьектов в установившемся режиме. Она содержит последовательно соединенные элемент сравнения, блок коррекции, сумматор, блок задержки, блок экстраполяции, выход которого соединен с вторыми входами элемента сравнения и сумматора.
Недостатком данной системы является низкая динамическая точность в переходном режиме.
Цель изобретения - повышение динамической точности системы в переходном режиме.
Поставленная цель достигается за счет введения в известную систему двух вычита- телей, второго сумматора, трех элементов памяти коэффициентов, счетчика, компаратора, усилителя, умножителя, второго блока задержки и двухканальнрго мультиплексора.
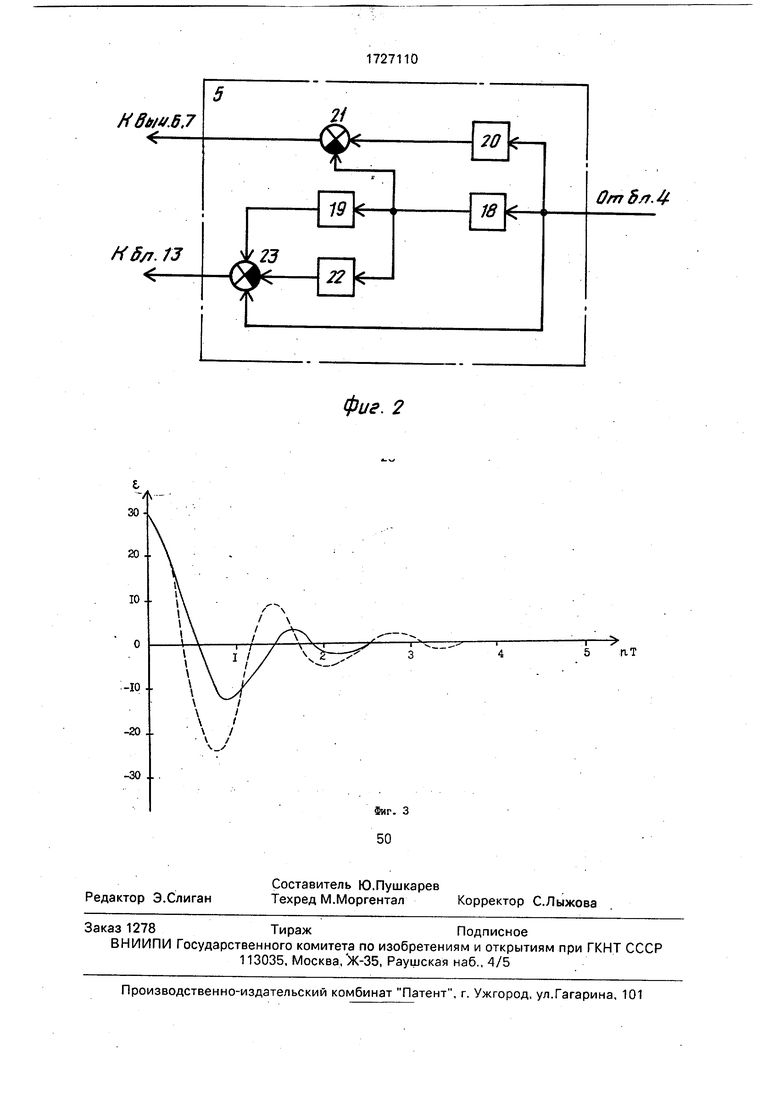
На фиг. 1 изображена структурная схема системы оценивания; на фиг. 2 - структурная схема блока экстраполяции.
Дискретная система оценивания (фиг. 1) содержит вычитатели 1, 6 и 7, блок 2 коррекции, сумматоры 3 и 14, блоки 4 и 8 задержки с операторами задержки , блок 5 экстраполяции, усилитель 9, счетчик 10, двухка- нальный мультиплексор 11, компаратор 12, умножитель 13, элементы 15-17 памяти коэффициентов.
В статическом состоянии система оценивания характеризуется следующими связями: содержит последовательно соединенные вычитатель 1, блок 2 коррекции, сумматор 3, блок 4 задержки, блок 5 экстраполяции. Первый вход вычитателя 1 и выход сумматора 3 являются соответственно информационным входом и выходом дискретной системы оценивания. Кроме того, система оценивания содержит вычитатели 6 и 7, сумматор 14, элементы 15-17 памяти коэффициентов, счетчик 10, компаратор 12, усилитель 9, умножитель 13, блок 8 задерж0 ки и двухканальный мультиплексор 11. Выход вычитателя 1 через последовательно соединенные блок 8 задержки и усилитель 9 подключен к первой группе информационных входов мультиплексора 11, соединенно5 го второй группой информационных входов с выходами элементов 15-17 памяти коэффициентов, адресным входом - с выходом счетчика 10 и первым входом компаратора 12. Первый выход блока 5 экстраполяции
0 подключен к первому входу умножителя 13, соединенного вторым входом с первым выходом мультиплексора 11, а выходом - с первыми входами сумматора 14 и вычитателя 6. Второй выход блока 5 экстраполяции
5 подключен к первому входу вычитателя 7 и второму входу вычитателя 6, соединенного выходом с вторым входом вычитателя 1. Второй выход мультиплексора 11 подключен к второму входу сумматора 14, соеди0 ненного выходом с вторым входом вычитателя 7, выход которого подключен к второму входу сумматора 3. Второй вход компаратора 12 соединен с шиной задания числа шагов, а выход - с информационным
5 входом счетчика 10, тактовый вход которого является тактовым входом дискретной системы оценивания.
При работе устройства возможны два режима работы: переходный и установив0 шийся.
В установившемся режиме устройство работает следующим образом.
Входной сигнал системы Х(п), представляющий собой сумму детерминированной
5 составляющей mx(n), центрированной случайной составляющей Х(п) и ошибок измерения f(n) (помехи), поступает на первый вход вычитателя 1, на его второй вход подается экстраполированное значение входного
0 сигнала Хэ(п). В установившемся режиме блоки 8-17 системы не работают, поэтому информация на первом входе вычитателя 6 и втором входе вычитателя 7 отсутствует. В этом случае экстраполированное значение
5 входного сигнала Хэ(п), сформированное блоком 5, проходит через вычитатели 6 и 7 без изменений. На выходе вычитателя 1 имеем сигнал невязки U(n), который поступает на блок 2 коррекции. На выходе сумма- тора 3 имеем сигнал оценки Х(п):
X(n) - 2X(n-1)-X(n-2) + K(n) U(n).(1)
Первые два члена в правой части выражения (1) являются сигналом Хэ(п), сформированным блоком 5 экстраполяции. Блок 5 экстраполяции синтезирован на основании известного метода трех полиномов из условия: входное воздействие на систему имеет видо
X(n) mx(n)+ X(n) + f(n),(2)
где mx(n) - детерминированная составляющая задающего воздействия Х(п);
Х(п)-его центрированная случайная составляющая;
f(n)- центрированная возмущающая составляющая (ошибки наблюдения).
Для исключения динамической ошибки в дискретной системе при оценивании координат объекта, описываемого выражением (2), необходимо иметь порядок астатизма v 2, а следовательно из метода трех полиномов определим полиномы
АЈ,п) ао(пХ1-Г12)и В(2,п) Ьо(п)(1-Г12). (3)
Характеристический полином выбираем из условия устойчивости системы.
C(Z,n) а0(п)-2Ьо(п)Г1 + bo(n). (4)
Используя выражение для оценки метода трех полиномов
A(Z,n)
(5)
получим
т
a)-2b0(n)Z%b0(nlzUeM+2t 0(n)Z -b0(
-2
а0(п)-2а0{г ги+а г :a0(hl-b0M
a0(nV2ae(h)2-Vo0(n)
:;U(z}
,отсм (6)
где U(n) - невязка, а ц0),
После преобразования (6) получим выражение для оценки в операторном виде
X(Z) 2X(Z)(Z) +
+U(ZXl-b0(n)) X3(Z) + +U(Z)(1-bo(rO),
(7)
где X3(Z) 2X(Z)(Z) - экстраполированное значение координаты;
0
5
0
5
U(ZX1-bo(n)) U(Z)K(n) - корректировочное значение.
Блок 5 экстраполяции, структурная схема которого изображена на фиг. 2, содержит блоки 18 и 19 задержки с оператором задержки , усилители 20 и 22 с коэффициентами усиления два и вычитатели 21 и 23.
На основании проведенного синтеза уравнения (7) построена часть блока 5, включающая в себя блок 18 задержки, усилитель . 20, вычитатель 21. Эта часть блока 5 используется устройством при работе как в установившемся, так и в переходном режиме.
Блоки 19, 22 и 23 используются устройством при работе только в переходном режиме.
Входным сигналом для блока 5 экстраполяции является сигнал с выхода блока задержки Х(п-1). Сигнал с первого выхода блока 5 поступает на первый вход умножителя 13, а сигнал с второго выхода в виде Хэ(п) - на первый вход вычитателя 7 и на второй вход вычитателя 6, через которые поступает соответственно на вторые сумматора 3 и вычитателя 1. Сигнал Х(п) формируется в виде (1), сигнал невязки U(n) - в следующем виде:
30
U(n) X(n)-2X(n-1) + X(n-2).
(8)
2
35
40
6)
45
50
55
Прежде, чем описывать работу устройства в переходном режиме, необходимо отметить, что в замкнутых системах оценивания, использующих для сглаживания (фильтрации) и управления только одни и те же весовые коэффициенты, существует противоречие между условиями уменьшения флюктуационных ошибок (условиями фильтрации) и условиями повышения динамической точности в переходном режиме. Это противоречие может быть разрешено с помощью введения дополнительных весовых коэффициентов по каналу управления. Тогда можно добиваться высокого качества переходного процесса как по каналу управления, так и по каналу оценивания, не увеличивая при этом флюктуационные ошибки.
В связи с изложенным полиномы A(Z,n), B(Z,n), C(Z,n) представим в виде
A(Z,n) (1-Z 1Al + ai(n)Z 1), B(Z,n) (1-Z-1)a(B0(n) + bi(n)r1,
C(Z,n) 1 + aiM botrOJZ 1 H- bo(n)-2
-2bi(n)Z + bi(n)Z
7-3
(9)
717271108
При оценивании процесса (2) обеспечимПринимая во внимание (12), найдем пе- требуемое качество переходного процессареходную составляющую ошибки в начально критериюный момент времени.
Учитывая, что канал наблюдения описы мин VIMHH + V2MMH + .,(Ю) 5вается выражением по методу трех полино .мов,
где VIMHH мин U2n(1), /2мин мин U2n(2) и
т.д.;и(п) Х(п)-Хэ(п),(15)
Un - переходная составляющая ошибки
наблюдения.10имеем
Для отыскания оптимальных коэффици-
ентов aiopt(n) обратимся к методу трех пол-0(0)п Х(0)-Хэ(0) Х0(0)-0 Х0.
иномов для невязки
Так как в первую часть уравнения (13)
A(Z,nVг, 15входит множитель Х0(п) 0 при п 1, 2, 3,
UЫ-с(2 п) X(п).( )то из данного выражения получим следую4 щие три уравнения:
H((o),.(0,
Из (11) при условии, что20 Ше)п ЧД)(Фо(°)
UtV- V On-eaUfoWJlXjO).
У.М- X еСЛИ (12)Здесь слагаемые, содержание 11П в праl J- ov , если nfO;вой части, образуют свободную составляю25 щую ошибки, а Х0(0) - вынужденную, имеемДля квадратов ошибок имеем
Un(n) C(-i)(Z,n) Un(n) + A(Z,n) X0(n),U Wn l OlnlV hill l Xo (0)F, ,
где полином C(-i)(Z,n) - это полином C(Z,n) 30Ua(2)n,0(0(01 + без свободного слагаемого.+П-2а,(2.еКо(0)2
Следовательно.uU K MMJ C(.,)(Z.n)Un(n)-ijcb(a). ()з) ч ОМЛ Г в Мх оМР,.
A(Z,n) X0(n) иВын(п),Дальнейшее решение задачи основывается на принципе оптимальности Белмана,
есть свободная и вынужденная составляю- согласно которому каждое последующее оп- щие динамической ошибки в переходном тимальное значение коэффициента ai(n) режиме. И та и другая составляющие зави- 40 получается относительно предыдущего со- сят от коэффициентов ai(n), причем проти- стояния, полученного оптимальным обра- воречивым образом. Поэтому существуют зом.
оптимальные значения коэффициентовНа первом шаге оптимизации имеем
aiopt(n), удовлетворяющие критерию (10).
45 2
Для отыскания минимальных значений - U WneV,-MijH{ a(((llJ Х0(01Г VMMH критерия качества I вводятся весовыеrQ с
коэффициенты Г и F по свободной и вынуж-L iv. J J -o I J
денной составляющей соответственно.ЭУ| „, .-i „г ,..лг.)
Из (11) с учетом (12) и (9) получим следу- 50 ЭсЦО Х°l0lt2La|l4l 2beH}JП (,№-2|Р,0. ющее разностное уравнение:
как П + Fi 1, то
- U(n)n -tiU(n-1)n-f2U(h-2)n-f3U(n-3)n +
Х0(п) + ai(n) - 2 X0(n-1) + 1-2ai(n) Х0(п-2) +aiopt(1) 2 Ь0(1) Гт + Fi.(16)
ai(n) Хо(п-З),(13) 55
где Ei ai(n)-2bo(n),Поэтому
h bo(n)-2bi(n),(14)
Рз Ь1(п).U2n(1)opt aiopt(1h2bo(1)j2 Х20(0)Г1 +
aiopt(1)(0)Fi. Второй шаг
О2(йя-V WWH , Ы2ИЬо()2
a,Wa,(e)L М-гад М -20 x5(0)F2,
| eM-2b0(VnpV
od(Vi)
-ea,(2)x)(-2F2)0; opt
а7
г
Третий шаг
B WB-V,-- мин
Q,ClWi«1Q,ft
a,(3)-2b0(3)V(2)
ЗЛмЧ
з
4b«(a)-2bl&OY()0If4b:f3)x02(.af(3)xo2(o)F3
(o((J)-2bbfe)uZ(2)(3))(f(o) ORL , „MuVlftj
Ч fiWV
(18)
В момент включения устройства на вход системы поступает ступенчатое воздейстai(n).
Если полиномы A(Z,n) и B(Z,n) задать в
виде
AM-O-rflVaMz-1;,|
В(г, z-|)(n)b,(n)z-|J +a Wz-1J,
(19)
При выбранных полиномах A(Z,n), B(Z,n), C(Z,n) коэффициент ai(n) не входит в управление. Это приводит к ухудшению ка- 30 вие вида (12), обусловленное априорной не- чества фильтрации. Чтобы снять этот недо- определенностью состояния объекта. Для статок, необходимо в разнице полиномов того, чтобы улучшить качество переходного C(Z,n)-B(Z,n) исключить слагаемые, содер- процесса заранее по формулам (16)-(18), вы- жащие коэффициенты ai(n). Это можно еде- числяются коэффициенты ai(1), at(2), ai(3) и лать лишь в том случае, если полином C(Z,n) 35 записываются в блоки 15-17. Количество и B(Z, N ) включают в себя коэффициенты шагов, равное трем, определяется порядком характеристического полинома при ступенчатом воздействии.
Процесс управления в переходном ре- 40 жиме реализуется устройством при помощи блока 8 задержки, усилителя 9 с коэффициентом усиления bi(n), счетчика 10, двухка- нального мультиплексора 11, компаратора 12, умножителя 13, сумматора 14, элемента 45 15 хранения коэффициента ai(1), элемента
16хранения коэффициента ai(2), элемента
17хранения коэффициента ai(3).
Перед началом работы устройства на второй вход компаратора 12 подается код N
50 числа шагов работы системы в переходном режиме. Для рассматриваемого случая N 3. На вход счетчика 10 поступает последовательность импульсов пТ, синхронная моментам выдачи информации на обработку.
55 Выходные сигналы счетчика 10 поступают на адресный вход мультиплексора 11 (в качестве которого может быть использована, например, микросхема К155КП2). В первом такте коэффициент ai(1) считывается из элемента 15 памяти и проходит через мультито из выражения по методу трех полиномов для C(Z,n)
C(Z,n)
A(z.hV-B(Z.nlF3(2) -Fj(Z)
(20)
найдем выражения для алгоритмов оценивания и управления в переходном режиме. Согласно (20)
C(Z,n)-BZ,n) 1-b0(n)-bi(n)z
,-1
(21)
Поэтому выражение для оценки примет
вид А А лл
X(n) 2X(n-1)-X(n-2)-ai(n)X(n-1) +
,
172711010
.AA
+ 2ai 1(n)X(n-2)-ai(n)X(n-3) +
+K(n)U(n)-bi(n}U(n-1).
Для того, чтобы система была устойчивой, необходимо выполнить условие
-1А
(l-rro+aitn Vl-FsCZ).
10 Здесь выражение для функции F3(z) (программы управления) будет иметь вид
7-3
F3(Z) (2-ai(n) + (2ai(nH)Z -ai(n)Z
15 и, следовательно, алгоритм управления примет вид
20
Хэ(п) 2X(n-1)-X(n-2)-ai(n)X(n-1) + + 2ai(n)X(n-2)-ai(n)X(n-3). (23)
Таким образом, выбор полиномов А и В в соответствии с выражением (19) создает условия для оптимальных переходных про- цессов без нарушения условий фильтрации В переходном режиме устройство работает следующим образом.
В момент включения устройства на вход системы поступает ступенчатое воздействие вида (12), обусловленное априорной не- определенностью состояния объекта. Для того, чтобы улучшить качество переходного процесса заранее по формулам (16)-(18), вы- числяются коэффициенты ai(1), at(2), ai(3) и записываются в блоки 15-17. Количество шагов, равное трем, определяется порядком характеристического полинома при ступенчатом воздействии.
(19)
(20)
(21)
плексор 11 на второй вход умножителя 1Л3, в котором умножается на сигнал Х(п-1)-2Х(п- 2) + Х(п-З), сформированный блоками 18,19 и 20 и вычитателем 23 блока 5. На выходе умножителя 13 формируется сигнал ai(1)X(n-1)-2ai(1)X(n-2) + ai(1)X)n-3). В тоже время по второму каналу мультиплексора 11 поступает сигнал bi(1)U(n-1), сформированный блоками 8 и 9, на второй вход сумматора 14. Информация с выхода умножителя 13 поступает на первый вход сумматора 14 и первый вход вычитателя 6. На выходе сумматора 14 имеем сигнал
ai(1) X (n-1)-2ai(1)X(n-2) + ai(1)X(n-3) + bi(1)U(n-1).
В результате на выходе вычитателя 6 имеем сигнал управления (23), а на выходе вычита- теля 7 сигнал Ал
2X(n-1)-X(n-2hai(1)X(n-1) + 2ai(1)X(n- 2)-ai(1)X(n-3)-bi(1)U(n-1), который принимает участие в формировании сигнала оценки (22). В следующих двух тактах формирование рассмотренных сигналов осуществляется аналогично для коэф- фициентов ai(2), ai(3), bi(2), bi(3). Коэффициент Ы(п) определяется из условий устойчивости системы и в рассматриваемом случае является постоянным, т.е. bi(1) bi(2) bi(3). При достижении счетчиком 10 числа N компаратор 12 вырабатывает сигнал, блокирующий работу счетчика 10. Работа системы в переходном режиме на этом заканчивается. Количество шагов оптимизации N рассчитывается на основе принципов оптимальности Белмана, уравнения (16)- (18).
С целью подтверждения эффективности предлагаемой системы было проведено цифровое моделирование на ЭВМ. Для расчета коэффициентов ai(n) принимались Х0 30 м, Т 0,1 с. Результаты моделирования приведены на фиг. 3, где пунктиром показа- ны ошибки оценки в переходном режиме для системы с ai(n) 0, а сплошной - с использованием ai(n) 0, где коэффициенты ai(n) принимали значение: 2; 0,615; 2 соответственно. Данным значениям соответствуют весовые коэффициенты Г F 0,5.
Анализ результатов моделирования показал, что применение блоков 8-17 позволяет повысить динамическую точность системы в переходном режиме. Время регулирования переходного процесса уменьши0
5
0
5 0 5
0 5 0
5
лось с tp 3,6 с до tp 2,5 с, а перерегулирование - с о 80% до 40%. Ошибка оценки еуменьшилась с 24 м до 12 м. Видно, что для предлагаемого устройства динамическая точность в переходном режиме повысилась в два раза (при заданных условиях), что особенно важно в системах обработки информации, в частности, при выдаче целеуказанной системе оценивания при захвате цели.
Формула изобретения
Дискретная система оценивания, содержащая последовательно соединенные первый вычитатель, блок коррекции, первый сумматор, первый блок задержки, блок экстраполяции, первый вход первого вычитателя и выход первого сумматора являются соответственно информационными входом и выходом дискретной системы оценивания, отличающаяся тем, что, с целью повышения динамической точности системы, в нее введены два вычитателя, второй сумматор, три элемента памяти коэффициентов, счетчик, компаратор, усилитель, умножитель, второй блок задержки и двухканальный мультиплексор, выход первого вычитателя через последовательно соединенные второй блок задержки и усилитель подключен к первой группе, информационных входов двухканального мультиплексора, соединенного второй группой информационных входов с выходами элементов памяти коэффициентов, адресным входом - с выходом счетчика и первым входом компаратора, первый выход блока экстраполяции подключен к первому входу умножителя, соединенного вторым входом с первым выходом двухканального мультиплексора, а выходом - с первыми входами второго сумматора и второго вычитателя, второй выход блока экстраполяции подключен к первому входу третьего вычитателя и второму входу второго вычитателя, соединенного выходом с вторым входом первого вычитателя, второй выход двухканального мультиплексора подключен к второму входу второго сумматора, соединенного выходом с вторым входом третьего вычитателя, выход которого подключен к второму входу первого сумматора, второй вход компаратора соединен с шиной задания числа шагов, а выход - с информационным входом счетчика, тактовый вход которого является тактовым входом дискретной системы оценивания.
фиг. 2
| Гришин Ю.П., Казаринов Ю.М | |||
| Динамические системы, устойчивые к отказам | |||
| М.: Радио, 1985, с | |||
| Способ изготовления электрических сопротивлений посредством осаждения слоя проводника на поверхности изолятора | 1921 |
|
SU19A1 |
Авторы
Даты
1992-04-15—Публикация
1989-11-03—Подача