Изобретение мапшностроенил и .: эовано для моделп я, обработки цетале, верхностями ;:л . 1))1н м: в и с с л е д о т: -1 и и я х 1 I нологиче к1 к пю . обработки np . f
о II- ctiTi H ;ei- .
J-lHr- , rr.llfH
к области
и о ПОЛЬ L Oiieccaиных ПОфир:|1и ь inplii-iep
jiiTTv ill ч 1ПИ)- техi 1) -.- ч rjOI ifiCCt - ТЧ . г и (1 :; ; I о ж Н ЫХ
noBepxHocTeii п - Т--л: й . иостГ
мой поверхности детали;
- - криволинейные (гауссовы) координаты на формообразуемой поверхности детали, ;-лавные радиусы кривизны Н
1А и R гд м г л, могут быть определены как корни квадратного урав-
то
ч



| название | год | авторы | номер документа |
|---|---|---|---|
| Инструмент для обработки криволинейных поверхностей | 1986 |
|
SU1355378A2 |
| Способ автоматизированного формообразования оболочки переменной кривизны обтяжкой листовой заготовки | 2024 |
|
RU2838191C1 |
| Инструмент для упрочнения деталей,ограниченных поверхностями сложной формы | 1986 |
|
SU1428563A1 |
| Способ изготовления зубчатых колес с профильной модификацией зубьев | 1989 |
|
SU1683913A1 |
| Способ шевингования зубчатых колес двумя дисковыми шеверами и станок для его осуществления | 1988 |
|
SU1768359A1 |
| Роликовый червячный обкатник | 1987 |
|
SU1466861A1 |
| СПОСОБ ФОРМООБРАЗОВАНИЯ ОБТЯЖКОЙ ТОНКОЛИСТОВЫХ ДЕТАЛЕЙ ОБОЛОЧЕК ДВОЙНОЙ КРИВИЗНЫ ДВОЯКОВЫПУКЛОЙ ФОРМЫ | 2014 |
|
RU2573859C2 |
| СМЕННАЯ РЕЖУЩАЯ ПЛАСТИНА | 2008 |
|
RU2364475C1 |
| МНОГОЗАХОДНЫЙ ЧЕРВЯК И ИНСТРУМЕНТ ДЛЯ ОБРАБОТКИ МНОГОЗАХОДНЫХ ЧЕРВЯКОВ | 1991 |
|
RU2101587C1 |
| Способ моделирования процесса электромеханической обработки зубчатых колес | 1987 |
|
SU1412862A1 |

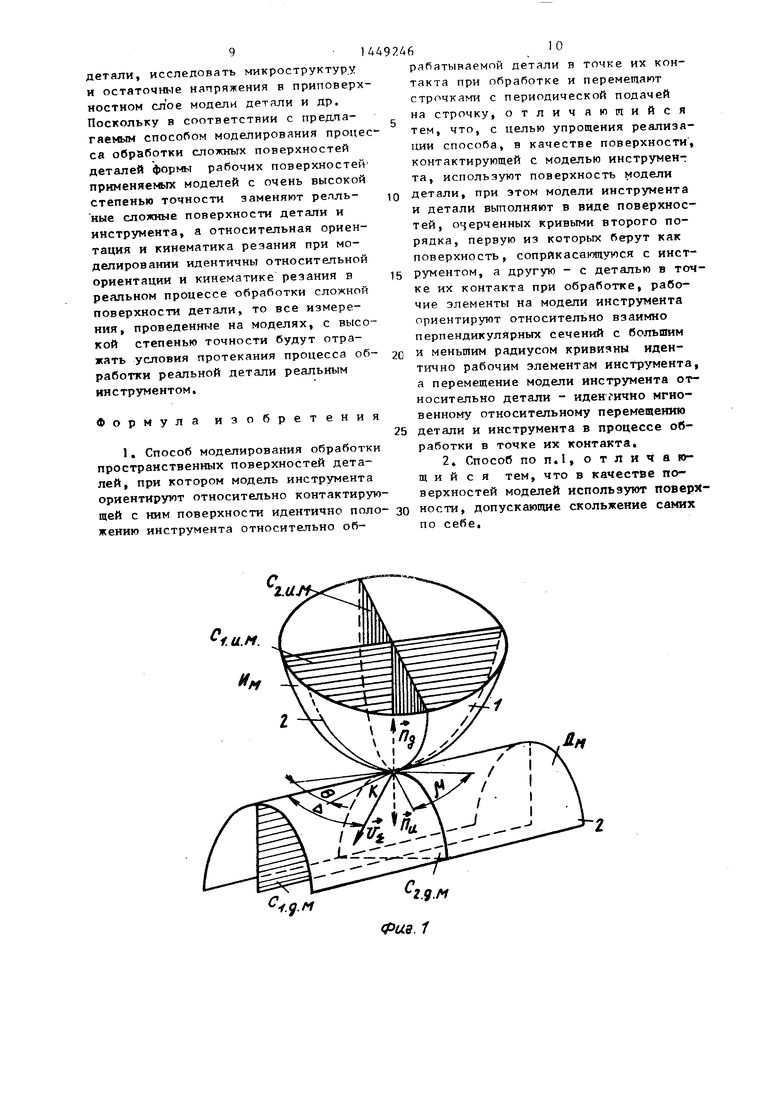
Изобретение относится к области машиностроения и может быть использовано для моделирования процесса обработки деталей, ограниченных поверхнотстями сложной формы, например, в исследованиях по оптимизации технологических параметров процесса обработки пространственно-сложных поверхностей деталей методом построчного огибания на многокоординатных станках с ЧПУ. Цель изобретения - упрощение реализации за счет упрощения конструкции моделей и возможности использования универсального оборудования. Способ моделирования осуществляют моделями детали и инструмента. Модели инструмента и детали выполняют в виде поверхностей, очерченных кривыми второго порядка. Кривизна рабочей поверхности моделей детали и инструмента в двух взаимно перпендикулярных сечениях равны кривизне инструмента и детали. Модели детали и инструмента вводят в контакт друг с дрзггом, ориентируют одну относительно другой так, чтобы усол между взаимно перпендикулярными сечениями с большим и меньшим радиусами кривизны бал равен углу между этими сечениями на детали и инструменте. Рабочие элементы на модели инструмента ориентируют идентично раЬочим элементам на инструменте. Затем моделям придают относительное движение, идентичное мгновенному относительному движению детали и инструмента в точке контакта, которая соответствует ке контакта, условия в зоне которой моделируются. В качестве поверхностей второго порядка могут использоваться поверхности, допускающие скольжение самих по себе. 1 з.п. ф-лы, 2 ил. СЛ
(L, Mj)R ,,- +
jL - )R,.+ Е, Р 0. Е о. РЛ ) Ь I
(2)
и L, М,. N
, ig, oijMb,j, га, п гауссовы коэффициенты соответствен- первой и второй основных квадратичных форм (первой и второй диффе- зенцийльмых форм Гаусса) формоойра- уемой поверхности детали, вычисленв точке К. Вольший корень квадратного урав2) соответствует значению радиуса кривизны R, д ;, а меньптй - значению радиуса кривизны R ад./ц.
Равенство главных радиусов кри- формообразуемой поверхности лета,пи соответствующим значениям тавных радиусов кривизны моделирую ей поверхности Д на основании гЬормулы Эйлера
1 /-Ч
R - ()
I, Л,« t-A-
RAM текущее значение нормального радиуса кривизны квадрики
в произвольном плоском нормаль сечении (ив покаяама)(Проходящем черея точку К под углом V J 1-лявному сеченто С t щ осио- вание утверждлть, что в произвольном плоском нормальном сячеяии радиусы кривизны поверхности детали моделируюцеЛ ее поверхности Л ,и будут равны друг другу. Ms этого следует, что вытолиение квадрики Д соприкасакмчейся с поверхностью .етали гарантированно обеспечивает идентичность друг другу поверхнос- )ей детали и Д в дифференциальной окрестности точки К с точностью-не , чем до членов второго поряд- 10СТИ,
Ия условия соприкосновения квадрики И к исходной инструментальной поверхности И следует, что вяаимно перпендикулярные главные сечения С,ц и С. (не покауяны) игхоц- ной инструментальной поверхности совпадают с соответствутошими вяаим- но перпендикулярными главныьш сечениями С „ „моделирутощей поверхности И. Кроме того, главные радиусы кривизны П , и R , исходной инструментальной поверхности в точности равны соответ твующим главным радиусам кривизны К i ми R „, л, моделирующей поверхности И, Если уравнение исходной инструментальной поверхности в той же системе декар- товых координат, что и уравнение (1) обрабатываемой поверхности детали, задано в параметрической формс- уравнениями
Хц Х,(и,; V, );
Y,. Y,(U,; Vj;
55и 7.„(и,; Vj,
Uu. V,
где Х,, У„, Zj, - координаты теку-
щей точки формообразующей исходной инструментальной поверхности; - криволинейные (гауссовы) координаты на формообразующей исходной инструменталь ной поверхности,
то главные радиусы кривизны R , R, и R, „.„ R.M могут быть определены как корни кв-адратного - уравнения
(, - М)Е2. (, - - 2FyMjR,+ О , (5)
где Е„, Fy, d,,H L,, М, N,, - га- уссовы коэффициенты соответственно первой и второй основных квадратичных форм (первой и второй дифференциальных форм Гаусса) формообразующей исходной инструментальной по- верхности, вычисленные в точке К (вычисление значений коэффициентов уравнения (5) производится по тем же формулам, что и вычисление коэффициентов уравнения (2).
Больший корень квадратного уравнения (5) соответствует значению радиуса кривизны R , vj.v, а меньший - значению радиуса кривизны Н « .
-с 10, 15 -
0
i sin tt
R
.,(6)
25
i
ЗО- 5
40
)
45 gQgg
Рявенстро ггганных радиуг -н Kp:i- визны формообразующее исходттой инструментальной поверхности соответствующим значениям главных радиусов кривизны моделируюргей поверхности И на основании формул Эйлера 1 ,. .
,м.« 7 j. г Де 1(.„- текущее значение нормального радиуса кривизны квадрики Ид, в произвольном плоском нормальном сечении (не показано , проходящем через точку К под углом v к главному сечению С ,д, , дает основание утверждать, что н произвольном плоском нормальном сечении радиусы кривизны исходной инструментальной поверхности и моделир тощей поверхности Ид, равны друг другу. Из этого следует, что выполнение поверхности Ид,) соприкасающейся с исходной инструментальной поверхностью, гарантированно обеспечивает идентичность одна другой поверхностей инструмента и И ц в дифференциальной окрестности точки К с точностью не менее чем до членов второго порядка малости.
На модели 1 И сохраняют неизменной ориентац№ рабочгтх элементов 2 (режущих кромок, упрочняющих ленточек и т.п.) относительно главных сечень й С иС. Для этого сначала определяют ориентацию главных сечений С i, ц и С и исходной инструментальной поверхности относительно координатных 11 „ - и V,-ли- ний. Ориентация любого нормального сечения однозначно определяется от- нощением (), значения которого для главных срчсттй С , и С - ,, могут быть найдены как корни квадратного уравнения
(б,м„ - F,Nj() + (i,L, - ) -йО- (n,L. - ЕиМ,)
0. ,(7)
При ортогональной (U,. : V )-параИ и
метризации исходной инструментальной поверхности И отнощение (dVy/dU,) определяет величину тангенса угла 5 наклона главных сечений С , 1 т и координатным линиям. В большинстве случаев (Ujj;Vy) параметризация поверхности И, как правило, является изогональной.
51ДДЧ2 66
Поэтому при ИПОГС1НЯПЫЮ11 плрлмет-зянсО спедует ряссчнтыв.чть по форрнзации неличину углл , (не пока-муле
sin у
Ytf. dllu
, dVn v7„ dVn. ,
- 2 Ли
dU,
dU
где угол между координатными
Un- и V -линиями, измеренный в точке К. Угол равен:
и„ arccos( j 6) .
(9)
.cos
, EydUndVv, + Fv,(dU«Jv + dV«(fUu) +сГ,ЛУи(„ Ч и -
+ 2F,.y + f dV /Е,(Ги + +6,Vj
где буквой tf обозначено дифферен-И -линии, то вследствие того, что
цирование вектора, касательного к25 вдоль координатной U -линии параметр
Uy-координатной линии. const, поэтому fV 0. С учеПоскольку речь идет об угле нак-том этого угол Ijr м рявен лона кривой линии к координатной
cos
EHdUu + FHVv
V EydU J, + + 6 dV, t
Алгебраическая сумма углов и V определит искомую величину уг- ла наклона 6 ( к + рабочего элемента 2 к первому главному сечению С ,.г, .
Из изложенного следует, что расположение рабочего элемента 2 под углом 6 еи(м+)к первому главному сечению моделирующей поверхности И гарантированно обеспечивает идентичность расположения рабочего элемента 2 на моделирующей поверхности Нерасположению соответствующего рабочего элемента на исходной инструментальной поверхности в дифференциальной окрестности точки К с точностью не менее, чем до членов второго порядка малости.
Моделирующие пояерхности Д ;i, и И располагают одну относительно другой под углом ориентации fx , равным углу относительной ориентации, поверхности детали и исходной инструментальной поверхности. Угол относительной ориентации поверхностей
sinu.
(8)
Рабочий элемент 2 в точке К наклонен к координатньтм ( i,; и линиям. Величина угла наклона pafio- чего элемента к и„-линии может быть рассчитана по формуле
(Ю)
(11)
детали и инструмента в точке К их касания измеряется как угол между соответствуюишми главными секущими плоскостями, а именно как угол между главными секущими плоскостят и С , и С или, что то же самое, как
угол между главными секущими плоскостями С д и С ( . Для определения величины угла относительной ориентации (U достаточно по известным формулам рассчитать значение угла
между двумя векторами, касательньши к линиям пересечения поверхности детали главным сечением , а исходной инструментальной поверхиости - главным сечением G , „ . Из изложенного следует, что по предлагаеиому способу относительная ориентация моде- лирумвц х поверхностей Ид, в дифференциальной окрестности точки К с точностью не менее чем до членов второго порядка малости идентична относительной ориентации детали и инструмента в процессе ойработки. Моделирующим поверхностям Д и И „придают относительное движение
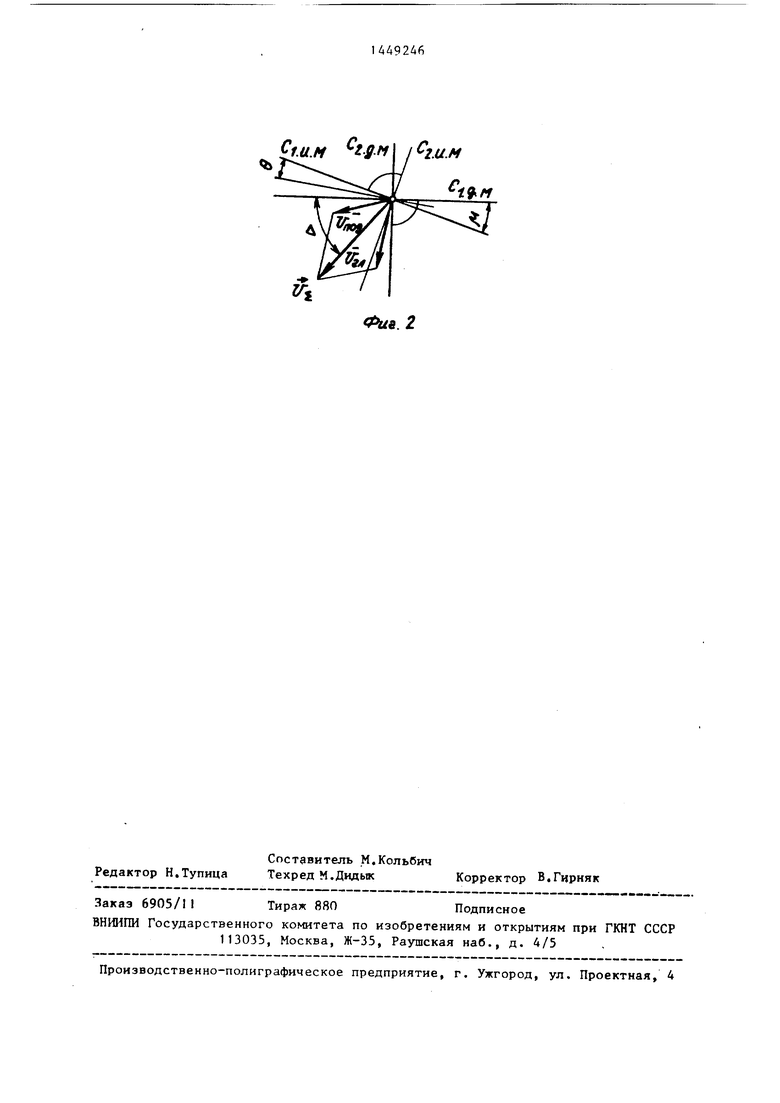
с ретультирующей скорогтт-и V , , яп- ляющейся noKTopfion cyMMoff скорости главного лрнжения V,-,, и скорости движения поллчи . Отиоситепьное движение поверхностей Л„ и И с результирующей скоростью V - по характеру и натравлеиию соответствует мгновенному относительному лвижению детали и инструмента в чроцессе моделируемой обработки, то достигается тем, что при моделировании величина угла и между векторами результирующей скорости V j и первым гла ным сечением С поверхности Д назначается в точности равной величине угла между вектором результиру щей скорости У и первым главньм сечением С обрабатьтаемой детали а модуль вектора относительной скорости IVg I одинаков как при моделировании, так и в процессе обработки
Из изложенного следует, что по предлагаемому способу относительное движение моделируюгцих поверхностей Л м м идентично мгновенному относительном движению детали и инструмента в процессе моделируемой обработки.
Моделирование процесса обработки деталей, ограниченных поверхностями сложной формы, в ряде случаев может быть произведено поверхностями Д и И, одна из которых, либо одновременно обе, допускают скольжение самих по себе. В самом общем случае такие поверхности должны представлять собой винтовые поверхности постоян- ного шага. Если винтовой поверхности придать винтовое движение вдоль ее оси с параметром движения, равным по величине и направлению винтовому параметру самой поверхности, то получим огибающую последовательных положений исходной винтовой поверхности, причем огибающая и исходная винтовая поверхности окажутся взаимно конгруэнтными. Следовательно, такая квадрика допускает скольжение, самой по себе.
Частным случаем поверхностей,допускающих скольжение самих по себе, являются поверхности вращения (для них винтовой параметр равен нулю) и цилиндрические поверхности (для них винтовой параметр равен бесконечности). Еще более частными случаями поверхностей, допускающих скольжение самих по себе, будут штос,
. 4Д024Г18
кость, сфера, круглые конус и цилиндр и др.
Выполнение моделирующих поверх- g ностей Ид, (одной или одновременно обеит:) в виде поверхностей, допускающих скольжение самих по себе, позволяет упростить технологию изготовления моделей, а в ряде слу- 10 чаев перейти от мгновенных относительных движений поверхностей Дд и Ид, к непрерывным их относительным движениям, чем может быть достигнуто повыщение эффективности модели- 15 рования.
При исследовании процесса обработки сложных поверхностей деталей указанную информацию можно использовать следующим образом. Для выб- 20 ранной точки на сложной поверхности детали изготавливают модель детали так, чтобы главные кривизны рабочей поверхности модели были в точности равны главным кривизнам обрабатывае- 25 мой сложной поверхности детали (это достигается при аппрЬксимации сложной поверхности детали в точке ее касания с инструментом поверхностью второго порядка). Модель детали из- 30 готавливают из того же и так же предварительно обработанного материала, что и деталь. Аналогично получают и модель используемого режущего инструмента. После этого моде- 35 ли детали и инструмента вводят в
контакт друг с другом, соответствующим образом ориентируют друг относительно друга путем поворота вокруг контактной нормали так, чтобы 40 угол между первыми (или, что то же самое, между вторыми) главными секущими плоскостями моделирующих поверхностей был в точности равен углу между первыми (или вторыми) глав- 45 ными секущими плоскостями моделируемых поверхностей детали и инструмента. Затем моделям придают относительное движение, идентичное мгновенному относительному движению детали 50 и инструмента в той их общей точке (точке контакта), условия обработки в окрестности которой моделируется. В процессе и после реализации такого способа моделирования можно 55 производить измерения температур в зоне резания, сил резания, величина износа режущих кромок инструмента (его модель), шероховатости обработанной рабочей поверхности модели
детали, исследовать микроструктур.у и остаточные напряжения в приповерхностном слое модели детали и др. Поскольку в соответствии с предпа- гаемым способом моделирования процесса обработки сложных поверхностей деталей формы рабочих поверхностей применяемых моделей с очень высокой степенью точности заменяют реальные сложные поверхности детали и инструмента, а относительная ориентация и кинематика резания при моделировании идентичны относительной ориентации и кинематике резания в реальном процессе хэбработки сложной поверхности детали, то все измерения, проведенные на моделях, с высокой степенью точности будут отражать условия протекания процесса обработки реальной детали реальным инструментом.
Формул
зобретения
ч.д.м
49246
10
10
15
20
25
30
рабатываемой детали в точке их контакта при обработке и перемещают строчками с периодической подачей на строчку, отличающийся тем, что, с целью упрощения реализации способа, в качестве поверхности, контактирующей с моделью инструмент та, используют поверхность модели детали, при этом модели инструмента и детали выполняют в виде поверхностей, очерченных кривыми второго порядка, первую из которых берут как поверхность, соприкасающуюся с инструментом, а другую - с деталью в точке их контакта при обработке, рабочие элементы на модели инструмента ориентируют относительно взаимно перпендикулярных сечений с большим и меньшим радиусом кривизны идентично рабочим элементам инструмента, а перемещение модели инструмента относительно детали - иден.-ично мгновенному относительному перемещению детали и инструмента в процессе обработки в точке их контакта.
Лп
ir
г.и.м
Фий.2
| Способ моделирования обработки пространственных поверхностей | 1985 |
|
SU1304991A1 |
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
Авторы
Даты
1989-01-07—Публикация
1987-02-17—Подача