Изобретение относится к цифровой вычислительной технике и предназначено для использования в универсальных и специализированных вычислительных устройствах.
Цель изобретения - сокращение аппаратурных затрат.
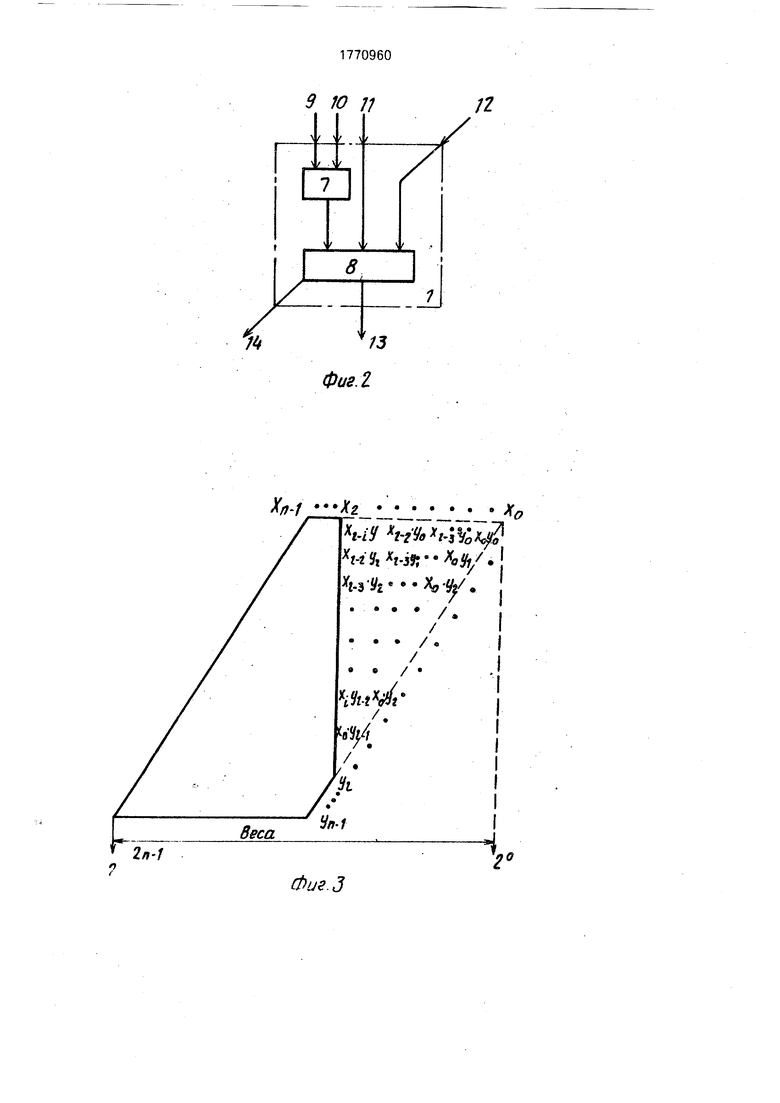
На фиг.1 изображена функциональная схема устройства для умножения; на фиг.2 - функциональная схема ячейки; на фиг.З - разряды частичных произведений, теряющиеся при вычислениях; на фиг.4 - случай наибольшей ошибки вычислений со знаком минус ; на фиг 5 - то же со знаком плюс.
Устройство для умножения (фиг.1) содержит матрицу из nxk вычислительных ячеек 1, группу из (2n - k - 1) элементов И 2, (п+1)-разрядный сумматор 3, входы множимого 4.1-4.П и множителя 5.1-5.П, выходы 6.1-6(k+1) результата устройства.
Вычислительная ячейка 1 (фиг.2) содержит элемент И 7 и одноразрядный сумматор 8, первый 9, второй 10, третий 11 и четвертый 12 информационные входы, выходы суммы 13 и переноса 14 ячейки.
Устройство для умножения работает следующим образом.,
В исходном состоянии на входах 4.1-4,п и 5.1-б.п установлены сигналы О. Процесс вычисления начинается с подачи из входы 4.1-4.п разрядов множимого и на входы 5.1 - 5.п разрядов множителя. По окончании переходного процесса в матричной схеме и (п+1)-разрядном параллельном сумматоре разряды произведения установлены на выходах 6.1-6.k+1.
Устройство обеспечивает минимум п- разрядную точность вычислений.
Матричная схема (фиг.1) состоит из k колонок, которые вычисляют старшие (k-n+l) разрядов частичных произведений остальных рядов, с (2n-k)-ro до n-го. и суммируют их. При этом разряды с первого по (2п-Ы)-й частичных произвелоний каждого 1-го ряда теряются (M,...,2n-k-1). Эти разряды частичных произведений изображены на фиг. Группа элементов И 2 вычисляет разряды частичных произведений в весе 2 (l 2n-k- 1). Выходы элементов И 2 группы соединены с четвертыми информационными Еходами
9
fe
VI
I
g
(переноса) вычислительных ячеек 1 (1+1}-й колонки, имеющими вес 21. Таким образом, разряды частичных произведений в весе 2 суммируются в основным результатом, вычисляемым матричной схемой, с вессни 21. В результате этого, если в 1-м ряду (N1,1) разряд частичного произведения с весом 2 равен нулю, а разряды с меньшими весами равны единице, возникает частичная ошибка со знаком минус. Аналогично, если разряд с весом 2 равен единице, а разряды с меньшими весами равны нулю, возникает частичная ошибка со знаком плюс. Благодаря тому, что ошибки со знаком плюс и минус в разных радах частич- но компенсируют друг друга, полная ошибка результата вычислений уменьшается.
Применение такого подхода вызывает в общем случае появление ошибки, изменяющейся в зависимости от величины операндов от максимальной со знаком минус до максимальной со знаком плюс, со средним значением, равным нулю.
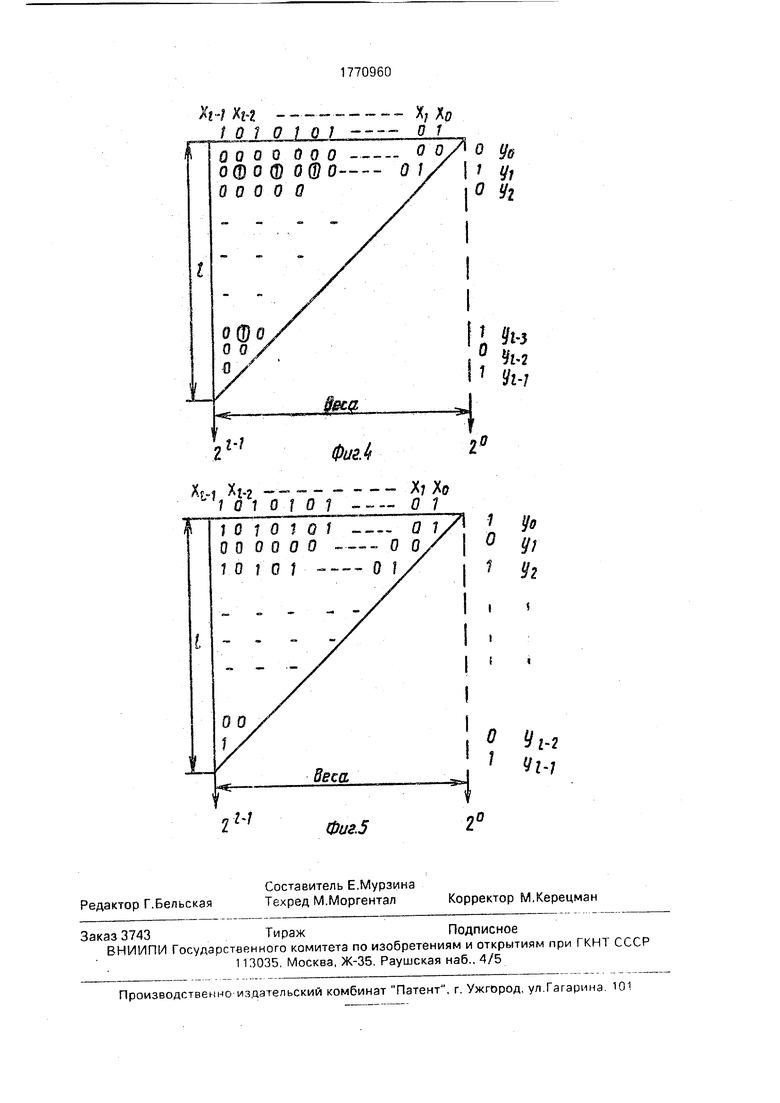
Максимальная ошибка со знаком минус получается, когда максимальное число частичных ошибок со знаком минус не компенсируется частичными ошибками со знаком плюс, т е. когда разряд частичного произведения каждого ряда в весе 2 равен нулю а возможно большее число разрядов с меньшими весами этого частичного произведения равно единице. Этот случай отражен на фиг 4. Кружками обведены разряды частичных произведений, которые в сумме создают ошибку.
Для определения величины ошибки суммируют частичные ошибки всех рядов, полагая { нечетным:
(21-2 + 2 и +
21) + ( + 2м +
...+ 23 + 0)+ ... +) + 0 + . . +... + 0 + + 0) -4г2124 -4г2м + .,. + 21.
Чтобы определись величину е-, переходят к более простому выражению, превышающему по величине е+
е Ll2 2i-2 + е- 2 2 2
+ 1-2-1+ -
Таким образом, справедливо неравенство
е- е-1 S -Ф ъ |о-2)2-3
Случай, приводящей к наибольшей ошибке со знаком плюс, противоположен вышеизложенному случаю наибольшей ошибки со
знаком минус. Она возникает, когда «акси- мальное число частичных ошибок со знаком плюс не компенсируется частичными ошибками со знаком минус. Этот случай отражен на фиг.5. Максимальная ошмбка
со знаком плюс несколько отличается по абсолютной величине от максимальной ошибки со знаком минус, но не превышает S по выражению (3). Таким образом, справедливы соотношения
е-
le±l §0-2)н
Максимальная относительная ошибка, возникающая при вычислениях s предлагаемом устройстве для 24-разрядных чисел с плавающей запятой (считая, что число отброшен- ных колонок 1 24) определяется из соотношения
е±
Xmln
J-22-221
4U&
-.24.81
-2 0 -20,19 046
Таким образом, предлагаемое устройство обеспечивает по меньшей меро 20-разрядную точность, в отличие от
0 устройства-прототипа, обеспечивающего лишь 18-разрядкую точность.
Отсюда следует, что для обеспечения такой же точности, как в устройстве-прототипе, предлагаемое устройство требует на
две колонки вычислительных ячеек меньше, чем устройство-прототип. При этом для данного примера максимальная относительная ошибка равна
50
Emax-97-921
е± 3 l l
Xmin
223.223
,23

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения | 1989 |
|
SU1697078A1 |
| Параллельный сумматор | 1981 |
|
SU1018114A1 |
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| Устройство для умножения | 1980 |
|
SU1005039A1 |
| Матричное вычислительное устройство | 1982 |
|
SU1034032A1 |
| Вычислительное устройство | 1982 |
|
SU1164697A1 |
| КОНВЕЙЕРНЫЙ АРИФМЕТИЧЕСКИЙ УМНОЖИТЕЛЬ | 2013 |
|
RU2546072C1 |
| Устройство для умножения | 1989 |
|
SU1714592A1 |
| Матричное вычислительное устройство | 1988 |
|
SU1541599A1 |
| Вычислительная ячейка | 1985 |
|
SU1287145A1 |

Изобретение относится к цифровой вычислительной технике и предназначено для использования в универсальных и специализированных вычислительных устройствах. Цель изобретения - сокращение аппаратурных затрат за счет уменьшения числа колонок вычислительных ячеек и реализации коррекции результата, выполняемой введенной в устройство цепочкой элементов И. 5 ил.
Выражение (2) является частичной суммой бесконечно убывающей геометрической прогрессии, полная сумма которой равна
4 I :3
,-Ъ -2
(3)
Формула изобретения
Устройство для умножения, содержащее матрицу из nxk вычислительных ячеек (где п - разрядность операндов, k - количество колонок в матрице, k (tog2n)-3J v,
(л 1)-разрядный параллельный сумматор причем первый и второй входы (i }-й вычислительной ячейки матрицы (I - номер строка, ,..,n, j - номер столбца, , ,,п) соединены соответственно с входом 1-го разряда мчохимого и вчодоп j-ro разряда множителя устройства, третий вход р-й вычислительной ячейки, в каждой 1-й колонке маюиич соединен соответственно с выходом суммы (р-1)-й вычислительной ячейки в каждой 1-й колонке матрицы (,...,п:
), четвертый вход р-й вычислительной
ячейки первого столбца матрицы соединен соответственно с выходом перекоса (р-1)-й ек- иеллтельчой ячейки первого столбца матрицы, третий вход первой вычислительной ячейки в каждой 1-й колонке матрицы соединен с входом логического нуля устройства, выход cyMMbi (ti,|J-n вычислительной ячейки матрицы соединен соответственно с первыь входа; 1 i-го разряда (и4- -разрядного параллельного сумматора второй вход (лН)-го разряда которого соединен с выходов переноса (1,1)-й вычислительной ячейки матрицы, выходы разрядов разрядного параллального сумматора соединены « V 83 Ч
ответственно с выходами старших рлзрядив результата устройства, отличающееся гем. что, с целью сокращения аппаратурных затрат, в него введена группа из (2n-k-1)
элементов И, причем первый вход гп-го элемента И группы соединен соответственно с входом (2n-k-m)-ro разряда множимого устройства (т 12п-1 -1), второй вод m-го эле
мента И группы соединен соответственно с
входом m-ro разряда множителя устройства, выходы элементов И группы соединены с четвертыми входами соответствующих вычислительных ячеек - колонки матрицы, выход переноса (1,1)-й вычислительной ячейки
матрицы, кроме (n.j)-x вычислительных ячеек матрицы, соединен соответственно с четвертым входом (К1,)-й вычислительной ячейки матрицы, выход переноса (n,j)-n вычислительной ячейки матрицы соединен соответственно с вторым входом (К1)-разряда (пд 1)-разрядкого параллельного сумматора, выход суммы (l.n)-x вычислительных ячеек матрицы, кроме (п,п)-й вычислительной ячейки матрицы, соединен соответственно
с (n-k) выходами младших разрядов результата устройства.
4я. 4.п-1
Фие.1
1
V M M
Фиг. 2
Хп-1
хг-г, Xt ifXofi/. . /.
Фие.З
/
П
и
Х|-/ Хн / 0 1
Фиг. 4
1 Q 1 0 1 Q
000000
10 0 1 1 .
Bsca
Xj Ко
0 1
7 0
У
9t
У2
0 91.1
1 Vz-7

| Самофалов К.Г | |||
| и др | |||
| Прикладная теория цифровых автоматов | |||
| - Киев, Высшая школа, 1987, с.95, рис.4.6 | |||
| Патент США № 4598382, кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1992-10-23—Публикация
1989-05-22—Подача