Изобретение относится к вычислительной технике и может быть использовано в универсальных и специализированных а|зифметических устройствах.
Цель изобретения - повышение отказоустойчивости устройства.
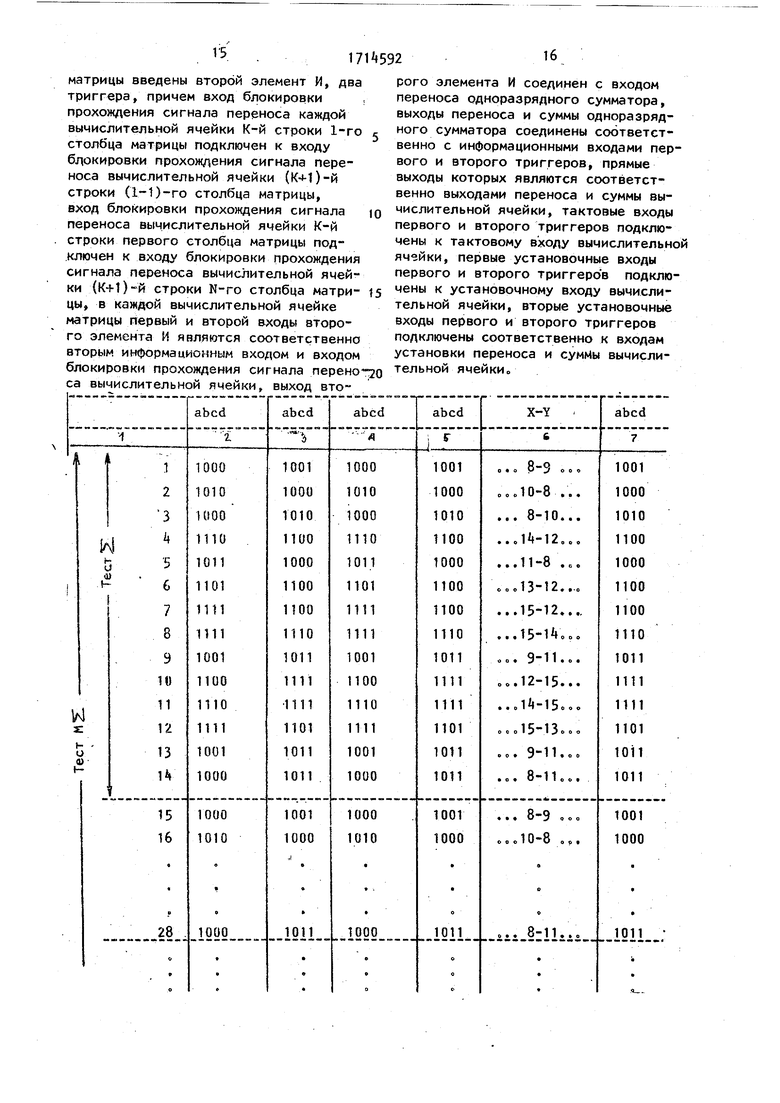
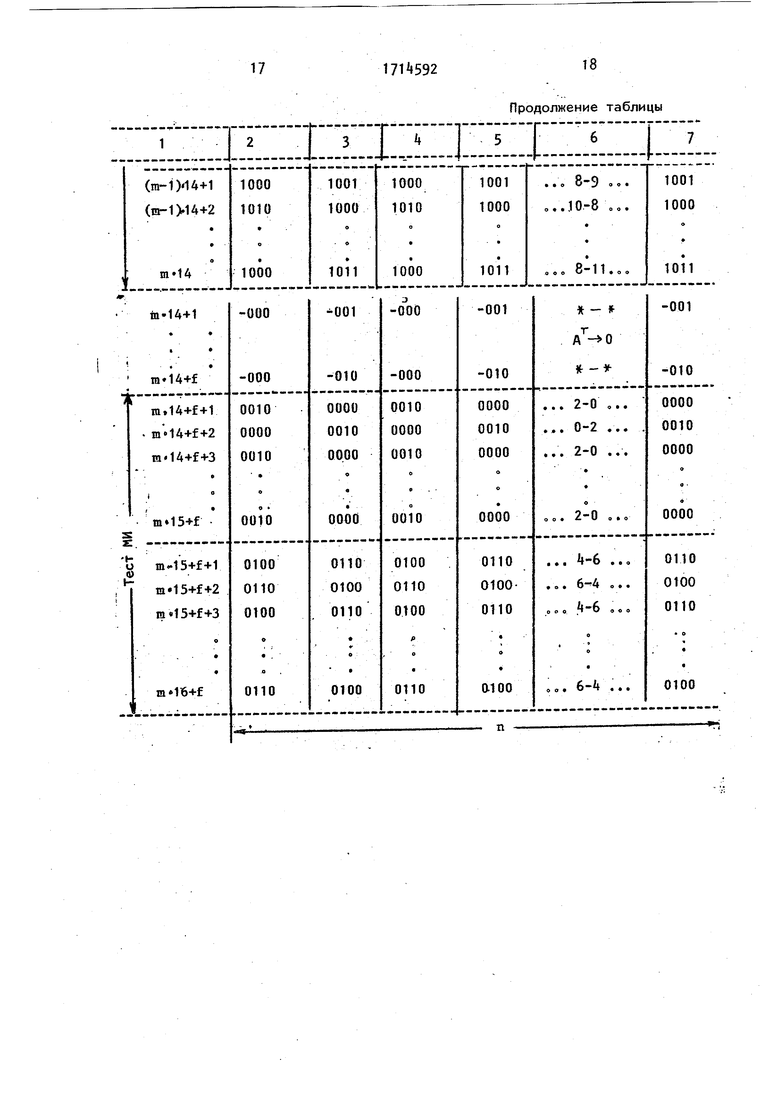
В таблице показано распределение входных тестовых наборов во времени.
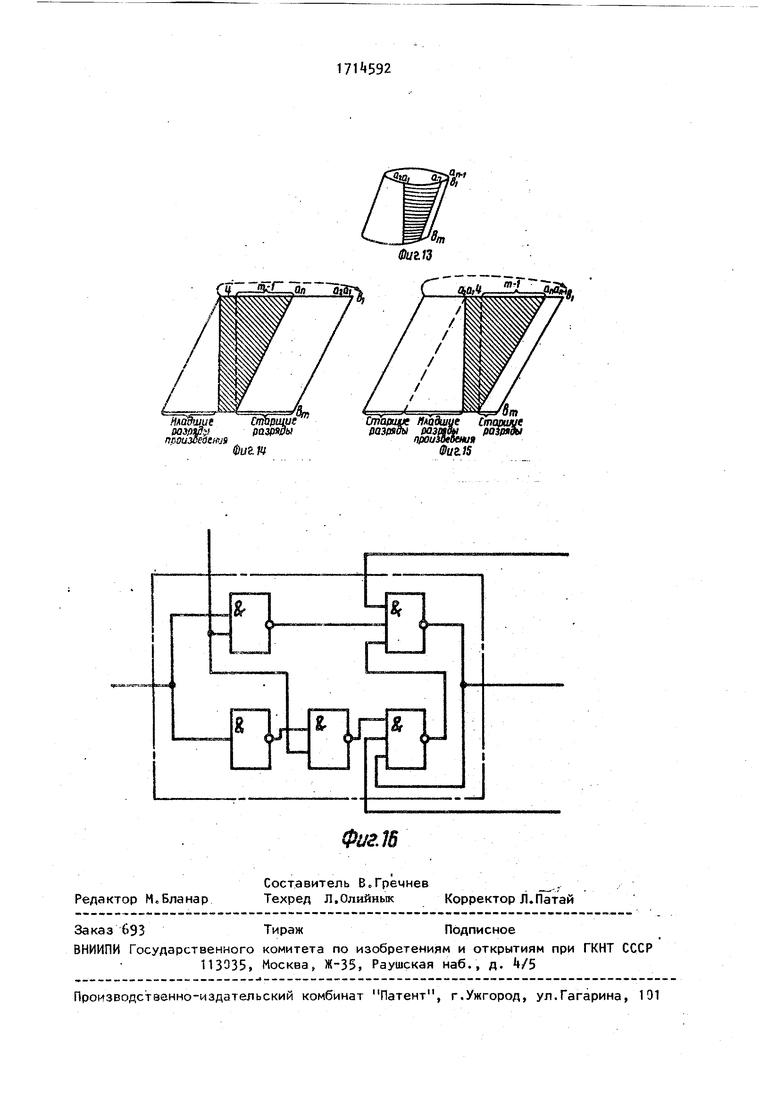
На фиг. 1 приведена функциональная схема устройства; на фиг. 2 - функциональная схема вычислительной ячейки последней строки матрицы; на фиг. 3 и 4 - временные диаграммы работы устройства в режиме вычислений и; подготовительном режиме соответственно} на фиго 5 таблица входных тестовых наборов ячейки матрицы; на . фиГо 6-12 - пояснения принципа Лока- лизации Неисправной вычислительной ячейки матрицы; на фиг, 13-15 - примеры расположения рабочей и нерабочей
зон матрицы; на фиг. 1б - функциональная схема одной из реализаций триггера на элементах И-НЕ.
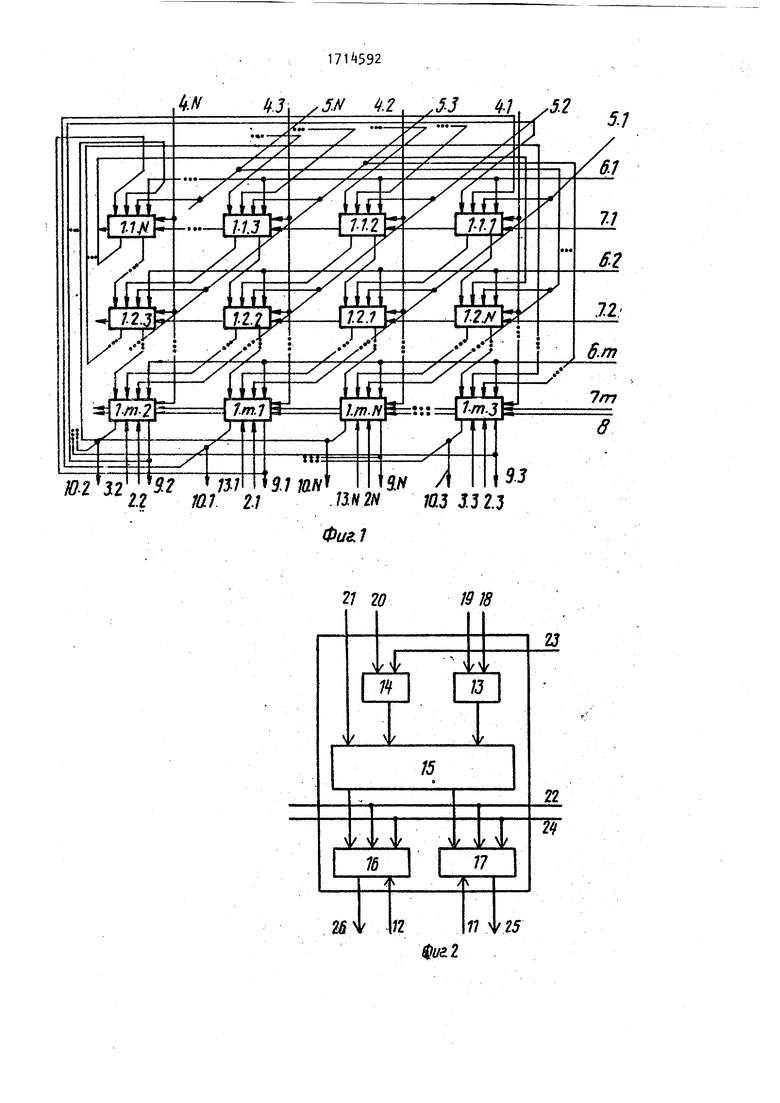
Устройство (фиг. 1) содержит матрицу 1 вычислительных ячеек, входы 2 и 3 установки суммы и переноса устройства соответственно, вход блокировки прохождения сигнала переноса устройства, входы 5 и 6 множимого и множителя устройства соответственно., тактовый вход 7 и установочный .вход 8 устройства, выходы 9 и 10 результата и переноса устройствасоответственно.
Вычислительная ячейка последней строки матрицы 1 (фиг 2) содержит установочные входы 11 и 12 суммы и переноса вычислительной ячейки соот.ветственно, элементы И 13 и 1, одноразрядный сумматор 15, триггеры 16 и 17 вход 18 блокировки первого oneранда и информационные входы в числительной ячейки, тактовый, вход 22 вычислительной ячейки, вход 23 блокировки прохождения сигнала переноса вычислительной ячейки, установо ный вход 2А, выход 25 суммы и выход 26 переноса вычислительной ячейки Вычислительные ячейки других стро матрицы 1 отличаются темр что в них отсутствуют установочные входы триг герое 16 и 17. Устройство работает следующим образом. Устройство для умножения может работать в подготовительном режиме и режиме вычислений, В подготовительном режиме производится тестирование устройства и ло кализация неисправной вычислительной ячейки, Режим вычислений подразделяется н два подрежима: подрежим при наличии неисправной вычислительной ячейки и подрежим при отсутствии неисправной вычислительной ячейки Раб эта матрицы в этих подрежимах отличается только положением рабочей 3OHUf ToG. области матрицы умножения в которой производятся вычисления, и нерабочей зоны (фиг„ 14 - 16). Вычислительные ячейки всех рядов матрицы умножения, кроме последнего ряда, описываются системой уравнений S(t+1) ((ab)©c©d) у S(t)y; p(t+1) (cd+abd + abc)y )ylz Вычислительные ячейки последнего ряда матрицы умножения описываются уравнениями S(t+1)(ab)®c®d)y©S(t)y3g; p(t+1)(cd+abc + abd)y + p(t)yj (2) где a,b,c,d - сигналы на информацион ных входах вычислитель ных ячеек матрицы 1J разряды операндов множимого и множителя соо ветственно/ разряд частичной суммы разряд переноса; S(t),p(t) - сигналы на выходах сум мы и переноса вычислительных ячеек в момент времени t; у - сигнал на тактовом входе вычислительной ячей-i ки матрицы 1; i g - сигнал на установочном входе вычислительной ячейки матрицы 1; Z - сигнал на входе блокировки прохождения сигнала переноса матрицы 1, Как видно из (1) и (2) подачей сигналов О на входы блокировки f,1 ,N устройства можно блокировать входы переноса соответствующих вычислительных ячеек матрицы 1, тем самым запрещая распространение возможной ошибки по цепям переноса. Блокируемая вычислительная ячейка первого ряда матрицы Г, имеющая наибольший порядковый номер внутри ряда с учетом циклической структуры матрицы, является первой ячейкой рабочей зоны, а именно младшим разрядом операнда множимого. На информационные входы вычислительных ячеек первого ряда нерабочей зоны матрицы подаются сигналы О (кроме информационных входов b - множителя), что в сочетании с входами блокировки, исходя из (1) и (2), позволяет исключить из работы всю нерабочую зону матрицы умножения. Рабочая и нерабочая зоны определяются значениями на соответствующих информационных входах и входах блокировки В подрежимевычислений без неисправной вычислительной ячейки положение рабочей и нерабочей зон произвольно (фиг, И), В подрежиме вычислений при наличии неисправной вычислительной ячейки нерабочая зона совмещается с областью матрицы 1, в которой локализована неисправная вычислительная ячейка (фиг 16), посредством подачи сигналов О на соответствующие блокировочные и информационные входы. Рабочая зона устанавливается в области матрицы 1, не содержащей неисправности, путем подачи на соответствующие входы блокировки сигналов 1 вычисления производятся в рабочей зоне и в обоих подрежимах осуществляются аналогично. Работа устройства в подрежиме вычислений без неисправной вычислительной ячейки протекает следующим образом.
i Пусть положение рабочей и нерабо.чей зоны такое, как показано на
фиг. 15
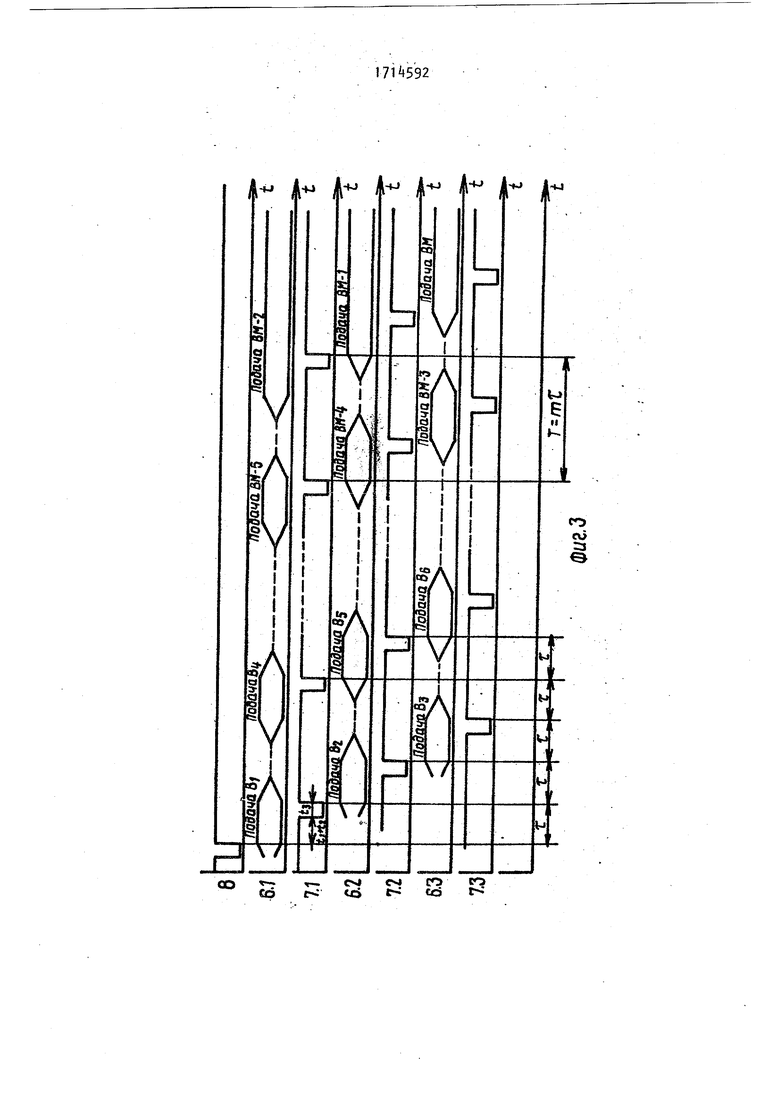
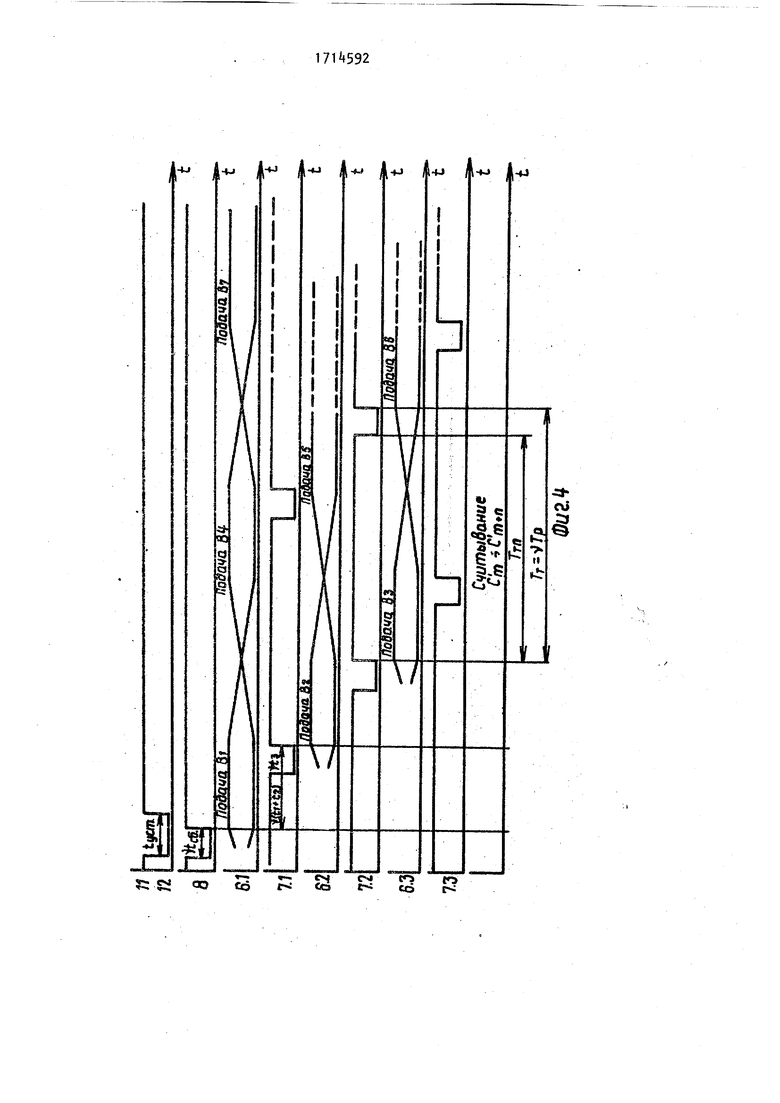
Процесс вычисления происходит в рабочей зоне устройства о В исходном состоянии на тактовых входах 7.1, 7.2,...,7.т устройства и установочном входе 8 устройства установлены сигналы 1 (фиг„4, m 3). Перед на чалом вычислений на вход 8 устройства подается отрицательный импульс Сброс, длительностью Импульс Сброс устанавливает в нулевое состяние выходы суммы и переносов вычислительных ячеек последнего ряда матрицы 1 умножения т.1 - т.п.
Устройство для умножения работает в конвейерном режиме. Процесс вычисления начинается с подачи на входы 5.1-5.П устройства разрядов aj(,c,..,a п-разрядного множимого А и младшего ;разряда В т-разрядного множителя В на вход 6.1 устройства, момент пода;чи совпадает с задним фронтом импульса Сброс и его полагают началом отсчета. Весь процесс вычислениям вычислительной ячейке матрицы 1 можно разделить во времени на три периода: время прохощения информационных сигналов через элементы И 13 и 14 (фиго2) t4; время прохождения сигналов в сумматоре 15 t и время запоминания информации в элементах памяти tj,
Через время t + t на вход устройства подается сигнал О,.разрешающий прохождение результатов суммирования 1 о 1.1 - 1.1оП вычислительных ячеек матрицы 1 на входы триггеров 16 и 17о Через время t на вход 7о1 устройства подаётся сигнал 1, обеспечиваю1чий запоминание результатов вычислений в первом ряду матрицы 1 на требуемое время и запрещаюи4ий появление на выходах триггеров 16 и 17 другой информации.
Одновременно с .подачей на вход 7о1 устройства сигнала О начинается hoдгoтoвкa к вычислениям во втором ряду матрицы 1, Тое. на входе 6.2 уст ройства устанавливается второй разряд Б множителя В и через время t + (t + t) на входах триггеров 16 и 17 вычислительных ячеек второго ряда устройства присутствуют резуль:таты вычисленияв первом ряду. Поэтому, через время tf + tg на вход 7.2 устройства подается сигнал О, разрешающий прохождение результатов вычислений второго ряда матрицы 1 на входы триггеров 1б и 17 этого ряда. Одновременно с подачей сигнала О на вход 7.2 устройства начинается подготовка к вычислениям в третьем ряду вычислительных ячеек матрицы К I С уметом обозначения t; i , в момент времени 2t на вход устройства подается сигнал 1. Аналогично процесс вычисления продолжается до.т-го ряда Разряд Ь множителя В подается на вход 6.m устройства к моменту (т-1). В момент времени m t- t на вход 7«.и устройства подается сигнал О. В момент времени т на вход 7.1П устройства подается сигнал 1. Далее процесс вычисления протекает циклически. Пока идет вычисление и запоминание результата в т-м ряду на первом ряду идет подготовка к вычислению.
К моменту времени mt на вход 6„1 устройства подается разряд в,у,.( множителя В. В момент времени (т+1). -t на вход 7а1 устройства подается сигнал О, разрешая прохождение результатов вычислений на выходы триггеров 1б и 17 вычислительной ячейки матрицы 1 и их запоминание, В момент времени (т-«-1) на вход 7о1 устройства подается сигнал 1, обеспечивающий фиК сацию на выходах триггеров 16 и 17 ячейки вычислительной информации и запрещающий поступление на выходы ячеек новой информации. Процесс вычислений осуществляется аналогично После подачи всех М разрядов операнда В на входах 6.1-6от устройства устанавливаются сигналы О, а процесс вычисления продолжается, пока разряды результата С - установятся на входах 9о1 - УоШ и 10о1 - 10.т устройства в двухразрядном коде. Отказоустойчивость устройства для умножения обеспечивается за счет периодического тестирования, локализации неисправного функционального модуля, если он имеется, и реконфигурации матрицы 1 для его нейтрализации. Работа устройства в подготовитель/ном режиме отличается от работы в режиме вычислений тем, что в исходном состоянии на входы 2„1 - 2,N, З 3.N поданы соответствующие разряды первого и второго установочного тестового операнда. Длительность tu.
установочного импульса на входах 2 и 3 устройства
t tcep 3) этот импульс устанавливает на выходах суммы и переноса вычислительных ячеек то.N - т„1 матрицы 1 сигналы, соответствущие разрядам первого и второго установочного тестового one™ ранда Затем осуществляется подача тестовых значений первого операнда А (множимого) и второго операнда (множителя) аналогичнотому, как это осуществлялось в режиме вычислений
Период управлящих сигналов Т (фиго ) в подготовительном режиме определяется временем Тд необходимым для анализа тестовых откликов (в двухрядном коде) с соответствукн-чих выходов - 9.N и 10,1 - 10„Н устройства после каждых та циклов работы Необходимо, чтобы S: Тд являлось частью Т, в течение которой вычислительная ячейка запоминает значение ,S3 выходах триггеров 16 и 1 (фиг. ). Считаютf что Т F Р где Jf - коэффициент уменьшения та ктовой опорной -частоты, используемой . при формировании управляющих сигналов,
локализации неисправной вычислительной ячейки матрицы 1 осуществляется тестирование матрицы за счет начальной установки (установочных тес товых операндов) и подачи таких значений входных тестовых операндов А и что на каждую вычислительную . ячейку матрицы 1 в процессе тестового вычисления поступают все входные тес товые наборы При этом тестовые операнды подбираются таКр что картина распределения входных тестевых наборов в матрице умножения повторяется в каждом р-м столбце (, фиг.6), что обеспечивает идентичность тестовых откликов ячеек каждого столбца, т.е. при все ячейки стоящие на четных (нечетных) позициях в рядах матрицы умножения в процессе тестирования имеют одинаковые тестовые отклики (выходы суммы и переноса)о Если предположить, что в матрице умножения есть одна Неисправная вычислитель нал ячейка, то в результате ее неисправности возникнет ошибка в тестовом вычислении, которая за m тактов работы может вызвать групповую ошибку и изменить выходы суммы и переноса ячеек в последнем ряду матрицы,
доступном для наблюдателя, нарушив идентичность соответствущих откликов
Тогда, если организовать сравнение тестовых откликов по р идентичным группам, число неверных тестовых откликов будет меньше числа верных внутри идентичной группы (полагают, что N та для большинства практических реализаций), что позволяет локализовать неверные тестовые отклики внутри идентичной группы через голосование Локализовав неверные тестовые отклики, можно с точностью, в худшем случае до тп позиций столбца, определить область локализации неисправной вычислительной ячейки. Так как размерность матрицы 1 N;(m, где N n+in+k (п - разрядность множимого), то возможно выполнение вычислений в различных областях матрицы 1, соответствущих различным положениям рабочей зоныо При этом необходимо обеспечить совмещение блокируемой области матрицы 1 (нерабочей зоны) размерностью т+К с областью локализации неисправной вычислительной ячейки размерностью т, используя при этом кольцеоую структуру матрицы 1. В результате влияние неисправной вычислительной ячейки, в дальнейшем, на вычисления в рабочей зоне нейтрализуется. При этом, соответственно, изменяется порядок нумерации входных (множимого) и выходных (результата) шин.
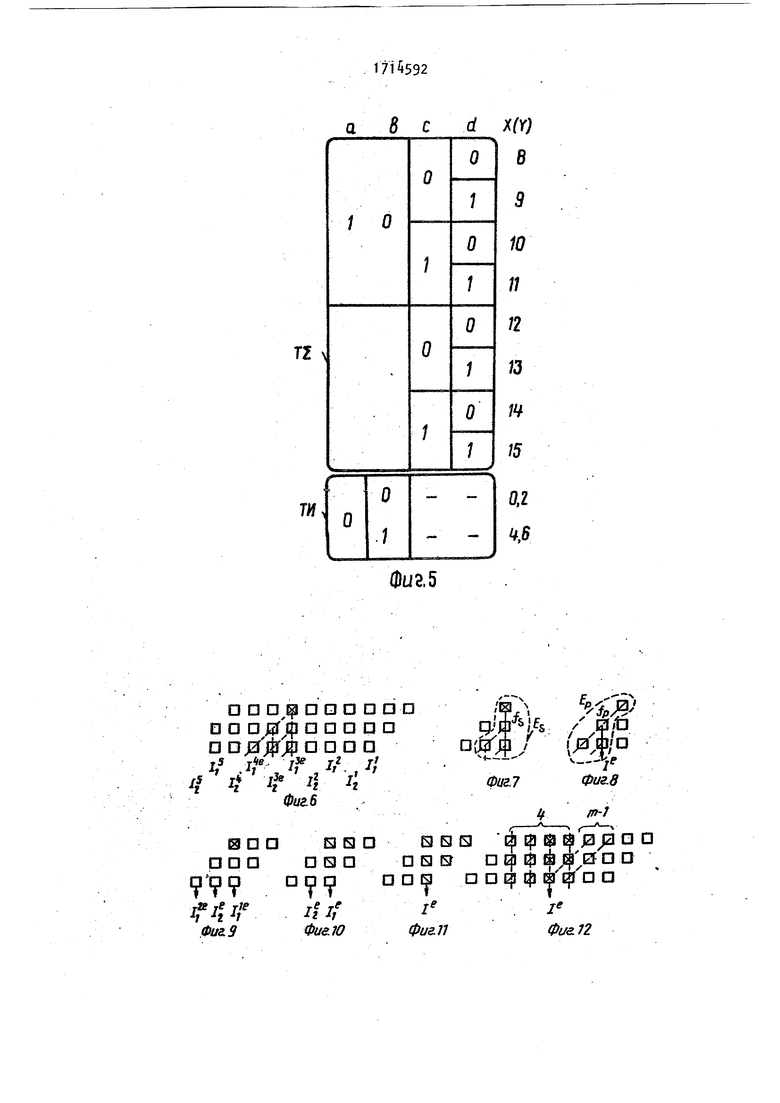
Вычислительная ячейка является четырехвходовой, на ее информационные входы поступают входные наборы в формате а - двоичный разряд множимого, ь- двоичный разряд множителя, с - разряд частичного произведения, d - разряд переноса.
Для исчерпываюи{его тестирования функциональных модулей в составе вычислительной ячейки Необходимо 10 тестовых входных наборов, вторые в формате abed представлены на фиг.5, причем восемь тестовых наборов для исчерпывающего тестирования одноразрядного трехвходового сумматора (т 21) и два входных тестовых набора из четырех (ТИ) для исчерпываю1цего тестирования двухвходового элемента И вычислительной ячейки, которые не покрываются Т21«
На фиг. 6 приведен пример распределения входных тестовых наборов в формате развернутой во времени замкнутой конвейерной матрицы 91 (число столбцов р равно 2), которая для удобства восприятия представлена в ортогональном виде. Каждому числу в формате abcd (фиг. 6).соответствует десятичное число X(Y) (фиго 5). Для удобства ан лиза распределения входных тестовых наборов в двух столбцах (фиг.6) приведено также десятичное выражение Xтестовых входных наборов, соответствующих двум соседним столбцам Тест включает восемь входных тестовых наборов (T2ij фиго5) для подачи кот рых необходимо (для рассматриваемого примера) Ti тактов работы матрицы умножения, образущих условно цикл. Тест, обеспечивая за m циклов при ложение каждого из восьми входных тестовых наборов к каждой вычислител ной ячейке, обеспечивает исчерпывающее тестирование всех вычислительных ячеек матрицы умножения за т.14 тактов работы матрицы умножения, Для завершения тестирования двухаходового элемента И вычислительной ячейки необходимо подать еще два входных тестовых набора (ТИ, фиг,5). Для этого разряды множимого А устанавливаются в ноль, не прерывая pat5oты матрицы, так как на (т„14-1)и (т. 14-2)-м тактах работы матрицы разряды множителя В равны нулю, и элементы соответствующих рядов матри цы заблокированы, что позволяет либо осуществить установку А в ноль за эти два такта, либо при необходимости использовать дополнительно еще f тактов, что определяется временем сброса соответствующего регистра, хранящего разряды А . Затем осуществляется еще 2т TaKtoB работы матри цы (тест ми), в которых на входы эле ментов И всех вычислительных ячеек матрицы подаются два входных тестовы набора (в формате abcd ) 01 - и 00 , которым фактически соответствует 0100, 0110 и 0010, 0000 (фиг,5 и 6). Значения установочных тестовых операндов (фиг. 6) разрядности N устанавливаются за счет подачи на входы 2o1-27N устройствасигналов О, на входы Зо1,ЗоЗ,3.5,.оо сигналов 1, на входы 3.2,3.4;3о6,,.. сигналов О (реализация установки . -описана, фиг. А). Значения всех N разрядов входного тестового операнда А на 1 - т. 14 тактах работы равны 1, на остальных О. Значение входного тестового операнда В (младшие разряды слева) представляет собой конкатенацию К,,, К и в Т ПГ В 1 f-- где в 0011101110000 к, 000, К„ 111,,.11 Разрядность операнда В равна RJ где R т. 16 + f, где f - дополнительное число тактов, достаточное для сброса А в ноль (на практике f 0-2), Если предположить, что m 3 (фиго 1), то после первых трех тактов работы (первый цикл) матрицы 1 с вы- хода вычислительных ячеек последнего ряда матрицы 1 снимаются разряды (в двухрядном коде) старшей части частичного произведения (фиг.), анализируются на идентичность внутри соответствующих групп и, если обнаружена ошибка - неверный тестовый отклик (или отклики), то тестирование прерывается, неисправный функциональный модуль локализуется, соответствующие ячейки матрицы блокируются, причем блокируемый столбец организован по следующему правилу: произвольная ячейка i,j (где i - номер ряда, j - порядковый номер ячейки внутри ряда) соединена в столбце с ячейками (i-1, j + 1) и (i+1, , т,е. порядковый номер ячейки внутри соседнего вышерасположенного ряда на единицу больше, а порядковый номер ячейки внутри соседнего нижерасположенного ряда на единицу меньше. Таким образом, осуществляется условно называемая вертикальная блокировка несправных ячеек. Рассмотрим пример, N 10, m 3 (фиг, 7), .квадраты соответствуют ячей ам . матрицы, неисправен функциональый модуль в ячейке первого ряда матицы (обозначение S ), В результате еисправности возникает область Е озможного распространения ошибки, оторая определяет возможную группоую ошибку по входам суммы-переноса рех (т 3) ячеек последнего ряда атрицы. Неисправность функционального моуля ячейки умножения может вызвать ошибку либо на выходе суммы, либо на выходе переноса, ли(5о на обоих одновременное Если ошибка проявилась по выходу суммы fg (фиго 8)j она определяет область распространения ошибки Eg, если по переносу fp (фиг, 9) то область Ер о Лействие неисправности всегда распространяется по цепям сум МЫ (показано сплошной линией) либо |В этой же позиции при Eg, либо при :Ер, либо в следующей при Ер, обеспечивая наблюдаемость на выходах вычислительных ячеек последнего ряда матрицы Тестовые отклики ячеек на четных 1, и нечетных 1 позициях ячеек пос леднего ряда матрицы 1 идентичны (фиго 6). Тогда, сравнивая b«-1j между .собой определяют, что 1 ошибочен (в общем случае) Таким образом, определяются ошибочные отклик Рассмотрим пример, предположив, что на .одном из циклов тестирования обнаружилось три (фиг«10), два (фиг.П) и один (фиго12) ошибочных откликч о, что включает а себя все возможные случаи о При ошибочных от rtijJo 4/д кликах П i- 12 t 1J положение неи.справной ячейки определяется однознач но (Ш J фиг о 10). Возможны три вероятных положения неисправной вычислительной ячейки ( И , фигеП), а пять возмо«( положений неисправной ячейки соответствуют худшему случаю (фиг.12)о Из фиго12 видно, что поло женив неисправной вычислительной ячейки можно локализовать в худшем случае до m 3 позиций (позиция соответствует столбцу или одной линии шины блокировки if фиг. 1)х На фиГе1 показано, что для осуществления надежной блокировки всех предполагаемых неисправных вычислительных ячеек необходимо блокировать два столбца (фиг. 13, S ) вероятность неисправ ности которых (фиго 12) наиболее высо ка, кроме того, необходимо заблокировать два столбца, соседних с неисправными (фиг.13, И)« Дублирование при блокировке двух столбцов (фиго13 13 ) позволяет не проводить специал ное тестирование входов блокировки Таким образом, полностью необходимо блокировать Четыре столбца матрицы умноженияо При замыкании матрицы умножения имеется возможность не снижать точность вычислений, т,ёо получать и младшие и старшие разряды произведения о С этой целью в состав матрицы умножения дополнительно введены т-1 столбцово Следовательно, суммарное число столбцов, которые необходимо дополнительно ввести в структуру матрицы умножения с целью повышения отказоустойчивости, равно сумме т-1 т+3, так как в об1чем случае введены будут пн-К столбцов, то К Зо При такой избыточности не снижается точность вычислений Таким образом, если неисправная вычислительная ячейка матрицы 1 локализована и позиция тестового отклика наблюдаемого последнего ряда (с учетом циклической структуры матрицы) 1 (1 1, N), то блокируется четыре позиции от (1 + m + 1) до (1 m - 2) первого ряда матрицы, причем вход блокировки ()-й вычислительной ячейки первого ряда соединен с входом блокировки (1 + m г 1)-й вычислительной ячейки второго ряда, .с входом блокировки ()-й вычислительной ячейки третьего ряда и ТоДо На входы блокировки указанных четырех столбцов подаются логические О, на всех остальных входах блокировки присутствуют логические 1, Четыре блокированных столбца совместно с вычисли- : тельными ячейками ra-l дополнительных столбцов составляют нерабочую зону матрицы умножения Рабочая зона (младший разряд) начинается с вычис- , лительной ячейки (1+га+2) первого ряда матрицы. Для возможности получения младших разрядов произведения необходимо на все информационные входы (кроме входа операнда множителя В) вычислительных ячеек нерабочей зоны подавать в подрежиме вычислений сиг-, налы логического О, что реализуется через соответствующие входы установки. В дальнейшем все вычисления проводятся при данном положении рабочей зоны., Если в первом цикле тестирования ошибка не обнаружена, то тестовое вь1числение продолжается до тех пор, пока не обнаружится ошибка или пока не приложены все входные тестовые наборы, осуществляющие исчерпывающее тестирование каждой вычислительной ячейки Если при тестировании ошибка не обнаружена, то полагают, что матрица умножения исправна относительно принятой модели неисправности одной вычислительной ячейки. которая заключается в произвольном изменении соответствукхцей ей таблицы истинности (смо таблицу), при которой она остается комбинационной схёмойРабота матрицы в подрежиме вычислений при наличии неисправной вычислительной ячейки (локализованной в пoдгotoвитeльнoм режиме) аналогична работе в подрежиме вычислений без не исправной ячейки, за исключением тог что в исходном состоянии на входы .l+m+1 - До1 + т-2 подаются сигналы логического О, а также на инфор мационные входы вычислительных ячеек первого ряда нерабочей зоны матрицы умножения (кроме входов операнда множителя В) подаются логические сигнал,ы О (в рассматриваемом приме ре - это бходь операнда 5о1 + пи-1 5,1 + га-4, при m 3). Таким образом, за счет периодичес кого тестирования, локализации по рассмотренному на примере алгоритму, реализуемому любым доступным программным или аппаратным способом, и последующей реконфигурацией обеспечйвается отказоустойчивость устройства к неисправности одной вычислительной ячейки матрицы 1 без сниже ния точности результата вычисления Предлагаемый подход к локализации неисправных ячеек предполагает, что информационные шины матрицы 1 исправ Формула изобретения Устройство для умножения,- содержащее матрицу из m х N вычислительных ячеек (N m+ntP), где п - разрядность множимого} Рит- произвольные числа), причем первый информационный вход каждой из вычислительных ячеек i-ro столбца матрицы подключен к i-му разряду входа множимого устройства ( e.N), входы блокировки первого слагаемого всех вычислительных ячеек j-й строки матрицы подключены к j-му разряду входа множителя устройства, выход переноса каждой вычислительной ячейки К-й строки i-ro столбца матрицы соединен с вторым информационным входом вычислительной ячейки (К+1)-й строки i-ro столбца матрицы (1 Кет-1), выход переноса вычислительной ячейки т-й строки i-ro столбца матрицы соединен с вторым информационным входом вычислительной ячейки первой строки i-ro столбца матрицы, выход суммы каждой вычислительной ячейки К-й ;строки 1-го столбца матрицы соединен с третьим информационным входом вычислительной ячейки (К+1)-й строки (1-1)-го столбца матрицы, выход суммы каждой вычислительной ячейки т-й строки 1-го столбца матрицы соединен с третьим информационным входом вычислительной ячейки первой строки (1-1)-го столбца матрицы (), выход суммы каждой вычислительной ячейки К-й строки первого столбца матрицы соединен с третьим информационным входом вычислительной ячейки (К+1)-й строки N-ro столбца матрицы, выход суммы вычислительной ячейки т-й строки первого столбца матрицы соеди-нен с третьим информационным входом вычислительной ячейки первой строки N-ro столбца матрицы, тактовые входы вычислительных ячеек j-й строки матрицы подключены к j-му разряду Тактового входа устройства, установочные входы вычислительных ячеек т-й строки матрицы подключены к установочному входу устройства, выходы суммы и переноса вычислительных ячеек ш-й строки матрицы подключены к соответствующим разрядам выходов результата и переноса устройства, соответственно, входы установки переноса и суммы вычислительных ячеек т-й строки матрицы подключены к .соответствующим разрядам входов установки переноса и суммы устройства соответственно, входы блокировки прохожде- ния сигнала переноса вычислительных ячеек первой строки матрицы подключены к соответствующим разрядам входа блокировки устройства, каждая вычислительная ячейка матрицы содержит одноразрядный сумматор и первый элемент И, причем первый и второй входы первого элемента И являются соответственно пе1эвым информационным входом и входом блокировки первого операнда вычислительной ячейки, выход первого элемента И соединен с входом первого операнда одноразрядного сумматора, вход второго операнда которого подключен к третьему информационному входу вычислительной ячейки, о т л и-чающееся тем, что, с целью повышения отказоустойчивости устройства, в каждую вычислительную ячейку
матрицы введены второй элемент И, два триггера, причем вход блокировки прохождения сигнала переноса каждой вычислительной ячейки К-й строки 1-го столбца матрицы подключен к входу блокировки прохождения сигнала переноса вычислительной ячейки ()-й строки (1-1)-го столбца матрицы, вход блокировки прохождения сигнала переноса вычислительной ячейки К-й строки первого столбца матрицы подключен к входу блокировки прохождения сигнала переноса вычислительной ячейки {К+1)-й строки N-ro столбца матрицы, в каждой вычислительной ячейке матрицы первый и второй входы второго элемента И являются соответственно вторым информационным входом и входом блокировки прохождения сигнала перено са вычислительной ячейки, выход второго элемента И соединен с входом переноса одноразрядного сумматора, выходы переноса и суммы одноразрядного сумматора соединены соответственно с информационными входами первого и второго триггеров, прямые выходы которых являются соответственно выходами переноса и суммы вычислительной ячейки, тактовые входы первого и второго триггеров подключены к тактовому входу вычислительно ячейки, первые установочные входы первого и второго триггеров подключены к установочному входу вычислительной ячейки, вторые установочные входы первого и второго триггеров подключены соответственно к входам установки переноса и суммы вычислительной ячейки
Продолжение таблицы
«u
: К 00 to
d x(Y)






| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения | 1989 |
|
SU1688238A1 |
| Устройство для умножения | 1988 |
|
SU1603379A1 |
| Устройство для умножения | 1989 |
|
SU1697078A1 |
| Матричный умножитель | 1988 |
|
SU1615704A1 |
| Устройство для умножения | 1987 |
|
SU1501043A1 |
| НЕЙРОПРОЦЕССОР, УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИЙ НАСЫЩЕНИЯ, ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО И СУММАТОР | 1998 |
|
RU2131145C1 |
| Вычислительное устройство | 1989 |
|
SU1697077A2 |
| Конвейерное устройство для умножения шестнадцатиразрядных чисел | 1984 |
|
SU1291970A1 |
| Матричное вычислительное устройство | 1982 |
|
SU1034032A1 |
| Устройство для умножения | 1989 |
|
SU1770960A1 |
Изобретение относится к автоматике и вычислительной технике и может быть использовано в универсальных и специализированных арифметических устройствах^ Цель изобретения - повышение отказоустойчивости устройства. С помощью объединения вычислительных ячеек матрицы в циклическую структуру образуется возможность благодаря увеличению размерности матрицы по столбцам исключать неисправные t. вычислительные ячейки, смещая расположение ра
о D D П D D D D П ODD ЙГф a D a P П
по0адаара
r%..
;,
rZ T ,
7
rfe r2
г t Фиг 6
S Б) О
a DS П
°99
r r
f г // 06e;(
Фиг 5
if
/ И/П «я i/D
-r
Фиг.8 m-l
51 S 13 Ф Ф (
D П 51 ЕГ D 1 ф Ф
0 о D
аш аоц ф1я{ аа
Фиг ITФиг. 12
fli
т
Старщие Нладши paspsiobi разаа,
проишбоия
Фиг.}5
t
Е
Авторы
Даты
1992-02-23—Публикация
1989-07-24—Подача