сл
с


| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ТРЕХМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ | 1991 |
|
RU2051411C1 |
| Вычислительный узел цифровой моделисетки для решения дифференциальных уравнений в частных производных | 1975 |
|
SU608165A1 |
| Устройство для решения двумерных задач математической физики | 1991 |
|
SU1833891A1 |
| Вычислительный узел цифровой моделисетки для решения дифференциальных уравнений в частных производных | 1975 |
|
SU546891A1 |
| Вычислительный узел цифровойСЕТОчНОй МОдЕли для РЕшЕНия диффЕРЕН-циАльНыХ уРАВНЕНий B чАСТНыХ пРОизВОд-НыХ | 1978 |
|
SU798858A1 |
| Вычислительный узел цифровой сеточнойМОдЕли для РЕшЕНия диффЕРЕНциАльНыХуРАВНЕНий B чАСТНыХ пРОизВОдНыХ | 1979 |
|
SU798859A1 |
| Матричное устройство для решения уравнений в частных производных | 1985 |
|
SU1302276A1 |
| Сеточный микропроцессор | 1978 |
|
SU763904A1 |
| Вычислительный узел цифровойСЕТКи | 1979 |
|
SU800997A1 |
| Вычислительный узел цифровой сетки для решения дифференциальных уравнений в частных производных | 1981 |
|
SU976448A1 |
Изобретение относится к области вычислительной техники и может быть использовано при построении специализированных и проблемно-ориентированных процессоров для решения дифференциальных уравнений в частных производных эллиптического типа. Устройство содержит многовходовый сумматор, регистр сдвига, элемент И, четыре группы элементов задержки и группу элементов И. Предназначено для решения трехмерных задач математической физики, отличается от из- вестных высоким быстродействием и точностью решения и позволяет сократить Количество узлов цифровой сетки. 2 ил.
Изобретение относится к области вычислительной техники и может быть использовано при построении цифровых сеток и процессоров для решения задач математической физики.
Цель изобретения - повышение точности вычисления.
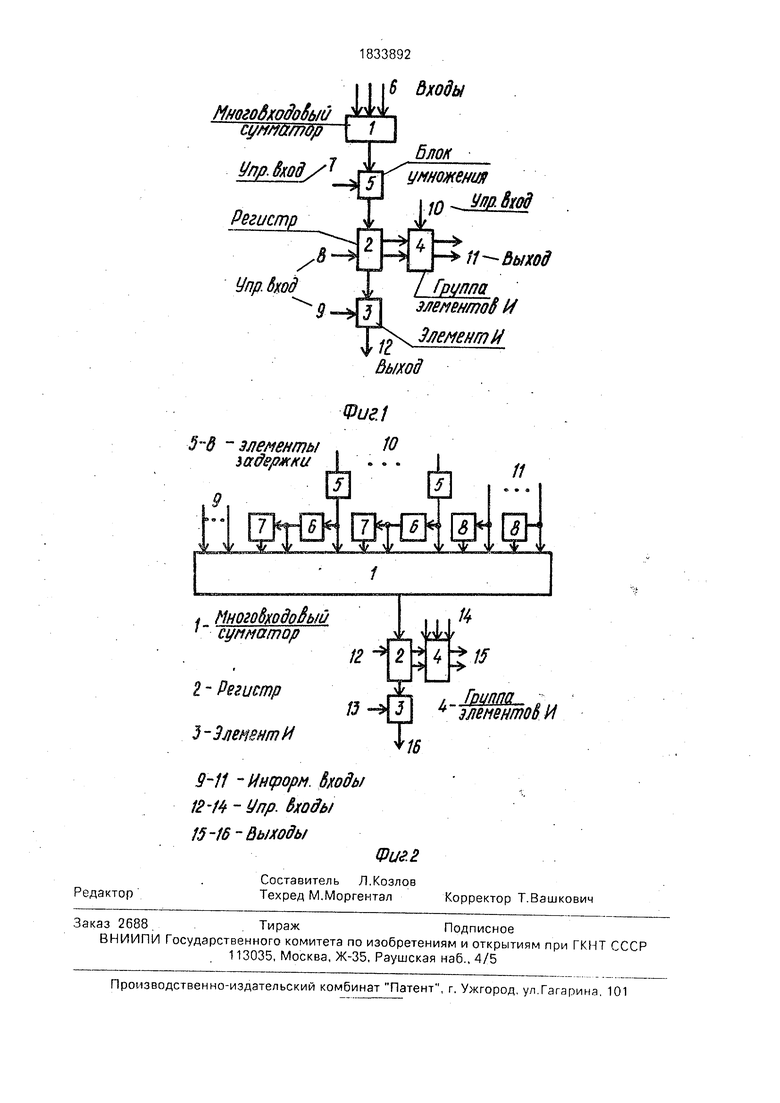
На фиг. 1 представлена схема предлагаемого узла.
Он содержит многовходовый сумматор 1, регистр сдвига 2, элемент И 3, группу элементов И 4, элементы задержки 5-8, первая 9, вторая 10 и третья 11 группы информационных входов, первый 12, второй 13 и третий 14 управляющие входы, параллельный 15 и последовательный 16 выходы результата узла.
Первая группа 9 информационных входов узла соединена с первой группой входов многовходового сумматора 1, выход которого соединен с информационным входом регистра сдвига 2, информационный выход которого соединен через элементы И группы 4 с параллельным выходе. результата 15 узла, последовательный выход результата 16 которого соединен через элемент И 3 с последовательным выходом регистра сдвига 2. Третий 14, второй 13 и первый 12 управляющие входы узла соединены соответственно с входами управления сдвигом регистра сдвига 2, вторым входом элемента И.З и вторыми входами элементов И группы 4. Вторая группа информационных входов 10 узла соединена через элементы 5
00
со ы со о ю
задержки первой группы с второй группой входов многовходового сумматора 1 и входами элементов 6 задержки второй группы, выходи которых соединены с третьей группой входов многовходового сумматора 1 и входами элементов 7 задержки третьей группы, выходы которых соединены с четвертой группой входов многовходового сумматора 1, пятая группа входов которого соединена с третьей группой информационных входов 11 узла и входами элементов 8 задержки четвертой группы, выходы которых соединены с шестой группой входов многовходового сумматора 1.
На первую 9 группу .информационных входов узла подается последовательный код восьми (для уравнения Лапласа) или девяти (для уравнения Пуассона) чисел младшими разрядами вперед. На вторую 10 и третью 11 группы информационных входов узла подается последовательный код соответственно шести и двенадцати чисел млад- шими разрядами вперед. Каждый очередной разряд этих чисел поступает на входы многовходового сумматора 1, на выходе которого формируется результат суммирования. Переносы в следующие разряды запоминаются на соответствующих элементах памяти (не показаны) многовходового сумматора 1 и используются в следующих тактах при суммировании следующих (1+1 и т.д.) разрядов чисел. При решении уравнения Пуассонана-один из информационных входов 9 первой группы подается последовательный код значения - 60h Fijk, где Fyk - значение первой части уравнения. На остальные информационные входы 9 первой группы подаются (синхронно с разрядами правой части) разряды значений (Ui± 1, J±i,k± 1) восьми ближайших угловых в двух соседних (i± 1) слоях узлов объемной сетки. На вторую 10 группу информационных входов подаются последовательным кодом разряды значений (Ui, ±1, k± 1: Ui ±1, j, k± 1; Ui ±1. j ±i.k) двенадцати ближайших по диагоналям в i-ом слое и двух соседних (I ±1) слоях узлов объемной сетки. На третью 11 группу информационных входов узла подаются последовательным кодом разряды значений .(Ui± 1. j, k; Ui. j± 1, k; Ui,j.k± О с последовательных выходов результата 16 соседних узлов по слою (i) столбцу 0) и строке (k) объемной цифровой модели-сетки (фиг.2). Эти значения чисел проходят через элементы задержки 5-8, на которых осуществляется задержка на один такт - время обработки одного разряда. В результате этого числа, поступающие на вторую 10 и третью 11 группы информационных входов
узла умножаются на коэффициенты четырнадцать и три соответственно. Задержка на один такт эквивалентна умножению на .коэффициент два, так числа, поступающие на
третью группу информационных входов 11, подаются на группы входов многовходового сумматора 1 непосредственно с коэффициентом единица и, пройдя через элементы задержки 8, с. коэффициентом два, т.е. суммарный коэффициент равен трем.
Для оперативного ввода значения - 6Qh Fijk во все узлы цифровой сетки и повышения быстродействия это значение может быть предварительно занесено параллельным кодом.на предусмотренный для этой цели регистр, на выходе которого под воздействием управляющих сигналов формируется последовательный код значения - 60h Fijk на каждой итерации решения.
Результат суммирования каждого разряда чисел, полученный на выходе многовходового сумматора 1, заносится в регистр сдвига 2. Код значения искомой функции Uijk на предыдущей r-ой итерации, содержащийся в-регистре сдвига 2, сдвигается на каждом такте под управлением сигнала, по- ступающего натретий 14 управляющий вход узла и выдается на последовательный выход 16 результата через элемент И 3 и на параллельный выход 15 результата через элементы И группы 4.- Элемент И 3 открывается сигналом, поступающим на второй 13 управляющий вход в течение всех п тактов (где п - разрядность чисел). После прохождения п
тактов элемент И 3 закрывается и в последующих семи тактах в узле осуществляется сдвиг регистра сдвига 2 на семь разрядов. При этом, происходит обработка семи старших разрядов чисел, поступающих с последовательных выходов 16 результата соседних узлов за счет их прохождения в течение от одного до семи тактов через элементы задержки 5-8. В течение (п+7) тактов в регистр сдвига 2 формируется код нового
приближенного значения искомого решения:
-
Ч 128
0
fu.zfu,.
L ;,j,xV - О НЁКт.ХГм.
+S(..m)
of.
()
Jil.K
(N M.kt,)
HJ..
+ U;t i.it,k)
j4
что и требуется для реализации зависимо55 сти Ј(iX;lx,;iu.
,(СлХ-1,л,Х,л,Л uVCu,,.,,k,,,,k,.
iH,,,x.,,0 i-i-diC1 нЛ1 tii(rl«lЈ8 u i l.jii.fcil uin,J4(,.i.,j-i,
uv
()
(rl
M
,1-1л..,1,),( + 1-(о(Л- 4
,,i,,,,()-ih4ik,
которая обеспечивает аппроксимацию дифференциального оператора Лапласа для трехмерного уравнения Лапласа с погрешностью до Ь , а для уравнения Пуассона с погрешностью до h6 или h4, в зависимости от функции правой части F..
Последующие итерации осуществляются аналогично и, когда решение получено, при сравнении результатов на двух последующих итерациях, на первый 12 управляю- цшА вход поступает сигнал, который открывает группу 4 элементов И, через кото рую результат решения выдается из регистра сдвига 2 на параллельный выход 15 результата узла.
По сравнению с прототипом, в предлагаемом устройстве обеспечивается более высокая точность решения, поскольку погрешность аппроксимациидифференциаль- ного оператора для уравнения Лапласа в нем определяется восьмым порядком степени шага дискретизации (h ), а в прототипе - вторым порядком (h ). Поскольку при pea; лизации устройства цифровой сетки для ре- шения трехмерного уравнения Лапласа или Пуассона необходимое количество узлов равно 1 /h , то использование предлагаемого узла для построения цифровой сетки позволяет сократить аппаратурные затраты сетки за счет существенного уменьшения количества узлов, поскольку шаг дискретизации (h) для заданной точности решения может быть значительно увеличен по сравнению с вариантом прототипа. Так, напри- мер, если требуется получить решение уравнения Лапласа с точностью (5 10 , то шаг для предлагаемого узла равен 0,1, а для прототипа - 0,0001. Тогда цифровая сетка должна содержать для предлагаемого устройства 1000 узлов или 10 узлов - прототипа. Это обусловлено тем, что точность решения в предлагаемом устройстве в (1 /h ) раз выше точности прототипа. Кроме того, существенно сокращается количество ите- раций для достижения решения, поскольку количество итераций пропорционально
квадрату числа узлов, т.е. повышается быстродействие устройства в 1 /h6 раз.
Формула (1) аппроксимирует дифференциальный оператор исходного уровня Лапласа с п огрешностью 0(h8), что проверяется путем разложения дифференциального оператора в узлах объемной матрицы в ряд Тейлора и суммирование их с коэффициентами по формуле (1).
Формула изобретения Вычислительный узел устройства для решения уравнений в частных производных, содержащий многовходовый сумматор, регистр сдвига, элемент И и труппу .элементов И, причем первая группа информационных входов соединена с первой группой входов многовходового сумматора, информационный выход регистра сдвига соединен с первыми входами элементов И группы, вторые входы и выходы, которых соединены соответственно с первым управляющим входом узла и с параллельным выходом результата узла, последовательный выход регистра сдвига соединен с первым входом элемента И, второй вход и выход которого соединены соответственно с вторым управляющим входом узла и последовательным выходом результата узла, третий управляющий вход узла соединен с входом управления сдвигом регистра сдвига, отличающийся тем, что, с целью повышения точности вычисления, он содержит четыре группы элементов задержки, причем вторая группа информационных входов узла соединена через элементы задержки первой группы с второй группой входов многовходового сумматора и входами элементов задержки второй группы, выходы которых соединены с третьей группой входов многовходового сумматора и входами элементов задержки третьей группы, выходы .которых соединены с четвертой группой входов многовходового сумматора, пятая группа входов кеторого соединена с третьей группой информационных входов узла и входами элементов задержки четвертой, группы, выходы которых соединены с шестой группой входов многовходового сумматора, выход которого соединен с информационным входом регистра сдвига.
Ш5 Входы
fl u VUVVOIu Г,
сумйтЬр г / I
7 1 Блок Упр. Ы/ jjjK умножения
ТГ Регистрф X
л v С..
11--Выхо
&
Фиг/
элементы , тдержки Л
5
Hh&
.-еЖ
/„ t
Многоходовый супматор
I - Регистр 3-Злеп8нтИ
/J-
С..
11--Выход
л
/ Группа
х I эле меняю8 И J J
у Элемент И Выход
10
11
f
du
/4
12
.#
/ Гриппа в элененто&И
| Катков А.Ф., Романцев В.П | |||
| Комбинационная цифровая сетка для решения уравнений математической физики - Рефераты докладов IV Всесоюзного совещания Математическое моделирование | |||
| Теория и методы гибридных вычислений | |||
| Таллинн, 1973, с.37-40 | |||
| Вычислительный узел цифровой моделисетки для решения дифференциальных уравнений в частных производных | 1975 |
|
SU608165A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1993-08-15—Публикация
1991-05-05—Подача