Известен способ многотактного выполнения логических операций, при котором операция «ИЛИ осуществляется синхронной подачей входных сигналов на входы элемента «ИЛИ, а операция «И и «ИЕ реализуется подачей сигналов входных последовательностей по очереди на входы «1 и «О элемента .памяти.
Предложенный снособ отличается от известных тем, что, с целью упрощения и повыщения надежности выполнення логических операций, входные последовательности сигналов с элементов яамяти и «ИЛИ подают без промежуточных вентилей па другие элементы памяти и «ИЛИ, а логическую функцию считают выполненной, если хотя бы один из сигналов выходной последовательности логической схемы является заданной функцией ее входных сигналов.
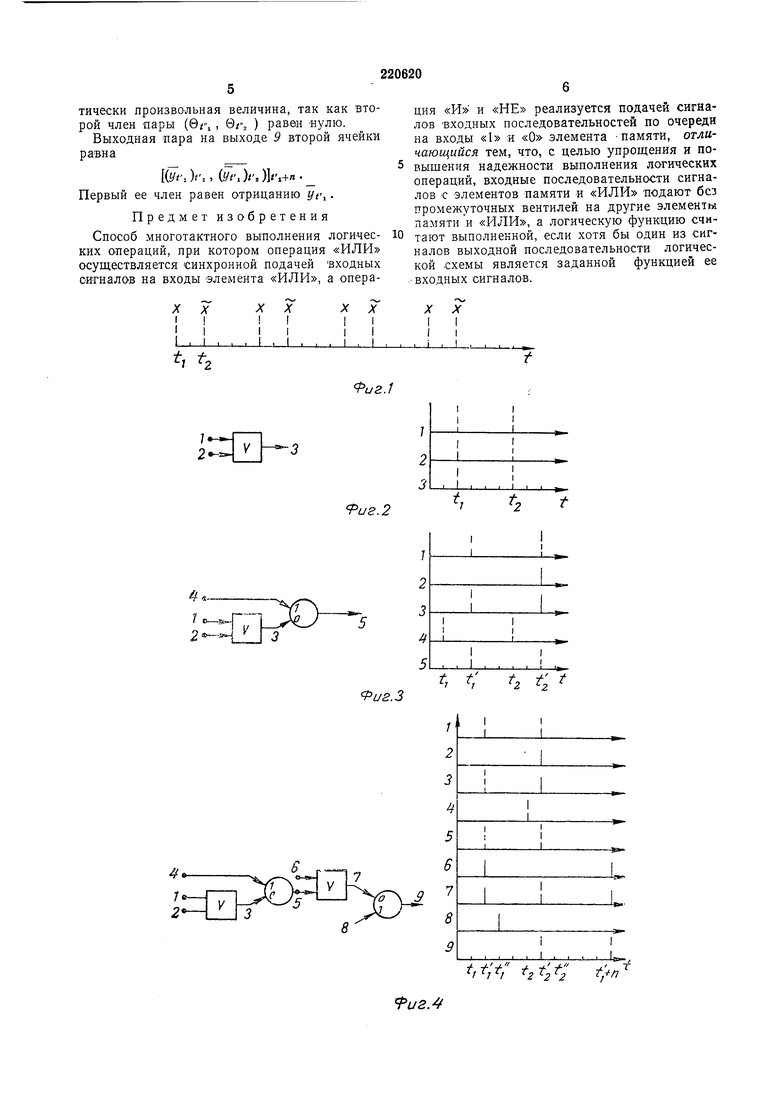
На фиг. 1 представлена временная последовательность двоичных сигналов: на фиг. 2- схема, реализующая дизъюнкцию -пар; на фиг. 3 - схема, реализующая конъюнкцию пар; на фиг. 4 - схема, реализующая отрицание нары.
В многотактных схемах используется возможность строить логические схемы без совпадения логических сигналов. Этот способ рассмотрим на примере четырехтактной феррит-триодной схемы. На вход записи «1 феррит-триодной ячейки «памяти (ФТЯ) во время первого такта подается сигнал х, а во время второго такта на вход записи «О этой же ячейки подается сигнал у (на этот же вход во время четвертого такта подается тактовый
сигнал 0). Выход этой ячейки во время второто такта эквивалентен операции «И над входными сигналами х и у, а во время четвертого такта - онерации «ЗАПРЕТ, т. е. выход ячейки описывается парой функции
«И и «ЗАПРЕТ. Чтобы выполнить одну из этих операций известным способом, последовательно с выходом ячейки подсоединяется вентиль, управляемый некоторым тактовым сигналом. Если, например, этот тактовый сигнал открывает вентиль во время второго такта и не открывает его во время четвертого такта, то выход вентиля во время второго такта эквивалентен операции «И, а в остальные моменты цикла сигнал на выходе равен
нулю. Недостатком этого способа является наличие вентиля после каждой феррит-триодной ячейки, так как это существенно ycлoлvняет схему. Важно отметить, что необходимость вентиля вытекает из того, что одна из
пары функций «И и «ЗАПРЕТ, которые
описывают выход ячейки, рассматривается как ляться от «помех. Более того, в этом случае существенным образом используются пары функций, которые в общем случае могут отличаться от функций «И и «ЗАПРЕТ. Поэтому такие пары функций /i и /о будем записывать в виде (fi, /2). На фигурах представлены временные диаграммы, поясняющие работу схем. Сигналы, которые могут быть равны либо «О, либо d, обозначаются на диаграммах пунктирами. Сигналы, тождественно равные «1 (тактовые сигналы), изображаются сплощными линиями. На фигурах цифрами указываются входы и выходы схем «11ЛИ и ячеек «памяти. Предлагаемый способ позволяет выполнять любую логическую функцию, используя лищь многотактные регистры, схемы «ИЛИ и специальное представление информации в виде пар сигналов, при этом к сигналам в схеме не предъявляется никаких специальных требований. Поясним понятие пары сигналов. Пусть имеется временная последовательность некоторых двоичных сигналов х и х (см. фиг. 1) Х(, , Xt,....X , , (к 0, 1,2,...) Индексы внизу справа указывают соответствующие моменты времени. Пусть при этом в остальные моменты времени сигналы л: и л тождественно равны нулю и i i 54. Эта последовательность полностью описывается циклическими парами сигналов „.,-0,1,2), для которых вводим обозначение (Xt , xt.,), При описании логических схем подробно рассматривается один какой-нибудь цикл, например нулевой (Л 0). В частном случае может оказаться, что , тогда получается обычное представлепие информации в многотактных схемах. Например, выход ФТЯ, опрашиваемой тактовым генератором в моменты /i-f4.ft , описывается переменной Xt или парой (xt, , Xt,). Пара (х, X) равна, по определению функции если выполняется по крайпей мере одно из равенств. Для определенности будем считать, что должно выполняться первое условие. Покажем, что, используя обычные схемы, многотактные регистры сдвига и схемы «ИЛИ, над парами сигналов можно выполнять операции «ИЛРЬ, «И и «НЕ. Таким образом, реализовать любую логическую функцию, так как перечисленные элементарные операции образуют полный набор. Пример 1. Дизъюнкция пар реализуется схемой на фиг. 2. Пусть на входы У и 2 обычной схемой «ИЛИ подаются соответственно две лары (Х(, , xt,) и (г//, , , равные соответственно Xt, м yt, Так как пары поступают на входы схемы «ИЛИ синхронно, то ее шина 3 описывается парой (xt / yt , t, У yt, ) Эта пара равна функции Xt yt,Следовательно, схема «ИЛИ преобразует входные пары в выходную пару, равную дизъюнкции входных пар. Пример 2. Конъюнкция пар реализуется схемой на фиг. 3. На вход 4 феррит-триодной ячейки «памяти в я-тактпой схеме подается пара (xt , Xt), а на щину 3 записи пара (yt,yi, V 0rJ, где ©Гг -тактовый сигнал, эквивалентный а t, 4, tl и t связаны соотношениями ti fi t to, t2 - ,. Пара (У(,,У1, V Qf, ), получается на выходе 5 схемы «ИЛИ из пары (yt, Ус,) на входе 1 и пары (Qfi , Qr, ) на входе 2. Выход 5 упомянутой ячейки «памяти описывается парой (Xi, yf,)t ,(Х(, yt, V t, равной операции «И над сигналами Xt и yt . Таким образом, с помощью простой ячейки «памяти и схемы «ИЛИ, преобразуя входные пары, можно получить выходную пару, равную логическому произведению входных. Пример 3. Схема задержки пары. Полагая в предыдущем примере, что пара (yti, Ус, / Qf,) равна паре (9,, Qt,), получаем выходную пару ячейки «памяти. (Or.,Jr., которая равна входной, но сдвинута во времени относительно первой. Так осуществляется задержка пары. Видно, что при этом «расстояние во времени между членами пары можно менять. Пример 4. Отрицание пары (фиг. 4). Покажем, как выполнить логическое отрицание пары, т. е. из пары (у, у) получить паРУ (.. у}, где у - какая-то не интересующая нас функция. Если в примере 2 взять в качестве пары (х, х) пару (0, , 0,, ) на входе , то выход 5 ячейки эквивалентен паре г/г, , , которую Подаем на вход схемы ИЛИ. С помощью этой схемы, подавая на еВХОД 6jiapy (Qi, , получаем пару V Ус, (yti )t, Эту пару подаем на ход 7 записи «О другой ячейки «памяти на ход 8 записи «1 которой подается пара вг, ,0rJ, причем t,t, + n-l,
тически произвольная величина, так как второй член пары (бг, , Qt ) равен нулю.
Выходная пара на выходе 9 второй ячейки равна
(t/rjr., (i/i.K)K+n- Первый ее член равен отрицанию г/г,
Предмет изобретения
Способ многотактного выполления логических операций, при котором операция «ИЛИ осуществляется синхронной подачей входных сигналов на входы элемента «ИЛИ, а оцерация «И и «НЕ реализуется подачей сигналов ВХОДНЫХ последовательностей по очереди на входы «1 :и «О элемента -памяти, отличающийся тем, что, с целью упрощения и повьшения надежности выполнения логических операций, входные последовательности сигиалов С элементов памяти и «ИЛИ подают без промежуточных вентилей на другие элементы памяти и «ИЛИ, а логическую функцию считают выполненной, если хотя бы один из сигналов выходной последовательности логической схемы является заданной функцией ее -ВХОДНЫХ сигналов.

| название | год | авторы | номер документа |
|---|---|---|---|
| МОДУЛИ СТРУЙНОЙ ПНЕВМО- и ГИДРОАВТОМАТИКИ | 1967 |
|
SU195721A1 |
| ПНЕВМАТИЧЕСКОЕ УНИВЕРСАЛЬНОЕ ЛОГИЧЕСКОЕУСТРОЙСТВО | 1969 |
|
SU241796A1 |
| ЦИФРОВОЕ ВЫЧИСЛИТЕЛЬНО-ЛОГИЧЕСКОЕ УСТРОЙСТВО | 1970 |
|
SU273523A1 |
| Логическое запоминающее устройство | 1972 |
|
SU442512A1 |
| СПОСОБ ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ НА ЗАПОМИНАЮЩЕМ ЭЛЕМЕНТЕ | 1966 |
|
SU224160A1 |
| Логическое запоминающее устройство | 1972 |
|
SU464017A1 |
| Система для автоматизированногопРОЕКТиРОВАНия и упРАВлЕНия TEXHO-лОгичЕСКиМи пРОцЕССАМи B МиКРОэлЕКТРО-НиКЕ | 1976 |
|
SU805322A1 |
| Микропроцессор | 1983 |
|
SU1141419A1 |
| РЕКУРСИВНЫЙ ЦИФРОВОЙ ФИЛЬТР | 1992 |
|
RU2075826C1 |
| МНОГОФУНКЦИОНАЛЬНЫЙ ФЕРРИТ-ДИОДНЫЙ КОММУТАЦИОННЫЙ ЛОГИЧЕСКИЙ ЭЛЕМЕНТ | 1968 |
|
SU207474A1 |



Даты
1968-01-01—Публикация