Изобретение относится к области автоматики и вычислительной техники и предназначено для преобразования двоичного кода в десятичный код или код с любым другим основанием.
Известны двоично-десятичные преобразователи, использующие суммирующие (счетные) схемы, в которых преобразование кода осуществляется последовательно.
Предложенное устройство отличается тем, что оно содержит пирамидальные сумматоры всех разрядов числа с новым основанием, при этом число разрядов первого сумматора, на котором выделяется младший разряд числа с новым основанием, равно разрядности преобразуемого двоичного кода, а максимальное число связей между разрядами сумматора равно новому основанию (при его четности) или его удвоенному числу (при его .нечетности), половина выходов каждого разряда старщих численных значений нового основания соединена с помощью логических элементов «И- ИЛИ, выходы которых связаны с соответствующими входами разрядов сумматора следующего (старшего) разряда числа с новым основанием.
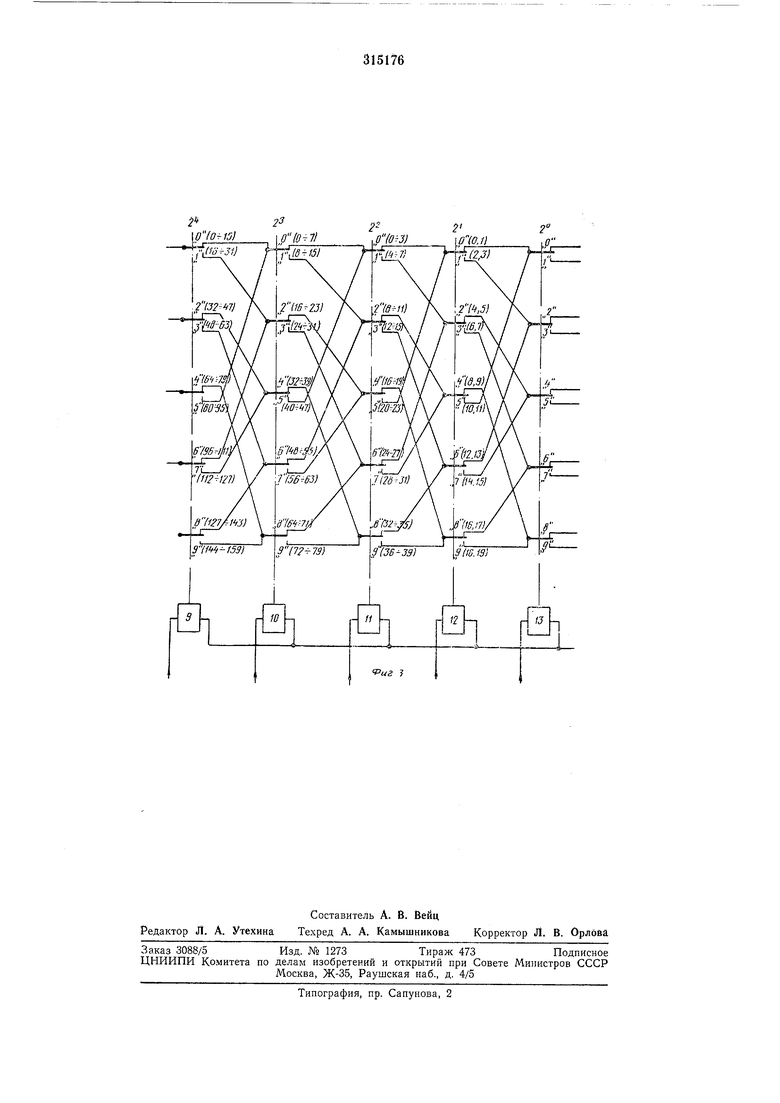
фиг. 3 -пять последних ячеек сумматора для любого целого числа.
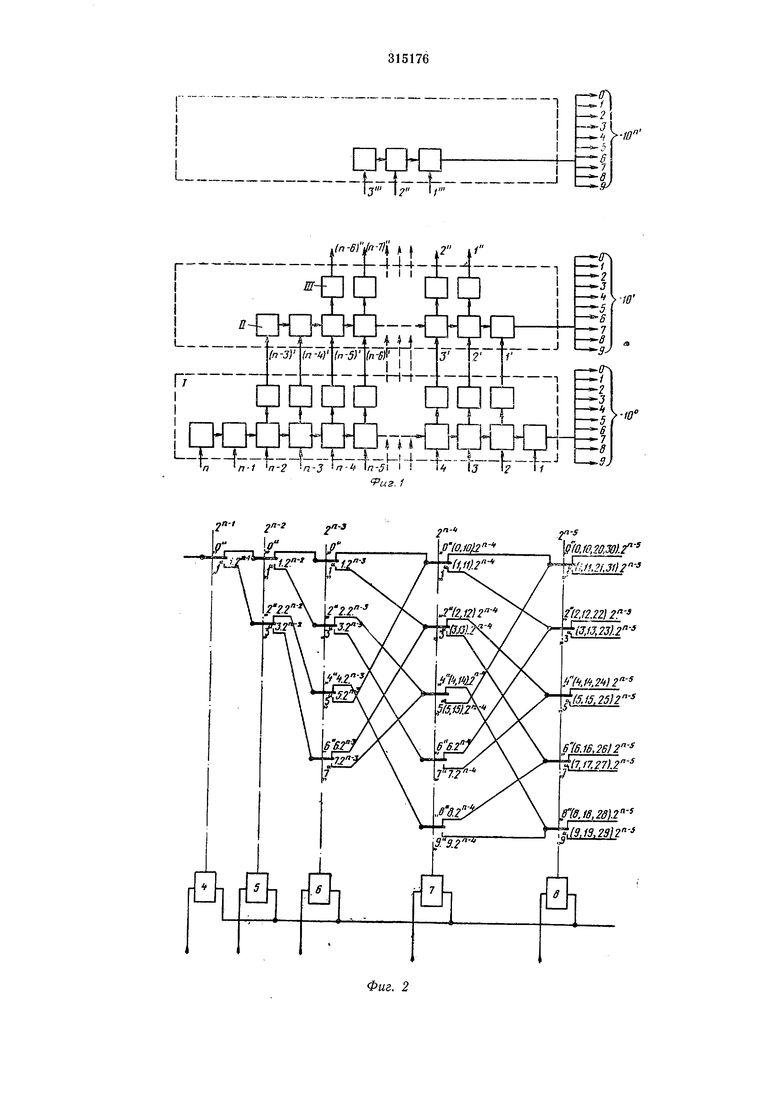
Устройство содержит релейно-диодные сумматоры I, число которых равно разрядности десятичного числа, контактные группы реле ячеек П и диодные сборки 1П. Число ячеек 1-я, а входов О-9.
Первый сумматор (на фиг. 1 нижний) - сумматор единиц десятичного числа - образуется контактами входных реле. На обмотки этих реле по п цепям (п - число разрядов двоичного кода) подается запитывающее напрял ение в соответствии с двоичным кодом (запитываются обмотки реле разрядов со значением 1). Внутри сумматора связь между ячейками П осуществляется от старшего разряда к младшему.
С десяти выходов первого сумматора снимается инфор.мация о единицах десятичного числа, а также информация о числе десятков в виде двоичного кода.
Двоичный код числа десятков подается на второй сумматор, который со своих десяти выходов выдает это число. С сумматора десятков снимается двоичный код числа сотен и т. д.
Контакты реле ячеек сумматора единиц десятичного числа (фиг. 2) образуют пирамиду, в вершине которой - контакты реле старшего двоичного разряда, а в основании пирамиды - контакты реле младшего разряда двоичного кода (на схеме под контактами указано числовое значение разрядов двоичного числа). Для каждого числа в пирамиде образуется единственная сквозная цепь от вершины пирамиды до одного -из ее оконечных выходов, и появление напряжения на том или ином контакте пирамиды определяется значением данного и всех старших разрядов двоичного кода.
Так, например, на выходе «3 ячейки 5 напряжение появляется только в том случае, если значение двух старших разрядов двоичного числа соответствует единицам, т. е. число равно а напрялсение на выходе «1 ячейки 7 появляется, если двоичное число равно или и т. д.
При данном соединении ячеек пирамиды десять ее выходов соответствуют значению единиц десятичного числа. Для того, чтобы убедиться в этом следует положить п равным любому числу. Если, например , то значение младшего разряда числа 2 . В этом случае на нулевом выходе «О сумматора напряжение появится, когда число имеет нуль единиц, т. е. О, 10, 20, 30, на выходе «1, - когда число единиц равно «1, т. е. 1, 11, 21, 31 и т. д.
На фиг. 3 на контактах реле указано, в каких пределах может находиться преобразуемое число в зависимости от значения данного и всех младших разрядов. Если на выходе десятичного сумматора значение чисел лежит в пределах десятка () 2°, то на выходе предпоследней ячейки значения чисел ограничиваются пределами двух десятков (O-f-9) 2, на выходе следуюш,ей ячейки в пределах четырех десятков (0-н9) 2 и т. д.
Появление напряжения на любом из верхних пяти выходов «О, «1, «2, «3 и «4 ячейки 12 свидетельствует о том, что преобразуемое число в своих последних двух младших разрядах имеет значение OO-f-09, или , или 40-Г-49 или 60-f-69 и, наконец, 80-Г-89. Появление же напряжения на одном из нижних пяти выходов ячейки 12 («5, «6, «7, «8, «9) возможно, если число лейцит в пределах lO-f-19, или 30-н39, или 50-f-59, или 70-f-79, или 90-н99.
Следовательно, в первом случае число десятков преобразуемого кода четно и потому младший разряд двоичного кода числа десятков равен нулю. Во втором случае число десятков нечетно и поэтому младший разряд двоичного кода, выралкающего число десятков, равен единице.
По сходным рассуждениям наличие напряжения на верхних пяти выходах ()
реле ячейки // свидетельствует о том, что второй разряд двоичного кода, выражающего число десятков, равен нулю, а наличие напряжения на одном из выходов () показыва-ет, ч го он равен единице.
Таким образом можно снять полную информацию в двоичном коде числа десятков. В общем случае число разрядов двоичного кода, выражающего число десятков, на три меньше, чем разрядность двоичного кода,
подлежащего преобразованию, так как младший разряд двоичного кода, выражающего числа десятков, снимается с выходов реле ячейки 12, а старший - с контактов реле ячейки 6 с выходов «5, «6, «7 (реле ячейки 4 и 5 не имеют выходов ).
С сумматора десятков с помощью диодных сборок запитывается сумматор сотен и т. д. Сумматор старшего разряда десятичного числа выполняется без диодных сборок.
предмет изобдетения
Преобразователь двоичного кода в код с любым другим основанием, использующий
принцип преобразования кодов на сумматорах и логических элементах, отличающийся тем, что, с целью повышения быстродействия и упрощения схемы, он содержит пирамидальные сумматоры всех разрядов числа с новым
основанием, при этом число разрядов первого сумматора, на котором выделяется младший разряд числа с новым основанием, равно разрядности преобразуемого двоичного кода, а максимальное число связей между разрядами сумматора равно новому основанию (при его четности) и его удвоенному числу (при его нечетности), половина выходов каждого разряда старщих численных значений нового основания соединена с помощью логических
элементов «И-ИЛИ, выходы которых связаны с соответствующими входами разрядов сумматора следующего (старшего) разряда числа с новым основанием.
:Л
/ .(
.
s
-7
-8, S
Ij 2 It

| название | год | авторы | номер документа |
|---|---|---|---|
| Преобразователь двоичного кода в двоично-десятичный код угловых единиц | 1986 |
|
SU1349008A2 |
| Преобразователь двоичного кода в двоично-десятичный | 1984 |
|
SU1277402A1 |
| Преобразователь двоичного кода угла в двоично-десятичный код градусов и минут | 1983 |
|
SU1116425A1 |
| Преобразователь кодов | 1989 |
|
SU1619402A1 |
| Преобразователь двоично-десятичного кода в двоичный | 1973 |
|
SU517890A1 |
| Преобразователь последовательного двоичного кода в параллельный двоично-десятичный код | 1982 |
|
SU1084780A1 |
| Преобразователь двоичного кода в двоично-десятично-шестидесятиричный код | 1979 |
|
SU860054A1 |
| Преобразователь двоичного кода в двоично-десятично-шестидесятиричный код | 1988 |
|
SU1529457A2 |
| Преобразователь кодов | 1978 |
|
SU744548A1 |
| Преобразователь двоичного кода в двоично-десятичный код | 1982 |
|
SU1097995A1 |

-s
4l0.10,20Mf ,2i.3t)
212Д. iJ,23).
Даты
1971-01-01—Публикация