К авторскому свидетельству С. Д. Понамарева, заявленно.1у I июня 19 ;3 года (спр. о перв. jNs 129625).
О с.ыдаче аьторского свидетельства опубликовано Л kian 1934 года.
В технике при решении целого ряда практических задач встречается необходимость брать определенные интегралы
типа
I f(ij) dx, где / р (ж).
Например, при определении статического момента S, или момента инер ции /д. какой-либо площади относительно оси XX (фиг. 1 и 2) приходится вычислять интегралы: .
ryldx
ry.ax г --J 2 +j
S.
и т. д.
Если функция 7/ (ж) задана аналитически, то, во бще говоря, интегрирование может быть выполнено, но обычно это связано с большими математическими выкладками, что требует много времени и умственного напряжения, тем более, что очень часто отдельные участки кривой выражаются разными уравнениями. Не менее часто встречаются фигуры, очерченные линиями, полученными из конструктивных соображений или экспериментально; в этих случаях y (f(x) остается аналитически неизвестной, и тогда можно применять только графические способы, которые также требуют много времени и кропотливой работы.
Уже с давних пор все проектные организации и научные учреждения снабжены планиметрами, - приборами, позволяющими определять площади фигур, ограниченных любыми линиями. С математической точки зрения можно сказать, что планиметр есть прибор, позволяющий брать определенные интеь
гралы типа I ydx, где У («).
Предлагаемый прибор имеет целью расширить область применения плани метра и позволяет не только брать указанные выше ; нтегралы, но возможность йеханическим путем вычислять, например, интеграл Мора
1 М Mj dx, которой, как известно,
юд
играет громадную роль в теории сооружений, так как с помощью его находятся деформации различных систем.
Возможность брать этот интеграл механическим способом значительно упрощает технику расчетов и позволяет внедрить формулу Мора в ряд отделов строительной механики, где до сих пор она применялась лишь в очень слабой степени, в виду сложности аналитических выкладок, например, в расчет кривого бруса большой кривизны и т. д.
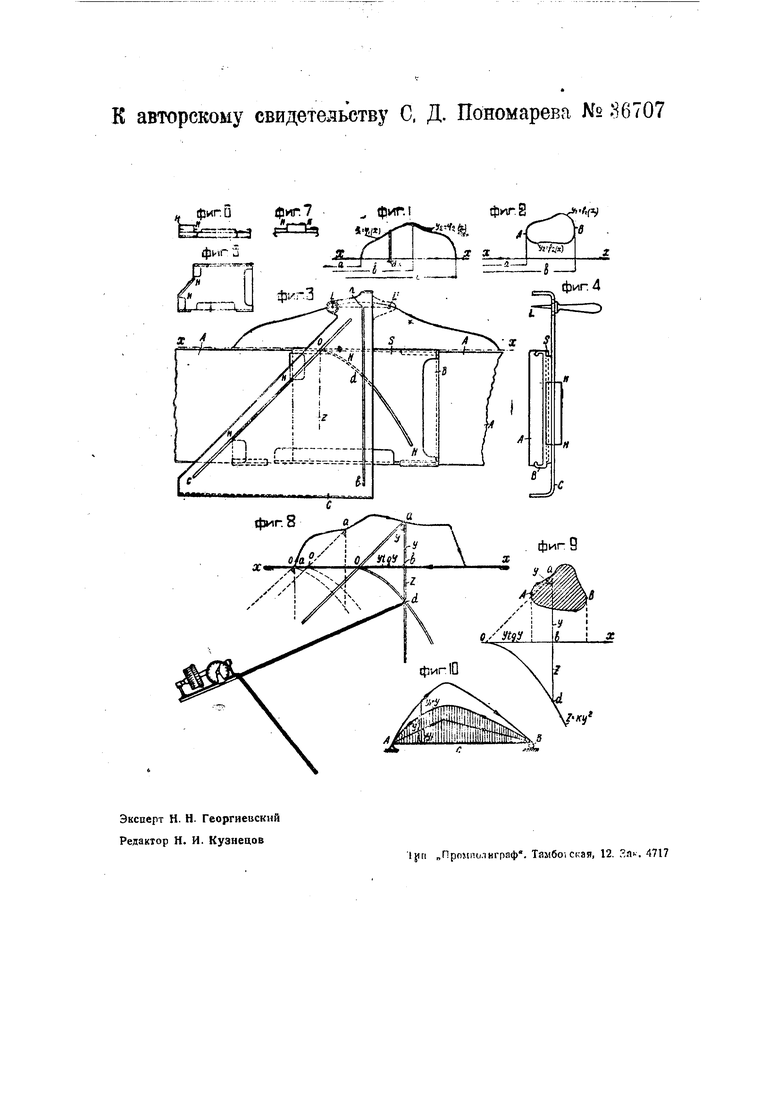
На чертеже фиг 1 и 2 поясняют графически определение статического момента S, или момента инерции У, какой-либо площади относительно оси жж; фиг. 3-вид прибора сверху; фиг. 4 - вид сбоку; фиг- 5-7 деталь движка в различных проекциях; фиг. 8-схема, поясняющая пользование прибором, фиг, 9 и 10-графики, относящиеся к нахождению статического момента -.У,. и центра тяжесТи фигуры относительно оси жж и к определению прогиба балки в некоторойТочке ее.
Предлагаемый прибор имеет следующее устройство. Вдоль Нланшайбы А (фиг. 3, 4) моЖёт поступательно двигаться движок В, с шаблоном S, на котором сделан прорез О NN по кривой (y), шириною около мм. Шаблон устроен сменным для того, чтобы можно было применять прибор при различных функциях (y).
Ось уу у кривой прореза (y) должна совпадать с осью хх заданной кривой и поэтому наиболее удобно, чтобы она помещалась на краю движка (ось SZ уу, начало координат точка О).
Относительно движка перемещается пластинка С с нанесенным на ней
угольником аЬс (угол при вершине и равен 45°) Одна из сторон угольника иЬс, представляющая прямой прорез шириною в 1-1,5 мм, всегд 1 „п рп|ендикулярна к ребру планшайбы А, а следовательно, и к краю движка В и взаимно совмещенным осям хх и уу кривой- (t/).- Другая сторона угольника аде всегда прохсадит через начало координат О кривой (y),B каком бы положении движок В и угольник С ни находились. Для осуществления такой связи между угольником и движком на последнем имеется прямолинейная направляющая НН, проходящая Через начало координат О, а сторона угольника ; «ос представляет собою прорез; таким образом, угольник будет скользить по направляющим относительно двхжка с соблюдением указанных выше условий.
в вершине угольника а (фиг. 3) помещается игла, которая для удобства может быть вынесена в сторону параллельно Оси L или L. Это будет лишь смещать заданную кривую относительно прибора. Установив неподвижно планшайбу так, чтобы ось уу, совпадающая с краем движка, совмещалась с осью XX заданной кривой, обводят иглой /- или L заданную кривую по стрелке часов и ось хх справа налево (или наоборот). При этом пластинка С и дзижск В перемещаются вдоль п-ланшайЬы А, а шпиль планиметра, помещенный в точке d пересечения двух npopejOB NN и аА, увлекаемый первым и направляемый последним, будет описывать кривую (y).
Счетчик планиметра даст нам
ьь
j sdx f f(y}dx.
aa
Действительно (фиг. 8) ад::. Если - 45°, то у; если же сделать угол 9 не 45°, а любой, то OZ) иногда это будет лишь менять масштаб и может быть удобно использовано; M (i/). Шпиль планиметра, связанный с точкой d, будет описывать кривую z f(y, а его счетчик даст нам интересующий нас интеграл.На фиг. 8 указано применение прибора, заключающееся в том, что с помощью угольника и шаблона возможно перемещать шпиль планиметра по требуемой кривой без построения этой кривой, и таким образом получать
I f(y)dx, если графически задано
о,
у л{х).
Пример 1. Найти статический мо мент у. и центр тяжести фигуры (фиг 9) относительно оси хх.
Имеем:
аЬ - у; Ob - yig s-pij, где p ig.
.
Установив иглу а в точке А фигуры, записываем отсчет по счетчику планигчетра, затем обводим иглу а по контуру фигуры по часовой стрелке; возвратившись в точку А, вновь записываем показания счетчика; разность конечного и начального показаний дает нам площадь F фигуры, у которой ординаты всех точек равны 1/.
F -ГУ
S.
2Ар
F
Помощью планиметра легко находим /- плошадь заданной фигуры.
Для того, чтобы найти момент инерции этой фигуры ртносительно оси жж, надо воспользоваться другим шаблоном,
для которого z ky , тогда У,, ,
Таким образом мы видим, что определение центра тяжести и момента инерции любых фигур, т. е. решение двух больших задач требует всего лишь двух шаблонов.
Пример 2. Особое значение, как уже указывалось выше, прибор приобретает в решении интеграла Мора SMM dx, где M - f(x) и М (х) заданы эпюрами изгибающих моментов, например, требуется определить прогиб балки в некоторой точке С (фиг. 10).
1)Строим балку в масштабе мм - а см.
2)Строим эпюру от единичной нагрузки 1 р см, т. е. .
3)Строим эпюру изгибающих моментов, откладывая ординаты от оси хх и от единичной эпюры одновременно в масштабе 1 , т. е, М.у.
з;-2Х.2
/
I jSfMj(fЖ «рY I ,
ж,а,
НО
а2х у
J щ dx 2- / (
а
a;i
f. «2
(У + У. -
Г52- j 1/1 - J у
Т. е.
MM, dx - I J (y + yiYdxa, Laij
X2«2
- J 7// (Zo; - J / dx .
Ж «IJ
Каждый из интегралов, стоящих в квадратных скобках, берется как статический момент с помощью шаблона
Х2
s /fj/, так что I г/ dx ,- где
3 kp
JkD
Ж
F площадь эпюры, ординаты
„2 .2
равны Jcp у, г. е.
.Г2
I MM,da:(F,F
XI
2 3 V Р I о
2 k/
Движение иглы L прибора стрелками.
Сперва, перемещением иглы по часовой стрелке, обводится кривая (l/+yjl 9 (ж), затем кривая (а;), против стрелки часов, затем ось Х слева направо и, наконец, 1/1 4(7) .п отив стрелки часов. Счетчик планиметра, шпиль которого помещен в криволинейном прорезе, сразу даст нам Й- прогиб - О- (k 1) могут
2А;р /
равняться 1).
Таким образом, достаточно, не отрывая руки, обвести иглой прибора кривые / -J- /1, у и 2/1 и уможить получившуюся плои-1адь, подсчитанную по планиметру, на ч и прогиб найден при эпюрах любой сложности, т. е. даже в тех случаях, когда применение общеизвестного правила Верещагина является затруднительным.
Совершенно так же решается вопрос об определении деформаций кривого бруса; здесь интеграл Мора имеет вид
Ж1
I ЖМ| ds и он берется механически,
ж
только что описанным способом. Необходимо лишь эпюры построить на развертке оси бруса, т. е. дать графически Ж : 5 (S) и Ж, - ({v (s).
Приведенные примеры показывают, каким образом решаются с помощью предлагаемого прибора довольно сложные задачи, которые приходится решать в повседневной инженерной практике. Полная механизация .решения .не только сократит математические выкладки и с-ьэкономит много рабочих часов, но прибор позаолит передать решение этих вопросов работникам средней квалификации и освободит инженеров от сложных и утомительных подсчетов, которые приходится делать
Предмет изобретения.
Прибор для вычисления определенъ
/дй
их по заданных интегралов типа
ному графически У (), Отличающийся применением ходящего по планшайбе А движка В со сменнь11м шаблоном (S, на котором имеется прорез N по кривой /(/) и поверх которого может перемещаться пластинка С с нанесенными на ней в виде угольника прорезами аЬ и ас, из которых прорез аЪ перпендикулярен к ребру планшайбы А, и место его пересечения А с прорезом NN на шаблоне предназначено для помещения шпиля планиметра, а прорез ас всегда проходит через начало О координат кривой s f (г/) на шаблоне 8, причем пластинка С снабжена иглой L, помещенной в одной из точек прямой, проходящей через верщину а угольника аЪс параллельно ребру лланщайбы 4 и служащей для обвода заданной графически кривой.



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для анализа периодических кривых | 1936 |
|
SU49506A1 |
| Планиметр | 1928 |
|
SU14655A1 |
| ПРИБОР ДЛЯ ГАРМОНИЧЕСКОГО АНАЛИЗА | 1935 |
|
SU47116A1 |
| Планиметр | 1930 |
|
SU18407A1 |
| ФУНКЦИОНАЛЬНЫЙ ИНТЕГРИМЕТР | 1968 |
|
SU212562A1 |
| ПРИБОР ДЛЯ ПОСТРОЕНИЯ ЭПЮР ПЕРЕРЕЗЫВАЮЩИХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ БАЛОК | 1937 |
|
SU62172A1 |
| Прибор для вычерчивания кривых, линейно зависящих от наперед заданной шаблоном или чертежом кривой у=f(х) | 1935 |
|
SU51027A1 |
| Функциональный дифференцио-интеграф | 1955 |
|
SU118616A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО ПРОИЗВОДСТВА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ | 1932 |
|
SU36063A1 |
| Интегратор для измерения телесных углов | 1936 |
|
SU49291A1 |


Авторы
Даты
1934-05-31—Публикация
1933-06-01—Подача