Аналитический метод преподавания математики имеет вполне отвлеченный характер и поэтому иногда трудно усваивается учащимися. В противоположность этому графический метод, вследствие большей наглядности, значительно облегчает понил{ание сущности основных положений высшей математики. При этом процесс построения производной может помочь усвоению сущности аналитического метода нахождения производной данной функции.
Эти особенности характеризуют предлагаемое учебное пособие.
С помощью предлагаемого учебного пособия можно в промышленности определять скорость протекания любого процесса по опытному графику.
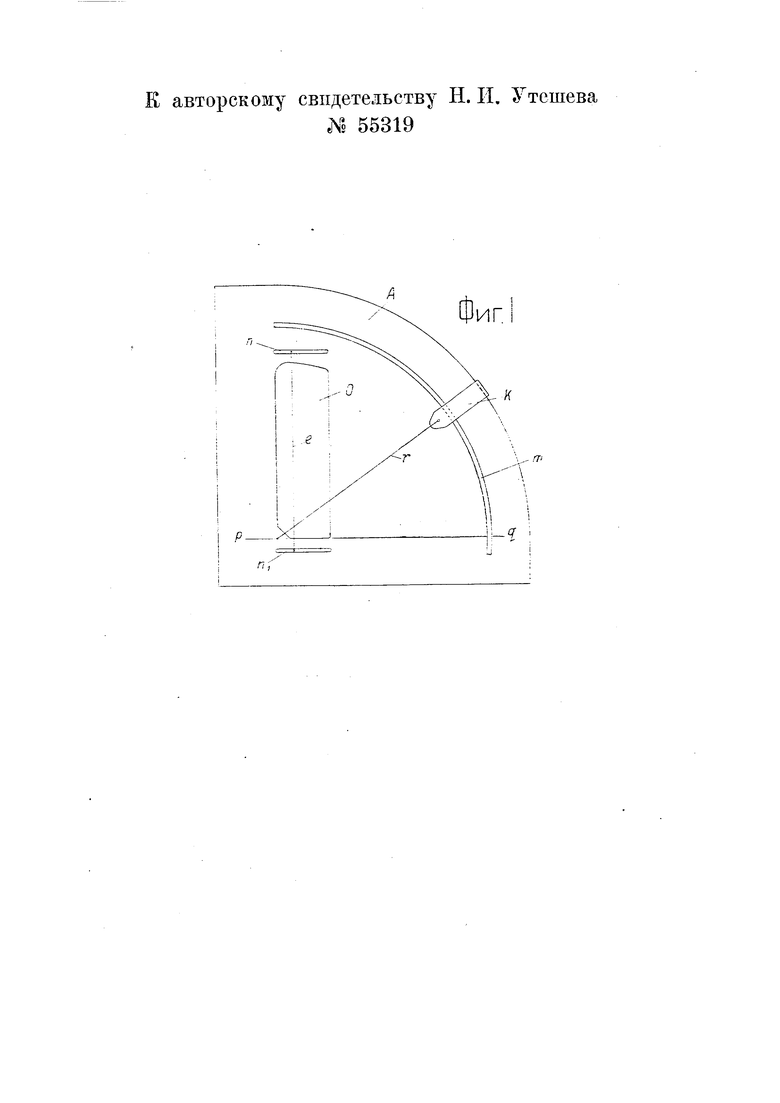
Сущность изобретения поясняется чертежом, на котором фиг. 1 изображает предлагаемое учебное пособие, фиг. 2 иллюстрирует построение производной с помощью предлагаемого учебного пособия и фиг. 3-проведение касательной к кривой с небольшим радиусом кривизны.
Сектор Л снабжен дуговым прорезом т, служащим для пропуска обоймы k. Последняя служит для перемещения радиуса г, выполненного в виде нити, натянутой между центром сектора и обоймой k. В вырезе О находится нить /, которую можно перемещать по прорезам я и «1 и устанавливать на одном из делений масштаба, нанесенного на прорезах п и «,. Прямая pq проходит через центр сектора и направлена по оси ОХ. Нить / направлена по оси OY. Деление, через которое проходит нить /, дает длину отрезка от начала координат до нити /, т. е. длину отрезка Дх.
Величина этого отрезка показывает, в каком масштабе будет произведено построение производной.
Производная в какой-либо точке кривой определяется как тангенс угла между касательной, проведенной к кривой в этой точке, и положительным направлением оси ОХ и
равна отношению д. Из соотно.
шения (Л)-АЛ: следует, что в прямоугольных треугольниках, по
строённых на упомянутых касательных с катетами, равными Дл;, вторые катеты дают величину производной, увеличенную в Дх раз.
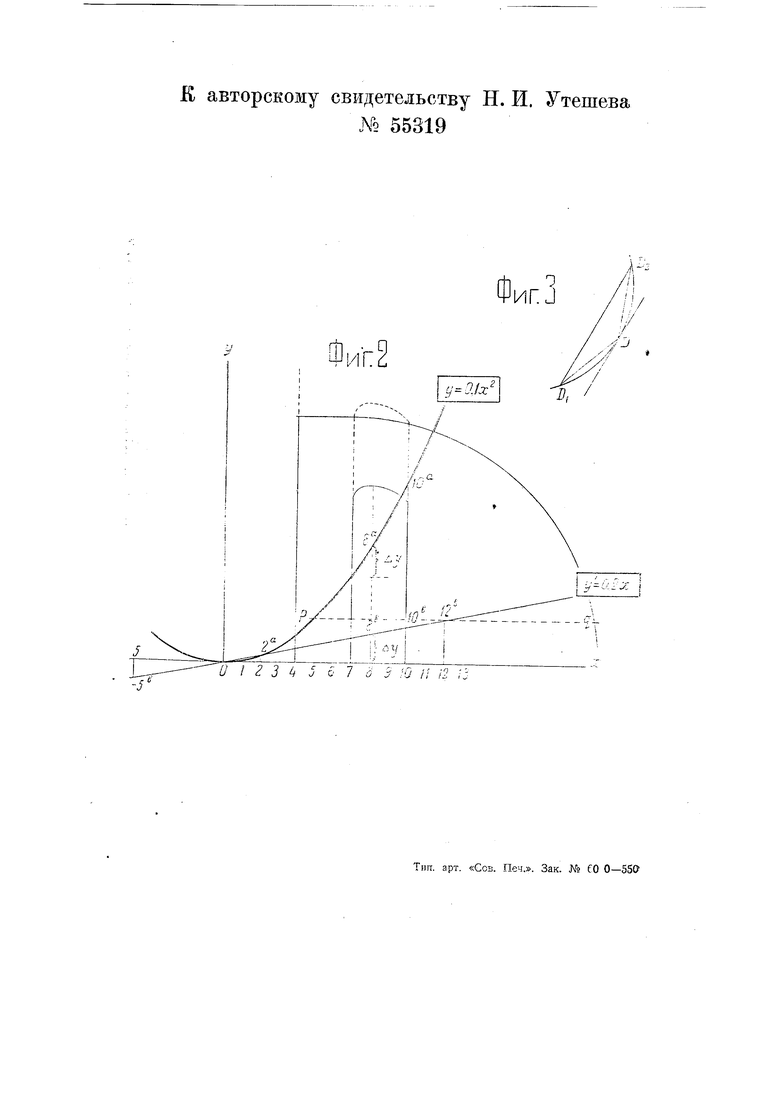
На фиг. 2 графически изображена функция у 0,1 л2. Построение производной (например, для точки S) состоит из следующих приемов. Устанавливают прежде всего нить I на делении i (ДА 1), затем накладывают прибор на чертеж так, чтобы нить / совпала с ординатой 8. Перемещая прибор и нить / вдоль этой ординаты, следят за тем, чтобы радиус г совпал с касательной к кривой в точке 8а. Отрезок нити / от прямой pq до точки пересечения радиуса г с нитью / равен искомой производной у Ь.у. Переместив прибор по ординате 8 до совпадения прямой pq с осью ОХ, отмечают эту производную точкой 8.
Подобным же образом строятся производные и для других точек графика (на фиг. 2 точки 2, 10, 12).
При другом масштабе чертежа нить / соответственно перемещают по прорезам п и HI.
Если угол между касательной и положительным направлением оси ОХ тупой и тангенс угла отрицательный, то пользуются обратной стороной прибора. Найденные значения производных - Дз/ откладывают по ординатам не вверх, а вниз от оси ОХ (см., например, построение производной для точки 5).
При построении касательной нет надобности устанавливать нить г в точке касания. Достаточно установить нить г параллельно участку данной кривой, если участок кривой имеет небольшую кривизну и весьма близок к прямой. В случае большой кривизны участка можно применить следующий способ построения касательной. От данной точки D кривой (фиг. 3) откладывают вправо и влево равные отрезки DDi и DD-, затем соединяют полученные точки прямой
DjD.j и устанавливают нить г по этой прямой или параллельно ей.
С этим прибором можно решить обратную задачу. Чтобы построить интегральную кривую по данной производной, например
У0,2л rfx 0,lx2 + C,
поступают следующим образом.
Пусть дано графическое изображение производнойз 0,2д;(фиг.2). Таким образом для каждой точки оси ОХ известны направления касательных к искомой кривой.
Прямые, параллельные этим касательным, проводятся в соответствующей последовательности из начала координат О до встречи с первой ординатой, оттуда до пересечения со второй и т. д.
Если взять вместо точки О другую точку, расположенную по оси ординат выше или ниже точки О, то получится кривая, все точки которой снижены или повышены по сравнению с первой интегральной кривой. Это семейство кривых наглядно иллюстрирует неопределенность задачи
yo,2x rfx 0,l д:з-|-С.
Предмет изобретения.
Учебное пособие для графического построения производной функции по заданному ее графику, отличающееся тем, что оно выполнено в виде квадранта со сквозным вырезом, снабженного поворотным вокруг центра радиусом в виде нити, служащим касательной к данной кривой, и параллельной одной из сторон квадранта передвижной нитью, точка пересечения которых определяет элементы для графического построения производной в любой точке графика заданной функции.
Е авторскому свидетельству Н. И. Утешева
JSs 55319

| название | год | авторы | номер документа |
|---|---|---|---|
| Демонстрационный прибор по математике | 1982 |
|
SU1075291A1 |
| Учебно-демонстрационный прибор | 1991 |
|
SU1808137A3 |
| Прибор для воспроизведения кривых | 1987 |
|
SU1511154A1 |
| Способ раскроя цельнокроенных деталей одежды | 1976 |
|
SU997653A1 |
| Учебный прибор по математике | 1986 |
|
SU1370661A1 |
| Счетный прибор | 1947 |
|
SU82753A1 |
| Учебный прибор по тригонометрии | 1972 |
|
SU1642495A1 |
| Измерительно-вычислительный координатный прибор | 1936 |
|
SU49504A1 |
| Прибор для вычерчивания спирали Архимеда | 1990 |
|
SU1815242A1 |
| СПОСОБЫ ДЛЯ ГРАФИЧЕСКОГО ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОКРУЖНОСТИ И УСТРОЙСТВА ДЛЯ ИХ ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2154805C2 |

Е авторскому свидетельству Н. И. Утешева
Ко 55819
Авторы
Даты
1939-01-01—Публикация
1937-06-25—Подача