(54) САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ

| название | год | авторы | номер документа |
|---|---|---|---|
| ЛИЙ | 1973 |
|
SU379889A1 |
| СПОСОБ САМОНАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОМ | 2014 |
|
RU2578630C2 |
| Самонастраивающаяся по входному сигналу система управления | 1987 |
|
SU1529176A1 |
| АДАПТИВНАЯ СИСТЕМА ДЛЯ РЕГУЛИРОВАНИЯ И СТАБИЛИЗАЦИИ ФИЗИЧЕСКИХ ВЕЛИЧИН | 2011 |
|
RU2457529C1 |
| АДАПТИВНАЯ СИСТЕМА ДЛЯ РЕГУЛИРОВАНИЯ И СТАБИЛИЗАЦИИ ФИЗИЧЕСКИХ ВЕЛИЧИН | 2012 |
|
RU2522899C1 |
| Самонастраивающийся регулятор | 1979 |
|
SU847273A1 |
| Система управления | 1981 |
|
SU996995A1 |
| Самонастраивающаяся система управления с эталонной моделью | 1980 |
|
SU877471A1 |
| Адаптивная система управления | 1980 |
|
SU980070A1 |
| Самонастраивающаяся система комбинированного регулирования | 1985 |
|
SU1254433A1 |


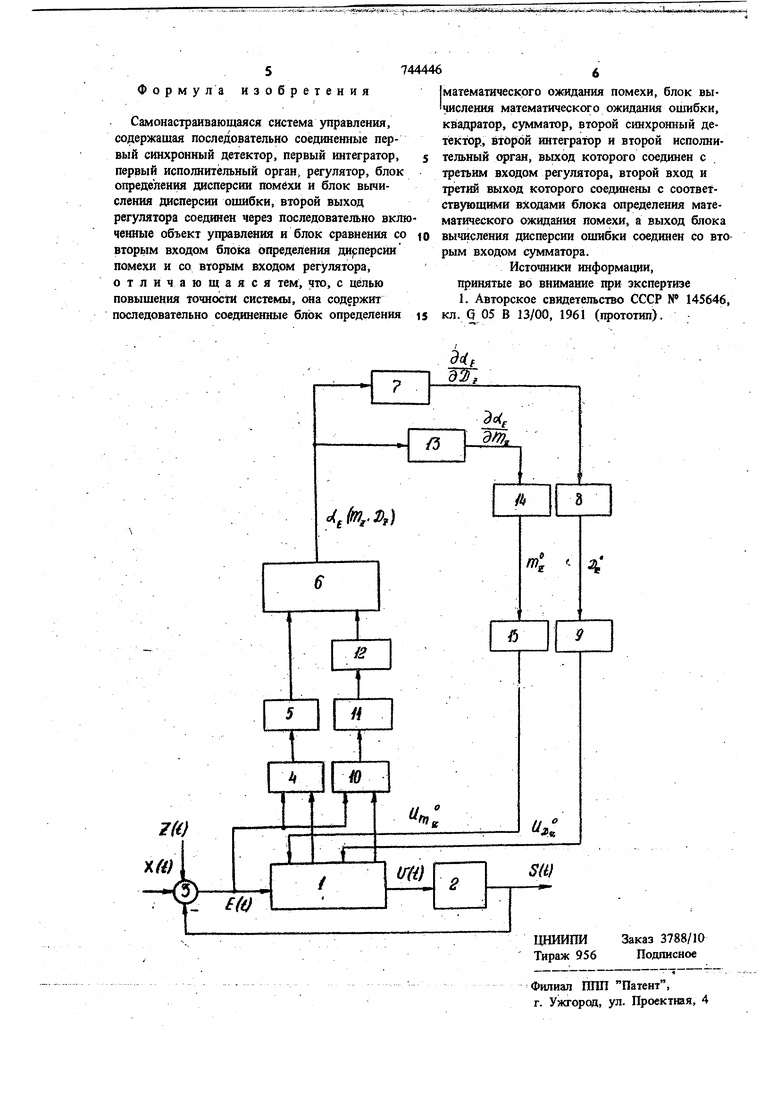
Изобретение относится к автоматическому управлению и может быть использовано в оптимальных самонастраивающихся следящих системах. Известны работы по исследованию и созданию экстремальных систем, обеспечивающих экстремум заданного показателя качества систем при неполной априорной инс юрмавди о входных сигналах в системе. Наиболее близким техническим решением является самонастраивающаяся следящая система, содержащая последовательно соединенные первый синхронньш детектор, первый интегратор, первый исполнительный орган, регул тор, блок определения дисперсии помехи и бл вычисления дисперсии ошибки, второй выход регулятора соединен через последовательн включенные объект управления и блок сравнения со вторым входом блока определения дисперсии помехи и со вторым входом регулятора И. Однако недостатком известной системы является то, что в качестве измеряемых характеристик выбраны спектральные плотности что ограничивает класс применяемых- систем, сигналов и вид критериев. Входные сигналы и системы должны быть стационарными, а критерий - среднеквадратическое отклонение , т.е. случай при нулевом математическом ожидании ошибки, что на практике встречается достаточно редко, что уменьшает точность системы управления. Цель изобретения - повышение точности за счет введения оптимальной самонастройки при учете на входе нестационарного случайного процесса с;неизвестнымиДисперсией и математическим ожиданием помехи. Поставленная цель достигается тем, что она содержит последовательно соединенные блок определения математического ожидания помехи, блок вычисления математического ожидания ошибки, квадратор, сумматор, второй синхронный детектор, второй интегратор и второй исполнительный орган, выход которого соединен с третьим входом регулятора, второй вход и третий выход которого соединены с соответствующими входами блока определения математического ожидания помехи, а выход блока вычисления дисперсии оигибки соединен со втон рым входом сумматораТакое устройство обеспечивает оптимальную самонастройку системы по критерию минимума, второго начального момента ошибки. Е О) учитывающего не только диснерсию ошибки, но и математическое ожидание т. На чертеже представлена функчаюнальная схема, реализующая самонастраивающуюся систему управления. Система содержит регулятор 1, объект 2 управления, блок 3 сравнения, блок 4 определения дисперсии/помехи, блок 5 вычисления дисперсии ошибки, сумматор 6, первый синхронный детектор 7, первый интегратор 8, пер вый исполнительный орган 9, блок 10 определения математического ожидания помехи, блок 11 вычисления математического ожидания ошибки, квадратор 12, второй сш хронный детектор 13, второй интегратор 14, второй исполнительный орган 15.- . На основной контур лннеЙ1 ой системы, состоящей из регулятора 3 и объекта управления 2, действует нестадаодарньш случайный сигнал ощибки E(t), являющийся суммой некорррелированных между собой полезного сигнала X(t) и помехи 2(t) И определяющийся по формуле E(t)X(t) + Z(t)-S(t). .Известны математическое ожидание mx(t) и корреляцион ная функция KX() э также нормированная корреляционная фуикыдя помехи RzC)- Мате: матическое ожвдание помехи т и дисперсия Ог и их закон, распределения неизвестен. Поскольку перед началом работы следящей системы неизвестны вероятностные характеристики помехи Dj; и Шг Для оптималь, ной системы, необходим контур самонастрой км, который настраивал бы параметры DZ и гпгна экстремальные значения, что обеспечивало бы оптимальную систему по критерию минимума второго начального молзента ousuSКИ ().. Система содержит два канзла: формирова тель дисперсии ошибки - Dp с помоиаю последовательного включен1 я блока 4 определе ния дисперсии помехи D, на который поступа ют,сигналы с одного из выходов и входа регулятора 1 и блока 5 вычисления дисперсии ошибки Dg. выходом соедийеш1ого с сумматором (самонастройки) 6, и формирователь квадрата матемапетеского ожидания ошиб ки т|, включающий последовательно соеднненные блок 10 определения математического . ожидания помехи mz, на который поступают сигналы с выхода регулятора 1 и сигнал ошибки системы Е(г), блок 11 вычисления математического ожидания ошибки rrig квадратор 12 и сумматор (самонастройки) 6. Выход сумматора 6 подключен с первым и вторым синхронными детекторами 7, 13 по соответствующим каналам неизвестных вероятностаых характеристик помехи DZ и mz- Выходы синхронных детекторов 7,13 через последрвател|(НО включенные первый и второй интеграторы 8,14 и первый и второй исполнительные органы 9,15 замкнуты на регулятор 1 основного контура системы управления. Во время работы системы по информащш со входа регулятора 1, поступающей в соответсвуюшиё блоки, вычисляются математические ожидания, а taкжe дисперсии помехи и ошибки с использованием начальной информавди. С выхода сумматора 6 сигнал напр жения, пропорциональный критерию оптимальности самонастройки (1) в функции от известных произвольных параметров т, й OcCmz, DZ), поступает в синхронные детекторы 7,13. Чтобы осуществлялась оптимальная самонастройка, т.е. чтобы вместо произвольных значений гпг и D в критерии использовались оптиматйные значения т| и Of, необходимо определить производные от критерия по параметрам, поэтому по каждому каналу отдельно ищутся компоненты градиента в виде, ,,1),) ,.Т) Движение к экстремуму (минимуму) критерия реализуется с помощью градиентного метода, используя, например, систему реверсивных двигателей . .. Ь .. где К - некоторое положительное число. С выхода Ю теграторов 8,14 напряжение, пропорциональное значениям ml и DZ воздействует на реверсивные двигатели исполнительных оргшюв 9,15, которые формируют алгоритм регу.1гятора (путем изменен параметров корректаруюшего контура), так чтобы значение критерия «g, характеризующее ощибку системы было минимально, т.е. чтобы реапьная характеристика системы приближалась к значению. обеспечиваюихему экстремум выбранного критерия оптимальности. Главным достоинством предлагаемой системы является максимальный учет действующих помех при работе системы в реальных условиях, , что обеспечивает высокую точность отработки .полезного сигнала.
Авторы
Даты
1980-06-30—Публикация
1978-04-20—Подача