1
Изобретение относится к цифровой вычислительной технике и может найти применение при аппаратном вычислении квадратов тригонометрических .или гиперболических синуса и косинуса.
Известен цифровой функциональный преобразователь, содержащий сумматоры, регистры сдвига, логические схе- ,|Q мы, схемы анализа У
Недостатком его является невозможность вычисления квадратов синуса . и косинуса. Наиболее близким техническим ре- 15 шением к данному изобретению является цифровой функциональный преобразователь, содержащий сумматоры-вычитатели, регистры, блоки сдвига, блок памяти и блок управления, причем 20 первый выход перво го регистра соединен с первым входом первого сумматора-вычитателя, выход которого соединен со входом первого регистра, второй выход которого соединен с пер- 25 в-ым входим первого блока сдвига, выход второго сумматора-вычитателя соединен со входом второго регистра, первый выход которого соединен с пер.вым входом второго блока сдвига, 30
tt f jsaxtf- - выход третьего сумматора-вычитателя соединен со входом третьего регистра, первый выход которого соединен с первым входок четвертого сумматора-вычитателя, ко второму входу которого подсоединен первый выход третьего блока сдвига, а выход четвертого сумматора-вычитателя соединен с первым входом третьего сумматора- вычитателя/ второй выход третьего регистра соединен с первым входом -Третьего блока сдвига, выход пятого сумматора-вычитателя соединен со входом четвертог о регистра, первый выход которого соединен с первым входом пятого- суг/виатора-вычитателя, на второй вход которого подсоединен выход блока памяти, выходы блока управления соединены со входами сдвига регистров, вторыми входами блоков сдвига и входом блока памяти L2J
Устройство содержит,кроме того, коммутатор.
Недостатком его является невозможность вычисления синуса двойного аргумента.
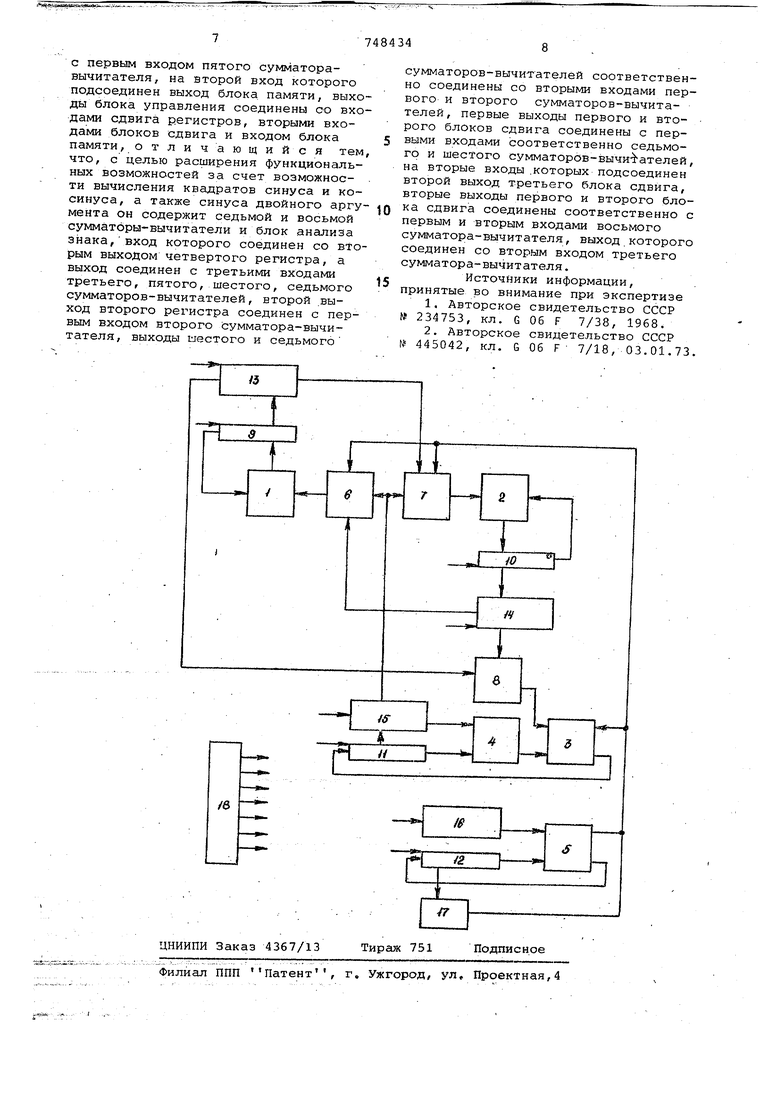
Цель изобретения - расширение функциональных возможностей за счет воз.можности вычисления квадратов синуса и косинуса, а также синуса двойного аргумента. Цель достигается тем, что цифрово функциональный преобразователь содер жит седьмой и восьмой сумматоры-вычитатели и блок анализа знака, вход которого соединен со вторым выходом четвертого регистра, а выход соедине с третьими входами третьего,-пятого jmecToro и седьмого сумматоров-вычита лей, второй выход второго регистра соединен с первым входом второго сум Матора-вычитателя, выходы шестого и седьмого сумматоров-вычитателей соот ветственно соединены со вторыми входами первого и второго сумматоров-вы читателей, первые выходы первого и второго блоков сдвига соединены с пе выми входами соответственно седьмого и шестого сумматоров-вычитателей, на вторые входы которых подсоединен второй выход третьего блока сдвига, вторые выходы первого и второго бло ков сдвига соответственно соединены с первым и вторым входами восьмого сумматора-вычитателя, выход которого соединен со вторым входом третьего сумматора-вычитателя. Устройство представлено на черте же. Устройство содержит сумматорывычитатели 1-8; регистры 9-12; блоки 13-15 сдвига; блок 16 памяти, блок 17 анализа анака, блок 18 управления. . Сумматоры-вычитатели 1-8 выполнены в виде одноразрядной комбинационной схемы. Регистры 9-12 являются обычными сдвигающими накопител ными регистрами. Блоки 13-15 сдвига состоят, например, из двух сдвигающих регистров,БЛОК 16 памяти может бать выполнен в виде одностороннего запоминающего устройства с поразряд ным считыёанием каждым тактовым импульсом одновременно двух констант. Влок 17 анализа зцака может быть выполнен, например, в виде триггера и элемента И. Блок 18 управления мо жет быть выполнен, например, в виде генератора тактовых импульсов, счет чиков, логически;х элементов. Устройство работает следующим об зом. .... , В основу вычисления указанных тригонометрических.или гиперболичес ких, .функций положен принцип одновре менного решения в итерационном процессе системы разностно-итерационны соотношений. Алгоритм вычисления тр . гонометрических указанных функций может быть представле.н в виде следующей системы рекуррентных Соотношений.: ,ej.r0j Vj« c 2l.« t при ,i,...ri. при ftj 0 j гJj- jz22 J. u -cose, .j22:j Uj2-2j to - 5. v j r jv jUj2-i-c.. Z -2-Sin2e. Алгоритм вычисления-указанных гиперболических функций может быть представлен в виде следующей систеы рекуррентных соотношений: e.r j-l rthrJ . ..n. 4iir4 j j2-2-J- « j22j . 4,°. j.r4i j, 2 2-Jt j. 2-2j. u). .2-2J.(UjZ-J.c.Wj 2--; . Алгоритмы для вычисления тригонометрических или гиперболических функ-. дий разли,чаются константами (arctg и arth 2- соответственно) и знаками перед вторым членом третьего соотношения и перед вторым и четвертыгчленами пятого соотношения. Кроме трго коэффициент удлинения для тригонометрических функций равен K. -гГ (1+2- 1,646759996, для гиперболических функций К .П ()V2 0,8297816. Вычибления указанных функций в данном цифровом функциональном преобразрвателе осуществляются следующим. образом. Первоначально в четвертый регистр 12 заносится значение аргумента 0, в первый регистр 9 заносится зна ение l/Kfi , во второй и третий регистры 10 и 11 заносятся нулевые.значения. В любой J-и итерации с выходов блока 18 управления вьодается последовательность (серия) тактовых импульсов, которые сдвигают содержания блоков 13-15 сдвига, продвигают содержания этих блоков и регистров 9-12 и очередную константу из блока 16 на соответствующие входы сумматороввйчитателёй 1-8. Результаты алгебраического суммирования в сумматорах-вычитателях 1-3 и 5 с выходов последних записываются мпадши1ми разрядами вперед в освобождающиеся при сдвиге старшие разряды регистров 9-12 и продвигаются к их началу. После выполнения n+m тактов, где п - числб разрядов аргумента, m 1од п число дополнительных защитных разрядов для компенсации погрешности усечения чисел при сдвиге, в регистрах 9-12 содержатся результаты j-й итерации. Общее число итераций равно п+1.По знаку содержания четвертого регистра -12 в конце каждой итерации в бло ке 17 анализа знака вырабатывается сигнал qj, определяющий на следующей итерации для тригонометрических функций при qj +1 сложение в сумм торах-вычитателях 1-3 и 7, вычитани в сумматорах-вычитателях 4-6 и 8, при 0 -1 сложение в сумматорахвычитателях 1, 2, 5 и 6, вычитание в сумматорах-вычитателях 3, 4, 7 и Для гиперболических функций при qj +1 в сумматорах-вычитателях 1-4, 6-8 выполняется сложение, в сумматоре-вычитателе 5 выполняется вычитание. При qj -1 в сумматорах вычитателях 1, 2, 4, 5 и 8 выполняется сложение, в сумматорах-вычитателях 3, б и 7 выполняется вычитание. Режим сложения-вычитания в сум маторах-вычитателях 4, В и 6 опреде ляется сигналом, подаваемым на специальный вход этих сумматоров-вычитателей с блока 18 управления, в за висимости от требуемой системы функ ций (на чертеже связи сумматоров-вы читателей 4, 8 и 6 с блоком 18 для Упрощения не показаны), Этот сигнал в сумматоре-вычитателе 6 при вычислении гиперболических функций инвер тирует подаваемый сигнал qj. В любой j-ой итерации содержание Uj регистра 9 передается в блок 13 сдвига, с выходов которого на сумматоры-вычитатели 7 и 8 соответствен но выдаются значения Uj и Uj 2 Содержание wj регистра 10 передается в блок 14 сдвига, с выходов которого на сумматоры-вычитаТели б и 8 соответственно выдаются значения Wj и Wj 2 Содержание Zj .регистра 11 передается в блок 15 сдвига, с выходов которого на сумматорывычитатели 4 и б, 7 соотв.етственно . выдаются значения Zj и 1у 2-2 Результаты суммирования-вычитания и сумматоре-вычитателе б, (в зависимости от типа вычисляемых функций и значения цифры qj) суммируются с со держанием Uj регистра 9 в сумматоревычитателе 1 и записываются в регис 9. Аналогично записываются результаты суммирования-вычитания с выхода сумматора-вычитателя 7 через сум матор-вычитатель 2 в регистр 10. Вы читание или суммирование в сумматорах-вычитателях 4 и 8 выполняется в зависимости от типа вьачисляемых функций. Результаты операций с выходов сумматоров-вычитателей 4 и 8 через сумматор-вычитатель 3 записываются в регистр 11. Из содержания ej регистра 12 в сумматоре-вычитате ле 5 вычитается (или суммируется с ним) значение очередной константы arctg 2J(или. arth 2- ). Знак содер,жания ©J регистра 12 определяет значение очередной цифры q; для управления режимом сложения-вычитания в сумматорах-вычитателях 3,5-7. На следующей j+1 итерации вычисления производятся аналогичным образом. После выполнения п+1 итераций содержание регистра 9 является квадратом функции косинуса, содержание регистра 10 - квадратом функции синуса, содержание регистра 11 - синусом двойного аргумента (причем производится структурно сдвиг на один разряд влево от двоичной запятой). Содержание регистра 12 равно нулю. Время вычисления указанных функций в тригономе рической системе равно в тактах Т + n(m+2)+ (m+2). Время вычисления указанных функций в гиперболической системе несколько больше, так как необходимо повторять по два раза итерации с номерами 4, 13, К, ( ЗК-i-l) , . . . Изобретение позволяет за один цикл вычисления одновременно вычис- . лить квадраты синуса и косинуса заданного аргумента, а также синус двойного аргумента в тригонометрической или гиперболической системе. Время вычисления даже одной из укаг занных функций значительно меньше времени вычисления традиционными способами в известных устройствах. Формула изобретения Цифровой функциональный преобразователь , содержащий сумматоры-вычитатели, регистры, блоки сдвига, блок памяти и блок управления, причем первый выход первого регистра соединен, с первым входом первого сумматора-вычитателя, выход которого соединен со входом первого регистра, второй выход которого соединег с первым входом nepBorq блока сдвига, выход згорого сумматора-вычитателя соединен со входом второго регистра, первьй выход которого соединен с первым входом второго блока сдвига, выход третьего сумматора-вычитателя соединен со входом третьего регистра, первый выход которого соединен с первым входом четвертого сумматора-вычитателя, ко второму входу которого подсоединен первый выход третьего блока сдвига, а выход четвертого сумматора-вычитателя соединен с первым входом третьего сумматора-вычитателя, второйвыход Третьего регистра соединен с первым входом третьего блока сдвига, выход пятого сумматора-вычитателя соединен со входом четвертого регистра, первый выход которого соединен


| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой функциональный преобразователь | 1979 |
|
SU922733A2 |
| Устройство для вычисления тангенса | 1975 |
|
SU650073A1 |
| Цифровой функциональный преобразователь | 1977 |
|
SU678488A1 |
| Устройство для вычисления тригонометрического тангенса | 1973 |
|
SU537344A1 |
| Цифровой функциональный преобразователь | 1975 |
|
SU607223A1 |
| Устройство для вычисления гиперболического тангенса | 1973 |
|
SU526890A1 |
| Устройство для вычисления обратного кругового синуса | 1973 |
|
SU478313A1 |
| Устройство для вычисления обратного гиперболического тангенса | 1973 |
|
SU465630A1 |
| Цифровой функциональный преобразователь | 1977 |
|
SU684551A1 |
| Устройство для вычисления корня к-ой степени | 1976 |
|
SU736096A1 |


Авторы
Даты
1980-07-15—Публикация
1976-10-01—Подача