1
Изобретение относится к автоматике и вычислительной технике и может найти применение как автономное устройство для решения системы линейных уравнений или в комплексе ЭВМ.
Известно устройство для решения системы линейных алгебраических уравнений, содержащее тХп блоков формирования коэффициентов, сумматоры, регистры, цифровые интеграторы, блоки умножения 1.
Недостатком известного устройства является значительная сложность структуры.
Наиболее близким по технической суш,ности к изобретению является устройство, содержаш,ее регистры, и сумматоры приращений, блоки памяти коэффициентов, блоки умножения, первые входы которых соединены с выходами блоков приращений, а вторые - с выходом блока памяти коэффициентов, сумматор, группа входов которого соединена с выходами блоков умножения, блок памяти невязок, коммутатор 2.
Недостаток известного устройства состоит в сложности структуры и быстром росте оборудования при увеличении порядка системы. Это обуславливается тем, что с ростом числа уравнений и неизвестных необходимо увеличить количество сумматоров приращений и блоков умножения для подсчета невязок, так как время вычисления.
расходуемое, главным образом, на умножение, растет пропорционально квадрату числа неизвестных.
Цель изобретения - упрощение устройства и повышение быстродействия.
Достигается это тем, что устройство для решения системы линейных уравнений, содержащее блок памяти коэффициентов, блок памяти неизвестных, сумматор, сумматор приращений, блок умножения, первый и второй входы которого соединены соответственно с первыми выходами блока памяти коэффициентов и блока памяти неизвестных, блок управления, первый и второй выходы которого соединены соответственно с входом блока памяти коэффициентов и первым входом блока памяти неизвестных, содержит блок памяти взвешенных координатных приращений, элемент
ИЛИ и блок памяти знака, причем второй выход блока памяти коэффициентов соединен с первым входом элемента ИЛИ, выход которого соединен с входом сумматора, выход которого соединен с первым входом
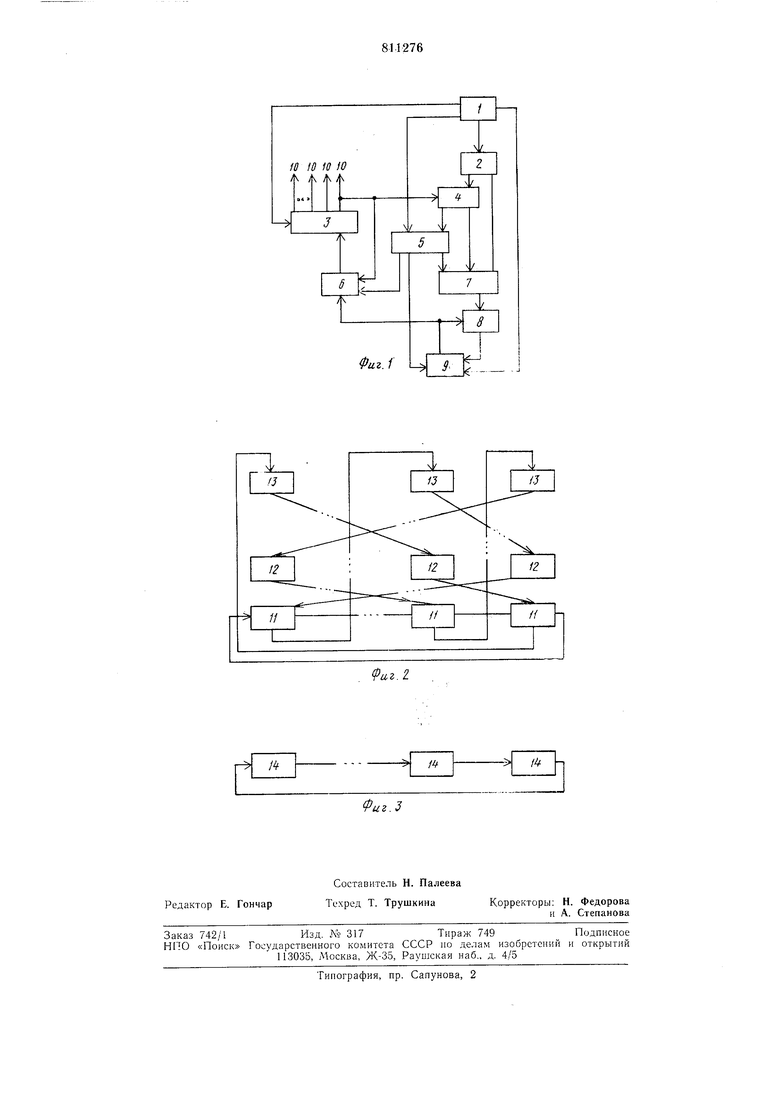
блока памяти знака, второй вход которого соединен с третьим выходом блока управления, четвертый выход которого подключен к первому входу блока памяти взвешенных покоординатных приращений, первый и второй выходы блока умножения подключены соответственно к вторым входам элемента ИЛИ и блока памяти взвешенных покоординатных приращений, первый, второй и третий выходы которого подключены соответственно к первому входу сумматора приращений и к третьим входам элемента ИЛИ и блока памяти знака, выход которого соединен с управляющими входами сумматора и сумматора приращений, второй вход которого соединен с первым выходом блока памяти неизвестных, второй вход которого соединен с выходом сумматора приращений. На фиг. 1 представлена блок-схема устройства; на фиг. 2 - схема блока памяти коэффициентов; на фиг. 3 - схема блоков памяти неизвестных и взвешенных покоординатных приращений. Устройство включает блок управления 1, блок памяти коэффициентов 2, блок памяти неизвестных 3, блок умножения 4, блок 5 памяти взвешенных покоординатных приращений, сумматор приращений 6, элемент ИЛИ 7, сумматор 8, блок 9 памяти знака, выходы устройства 10. Блок памяти коэффициентов содержит первую группу регистров 11, вторую группу регистров 12, п-к группу регистров 13. Блоки памяти неизвестных и памяти взвешенных покоординатных приращений содержат группу регистров 14. Устройство реализует следующий алгоритм вычисления корней системы. Рещением системы линейных уравнений 2 aijXi-bi-Q, ,..., п или в матричной форме АХ В, где А , Х ij 1, ...п является точка пересечения (п-1)-мерных гиперплоскостей (1) в /г-мерном евклидовом пространстве. Для нахождения решения системы был использован модифицированный метод Гаусса-Зейделя. Классический метод Гаусса-Зейделя состоит в преобразовании системы (2) к виду Х АХ + В и решений системы (3) методом последовательных итераций Х , А 1,2...п, начиная с некоторого начального приближения XQ. Основное отличие модифицированного метода Гаусса-Зейделя более понятно в геометрической интерпретации. Для подсчета не использовалась явная форма (4) вычисления Х через остальные 5 10 15 20 25 30 35 40 45 50 55 (50 65 переменные. Вместо этого использовалось то свойство п-мерного евклидова пространства, что калсдая (п-1)-мерная гиперплоскость (1) делит его на два пространства. Если теперь в левую часть уравнения гиперплоскости подставить координаты точки, лежащей в одном из полупространств, то значение этого выражения будет положительное, а для точки из другого полупространства -отрицательное. Алгоритм точки пересечения гиперплоскости (1) (корней системы) состоит в следующем. Шаг 1. Вычислить знак левой части очередного t-ro уравнения из (1) в достигнутой к данному моменту точке. В начале работы алгоритма на этом шаге вычисляется знак левой части первого уравнения системы в начальной точке XQ. Перейти к щагу 2. Шаг 2. С учетом результата шага 1 и знака аи начинается последовательное изменение Хг на величину h с тем, чтобы пересечь t-ую гиперплоскость, т. е. изменить знак левой части t-ro уравнения. Когда после очередного изменения х, это произойдет, то вернемся к предыдущему значению Хг И можем утверждать, что Хг отличается от точного значения, вычисленного по формуле (4), меньше, чем h. В целях уменьшения объема вычислений не подсчитывается каждый раз значение выражения всей левой части t-ro уравнения, а заранее подсчитывается взвешенное приращение autij этого выражения при изменении х, на величину /I. Это позволило сократить число умножений до минимума и ускорить подсчет решения. Далее перейти к шагу 3. Шаг 3. Если по всем координатам происходит изменение знака левой части уравнений гиперплоскостей после первого приращения Xi, , 2 ... п, то перейти к шагу 5, если не происходит - то к шагу 4. Шаг 4. Выбрать следующее (г-М)-ое уравнение из (1) и следующую (+1)-ую координату Xi+i. Если (г+1) превысило h, то следующий номер уравнения и координаты равен 1. Перейти к шагу I. Шаг 5. Изменить величину приращения коорди1нат h на /2 и величины взвешенных покоординатных приращений auh по . Если число .изменения h меньше заданного числа т, то перейти к шагу 1, иначе закончить решение задачи. Устройство работает следующим образом. В исходном состоянии сумматор 8 обнулен, в блоке памяти 2 хранятся коэффициенты системы, причем в первой группе регистров 11 (см. фиг. 2) размещены коэффициенты 1-го уравнения, во второй группе 12 - коэффициенты второго уравнения и т. д. до п. В первом регистре г-ой группы хранится коэффициент при первом неизвестном, во втором - при втором и т. д. Неизвестные Xi хранятся в блоке памяти 3 и размещаются в регистрах, начиная с нервого порядка, соответствующем их номеру. Начальное значение всех Хг равно h. Работа устройства по выполнению щага 1 алгоритма решения системы линейных уравнений начинается с передачи 1-го коэффициента и первой координаты в блок умножения 4, результат умножения через элемент ИЛИ / поступает на сумматор 8 и складывается с его содержанием. Пронзведение aahi, являющееся взвешенным координатным приращением левой части уравнения (1), записывается в блок памяти о. Затем производится сдвиг информации но регистрам в первой группе блока S и блоке 3 и процесс повторяется. Запись результата умножения в олок памяти 5 отсутствует. После п сдвигов, умножений и сложений в сумматор дооавляется свободный член Ьг из блока памяти 2 через элемент ИЛИ. Знак результата сумматора, являющийся знаком левой части уравнения (1), запоминается в блоке 9. Далее начинается выполнение шага 2. Для этого взвешенное приращение левой части уравнения (1) из блока памяти 5 поступает на су.м.матор, а приращение координат h из блока памяти о поступает на су.мматор приращений. Знак операции, производимой в сумматорах, определяется в олоке 9 с учето.м знаков результата шага 1 и знака ац- Если после дооавления взвешенного приращения знак левой части уравнения не изменился, то к текущей координате, поступающей на сум.матор приращеиий с нервого регистра блока памяти 3, добавляетсяприращение h, поступающее из блока памяти 6, результат сум.мирования записывается в тот же регистр Олока 3. Если знак левой части уравнения (i) изменился, приращение h не добавляется. Блок 9 проверяет условие, записанное в шаге 3 алгоритма решения системы уравнений. Если условие не выполняется, то переходим к выполнению шага 4. Оно включает: обпуленне сумматора 8 и знака левой части уравнения (1) в блоке 9, перепись коэффициентов из группы с номером i в i-1, а из первой группы в п-ю, один сдвиг информации но регистрам в блоках иамяти неизвестных 3 и памяти взвещенных покоординатных приращений 5, переходим к выполнению шага 1. Если условие шага 3 выполняется, то переходим к шагу 5, при котором происходит уменьшение приращений h и aah в блоке памяти 5 путем поразрядного сдвига содержимого регистров на один разряд вправо. Вся работа синхронизируется сигналами блока управления 1 и заканчивается, если число изменений h больше заданного. Введение новых блоков и новых констРуктивных связей позволило уменьшить количество операции у.множения, а следовательно, повысить быстродействие устройства. Количество блоков у.множения не увеличивается с ростом неизвестных в системе уравнений Формула изобретения Устройство для рещения системы линейных алгебраических уравнений, содержащее блок памяти коэффициентов, блок памяти неизвестных, сумматор, сумматор нрнращений, блок умложения, перВый и второй входы которого соединены соответственно с первыми входа.ми блока на,мяти коэффици.антОВ и блока па.мяти нензБОстных, блок управления, первый и второй выходы которого соединены ооогветственно с входом блока памяти коэффициентов и лервым входом блока памяти неизвестных, отличающееся те.м, что, с целью упрощения устройства и повышения быстродействия, оно содержит блок памяти ;взвешенных координатных приращений, элемент ИЛИ и блО(К памяти знака, причем второй выход блока иа.мяти коэффициентов соединен с первым входом эле.м-ента ИЛИ, выход которого соединен с входоМ сумматора,ВЫХОД которого ооеденен с первым входом блока .памяти знака, второй Вход которого соединен с третьим выходо.м блока управления, четвертый выход которого подключен к первому в.ходу олока памяти взвешенных координатных приращений, первый и второй выходы блока умножения подключены соответственно к вторым в.ходам элемента ИЛИ н блока памяти взвешенных покоординатных приращений, первый, второй и третий выходы которого подключены соответственно к первому входу сумматора приращений и к третьим входам элемента ИЛИ и блока па1мяти знака, выход которого соединен с управляющими входами сумматора н сумматора приращений, второй вход которого соединен с первым выходом блока памяти неизвестных, второй вход которого соединей с вы.ходом су.мматора приращений, Источники информации. принятые во внимание при экспертизе 1. Авторское свидетельство СССР - 559241, кл. G 06F 15/32, 1976. 2. Авторское свидетельство СССР JYo 564638, кл. G 06F 15/32, 1977 (Прототип).
Фиг. 1


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для решения систем линйныхАлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU824217A1 |
| Устройство для решения систем алгебраических уравлений | 1975 |
|
SU529468A1 |
| Устройство формирования оптимальных управляющих воздействий для обеспечения устойчивой работы сложных технических систем | 2017 |
|
RU2674281C1 |
| Устройство для решения системы алгебраических уравнений | 1981 |
|
SU966702A1 |
| Устройство для решения систем ли-НЕйНыХ АлгЕбРАичЕСКиХ уРАВНЕНий | 1978 |
|
SU811275A1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ УПРАВЛЯЮЩИХ ВОЗДЕЙСТВИЙ ДЛЯ ОБЕСПЕЧЕНИЯ УСТОЙЧИВОЙ РАБОТЫ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ | 2011 |
|
RU2475828C1 |
| Устройство для решения систем алгебраических уравнений | 1984 |
|
SU1203552A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1988 |
|
SU1566367A1 |
| Устройство для решения систем линейных алгебраических уравлений | 1972 |
|
SU564638A1 |
| Устройство для решения систем линейных дифференциальных уравнений | 1988 |
|
SU1525714A2 |


Авторы
Даты
1981-03-07—Публикация
1978-09-22—Подача