1
Изобретение относится к вычислительной технике и может быть использовано при построении вычислительных машин в системе остаточных классов.
Известно арифметическое устройство в системе остаточных классов, содержащее регистры операндов,регистры результатов, табличный сумматор,квадратор, дешифратор с соответствующими связями tij .
Недостатком устройства является работа только с целыми числами.
Наиболее близким к предлагаемому изобретению техническим решением является арифметичедкое устройство в системе остаточных классов, содержащее два регистра операндов, блок памяти таблиц, дешифраторы умножения, схемк передачи операндов, регистр хранения результатов операции, схему контроля, схемы выдачи результатов операции, причем выходы регистров первого и второго операндов соединены через схемы передачи операндов и дешифраторы умножения с блоком памяти таблиц, выходы которого соединены с входами регистра хранения результата операции и выходами схемы контроля, выходы .схемы контроля
и регистра хранения результата операции соединены со схемами результата операций.
Кроме того, устройство содержит схему определения знака и управления схемами передач операндов,логический элемент ИЛИ, а в регистры записи операндов и в регистр хранения результата операции введены
10 дополнительные разряды знака числа, выходы знаковых разрядов регистра записи операндов соединены со схемой определения знака и управления схемой передачи операндов, выходы ко15торой подсоединены к схемам передачи операндов и к первому входу элемента ИЛИ, выход которой соединен с знаковым разрядом регистра хранения результата операции, а второй вход
20 элемента ИЛИ соединен с выходом регистра контроля 2 .
Недостатке устройства также является работа только с целыми числами.
25
Цель изобретения - расширение функциональных возможностей устройства за счет обработки операндов целого и действительного типов.
Поставленная цель достигается тем, что устройство, содержащее ре30
гистры мантисс операндов, выходной регистр мантиссы, выходной регистр знака порядка, выходной регистр порядка, блок памяти таблиц, выход которого соединен с входом выходного регистра мантиссы, содержит блоки (Сдвига мантисс операндов, блок выравнивания порядков, регистра порядков операндов и регистры знаков порядков операндов, причем выходы регистров мантисс операндов соединен с информационными входг1ми соответствующих блоков сдвига мантисс операдов , выходы которых соединены с входами блока памяти таблиц,выходы регистров порядков операндов и регистров знаков операндов соединены с соответствугсщими входами блока выравнивания порядков, первый выход которого соединен с управляющими входами блоков сдвига мантисс операндов второй и третий выходы соединены с входами соответственно выходного регистра порядка и выходного регистра знака порядка, пятый, шестой и седьмой входы блока выравнивания порядков соединены с соответствующими входами блока памяти таблиц и являются управлякнцими входами Умножения, Слежения, Вычитания.
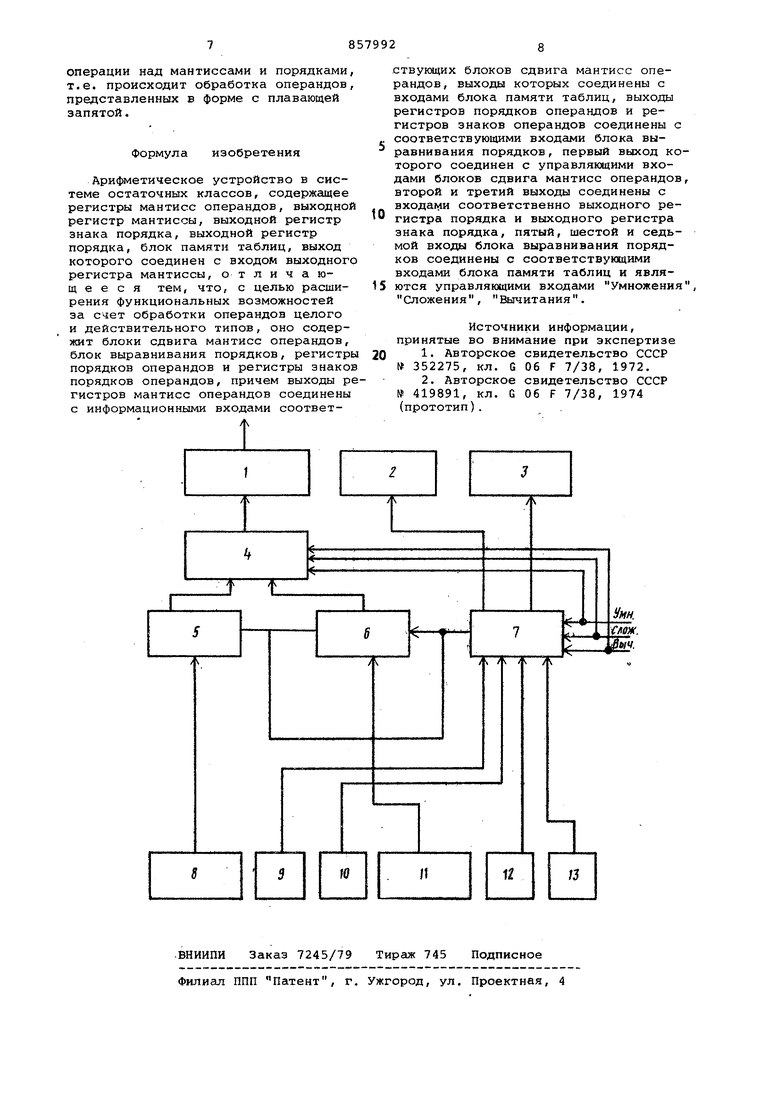
На чертеже представлена блок-схема устройства.
Устройство содержит выходной регистр 1 мантиссы, выходной регистр 2 знака порядка, выходной регистр 3 порядка,блок 4 памяти таблиц, блоки 5 и 6 сдвига мантисс операндов, блок 7 выравнивания порядков, регистр 8 мантиссы первого операнда, регистр 9 знака порядка первого операнда, регистр 10 порядка-первого операнда, регистр 11 мантиссы второго операнда, регистр 12 знака порядка второго операнда, регистр 13 порядка второго операнда.
В цифровых вычислительных мащинах, работающих в позиционных системах счисления, информация представляется,как правило, дробным числом. Поэтому при сопряжении таких ЦВМ необходимо выбрать масштаб так, чтобы для всех полученных масштабированных целых чисел, употребляемых в вычислениях, их максимальное значение по модулю было не больше максимально допустимого числа, представленного в . ЦВМ, работающих в СОК, а минимальное значение величины по модулю не мены1|е минимального допустимого, т.е. чтобы числа находились в пределах выбранного диапазойа.
В связи с этим целесообразно получить целочисленные мантиссы чисел, представленные в естественной или нормальной форме, соответственно в ЦВМ с фиксированной или плавающей запятой. Полученные целые числа, представленные в позиционной системе счисления, переводятся в СОК. В
таком случае ЦВМ, работающая в СОК, оперируется с целыми числами, полученными из дробных за счет введения масштаба. Известно, что масштабирование любого дробного числа, представленного в естественной или нормальной форме, осуществляется путем сдвига мантиссы влево на п разрядов, где п - количество разрядов мантиссы. Очевидно, полученный порядок масштаба мантиссы является порядком числа, если информация в ЦВМ,работакядей в позиционной системе счисления, представлена в естественной форме, и один из слагаемых порядка, в случае представления информации в 5 нормаль ной форме.
Тогда после масштабирования число запишется в виде
etn
(1)
MN
целочисленная мантисса, основание системы счисления,
е+п порядок (при естественной записи С 0). Мантисса и порядок записываются целыми числами.
Пример 1. в естественной форме число представлено в виде 0,101101. После введения масштаба это число будет записано в виде 101101.10 .
Пример 2.В нормальной форме число представлено в виде 0,100101. . После введения масштаба это число будет записано в виде 100101. .
Мантисса числа и порядок представлены в СОК. Для представления мантиссы используется система оснований СОК Р , P/j, -.РН , которая определяется диапазоном представленных в ЦВМ чисел. Для представления порядка отводится одно основание Р . При этом должно выполняться неравенство Pj 7/ , где Lfnc,- диапазон порядка, представленного в позиционной системе счисления.
Знак порядка целесообразно ввести в явном виде, тогда К чисел, которые однозначно определяют диапазон представления любого числа Z, в данном основании записываются ,-1). (2)
Любое число, являющееся элементом множества диапазона, может быть представлено в виде
х.,ц,...,а.п)51(уры..,ц., W
значения мантиссы числа X по основа иям
значения порядка по основанию PJ;
t - для положительного порядка , L - для отрицательного порядка.
Анализ показывает, что при таком представлении чисел в СОК получаем выигрыш в скорости обработки информации. ,
При производстве сложения (вычитания) чисел операции над мантиссами (cL.dj, .-- ,с1п)и порядками cLj чисел Xj выполняются последовательно, затем над мантиссами.
Операционная часть устройства будет состоять из устройств, оперирующих с мантиссами, и устройств, оперирующих с порядками.
При выполнении операций с порядками, каждый раз после вычитания или сложения порядков необходимо знать модуль разности для определения числа сдвигов мантиссы и знак разности порядков для определения, какую из мантисс нужно сдвинуть.
При сложении (вычитании) чисел, представленных в форме (выражение 3 сначала уравниваются порядком чисел затем сдвигается мантисса, а после производится арифметическая операция над мантиссами. Уравнивание порядков состоит в том, что больший порядок числа приводится к меньшему, и при этом соответственно увеличивается мантисса числа, у которого больший порядок,
Сдвиг мантиссы производится влево, что равносильно умножению мантиссы на число, равное разности порядков. Операция умножения в СОК однотактная. Арифметические операции сложения (вычитания) -тоже однотактные. Желательно, чтобы операция уравнивания порядков занимала немного времени, чтобы не снизить общую скорость обработки информации.
Процесс выполнения арифметической операции осуществляется следующим образом.
1.Определение разности и знака порядка. Разность порядков определяет число сдвигов влево, а знак разности порядков указывает, какую из мантисс нужно сдвинуть.
2.Сдвиг влево мантиссы с большим порядком.
3.Сложение (вычитание) мантисс. Сумма (разность) мантисс дает сумму (разность), а порядок равен порядку большего числа.
При уравнивании порядков могут встретиться следующие варианты;
Г. (dL5-l;dl5 lcL5,гдe JLj,y соответственно порядки чисел А и В. Если |cL5l |ol5),TOd5-d.j lcij l-lcJ.fi ;
Если ldl l lcLjl, |d.5l-|«1 5li переполнения нет.
в
Действительно, еслИ:, р. и Л| Р- ,
раз ность : 0 Id-j l-lolf К Pj-1. iл3 J
Модуль разности порядков определяет величину сдвига мантиссы 5 числа с большим порядком.
2. .,
Аиr iv.ijBi -.-л ijAi ijB
Если |oLj| IA5l.TO|cLjHd5|.(P.j-HJIHPrVl)
Здесь переполнения тоже нет, аналогично первого варианту.
I
3. ),dL5)oLjl,TOlct5-oi,|)ld..
В том случае имеет место переполнение , когда
/А, .
At,I iBi
,cLb-td|| Pj, (Рй)Модуль разности определяет величину сдвига.
4. ф-|4.ф-1 1Этот случай симметричен сле yщeмy с переменными ролями чисел.
При выполнении операции умножения значения порядков суммируются.
Устройство работает следующим образом.
При выполнении арифметических
операций на регистры 8 и 11 операндов заносятся мантиссы, на регистры 9 и 12 - знаки порядков, а на регистры 10 и 13 - значения порядков операндов. На блок 7 выравнивания порядков поступает информация о знакак порядков операндов и их значения и символы команд (Умножение, Вычитание, Сложение).
В зависимости от символа команды и знаков порядков блок 7 (в случае
Сложения или Вычитания) определяет разность порядков и мантиссу, которую необходимо сдвинуть, и выдает информацию на блоки 5 и б сдвига мантиссы операндов.
Кроме того, блок 7 выдает результат выравнивания порядков и знаки на выходные регистры 2 и 3.
Сдвиг мантиссы влево равносилен умножению. Эта операция одноактна. После сдвига информация передается наблок 4. В случае Умножения чисел блок 7 выдает разрешение на передачу мантисс на блок 4 без сдвига, а результат суммирования порядков и знак выдает на выходной регистр 2 и
3 соответственно. При выполнении операции блок 4 выдает результат суммирования, сложения и умножения мантисс на выходной регистр 1.
Таким образом, на выходном регистре формируется результат выполнения


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для выравнивания порядков чисел,представленных в системе остаточных классов | 1973 |
|
SU781812A1 |
| Арифметическое устройство | 1989 |
|
SU1656525A1 |
| Устройство для суммирования двух чисел с плавающей запятой | 1985 |
|
SU1405049A1 |
| Арифметическое устройство для обработки комплексных чисел | 1984 |
|
SU1223249A1 |
| Устройство для сложения и вычитания чисел с плавающей запятой | 1980 |
|
SU959070A1 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ | 2004 |
|
RU2292580C2 |
| Устройство для умножения чисел | 1981 |
|
SU999045A1 |
| Арифметическое устройство | 1978 |
|
SU809169A1 |
| Суммирующее устройство с плавающей запятой | 1982 |
|
SU1056182A1 |
| Арифметическое устройство | 1984 |
|
SU1193661A1 |



Авторы
Даты
1981-08-23—Публикация
1979-11-11—Подача