Описываемый способ позволяет разработать и изготовить аппаратуру, необходимую для дистанционного управления в копирующем режиме ходьбой антропоморфного шагающего робота.
Вначале рассматриваются способы изготовления датчиков, определяющих угловую ориентацию произвольно движущегося твердого тела /в данном случае - корпуса робота/.
В просмотренной мною литературе, касающейся проблемы создания антропоморфных шагающих роботов, говорится, что "Шагающий робот должен быть снабжен гироскопическим датчиком для определения ориентации в пространстве." /см. Е. П. Попов, А. С. Ющенко "Роботы и человек", Москва, 1984 г., стр. 63/.
Такие датчики, определяющие угловую ориентацию, необходимы для обеспечения устойчивой походки робота.
Однако механический "свободный" гироскоп имеет ряд очевидных изъянов, совокупность которых, по-видимому, и является одним из препятствий на пути создания полноценных шагающих роботов.
Первый, очевидный, но не основной, недостаток гироскопа - механическое вращение маховика и необходимость в постоянном поддержании этого быстрого вращения.
Второй изъян гироскопа /он менее очевиден, но зато гораздо более существенен/: т. н. "свободный" гироскоп, закрепленный на карданном подвесе, не является свободным в полной мере этого слова. Действительно, пусть в первый момент ось вращения "свободного" гироскопа направлена вертикально /фиг. 1/, где эллипсом изображен маховик гироскопа, вращающийся на оси O-O1. Малая /внутренняя/ рамка карданного подвеса обозначена буквами A, B, C, D. Она имеет ось вращения P-P1. Большая рамка карданного подвеса E, K, L, M вращается на оси N-N1 в подшипниках, закрепленных в корпусе робота. По идеи ось вращения маховика O-O1 должна всегда сохранять свое направление в пространстве, независимо от того, как изменится угловая ориентация корпуса робота, но это не так, в некоторых случаях возможно возникновение такой ситуации, когда ось O-O1 будет наклонена под воздействием внешних сил, изменяющих ориентацию корпуса робота. Рассмотрим эту ситуацию.
Введем правую тройку векторов 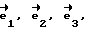 жестко связанную с осью O-O1 гироскопа. Орт
жестко связанную с осью O-O1 гироскопа. Орт 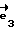 направим вдоль оси O-O1. Маховик гироскопа крутится, но векторы
направим вдоль оси O-O1. Маховик гироскопа крутится, но векторы 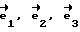 в этом кручении не участвуют. Вектор
в этом кручении не участвуют. Вектор 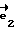 направлен вдоль оси P-P1, проходящей через подшипники внутренней рамки карданного подвеса. Вектор
направлен вдоль оси P-P1, проходящей через подшипники внутренней рамки карданного подвеса. Вектор 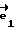 будет направлен "к нам". Введем теперь правую тройку векторов
будет направлен "к нам". Введем теперь правую тройку векторов 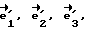 жестко связанную с корпусом робота. И пусть начальный момент, когда робот стоит вертикально, векторы
жестко связанную с корпусом робота. И пусть начальный момент, когда робот стоит вертикально, векторы 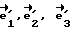 совпадают по своему направлению с ортами
совпадают по своему направлению с ортами 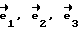 гироскопа. Теперь допустим, что робот из вертикального положения принял положение "упор лежа" /проще говоря, лег на живот/, тогда рамки карданного подвеса займут по отношению к гироскопу положение, изображенное на фиг. 2. Если теперь робот начнет перекатываться из положения "упор лежа" на спину, то рамки карданного подвеса находятся в таком положении /фиг. 2/, что не дают возможности оси вращения "свободного" гироскопа сохранить свое направление в пространстве. При перекатывании робота с живота на спину ось вращения гироскопа может оказаться повернута на 180o/я привожу здесь наиболее неблагоприятный случай/.
гироскопа. Теперь допустим, что робот из вертикального положения принял положение "упор лежа" /проще говоря, лег на живот/, тогда рамки карданного подвеса займут по отношению к гироскопу положение, изображенное на фиг. 2. Если теперь робот начнет перекатываться из положения "упор лежа" на спину, то рамки карданного подвеса находятся в таком положении /фиг. 2/, что не дают возможности оси вращения "свободного" гироскопа сохранить свое направление в пространстве. При перекатывании робота с живота на спину ось вращения гироскопа может оказаться повернута на 180o/я привожу здесь наиболее неблагоприятный случай/.
После такого перекатывания показания гироскопического датчика уже будут неверными. /Может возникнуть еще более худшая ситуация, когда ось маховика O-O1 будет погнута и гироскопический датчик ориентации выйдет из строя./ В реальных технических устройствах /ракетах, самолетах/ от указанного изъяна "свободного" гироскопа избавляются введением " разгрузочных двигателей", которые не дают рамкам карданного подвеса ложиться в одну плоскость. Но в любом случае механический гироскоп - это сложное устройство, которое плохо подходит для шагающего антропоморфного робота.
Возможно использование для шагающего робота в качестве датчиков, определяющих ориентацию, интерференционных лазерных гироскопов. Но такие интерферометры имеют большие размеры, требуют сложной юстировки, дороги и не очень надежны.
Целью настоящего изобретения является способ, с помощью которого можно изготовить компактные, надежные, технологичные в производстве датчики угловой ориентации.
Для этой цели предполагается использовать два различных по своим принципам устройства.
Первое из них - это жидкостной "датчик-отвес". Он позволяет определять начальное направление "верх-низ", а также позволяет измерять медленные наклоны тела, изменяющего ориентацию.
Второе из них - это жидкостной инерционный датчик, позволяющий измерять произвольные вращательные движения, имеющие значительное ускорение.
Датчик-отвес.
Рассматриваем проекции отвесной линии /линии "верх-низ"/ на три "единичные" окружности, вписанные в стороны куба /см. фиг. 3/. На фиг. 3 изображен куб со стороной в две условные единицы. В стороны куба вписаны три окружности единичного радиуса, т.е. с диаметрами в две условные единицы. Передние стенки куба изображены штриховкой, они как бы отсутствуют.
Введем в куб две системы координат: декартовы координаты X, Y, Z и полярные координаты θ, ϕ. Углы θ, ϕ изменяются в пределах 0o ≤ θ ≤ 180o и 0o ≤ ϕ ≤ 360o /см. фиг. 4/.
Углы θ и ϕ определяют ориентацию /наклон/ вектора отвесной линии относительно системы координат X, Y, Z /см. фиг. 4/. На фиг. 4 вектор отвесной линии обозначен сокращением "ОЛ" , проекция вектора отвесной линии обозначена сокращением "ПОЛ". Угол θ отсчитывается от оси Y системы координат X, Y, Z, т.е., если вектор отвесной линии совпадает /параллелен/ оси Y, то θ = 0o. А если вектор отвесной линии не параллелен оси Y, то угол θ ≠ 0o /см. фиг. 4/. Угол ϕ берет начало своего отсчета от оси X системы координат X, Y, Z и увеличивается, если проекция вектора отвесной линии смещается /поворачивается/ относительно системы координат от оси X в направлении оси Z /см. фиг. 4/.
Датчик - отвес устроен так: каждая единичная окружность представляет из себя набор фотоэлементов, расположенных по окружности /см. фиг. 5/. Перед "единичной окружностью фотоэлементов" устанавливается прозрачная дискообразная емкость-"кювета", заполненная прозрачной демпферирующей жидкостью /спиртом, керосином и т.д./. В этой кювете имеется небольшая, по отношению к общему объему кюветы, капелька ртути. На кювету от источника света падает излучение, освещая почти все фотоэлементы единичной окружности. Однако несколько фотоэлементов закрыты от источника света непрозрачной капелькой ртути. Эти закрытые фотоэлементы характеризуют наиболее низкую точку единичной окружности фотоэлементов /см. фиг. 5/. На фиг. 5 изображена "единичная окружность", состоящая только из 18 фотоэлементов. В реальной конструкции датчика-отвеса их должно быть гораздо больше, например тысяча.
Каждый фотоэлемент, принадлежащий единичной окружности, подключен одним своим выводом к своему индивидуальному тактируемому "Д" триггеру. Далее все "Д" триггеры подключены к приоритетному шифратору /см. фиг.6/. /"Единичную окружность - набор фотоэлементов, "Д" триггеры, приоритетный шифратор лучше изготовить в виде одной большой интегральной схемы, т.е. на одном кристалле. Возможно использовать в качестве измерительной "единичной окружности" "ПЗС окружность". Т.е. прибор с зарядовой связью, выполненный в виде окружности с последовательным опросом элементов.
По своей сути фиг. 6 - это "вид сбоку" на т.н. единичную окружность датчика - отвеса. Этот "вид сбоку" позволяет нам проследить связь элементов датчика - отвеса. На фиг. 6 цифрами обозначены: 1 - источник света, 2 - кювета, 3 - капля ртути, 4 - набор фотоэлементов, 5 - набор "Д" триггеров, 6 - приоритетный шифратор, 7 - электрические выводы из шифратора, на которых появляется двоичный код, характеризующий наиболее низкую точку данной единичной окружности датчика - отвеса.
Экранирование каплей ртути фотоэлементов вызывает появление на выходе приоритетного шифратора двоичного кода. Этот код, положение капли ртути, определяет проекцию отвесной линии на "единичную окружность".
В устройстве датчика-отвеса используются три "единичные окружности". Это дает нам возможность получить проекции отвесной линии на три взаимно перпендикулярные плоскости, см. фиг. 7. В результате мы получаем три угла α, β, γ, характеризующие наклон системы координат X, Y, Z относительно вектора отвесной линии.
Угол α принимает значения в интервале 0o ≤ α ≤ 360o и характеризует наклон системы координат X, Y, Z, полученный в результате вращения системы координат X, Y, Z вокруг оси X. Угол α берет свое начало /отсчет/ от оси Z , т. е. , если ось Z совпадает с вектором проекции отвесной линии на плоскость Z, O, Y, то угол α = 0o/см. фиг. 8 /. Направление отсчета угла α определяется исходя из условия, что правая система координат X, Y, Z совершает вращение вокруг оси X, которое определяется векторным произведением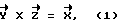
т. е. угол α возрастает, если в плоскости Z, О, Y вектор проекции отвесной линии смещается от оси Z в направлении к оси Y /см. фиг. 9 /.
Угол β принимает значения в интервале 0o≤β≤360o и характеризует наклон системы координат X, Y, Z, полученный в результате вращения системы координат X, Y, Z вокруг оси Y. Угол β берет свое начало /отсчет/ от оси X, т.е. , если ось X совпадает с вектором проекции отвесной линии на плоскость X, O, Z, то угол β = 0o/см. фиг. 10/. Направление отсчета угла β определяется исходя из условия, что правая система координат X, Y, Z совершает вращение вокруг оси Y, которое определяется векторным произведением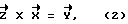
т. е. угол β возрастает, если в плоскости X, Y, Z вектор проекции отвесной линии смещается от оси X в направлении к оси Z /см. фиг. 11/.
Угол γ принимает значения в интервале 0o≤ γ ≤360o, и характеризует наклон системы координат X, Y, Z, полученный в результате вращения системы координат X, Y, Z вокруг оси Z. Угол γ берет свое начало /отсчет/ от оси Y, т. е. , если ось Y совпадает с вектором проекции отвесной линии на плоскость Y, O, X, то угол γ = 0o/см. фиг. 12 /. Направление отсчета угла γ определяется исходя из условия, что правая система координат X, Y, Z совершает вращение вокруг оси Z, которое определяется векторным произведением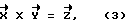
т.е. угол γ возрастает, если в плоскости Y, O, X вектор проекции отвесной линии смещается от оси Y в направлении к оси X /см. фиг. 13 /.
Теперь задача сводится к следующему: необходимо определить углы θ и ϕ, зная углы α, β, γ.
Ниже дан вывод формул, связывающих углы, α, β, γ с углами θ и ϕ. Эти формулы нужны для программирования ПЗУ /постоянного запоминающего устройства, см. фиг. 14/. Углы α, β, γ, как и углы θ и ϕ, образуют дискретный конечный набор значений, что и позволяет использовать ПЗУ при пересчете углов α, β, γ в углы θ и ϕ. На фиг. 14 цифрами 1, 2 и 3 помечены т.н. "единичные окружности", а 4 - ПЗУ. В данном случае каждая единичная окружность измеряет какой-то свой угол: α, β или γ, и представляет собой единую электронно-оптическую структуру, выполненную на одной подложке. /Предполагается, что топология каждой такой "единичной окружности" имеет структуру, идентичную блок-схеме, представленной на фиг. 6./ Задача фиг. 14 состоит в том, чтобы подчеркнуть применение ПЗУ для пересчета углов α, β, γ в углы θ, ϕ. Надо заметить, что на фиг. 14 отсутствуют несколько очень важных промежуточных блоков. /Более подробно эта структурная схема будет представлена на фиг. 66, после соответствующего описания./
Для вывода математических формул сделаем некоторые геометрические построения /см. фиг. 15 /. Где сфера "единичного" радиуса вписана в куб ABCDD'A'B'C'. В центре сферы берет начало система координат X', Y', Z'. Взаимная ориентация системы координат и куба такова, что оси X', Y', Z' ортогональны соответствующим граням куба. /Проекции сферы и куба на плоскости, перпендикулярные осям системы координат, дают нам три "единичные окружности", вписанные в квадраты, как это видно из фиг. 15./
Фиг. 15 позволяет разбить сферу на шесть угловых секторов. В зависимости от того, какую грань куба пересекает вектор отвесной линии, мы определяем угловой сектор.
Первый угловой сектор получится, если отвесная линия пересекает сторону ABCD куба /см. фиг. 16 /. В этом случае углы проекций отвесной линии на единичные окружности заключены в пределах
Значением угла γ пренебрегаем, т. к. мы имеем возможность вычислить наклон /углы θ и ϕ / по двум углам α и β.
Привожу математические формулы, позволяющие вычислить для первого сектора θ и ϕ по значениям углов α и β . Для этого рассмотрим следующие геометрические построения /см. фиг. 17/. Где совмещены центры двух "единичных окружностей", по которым производится отсчет углов α и β, с реперной точкой O' координат X', Y', Z'. Согласно этому рисунку вектор отвесной линии принадлежит первому угловому сектору. Проекции отвесной линии на соответствующие "единичные окружности" дают углы α и β.
Из фиг. 17 видно, что
ϕ = β. (5)
Угол θ находим из прямоугольного треугольника O'PN, см. фиг. 18, которая является частью фиг. 17. Вершина P треугольника O'PN равна 90o, поэтому угол θ можно найти как арктангенс отношения катетов NP и PO'
θ = arctg(NP:PO′). (6)
Но отрезок O'P, согласно фиг. 18, равен отрезку LM прямоугольного треугольника O'LM. А отрезок NP, согласно фиг. 18, равен гипотенузе KO' прямоугольного треугольника KLO'. Таким образом получаем
O′P = LM = |O′L|•tgα = 1•tgα; (7)
NP = KO′ = |O′L|:sinβ = 1:sinβ. (8)
Тогда формула 6 трансформируется в такой вид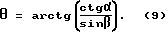
Это и есть искомая формула, связывающая для первого углового сектора углы α и β с углом θ.
Второй угловой сектор получится, если отвесная линия пересекает сторону ADD'A' куба /см. фиг. 15 /. В этом случае углы проекций отвесной линии на единичные окружности заключены в пределах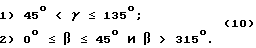
Значением угла α пренебрегаем.
Производим необходимые геометрические построения /см. фиг. 19 /. Откуда видно
ϕ = β (11)
Угол θ находим из прямоугольного треугольника O'PN, см. фиг. 20. Вершина P треугольника O'PN равна 90o, угол θ, как и в предыдущем случае, выражаем через арктангенс отношения катетов NP и PO'
θ = arctg(NP:PO′). (12)
С учетом того, что из прямоугольных треугольников KLO' и MPO' имеем
NP = (cosβ)-1 и PO′ = ctgγ. (13)
Получаем в окончательном виде формулу для нахождения угла θ: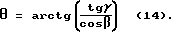
Третий угловой сектор получится, если отвесная линия пересекает сторону DCC'D' куба /см. фиг. 15/. В этом случае углы проекций отвесной линии на единичные окружности заключены в пределах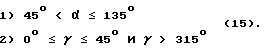
Значением угла β пренебрегаем.
Производим необходимые геометрические построения /см. фиг. 21 /. Она существенно отличается от похожей фиг. 17 тем, что в нее введена дополнительная линия LN. Это можно видеть на фиг. 22. Угол θ находим из прямоугольного треугольника O'LN как арктангенс отношения катетов LN и O'L /см. фиг. 23/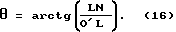
Учтем, что отрезок O'L равен единице, тогда формула 16 примет вид
θ = arctg LN, (17)
Отрезок LN находим с помощью теоремы Пифагора из прямоугольного треугольника LMN /см. фиг. 24/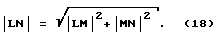
Катет LM получаем из прямоугольного треугольника O'LM /см. фиг. 25/
LM = tgγ. (19)
А катет MN получаем из прямоугольного треугольника O'LK /см. фиг. 26/
MN = LK = tg(90o-α) = ctgα (20)
Тогда формула 18 примет вид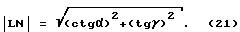
Отсюда получим в окончательном виде формулу для угла θ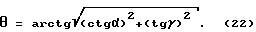
Формула для нахождения угла ϕ получается как арктангенс отношения катетов MN и LM прямоугольного треугольника LMN /см. фиг. 24/. С учетом формул 19 и 20 получим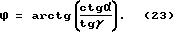
Здесь необходимо сделать еще несколько замечаний, связанных с формулой 23
Если угол γ = 0o и угол α < 90o, то угол ϕ = 90o.
Если угол γ = 0o и угол α > 90o, то угол ϕ = 270o.
Если угол γ = 0o и угол α = 0o, то угол ϕ имеет неопределенное значение.
Выражение "угол ϕ имеет неопределенное значение" становится понятным, если для системы координат X, Y, Z /см. фиг. 4/ построить "глобус наклонов" - сферу произвольного радиуса, с нанесенной на ее поверхности сеткой, состоящей из меридиан и параллелей /см. фиг. 27 /. Меридианы - это линии на поверхности глобуса наклонов, вдоль которых угол ϕ имеет постоянное значение. Параллели - это линии, вдоль которых угол θ сохраняет постоянное значение. Но на поверхности глобуса наклонов есть две особые, т.н. "полярные" точки. В этих точках угол ϕ имеет неопределенное значение, а при пересечении этих точек вдоль меридиана угол ϕ испытывает скачок в 180o. В полярных точках не надо знать значения угла ϕ, эти точки характеризуются другим углом, углом θ. Всякий раз, когда θ = 0o или θ = 180o означает, что вектор отвесной линии проходит через полярную точку, т.е. это означает, что система координат X, Y, Z наклонена в пространстве так, что вектор отвесной линии параллелен оси Y системы координат.
Четвертый угловой сектор:
Отвесная линия пересекает сторону ABB'A' куба /см. фиг. 15 /. В этом случае углы проекции отвесной линии на единичные окружности заключены в пределах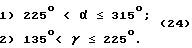
Значением угла β пренебрегаем. Геометрические построения выполнены в фиг. 28 - это общий вид.
Фиг. 29 выделяет из фиг. 28 только те элементы изображения, которые нужны нам для вывода формул. Из фиг. 29 видно, что для нахождения угла θ необходимо воспользоваться прямоугольным треугольником O'LN /см. фиг. 30 /. Катет LN треугольника O'LN связан с углом θ таким образом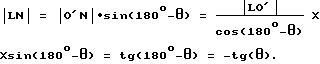
Т.е. получаем
θ = arctg(-|LN|). (25)
Отрезок LN находим с помощью теоремы Пифагора из прямоугольника LMNK /см. фиг. 31/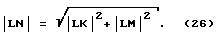
Отрезок LK находим с помощью фигуры 32, которая получается, если посмотреть на систему координат X', Y', Z', изображенную на фиг. 29 вдоль оси Z'. Имеем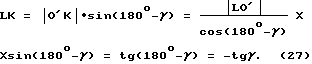
Отрезок LM находим из фиг. 33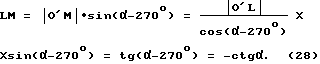
Формула 25 с учетом формул 26, 27 и 28 запишется так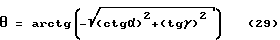
Угол ϕ согласно фиг. 31 ищем в виде арктангенса отношения отрезков LM и LK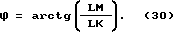
С учетом формул 27 и 28 получим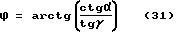
Здесь опять необходимо сделать несколько замечаний в связи с тем, что в секторе 4 находится полярная точка. Поэтому для формулы 31 имеем дополнения:
Если угол γ = 180o и угол α > 270o, то угол ϕ = 90o.
Если угол γ = 180o и угол α < 270o, то угол ϕ = 270o.
Если угол γ = 180o и угол α = 270o, то угол ϕ имеет неопределенное значение.
Пятый угловой сектор:
Отвесная линия пересекает сторону BCC'B' куба /см. фиг. 15 /. Углы проекции отвесной линии на единичные окружности заключены в пределах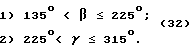
Значением угла α пренебрегаем. Геометрические построения /общий вид/ выполнены на фиг. 34. Фиг. 35 выделяет из фиг. 34 только необходимые элементы изображения, которые нужны для вывода формул. Мы видим из фиг. 35, что
ϕ = β. (33)
Угол θ находим из прямоугольного треугольника O'PN как арктангенс отношения катетов NP и O'P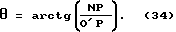
Отрезок NP получаем из прямоугольного треугольника О'LK, это демонстрирует фиг. 36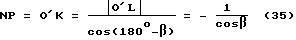
Согласно фиг. 37;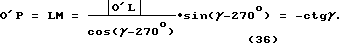
Тогда формула 34 запишется в таком виде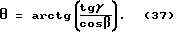
Шестой угловой сектор:
Отвесная линия пересекает сторону A'B'C'D' куба /см. фиг. 15/. Углы проекции отвесной линии на единичные окружности заключены в пределах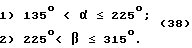
Пренебрегаем значением угла γ. Необходимые геометрические построения выполнены на фиг. 38 и 39, откуда видно
ϕ = β. (39)
Угол θ находим как арктангенс отношения катетов TN и O'T прямоугольного треугольника O'TN /см. фиг. 39/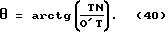
Отрезок TN получаем из треугольника O'LM /фиг. 40/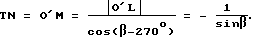
Отрезок O'T находим из треугольника O'LK /фиг. 41/;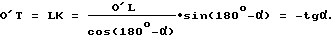
В окончательном виде формула для угла θ запишется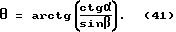
Достоинством предлагаемого жидкостного датчика - отвеса является его технологичность. Необходимо только изготовить соответствующую микросхему, содержащую в себе единичную окружность фотоэлементов, набор триггеров и шифратор. При современном уровне развития микроэлектронной промышленности это не составит особого труда. А дальше при окончательной сборке датчика-отвеса не будет больших проблем с настройкой. Например: пусть на эталонном /горизонтальном/ стенде во время сборки датчика-отвеса выяснилось, что микросхема, определяющая угол α, дает ошибочные показания /см. фиг. 42/. В этой ситуации специалисту, осуществляющему сборку, достаточно будет, учитывая показания контрольных приборов, слегка повернуть микросхему, а затем закрепить ее в нужном положении /см. фиг. 43/.
Другие датчики - отвесы, в основу работы которых положены иные технические решения, требуют более кропотливой настройки. Так в датчике - отвесе, выполненном на трех пружинных акселерометрах, расположенных вдоль осей системы координат X, Y, Z /см. фиг. 44/, необходимо учитывать разброс параметров трех акселерометров: небольшие различия в жесткости пружин, в трении, в массе инерционных грузиков. Все это делает настройку датчика - отвеса, состоящего из пружинных акселерометров, более трудоемкой.
Недостатком жидкостного датчика - отвеса является то, что он может выдавать точные показания только в том случае, если тело, на котором датчик - отвес установлен, совершает в пространстве в течение достаточно длительного времени поступательное /или почти поступательное/ движение, без сильных толчков и вращений, т.е. жидкостной датчик - отвес выдает правильные показания, если он достаточно долго находится в инерциальной /или почти инерциальной / системе отсчета.
/Здесь под выражениями: "в течение достаточно длительного времени" и "достаточно долго", подразумевается время, большее времени успокоения собственных колебаний /колебаний капелек ртути в кюветах/.
Жидкостной инерционный датчик ускоренных вращений.
Принцип действия:
Рассмотрим такое устройство, условно назовем его "измерительный виток":
Емкость, заполненная жидкостью, поделена на две камеры упругой мембраной /см. фиг. 45/, где V1 - первая камера, V2 - вторая камера, M - упругая мембрана.
Из одной камеры к другой идет трубка Т, также заполненная жидкостью. Трубка имеет форму окружности радиуса R.
При ускоренном вращении такого устройства вокруг точки "O" по разные стороны от мембраны создается перепад давления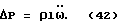
где ρ - плотность жидкости, l - длина окружности /длина трубки  - вращательное ускорение.
- вращательное ускорение.
Формула 42 получается по аналогии с формулой для расчета давления, создаваемого столбом жидкости в поле гравитационных сил. Только в нашем случае в роли "ускорения свободного падения" выступает вращательное ускорение 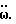
Под действием перепада давления ΔP упругая мембрана прогнется. Таким образом, следя за смещением мембраны, можно получить значение вращательного ускорения 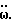 Тогда угол α′, на который повернулся в пространстве измерительный виток под воздействием вращательного ускорения
Тогда угол α′, на который повернулся в пространстве измерительный виток под воздействием вращательного ускорения  за время t, вычисляется по формуле
за время t, вычисляется по формуле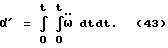
Мы должны иметь возможность измерять вращательные ускорения, происходящие вокруг любого произвольного направления /вокруг любой произвольной оси/, поэтому в жидкостном инерционном датчике вращательных ускорений необходимо использовать три таких измерительных витка. Причем каждый из этих измерительных витков будет иметь свою отдельную емкость и свою отдельную упругую мембрану, т.е. измерительные витки будут работать независимо друг от друга. Располагаться они будут в трех взаимно ортогональных плоскостях /см. фиг. 46/.
Из формулы 42 видно, что для повышения чувствительности прибора необходимо взять жидкость с возможно большей удельной плотностью ρ /например, ртуть/ и увеличить длину трубки Т /см. фиг. 45/. Длину измерительной трубки можно увеличить в несколько раз, но чтобы при этом весь прибор остался компактным, трубку придется свернуть особым - "спиралеобразным" образом. При этом необходимо тщательно следить за тем, чтобы случайно не образовались дополнительные /незапланированные/ петли, лежащие во взаимно ортогональных плоскостях. Это особенно важно, если общее число измерительных витков в "спирале" невелико. А если мы свернем трубку неправильно, то прибор будет давать неправильные показания. На фиг. 47 изображено как можно свернуть измерительную трубку. Фиг. 48 дает вид фиг. 47 слева. На фиг. 49 показана аксонометрическая проекция фиг. 47. Еще один возможный вариант сворачивания "спирали" представлен фиг. 50 - 52. Как видно здесь, на измерительной трубке образовались два бугорка. Наличие таких бугорков не оказывает влияния на правильность функционирование прибора, несмотря на то, что они не лежат в одной плоскости с основными измерительными витками. Дело в том, что воздействие двух таких бугорков на жидкость, заполняющую измерительную трубку, взаимно компенсируются. Возможно свернуть измерительную трубку в многовитковую спираль - соленоид, намотав ее на катушку в несколько слоев /подобно тому, как наматывают медную проволоку при изготовлении электромагнита/ см. фиг. 53. Эта последняя конструкция в виде катушки - солиноида обладает наибольшей чувствительностью, а появление нескольких дополнительных витков во взаимно ортогональных плоскостях уже не страшно, т.к. их влиянием на точность прибора можно пренебречь. Конечно, после сворачивания измерительной трубки в соленоид или в "спираль" формула 42 уже не будет выполняться абсолютно точно, но это тоже не страшно, ведь прибор в любом случае придется градуировать эмпирически.
Предлагаемый здесь жидкостной инерционный датчик ускоренных вращений реагирует только на вращательные ускорения /на изменение угловой ориентации тела в пространстве/ и полностью игнорирует прямолинейные ускорения тела /ускорения, возникающие при поступательном движении тела/.
Жидкостной инерционный датчик ускоренных вращений предназначен измерять значительные вращательные ускорения, этим самым он компенсирует недостатки жидкостного датчика - отвеса /см. выше/, который не может работать в неинерциальных системах отсчета.
Смещение мембраны в жидкостном инерционном датчике ускоренных вращений можно определить, воспользовавшись изменением электрической емкости, т.е. мембрана должна будет выполнять роль одной из обкладок конденсатора переменной емкости. Это демонстрируется фиг. 54, где изображены два конденсатора переменной емкости C1 и C2, соединенных между собой последовательно. Причем изменение емкостей этих конденсаторов взаимно противоположно, т.е., если емкость одного конденсатора увеличивается, то емкость другого в это время обязательно уменьшается, и наоборот. От конденсатора С2 идут выводы, к которым подключается измерительный прибор, здесь по сути дела получился емкостный делитель напряжения. На конденсаторы подается эталонное синусоидальное напряжение Uоп, имеющее фиксированную частоту и амплитуду.
В зависимости от того, какая жидкость используется в жидкостном датчике: диэлектрик /керосин/ или проводник электрического тока /ртуть/, возможны следующие конструкции датчика:
Фиг. 55.. В качестве жидкости, заполняющей датчик, используем диэлектрик /керосин/. Тогда применяется только одна мембрана: M, она выполняет роль обкладки электрического конденсатора. Другие две обкладки: K1 и K2 размещены непосредственно внутри камер V1 и V2, заполненных керосином. От мембраны и от двух других обкладок сделаны соответствующие электрические выводы.
Если в качестве жидкости, заполняющей инерционный датчик ускоренных вращений, используется проводник электрического тока, например, ртуть, то надо воспользоваться иной конструкцией датчика /см. фиг. 56/. Здесь применены уже две упругие металлические мембраны: M1 и M2. Между ними установлена металлическая распорка P, упирающаяся в мембраны выпуклыми /скругленными/ поверхностями. Вершины /центральные точки/ скругленных поверхностей металлической распорки припаяны к соответствующим мембранам. Таким образом, проводящая жидкость /ртуть/, мембраны M1, M2 и распорка P представляют из себя один сплошной проводник. Распорка является конденсаторной обкладкой. Напряжение с нее снимается с помощью вывода K3, который одним своим концом погружен в ртуть. Две другие конденсаторные обкладки K1 и K2 выполнены в виде шайб, насаженных своими центральными отверстиями на внешние поверхности камер V1 и V2, изготовленных из диэлектрика. /Здесь необходимо заметить, что отношение суммарной массы мембран M1, M2 и распорки P к объему воображаемого цилиндра Vц, основаниями которого являются мембраны /см. фиг. 57/, должно равняться плотности жидкости, используемой в датчике,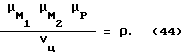
Иначе датчик ускоренных вращений окажется чувствительным к поступательным ускорениям, что крайне нежелательно./
Основным достоинством жидкостного инерционного датчика вращений является его простота по сравнению с другими устройствами, выполняющими аналогичную роль. Например, по сравнению с лазерными интерференционными гироскопами, изготовленными с использованием оптических волокон. Однако жидкостной инерционный датчик вращений имеет один достаточно серьезный недостаток: в нем используется упругий элемент - мембрана, которая может послужить источником т.н. возвращающей силы. Как следствие, в датчике возможно появление колебаний и, конечно, резонанса при определенной частоте. Надо сказать, что по своей сути жидкостной инерционный датчик вращательных ускорений представляет из себя модифицированный пружинный датчик - акселерометр, см. фиг. N 44. В данном случае в жидкостном инерционном датчике ускоренных вращений роль инерционной массы играет жидкость, а роль пружины - упругая мембрана. Так что вполне естественно, что жидкостному инерционному датчику ускоренных вращений, как и всякому датчику ускорений с инерционной массой присущ этот недостаток: опасность возникновения резонанса. Однако в технике сплошь и рядом применяются датчики-акселерометры, главным образом в навигационных системах кораблей, самолетов, баллистических ракетах. И это несмотря на опасность появления резонанса. Надеюсь, что и жидкостной инерционный датчик ускоренных вращений найдет свое применение в технике, несмотря на опасность проявления резонанса, тем более, что существуют способы, позволяющие существенно ослабить влияние резонанса на точность измерений:
Во - первых, сама жидкость, заключенная в трубке, может выполнить роль демпферирующего элемента и погасить резонансные колебания. Дело в том, что при колебаниях жидкость должна будет поочередно перетекать в небольших количествах по трубке Т то в одну камеру V1, то в другую V2. /см. фиг. N 45/, при этом жидкость будет тереться о стенки трубки Т, гася возникшие колебания.
Во - вторых, можно разработать активные способы борьбы с резонансными колебаниями. Для этого необходимо перенести путем соответствующего изначального подбора основных характеристик датчика /подбором упругости мембраны, подбором длины и сечения измерительной трубки/ резонансную частоту датчика в область высоких частот, т.е. в такую область, которая абсолютно не характерна для тела, изменения угловой ориентации которого мы измеряем. /Например, частота вращений /колебаний/ корпуса антропоморфного шагающего робота скорее всего будет меньше 5 Гц. В этом случае мы должны перевести частоту собственных колебаний жидкостного инерционного датчика ускоренных вращений в область порядка 10 Гц./ Далее в электрические цепи, предназначенные для снятия показаний с жидкостного инерционного датчика, необходимо будет ввести полосно - подавляющий фильтр, а в цепь обратной отрицательной связи - узкополосный фильтр. Причем резонансная частота этих фильтров должна совпадать с частотой резонанса жидкостного инерционного датчика ускоренных вращений.
Применение в электронных цепях таких фильтров позволит выделить интересующую нас низкочастотную составляющую вращений тела /корпуса робота/, даже в том случае, если резонанс в датчике все же наступит. Фиг. 58 и 59 поясняют это.
На фиг. 58 изображен график колебаний электрического напряжения, снимаемого с датчика, до фильтров. А фиг. 59 показывает, что через фильтры прошла только низкочастотная составляющая напряжения.
Электрические цепи, с помощью которых можно снимать показания с жидкостного инерционного датчика ускоренных вращений, могут иметь такую структуру: /см. фиг. 60/.
На фиг. 60 имеются следующие элементы: конденсаторы С1 и C2 изображают собой мембрану и обкладки K1 и K2 датчика ускоренных вращений. Эти конденсаторы подключены к генератору переменного напряжения Uоп, фиксированной частоты и амплитуды. Напряжение, снимаемое с мембраны датчика /на схеме мембрана помечена буквой "М"/, подается на полосно - подавляющий фильтр 1. Далее сигнал усиливается усилителем 2, у которого в цепи обратной отрицательной связи встроен узкополосный фильтр 3. Применение фильтров устраняет высокочастотную составляющую, соответствующую резонансным колебаниям датчика. Далее используется диодный мост 4, выпрямляющий напряжение. За ним стоит фильтр L-C3, сглаживающий колебания несущей частоты, возникшие в цепях от генератора переменного напряжения Uоп. На вход устройства выборки - хранения 5 поступает только низкочастотная составляющая, характеризующая изменение угловой ориентации тела /корпуса робота/. Затем идет аналого-цифровой преобразователь 6, вслед за которым стоит программируемое постоянное запоминающее устройство 7, на выходе которого получается двоичный код. /ППЗУ 7 необходимо для настройки датчика. / В предложенной схеме используются две независимые земли" 31 и З2.
Существует еще одна возможность существенно ослабить угрозу возникновения резонансных колебаний в датчике. Для этого необходимо превратить распорку Р /см. фиг. 56/ в "Прибор Фрама для уменьшения вибраций", смотри книгу: Н. В. Розе "Динамика твердого тела" Ленинград 1932 г. стр. 285 - 289. Однако здесь эту возможность я рассматривать не буду, т.к. полагаю, что достаточно уже рассмотренных способов гашения колебаний.
Как видно из фиг. 60, мы получаем на выходах ППЗУ значение вращательного ускорения 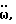 а нам для дальнейших применений понадобится значение угла α′, на который произошел поворот корпуса робота за время t под воздействием вращательного ускорения
а нам для дальнейших применений понадобится значение угла α′, на который произошел поворот корпуса робота за время t под воздействием вращательного ускорения 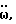 см. формулу (43). Поэтому рассмотрим метод численного интегрирования значений вращательных ускорений. Интегрирование будем производить с помощью цифровой /двоичной/ электроники.
см. формулу (43). Поэтому рассмотрим метод численного интегрирования значений вращательных ускорений. Интегрирование будем производить с помощью цифровой /двоичной/ электроники.
Предполагается, что в первые секунды после включения электропитания корпус робота неподвижен или малоподвижен. Это дает нам возможность получить начальные условия для "задачи определения угловой ориентации корпуса робота", т.е. мы можем определить начальное направление "вниз". За те первые секунды, пока робот остается неподвижным, электроника жидкостных датчиков ориентации успеет выдать показания тысячи раз. Часть из этих показаний надо будет запомнить - они нужны для вычислений.
Изменение угловой ориентации корпуса робота "с точки зрения электроники" происходит медленно, т.е. электроника работает гораздо быстрее, чем происходят повороты корпуса робота в пространстве. Производим выборку значений вращательных ускорений 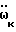 через равные промежутки времени Δt.
через равные промежутки времени Δt.
Вначале найдем скорость поворота корпуса робота, которая получается в результате вращательных ускорений 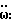

Используем аппроксимацию: заменим интегрирование суммированием площадей трапеций, заключенных под графиком функции /см. фиг. 61/. Здесь надо особо подчеркнуть один принципиальный момент: из графика, изображенного на фиг. 61, видно, что в первые мгновения значения функции  равны нулю. Это крайне необходимое условие, а вовсе не случайность! Только при соблюдении этого обстоятельства можно выполнить интегрирование.
равны нулю. Это крайне необходимое условие, а вовсе не случайность! Только при соблюдении этого обстоятельства можно выполнить интегрирование.
Тогда скорость вращения корпуса робота, полученная под воздействием вращательных ускорений  за конечное время ti, выражается формулой
за конечное время ti, выражается формулой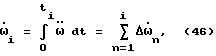
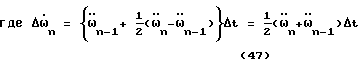 -
-
площадь элементарной трапеции, заключенной под графиком функции 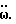 Это есть приращение угловой скорости вращения за "бесконечно малое" время Δt, прошедшее между моментами времени tn-1 и tn.
Это есть приращение угловой скорости вращения за "бесконечно малое" время Δt, прошедшее между моментами времени tn-1 и tn.
Тогда формула (6) перепишется так: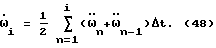
Полная скорость вращения корпуса робота получается с учетом начальных условий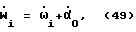
где 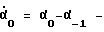 начальная малая скорость, полученная из показаний датчика - отвеса. /Напомню, что датчиком - отвесом можно пользоваться, когда робот малоподвижен, например, сразу после включения электропитания./ В общем случае α0, хотя и малая, но все-таки отличная от нуля величина, поэтому ее надо учитывать. Вычисляется она как разность угла α0, измеренного в момент времени to, и угла α-1, измеренного в момент - t-1 и запомненного электроникой.
начальная малая скорость, полученная из показаний датчика - отвеса. /Напомню, что датчиком - отвесом можно пользоваться, когда робот малоподвижен, например, сразу после включения электропитания./ В общем случае α0, хотя и малая, но все-таки отличная от нуля величина, поэтому ее надо учитывать. Вычисляется она как разность угла α0, измеренного в момент времени to, и угла α-1, измеренного в момент - t-1 и запомненного электроникой.
Полный поворот корпуса робота, произошедший за время ti, определяется формулой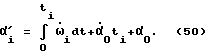
где первый член описывает поворот, полученный роботом, под воздействием вращательных ускорений за промежуток времени, прошедший между моментами to и ti.
Второй член описывает угол, на который поворачивается корпус робота под воздействием малой начальной скорости 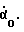 Третий член - это начальный угол α0, т. е. угол, на который был повернут корпус робота в момент времени to, его значение получено от датчика - отвеса.
Третий член - это начальный угол α0, т. е. угол, на который был повернут корпус робота в момент времени to, его значение получено от датчика - отвеса.
Используем аналогичный прием: заменяем интегрирование суммированием по площадям /см. фиг. 62/. Тогда формула (50) будет записана так: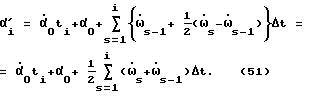
Перепишем это в более наглядной форме: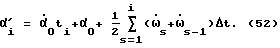
Из формулы (52) видно, что полный угол, на который повернулся в пространстве корпус робота под воздействием произвольных ускорений, можно найти, если представить его так: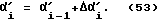
где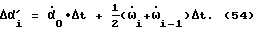
Эти две последнии формулы (53) и (54) более удобны по сравнению с формулой (52), т. к., основываясь на них, легче организовать "бесконечный вычислительный цикл" /см. фиг. 63 и 64/. К формулам (53) и (54) необходимо еще добавить начальные условия:
начальную скорость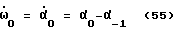
и начальное ускорение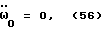
а также добавим еще одну формулу, которая получается из формулы (48),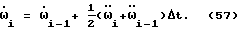
Комментарии:
В соответствии с формулой (53) угол 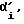 на который повернулся в пространстве корпус робота к моменту времени ti, вычисляется как сумма двух слагаемых:
на который повернулся в пространстве корпус робота к моменту времени ti, вычисляется как сумма двух слагаемых:
Первое слагаемое: 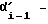 это значение угла, на который был повернут корпус робота к моменту ti-1. К моменту ti угол
это значение угла, на который был повернут корпус робота к моменту ti-1. К моменту ti угол 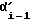 должен быть вычислен и запомнен электроникой.
должен быть вычислен и запомнен электроникой.
Второе слагаемое: 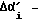 это причащение угла поворота корпуса робота, возникшее за время Δt, прошедшее между моментами ti-1 и ti. Значение
это причащение угла поворота корпуса робота, возникшее за время Δt, прошедшее между моментами ti-1 и ti. Значение 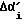 вычисляется электроникой робота с учетом формул (55), (56) и (57), на основе показаний датчика - отвеса.
вычисляется электроникой робота с учетом формул (55), (56) и (57), на основе показаний датчика - отвеса.
Объясню как работает алгоритм, изображенный на фиг. 63 и 64.
Сразу после включения электропитания робота начинается вычислительный процесс, заданный указанным алгоритмом.
В блоке 2 происходит присвоение начальных значений некоторым параметрам. Целочисленный параметр J необходим для организации разветвлений в "бесконечном цикле", в зависимости от проверки выполнения условия. /Блок 2 играет еще одну очень важную роль, которая не отображена полностью в этом алгоритме. Дело в том, что выполнение "бесконечного цикла" время от времени будет прерываться, а вычислительный процесс будет возвращен к блоку 2. Причины возникновения таких прерываний будут объяснены позже, в разделе, где обсуждается вопрос доминирования датчика одного типа над датчиком другого типа, т. е. в зависимости от динамики изменения угловой ориентации корпуса робота./
Ввод текущих показаний от жидкостного датчика - отвеса и от жидкостного инерционного датчика ускоренных вращений на представленном алгоритме изображен блоком 3.
Блок 4 обеспечивает тот самый режим прерывания, о котором было сказано выше.
Блок 5 - проверка выполнения условия, если J = 0, то переходим к блоку 6.
В блоке 6 производим некоторые присвоения. Параметру J присваивается значение единица. Углу 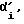 на который повернут корпус робота, присваивается текущее значение угла αi, измеренное датчиком - отвесом. А также в блоке 6 происходит присвоение переменной
на который повернут корпус робота, присваивается текущее значение угла αi, измеренное датчиком - отвесом. А также в блоке 6 происходит присвоение переменной 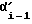 текущего значения угла αi, это - "задел на будущее" - в следующем периоде выполнения цикла нынешнее значение αi будет уже считаться предыдущим.
текущего значения угла αi, это - "задел на будущее" - в следующем периоде выполнения цикла нынешнее значение αi будет уже считаться предыдущим.
Блок 7 обозначает вывод значения полного угла  на который повернулся корпус робота. После этого мы вновь возвращаемся к блоку 3, это показано стрелкой. Теперь начинается новый период цикла.
на который повернулся корпус робота. После этого мы вновь возвращаемся к блоку 3, это показано стрелкой. Теперь начинается новый период цикла.
Опять в блоке 3 происходит ввод текущих значений, выдаваемых датчиком - отвесом и инерционным датчиком ускоренных вращений. После этого мы спускаемся к блоку 5, если нам удалось пройти блок 4. Теперь значение параметра J = 1, поэтому мы направляемся к блоку 8, где происходит проверка условия.
После этого мы попадаем в блок 9, где на основе предыдущего и нынешнего показания датчика - отвеса происходит вычисление начальной угловой скорости поворота корпуса робота.
В блоке 10 производятся присвоения. Параметру J присваивается значение "двойка", это необходимо нам для того, чтобы в следующий период можно было перейти на другую ветвь алгоритма. Полный угол 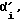 на который повернулся в пространстве корпус робота, получается присвоением текущего значения угла αi, измеренного датчиком - отвесом. Переменная
на который повернулся в пространстве корпус робота, получается присвоением текущего значения угла αi, измеренного датчиком - отвесом. Переменная 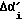 получает значение
получает значение 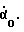 /Как уже ранее указывалось
/Как уже ранее указывалось 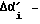 это приращение угла поворота корпуса робота, возникшее за промежуток времени Δt. /. Все остальные присвоения, осуществленные в блоке 10, необходимы, чтобы обеспечить работу алгоритма в следующем периоде, т.е. "нынешние значения становятся предыдущими" и запоминаются - записываются в соответствующие ячейки памяти. Так нынешняя скорость
это приращение угла поворота корпуса робота, возникшее за промежуток времени Δt. /. Все остальные присвоения, осуществленные в блоке 10, необходимы, чтобы обеспечить работу алгоритма в следующем периоде, т.е. "нынешние значения становятся предыдущими" и запоминаются - записываются в соответствующие ячейки памяти. Так нынешняя скорость 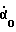 для следующего периода цикла становится предыдущей
для следующего периода цикла становится предыдущей 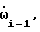 нынешний угол αi станет предыдущим
нынешний угол αi станет предыдущим 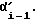
Далее переходим к блоку 11, который символизирует собой вывод информации: полного угла 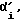 на который повернут корпус робота, и приращения угла поворота корпуса робота
на который повернут корпус робота, и приращения угла поворота корпуса робота 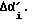 После чего, мы вновь возвращаемся к блоку 3.
После чего, мы вновь возвращаемся к блоку 3.
Теперь, по прошествии первых двух периодов цикла, корпус робота может подвергаться сильным произвольным вращательным ускорениям. Мы эти ускорения измеряем жидкостным инерционным датчиком ускоренных вращений /блок 3/. Ранее параметру в блоке 10 было присвоено значение 2, поэтому теперь после нескольких проверок на выполнение условий /блоки 4, 5, 8/ попадаем в блок 12, где осуществляется двойное интегрирование 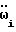 по времени. Этим самым мы получаем полный угол
по времени. Этим самым мы получаем полный угол 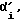 на который повернут корпус робота к моменту ti /блок 14/. В блоке 15 делаются необходимые присвоения для следующего периода цикла.
на который повернут корпус робота к моменту ti /блок 14/. В блоке 15 делаются необходимые присвоения для следующего периода цикла.
Блок 16 символизирует вывод информации, после чего мы вновь возвращаемся к блоку 3, и цикл становится "бесконечным".
Теперь основная роль в определении угловой ориентации корпуса робота перешла целиком к жидкостному инерционному датчику ускоренных вращений. Эта роль будет принадлежать ему до тех пор, пока угловая ориентация корпуса робота не станет изменяться равномерно в течение длительного времени /при этих условиях произойдет прерывание, изображаемое на алгоритме блоком 4, параметру J будет в блоке 2 присвоено значение ноль и т.д./.
Для нахождения полных углов β′ и γ′ можно представить аналогичные по своей структуре алгоритмы и формулы, аналогичные формулам (53), (54), (55), (56), (57).
Итак мы имеем в своем распоряжении три угла α′, β′, γ′, которые получены с учетом показаний датчиков двух типов, как датчика - отвеса, так и жидкостного инерционного датчика ускоренных вращений.
По изменению значений этих трех углов α′, β′, γ′ мы теперь можем определить изменение угловой ориентаций корпуса робота. Для этого введем правую систему координат XYZ, жестко связав ее с корпусом антропоморфного шагающего робота.
Здесь для наших теоретических построений необходимо воспользоваться теоремой Эйлера, которая утверждает:
"Если относительно некоторой системы отсчета S твердое тело имеет одну неподвижную точку, то перемещение твердого тела из любого положения в любое другое положение может быть совершено одним поворотом на определенный угол вокруг определенной оси, проходящей через неподвижную точку тела."
/Смотри книгу: И. И. Ольховский "Курс теоретической механики для физиков". М., 1970 г., стр. 148./
Пусть в течение достаточно длительного отрезка времени корпус робота, а вместе с ним и система координат XYZ, не изменял в пространстве своей угловой ориентации /такая ситуация, как я уже указывал, возникает в первые моменты сразу после включения электропитания антропоморфного шагающего робота. Робот еще неподвижен, а датчики угловой ориентации уже выдают свои показания./
Затем робот /совместно с системой координат XYZ. /начинает совершать в пространстве свои произвольные движения, изменяя при этом непредсказуемым образом свою угловую ориентацию.
В момент времени ti система координат XYZ имела наклон θi, ϕi. Пометим систему координат XYZ, наблюдаемую в момент времени ti индексом "i", так мы получим: Xi, Yi, Zi. Спустя один период Δt опроса датчиков в момент времени tk= ti + Δt датчики ориентации выдали показания: 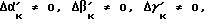 т. е. система координат XYZ совершила поворот в пространстве, перейдя в состояние, которое можно пометить индексом "k": Xk, Yk, Zk.
т. е. система координат XYZ совершила поворот в пространстве, перейдя в состояние, которое можно пометить индексом "k": Xk, Yk, Zk.
Период опроса датчиков Δt "с точки зрения" механики в нашем случае можно считать "бесконечно малым" отрезком времени, т.е. изменение угловой ориентации корпуса робота происходит медленно по сравнению со скоростью работы электроники. Поэтому за "бесконечно малое" время Δt /за период опроса датчиков ориентации/ корпус робота успеет изменить /свою ориентацию только на "бесконечно малые" величины: 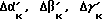 /это "бесконечно малые величины с точки зрения механики", но отнюдь не "с точки зрения" электроники/.
/это "бесконечно малые величины с точки зрения механики", но отнюдь не "с точки зрения" электроники/.
Как известно, бесконечно малые повороты коммутируют, поэтому они могут быть отождествлены с вектором, смотри книгу: И. И. Ольховский "Курс теоретической механики для физиков". М., 1970 г., стр. 151, где сказано примерно следующее: бесконечно малый поворот можно задать вектором, модуль этого вектора равен углу поворота, а прямая, на которой расположен вектор является мгновенной осью вращения.
В нашем случае вектор 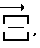 характеризующий бесконечно малое изменение ориентации корпуса робота, произошедшее за время Δt, будет иметь в системе координат Xi, Yi, Zi компоненты:
характеризующий бесконечно малое изменение ориентации корпуса робота, произошедшее за время Δt, будет иметь в системе координат Xi, Yi, Zi компоненты:  и длину /модуль/:
и длину /модуль/: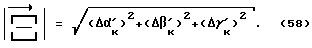
Теперь рассмотрим очень важный принципиальный момент, играющий фундаментальное значение в теории изготовления механизма подвеса - устройства, с помощью которого мы будем управлять ходьбой антропоморфного шагающего робота.
Мы имеем полное право разложить произвольный бесконечно малый поворот 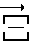 корпуса робота, совершаемый в пространстве вокруг мгновенной оси, иным /эквивалентным/ образом, а именно: как наклон корпуса робота, происходящий относительно вектора отвесной линии, и как поворот вокруг вектора отвесной линии, осуществляемый корпусом робота одновременно с наклоном.
корпуса робота, совершаемый в пространстве вокруг мгновенной оси, иным /эквивалентным/ образом, а именно: как наклон корпуса робота, происходящий относительно вектора отвесной линии, и как поворот вокруг вектора отвесной линии, осуществляемый корпусом робота одновременно с наклоном.
Таким образом любое произвольное изменение ориентации корпуса робота описывается тремя независимыми параметрами. Наклон корпуса робота относительно вектора отвесной линии определяется двумя бесконечно малыми углами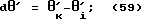
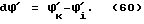
Поворот корпуса робота вокруг вектора отвесной линии определяется еще одним бесконечно малым углом dξ′, который вычисляется как скалярное произведение двух векторов: вектора отвесной линии - вектора единичной длины, с направлением, взятым момент ti, вектора 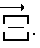 По сути мы здесь находим проекцию вектора
По сути мы здесь находим проекцию вектора 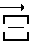 на единичный вектор отвесной линии /см. фиг. 65/.
на единичный вектор отвесной линии /см. фиг. 65/.
Единичный вектор отвесной линии имеет в момент времени ti в системе координат Zi,Yi,Zi компоненты /см. фиг. 4/: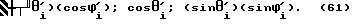
Таким образом угол dξ′ вычисляется по формуле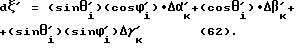
От дистанционного антропоморфного шагающего робота мы будем передавать по каналам связи на устройство управления три угла: 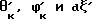 /см. фиг. 66/.
/см. фиг. 66/.
На блок - схеме, показанной на фиг. 66, соответствующими блоками изображены: жидкостной датчик - отвес и жидкостной инерционный датчик ускоренных вращений. /Об устройстве этих датчиков было рассказано выше./
Данные от датчиков поступают в блок вычислений и в блок управления.
Блок вычислений: его назначение состоит в том, чтобы на основе данных, поступающих от жидкостных датчиков, вычислить полные углы: α′, β′, γ′ и угол dξ′. Работа блока вычислений основана на алгоритме, представленном фиг. 63 и 64.
Кроме того, в блоке вычислений для расчета угла dξ′ используются значения углов θ′ и ϕ′ /см. формулу (63)/, полученных в предыдущий период. /Это на схеме показано стрелками, идущими от ПЗУ к блоку вычислений./
Блок управления, исходя из показаний жидкостных датчиков и из динамики изменения этих показаний, задает различные режимы работы блока вычислений. /На схеме, изображенной фиг. 66, "руководящее" воздействие блока управления на блок вычислений обозначено толстой стрелкой./
Постоянное запоминающее устройство /ПЗУ/ преобразует углы: α′, β′, γ′ в углы θ′ и ϕ′. /Об этом ранее уже говорилось, см. фиг. 14 и комментарии к ней./
Рассмотрим принципы работы блока управления.
Работа блока управления основана на следующем: исходя из данных, поступающих в блок управления от жидкостных датчиков, и на основе динамики изменения этих данных, необходимо определить режим изменения угловой ориентации корпуса робота и в соответствии с определенным режимом изменить режим расчета блока вычислений.
Для решения этой задачи необходимо будет вначале рассмотреть/правильнее сказать: "подсмотреть"/ как человек определяет свою угловую ориентацию в пространстве, т.е. необходимо посмотреть как функционируют человеческие органы равновесия.
У человека в голове имеются жидкостные инерционные "датчики ускоренных вращений", это т.н. "отолитовые органы". Имеется у человека и "датчик - отвес", но он не лакализован в каком-то конкретном месте организма, а "размазан" фактически по всему телу. Т.е. человек определяет направление внешних ускорений /в том числе и направление действия гравитационных сил/ с помощью всего своего тела. Под воздействием внешних ускорений отдельные части человеческого тела смещаются относительно друг друга, каким-то определенным образом, человек это чувствует и подсознательно определяет направление и интенсивность действия внешних ускорений.
Использование человеческим организмом подобного "датчика-отвеса" позволяет ему определять начальное направление "вниз". А отолитовые органы следят за последующими изменениями угловой ориентации человеческого тела /в том числе и за поворотами, происходящими вокруг вектора отвесной линии, а "датчик-отвес" повороты такого рода не замечает/.
Приведу конкретные примеры, на которых поясняется действие того или иного "датчика" в той или иной ситуации:
Первый, очень важный случай. Он часто встречается нам в практике: тело человека достаточно долго остается неподвижным или почти неподвижным, т.е. человеческий организм не испытывает больших ускорений и быстрых вращательных движений. Из этой ситуации человек подсознательно с помощью своего "датчика - отвеса" получает информацию о начальном направлении "вниз". В дальнейшем эта информация "о начальном направлении "вниз" человеку очень понадобится для определения своей угловой ориентации, когда его тело начнет двигаться неравномерно, т. е. когда появятся вращательные ускорения /см. второй случай/.
Применяя математическую терминологию, можно этот первый случай прокомментировать так: "нахождение начального направления "вниз" - это нахождение начальных условий в задаче об "определении угловой ориентации произвольно движущегося человеческого тела".
Второй, очень распространенный случай: человек передвигается пешим ходом по сильно пересеченной местности. При этом тело человека обязательно будет испытывать толчки и вращательные ускорения. В такой ситуации основную роль в определении угловой ориентации у человека играет отолитовый орган.
Эти два только что рассмотренных случая для нас наиболее важные, т.к. они наиболее типичны - природа создавала человека "исходя из предположения", что он /человек/ будет передвигаться прежде всего своим, пешим, ходом.
В дальнейшем человек сильно "избаловался", придумав различные технические средства передвижения, незапланированные первобытной природой: лодки, телеги, машины и т.д.... В этот список обязательно надо включить еще один механизм - центрифугу, которая, конечно, не относится к транспортным средствам передвижения, однако она является самым "коварным" техническим устройством для человеческих органов равновесия.
В результате применения технических средств органы равновесия человека часто оказываются в ситуациях, "нетипичных с точки зрения первозданной природы". Продемонстрирую это на примере центрифуги /см. фиг. 67/.
Схематически центрифуга устроена так: в подшипниках 1 и 2 установлена вертикальная ось вращения 3. На ней закреплен перпендикулярный стержень 4, в одном конце которого имеется противовес 5, а в другом подвешена "люлька" 6.
Человек /на фигуре он обозначен цифрой 7/ ложится в люльку 6, когда привод центрифуги выключен. После этого центрифуга приводится во вращение.
Спустя некоторое время, люлька 6 вместе с человеком 7 отклонится от своего начального положения под воздействием центробежной силы, изменив свой угол примерно на 90o по отношению к стержню 4 /см. фиг. 68/.
В этой ситуации показания различных "датчиков равновесия" человеческого организма крайне противоречивы. Отолитовый орган выдает следующие показания /см. фиг. 69/: "человек из горизонтального положения "встал на голову" и вертится вокруг своей оси с угловой скоростью, равной угловой скорости центрифуги".
А "датчик - отвес", "размазанный" по телу человека, в это время выдает совершенно другие показания /см. фиг. 70 /: "тело человека лежит горизонтально в непривычно сильном гравитационном поле".
Органы равновесия человека успешно справляются с указанным противоречием: человек признает правильным показания "датчика - отвеса".
Для создания дистанционного, антропоморфного робота, управляемого человеком в копирующем режиме, необходимо в блоке управления использовать алгоритмы, которые по возможности повторяли бы режимы работы органов равновесия человека.
На фиг. 71 и 72 даны такие алгоритмы блока управления.
Алгоритм, изображенный на фиг. 71, представляет из себя "бесконечный цикл". Назначение этого алгоритма - определять ситуации, когда корпус робота длительное время движется в пространстве без сильных вращательных ускорений. После чего из блока управления в блок вычислений должен быть подан сигнал прерывания /см. фиг. 63, блок 4/. Т.е. алгоритм, представленный фиг. 71 выявляет ситуации, удобные для измерения "начальных условий".
Блок 2, алгоритма, изображенного на фиг. 71, обозначает присвоение начального значения параметру S. Этот параметр будет необходим нам для измерения определенного промежутка времени.
Блок 3 обозначает ввод данных от жидкостных датчиков. Углы α, β и γ вводятся от соответствующих единичных окружностей датчика - отвеса. Вращательные ускорения: 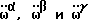 вводятся в алгоритм от соответствующих измерительных витков жидкостного инерционного датчика ускоренных вращений. /Здесь в рассмотрение введены вращательные ускорения с верхними индексами α, β, γ. Если
вводятся в алгоритм от соответствующих измерительных витков жидкостного инерционного датчика ускоренных вращений. /Здесь в рассмотрение введены вращательные ускорения с верхними индексами α, β, γ. Если 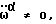 то это означает, что корпус робота вращается в пространстве c переменной угловой скоростью вокруг оси X системы координат XYZ, жестко связанной с корпусом робота /см. фиг. 7 /, т.е. угол α изменяется неравномерно. Аналогично, если
то это означает, что корпус робота вращается в пространстве c переменной угловой скоростью вокруг оси X системы координат XYZ, жестко связанной с корпусом робота /см. фиг. 7 /, т.е. угол α изменяется неравномерно. Аналогично, если 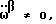 то угол β изменяется неравномерно. И, наконец, если
то угол β изменяется неравномерно. И, наконец, если 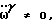 то γ изменяется неравномерно./
то γ изменяется неравномерно./
В блоке 4 производятся вычисления. Электроника рассчитывает: квадрат абсолютного значения угловой скорости вращения корпуса робота M, полученного на основе измерений датчика - отвеса, и квадрат абсолютного значения вращательного ускорения, F, полученного на основе данных, измеренных инерционным датчиком ускоренных вращений.
Далее идет блок 5 - это проверка выполнения условия. Если корпус робота не испытывает сильных вращательных ускорений: F≤C1, то переходим к блоку 6. А если имеются сильные вращательные ускорения: F>C1, то идем к блоку 10, где производится обнуление "секундомера" S= 0 и возвращаемся к началу цикла в блок 3.
Блок 6 - это то же проверка выполнения условия. Если условие: M<C2 выполняется, то это означает, что корпус робота не совершает в пространстве быстрых вращений.
Блоки 7 и 8 организуют "секундомер": если в течение длительного времени корпус робота изменяет свою угловую ориентацию медленно и равномерно, то "бесконечный цикл" алгоритма успевает прокрутиться много раз, проходя все время через одни и те же блоки с номерами: 3, 4, 5, 6, 7, 8. И каждый раз, при прохождении блока 7, значение параметра S будет увеличиваться на единицу - "секундомер тикает". В блоке 8 происходит сравнение времени, отмеренного "секундомером", с определенным временным интервалом, задаваемым константой С3. /Значение константы С3 подбирается с учетом скорости выполнения электроникой робота всех необходимых вычислительных операций алгоритма./ Как только "секундомер натикает" больше 2,5 - 3 секунд /S>C3/, происходит переход к блоку 9, т.е. электронным блоком управления будет подана команда прерывания /см. фиг. 66 и 63/. После этого "секундомер" будет обнулен: S=0 и выполнение цикла начнется снова.
Представленный фиг. 71 алгоритм электронного блока управления позволяет антропоморфному шагающему роботу передвигаться по сильно пересеченной местности пешим ходом, а также пользоваться фактически любыми видами транспортных средств.
На тот случай, если робот попадет в центрифугу, для блока управления разработан другой вычислительный алгоритм, изображенный на фиг. 72. Этот алгоритм будет постоянно "крутиться" в блоке управления, анализируя ситуацию, параллельно с алгоритмом, представленным фиг. 71.
Для робота, попавшего в центрифугу, наклон корпуса θ и ϕ должен определяться с помощью датчика - отвеса, а жидкостной инерционный датчик ускоренных вращений позволит узнать лишь: dξ - поворот корпуса робота вокруг вектора отвесной линии.
/Ранее мной употреблялись, аналогичные буквенные обозначения, но со штрихом: α′, β′, γ′, θ′, ϕ′, dξ′ это объяснялось тем, что в определении угловой ориентации корпуса робота основную роль играл жидкостной инерционный датчик ускоренных вращений. А для него я выбрал штрихованные переменные.
В ситуации, когда робот попадает в центрифугу, основная /доминирующая/ роль в определении угловой ориентации переходит к датчику - отвесу, для которого изначально были взяты переменные без штрихов: α, β, γ, θ, ϕ.
Теперь к этим пяти нештрихованным переменным добавляется еще одна нештрихованная переменная: dξ, значение которой рассчитывается по формуле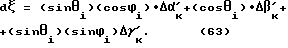
Т. е. наличие или отсутствие у переменной штриха показывает - какой датчик играл доминирующую роль при ее получении./
Физические принципы работы алгоритма, изображенного на фиг. 72, заключаются в следующем: если в течение 2 - 3 секунд наклон корпуса робота, измеренный датчиком - отвесом, существенно /более чем на 15o/ отличается от наклона, вычисленного с помощью жидкостного инерционного датчика ускоренных вращений, то наклон корпуса робота необходимо определять по датчику - отвесу.
В обычной ситуации, когда антропоморфный робот будет передвигаться по местности своим /пешим/ ходом, капельки ртути в датчике - отвесе будут совершать небольшие колебания около самых нижних точек единичных окружностей датчика. При этом направление "вниз", вычисленное на основе показаний жидкостного инерционного датчика ускоренных вращений, будет мало отличаться от истинного направления "вниз", полученного датчиком - отвесом. В течение длительного времени /например, в течение трех секунд/ показания датчиков различных типов несколько раз совпадут или будут очень близки друг к другу.
Иное дело в ситуации, когда робот попадет в центрифугу: здесь в течение длительного времени /например, в течение трех секунд/ показания датчика - отвеса и показания жидкостного инерционного датчика ускоренных вращений очень сильно разнятся, например, разнятся более чем на 15o. /В качестве примера можно посмотреть фиг. 67-70 и соответствующие комментарии к ним./
Такое длительное сильное различие в показаниях датчиков и позволит электронике блока управления прийти к выводу о том, что робот попал в центрифугу.
Я взял здесь в качестве "длительного времени" три секунды. Можно сказать, что эти три секунды - это "время адаптации", т.е. время привыкания робота к режиму центрифуги /или время отвыкания от режима центрифуги/.
Итак у нас имеются два вектора отвесной линии. Один вектор отвесной линии измерен датчиком - отвесом, другой вектор отвесной линии измерен жидкостным инерционным датчиком ускоренных вращений. Найти угол между этими двумя векторами можно с помощью скалярного произведения векторов.
По договоренности вектор отвесной линии имеет единичную длину, его компоненты в системе координат XYZ. такие /см. фиг. 4 /:
(sinθ)(cosϕ); (cosθ); (sinθ)(sinϕ). (64)
/Это были приведены компоненты вектора отвесной линии, измеренного датчиком - отвесом./
Для вектора отвесной линии, определенного с помощью жидкостного инерционного датчика ускоренных вращений, в записи компонент должны быть использованы штрихованные переменные:
(sinθ′)(cosϕ′); (cosθ′); (sinθ′)(sinϕ′). (65)
Тогда скалярное произведение между двумя единичными векторами отвесных линий даст нам косинус угла между ними и запишется: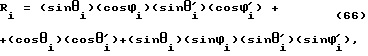
где переменной Ri обозначено значение косинуса угла, заключенного между двумя векторами отвесных линий, полученных в момент времени ti датчиками двух различных типов.
Для получения углов θ и ϕ, как и для получения углов θ′, ϕ′ можно воспользоваться одним и тем же ПЗУ /см. фиг. 66/, преобразующим углы α, β, γ в углы θ, ϕ. Дело в том, что жидкостной датчик - отвес срабатывает гораздо быстрее по сравнению с жидкостным инерционным датчиком ускоренных вращений. Действительно, чтобы снять показания с жидкостного датчика - отвеса достаточно подать запрашивающий стробирующий импульс на "Д" триггера датчика - отвеса, после чего на выходах приоритетных шифраторов появятся значения углов α, β, γ в двоичном коде. Т.е. время срабатывания датчика - отвеса определяется скоростью протекания переходных процессов в приоритетных шифраторах /см. фиг. 6 /. А жидкостной инерционный датчик ускоренных вращений работает гораздо медленнее. Это объясняется тем, что вначале необходимо аналоговый сигнал /электрическое напряжение / преобразовать с помощью АЦП в двоичный код, который затем преобразуется в другой двоичный код с помощью ППЗУ /см. фиг. 60 /. Затем уже этот преобразованный двоичный код используется для вычисления углов α′, β′, γ′ по алгоритму, представленному фиг. 63 и 64.
Так вот, в то время пока в блоке вычислений /см. фиг. 66/ будет производиться расчет углов α′, β′, γ′ на входы ПЗУ будут поданы значения углов α, β, γ и тогда на выходах ПЗУ появятся двоичные значения углов θ и ϕ. Эти значения будут переданы в блок управления /см. фиг. 66./, где они подлежат запоминанию и используются для дальнейших вычислений.
/Здесь возможно еще более эффективное использование ПЗУ, если в него помимо преобразования углов α, β, γ в углы θ и ϕ внести значения компонент вектора отвесной линии в двоичном коде. Тогда не придется в блоке управления пересчитывать углы в компоненты вектора./
Проследим как работает алгоритм.
Сразу после включения электропитания робота алгоритм, представленный фиг. 72, начинает работать. Этот момент обозначен блоком 1.
В блоке 2 осуществляется присвоение начальных значений параметрам: U и Т. Параметр U может принимать только два значения "ноль" или "единица". Начальное значение параметра U устанавливается равным нулю /U = 0/. В дальнейшем, в процессе функционирования робота, значение параметра U в результате выполнения алгоритма может измениться. Если U станет равным единице, то это означает, что робот попал в центрифугу и теперь в определении его угловой ориентации доминирует датчик - отвес.
Параметр Т необходим, чтобы отсчитывать "время адаптации". Этот параметр одновременно применяется как для определения продолжительности режима "привыкания" робота к центрифуге, так и для определения продолжительности режима "отвыкания" робота от центрифуги. Начальное значение параметра Т устанавливается равным -С /Т = -С/, где С - положительное, целое число. Его значение подбирается таким, чтобы время "адаптации" равнялось примерно 2 - 3 секундам.
Ввод данных от жидкостных датчиков двух различных типов осуществляется в алгоритме блоком 3.
Блок 4 представленного алгоритма символизирует операцию вычисления Ri - косинуса угла, заключенного между двумя векторами отвесных линий, направления которых измерены в момент времени ti жидкостными датчиками различных типов. /Я не стал вписывать формулу вычисления Ri непосредственно в алгоритм из-за ее громоздкости /см. формулу (66)/./
Блок 5 - проверка выполнения условия: если Ri меньше косинуса 15o, то это означает, что угол между двумя векторами отвесных линий, измеренных различными датчиками, больше 15o. А если, условие в блоке 5 для Ri не выполняется, т.е., если Ri больше или равно косинусу 15o, то значит угол между двумя векторами отвесных линий меньше 15o.
Сделаем допущение: пусть в первые минуты после включения электропитания робот не подвергается воздействию центробежных сил, т.е. находится в привычной, нормальной обстановке, например, передвигается по местности пешим ходом. В этой ситуации алгоритм, представленный фиг. 72, работает следующим образом: во время первого периода мы проходим блоки: 1, 2, 3, 4, 5. Т.к. робот не в центрифуге, то условие, записанное в блоке 5 не выполняется - угол, заключенный между двумя векторами отвесных линий, меньше 15o. Тогда переходим к проверке выполнения условия - блок 6. Согласно блоку 2: Т= -С, поэтому условие в блоке 6 не выполняется, переходим к блоку 7, где значение параметра Т уменьшается на единицу, теперь: Т=-С-1. Далее переходим к проверке выполнения условия в блоке 8 - условие выполняется, переходим к блоку 9 - присваиваем параметру: U значение "ноль" и возвращаемся к блоку 3.
Таким образом, в результате выполнения первого периода алгоритма, значение параметра Т стало: Т=-С-1., а параметру U присвоено значение "ноль".
Рассмотрим второй период цикла: последовательно проходим блоки с номерами: 3, 4, 5 и подходим к блоку 6. Теперь у нас Т=-С-1, поэтому условие в блоке 6 выполняется и мы переходим к блоку 3. Здесь надо сказать, что блок 6 /как и блок 10, представленного алгоритма/ предназначен для ограничения абсолютного значения параметра Т.
Теперь сколько бы не прошло периодов представленного алгоритма, параметр Т имеет значение, равное: -С-1, параметр U = 0. Так и должно быть, ведь робот не находится в центрифуге.
Сделаем другое допущение:
Пусть робот длительное время передвигался собственным /пешим/ ходом, а потом запрыгнул во вращающуюся центрифугу.
Так вот, с того самого момента когда робот окажется во вращающейся центрифуге, угол, образованный двумя векторами отвесных линий, измеренных жидкостными датчиками различных типов, окажется больше 15o. И теперь при прохождении каждого периода цикла будет выполняться условие, записанное в блоке 5, и вычисления пойдут по другой ветви алгоритма - блоки 5, 10, 11, 12, 13. Процессы, протекающие в этой, новой, ветви алгоритма, во многом аналогичны процессам, протекавшим в блоках 6, 7, 8, 9, за исключением того, что параметр Т теперь будет увеличиваться, а параметр U примет значение "единица", если Т станет больше С.
Представленный на фиг. 72 алгоритм позволяет антропоморфному шагающему роботу самостоятельно адаптироваться к центрифуге, ось вращения который может иметь в пространстве любую угловую ориентацию.
На этом я заканчиваю описание "вестибулярного аппарата" антропоморфного шагающего робота /жидкостных датчиков и необходимого им математического сопровождения/.
Перейду теперь к описанию механизма подвеса тела человека - оператора, т. е. к описанию устройства, позволяющего управлять движениями робота.
Механизм подвеса человека-оператора.
Перед нами стоит задача создания дистанционного антропоморфного шагающего робота. Такой робот будет обладать повышенной маневренностью, т. е. робот сможет свободно ходить на двух ногах по сильно пересеченной местности, приседать, ложиться, перекатываться с боку на бок, вставать, лазить по стремянкам и даже заниматься альпинизмом /в буквальном смысле этого слова/.
Управление роботом осуществляется в копирующем режиме с помощью следящей системы, одна часть которой представлена самим роботом, другая выполнена в виде управляющего костюма с жесткими элементами, надеваемого на человека-оператора. В каждом суставе антропоморфного робота и в каждом суставе управляющего костюма установлены датчики двух типов: один датчик измеряет угол сгиба сустава, второй - измеряет вращательный момент силы, приложенный к жестким элементам сустава. Данные от этих датчиков, установленных в корпусе дистанционно-управляемого робота, передаются по каналу связи на электронные логические цепи управляющего костюма. Одновременно на эти же логические цепи поступают данные и от датчиков, установленных в суставах управляющего костюма. Электроника анализирует эти данные и выдает необходимые управляющие команды на силовые приводы конечностей робота и управляющего костюма. Команды управления поступают к дистанционно управляемому роботу по соответствующим каналам связи.
Силовые, воздействия, оказываемые человеком-оператором на жесткие элементы какого-то сустава управляющего костюма, воспринимаются соответствующим датчиком, измеряющую момент силы. Если при этом на аналогичный сустав антропоморфного робота не действует равный по модулю и противоположный по направлению момент сил, то сустав управляющего костюма начинает сгибаться в направлении усилий, оказываемых оператором. Одновременно в том же направлении сгибается и аналогичный сустав антропоморфного робота. При этом электроника следит за тем, чтобы аналогичные суставы робота и управляющего костюма сгибались с одинаковой угловой скоростью и на одинаковый угол, т.е. должен выполняться принцип копирования. В свою очередь, если силовое воздействие внешних тел, окружающих робота не будет компенсироваться силовым воздействием со стороны оператора, то сустав робота и аналогичный ему сустав управляющего костюма начнут сгибаться в направлении силового воздействия, оказываемого на робота внешними телами. Все это позволяет человеку-оператору подсознательно ощущать непосредственно своими пропреоцепторами пространственное положение конечностей робота и усилия, оказываемые роботом на предметы, а также определять на ощупь форму предметов и их вес. Таким образом двигательная и чувствительная системы человека-оператора оказываются сочленены с механическими конечностями робота так, что последние становятся как бы естественным продолжением конечностей человека. Оператор получает в общем ту же самую информацию от конечностей робота, как если бы человек непосредственно своими руками манипулировал телами, окружающими робот.
Кроме того, электронные логические цепи, основываясь на данных, полученных от датчиков угловой ориентации корпуса робота, должны вносить соответствующие поправки в силовые воздействия, оказываемые управляющим костюмом на человека-оператора. Это необходимо для того, чтобы компенсировать гравитационную тяжесть конструктивных элементов робота и управляющего костюма, т.е. необходимо добиться, чтобы робот и управляющий костюм не висели бы своей тяжестью на руках и ногах человека-оператора независимо от его ориентации в пространстве. Иначе говоря, нужно сделать соответствующие "электронные противовесы". "
На данном этапе основное внимание при разработке подобного робота необходимо уделить конструкции механизма подвеса, с помощью которого мы должны подвесить в пространстве человека-оператора, одетого в управляющий активный экзоскелетон.
Механизм подвеса должен удовлетворять следующим двум требованиям:
1/ Не дать человеку - оператору соприкасаться своими конечностями с посторонними предметами: человек - оператор, например, не должен доставать ногами до пола, иначе это будет мешать управлению ходьбой робота.
Механизм подвеса должен придавать в пространстве телу человека - оператора ту же ориентацию, что и у корпуса робота, те же угловые скорости и те же вращательные ускорения - все это позволит обеспечить вертикальную ходьбу робота.
"Это позволит человеку ощущать своими органами равновесия все изменения, происходящие в угловой ориентации корпуса робота. При этом человек-оператор, осуществляя управление вертикальной ходьбой робота, будет подсознательно стремиться сохранить вертикальную устойчивость, непроизвольно изменяя соответствующим образом положение своих конечностей, из-за чего будет сохраняться и устойчивость вертикальной походки робота, т.к. он будет копировать все эти непроизвольные движения оператора.
Человек-оператор при управлении ходьбой робота будет испытывать примерно такие же ощущения как и при ходьбе в скафандре на механическом тренажере "беговая дорожка".
Таким образом от дистанционного робота по каналам связи на логические электронные цепи управляющего костюма и механизма подвеса передаются следующие телеметрические данные:
1/ данные об угловой ориентации корпуса робота,
2/ данные от датчиков, установленных во всех суставах робота,
3/ видеосигнал обстановки, окружающей робота,
4/ данные, характеризующие звуковую обстановку вокруг робота. /Последнее актуально для роботов-солдат и роботов-пожарных./
В свою очередь по соответствующим каналам связи к дистанционно управляемому роботу передаются:
1/ команды управления силовыми приводами суставов робота,
2/ сигналы, позволяющие роботу воспроизводить устную речь человека-оператора. /Последнее актуально для роботов- солдат и роботов-пожарных./"
Подобные роботы смогут найти применение в качестве роботов водолазов, роботов - солдат, роботов - шахтеров, роботов - пожарных и т.д.
Применение роботов в качестве солдат обсуждается позже, отдельным пунктом. А сейчас продемонстрирую применение роботов в качестве водолазов /см. фиг. N 73 - 78/, где нечетные фигуры изображают человека - оператора, одетого в управляющий костюм и подвешенного на механизме подвеса. Четные фигуры, имеющие номера: 74, 76, 78, изображают робота - водолаза.
Здесь обязательно надо сказать, что мы не сможем воспроизвести с помощью механизма подвеса поступательные ускорения, которые испытывает робот. Иначе человек - оператор должен был бы совершать в пространстве тот же путь, который проделывает робот. Траектория этого пути совпадала бы с траекторией пути робота. Например, в случае с роботом - водолазом, мы просто чисто физически не можем себе позволить, чтобы человек - оператор разгуливал по кораблю в управляющем костюме, свободно, как призрак, проходя сквозь все корабельные переборки.
Управляющий костюм должен оказывать силовое воздействие на человека - оператора. Это необходимо для того, чтобы человек - оператор имел такие же проприоцептивные ощущения, как и робот, т.е., если робот держит в своих руках какой - то предмет, то оператор, под силовым воздействием управляющего костюма, должен ощущать вес предмета, его форму и, что особенно важно, положение рук робота в пространстве. Аналогичные проприопептивные ощущения управляющий костюм создает для всех суставов тела человека - оператора.
На фиг. 73, 75, 77 у человека - оператора за спиной изображен ранец. Это объясняется тем, что в ранце размещаются "мышцы", ответственные за плечевые, шейные, поясные и тазовые суставы управляющего костюма. Размещение этих "мышц" за спиной у человека позволит освободить больше места спереди и сделает управление роботом более удобным.
Перейдем к более обстоятельному знакомству с устройством механизма подвеса.
Ранее указывалось, что ориентация корпуса антропоморфного робота задается тремя углами θ, ϕ и dξ /см. выше/. Первые два угла определяют наклон корпуса робота относительно вектора отвесной линии. Третий угол задает поворот корпуса робота вокруг вектора отвесной линии.
В механизме подвеса, для придания телу человеку - оператора той же ориентации, как и у корпуса робота, необходимо воспроизвести эти же углы θ, ϕ, dξ.
С корпусом антропоморфного шагающего робота жестко свяжем систему координат XYZ /см. фиг. 79 /. Теперь изменение угловой ориентации корпуса робота означает, что изменится и, угловая ориентация системы координат XYZ.
Задание углов θ и ϕ вектора отвесной линии в системе координат XYZ определяется так же, как было изображено на фиг. 4.
Если робот будет совершать "наклон вперед", то угол ϕ будет увеличиваться /см. фиг. 80 и 81/.
Если робот будет лежать на левом боку, то значение угла θ равно нулю /см. фиг. 82/. А если робот лежит на правом боку, то значение угла θ равно 180o /см. фиг. 83/.
Аналогичную систему координат XYZ жестко свяжем и с телом человека - оператора, подвешенного на механизме подвеса.
Механизм подвеса имеет следующую кинематическую схему:
Это шесть вложенных друг в друга колец. Пронумеруем их так, чтобы самое маленькое /внутреннее/ кольцо имело N 1, а самое большое /наружное/ кольцо - N 6, см фиг. 84.
В центре этой системы вложенных друг в друга колец находится человек - оператор, одетый в свой управляющий костюм. Жилет управляющего костюма жестко связан с кольцом 1 с помощью радиального стержня, который берет свое начало на внутренней поверхности кольца 1 и заканчивается на спине у человека - оператора /см. фиг. 85/.
У каждого кольца имеется два внешних выступа, лежащих на прямой, проходящей через центр кольца, т.е. лежащих на продолжении диаметра /см. фиг. 84 и 85 /. Кольца меньшего диаметра упираются своими выступами в кольца большего диаметра. Кольцо 6 лежит своими выступами на основании K1-K2 механизма подвеса /см. фиг. 84/.
/В случае если мы будем иметь дело с роботом - водолазом таким основанием для механизма подвеса будет жесткий каркас корабля, с которого производится управление роботом. А в случаях когда робот будет использоваться на суше, например, в качестве робота - солдата, основанием для механизма подвеса послужит каркас машины, с которой производится управление роботом./
Если внимательно посмотреть на фиг. 84, то можно заметить, что выступы колец с четными номерами /2, 4, 6/ лежат на одной прямой, которая направлена вдоль оси X системы координат XYZ жестко связанной с телом человека - оператора. А по отношению к выступам колеи с нечетными номерами можно заметить, что все они лежат на прямой, коллинеарной оси Y системы координат XYZ, связанной с телом человека - оператора.
Фиг. 84 здесь начерчена для того, чтобы дать общее представление о наборе деталей, из которых состоит механизм подвеса. На ней показан механизм подвеса в ситуации, когда все кольца лежат строго в одной плоскости, но в рабочей обстановке реальная конструкция механизм подвеса очень редко будет выглядеть подобным образом. Дело в том, что выступы на кольцах являются механическими осями, вокруг которых кольца поворачиваются друг относительно друга, это необходимо нам для того, чтобы можно было придавать телу человека - оператора определенную угловую ориентацию.
Перейдем к рассмотрению функций, которые выполняют представленные детали механизма подвеса;
Роль колец 5 и 6 состоит исключительно в том, чтобы оси - выступы кольца 4 всегда были расположены вдоль вектора отвесной линии /см. фиг. 86./
/Ниже будет показано, что одно из назначений кольца 4 - поворот тела человека - оператора на угол dξ вокруг вектора отвесной линии и именно поэтому оси - выступы кольца 4 должны всегда лежать на вертикальной линии./
По существу кольца 5 и 6 образуют здесь обычный карданный подвес, наподобие того, который применяется для механического гироскопа /см. фиг. 1/.
В качестве примера, демонстрирующего необходимость введения такого карданного подвеса, рассмотрим две ситуации.
Допустим, что с корабля в условиях морской качки производится управление роботом - водолазом. Датчики, установленные на корабле, будут следить за изменением углового крена судна и подавать необходимые команды на карданный подвес, образованный кольцами 5 и 6, сохраняя вертикальную ориентацию осей - выступов кольца 4.
Или другой пример. Машина, с которой управляют роботом-солдатом, стоит не горизонтально. В этой ситуации нас опять выручит карданный подвес - выступы кольца 4 будут установлены вертикально.
Полагаю, что здесь я достаточно полно раскрыл назначение карданного подвеса, образованного кольцами 5 и 6. Больше к этому вопросу уже не вернусь. /На всех последующих фигурах кольца 5 и 6 изображаться уже не будут, это делается в целях упрощения чертежей, для их лучшего понимания. Т.е. с данного момента мы условимся считать, что выступы - оси кольца 4 всегда расположены вертикально./
Вращая на выступах - осях кольцо 1 относительно кольца 2, мы сможем в механизме подвеса задавать телу человека -оператору угол ϕ /см. фиг. 85, 80 и 81/.
В механизме подвеса угол θ для тела человека - оператора в общем случае задается одновременным вращением двух колец 2 и 3.
Здесь придется сделать очень подробные объяснения, чтобы Вам стало ясно, почему для задания угла θ используются повороты двух колец.
Казалось бы, что для задания телу человека-оператора угла θ можно использовать вращение только одного кольца 2 /см. фиг. 87 и 88/, а кольцо 3 вообще выкинуть и этим существенно упростить конструкцию механизма подвеса. На самом деле подобное "упрощение" очень негативно скажется на работе механизма подвеса.
Дело в том, что если "выкинуть" кольцо 3, то в ситуациях, когда значение угла θ близко к 0o или 180o, в упрощенной конструкции механизма подвеса возникнут значительные сингулярности. Например:
Пусть робот длительное время лежит на левом боку так, что его наклон относительно вектора отвесной линии определяется двумя углами: θ= 1o ϕ = 270o т.е. пространственная ориентация робота напоминает фиг. 82. В упрощенной конструкции механизма подвеса аналогичный наклон телу человека-оператора задается соответствующим поворотом двух колец, имеющих номера 1 и 2 /см. фиг. 88/.
Допустим, что в какой-то момент робот незначительно изменяет наклон своего корпуса, так, что углы θ и ϕ приобретают значения: θ = 1o и ϕ = 0o. При этом для постороннего наблюдателя изменение ориентации корпуса робота кажется столь незначительным, что его положение в пространстве по-прежнему с большим успехом можно характеризовать фиг. 82. В системе координат XYZ, жестко связанной с корпусом робота, угол между двумя векторами отвесных линий, взятых в различные моменты времени, по своему абсолютному значению меньше 1,5o, так что "на глаз" изменение ориентации корпуса робота фактически незаметно.
Абсолютно иначе обстоит дело с приданием наклона θ = 1o, ϕ = 0o телу человека - оператора в упрощенном механизме подвеса /см. фиг. 89 /.
Если теперь обратить внимание на фигуры с номерами: 82, 88 и 89, то можно заметить явное несоответствие: робот лишь слегка изменил наклон своего корпуса, а в упрощенном механизме подвеса, для придания телу человека - оператора такого же наклона, пришлось очень быстро повернуть кольцо 1 на 90o, это и есть сингулярность, о которой я говорил.
Далее нами будет рассматриваться только "усложненная" конструкция механизма подвеса, в которой содержится кольцо 3, предназначенное для устранения сингулярностей подобного рода.
Каким образом кольцо 3 справляется с этой задачей я расскажу позже, а сейчас необходимо договориться о направлении отсчета и о начале отсчета углов, определяющих в механизме подвеса взаимные повороты колец.
На фиг. 84 кольца 1, 2, 3 и 4 имеют на одном из своих выступов "черную метку". Такие "черные метки" позволяют нам определить положительное направление отсчета углов, задающих взаимную ориентацию колец механизма подвеса:
"Угол между двумя кольцами возрастает, если кольцо меньшего диаметра поворачивается против часовой стрелки относительно кольца большего диаметра, при условии, что "черная метка" малого кольца направлена к нам."
Здесь было приведено самое общее правило, определяющее положительное направление поворотов, совершаемых друг относительно друга кольцами механизма подвеса. Это правило выработано на основе договора.
Перейдем к рассмотрению конкретных углов.
Угол μ задает поворот кольца относительно кольца 2. Он увеличивается, если тело человека - оператора совместно с кольцом 1 совершает по отношению к кольцу 2 "кувырки вперед" /см. фиг. 90 и 91 /. За начало отсчета угла μ берется такое взаимное положение колец 1 и 2, когда ось X системы координат XYZ, жестко связанной с телом человека - оператора, перпендикулярна плоскости кольца 2, а ось Z системы координат XYZ при этом направлена в сторону "черной метки" кольца 2 /см. фиг. 90/.
Угол λ задает поворот кольца 2 относительно кольца 3. Угол λ увеличивается, если кольцо 2 поворачивается относительно кольца 3 в направлении, оговоренном общим правилом, определяющим положительное направление взаимных поворотов колец механизма подвеса. Начало отсчета угла λ определим следующим взаимным положением колец 2 и 3 /см. фиг. 92./: кольцо 2 своей "черной меткой" направлено на нас и перпендикулярно к плоскости кольца 3. "Черная метка" кольца 3 по отношению к нам направлена в правую сторону, а "черная метка" кольца 1 направлена вниз.
Угол κ задает в механизме подвеса величину поворота кольца 3 относительно кольца 4. Он возрастает, если кольцо 3 поворачивается относительно кольца 4 в направлении, оговоренном общим правилом, определяющим положительное направление взаимных поворотов колец механизма подвеса. Началом отсчета угла κ выберем следующее взаимное положение колец 3 и 4 /см. фиг. 93 /: выступы - оси кольца 4 расположены строго вертикально, "черная метка" кольца 4 расположена внизу. Плоскость кольца 3 перпендикулярна плоскости кольца 4, а "черная метка" направлена направо. При этом "черная метка" кольца 2 направлена к нам.
/Вообще фиг. 93 изображает ситуацию когда все углы равны нулю: μ = 0o, λ = 0o, κ = 0o.
Изменяя в механизме подвеса значения углов μ, λ, κ, мы сможем задавать человеку - оператору такой же наклон, как и у корпуса робота.
/Необходимо заметить, что повороты на углы μ, λ, κ вокруг соответствующих выступов - осей механизма подвеса коммутируют - результат поворотов не зависит от последовательности их выполнения! Т.е. тело человека - оператора будет принимать один и тот же наклон θ, ϕ в пространстве при одних и тех же углах μ, λ, κ, независимо от очередности выполнения этих поворотов. Казалось бы, что это, противоречит известному утверждению о том, что: "результат двух /и более/ поворотов на конечные углы в самом общем случае зависит от последовательности выполнения этих поворотов" /см. И.И.Ольховский "Курс теоретической механики для физиков", 1970 г. М. стр. 150/. Однако это только что приведенное утверждение справедливо лишь при условии, что все повороты, как промежуточные, так и результирующий отсчитываются относительно абсолютно неподвижного пространства.
В случае же с механизмом подвеса только результирующий поворот /наклон тела человека - оператора/ рассматривается относительно абсолютного пространства, а все промежуточные повороты μ, λ, κ отсчитываются относительно жестких элементов конструкции механизма подвеса, поэтому-то повороты на углы μ, λ, κ и коммутируют. В этом при желании можно убедиться с помощью соответствующих геометрических построений./
Покажем, что конкретная пара углов θ и ϕ, определяющих наклон тела человека - оператора /подчеркиваю: наклон, а не ориентацию в пространстве/ в общем случае может быть реализована с помощью очень большого набора углов κ, λ, μ, если между этими углами существуют определенные соотношения.
Рассмотрим фиг. 94, где изображены кольца 1, 2 и 3.
Ранее мной указывалось, что для того чтобы придать телу человека - оператора такую же угловую ориентацию, как и у корпуса робота, необходимо в механизме подвеса определенным образом наклонить тело человека - оператора и одновременно повернуть его определенным образом вокруг вектора отвесной линии. Повороты тела человека - оператора вокруг вектора отвесной линии осуществляются в механизме подвеса за счет вращений кольца 4 вокруг его выступов - осей. Но сейчас, в данный момент, нас прежде всего интересуют наклоны тела человека - оператора относительно вектора отвесной линии, а не угловая ориентация вообще. Поэтому мы можем сейчас считать, что положение кольца 4 фиксировано в пространстве и рассматривать только повороты колец 1, 2, 3.
Жестко свяжем с кольцами 2, 3 и 4 системы координат: X2, Y2, Z2, X3, Y3, Z3 и X4, Y4, Z4 /на фиг. 94 в целях упрощения изображения кольцо 4 отсутствует, однако имеется связанная с ним система координат X4, Y4, Z4/.
Сейчас наша задача состоит в том, чтобы получить выражения / в виде формул/ для компонент вектора отвесной линии в системе координат: XYZ, жестко связанной с телом человека - оператора, последовательно выполнив с помощью механизма подвеса повороты κ, λ, μ.
Используем матрицы, описывающие повороты систем координат относительно друг друга.
Матрица A, описывающая поворот системы координат X3, Y3, Z3 относительно системы координат X4, Y4, Z4 получается, если мы смотрим на систему X4, Y4, Z4 из системы координат X3, Y3, Z3 после совершения кольцом 3 поворота на угол κ относительно кольца 4, т.е. мы рассматриваем ситуацию так, как если бы система координат X4, Y4, Z4 вместе с вектором отвесной линии совершали бы поворот относительно системы координат X3, Y3, Z3 как одно целое.
/В действительности, конечно, все обстоит наоборот: система координат X4, Y4, Z4 неподвижна, а вращение на угол κ совершает относительно нее система координат X3, Y3, Z3./
При нахождении матрицы A необходимо учитывать также взаимное положение систем координат X4, Y4, Z4 и X3, Y3, Z3 /колец 4 и 3/, когда κ = 0o, т.е. начало отсчета угла κ /см. фиг. 95/. А также необходимо учитывать и взаимное положение систем координат X3, Y3, Z3 и X4, Y4, Z4 после того как кольцо 3 повернулось относительно кольца 4 в положительном направлении отсчета угла κ /см. фиг. 96/.
Тогда в соответствии с фиг. 95 и 96 матрица A запишется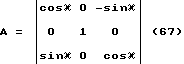
Аналогичные методы используются для получения других матриц:
Матрица В получается с помощью фиг. 97 и 98, она описывает поворот на угол λ системы координат X2, Y2, Z2 относительно системы координат X3, Y3, Z3: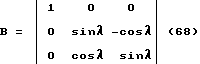
Матрица С получается с помощью фиг. 99 и 100, она описывает поворот на угол μ системы координат XYZ относительно системы координат X2, Y2, Z2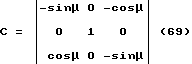
В соответствии с фиг. 94 компоненты вектора отвесной линии в системе координат X4, Y4, Z4 имеют постоянные значения
(0,0-1). (70)
Используя матрицы A, B, C найдем значение компонент вектора отвесной линии в системе координат XYZ. Для этого надо использовать матричное умножение: вначале умножим компоненты вектора отвесной линии /формула (70)/ на матрицу A, полученный результат затем умножим на матрицу B, а потом и этот результат умножаем на матрицу С. Таким образом мы получим компоненты вектора отвесной линии в системе координат XYZ в виде формул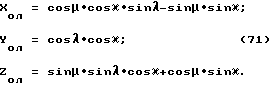
/Здесь надо обязательно заметить, что матрицы A, B и C между собой не коммутируют, несмотря на то, что повороты на углы κ, λ, μ коммутируют. Т.е. порядок выполнения матричного умножения в данном случае надо строго соблюдать./
С другой стороны мы, используя фиг. 4, можем для компонент вектора отвесной линии записать такие выражения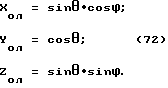
Напомню: сейчас я доказываю, что какой-то конкретный наклон θ, ϕ тела человека-оператора в механизме подвеса может быть получен в общем случае очень большим набором значений углов κ, λ, μ, если они удовлетворяют формулам 71.
Для примера рассмотрим такую ситуацию: вектор отвесной линии имеет в системе координат ориентацию, определяемую углами θ = 30o, ϕ = 0o. Тогда из формул (72) получаем
Xол=0,5; Yол=0,866; Zол=0. (73)
В механизме подвеса этот наклон тела человека - оператора относительно вектора отвесной линии может быть /в принципе/ реализован, если углы κ, λ, μ примут соответствующие числовые значения, указанные в какой-то /любой/ строке таблицы, приведенной на фиг. 101. Это как раз и есть наглядное доказательство того, что в механизме подвеса любой наклон тела человека-оператора в принципе мог бы быть получен бесконечным набором соответствующих комбинаций трех углов κ, λ, μ, удовлетворяющих выражениям 71 и 73.
В связи с этим перед нами возникает вопрос; "Как из такого бесконечного набора комбинаций углов κ, λ, μ выбрать оптимальную, обеспечивающую в механизме подвеса наиболее эффективный способ придания необходимого наклона телу человека- оператора? " - это необходимо для рациональной организации электроники механизма подвеса.
Чтобы ответить на поставленный вопрос надо вернуться к понятию "глобус наклонов" /см. выше и фиг. 27 /.
Изобразим глобусы наклонов вокруг корпуса робота и вокруг тела человека - оператора, так, как это показано на фиг. 102 и 103.
Робот свободен, он может двигаться /наклоняться/ так, как ему заблагорассудится. Понятие "глобус наклонов" для него не играет особой роли.
Тело же человека - оператора не является свободным, его ориентация в пространстве задается с помощью механизма подвеса, путем вращения соответствующих колец вокруг выступов осей. И именно здесь, в механизме подвеса, понятие "глобус наклонов" играет чрезвычайно важную демонстрационную роль.
Глобус наклонов, жестко связанный с телом человека - оператора, разобьем мысленно на три сектора, выделив на его поверхности два "полярных круга" и "экваториальную часть" /см. фиг. 104, где полярные круги затемнены/. Точки поверхности глобуса наклонов, принадлежащие одному полярному кругу удовлетворяют условию
θ ≤ 30o. (74)
Для другого полярного круга выполняется
θ ≤ 150o (75)
Так вот, если нам необходимо, чтобы вектор отвесной линии проходил для человека - оператора через экваториальную часть глобуса, то мы будем задавать такие наклоны тела человека - оператора исключительно только с помощью двух колец механизма подвеса: с помощью вращений кольца 1 и кольца 2. Угол же κ при этом должен быть равен нулю, т.е.
если: 30o < θ < 150o, то κ = 0o! (76)
Тогда в экваториальном секторе задание наклона тела человека- оператора будет осуществляться предельно просто: вращением кольца 1 мы будем устанавливать угол ϕ, а вращением кольца 2 угол θ.
Таким образом, если нам необходимо придать телу человека-оператора наклон, характеризуемый углами θ и ϕ, где угол θ заключен в интервале 30o < θ < 150o, то мы теперь можем это сделать уже только двумя способами в зависимости от того, к какому интервалу значений принадлежит угол λ: так, если мы выберем 0o ≤ λ1 ≤ 180o, то для задания углов θ и ϕ необходимо, чтобы углы λ1 и μ1 приняли следующие значения:
λ1 = θ; μ1 = ϕ, (77)
а если мы выбрали для угла λ интервал значений 180o < λ2 < 360o, то для задания тех же углов θ и ϕ необходимо, чтобы выполнялись равенства
λ2 = 360-θo; μ2 = ϕ+180o. (78)
/Вопрос о том, какой интервал значений угла λ выбрать для задания наклонов тела человека - оператора решается просто: договоримся, что электроника, обеспечивающая работу механизма подвеса, в первые мгновения после включения питания устройства должна всегда задавать режим 0o ≤ λ1 ≤ 180o. В дальнейшем, в процессе работы механизма подвеса, интервал значений угла λ может измениться и стать 180o < λ2 < 360o, но для этого в механизме подвеса вектор отвесной линии обязательно должен пройти через территорию полярного круга./
Теперь вместо бесконечного набора комбинаций углов κ, λ и μ, с определенными соотношениями между собой, мы имеем уже только две возможности, что, конечно же, является существенным упрощением ситуации.
/Пусть, например, на данный момент механизм подвеса задает телу человека-оператора наклон, характеризующийся углами θ и ϕ, одновременно от робота приходит информация о том, что наклон корпуса робота по отношению к вектору отвесной линии определяется иными углами θ′ и ϕ′. Электроника механизма подвеса вычисляет величины dθ = θ′-θ ≠ 0o и dϕ = ϕ′-ϕ ≠ 0o, которые выступают в качестве сигналов рассогласования. Задача механизма подвеса - придать такой наклон телу человека-оператора, что dθ = 0o и dϕ = 0o. И все, больше никаких особо сложных вычислений делать не придется, что позволяет очень сильно упростить электронные цепи механизма подвеса - фактически мы имеем здесь в достаточной степени простую, традиционную систему слежения./
Экваториальный сектор 30o < θ < 150o занимает на глобусе наклонов большую часть поверхности, примерно 86,6% площади сферы, поэтому в большинстве случаев в механизме подвеса можно будет воспользоваться относительно простой электроникой.
Из фиг. 105 и 106 становится ясно почему имеются только две возможности, реализующие один и тот же наклон тела человека- оператора относительно вектора отвесной линии, при условии, что 30o < θ < 150o.
На фиг. 105 и 106 изображены центральные детали механизма подвеса - кольца с номерами 1, 2, 3 и человек-оператор в управляющем костюме. В обоих случаях мы /внешние наблюдатели/ смотрим на механизм подвеса из одной и той же фиксированной точки, кольцо 3 неподвижно относительно нас, а вот кольца 2 и 1 совершают повороты.
В первом случае /фиг. 105/ имеем такие углы поворотов колец 1 и 2: λ1 = 45o и μ1 = 300o. Во втором случае /фиг. 106/: λ2 = 315o и μ2 = 120o.
Для демонстрации того факта, что наклоны тела человека- оператора в случае λ1 = 45o, μ1 = 300o и в случае λ2 = 315o, μ2 = 120o одинаковы, можно воспользоваться формулами (71). Поочередно подставим значения углов λ1 = 45o, μ1 = 300o, κ = 0o и λ2 = 315o, μ2 = 120o κ = 0o в формулы (71). В обоих случаях у нас получатся одни и те же значения компонент вектора отвесной линии в системе координат XYZ:
Xол=0,353; Yол=0,707; Zол=0,612, (79)
а это является бесспорным свидетельством того, что наклоны тела человека - оператора в обоих случаях одинаковы.
Теперь рассмотрим такие наклоны тела человека-оператора, осуществляемые механизма подвеса, при которых вектор отвесной линии попадает на территорию полярного круга глобуса наклонов.
Напомню, что я определил полярный круг как множество точек поверхности глобуса наклонов, имеющих угол θ ≤ 30o,/ другой полярный круг - множество точек с: θ ≥ 150o/.
Ранее я уже указывал, что любая точка θ, ϕ на поверхности глобуса может быть в принципе реализована очень большим набором углов κ, λ, μ. В связи с этим у нас возникла проблема выбора из большого набора углов κ, λ, μ оптимальной комбинации при задании телу человека-оператора необходимого наклона. Для точек экваториальной части глобуса (30o < θ < 150o) эта проблема решалась фиксацией значения угла κ : κ = 0o.
Тогда наклоны тела человека - оператора в механизме подвеса задаются поворотами колец 1 и 2 на углы λ и μ, значения которых вычисляются по формулам (77) или (78).
Для полярных кругов эта проблема устраняется иным путем;
Введем для точек глобуса, принадлежащих полярному кругу, понятие "соседние точки" - это такие две близкие точки на поверхности глобуса, которые отстоят друг от друга на одно деление угла θ или /и/ угла ϕ /см. фиг. 107 /.
На фиг. 107 точки: B, C, D являются соседними точками к точке A. Точки же: B, C уже не являются соседними к точке D, т.к. отстоят от нее на два деления угла ϕ.
Задача, стоящая перед нами, заключается в том, чтобы по возможности уменьшить /или вообще устранить/ сингулярности вблизи полярных точек глобуса наклонов. Математически это выражается так
|Δμ|+|Δλ|+|Δκ| _→ min, (80)
где Δμ = μ′-μ - разность углов между нынешним μ поворотом кольца 1 и будущим μ′ поворотом кольца 1, который необходимо задать для получения требуемого наклона тела человека-оператора.
Аналогично для Δλ и Δκ.
Для решения этой задачи введем два достаточно очевидных граничных условия:
1: Угол κ ≠ 0 только на территории полярного круга. При подходе из внутренних областей полярного круга к его периферии значение угла κ плавно стремится к нулю. За пределами полярного круга κ = 0o.
2: Если вектор отвесной линии имеет полярную координату θ, равную нулю при любом ϕ, то κ = 0o, λ = 0o, угол μ поворота первого кольца механизма подвеса может иметь произвольное значение.
Далее введем еще несколько условий:
3: Угол κ на территории полярного круга в общем случае неравен нулю и может принимать значения в интервале от -12 до +12 градусов. При этом абсолютное максимальное значение 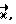 которое может принимать угол κ для данной θ, ϕ точки полярного круга, определяется углом θ и задается кривой, изображенной на фиг. 108 - параболой, плавно переходящей в прямые. /Эта кривая выражается в аналитическом виде с помощью алгоритма, представленного на фиг. 109. / Полученное таким образом значение
которое может принимать угол κ для данной θ, ϕ точки полярного круга, определяется углом θ и задается кривой, изображенной на фиг. 108 - параболой, плавно переходящей в прямые. /Эта кривая выражается в аналитическом виде с помощью алгоритма, представленного на фиг. 109. / Полученное таким образом значение 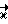 выступает в дальнейшем как "радиус-вектор
выступает в дальнейшем как "радиус-вектор 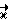 " или как "амплитуда
" или как "амплитуда 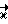 ".
".
4: У каждой θ, ϕ точки полярного круга имеется набор значений угла κt, который получается "как проекция радиус- вектора 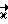 " с помощью формулы
" с помощью формулы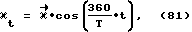
где 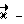 - "радиус-вектор", упоминавшийся в условии (3),
- "радиус-вектор", упоминавшийся в условии (3),
Т - "число секторов", на которые мы разбили воображаемую окружность, образованную радиус-вектором
t - целочисленный параметр: t ⊂ [0,T].
5: Для различных θ, ϕ точек полярного круга значение Т определяется в зависимости от значения θ:
если θ ⊂ ]0o,9o], то Т = 88; (82)
если θ ⊂ [10o,29o], то T = 4•(31 -θ ); (83)
если θ ≥ 30o, то T = 0. (84)
6: Для каждой θ, ϕ, точки полярного круга определяем набор значений угла λN, используя набор значений угла κt, полученный для данной точки полярного, и формулу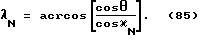
Здесь необходимо следить за знаком, который появляется перед λi. Договоримся, что если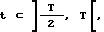
данные элементы "набора λN " имеют отрицательные значения. А если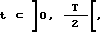
то такие элементы "набора λN " имеют положительные значения.
При этом количество элементов в "наборе λN " буде равно: N + T+2 /Элементы "набора λN " образованные при t=0  и при t=T/2
и при t=T/2  дадут в "набор λN " еще по одному элементу, таким образом и получается: N=Т+ 2, N ⊂ [2, 90].
дадут в "набор λN " еще по одному элементу, таким образом и получается: N=Т+ 2, N ⊂ [2, 90].
7: Набор значений угла μ для данной θ, ϕ точки полярного круга найдем с помощью формул
если λi > 0o, то μi = ϕ-Si; (86)
если λi < 0o, то μi = ϕ+180-Si; (87)
где Si поправка, вычисляемая по формуле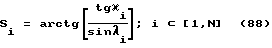
Таким образом, каждой θ, ϕ точке полярного круга ставится в соответствие набор троек углов κn, λn, μn, где n ⊂ [1,N]. Каждая такая тройка углов κi, λi, μi может реализовать в механизме подвеса наклон θ, ϕ тела человека-оператора.
Теперь допустим, что в какой-то момент времени вектор отвесной линии находится на территории полярного круга в точке с полярными координатами θ, ϕ, при этом внутренние кольца механизма подвеса, задающие наклон тела человека-оператора, повернуты относительно друг друга на определенные углы κ, λ, μ. Предположим, что у нас затем возникла необходимость изменить наклон тела человека-оператора таким образом, чтобы вектор отвесной линии оказался в θ′, ϕ′ точке полярного круга. Этой новой θ′, ϕ′ точке полярного круга соответствует набор троек углов 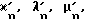 содержащий N элементов /N троек углов/, и определяемый в соответствии с вышеперечисленными семью условиями.
содержащий N элементов /N троек углов/, и определяемый в соответствии с вышеперечисленными семью условиями.
Остается из этого набора троек углов выбрать такую, которая максимально удовлетворяла бы формуле (80), и повернуть внутренние кольца механизма подвеса на эти углы. Таким образом проблема сингулярности вблизи полярных точек будет решена.
Представленные условия позволяют разработать алгоритм, который реализован автором заявки в виде демонстрационной программы DATAPK. BAS.
Для получения формулы (85) необходимо приравнять вторые строки формул (71) и (72), запишем:
cosθ = cosλ•cosκ, (89)
откуда уже легко получается формула (85).
Обоснуем формулы (86) и (88).
Из-за того, что на территории полярного круга угол κ в общем случае не равен нулю, выражение μ = ϕ /см. формулы (77)/ не выполняется, и мы должны теперь воспользоваться для вычисления угла μ формулой (86). Где S играет роль поправки.
Для обоснования формулы 86 используем следующий прием: допустим, что мы смотрим на систему координат XYZ так, что при любых ее наклонах ось Y всегда направлена строго на нас. Т.е. мы как будто все время жестко насажены своим глазом на ось Y системы координат XYZ и совершаем вместе с ней наклоны относительно вектора отвесной линии.
Пусть в начальный момент времени система координат XYZ имеет такую ориентацию, что вектор отвесной линии проходит через полярную точку глобуса наклонов θ = 0o, т.е. направлен по оси Y системы координат XYZ. Согласно второму условию, изложенному выше, подобная ориентация системы координат реализуется в механизме подвеса углами: κ = 0o, λ =0o, угол μ при этом может без ограничения общности равняться нулю. Выше мы договорились, что будем смотреть на систему координат XYZ так, что ось Y все время была бы направлена точно на нас. Тогда данная ситуация изображается фиг. 110.
Допустим, что в следующий момент система координат XYZ претерпела в пространстве наклон. Так, что λ > 0o. При этом мы /внешние наблюдатели/ также подверглись подобному наклону и система координат XYZ по-прежнему направлена своей осью Y строго "к нам". Однако вектор отвесной линии уже неколлинеарен оси Y и дает проекцию на плоскость XOZ, перпендикулярную оси Y системы координат XYZ. Из фиг. 111 видно, что проекция вектора отвесной линии лежит на оси X системы координат XYZ, а это означает, что ϕ = 0o.
Теперь допустим, что система координат XYZ была повернута механизмом подвеса вокруг оси Y, так, что угол μ получил положительное приращение. Тогда для нас /наблюдателей/ взаимная ориентация системы координат XYZ и вектора отвесной линии представится фиг. 112, из которой видно, что ϕ ≠ 0o и ϕ = μ.
И в заключение пусть система координат XYZ получит с помощью механизма подвеса положительное приращение угла κ: κ > 0o /cм. фиг. 113/. Откуда видно, что ϕ = μ+S.
Таким образом формула (86) получила свое обоснование.
Теперь докажем формулу (88). Для этого выполним ряд геометрических построений.
Пусть вначале ориентация системы координат XYZ в пространстве такова, что вектор отвесной линии совпадает по направлению с осью Y системы координат /см. фиг. 114 и 93/.
Эта ситуация реализуется в механизме подвеса, когда углы μ, λ, κ равны нулю, согласно второму условию, изложенному выше
Пусть в следующий момент механизм подвеса изменяет наклон системы координат XYZ так, что λ > 0o /см. фиг. 115/, при этом вектор отвесной линии остается на территории полярного круга, т.е. θ < 30o. Угол между осью X системы координат и проекцией вектора отвесной линии определяет значение угла ϕ, в данном случае ϕ = 0o.
Теперь допустил, что после этого система координат XYZ была еще раз наклонена механизмом подвеса, так, что угол κ получил положительное приращение и стал отличным от нуля: κ > 0o.
Поворот системы координат XYZ на угол κ осуществляется путем ее вращения вокруг прямой, перпендикулярной вектору отвесной линии, /в большинстве ситуаций эта прямая не совпадает с какой-то конкретной осью системы координат ХY2/. Поэтому задание механизмом подвеса положительного приращения угла κ, при котором угол κ становится отличным от нуля, представляется в системе координат XYZ как изменение направления вектора отвесной линии, причем угол между предыдущим направлением вектора отвесной линии и новым направлением равен приращению угла κ. Это показано на фиг. 116.
/Фиг. 114, 115 и 116 дают аксонометрические изображения системы координат XYZ на различных этапах ее эволюции, начиная от первого момента, когда λ = 0o, κ = 0o, и заканчивая моментом, когда λ = 10o, κ = 5o. Все эти три фигуры выполнены математически точно, т.е. перед тем, как чертить, я рассчитал параметры их элементов: направление и длину всех векторов. Но для дальнейших логических построений фиг. 114, 115 и 116 использовать неудобно./
Нарисую еще одну фиг. 117. Она несет такую же физическую нагрузку, как и фиг. 116. Однако в данном случае соотношения между элементами изображения сильно изменены /в частности, значительно увеличены величины углов λ и κ /. Такого рода искажения здесь вполне допустимы, они сделаны в чисто демонстрационных целях и в дальнейшем не повлияют на истинность приведенных логических построений.
Итак: на фиг. 117 изображены три некомпланарные луча, берущие начало в одной общей точке "О". Луч [O,A] символизирует собой ось Y системы координат XYZ. /см. фиг. 116/. Луч [O,B] изображает направление вектора отвесной линии в ситуации, когда система координат XYZ имела наклон: λ ≠ 0o, κ = 0o /см. фиг. 115 /. Угол между лучами [O,A] и [O,B] равен λ. Луч [O,F] совпадает по направлению с вектором отвесной линии, когда наклон системы координат задается в механизме подвеса углами: λ ≠ 0o, κ ≠ 0o /см. фиг. 116/. Угол между лучами [O,B] и [O,F] равен κ.
Рассечем луч [O, A] перпендикулярной плоскостью /см. фиг. 118 /. Тогда проекции лучей [O,B] и [O,F] на эту плоскость дадут нам отрезки [A,B] и [A, F]. Соединим точки B и F прямой линией, получим отрезок [B,F].
Таким образом мы получили четыре треугольника: Δ OAB, Δ OAF, Δ OBF и Δ ABF. Треугольники Δ OAB и Δ OAF - прямоугольные, т.к. катеты: [A,B] и [A,F] лежат в плоскости, перпендикулярной катету [O,A]. Плоскость треугольника Δ OAB перпендикулярна плоскости треугольника Δ OBF, т.к. в механизме подвеса оси, вращением вокруг которых задаются углы λ и κ, перпендикулярны друг другу.
В результате того, что две взаимно перпендикулярные плоскости: OBF и OAB пересекаются третьей плоскостью ABF, перпендикулярной к плоскости OAB, мы получаем, что углы: ABF и OBF - прямые.
Таким образом, все четыре треугольника, представленные на фиг. 118, прямоугольные. Сложенные вместе они образуют пространственную фигуру: треугольную наклонную пирамиду /см. фиг. 118 /. Плоская развертка этой пирамиды представлена фиг. 119 - здесь все треугольники лежат в одной плоскости. Напомню, что катет [A,B] треугольника OAB получился в результате проекции вектора отвесной линии на плоскость BAF, параллельной плоскости XOZ, в ситуации, когда наклон системы координат XYZ определяется углами λ = 10o, κ = 0o.
Гипотенуза [A,B] треугольника ABF получилась в результате проекции вектора отвесной линии на плоскость ABF, параллельной плоскости XOZ системы координат XYZ, в ситуации, когда λ = 10o, κ = 5o.
Т.е. величина угла BAF - есть величина искомого угла S /поправки/!
Из треугольников, приведенных на фиг. 119, найдем математическую формулу, необходимую для вычисления поправки S.
Сделаем допущение:
Пусть
|OB| = 1, (90)
Тогда
|BF| = tgκ и |AB| = sinλ. (91)
Отсюда уже легко получить: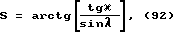
т.е. формула (88) доказана.
И наконец, обоснуем формулу (87). Для чего будем смотреть на систему координат XYZ так, что ось во всех случаях направлена точно на нас. Пусть в первый момент система координат имела такой наклон, что вектор отвесной линии был параллелен оси Y /см. фиг. 120/. Такая ситуация согласно второму условию, изложенному выше, в механизме подвеса получается, если μ =0o, λ = 0o, κ = 0o.
В следующий момент механизм подвеса изменяет наклон системы координат так, что λ < 0o, μ = 0o, κ = 0o /см. фиг. 121 /. Проекция вектора отвесной линии на плоскость XOZ системы координат XYZ оказалась в полуплоскости где X < 0.
Затем механизм подвеса еще раз изменил наклон системы координат, сделав κ > 0o, /см. фиг. 122 / теперь проекция вектора отвесной линии оказалась в той четверти координатной плоскости где: Z > О, X < 0. Тогда для фиг. 122 можно записать
ϕ = μ+180o+S, (93)
где μ без ограничения общности равно нулю. Отсюда получаем формулу (87).
В реальной конструкции механизма подвеса для поиска нужной тройки углов κ, λ, μ следует использовать специализированные электронные цепи, осуществляющие параллельную обработку информации. Структура этих цепей может быть такой, как это изображено на фиг. 123.
Набор ПЗУ /постоянных запоминающих устройств/ количеством 90 штук образует первый ряд электронных элементов. /На фиг. 123 таких ПЗУ изображено только три./
Поясню почему в первом ряду применяется 90 ПЗУ. Дело в том, что максимальная длина N = Т+2 набора троек углов κ, λ, μ может составлять 90. А в каждом ПЗУ первого ряда хранится только одна тройка углов, соответствующая конкретной θ, ϕ точке полярного круга. Отсюда и появляется набор из 90 ПЗУ.
На входы ПЗУ первого ряда через общую шину подаются значения θ′, ϕ′, характеризующие наклон, который мы собираемся придать телу человека-оператора. После чего на выходах ПЗУ первого ряда появляются значения троек углов, соответствующих наклону θ′, ϕ′. Причем на выходе каждого ПЗУ появляется только значения углов какой-то одной тройки κ′, λ′, μ′.
Далее эти значения троек углов в качестве операндов поступают на второй ряд электронных элементов, который состоит из 90 ПЛМ /программируемых логических матриц /. Каждая тройка углов, полученная от какого-то ПЗУ первого ряда, подается на свою "персональную" ПЛМ второго ряда. В качестве другого операнда на входы ПЛМ второго ряда из соответствующей общей шины поступают значения тройки углов κ, λ, μ, которая в данный момент реализует в механизме подвеса наклон θ, ϕ тела человека-оператора. На выходах ПЛМ появляются калиброванные значения абсолютных разностей троек углов - сравниваются значения κ, λ, μ внешней тройки углов и всевозможные значения троек углов κ′, λ′, μ′ которые будут задавать следующий θ′, ϕ′ наклон тела человека-оператора. Т.е. в ПЛМ второго ряда вычисляются такие выражения
Kn = |Δμ|+|Δλ|+|Δκ|, (94)
где n принимает значение от 1 до 90.
Одновременно с этим каждая ПЛМ второго ряда производит калибровку своего "персонального" выражения (94), дополняя его до наименьшего целого числа, превышающего или равного значению выражения (94). /Например, если в какой-то i-й ПЛМ второго ряда вычислено, что
Ki = |Δμ|+|Δλ|+|Δκ| = 2.56,
то на выходе i-й ПЛМ появится калиброванное значение этого выражения: Ki = 3, и т.д./
Затем полученные на ПЛМ колиброванные значения Kn попадают на входы дешифраторов /Дш/, где происходит их преобразование из двоичного разрядного кода в разрядный код с основанием единица. После чего преобразованные в дешифраторах значения подаются на общую шину. Причем эта разрядная шина с основанием единица, т.е. если на выходе каких-то ПЛМ второго ряда появляется калиброванное значение, равное нулю, то после дешифраторов на разрядном проводе шины, соответствующем нулю /это, например,- может быть первый провод "разрядной шины, с основанием единица"/, появляется положительный потенциал. А если одновременно с этим на выходах каких-то других ПЛМ второго ряда появляются калиброванные значения, равные пяти, то положительный потенциал появляется также и на разрядном проводе шины, соответствующем пяти /шестой провод шины/, таким образом на первом и шестом проводах шины появляются положительные потенциалы и т.д. Т.е. данная шина в своих разрядных проводах несет информацию одновременно о всех 90 Kn.
Далее к этой шине своими входами подключены электронные элементы четвертого ряда - девяносто ПЗУ. Одновременно к другим входам ПЗУ в качестве операндов от ПЛМ второго ряда в индивидуальном порядке поступают калиброванные значения Kn.
Назначение ПЗУ четвертого ряда состоит в том, чтобы сравнить индивидуальные калиброванные значения Ki, полученные от ПЛМ второго ряда, одновременно сразу со всеми Kn калиброванными значениями, имеющимися в наборе /в разрядной шине с основанием единица/.
В данном случае ПЗУ четвертого ряда выбирают из всего набора троек углов κ′, λ′, μ′, задающих в механизме подвеса будущий наклон тела человека-оператора, только те тройки углов, которые удовлетворяют выражению (80). Положительный потенциал появляется на выходе i-го ПЗУ четвертого ряда, если его индивидуальное K1 меньше или равно минимального значения всего набора троек углов.
Затем в схеме идет ряд логических элементов ИЛИ и НЕ-И применение которых позволяет устранить неоднозначность - выделить из нескольких троек углов, удовлетворяющих выражению (80), какую-то одну. Это осуществляется тем, что появление на выходе какого-то i-го ПЗУ положительного потенциала блокирует выходы всех (90-i) ПЗУ, расположенных справа от него.
В последнем ряду рассматриваемой электронной схемы располагается набор из 90 регистров, открывающих доступ на выходную шину единственной тройке углов κ′, λ′, μ′, удовлетворяющей всем семи условиям, изложенным выше.
Поворотами внутренних колец механизма подвеса на эти углы и будет задаваться новый наклон θ′, ϕ′ тела человека-оператора.
Скорость параллельной обработки информации в такой электронной структуре определяется только переходными процессами.
Здесь мною была описана только сама идея по созданию электронных цепей, осуществляющих быструю выборку из набора N = 90 нужной тройки углов, причем я сознательно опустил определенные нюансы.
Таким образом, здесь мы полностью рассмотрели вопросы, связанные с приданием телу человека-оператора того же наклона, что и у корпуса робота.
Но для того чтобы тело человека-оператора получило в пространстве определенную угловую ориентацию одного лишь наклона недостаточно, необходимо еще совершить поворот на определенный угол вокруг вектора отвесной линии /см. текст выше, где сказано, что любое изменение ориентации корпуса робота мы можем рассматривать как наклон корпуса робота относительно вектора отвесной линии и как поворот вокруг вектора отвесной линии, происходящий одновременно с наклоном./
Ранее я уже указывал, что в механизме подвеса поворот тела человека - оператора вокруг вектора отвесной линии осуществляется путем вращения кольца 4 относительно колец 5 и 6. Но кроме этого вращение кольца 4 выполняет еще одну очень важную "нейтрализующую" роль.
Рассмотрим эти вопросы подробнее.
Пусть в первый момент робот стоит вертикально /см. фиг. 79/.
Теперь допустим, человек-оператор принимает решение повернуть робота "направо". Тогда оператор начинает оказывать ногами соответствующее силовое воздействие на "штаны" управляющего костюма, что в свою очередь вызовет появление соответствующих усилий на ногах робота, после чего робот начнет поворачивать свой корпус направо. Такое небольшое изменение ориентации корпуса робота будет зафиксировано жидкостным инерционным датчиком ускоренных вращений, который перешлет по каналу связи информацию электронике механизма подвеса о том, что ориентация корпуса робота изменилась на величину: Δγ ≠ 0.
После чего механизм подвеса повернет кольцо 4 /а вместе с ним и тело человека - оператора / на угол Δγ и т.д., до тех пор, пока робот /и управляющий им человек-оператор/ полностью - на 90o - не совершат в пространстве поворот направо, задуманного человеком-оператором.
Процесс поворота робота и тела человека - оператора "направо" демонстрируется фиг. 79, 124, 125 и 126.
Вначале робот стоял вертикально см. фиг. 79, этому положению в механизме подвеса соответствовала ориентация тела человека - оператора, изображенная на фиг. 124. Фиг. 125 изображает робота уже после того, как он полностью выполнил поворот "направо", этому положению соответствует новая ориентация тела человека - оператора, задаваемая в механизме подвеса поворотом кольца 4 /см. фиг. 126/.
Теперь поговорим о "нейтрализующей" роли, выполняемой кольцом 4.
Для этого рассмотрим четыре позы, которые робот последовательно принимает в пространстве.
Пусть вначале наклон корпуса робота задается углами: θ = 40o, ϕ = 270o /см. фиг. 127/. В следующий момент робот начинает опускать верхнюю часть своего корпуса и одновременно с этим слегка перекатывается на живот, так, что углы θ = 40o, ϕ = 0o /см. фиг. 128/. Далее робот опять перекатывается на левое плечо и одновременно приподнимает нижнюю часть своего корпуса: θ = 40o, ϕ = 90o /см. фиг. 129/. И наконец, робот опускает свою нижнюю часть корпуса и слегка перекатывается на спину: θ = 40o, ϕ = 180o /см. фиг. 130/. Затем робот опять принимает позу, изображаемую фигурой 127, и весь цикл повторяется.
На глобусе наклонов тела человека - оператора, поворачиваемом в механизме подвеса, при подобных наклонах корпуса робота конец вектора отвесной линии будет описывать круги вокруг полярной точки: θ = 0o /см. фиг. 131/. И вот тут-то в механизме подвеса как раз и возникает тот нежелательный эффект, который нужно нейтрализовать поворотом кольца 4.
Обратите внимание на то, что на фиг. 127 - 130 ось Z системы координат XYZ, жестко связанной с корпусом робота, все время направлена в одну сторону, вдоль одного и того же азимута. Т.е. робот не совершает в пространстве реального вращения вокруг вектора отвесной линии, а только лишь наклоняется относительно него.
В то время как в механизме подвеса мы будем вынуждены вращать тело человека - оператора для придания ему необходимых наклонов /см. фиг. 132-135 /:
фиг. 132 соответствует позе робота, изображенной на фиг. 127,
фиг. 133 соответствует позе робота, изображенной на фиг. 128,
фиг. 134 соответствует позе робота, изображенной на фиг. 129,
фиг. 135 соответствует позе робота, изображенной на фиг. 130.
Таким образом в механизме подвеса при задании телу человека - оператора необходимого наклона /с помощью вращения колец 1, 2 и 3 / одновременно возникает нежелательное вращение вокруг вектора отвесной линии.
Чтобы нейтрализовать это нежелательное вращение тела человека - оператора вокруг вектора отвесной линии мы будем поворачивать кольцо 4 ему навстречу. Тогда тело человека - оператора не будет совершать в пространстве незапланированного поворота вокруг вектора отвесной линии. Именно в этом и заключается нейтрализующая роль кольца 4.
Итак, в механизме подвеса кольцо 4 за "бесконечно малый" промежуток времени: dt должно в общем случае повернуться вокруг своих выступов - осей /см фиг. 86, 93 /на угол:
dψ = dξ-dN, (95)
где величина угла dξ вычисляется по формуле (62). Физический смысл поворота на этот угол dξ был раскрыт ранее.
Величина нейтрализуемого вращения dN вычисляется по формуле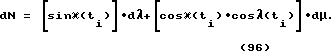
По своей сути величина dN - это угол нежелательного вращения, на который повернется тело человека - оператора вокруг вектора отвесной линии за время dt при задании ему необходимого наклона: θi+1, ϕi+1.
Бесконечно малый промежуток: dt берется между двумя близкими моментами времени ti и ti+1:
dt = ti+1 - ti. (97)
Значения дифференциалов dλ и dμ вычисляются исходя из текущего и будущего наклонов тела человека - оператора. Т.е. в момент времени ti тело человека- оператора имеет наклон: θi, ϕi, который в механизме подвеса задан углами μi, λi, κi. Одновременно от робота по каналу связи к нам пришла информация, что наклон корпуса робота определяется иными углами θi+1, ϕi+1, близкими по своим значениям к углам θi, ϕi.
Для придания телу человека - оператора подобной угловой ориентации /как и у корпуса робота/ мы будем должны повернуть за время dt кольца 1, 2, 3, 4 на углы dμ, dλ, dκ и dψ.
Перед тем как выполнить повороты на эти углы электроника механизма подвеса должна вычислить их значения.
Дифференциал dμ вычисляется как разность будущего значения угла μi+1 и текущего значения угла μi:
dμ = μi+1-μi, (98)
где значение будущего угла μi+1 электроника механизма подвеса извлекает из набора ПЗУ, куда "зашиты" значения углов поворотов колец μ, λ, κ как функции от углов θ, ϕ, определяющих наклон /см. текст выше/.
Аналогичным образом вычисляются дифференциалы dλ и dκ:
dλ = λi+1-λi; (99)
dκ = κi+1-κi. (100)
В формуле (96) перед дифференциалами dλ и dμ стоят коэффициенты [sinκ(ti)] и [cosκ(ti)•cosλ(ti)], значения которых берутся на текущий момент времени ti.
Обосную формулу (96).
Для этого рассмотрим следующий пример:
Допустим, что у нас имеется твердое тело, вращаемое на механической оси A-B см. фиг. 136 /. Ось вращения A-B направлена под углом θ к вектору отвесной линии. Введем в рассмотрение две системы координат: систему XYZ и систему XoYoZo, такие, что ось Zo системы XoYoZo направлена противоположно вектору отвесной линии, оси Yo и Y совпадают /совмещены/ и направлены под углом 90o к оси Zo, ось X сонаправлена с механической осью вращения A-B, а ось Xo компланарна оси X /см. фиг. 137./.
Несмотря на то, что твердое тело вращается вокруг оси A-B, системы координат XoYoZo и XYZ неподвижны в пространстве, т.е. твердое тело не вовлекает во вращение системы координат.
Угол N, на который происходит вращение твердого тела вокруг оси Zo /вокруг вектора отвесной линии/, определим как дугу, описываемую в пространстве единичным радиус - вектором, перпендикулярным оси Zo. Вращение этого единичного радиус - вектора вокруг оси Zo рисует в плоскости XoOYo окружность единичного радиуса, которая на фиг. 138 выглядит как эллипс. /Единичный радиус - вектор пока что не связан ни с какой конкретной материальной точкой твердого тела./
Теперь выберем в твердом теле материальную точку "A", располагающуюся на расстоянии 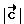 от оси вращения A-B. /см. фиг. 138/.
от оси вращения A-B. /см. фиг. 138/.
На фиг. 138 показан общий вид систем координат XoYoZo и XYZ /здесь использованы аксонометрические проекции/, большой эллипс изображает единичную окружность, описываемую в пространстве вокруг оси Zo единичным радиус - вектором, а малый эллипс изображает окружность, описываемую материальной точкой "A" при вращении материального твердого тела вокруг механической оси A-B.
Найдем вектор линейной скорости материальной точки "A" в момент, когда она пересекает единичную окружность при вращении твердого тела вокруг оси Х. Далее мы находим проекцию этой линейной скорости на касательную к единичной окружности, проведенную в точке, где вектор  пересекает окружность. Отсюда мы уже легко можем найти угловую скорость, которую имеет материальная точка "A" по отношению к оси Zo в момент прохождения точкой "A" плоскости XoOYo.
пересекает окружность. Отсюда мы уже легко можем найти угловую скорость, которую имеет материальная точка "A" по отношению к оси Zo в момент прохождения точкой "A" плоскости XoOYo.
Точка "A" была выбрана нами в твердом теле достаточно произвольно, понятие: "единичный радиус-вектор" также имеет достаточно произвольную интерпретацию. Отсюда мы получаем проекцию вектора угловой скорости на ось Zo для всех точек твердого тела, когда они в своем вращении пересекают плоскость XoOYo.
Фиг. 139 дает нам изображение фиг. 138 сверху, так что ось Zo системы координат XoYoZo направлена к нам.
Фиг. 140 дает вид фиг. 138 сбоку, так что ось Yo системы координат XoYoZo направлена к нам.
На фиг. 138 и 139 был введен в рассмотрение единичный радиус-вектор 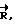 лежащий в плоскости XoOYo. Этот вектор берет свое начало в точке "О" и заканчивается в той точке единичной окружности, через которую материальная точка "A" пересекает плоскость XoOYo.
лежащий в плоскости XoOYo. Этот вектор берет свое начало в точке "О" и заканчивается в той точке единичной окружности, через которую материальная точка "A" пересекает плоскость XoOYo.
Как видно из фиг. 139, вектор 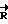 имеет в системе координат XoYoZo следующие компоненты:
имеет в системе координат XoYoZo следующие компоненты:
(cosρ, sinρ, 0). (101)
Теперь с помощью матрицы, описывающей переход от системы координат XoYoZo к системе XYZ /см. фиг. 140/: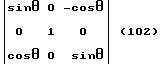
можно записать компоненты вектора  в системе координат XYZ:
в системе координат XYZ:
(cosρ•sinθ, sinρ, cosρ•cosθ). (103)
Отсюда уже легко получить компоненты вектора  в тот момент, когда материальная точка "A" пересекает при своем вращении единичную окружность, лежащую в плоскости XoOYo:
в тот момент, когда материальная точка "A" пересекает при своем вращении единичную окружность, лежащую в плоскости XoOYo:
(0, sinρ, cosρ•cosθ). (104)
Найдем с помощью векторного произведения компоненты вектора линейной скорости материальной точки "A" в системе координат XYZ. Для этого рассмотрим векторное произведение двух векторов: вектора  и вектора
и вектора  задающего вращение твердого тела. Вектор
задающего вращение твердого тела. Вектор  имеет в системе координат XYZ следующие компоненты:
имеет в системе координат XYZ следующие компоненты: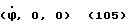
Тогда вектор линейной скорости материальной точки "A" :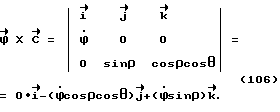
Т.е. через компоненты линейная скорость материальной точки "A" в системе XYZ запишется так: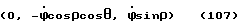
Теперь перейдем от системы координат XYZ к системе координат XoYoZo. Для этого транспонируем матрицу, записанную в выражении (102)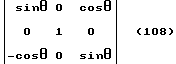
Тогда вектор линейной скорости материальной точки "A" в системе координат XoYoZo имеет следующие компоненты: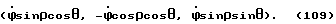
Найдем проекцию этого вектора линейной скорости на касательную к единичной окружности в точке, где заканчивается вектор  /см. фиг. 141/. Для этого необходимо вначале определить единичный вектор, перпендикулярный вектору
/см. фиг. 141/. Для этого необходимо вначале определить единичный вектор, перпендикулярный вектору  и лежащий в плоскости XoOYo. Такой вектор в системе координат XoYoZo имеет компоненты /см. фиг. 141 /:
и лежащий в плоскости XoOYo. Такой вектор в системе координат XoYoZo имеет компоненты /см. фиг. 141 /:
(sinρ, -cosρ, 0). (110)
Искомая нами проекция вектора линейной скорости материальной точки "A" на касательную определяется скалярным произведением вектора линейной скорости /выражение (109)/ и единичного вектора, касательного к окружности /выражение (110)./:
Итак, мы получили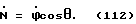
/О том, что связь между  и
и  будет именно такой, можно было догадаться. Собственно говоря, я так и поступил, а здесь уже просто подогнал доказательство под интуитивно полученный ответ./
будет именно такой, можно было догадаться. Собственно говоря, я так и поступил, а здесь уже просто подогнал доказательство под интуитивно полученный ответ./
Теперь уже не составит труда объяснить появление формулы (96).
Первое слагаемое [sinκ(ti)•dλ, записанное в формуле (96), определяет величину поворота тела человека - оператора вокруг вектора отвесной линии, когда кольцо 2 поворачивается в механизме подвеса на угол dλ. По своей сути выражение [sinκ(ti)•dλ - это проекция "вектора вращения" 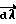 на вектор отвесной линии. /Появление перед dλ "sin" а не "cos", как это казалось бы следует из формулы (112), объясняется тем, что в механизме подвеса угол κ берет свое начало /начинает свой отсчет/ в положении, когда плоскость кольца 3 перпендикулярна вектору отвесной линии /см. фиг. 93 //. Второй член суммы (96) определяет величину поворота тела человека - оператора вокруг вектора отвесной линии, вызванного вращением dμ кольца 1 механизма подвеса. Перед дифференциалом dμ имеется коэффициент, состоящий из произведения косинусов, его появление объясняется формулой (89).
на вектор отвесной линии. /Появление перед dλ "sin" а не "cos", как это казалось бы следует из формулы (112), объясняется тем, что в механизме подвеса угол κ берет свое начало /начинает свой отсчет/ в положении, когда плоскость кольца 3 перпендикулярна вектору отвесной линии /см. фиг. 93 //. Второй член суммы (96) определяет величину поворота тела человека - оператора вокруг вектора отвесной линии, вызванного вращением dμ кольца 1 механизма подвеса. Перед дифференциалом dμ имеется коэффициент, состоящий из произведения косинусов, его появление объясняется формулой (89).
В формулу (96) не входит дифференциал dκ, т.к. оси - выступы кольца 3 всегда остаются перпендикулярными вектору отвесной линии и проекция вектора 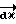 на вектор отвесной линии всегда равна нулю. Однако повороты кольца 3 изменяют наклоны выступов - осей колец 1 и 2, поэтому-то значение угла κ и входит через "sin " и "cos" в коэффициенты, стоящие перед dλ и dμ.
на вектор отвесной линии всегда равна нулю. Однако повороты кольца 3 изменяют наклоны выступов - осей колец 1 и 2, поэтому-то значение угла κ и входит через "sin " и "cos" в коэффициенты, стоящие перед dλ и dμ.
Предложенная здесь конструкция механизма подвеса обладает еще одним достоинством, заключающимся в том, что при задании наклонов тела человека-оператора сингулярные эффекты могут проявляться в механизме подвеса только тогда, когда антропоморфный робот находится в максимально устойчивом положении - лежит на правом или левом боку, поэтому сингулярные эффекты не отразятся на устойчивости вертикальной походки робота.
Предложенный здесь способ /физическая теория механизма подвеса и датчиков угловой ориентации/ позволяет изготовить дистанционно управляемый, копирующий, антропоморфный, шагающий робот, имеющий повышенную маневренность и повышенную проходимость /по сравнению с роботами, передвигающимися на колесном или гусеничном ходу /.
Способ защиты электроники антропоморфного робота от воды.
По этому способу наружное покрытие робота состоит из двух слоев. Первый слой - сборные щитки, изготовленные из нержавеющих сплавов. Одно из назначений этих "рыцарских доспехов" - защитить внутренности робота от колюще-режущих воздействий окружающих предметов. Для этого металлические щитки должны полностью прикрывать собой поверхность робота. В тех местах, где у робота размещаются суставы, щитки должны при необходимости заходить друг за друга, чтобы не мешать роботу сгибать сустав.
Под металлическими щитками находится сплошная полимерная оболочка, наподобие той, которая надевается на тело человека-водолаза, работающего в трехболтовом водолазном снаряжении. /Вероятно, эту оболочку будет лучше изготовить не из резины, а из нейлона, который, как мне известно, более стойко переносит воздействие углеводородных соединений./
В тех местах, где у робота располагаются наиболее подвижные суставы /плечевые, тазовые, коленные,.../ между металлическими щитками и полимерной оболочкой должна располагаться кольчужная прокладка - структура, сплетенная из металлических колец.
Назначение этой кольчужной прокладки состоит в том, чтобы предохранить полимерную оболочку от случайного защемления металлическими щитками и от разрыва, когда робот сгибает сустав и щитки заходят друг за друга. /Кольца кольчуги должны иметь достаточно крупные размеры, чтобы не попасть между щитками, а сами щитки должны быть тщательно подогнаны друг к другу, чтобы зазор между ними был по возможности меньше.
При погружении робота - водолаза на глубину вода, конечно, легко проникнет в щели между металлическими щитками и сквозь кольца кольчуги, но она не сможет пройти дальше внутрь робота через герметичную, сплошную, полимерную оболочку.
С увеличением глубины погружения робота - водолаза будет возрастать и давление воды на полимерную оболочку. Однако полимерная оболочка будет сохранять объем, заключенный внутри нее, т.к. она заполнена "несжимаемой" жидкостью /керосином или соляркой/. Поэтому нам удастся предотвратить сжатие и разрыв полимерной оболочки под воздействием возрастающего внешнего давления воды.
Таким образом электроника робота - водолаза все время будет находиться в неагрессивной, диэлектрической среде /в керосине или в солярке/, этим мы и сможем защитить ее от воздействия морской воды.
Примечание:
Диэлектрическая жидкость, заполняющая полимерную оболочку, играет роль смазки для внутренних механизмов робота - водолаза /при этом ее можно даже принудительно нагнетать между трущимися поверхностями суставов робота/. На суше "рыцарские доспехи" робота - водолаза предотвращают "раздувание" полимерной оболочки в нижней части робота под воздействием веса диэлектрической жидкости, заключенной в полимерной оболочке.
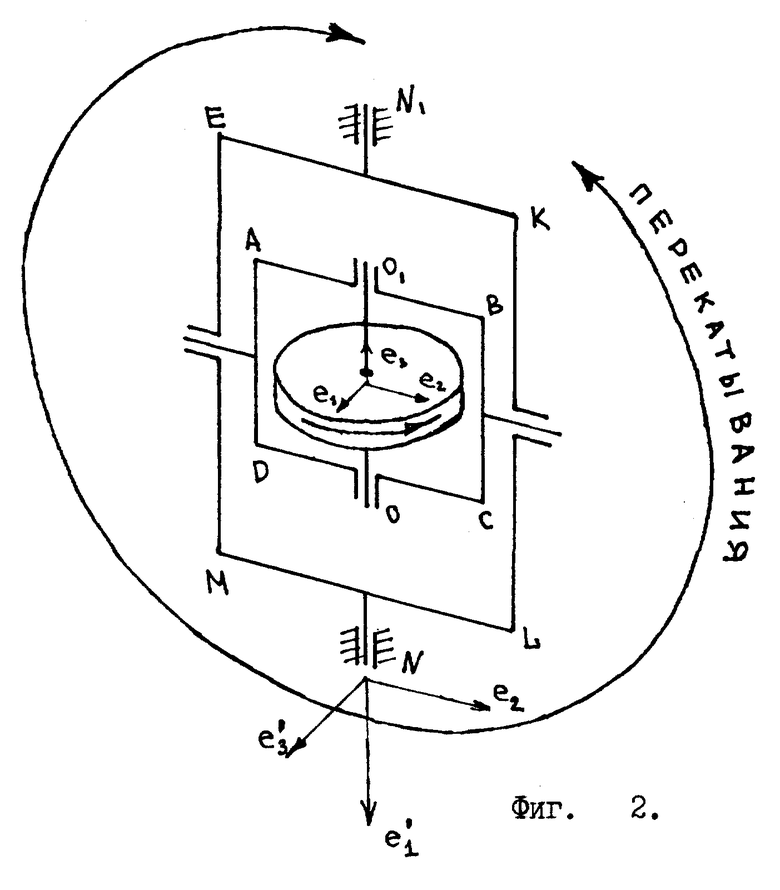
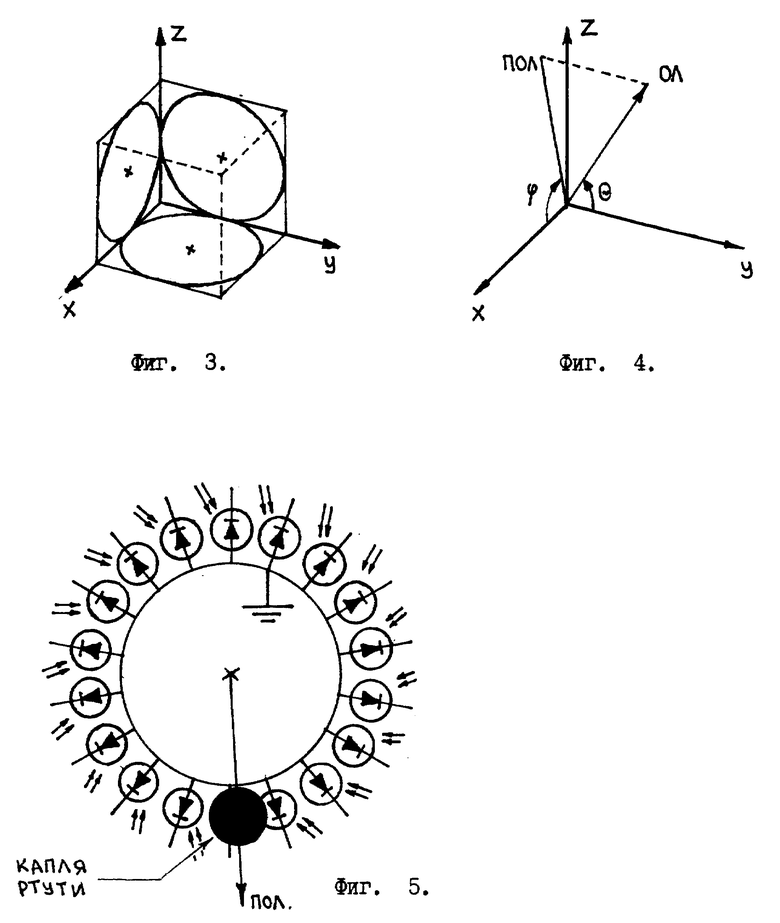
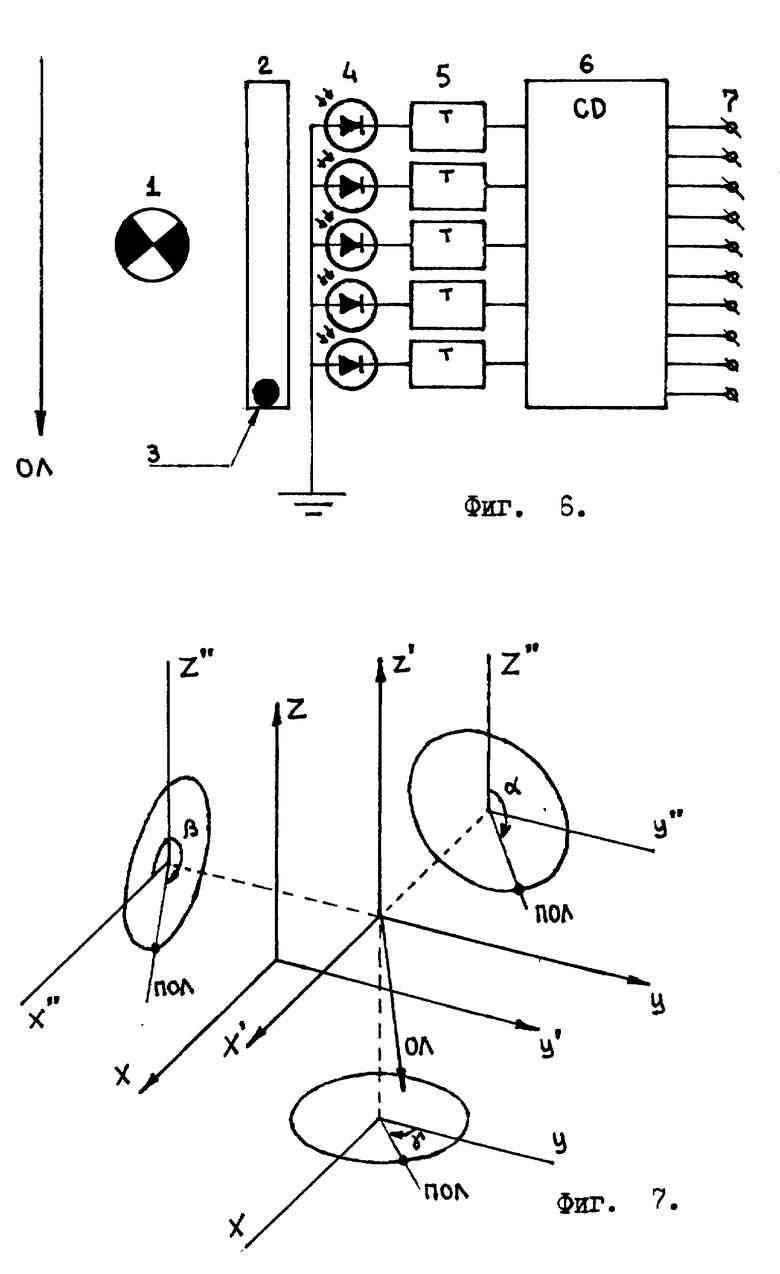
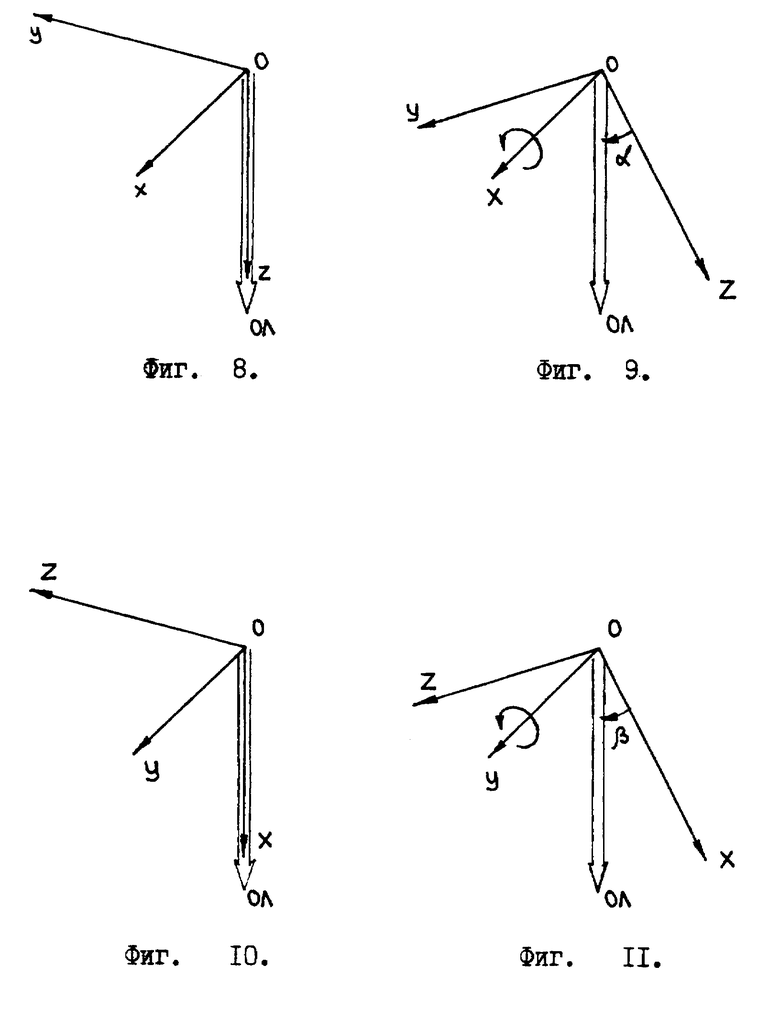
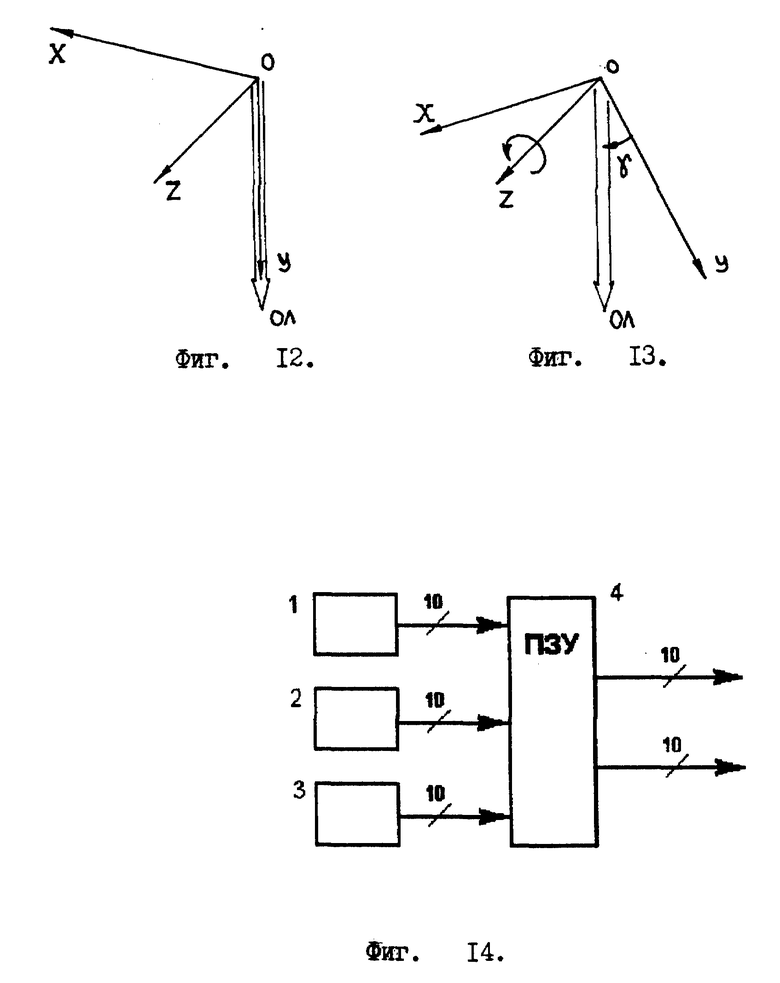
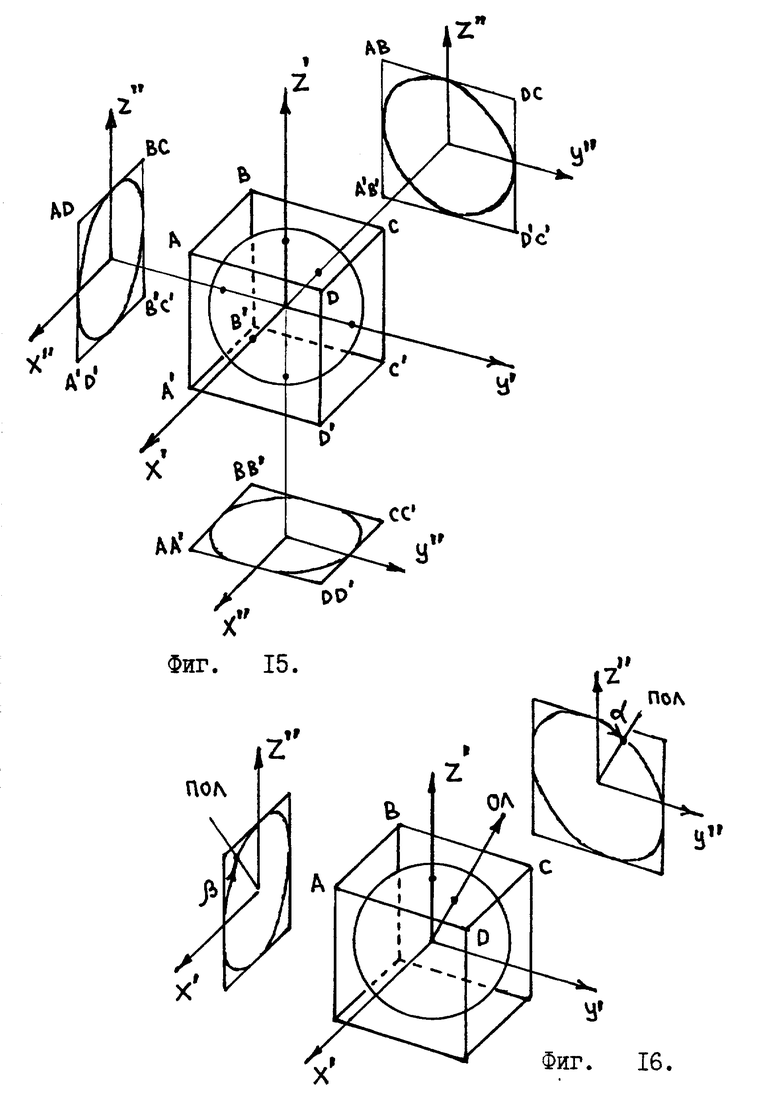
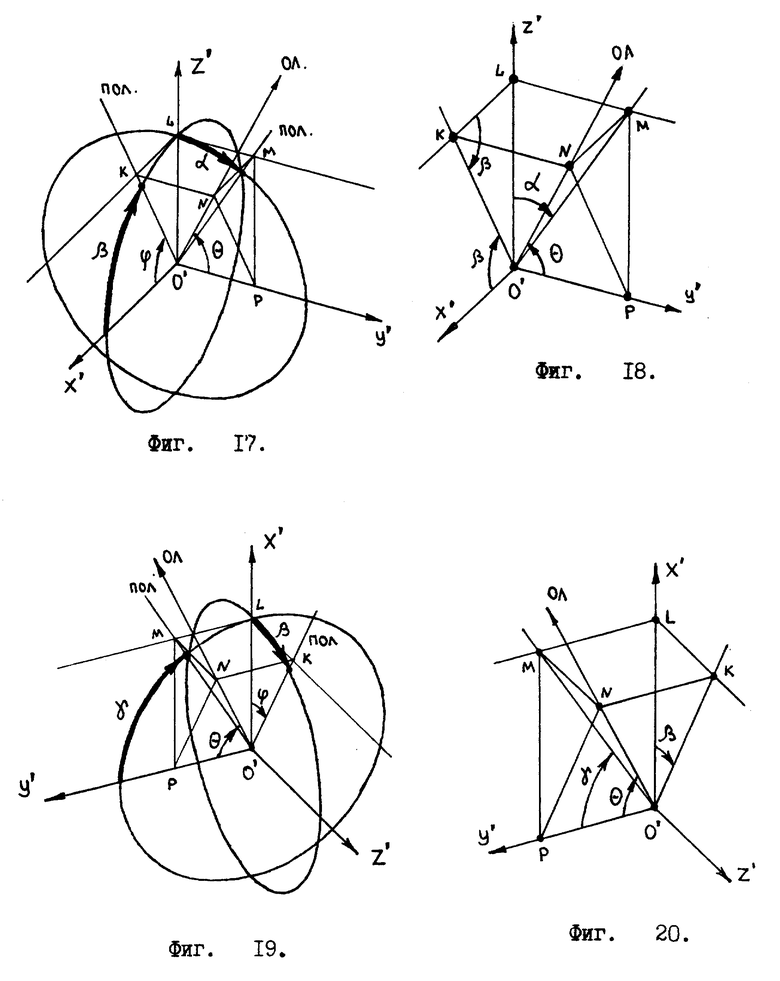
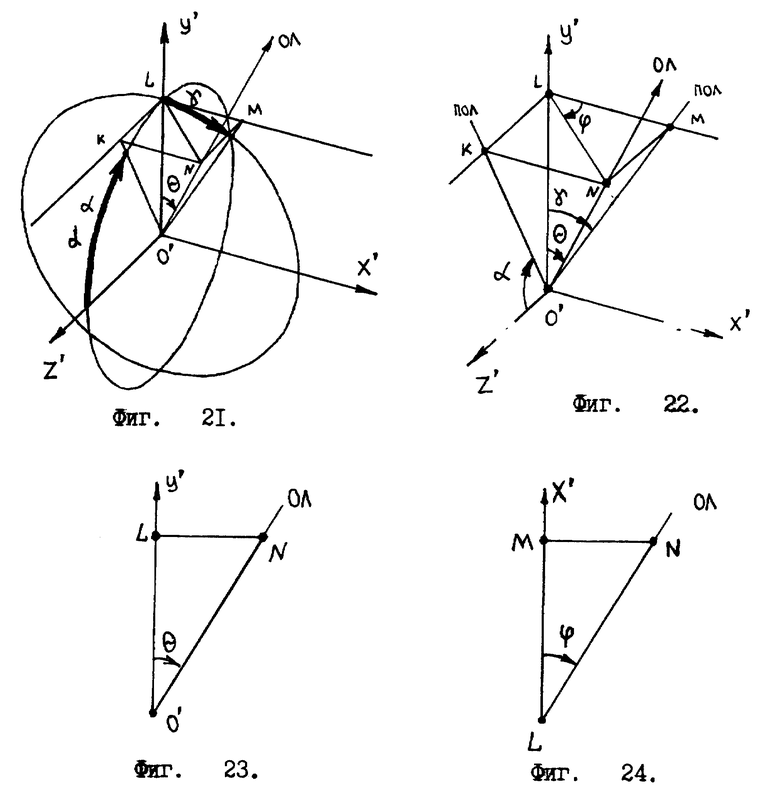
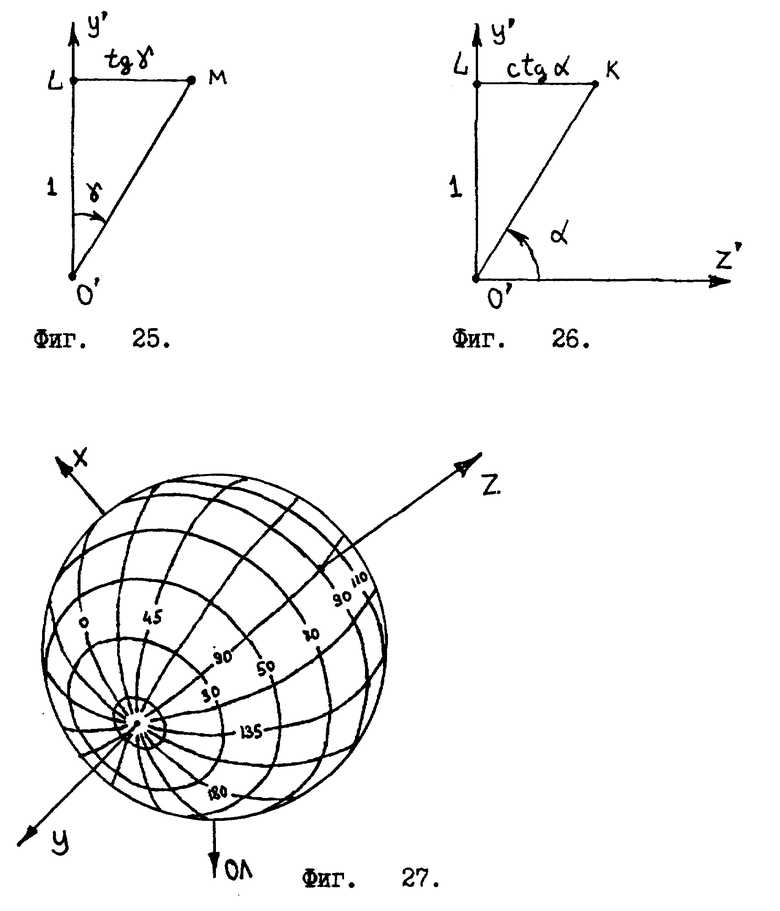
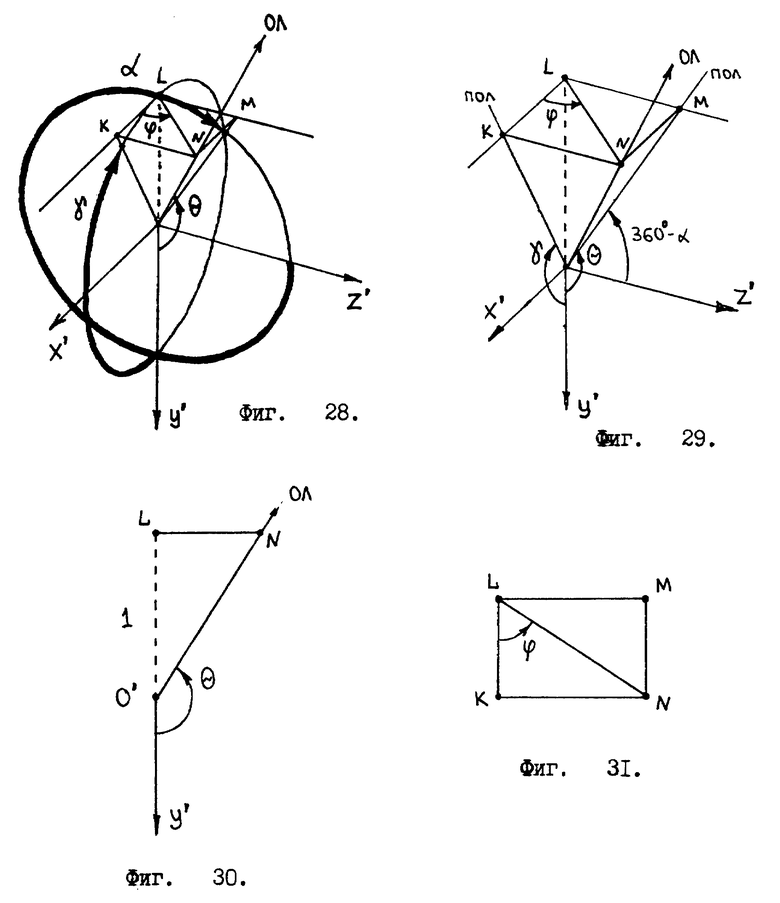
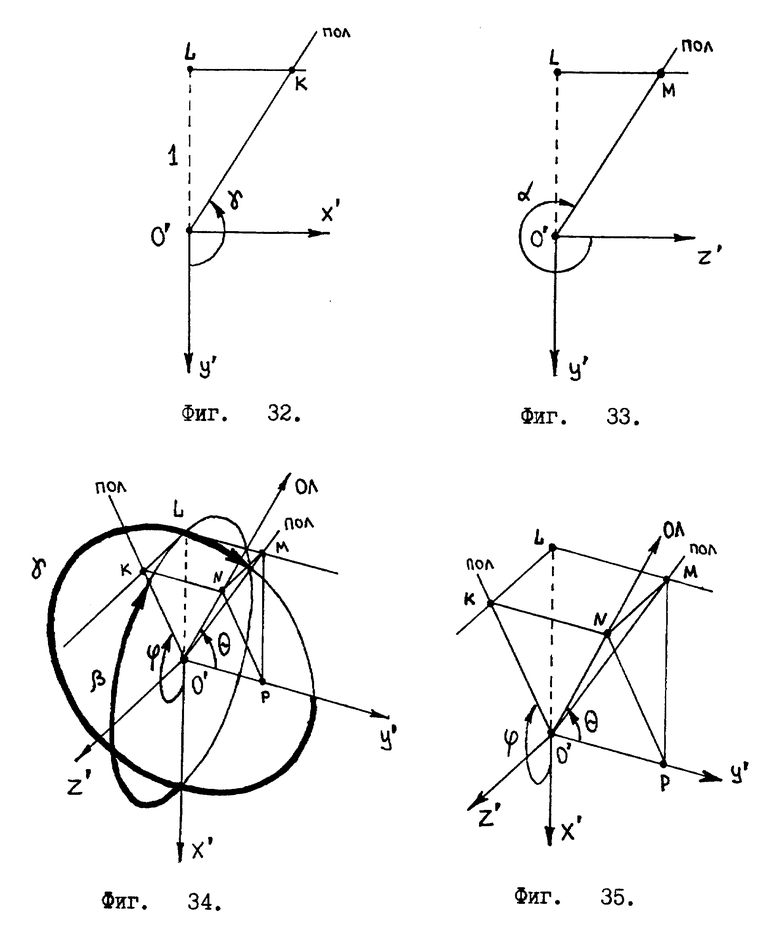
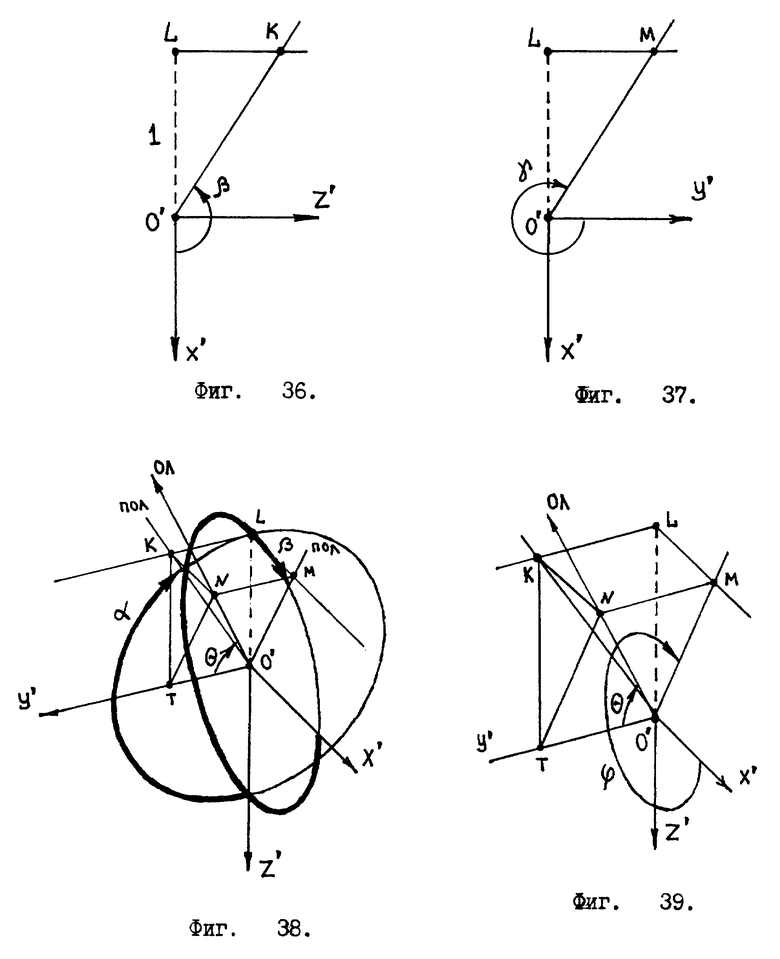
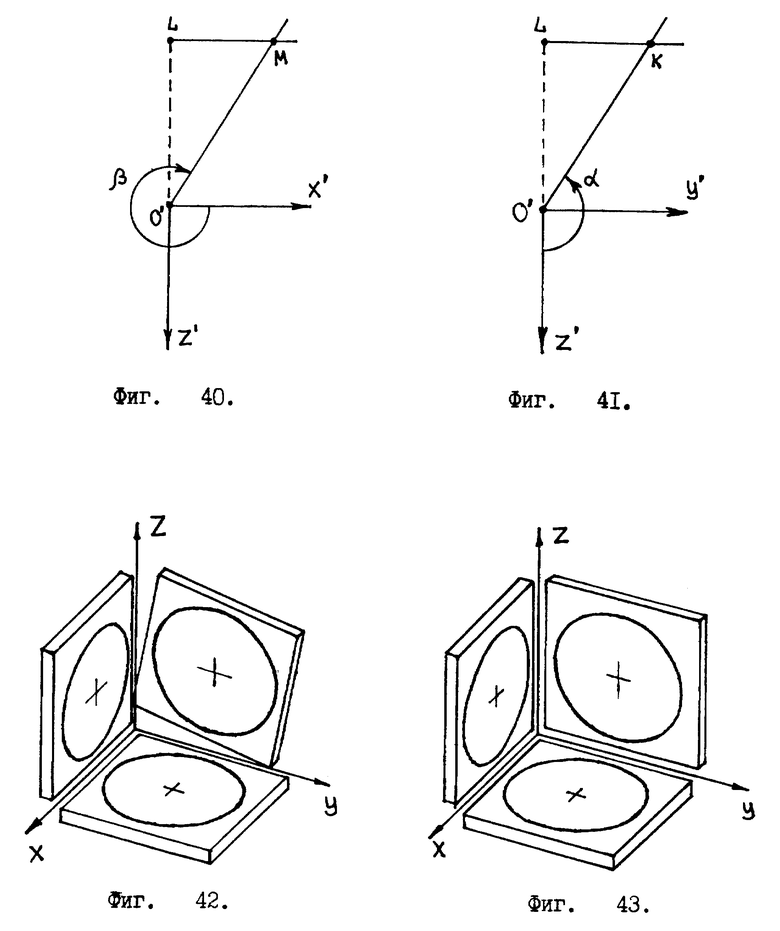

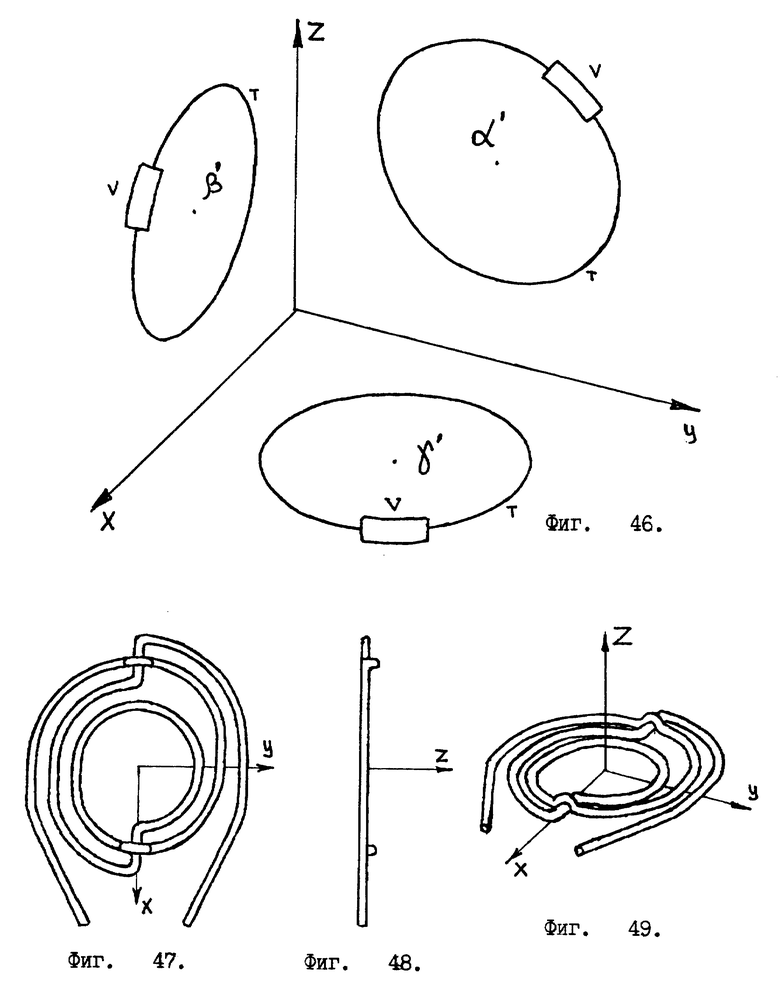
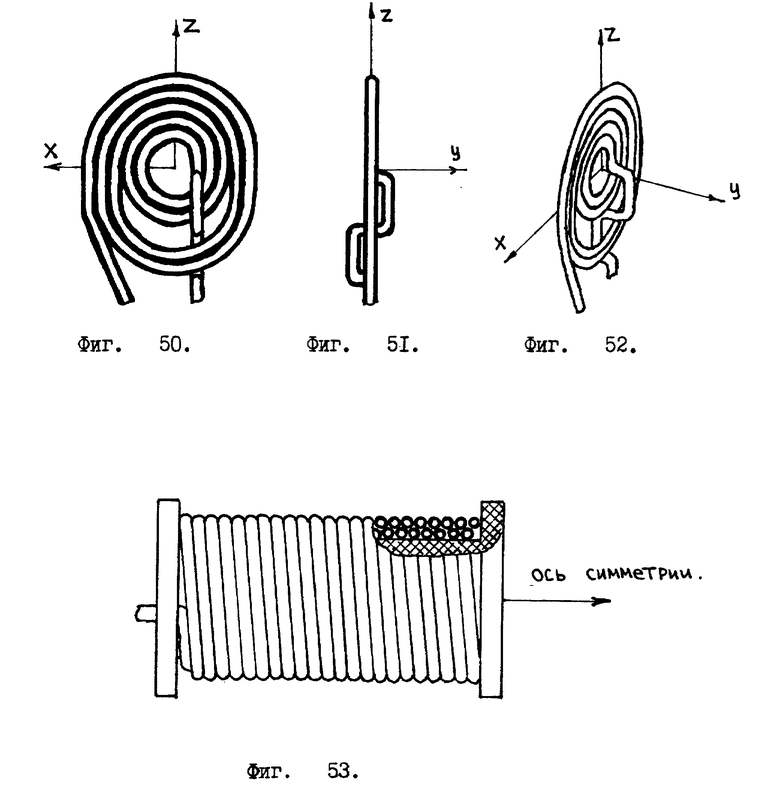
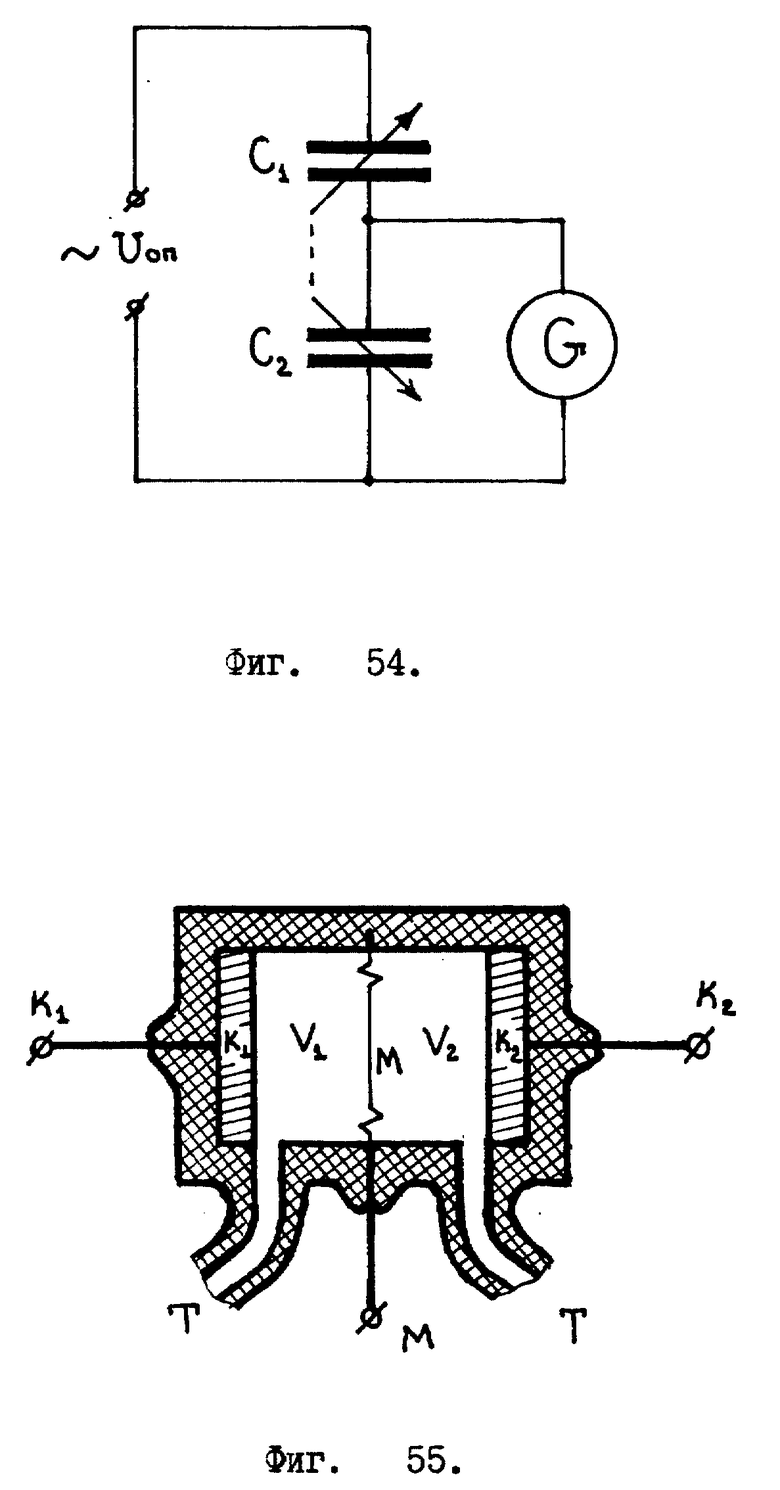
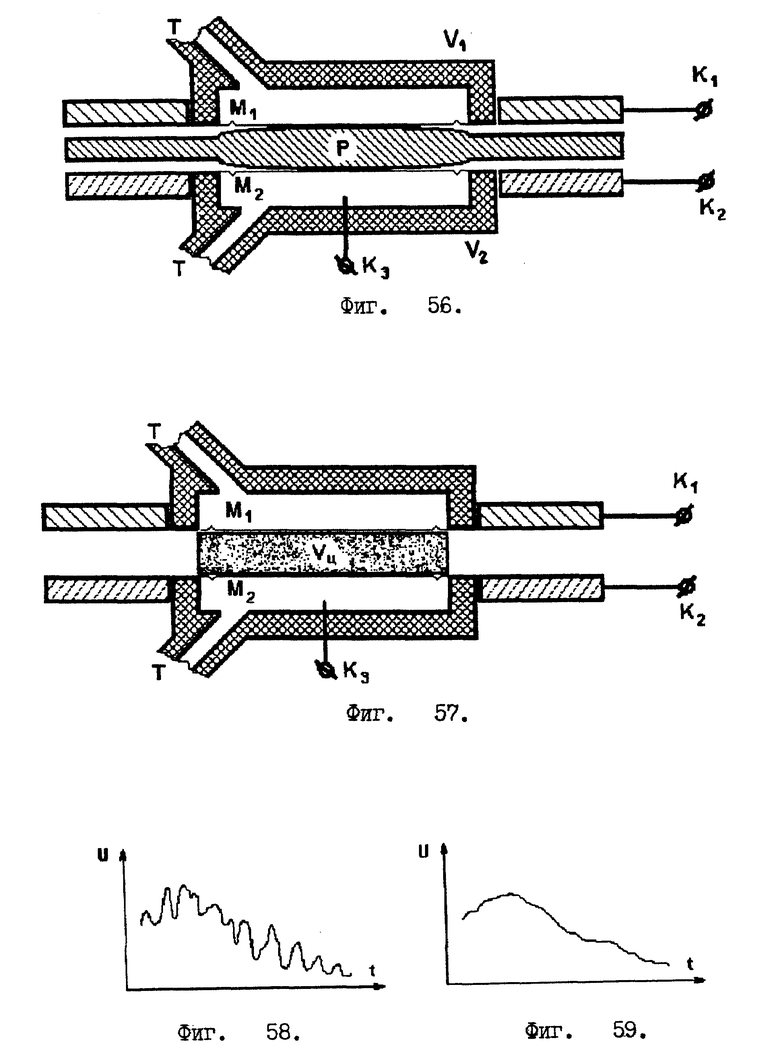
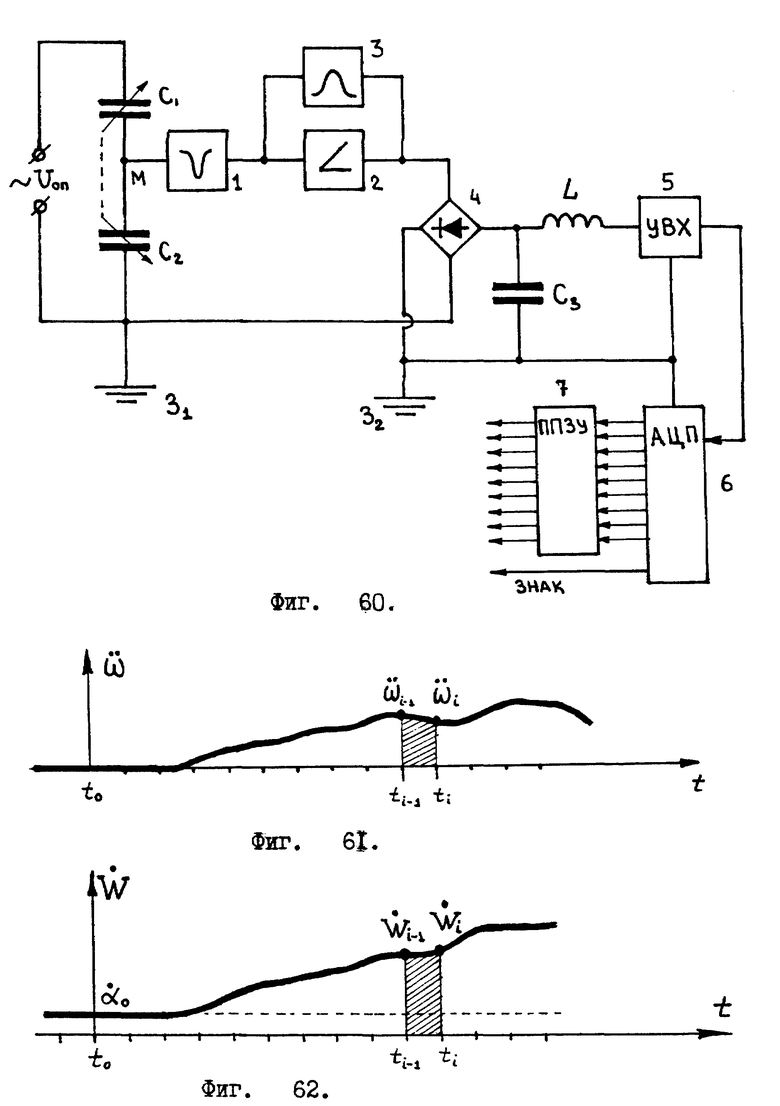
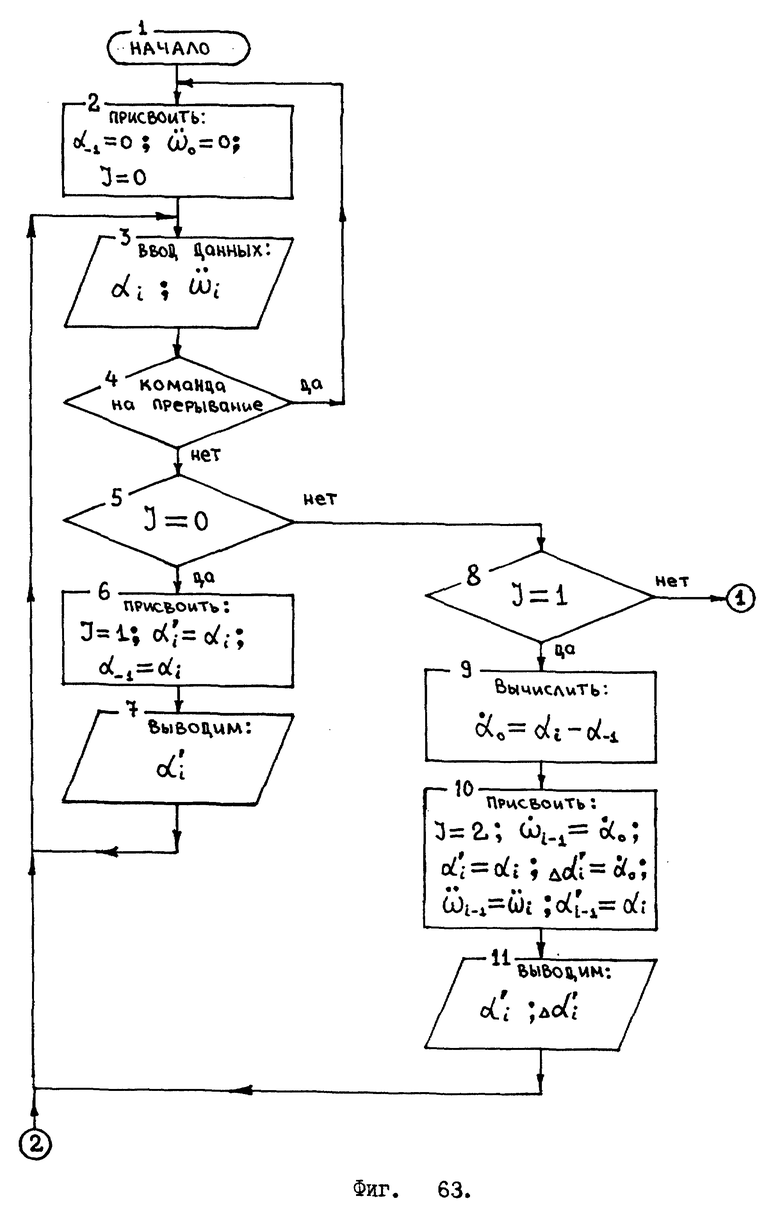
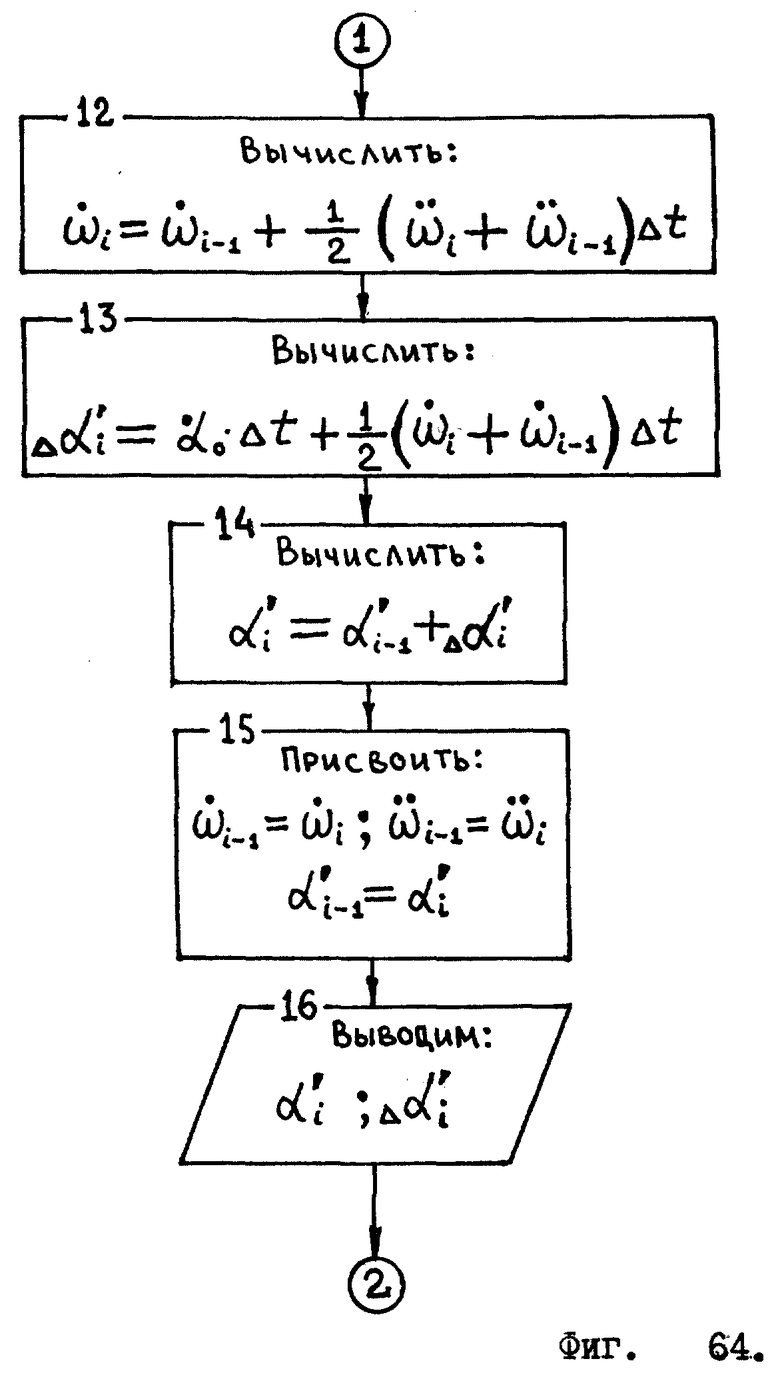
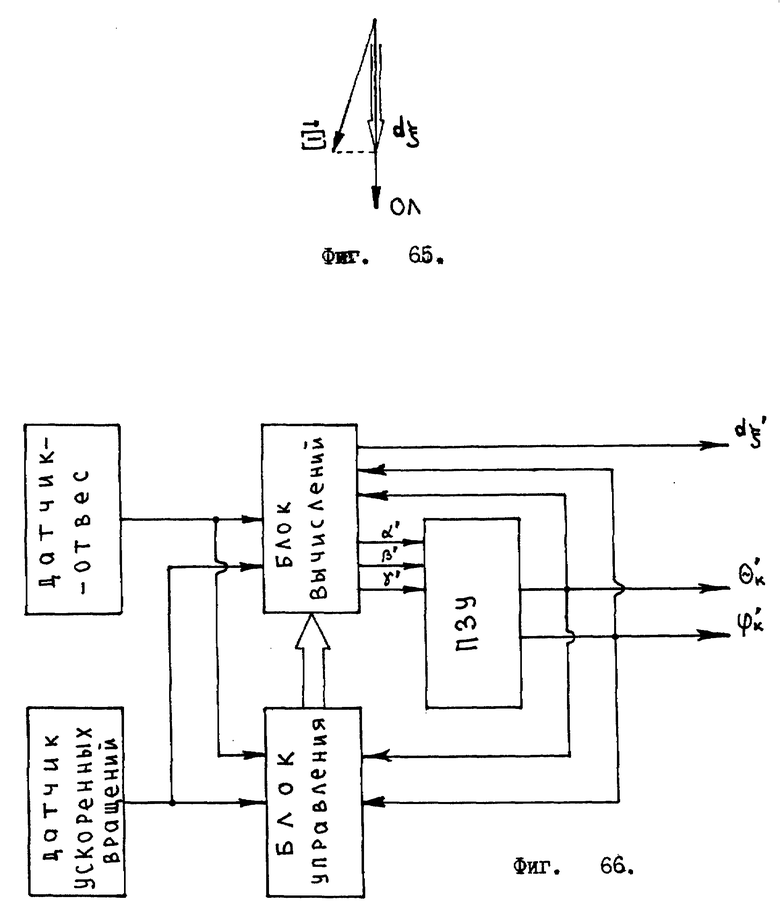
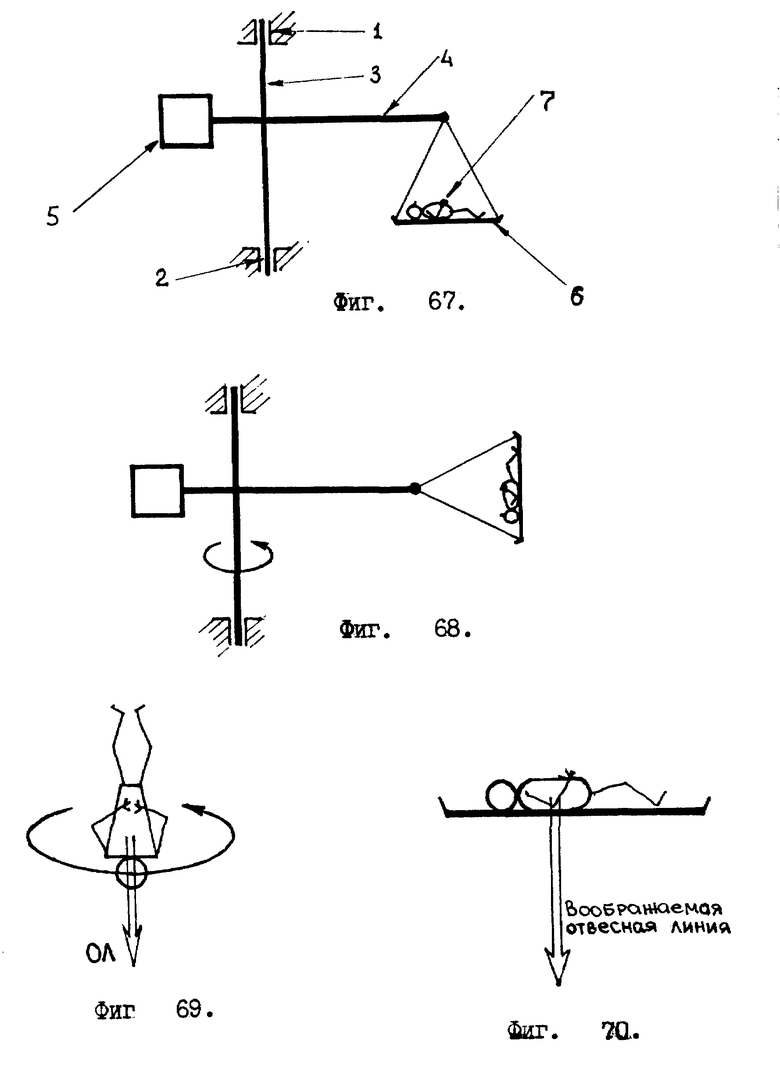
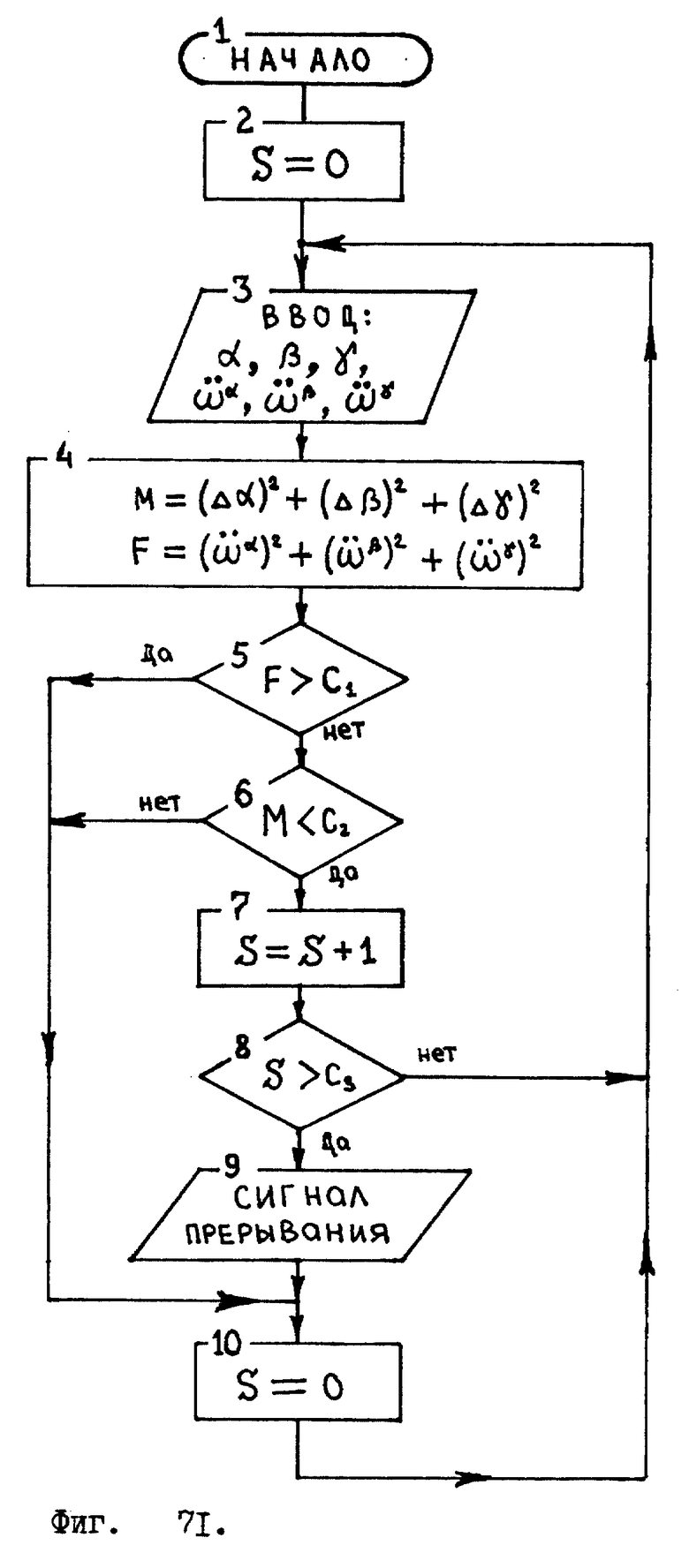
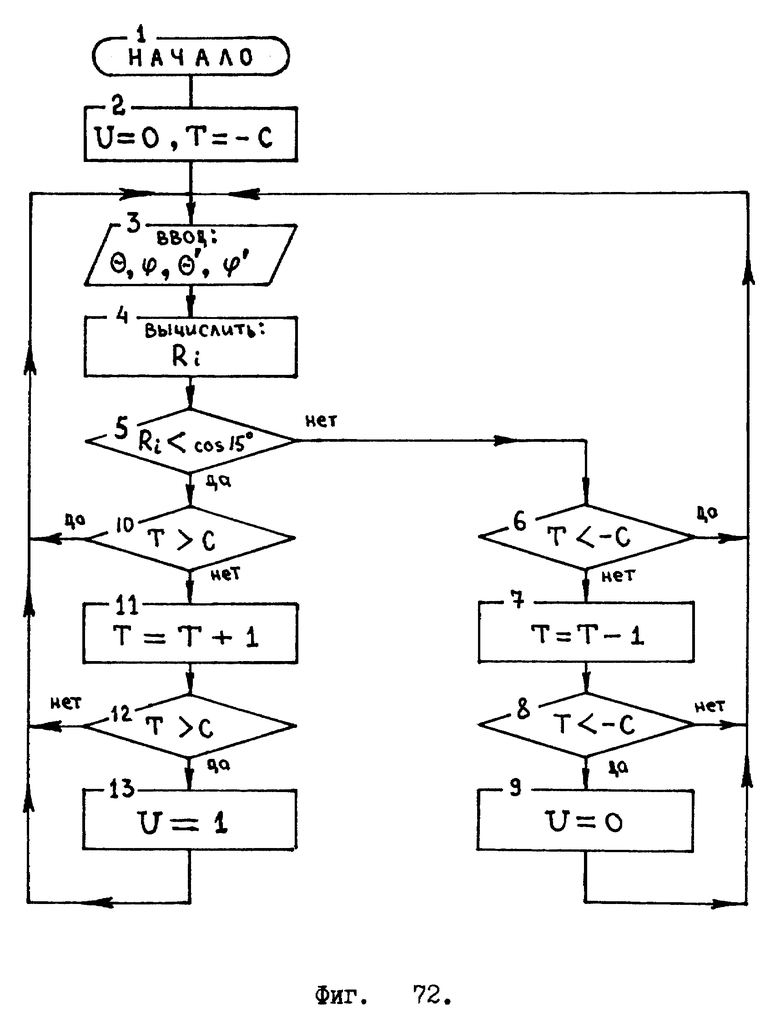
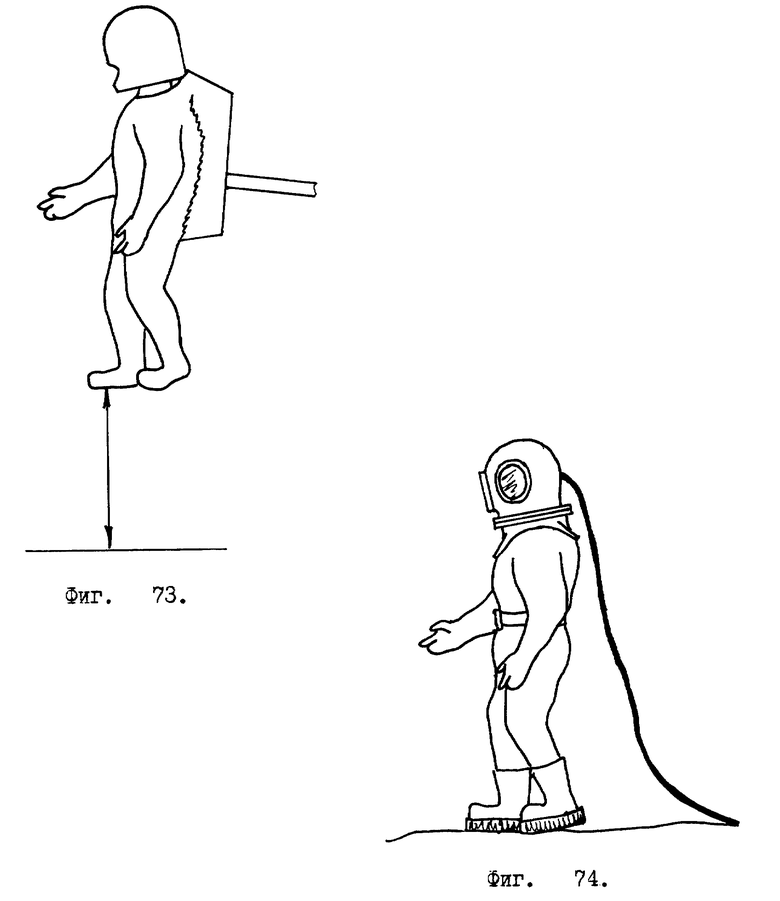
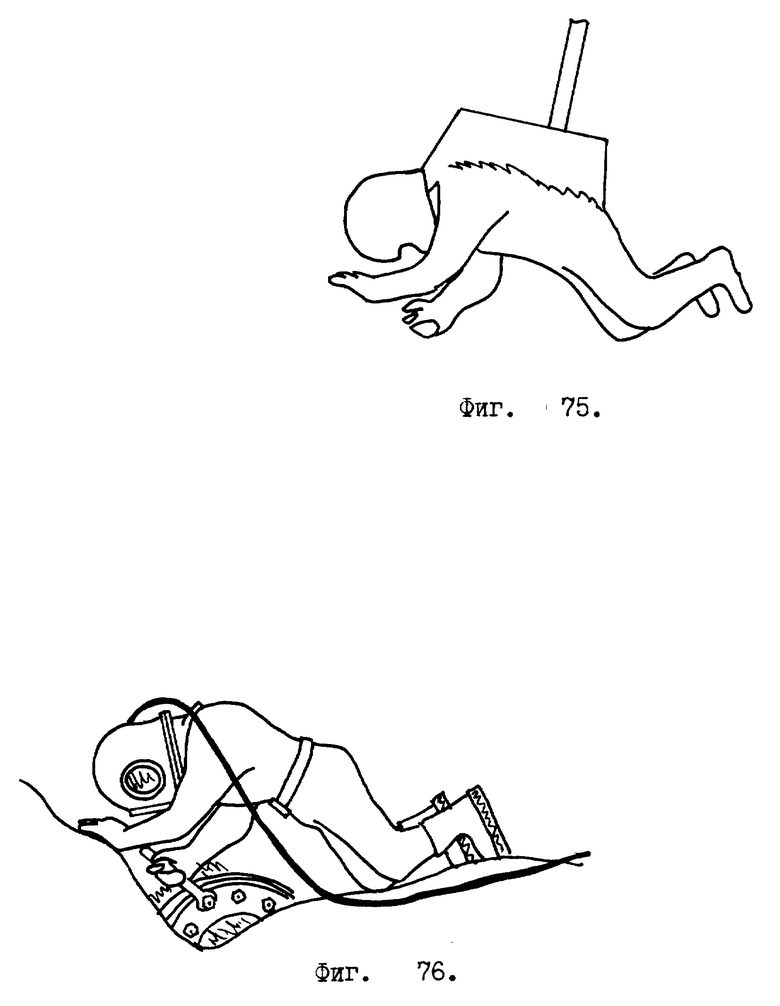
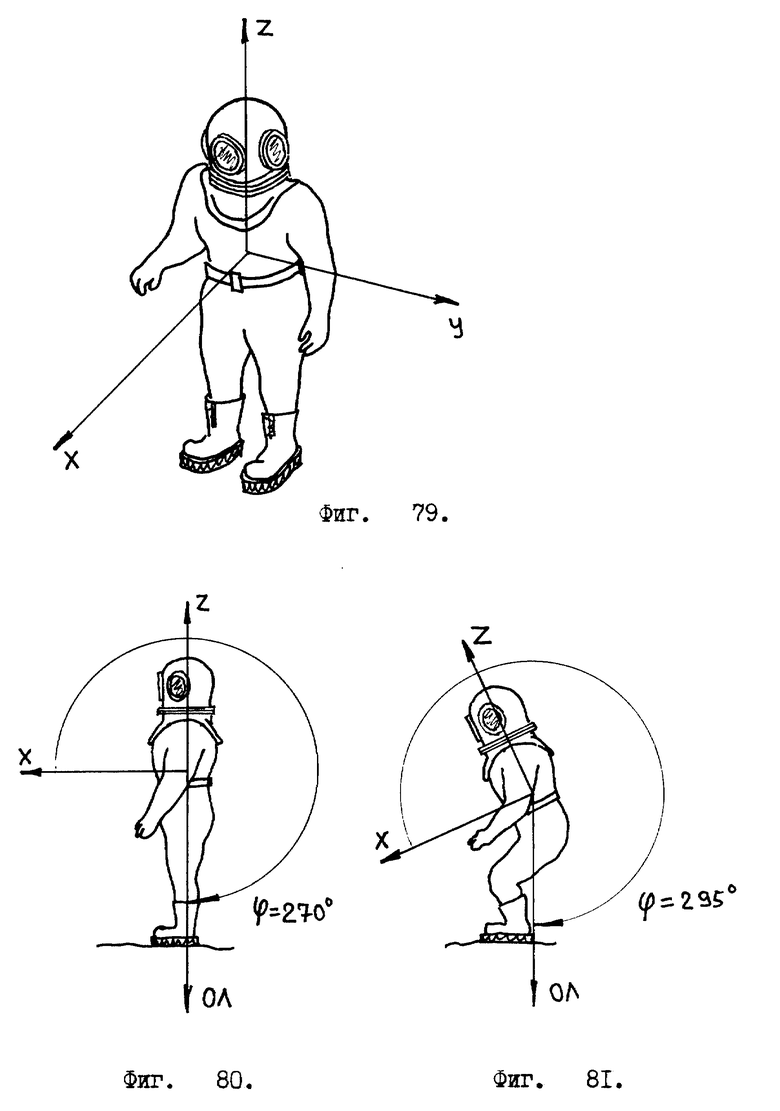
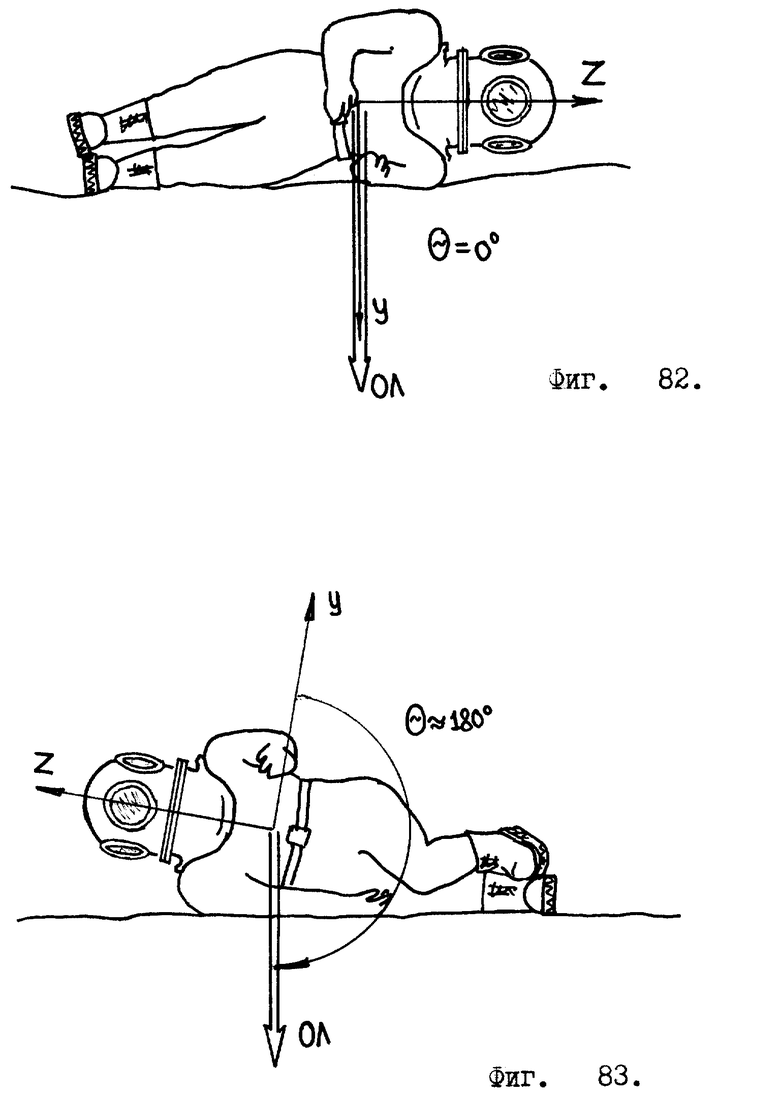
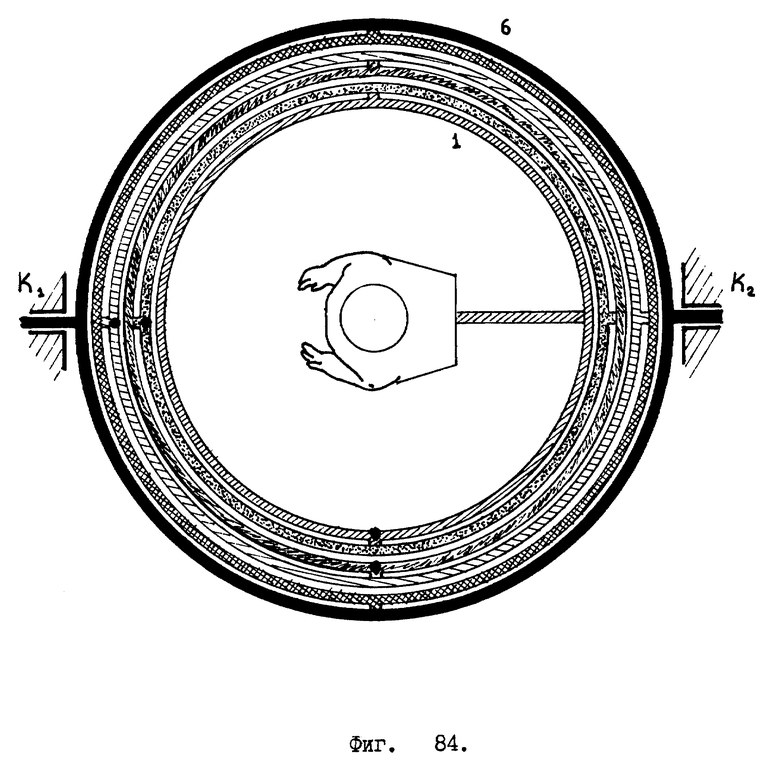

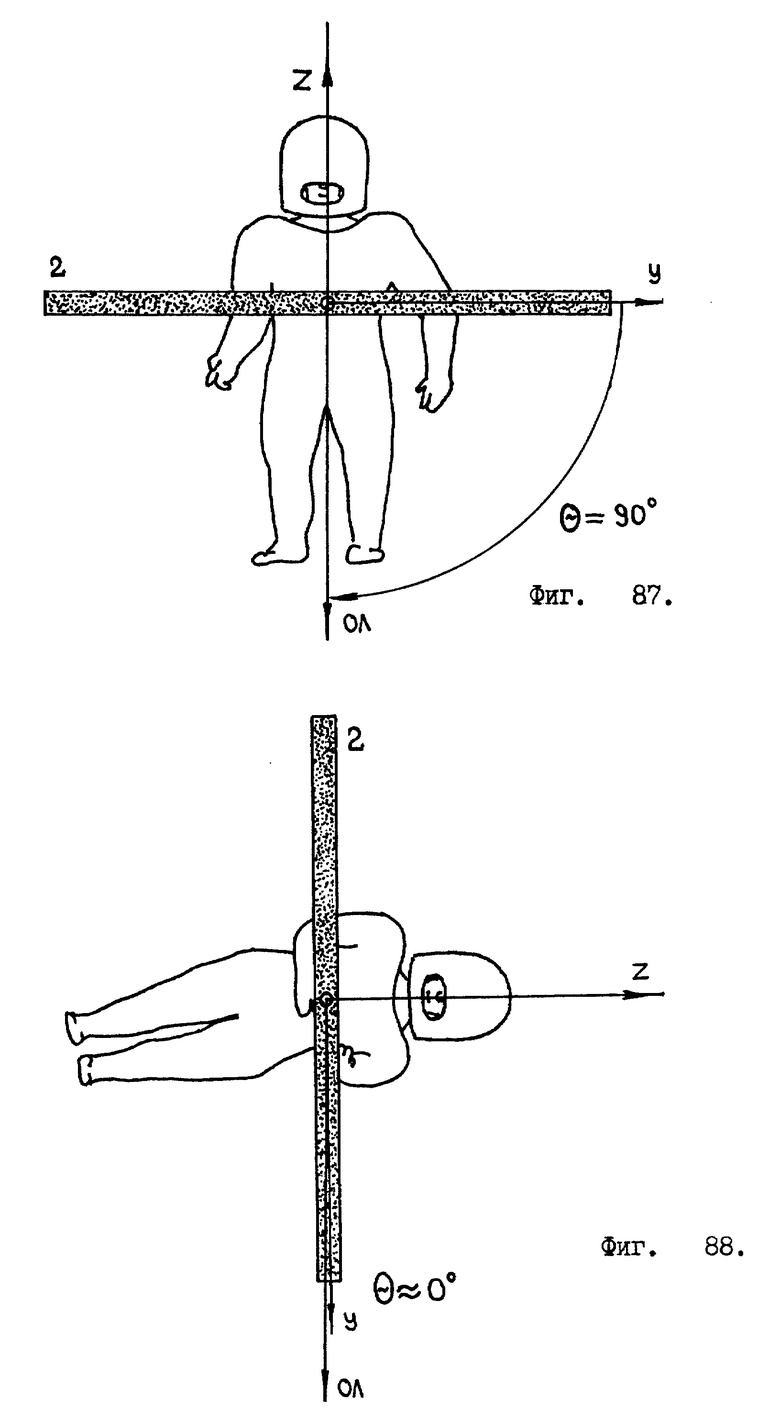
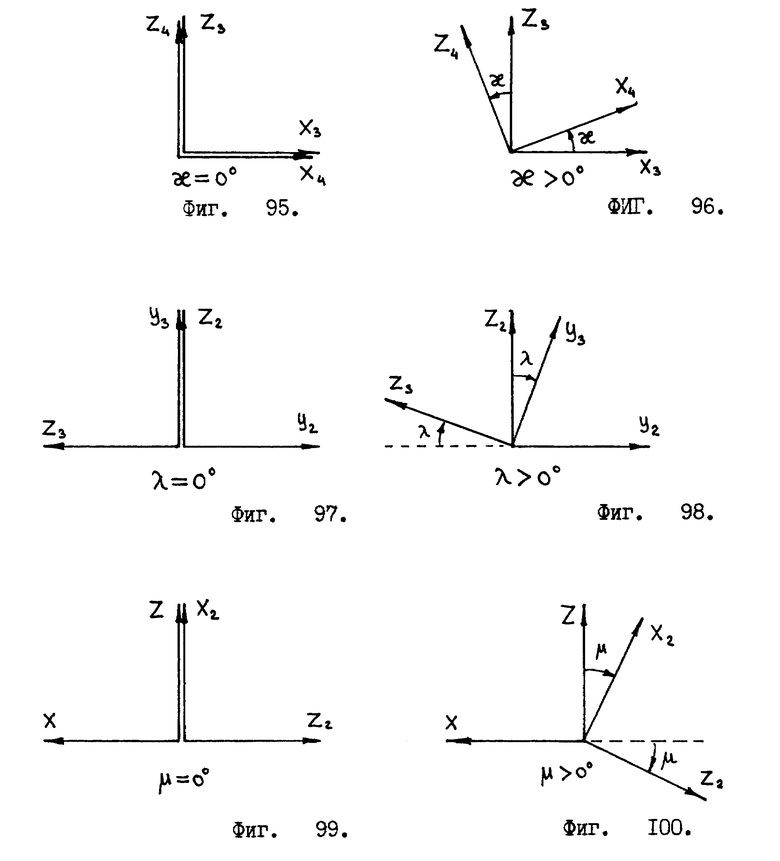
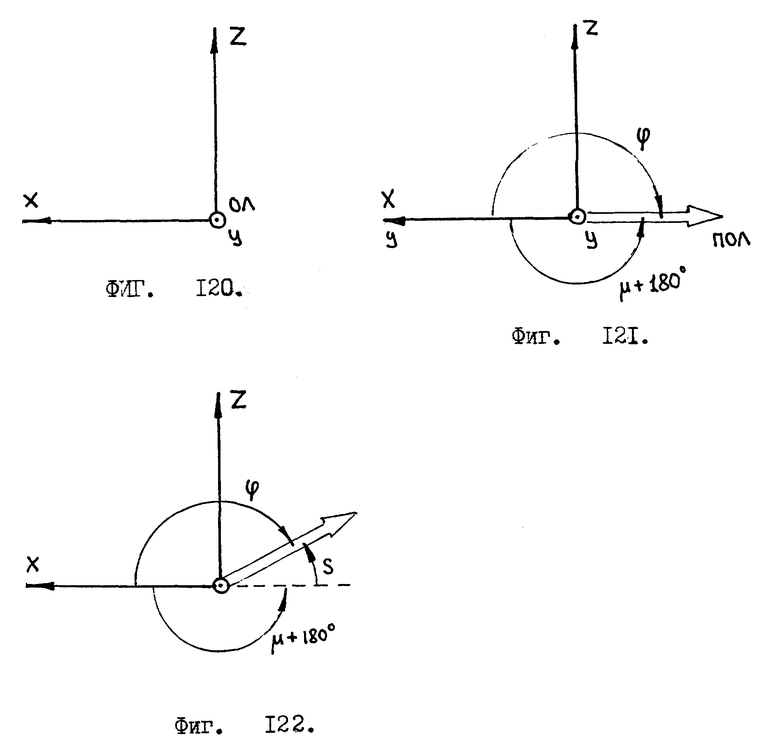
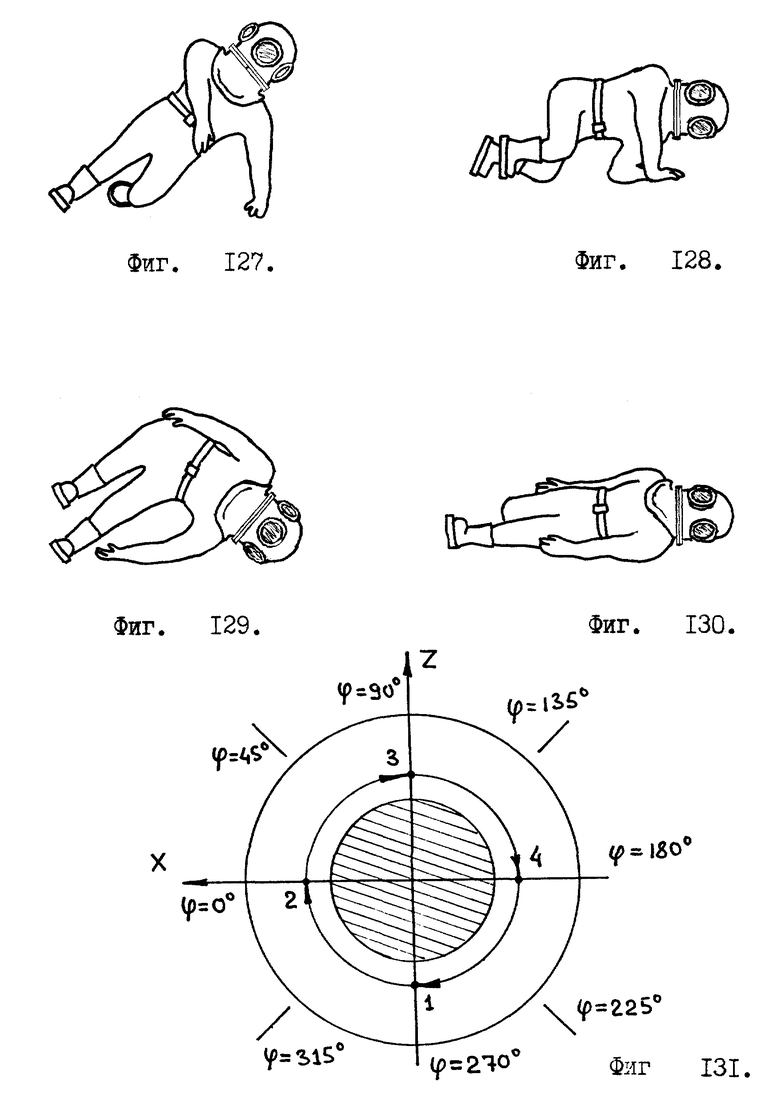
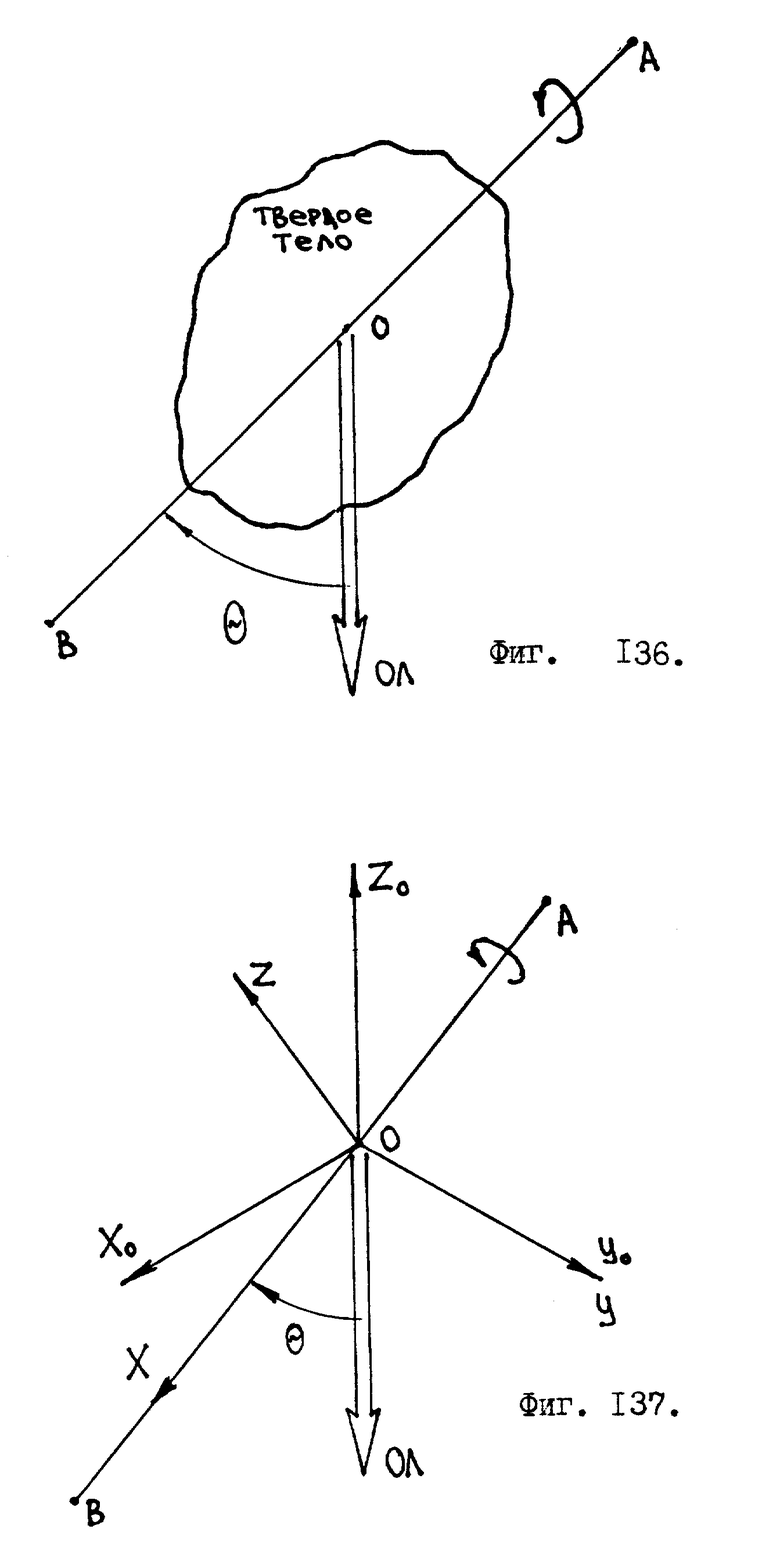
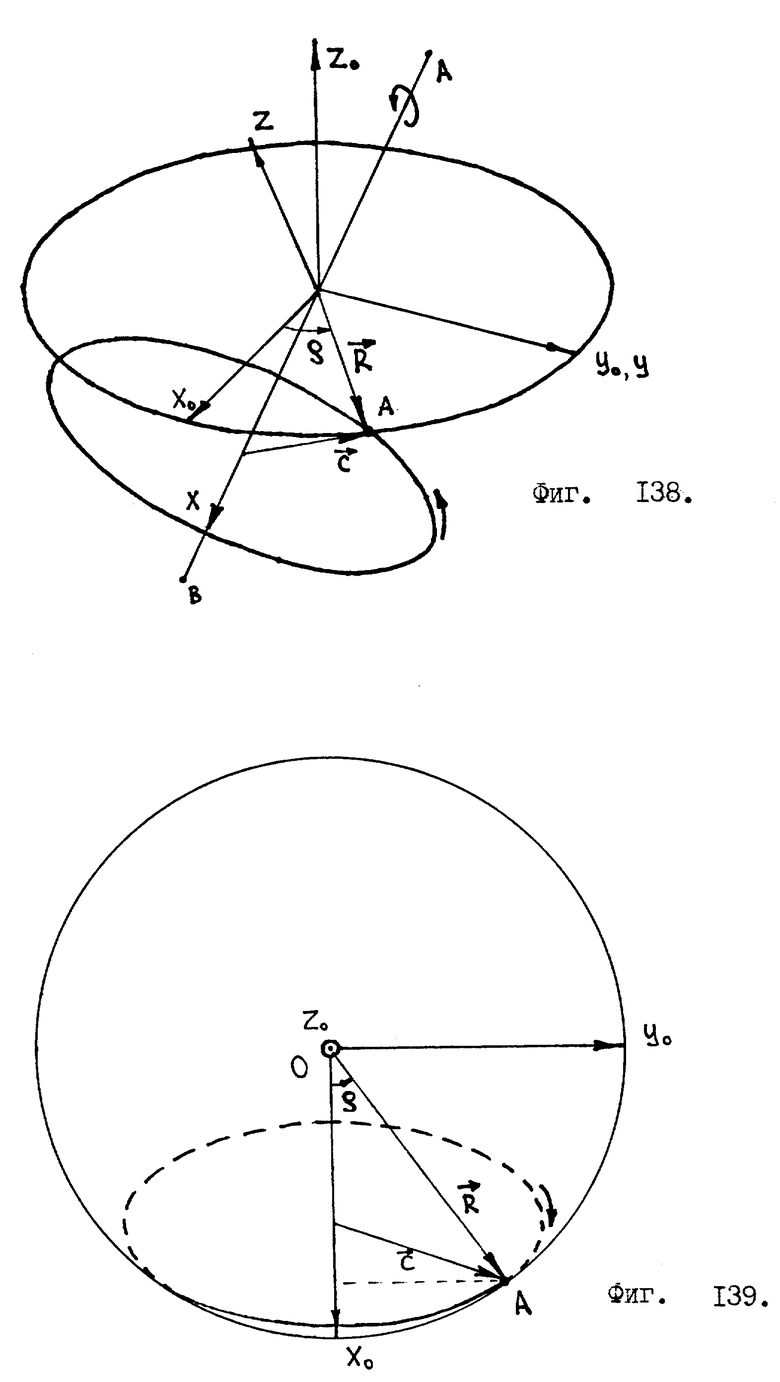
Изобретение относится к робототехнике и может быть использовано, например, в военном деле или при водолазных работах. Технический результат: повышение качества управления. Сущность изобретения: данные об угловой ориентации робота передаются по каналу связи на следящий механизм подвеса, который придает телу человека-оператора такую же угловую ориентацию, как и у корпуса робота, что позволяет человеку ощущать своими органами равновесия все изменения, происходящие в угловой ориентации робота. Это в конечном итоге позволяет повысить качество управления роботом. 5 з.п. ф-лы, 141 ил.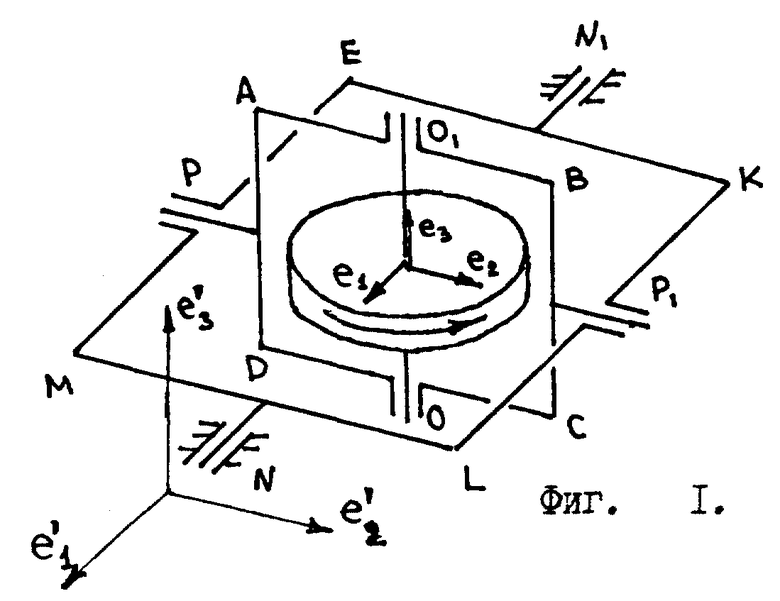
| КОМПЛЕКСНОЕ СВЯЗУЮЩЕЕ ДЛЯ ПОЛУЧЕНИЯ УГОЛЬНЫХ БРИКЕТОВ | 2011 |
|
RU2467060C1 |
| УСТРОЙСТВО И СПОСОБ ЗАЩИТЫ КОМПРЕССОРА И ОХЛАДИТЕЛЯ ВОЗДУХА ТУРБОНАДДУВА В ДВИГАТЕЛЕ ВНУТРЕННЕГО СГОРАНИЯ, ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ И УСТРОЙСТВО УПРАВЛЕНИЯ | 2010 |
|
RU2555091C2 |
| US 3535711 A, 27.10.70 | |||
| Задающее устройство для дистанционного управления роботом - манипулятором | 1991 |
|
SU1825730A1 |
Авторы
Даты
1999-08-10—Публикация
1997-04-03—Подача