Изобретение относится к цифровой вычислительной технике и рекомендуется в качестве перифирийного процессора для выполнения операций вращения вектора в трехмерном пространстве, в частности для решения широкого класса задач морской и воздушной навигации.
В известных устройтвах (например, авт. св. СССР №1460720, кл. G 06 F 7/544, 1989 г., бюл.№7) поворот вектора (кватернионное преобразование) осуществляется вокруг равнонаклоненной оси вращения, что ограничивает разновидность ортогональных преобразований.
Наиболее близким по технической сущности (прототипом) является устройство преобразования координат (авт. св. СССР №1472902, кл. G 06 F 7/544, 1989 г., бюл.№14), содержащее с первого по шестой регистры, с первого по шестой сумматоры-вычитатели, с первого по шестой блоки умножения и блок управления, причем первые выходы первого, второго и третьего регистров соединены с входами первых операндов соответственно первого, второго и третьего сумматоров-вычитателей, выходы которых соединены с входами первых операндов соответственно четвертого, пятого и шестого сумматоров-вычитателей, выходы которых соединены с первыми входами соответственно первого, второго и третьего регистров, первые выходы четвертого, пятого и шестого регистров соединены соответственно с объединенными попарно первыми входами первого и второго, третьего и четвертого, пятого и шестого блоков умножения, выходы которых подключены к входам вторых операндов одноименных сумматоров-вычитателей, вторые входы (выходы) первого, второго и третьего регистров соединены двухнаправленными связями с интерфейсной шиной, к которым подключены также входы четвертого, пятого и шестого регистров, а объединенные попарно входы оператора направления вращения первого и второго, третьего и четвертого, пятого и шестого сумматоров-вычитателей соединены соответственно с первым, вторым и третьим выходами блока управления.
В таком устройстве вращение вектора осуществляется численным интегрированием по формуле прямоугольников, что ограничивает точность и шаг решения задач. Кроме того, интегрирование по Риману с постоянными шагами по углам на всем интервале вращения затрудняет решение задач в реальном масштабе времени.
Технический результат предлагаемого решения заключается в повышении точности и увеличении шага вращения вектора.
В предлагаемом устройстве приращение 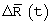 вектора
вектора 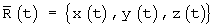 , вращаемого с угловой скоростью
, вращаемого с угловой скоростью 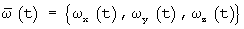 на интервале времени Δt, описывается интегралом Стилтьеса
на интервале времени Δt, описывается интегралом Стилтьеса
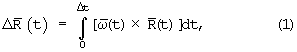
который представляется в виде
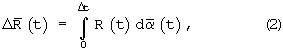
где 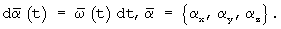
В проекциях на оси координат трехмерного пространства интеграл (2) преобразуется к выражениям
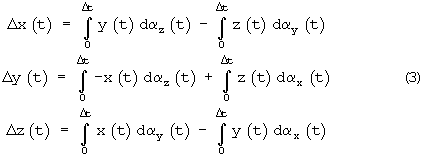
Каждый из интегралов системы (3) вычисляется по формуле трапеций
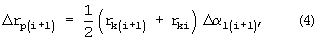
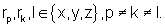
Неизвестные координаты rk(i+1), входящие в правые части приращений (4) заменяются их экстраполированными значениями
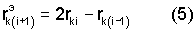
и окончательное выражение для приращений (4), то есть для каждого из интегралов (3) имеет вид
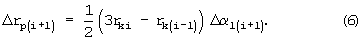
Точкам i-1, i, i+1,... соответствует значение времени ti-1, ti, ti+1,..., причем шаг Δt=const.
Суммируя попарно приращения интегралов (3), каждый из которых Δrр=Δr(k,l) вычисляется по алгоритму (6) с соответствующими индексами k и l, и присваивая интегралам оператор направления вращения ζl, получим окончательные выражения для приращения координат
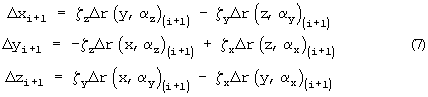
Соответственно, текущие значения координат вектора 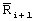 равны
равны
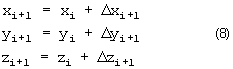
При соответствующем задании значений ζ1={+1,0-1} выполняются все возможные ортогональные преобразования вектора в трехмерном пространстве, включая обратные преобразования прямоугольных координат в сферические.
Для реализации вычислений по описанному алгоритму, включая обратные преобразования, устройство дополнительно содержит шесть регистров (с седьмого по двенадцатый), три сумматора-вычитателя (с седьмого по девятый), три элемента задержки, три трехвходовых сумматора-вычитателя и имеет шесть дешифраторов, причем третьи входы первого, второго и третьего регистров соединены соответственно с входами седьмого, восьмого и девятого регистров, выходы которых подключены соответственно к вычитающим входам первого, второго и третьего трехвходовых сумматоров-вычитателей, первый выход первого регистра соединен также через первый элемент задержки и непосредственно с суммирующими входами первого трехвходового сумматора-вычитателя, выход которого соединен с вторыми входами второго и третьего блоков умножения, первый выход второго регистра соединен также через второй элемент задержки и непосредственно с суммирующими входами второго трехвходового сумматора-вычитателя, выход которого соединен с вторыми входами первого и шестого блоков умножения, первый выход третьего регистра соединен также через третий элемент задержки и непосредственно с суммирующими входами третьего трехвходового сумматора-вычитателя, выход которого соединен с вторыми входами четвертого и пятого блоков умножения, вторые выходы четвертого, пятого и шестого регистров соединены соответственно с входами вторых операндов седьмого, восьмого и девятого сумматоров-вычитателей, выходы которых и входы первых операндов соединены соответственно с первыми входами и первыми выходами десятого, одиннадцатого и двенадцатого регистров, третьи выходы первого, второго и третьего регистров также соединены соответственно с входами первого, второго и третьего дешифраторов, вторые выходы десятого, одиннадцатого и двенадцатого регистров соединены соответственно с входами четвертого, пятого и шестого дешифраторов, выходы дешифраторов с первого по шестой соединены с одноименными входами блока управления, четвертый, пятый и шестой выходы которого соединены соответственно с входами оператора направления вращения седьмого, восьмого и девятого сумматоров-вычитателей, а третьи входы (вторые выходы) десятого, одиннадцатого и двенадцатого регистров и седьмой вход (выход) блока управления соединены двухнаправленными связями с интерфейсной шиной.
На чертеже представлена функциональная схема устройства, где обозначены:
- 1-6, 25, 26, 27, 31, 32, 33 - регистры;
- 7, 8, 9 - элементы задержки;
- 10, 11, 12 - трехвходовые сумматоры-вычитатели;
- 13-18, 28, 29, 30 - сумматоры-вычитатели;
- 19-24 - блоки умножения;
- 34-39 - дешифраторы;
- 40 - блок управления;
- 41-46 - внутренние связи выходов дешифраторов с одноименными входами блока управления;
- 47-52 - внутренние связи выходов блока управления с одноименными входами сумматоров-вычитателей;
- 53 - интерфейсная шина.
При преобразованиях координат по алгоритмам (7), (8) с учетом (6) устройство работает следующим образом. Перед началом вычислений (i=0) в регистры 1, 3, 6 и 25, 26, 27 записываются координаты хо, уо, zo и приращения углов Δαz, Δαу, αx, соответственно. На последующих итерациях при вычислениях в реальном времени перед каждым шагом (i+1) в регистры 25, 26, 27 заносятся текущие приращения углов Δαz(i+1), Δαy(i+1), Δαх(i+1). При преобразованиях в ускоренном масштабе времени (например, проигрывании маневра судна) и решении задач, не связанных со шкалой времени, приращения углов целесообразно задавать постоянными на всех итерациях до полной отработки углов αх, αу, αz.
Операторы направления вращения ζx (49), ζу (48) и ζz (47), задающие вид операции сумматоров-вычитателей 13-18, в данном случае принимаются равными "1", если вращение по соответствующему углу αх, αу, αz выполняется, и "0" в противном случае. Направление вращения по соответствующему углу αx, αy, αz определяется знаками приращений Δαz, Δαу, Δαx.
В текущей итерации координата xi из регистра 1 через элемент задержки 7 (2хi) поступает на первый суммирующий вход и непосредственно на второй суммирующий вход сумматора-вычитателя 10, а на его вычитающий вход из регистра 2 поступает координата xi-1. В результате получается величина (3хi-xi-1). Аналогичным образом на сумматорах-вычитателях 11 и 12 вычисляются величины (3уi-yi-1) и (3zi-zi-1). При параллельной обработке информации элементы задержки 7, 8, 9 исключаются и умножение на "2" операндов хi, yi, zi осуществляется соответствующей перекоммутацией разрядов между регистрами 1, 3, 6 и сумматорами-вычитателями 10, 11, 12 соответственно. На блоках умножения 19 и 20 вычисляются удвоенные значения алгоритма (6)
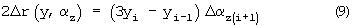
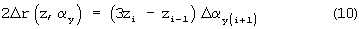
разность которых с операторами ζz и ζу дает удвоенное значение приращения Δxi+1 (первой строки алгоритма (7)). Умножение выражений (9) и (10) на коэффициент 1/2 осуществляется соответствующей перекоммутацией разрядов произведений между блоками умножения 19, 20 и сумматорами-вычитателями 13, 14 соответственно. На сумматоре-вычитателе 13 вычисляется величина
 ,
,
а на сумматоре-вычитателе 14 - координата
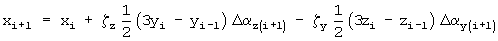 ,
,
записываемая в регистр 1 с одновременной перезаписью из регистра 1 в регистр 2 координаты хi.
Аналогичным образом в канале координаты у (регистры 3, 4, элемент задержки 8, сумматоры-вычитатели 11, 15, 16 и блоки умножения 21, 22) вычисляются значения yi+1, а в канале координаты z (регистры 5, 6, элемент задержки 9, сумматоры-вычитатели 12, 17, 18 и блоки умножения 23, 24) вычисляется значение zi+1.
Операторы вращения ζα z (50), ζα y (51), ζα x (52) при вращении вектора по текущим приращениям углов Δαz, Δαу, Δαx равны нулю. Сумматоры-вычитатели 28, 29, 30 и дешифраторы 34-39 не работают.
При повороте вектора на заданные углы αz, αу, αx их значения вносятся в регистры 31, 32, 33 соответственно. Для одновременного приведения вектора в конечную точку по всем трем углам шаги вращения задаются следующим образом. Максимальный шаг Δαl определяется из погрешности, обусловленной остаточным членом формулы трапеций, и с этим шагом отрабатывается максимальный угол αl. Шаги оставшихся двух углов будут равны
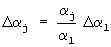 (j-1).
(j-1).
Шаги Δαl, l=[z,y,x} имеют знаки углов αl и заносятся соответственно в регистры 25, 26, 27. Операторы ζα l=1, если αl≠0 и на сумматорах-вычитателях вычисляются текущие значения отрабатываемых углов
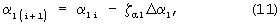
перезаписываемые в регистры 31, 32, 33. Вычисление текущих координат xi+1, уi+1, zi+1 выполняются по вышеприведенному описанию вращения вектора по текущим приращениям Δαl.
Дешифраторы 37, 38, 39 фиксируют нулевые значения соответствующих углов αl. При этом ζα l=0 и вращение завершается.
Приведенное описание вращения вектора остается неизменным при любых его преобразованиях. Частные случаи вращения задаются операторами ζα l. При ζx=ζα x=ζy=ζα y=ζz=ζα z=1, как описано выше, имеет место кватернионное преобразование. При задании двух любых операторов единицами, а третьего - нулю ось вращения кватернионного преобразования будет лежать в плоскости единичных операторов. При последующем задании нулевого оператора единичным, а единичных - нулями третий поворот выполняется в плоскости нулевых операторов вокруг оси единичного оператора. При последовательном задании одного из операторов единицей, а остальных - нулями будут выполнятся последовательные (плоские) повороты вокруг осей единичных операторов.
При обратных преобразованиях вычисляются модуль вектора и его угловое положение или его проекция на любую из плоскостей трехмерного пространства и угловое положение этой проекции в данной плоскости. Текущие координаты х, у, z вычисляются по алгоритмам (7) и (8) с учетом (9) и (10), а углы - по алгоритму (11), как описано выше. Отличие состоит лишь в задании операторов направления вращения ζl.
При задании ζх=ζу=0, а
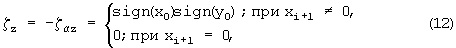
вектор вращается вокруг оси z (по углу αz). При исходных координатах х0, у0, z0 и достижении условия ζz=0 получим проекцию вектора на плоскость хоу
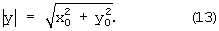
Одновременно задавая αz0=0 и шаг Δαz при ζαz=0 на сумматоре-вычитателе 28 (в регистре 31) получим угол между проекцией (13) и осью у: αz=(i+1)ζαzΔαz, равный
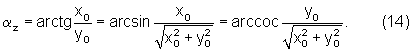
После выполнения описанного поворота проекция (13) совмещается с осью у, координата х=0, а z=z0. Задавая по аналогии с (12) операторы ζх, ζу и ζαх, ζαу, получим соответственно проекции вектора на плоскости yoz и хоу вида (13) и углы αx, αу вида (14).
После любого из описанных плоских вращений можно выполнить поворот в плоскости, образованной осью предыдущего вращения, и осью, с которой совмещена проекция предыдущего вращения. Например, задаваясь после получения преобразования (13), (14) операторами 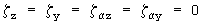 , а
, а 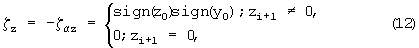
получим вращение вокруг оси х (по углу αх). При достижении условия ζх=0 получим проекцию исходного вектора 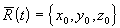 на ось z
на ось z
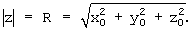
Одновременно, задавая αx0=0 и шаг Δαx,получим угол между вектором 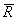 и осью z: αx=(i+1)ζαxΔαx, равный
и осью z: αx=(i+1)ζαxΔαx, равный
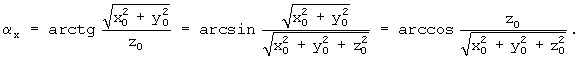
Окончание вращения по соответствующему углу (ζx=0, или ζу=0, или ζz=0) фиксируется соответствующими дешифраторами 34, 35, 36. Координаты х, у, z фиксируются в регистрах 1, 3, 5, а углы αz, αy, αx - в регистрах 31, 32, 33 соответственно.
Логика работы блока управления 40 (формирования операторов ζl, ζαl) такова:
- при отработке приращений Δαz, Δαу, Δαx
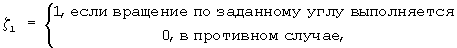
ζαl=0;
- при отработке углов αz, αy, αx
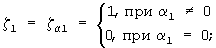
- при обратных преобразованиях
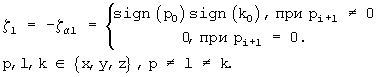
Вид преобразования (код операции) заносится в блок управления 40 с интерфейсной шины 53.
| название | год | авторы | номер документа |
|---|---|---|---|
| Вычислительное устройство | 1983 |
|
SU1167604A1 |
| Устройство преобразования координат | 1987 |
|
SU1472902A1 |
| Устройство для определения модуля трехмерного вектора | 1983 |
|
SU1142830A1 |
| Устройство для преобразования координат вектора в трехмерном пространстве | 1986 |
|
SU1403062A1 |
| Вычислительное устройство | 1983 |
|
SU1164696A1 |
| Устройство для вычисления модуля трехмерного вектора | 1989 |
|
SU1672442A1 |
| Устройство для выполнения преобразования координат | 1987 |
|
SU1462299A1 |
| Вычислительное устройство | 1988 |
|
SU1522196A1 |
| Устройство для вычисления эллиптических функций | 1987 |
|
SU1474641A2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1992 |
|
RU2029356C1 |
Изобретение относится к цифровой вычислительной технике и может быть использовано в качестве периферийного процессора для выполнения операций вращения вектора в трехмерном пространстве. Техническим результатом является повышение точности и увеличение шага вращения, а также возможность решения задач в реальном масштабе времени, что достигается за счет вращения вектора методом численного интегрирования по Стилтьесу по формуле трапеций. Указанный результат достигается за счет того, что устройство содержит двенадцать регистров, три элемента задержки, три трехвходовых сумматора-вычитателя, девять сумматоров-вычитателей, шесть блоков умножения, шесть дешифраторов, блок управления, интерфейсную шину. 1 ил.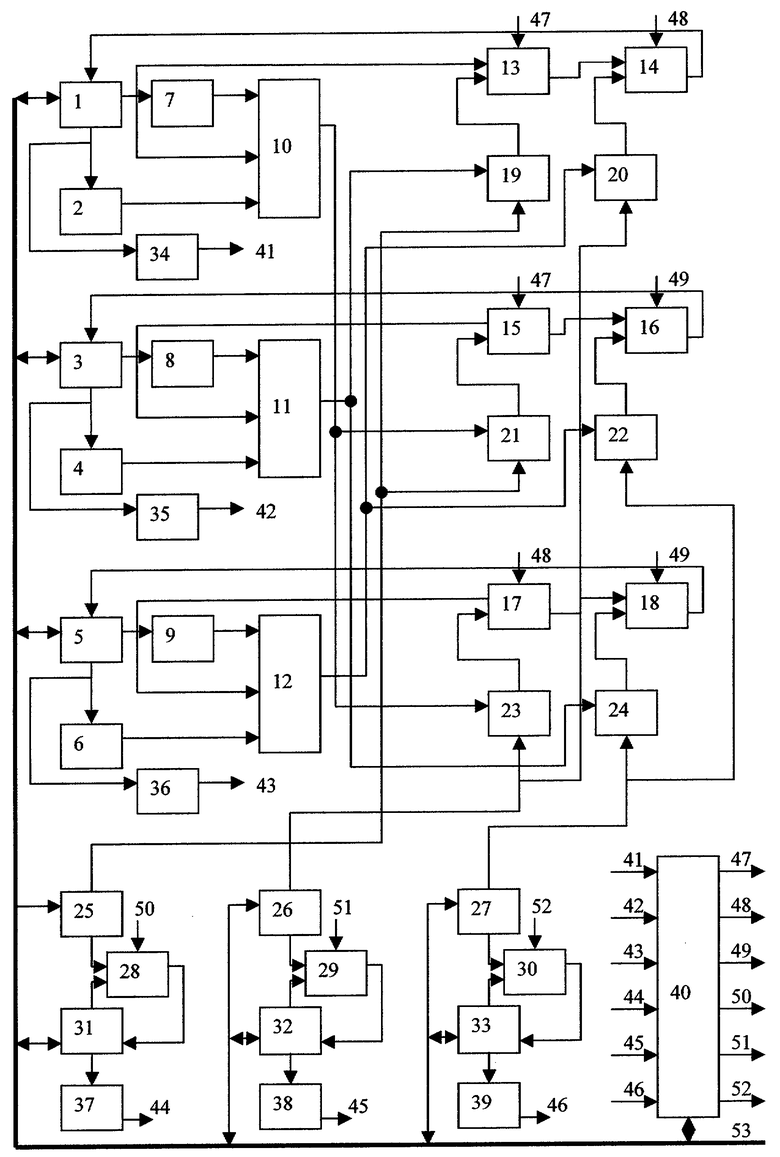
Арифметическое устройство, содержащее с первого по шестой регистры, с первого по шестой сумматоры-вычитатели, с первого по шестой блоки умножения и блок управления, причем первые выходы первого, второго и третьего регистров соединены со входами первых операндов соответственно первого, второго и третьего сумматоров-вычитателей, выходы которых соединены со входами первых операндов соответственно четвертого, пятого и шестого сумматоров-вычитателей, выходы которых соединены с первыми входами соответственно первого, второго и третьего регистров, первые выходы четвертого, пятого и шестого регистров соединены соответственно с объединенными попарно первыми входами первого и второго, третьего и четвертого, пятого и шестого блоков умножения, выходы которых подключены ко входам вторых операндов одноименных сумматоров-вычитателей, вторые входы (выходы) первого, второго и третьего регистров соединены двунаправленными связями с интерфейсной шиной, к которым подключены также входы четвертого, пятого и шестого регистров, а объединенные попарно входы оператора направления вращения первого и второго, третьего и четвертого, пятого и шестого сумматоров-вычитателей соединены соответственно с первым, вторым и третьим выходами блока управления, отличающееся тем, что в него введены шесть регистров (с седьмого по двенадцатый), три сумматора-вычитателя (с седьмого по девятый), три элемента задержки, три трехвходовых сумматора-вычитателя и шесть дешифраторов, причем третьи выходы первого, второго и третьего регистров соединены соответственно со входами седьмого, восьмого и девятого регистров, выходы которых подключены соответственно к вычитающим входам первого, второго и третьего трехвходовых сумматоров-вычитателей, первый выход первого регистра соединен также через первый элемент задержки и непосредственно с суммирующими входами первого трехвходового сумматора-вычитателя, выход которого соединен со вторыми входами второго и третьего блоков умножения, первый выход второго регистра соединен также через второй элемент задержки и непосредственно с суммирующими входами второго трехвходового сумматора-вычитателя, выход которого соединен со вторыми входами первого и шестого блоков умножения, первый выход третьего регистра соединен также через третий элемент задержки и непосредственно с суммирующими входами третьего трехвходового сумматора-вычитателя, выход которого соединен со вторыми входами четвертого и пятого блоков умножения, вторые выходы четвертого, пятого и шестого регистров соединены соответственно со входами вторых операндов седьмого, восьмого и девятого сумматоров-вычитателей, выходы которых и входы первых операндов соединены соответственно с первыми входами и первыми выходами десятого, одиннадцатого и двенадцатого регистров, третьи выходы первого, второго и третьего регистров также соединены соответственно со входами первого, второго и третьего дешифраторов, вторые выходы десятого, одиннадцатого и двенадцатого регистров соединены соответственно со входами четвертого, пятого и шестого дешифраторов, выходы дешифраторов с первого по шестой соединены с одноименными входами блока управления, четвертый, пятый и шестой выходы которого соединены соответственно со входами оператора направления вращения седьмого, восьмого и девятого сумматоров-вычитателей, а третьи входы (вторые выходы) десятого, одиннадцатого и двенадцатого регистров и седьмой вход (выход) блока управления соединены двухнаправленными связями с интерфейсной шиной.
| Устройство преобразования координат | 1987 |
|
SU1472902A1 |
Авторы
Даты
2006-01-20—Публикация
2004-04-21—Подача