Изобретение относится к области радиоизмерений, в частности к измерениям фазового сдвига сигнала в присутствии помех, и может быть использовано при разработке систем поиска и измерения параметров сигналов, искаженных интенсивными помехами, например, при разработке навигационных систем или помехоустойчивых систем передачи информации.
Известны цифровые корреляционные способы измерения фазового сдвига (см., например, Чмых М.К. Цифровая фазометрия. - М.: Радио и связь, 1993), в которых, как и в предлагаемом способе, исследуемый сигнал S преобразуют в цифровой сигнал и измеряют фазовый сдвиг с использованием цифрового опорного сигнала 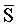 , кроме того, в таких способах вычисляют взаимокорреляционную функцию
, кроме того, в таких способах вычисляют взаимокорреляционную функцию 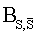 исследуемого сигнала и опорного сигнала, а также нормированную взаимокорреляционную функцию
исследуемого сигнала и опорного сигнала, а также нормированную взаимокорреляционную функцию
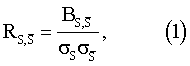
где σ2 s, 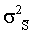 - дисперсии соответственно измеряемого и опорного сигналов. Далее фазовый сдвиг между опорным и измеряемым сигналом определяют по тригонометрической функции
- дисперсии соответственно измеряемого и опорного сигналов. Далее фазовый сдвиг между опорным и измеряемым сигналом определяют по тригонометрической функции
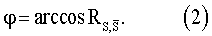
Существенным недостатком корреляционных способов измерения фазового сдвига является появление систематических погрешностей при исследовании сигнала, аддитивно искаженного белым шумом θ, когда
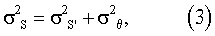
где σ2 s' - дисперсия исследуемого сигнала, не искаженного шумом, σ2 θ - дисперсия шума, искажающего исследуемый сигнал. Еще одним недостатком корреляционного способа измерения фазового сдвига является значительная зависимость результата измерения от уровня нелинейных искажений измеряемого сигнала.
Известен также способ измерения фазового сдвига по патенту РФ №2099721, кл. G 01 R 25/04, опубл. 20.12.1997, в котором, как и в предлагаемом способе, измеряемый сигнал дискретизируют, преобразуют в цифровой сигнал, используют опорный цифровой сигнал, суммируют коды сигналов и вычисляют фазовый сдвиг. Кроме того, в отличие от предлагаемого, в известном способе формируют группы из взятых последовательно k выборок дискретизированного цифрового измеряемого сигнала, с частотой дискретизации, уменьшенной в k раз, формируют одно- или многоразрядные цифровые сигналы, зависящие от группы k выборок дискретизированного цифрового измеряемого сигнала и номера группы k выборок цифровых синусной и косинусной составляющих опорного сигнала, которые поступают на суммирование их кодов. Однако при шумовой составляющей измеряемого сигнала, отличной от белого шума (в силу использования в качестве опорного сигнала синусных и косинусных колебаний, имеющих в некоторых условиях измерения отличную от нуля корреляцию с шумовой составляющей измеряемого сигнала), известный способ может иметь значительную погрешность измерения, особенно при большом отношении шум/сигнал.
Наиболее близким к предлагаемому является способ по Чмых М.К. Цифровая фазометрия, М.: Радио и связь, 1993, прототип, в котором как и в предлагаемом способе, исследуемый сигнал дискретизируют, преобразуют в цифровой сигнал, используют опорный цифровой сигнал. Путем суммирования попарных произведений кодов отсчетов исследуемого и опорного сигнала приближенно оценивают первое значение функционала правдоподобия
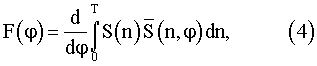
(являющегося производной от корреляционного интеграла опорного сигнала 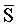 и исследуемого сигнала S), где T - длина отрезков сигналов
и исследуемого сигнала S), где T - длина отрезков сигналов 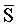 и S, для которых определяется степень коррелированности. Последовательно изменяя значение сдвига ϕ между цифровым опорным сигналом и цифровым исследуемым сигналом, добиваются нуля оценки функционала (4), соответствующего нулевому фазовому сдвигу между опорным и исследуемым сигналом. Значение ϕ*: F(ϕ*)=0 преобразуют в код фазового сдвига. Однако при коррелированности опорного сигнала и помех (особенно при большом отношении шум/сигнал) значение нуля оценки функционала (4) может не соответствовать фактическому нулевому сдвигу между опорным и исследуемым сигналом, что приводит к погрешности в измерении фазового сдвига.
и S, для которых определяется степень коррелированности. Последовательно изменяя значение сдвига ϕ между цифровым опорным сигналом и цифровым исследуемым сигналом, добиваются нуля оценки функционала (4), соответствующего нулевому фазовому сдвигу между опорным и исследуемым сигналом. Значение ϕ*: F(ϕ*)=0 преобразуют в код фазового сдвига. Однако при коррелированности опорного сигнала и помех (особенно при большом отношении шум/сигнал) значение нуля оценки функционала (4) может не соответствовать фактическому нулевому сдвигу между опорным и исследуемым сигналом, что приводит к погрешности в измерении фазового сдвига.
Задача помехоустойчивого измерения фазового сдвига является в настоящее время актуальной. Измерение фазового сдвига используется системами навигации с различными характеристиками измерения дальности и координат объектов. От таких систем требуется максимальная точность измерения при минимальной сложности и вычислительных затратах. Например, требования точности измерения координат и углового положения, предъявляемые к спутниковым системам глобальной навигации, определяют погрешность измерения, составляющую до 10-2 м. Как правило, измерения фазового сдвига сигнала системами навигации осуществляются в условиях помех различного характера и интенсивности. Различная природа помех (наводки от других радио систем и приборов, отражение от окружающих объектов, помехи в каналах связи) обуславливает сложный характер искажений исследуемого сигнала. Кроме того, отношение шум/сигнал чаще всего не известно, и его определение является дополнительной задачей. Перечисленные факторы затрудняют точное измерение фазового сдвига, основанное на сравнении измеряемого сигнала с эталонным сигналом с известным фазовым сдвигом. Объясняется это тем, что в случае коррелированности помехи и эталонного сигнала появляется смещение максимума функционала правдоподобия (или нуля его производной), являющегося критерием схожести измеряемого и эталонного сигнала в смысле фазового сдвига. Степень смещения максимума функционала правдоподобия, соответствующего корреляционному интегралу
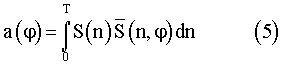
при S(n)=S'(n)+θ(n), где S'(n) - измеряемый сигнал, θ(n) - аддитивные помехи, a S(n) - наблюдения, зависит от второго слагаемого выражения
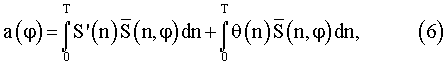
и определяется степенью коррелированности θ и 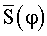 . При этом одним из вариантов снижения ошибок измерения может быть фильтрация наблюдаемого сигнала. Однако задача фильтрации помех при корреляции θ и S', отличной от нуля, является достаточно трудоемкой, малоэффективной и требует определения отношения шум/сигнал.
. При этом одним из вариантов снижения ошибок измерения может быть фильтрация наблюдаемого сигнала. Однако задача фильтрации помех при корреляции θ и S', отличной от нуля, является достаточно трудоемкой, малоэффективной и требует определения отношения шум/сигнал.
Предлагаемый способ измерения фазового сдвига в условиях интенсивных помех имеет следующие существенные признаки, сходные с прототипом. Исследуемый сигнал S дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов, представленных цифровыми кодами. Используют опорный цифровой сигнал 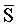 . Путем суммирования произведений кодов опорного и исследуемого сигнала получают первое значение оценки функционала правдоподобия
. Путем суммирования произведений кодов опорного и исследуемого сигнала получают первое значение оценки функционала правдоподобия
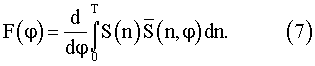
Последовательно изменяя значение сдвига ϕ между цифровым опорным сигналом и цифровым исследуемым сигналом, вычисляют значения оценок функционала правдоподобия (7). Требуемая точность измерения, в зависимости от знака функционала правдоподобия, достигается сдвигом опорного сигнала влево на m≥1 дискретных отсчетов, что соответствует увеличению значения ϕ (или вправо, что соответствует уменьшению значения ϕ). Для этого при сдвиге, например вправо, из начала опорного сигнала убирают m отсчетов и добавляют их в его конец. Если значение ϕ уменьшается, m отсчетов добавляют к началу опорного сигнала, убирая соответственно m отсчетов из его конца. Значение m фиксировано в течение всего времени измерения. При значении оценки функционала (4) равном нулю, сдвиг ϕ*: F(ϕ*)=0 преобразуют в код фазового сдвига, используя формулу
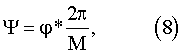
где М - число дискретных отсчетов в периоде исследуемого сигнала.
Во всех случаях, на которые распространяется испрашиваемый объем правовой охраны, повышение точности измерения фазового сдвига сигнала в присутствии интенсивных помех достигается тем, что в предлагаемом способе дополнительно используют оценку 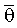 шумовой составляющей исследуемого сигнала θ, коррелированную с шумовой составляющей исследуемого сигнала θ. Оценку
шумовой составляющей исследуемого сигнала θ, коррелированную с шумовой составляющей исследуемого сигнала θ. Оценку 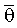 дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов. Отсчеты оценки
дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов. Отсчеты оценки 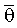 добавляют к отсчетам цифрового опорного сигнала перед вычислением очередного значения оценки функционала
добавляют к отсчетам цифрового опорного сигнала перед вычислением очередного значения оценки функционала
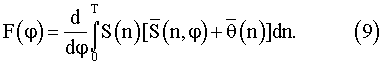
Процедуру добавления отсчетов 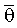 к отсчетам опорного сигнала производят для каждого очередного положения опорного сигнала, получаемого сдвигом на m отсчетов. При этом значения оценок функционала (9) получают как разности соседних значений сумм попарных произведений отсчетов исследуемого и каждого из получаемых положений опорного сигнала.
к отсчетам опорного сигнала производят для каждого очередного положения опорного сигнала, получаемого сдвигом на m отсчетов. При этом значения оценок функционала (9) получают как разности соседних значений сумм попарных произведений отсчетов исследуемого и каждого из получаемых положений опорного сигнала.
Благодаря тому, что 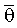 и θ коррелированны, при помехах θ, коррелированных с опорным сигналом
и θ коррелированны, при помехах θ, коррелированных с опорным сигналом 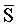 , и большом отношении шум/сигнал выборочная корреляционная функция сигналов S'+θ и
, и большом отношении шум/сигнал выборочная корреляционная функция сигналов S'+θ и 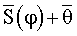 имеет максимум (ноль производной), соответствующий максимуму выборочной корреляционной функции S' и
имеет максимум (ноль производной), соответствующий максимуму выборочной корреляционной функции S' и 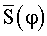 . При этом соответствие максимумов корреляционных функций для сигналов S'+θ и
. При этом соответствие максимумов корреляционных функций для сигналов S'+θ и 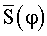 и сигналов S' и
и сигналов S' и 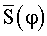 имеет место не всегда. Объясняется это тем, что при большом отношении шум/сигнал максимум выборочной корреляционной функции определяется в большой степени корреляцией θ и
имеет место не всегда. Объясняется это тем, что при большом отношении шум/сигнал максимум выборочной корреляционной функции определяется в большой степени корреляцией θ и 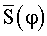 , которая может быть достаточно низкой при нулевом фактическом сдвиге исследуемого и опорного сигнала и, наоборот, высокой при не нулевом сдвиге. В случае же определения корреляции между сигналами S'+θ и
, которая может быть достаточно низкой при нулевом фактическом сдвиге исследуемого и опорного сигнала и, наоборот, высокой при не нулевом сдвиге. В случае же определения корреляции между сигналами S'+θ и 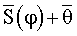 выборочная корреляционная функция имеет большие значения при всех ϕ (в силу большой корреляции
выборочная корреляционная функция имеет большие значения при всех ϕ (в силу большой корреляции 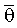 и θ), однако максимум значений достигается при максимуме корреляции S' и
и θ), однако максимум значений достигается при максимуме корреляции S' и 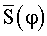 . Причем это выполняется и при разных уровнях
. Причем это выполняется и при разных уровнях 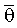 и θ, т.е. при неизвестном отношении шум/сигнал.
и θ, т.е. при неизвестном отношении шум/сигнал.
В частном случае реализации способа измерения фазового сдвига в условиях интенсивных помех исследуемый сигнал S дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов, оценку шума 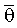 дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов. Используют опорный цифровой сигнал
дискретизируют, преобразуют в цифровой сигнал, содержащий N дискретных отсчетов. Используют опорный цифровой сигнал 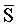 . На этапе измерения сначала (ϕ=0) к дискретным отсчетам опорного сигнала
. На этапе измерения сначала (ϕ=0) к дискретным отсчетам опорного сигнала 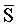 прибавляют дискретные отсчеты оценки шума
прибавляют дискретные отсчеты оценки шума 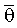 , получают первое значение суммы попарных произведений отсчетов исследуемого сигнала S и смеси
, получают первое значение суммы попарных произведений отсчетов исследуемого сигнала S и смеси 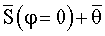 , значение ϕ увеличивают на m отсчетов (из начала опорного сигнала
, значение ϕ увеличивают на m отсчетов (из начала опорного сигнала 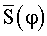 убирают m отсчетов и добавляют их в его конец), получают значение смеси
убирают m отсчетов и добавляют их в его конец), получают значение смеси 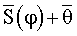 , находят второе значение суммы попарных произведений отсчетов исследуемого сигнала S и смеси
, находят второе значение суммы попарных произведений отсчетов исследуемого сигнала S и смеси 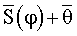 . Путем вычитания из предыдущего значения суммы попарных произведений отсчетов S и
. Путем вычитания из предыдущего значения суммы попарных произведений отсчетов S и 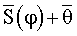 последующего значения суммы получают первое значение оценки функционала правдоподобия (9). В зависимости от ее знака значение ϕ увеличивают или уменьшают на m отсчетов. Изменение значения ϕ может производиться и независимо от знака текущего значения оценки функционала правдоподобия (9), тогда ϕ каждый раз увеличивают на m отсчетов, вычисляют следующую сумму попарных произведений отсчетов S и
последующего значения суммы получают первое значение оценки функционала правдоподобия (9). В зависимости от ее знака значение ϕ увеличивают или уменьшают на m отсчетов. Изменение значения ϕ может производиться и независимо от знака текущего значения оценки функционала правдоподобия (9), тогда ϕ каждый раз увеличивают на m отсчетов, вычисляют следующую сумму попарных произведений отсчетов S и 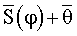 , а затем следующее значение оценки функционала правдоподобия (9). Процедуру повторяют до получения нуля оценки функционала правдоподобия (9). При этом нулю оценки функционала правдоподобия может соответствовать изменение ее знака с плюса на минус. Значение ϕ, соответствующее нулю оценки функционала правдоподобия, преобразуют в код фазового сдвига. Для обеспечения коррелированности
, а затем следующее значение оценки функционала правдоподобия (9). Процедуру повторяют до получения нуля оценки функционала правдоподобия (9). При этом нулю оценки функционала правдоподобия может соответствовать изменение ее знака с плюса на минус. Значение ϕ, соответствующее нулю оценки функционала правдоподобия, преобразуют в код фазового сдвига. Для обеспечения коррелированности 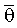 и θ, оценка шума
и θ, оценка шума 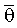 может быть получена, например, из частотного канала, смежного каналу связи измеряемого сигнала.
может быть получена, например, из частотного канала, смежного каналу связи измеряемого сигнала.
По мнению авторов, с учетом имеющихся у них сведений, предложенная совокупность существенных признаков не известна из уровня техники и соответствует критериям новизны и изобретательского уровня.
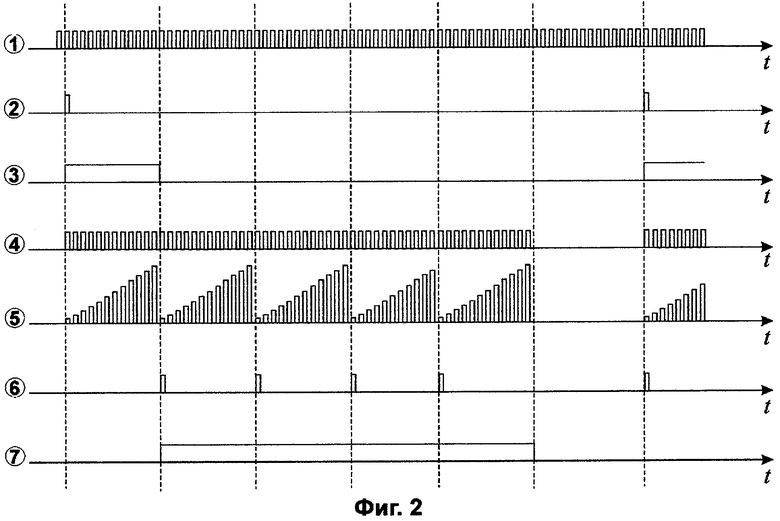
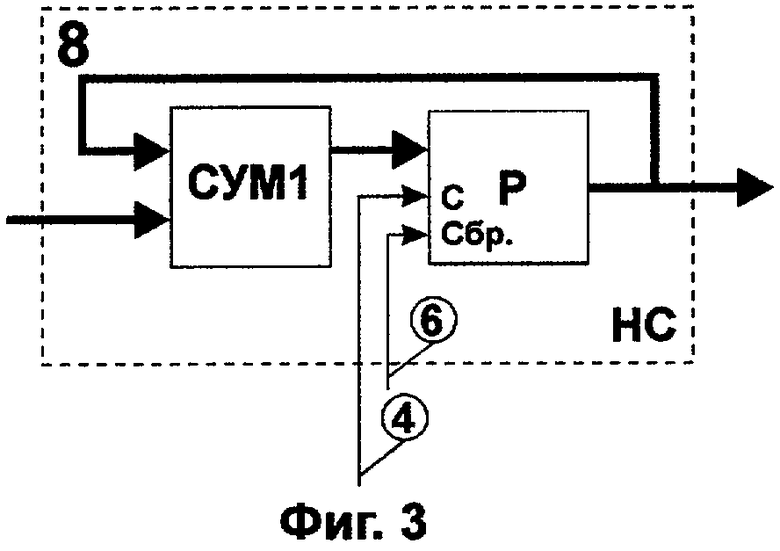
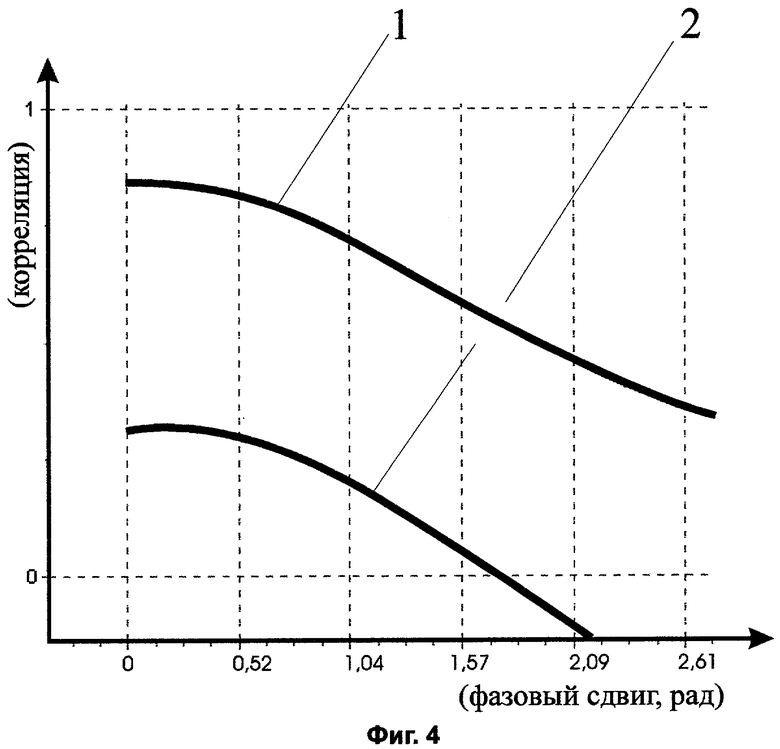
Изобретение поясняется графическими материалами: на фиг.1 представлена функциональная схема устройства измерения фазового сдвига в условиях интенсивных помех, осуществляющего заявляемый способ; на фиг.2 изображены диаграммы сигналов, используемых устройством измерения фазового сдвига в условиях интенсивных помех; на фиг.3 изображена функциональная схема накапливающего сумматора; на фиг.4 представлены графики зависимости корреляции опорного и измеряемого сигнала от их фазового сдвига.
Способ измерения фазового сдвига в условиях интенсивных помех поясняется реализующим его устройством. Работу устройства измерения фазового сдвига в условиях интенсивных помех можно подразделить на два этапа: первый - запись исследуемых сигналов, второй - определение фазового сдвига. Для начала работы первого этапа на первый вход блока управления (БУ) 12 подают импульс (см. сигнал 2 фиг.2), в результате чего триггер БУ 12 формирует сигнал записи (см. сигнал 3 фиг.2). Адреса кодов записи запоминающих устройств (ЗУ) 1, ЗУ 2 и ЗУ 3 формируются счетчиком БУ 12, который увеличивает значение адреса при каждом поступлении на его вход импульса со схемы И БУ 12 (см. сигнал 4 фиг.2) и обнуляет значение адреса, если оно равно значению адреса кода последнего отсчета исследуемого сигнала, поступающему на адресный вход БУ 12. При этом на один вход схемы И БУ 12 поступает синхросигнал (см. сигнал 1 фиг.2), а на другой вход - сигнал со схемы ИЛИ БУ 12, формирующийся при поступлении на вход схемы ИЛИ БУ 12 сигнала записи (см. сигнал 3 фиг.2). Коды отсчетов исследуемого сигнала, опорного сигнала и оценки шума записываются соответственно в ЗУ 1, ЗУ 2 и ЗУ 3. Для этого на информационные входы ЗУ 1, ЗУ 2 и ЗУ 3 поступают коды отсчетов исследуемого сигнала, опорного сигнала и оценки шума. В течение времени записи на первые управляющие входы ЗУ 1, ЗУ 2, ЗУ 3 поступает сигнал с выхода триггера БУ 12, разрешающий запись в ЗУ 1, ЗУ 2 и ЗУ 3 и обнуляющий задним фронтом счетчик 4. Одновременно на вторые управляющие входы ЗУ 1, ЗУ 2 и ЗУ 3 поступают синхроимпульсы с выхода схемы И БУ 12 (см. сигнал 4 фиг.2), разрешающие запись кодов отсчетов: исследуемого сигнала в ЗУ 1, опорного сигнала в ЗУ 2, оценки шума в ЗУ 3, при этом на адресные входы ЗУ 1, ЗУ 2, ЗУ 3 поступают адреса кодов со счетчика БУ 12 (см. сигнал 5 фиг.2).
После записи кодов отсчетов исследуемого сигнала, опорного сигнала и оценки шума в ЗУ 1, ЗУ 2 и ЗУ 3 переходят к измерению фазового сдвига. При этом ЗУ 1, ЗУ 2 и ЗУ 3 переводятся в режим чтения сигналом, поступающим на их первые управляющие входы с выхода триггера БУ 12, изменяющего фронт сигнала (см. сигнал 3 фиг.2), при поступлении на его первый вход первого импульса со схемы сравнения БУ 12 (см. сигнал 6 фиг.2), данный импульс также обнуляет счетчик БУ 12. Далее, счетчик БУ 12 при поступлении на его вход импульса со схемы И БУ 12 (см. сигнал 4 фиг.2) формирует адреса кодов чтения запоминающих устройств ЗУ 1, ЗУ 2 и ЗУ 3. При этом на второй вход схемы И БУ 12 поступает синхросигнал (см. сигнал 1 фиг.2), а на первый вход - сигнал со схемы ИЛИ БУ 12, формирующийся при поступлении на ее первый вход сигнала со схемы сравнения 10 (см. сигнал 7 фиг.2).
Измерение начинается с первого цикла. При поступлении синхроимпульса с выхода схемы И БУ 12 на вторые информационные входы ЗУ 1, ЗУ 2 и ЗУ 3, на выходы ЗУ 1 и ЗУ 3 поступают коды отсчетов с адресом, поступившим на их адресные входы с выхода счетчика БУ 12, а на выход ЗУ 2 - код отсчета с адресом, поступившим с выхода сумматора 7. При этом на первый вход сумматора 7 с выхода счетчика 4 поступает код сдвига опорного и измеряемого сигналов (при первом цикле измерения равный нулю), на второй вход сумматора 7 поступает адрес с выхода счетчика БУ 12. Коды отсчетов с выходов ЗУ 2 и ЗУ 3 поступают соответственно на первый и второй входы сумматора 6, с выхода которого сумма кодов отсчетов подается на второй вход умножителя 5, на первый вход которого поступает код отсчета с выхода ЗУ 1. На первый вход накапливающего сумматора (НС) 8 поступает код с выхода умножителя 5, запись кода происходит при поступлении на второй вход НС 8 синхроимпульса с выхода схемы И БУ 12 (см. сигнал 4 фиг.2). В течение одного этапа измерения с выхода схемы И БУ 12 синхроимпульсы подаются до тех пор, пока адрес на выходе счетчика БУ 12 не будет равным адресу, поступающему на адресный вход БУ 12. Когда адрес на выходе счетчика БУ 12 становится равным адресу, поступающему на адресный вход БУ 12 на выходе схемы сравнения БУ 12 формируется импульс, разрешающий запись кода суммы в регистр (Р) 9 и обнуляющий счетчик БУ 12 и НС 8. При этом с выхода НС 8 код суммы поступает на первые входы Р 9 и блока сравнения (БС) 10. На выход Р 9 поступает код суммы, находившийся в Р 9 до записи очередной суммы. Для первой суммы код равен нулю. Код с выхода Р 9 поступает на второй вход БС 10, на выходе которого образуется сигнал, отражающий результат сравнения сумм на первом и втором входах БС 10 (см. сигнал 7 фиг.2). Сигнал с выхода БС 10 поступает на первый вход схемы И 11 и, если на выходе БС 10 формируется перепад, является выходным сигналом для считывания кода сдвига на выходе устройства, при этом схемой ИЛИ БУ 12 прекращается формирование сигнала, пропускающего синхроимпульсы (см. сигнал 1 фиг.2) через схему И БУ 12. В противном случае (если на выходе БС 10 не образуется перепад) сигнал, формируемый схемой сравнения БУ 12 (см. сигнал 6 фиг.2), проходит через схему И 11 и поступает на первый вход счетчика 4, в результате чего код на выходе сумматора 7 увеличивается на единицу и происходит переход к следующему циклу измерения. При каждом цикле измерения со схемы И БУ 12 поступает число импульсов, равное числу отсчетов в измеряемом сигнале, а с выхода схемы сравнения БУ 12 один импульс (см. сигнал 6 фиг.2).
ЗУ 1, ЗУ 2, ЗУ 3, первый и второй сумматоры, накапливающий сумматор, схема сравнения 10 и схема сравнения БУ 12, схема И 11 и схема И БУ 12, 4 и счетчик БУ 12, схема ИЛИ БУ 12, а также регистр 9 и триггер БУ 12 могут быть реализованы, например, ИМС серии 555. Для реализации умножителя 5 могут быть использованы ИМС серии 1802. Накапливающий сумматор 8 может быть выполнен в соответствии с функциональной схемой, изображенной на фиг.3. Таким образом, предлагаемый способ удовлетворяет критерию промышленной применимости.
Устройство, реализующее заявляемый способ измерения фазового сдвига в условиях интенсивных помех, было смоделировано на ПЭВМ в среде Delphi. Испытания проходили в следующих экспериментальных условиях: в качестве измеряемого сигнала использовалось синусоидальное колебание аддитивно зашумленное моделированным шумом. Шум моделировался авторегрессионной моделью вида
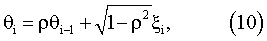
где ρ=0,7, θ0=0, ξi - равномерно распределенные случайные величины с нулевым математическим ожиданием и единичной дисперсией; отношение шум/сигнал 5 дБ. В качестве оценки шума использовался сигнал, также смоделированный моделью (10). Отношение (оценка шума)/(шум в сигнале) было выбрано равным 1 дБ. На фиг.4. приведены характерные зависимости корреляции опорного и измеряемого сигнала от их фазового сдвига. Кривая 1 соответствует корреляционной функции заявляемого способа, кривая 2 - корреляционной функции способа прототипа. Значение сдвига, соответствующее максимуму корреляционной функции, в каждом опыте считалось результатом измерения фазового сдвига. Как показала опытная проверка, заявляемый способ обеспечил следующие результаты: доверительный интервал абсолютной погрешности измерения фазового сдвига (-0,0028; 0,0028) рад при доверительной вероятности 0,976. Смоделированный и испытанный в тех же условиях способ прототип при доверительной вероятности 0,976 показал доверительный интервал абсолютной погрешности измерения фазового сдвига (-0,0374; 0,0374) рад.
Апробация подтвердила достижение технического результата - повышение точности измерения фазового сдвига сигнала в присутствии интенсивных помех.
Способ может быть использован при разработке навигационных систем или помехоустойчивых систем передачи информации. Используют опорный сигнал, очередное положение которого относительно исследуемого получают путем сдвига опорного сигнала, например, вправо. Отсчеты опорного сигнала суммируют с отсчетами оценки шумовой составляющей исследуемого сигнала, коррелированной с шумовой составляющей исследуемого сигнала. Вычисляют оценку функционала правдоподобия, являющегося производной от корреляционного интеграла исследуемого и опорного сигналов. Операции сдвига опорного сигнала, суммирования его отсчетов с отсчетами оценки шума и вычисления значения оценки функционала правдоподобия повторяют до получения нуля оценки функционала правдоподобия. Значение сдвига между опорным и исследуемым сигналом, соответствующее нулю оценки функционала правдоподобия, преобразуют в код фазового сдвига. Способ позволяет снизить погрешность определения фазового сдвига в условии помех, коррелированных с исследуемым сигналом, при низком отношении сигнал/шум. 1 з.п. ф-лы, 4 ил.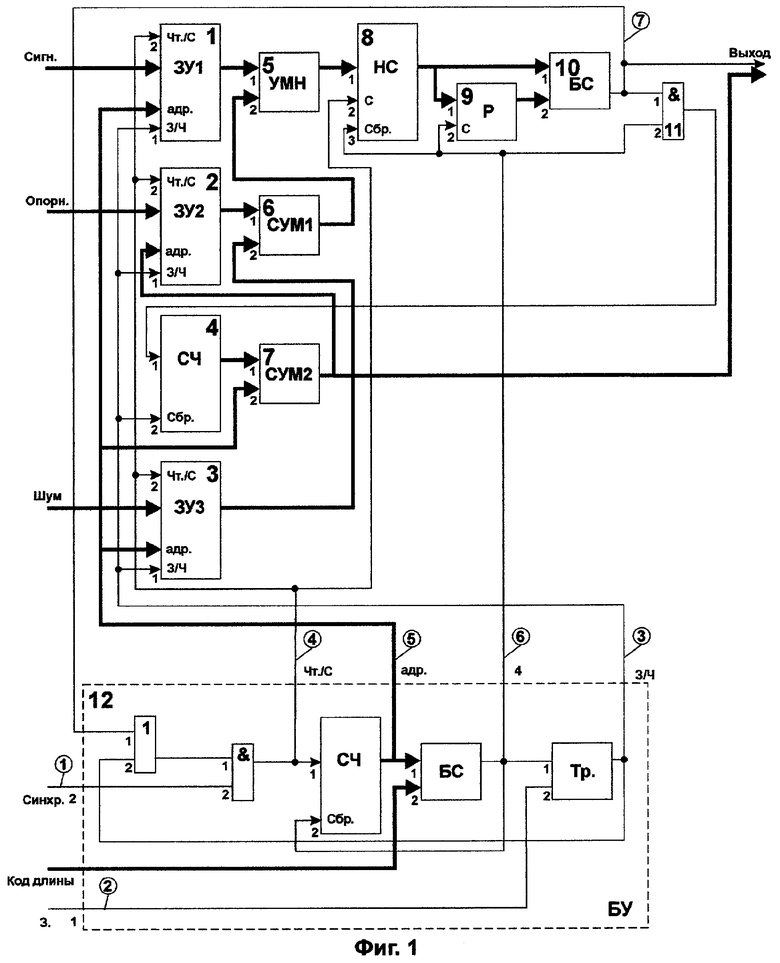
| ЧМЫХ М.К | |||
| Цифровая фазометрия | |||
| - М.: Радио и связь, 1993, с.143 | |||
| СПОСОБ ИЗМЕРЕНИЯ ФАЗОВОГО СДВИГА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1996 |
|
RU2099721C1 |
| US 5847558 А, 08.12.1998. | |||
Авторы
Даты
2006-08-20—Публикация
2005-05-11—Подача