Изобретение относится к способам выбора режимов резания и может быть использовано в производстве при разработке технологических процессов. Способ включает определение динамической податливости упругой системы станка при помощи электромагнитного вибратора и виброзаписывающей аппаратуры с последующим построением математической модели упругой системы в виде суммы колебательных звеньев и определением устойчивости и критической ширины фрезерования.
Технический результат - выбор режимов резания, исходя из условия устойчивости процесса резания.
Сущность изобретения заключается в следующем: строится амплитудно-фазочастотная характеристика (АФЧХ) системы станок-приспособление-инструмент-заготовка при заданном отношении ширин торцевой и цилиндрической части концевой фрезы. Затем с учетом параметров этой АФЧХ вычисляется ширина фрезерования.
Динамическая характеристика процесса резания для i-го зуба фрезы в линейной постановке может быть записана в следующем виде (см. Кудинов В.А. Динамика станков / М.: Машиностроение, 1966. - 358 с.):
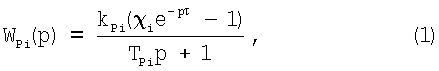
где kpi - коэффициент резания на i-м зубе фрезы; χi - коэффициент перекрытия; 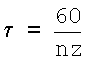 - время поворота фрезы на один зуб (здесь n - частота вращения фрезы; z - число зубьев фрезы); р - параметр преобразования Лапласа;
- время поворота фрезы на один зуб (здесь n - частота вращения фрезы; z - число зубьев фрезы); р - параметр преобразования Лапласа; 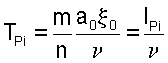 - постоянная времени стружкообразования, зависящая от скорости резания (здесь
- постоянная времени стружкообразования, зависящая от скорости резания (здесь 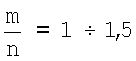 - постоянный коэффициент; а0 - заданная толщина срезаемого слоя или подача на зуб;
- постоянный коэффициент; а0 - заданная толщина срезаемого слоя или подача на зуб; 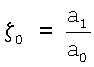 - усадка стружки; ai - толщина стружки; ν - скорость резания; lpi - некоторый путь движения резца, определяющий формирование силы резания). При необходимости учет нелинейности можно осуществить согласно методике, изложенной в работе Санкин Ю.Н., Н.Ю.Санкин Устойчивость фрезерных станков при нелинейной характеристике процесса резания // СТИН, 2002. - №6, - с.24-27.
- усадка стружки; ai - толщина стружки; ν - скорость резания; lpi - некоторый путь движения резца, определяющий формирование силы резания). При необходимости учет нелинейности можно осуществить согласно методике, изложенной в работе Санкин Ю.Н., Н.Ю.Санкин Устойчивость фрезерных станков при нелинейной характеристике процесса резания // СТИН, 2002. - №6, - с.24-27.
Рассмотрим процесс фрезерования концевой фрезой, когда основной съем материала осуществляется цилиндрической частью фрезы при получистовой/чистовой обработке заготовок (Фиг.1).
На Фиг.1 αцi - угол наклона силы Рцi к обрабатываемой плоскости; βцi - угол между горизонтальной проекцией Рxyцi и осью xцi системы координат, связанной с i-м зубом фрезы; ψцi - угол, определяющий текущее положение цилиндрической части i-го зуба относительно осей X, Y, Z неподвижной системы координат с центром 0 на оси фрезы; αmi - угол наклона силы Рmi к обрабатываемой плоскости; βmi - угол между горизонтальной проекцией Pxymi и осью хmi; ψmi - угол, определяющий текущее положение торцевой части i-го зуба относительно осей X, Y, Z; ε - угол винтовой канавки;
ψцi=ψmi-Δψi,
где Δψi - разность углов, определяющих положение зубьев цилиндрической и торцевой части фрезы, относительно единой системы координат.
 ,
,
где D - диаметр фрезы, Вц - предполагаемая ширина фрезерования.
Проекции силы Рцi на оси xцi уцi, zцi определяются следующим образом:
Рxцi=P0 цiCosαцi·Cosβцi;
Рyцi=-Р0 цiCosαцi·Sinβцi;
Pzцi=P0 цiSinαцi.
Проекции силы Рцi на оси X, Y, Z будут:
РXцi=Р0 цiCosαцi·Sin(βцi+ψцi);
РYцi=Р0 цiCosαцi·Cos(βцi+ψцi);
PZцi=Р0 цiSinαцi.
Орт силы Рцi:
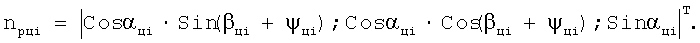
Орт нормали к поверхности резания цилиндрической частью зуба:

Учитывая, что  получаем:
получаем:
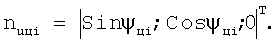
Проекции силы Рmi на оси xmi, ymi, zmi:
Pxmi=P0 miCosαmi·Cosβmi;
Pymi=-P0 miCosαmi·Sinβmi;
Pzmi=P0 miSinαmi.
Проекции силы Pmi на оси X, Y, Z будут:
PXmi=P0 miCosαmi·Sin(βmi+ψmi);
PYmi=P0 miCosαmi·Cos(βmi+ψmi);
PZmi=P0 miSinαmi.
Орт силы Pmi:
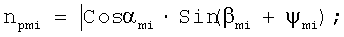
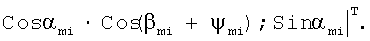
Орт нормали к поверхности резания торцевой частью зуба:
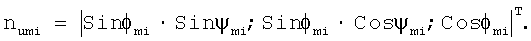
Так как φmi=0, получаем:
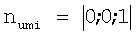
Суммарная сила резания записывается следующим образом:

где 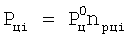 ,
, 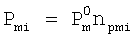
Модуль силы резания на i-м зубе:
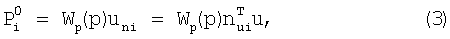
где uni - проекция относительного перемещения между резцом и заготовкой на нормаль к поверхности резания, u - относительное перемещение между фрезой и заготовкой от действия всех сил резания на зубьях.

где W(p) - суммарная передаточная функция несущей системы станка и заготовки.
Учитывая (3), выражение (2) можно представить в виде:
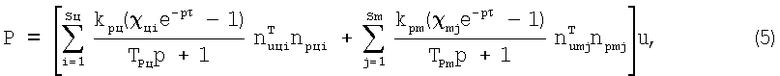
где kpц=kBц - коэффициент резания для цилиндрической части зуба; kmц=kBm - коэффициент резания для торцевой части зуба; Вц, Вm - ширины срезаемого слоя соответственно цилиндрической и торцевой частью фрезы; k - коэффициент удельной силы резания.
Отсюда:
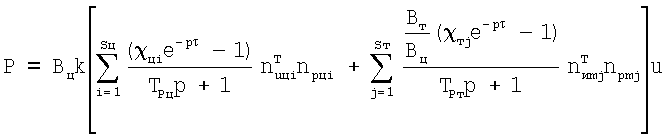 .
.
Принимая характеристику резания одинаковой на всех зубьях, получим:
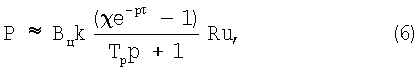
где 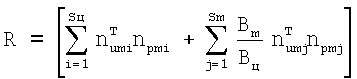 - матрица коэффициентов направления, Тр - постоянная времени стружкообразования, χ - общий коэффициент перекрытия, обычно близкий по значению к единице.
- матрица коэффициентов направления, Тр - постоянная времени стружкообразования, χ - общий коэффициент перекрытия, обычно близкий по значению к единице.
Подставив (6) в (4), получим:

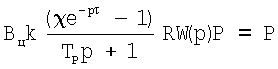
Так как Р=Р0np (np - орт силы Р), то:
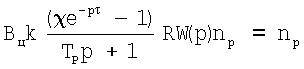
Умножим скалярно обе части равенства на nр.
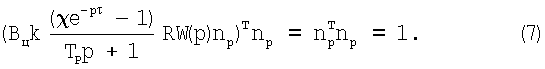
При этом данное равенство возможно только тогда, когда левая часть принимает вещественное значение, при этом р=iω.
Из равенства (7) получим ширину срезаемого слоя на цилиндрической части при фиксированном отношении Вц/Вm:
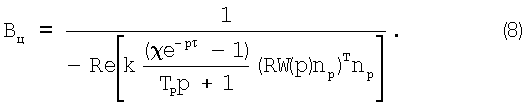
Дальнейший расчет осуществляется согласно методике, описанной в Справочнике технолога - машиностроителя. Т.2. Изд. 4-е / Под ред. А.Г.Косиловой, Р.К.Мещерякова. М.: Машиностроение, 1985, 496 с.
Рассмотрим расчет критической ширины срезаемого слоя на примере получистовой обработки детали «балка пола» самолета ТУ-204, когда в процессе резания участвуют боковая и торцевая часть фрезы.
Конечноэлементная модель секции обрабатываемой заготовки, построенная согласно методике, изложенной в работе Санкин Ю.Н., С.А.Явкин. Метод конечных элементов в задаче нестационарных колебаний тонких плит при внезапном нагружении // Вестник УлГТУ, 2004. - №2. - С.23-27.
Конечноэлементная модель рассматриваемой секции представлена на Фиг.2. АФЧХ заготовки представлена на Фиг.3. Ввиду того, что податливость заготовки в направлении ОХ существенно ниже, чем податливость в других направлениях, податливость станка ФП-9, на котором обрабатывается заготовка, во всех 3-х направлениях не менее чем на 2 порядка ниже, то в расчете составляющей динамической податливости по направлению оси х пренебрегаем (см. Санкин Ю.Н., С.А.Явкин. Устойчивость обработки тонкостенных заготовок на фрезерных станках // СТИН, 2005. - №5. - С.3-5.).
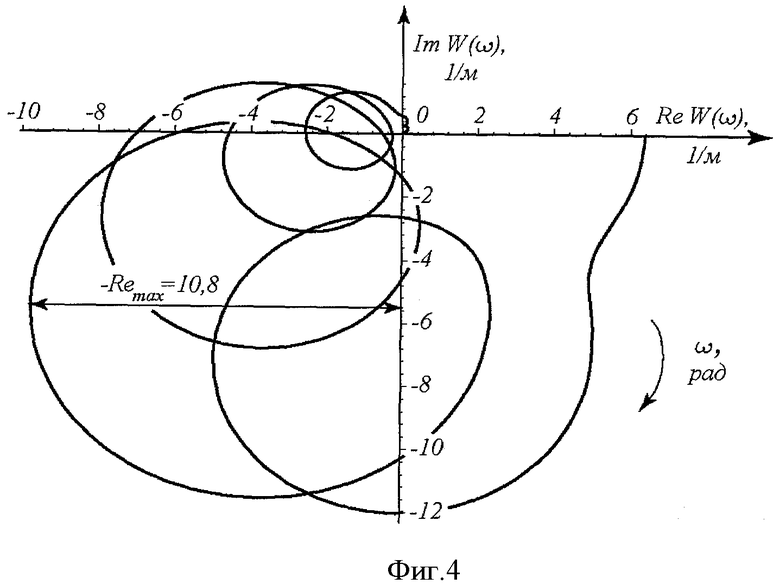
АФЧХ разомкнутой системы (знаменатель выражения (8)) приведена на Фиг.4. При этом полагалось отношение 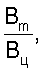 равное 0,34, где Вm=11,2 мм; Вц=33,5 мм.
равное 0,34, где Вm=11,2 мм; Вц=33,5 мм.
Результаты расчета показали, что при такой толщине среза устойчивым является режим, когда ширина среза не превышает 46 мм.


Способ заключается в том, что определяют динамическую податливость упругой системы станка с использованием электромагнитного вибратора и виброзаписывающей аппаратуры с последующим построением их математической модели в виде совокупности колебательных звеньев и определяют критическую ширину фрезерования по приведенной формуле. Технический результат: выбор режимов резания, исходя из устойчивости процесса резания. 4 ил.
Способ определения критической ширины фрезерования концевой фрезой, заключающийся в том, что определяют динамическую податливость упругой системы станка с использованием электромагнитного вибратора и виброзаписывающей аппаратуры с последующим построением их математической модели в виде совокупности колебательных звеньев и определяют критическую ширину фрезерования Вц по формуле:
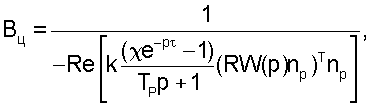
где k - коэффициент удельной силы резания;
χ - коэффициент перекрытия;
р - параметр преобразования Лапласа;
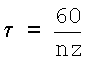 - время поворота фрезы на один зуб, где n - частота вращения фрезы, z - число зубьев фрезы;
- время поворота фрезы на один зуб, где n - частота вращения фрезы, z - число зубьев фрезы;
 - постоянная времени стружкообразования, зависящая от скорости резания, где
- постоянная времени стружкообразования, зависящая от скорости резания, где 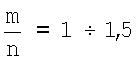 - постоянный коэффициент;
- постоянный коэффициент;
W(p) - суммарная передаточная функция несущей системы станка и заготовки;
а0 - заданная толщина срезаемого слоя или подача на зуб;
 - усадка стружки;
- усадка стружки;
a1 - толщина стружки;
v - скорость резания;
lр - некоторый путь движения зуба фрезы, определяющий формирование силы резания;
np - орт силы резания;
R - матрица коэффициентов направления, которую рассчитывают по формуле
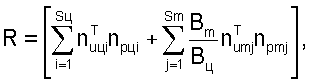
где Вц, Вm - ширина фрезерования соответственно цилиндрической и торцевой частей фрезы;
nuцi - орт нормали к поверхности резания цилиндрической частью зуба;
numj - орт нормали к поверхности резания торцевой частью зуба;
npцi - орт силы резания цилиндрической части зуба;
npmj - орт силы резания торцевой части зуба;
Sц, Sm - количество зубьев на цилиндрической и торцевой частях фрезы соответственно.
| СПОСОБ УПРАВЛЕНИЯ ТРАЕКТОРИЕЙ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ИНСТРУМЕНТА И ОБРАБАТЫВАЕМОЙ ДЕТАЛИ | 0 |
|
SU240452A1 |
| СПОСОБ УПРАВЛЕНИЯ УРОВНЕМ КОЛЕБАНИЙ В МЕТАЛЛОРЕЖУЩИХ СТАНКАХ | 1996 |
|
RU2111091C1 |
| СПОСОБ ПОСТРОЕНИЯ ДИНАМИЧЕСКОЙ МОДЕЛИ ЭКВИВАЛЕНТНОЙ УПРУГОЙ СИСТЕМЫ МЕТАЛЛОРЕЖУЩЕГО СТАНКА В ЗОНЕ РЕЗАНИЯ | 1996 |
|
RU2130598C1 |
| US 3744353 A, 10.07.1973. | |||
Авторы
Даты
2009-03-20—Публикация
2007-03-20—Подача