Настоящее изобретение относится прежде всего к способу моделирования для временной характеристики состояния объема стали с помощью вычислительной машины,
- причем объем стали моделируют в вычислительной машине с помощью множества элементов объема,
- причем состояние объема стали в определенный момент времени содержит для каждого из элементов объема величины, которые являются характеристическими для энтальпии, имеющейся в этот момент времени в соответствующем элементе объема, и для относительных содержаний, в которых сталь присутствует в этот момент времени в соответствующем элементе объема в фазах аустенит, феррит и цементит,
- причем вычислительная машина для по меньшей мере одного из элементов объема определяет временную характеристику характеристических величин путем решения уравнения теплопроводности и уравнения фазового превращения.
Затем настоящее изобретение относится к носителю данных с запомненной на носителе данных компьютерной программой для осуществления подобного способа моделирования и к вычислительной машине с массовым накопителем, в котором отложена компьютерная программа так, что вычислительная машина при вызове компьютерной программы осуществляет подобный способ моделирования.
Наконец, настоящее изобретение относится еще к устройству воздействия для воздействия на температуру действительного объема стали, в частности, участку охлаждения, который управляется вычислительной машиной, а также к стали, которая прошла через такое устройство воздействия.
Подобные способ моделирования и соответствующие объекты известны. Например, делается ссылка на DE-B4-10129565 и, в частности, на DE-B3-10251716 заявителя.
В процессе автоматизации обработки стали моделирование температуры металла имеет особенное значение. При этом является принципиально несущественным, происходит ли моделирование температуры металла относительно объема стали, который находится в печи, или, например, проходит через процесс прокатки или процесс охлаждения. Фазовые превращения, которые могут появляться в металлах также внутри твердой фазы, затрудняют при этом вычисления с уравнением теплопроводности. Если является необходимым точный расчет, в определение временной характеристики состояния объема стали должно привлекаться фазовое превращение.
В частности, в стали фазовое превращение происходит только замедленно, поскольку появляющиеся температурные изменения являются таким большими, что превращение не может следовать за температурным изменением. Часто это вызывается легирующими элементами, которые добавлены к стали.
Причина для этого замедленного превращения - в примере стали - лежит в наличии в стали углерода. Так как углерод хотя относительно хорошо растворяется, например, в аустените, однако только в очень малой, практически пренебрежимой степени в феррите. Тем самым фазовые превращения аустенита в феррит замедляются, поскольку углерод в аустените сначала должен продиффундировать прежде, чем может образоваться феррит.
Аустенит может также еще образовывать другую фазу, а именно цементит. Цементит образует вместе с ферритом смешанную фазу, которую также обозначают как перлит. На первый взгляд представляется совершенно не ясным и почти безнадежным, корректно учитывать такой сложный процесс при уравнении теплопроводности.
В уровне техники прежде всего использовались следующие решения:
- Моделирование фазового превращения сильно упрощалось.
- Моделирование фазового превращения производили в предварительном расчете с приближенной температурной характеристикой. Затем фазовое превращение фиксировали. Экзотермические процессы при фазовом превращении учитывались с помощью источников тепла в уравнении теплопроводности Фурье. Эта связь фазового превращения в форме источников тепла с уравнением теплопроводности Фурье однако решает проблему только мнимо. Так как более точное рассмотрение показывает, что подход является физически ошибочным. Это видно, в частности, из того, что источники тепла должны параметрироваться отдельно, что при корректном решении не требуется.
Из DE-B4-10129565 известен уже значительно улучшенный подход, при котором уравнение теплопроводности составлено корректно. Уравнение фазового превращения является справедливым только для двухфазной системы (например, системы аустенит-феррит). Расширение на трехфазную систему (например, систему аустенит-феррит-цементит) не является возможным без проблем. Также появляющиеся там в уравнении теплопроводности величины теплопроводность и температура зависят только от энтальпии и относительного содержания фаз. Зависимость от относительного содержания фаз при этом является достаточной, так как на основе произведенного там рассмотрения чисто двухфазной системы второе относительное содержание фаз получается в неявном виде из обстоятельства, что сумма обоих относительных содержаний фаз должна быть равна единице.
В также упомянутой уже DE-B3-10251716 теплопроводность и температура являются функциями, которые зависят от энтальпии и относительных содержаний всех рассмотренных фаз. В случае трехфазной системы, например, системы аустенит-феррит-цементит, упомянутой в DE-B3-10251716, теплопроводность и температура являются таким образом функциями, которые зависят от энтальпии и всех фаз.
Попытки реализации способов обоих названных последними описаний хотя и приводят к значительно лучшим результатам, чем до сих пор. Однако, тем не менее все же появлялись отклонения между поведением объема стали, определенным в соответствии со способом моделирования, и фактическим поведением соответствующего действительного объема стали.
Из специальной статьи ”Компьютерное моделирование процесса закалки стали с использованием модели многофазного преобразования” авторов Тамас Рети и др., появившейся в Computational Materials Science 22 (2001), с.261 до 278, известно, что фазовое превращение аустенита в феррит, перлит и бейнит зависит от концентрации углерода в аустените. В этой статье концентрацию углерода в фазе аустенит устанавливают равной концентрации углерода в рассмотренной стали в целом.
Задача настоящего изобретения состоит в создании способа моделирования названного выше вида и вместе с тем соответствующих объектов, посредством которых является возможным качественно более высокое моделирование объема стали, причем одновременно необходимые для этого затраты машинного времени поддерживаются малыми.
Задача решается за счет того, что соответственно одной из характеристических величин является локально неизменная внутри соответствующего элемента объема средняя концентрация внедренных элементов в фазе аустенит соответствующего элемента объема, относительное содержание фазы аустенит в соответствующем элементе объема и энтальпия соответствующего элемента объема так, что относительное содержание фаз феррит и цементит в соответствующем элементе объема являются величинами, выведенными из характеристических величин. Внедренными элементами являются при этом элементы, которые занимают при поглощении в железе междоузельное положение. Примерами внедренных элементов являются углерод и азот. Противоположностью к внедренным элементам являются замещающие элементы. Эти элементы замещают атомы железа в их положениях в узлах решетки. Примерами замещающих элементов являются марганец и никель.
В действительности концентрация внедренных элементов в фазе аустенит является локально зависимой. Точнее, в рамках способа моделирования следовало бы поэтому учитывать точное распределение внедренных элементов в фазе аустенит. Этот образ действий приводит однако к экстремально высоким затратам машинного времени на вычисления, однако остается почти без влияния на качество моделирования.
При соответствующем изобретению образе действий не требуется применять в явном виде относительные содержания фаз в качестве параметров. Поскольку, если pA, pF и pZ обозначают относительные содержания фаз аустенит, феррит и цементит в соответствующем элементе объема, справедливо соотношение
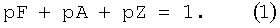
Если далее cA, cF и cZ обозначают соответствующую, локально неизменную внутри соответствующего элемента объема среднюю концентрацию внедренных элементов в фазах аустенит, феррит и цементит в соответствующем элементе объема, а с общее относительное содержание внедренных элементов в соответствующем элементе объема, далее справедливо
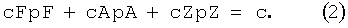
Общее относительное содержание с внедренных элементов в стали при этом можно без проблем рассматривать в качестве постоянной. Так как далее средняя концентрация cF внедренных элементов в фазе феррит, как известно, приблизительно равна нулю, в уравнении 3 ею можно практически пренебречь. Также значение cZ для цементита является известной постоянной, а именно 0,25. Уравнение 3 можно поэтому упростить до
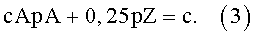
В уравнениях 1 и 3 поэтому имеются пять величин, а именно относительные содержания pA, pF и pZ фаз аустенит, феррит и цементит, а также локально неизменная средняя концентрация cA внедренных элементов в фазе аустенит и общее относительное содержание с внедренных элементов в стали. При задании трех независимых из этих пяти величин тем самым сразу же и непосредственно являются тем самым однозначно определимыми две остальные величины.
В частности, на основе уравнения 3 сразу же получается относительное содержание pZ фазы цементит
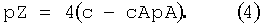
На основе уравнения 1 тем самым сразу же определено также относительное содержание pF феррита в по меньшей мере одном элементе объема.
С помощью такого образа действий является возможным, в частности, определение относительных содержаний фаз pF и pZ фаз феррит и цементит в соответствующем элементе объема и тем самым определение всех существенных входных параметров, без необходимости выполнения операций деления. Избежание операций деления имеет, в частности, преимущество возможность исключения высоких затрат машинного времени для выполнения операций деления и также исключение необходимости предусматривать особое регулирование для случая, что делитель принимает значение нуль. Далее, избегаются неточности, которые, с другой стороны, получались бы за счет того, что в частном случае нужно выполнять деление на малые значения.
Тем не менее является простым образом возможным, что вычислительная машина в рамках решения уравнения теплопроводности и/или в рамках решения уравнения фазового превращения определяет для по меньшей мере одного элемента объема зависимость между энтальпией и температурой и при этом учитывает, что зависимость между энтальпией и температурой зависит от концентрации внедренных элементов в фазе аустенит соответствующего элемента объема.
В уровне техники до сих пор тем не менее пытались определять зависимость между энтальпией и температурой на основе уравнения

причем eA, eF и eZ являются функциями, которые описывают соответственно зависимость между энтальпией и температурой в по меньшей мере одном элементе объема для случая, что элемент объема имеется исключительно в фазе аустенит, феррит или, соответственно, цементит. Этот образ действий хотя и является корректным по подходу, однако он не учитывает того, что зависимость между энтальпией и температурой в фазе аустенит зависит также от концентрации внедренных элементов в фазе аустенит. В противоположность этому в случае настоящего изобретения можно учитывать эту зависимость без проблем в функции eA.
Предпочтительным образом вычислительная машина уже до моделирования временной характеристики состояния объема стали определяет для множества значений характеристических величин зависимость между энтальпией и температурой и запоминает ее в виде поля опорных точек. Так как за счет этого является возможным, что вычислительная машина в рамках моделирования временной характеристики состояния объема стали определяет температуру, имеющуюся в по меньшей мере одном элементе объема, на основании поля опорных точек. Поскольку за счет этого могут быть значительно уменьшены затраты машинного времени для решения уравнения теплопроводности и уравнения фазового превращения. При этом предварительное определение становится возможным только за счет того, что концентрация внедренных элементов внутри по меньшей мере одного элемента объема предполагается как локально неизменная.
Аналогичным образом является также возможным, что вычислительная машина уже до моделирования временной характеристики состояния объема стали определяет для множества значений характеристических величин зависимость между энтальпией и теплопроводностью и запоминает в виде поля опорных точек. Поскольку за счет этого становится возможным, что вычислительная машина в рамках моделирования временной характеристики состояния объема стали определяет теплопроводность, имеющуюся в по меньшей мере одном элементе объема, на основании поля опорных точек.
Теоретически также при теплопроводности возможно учитывать зависимость теплопроводности в фазе аустенит от концентрации внедренных элементов в фазе аустенит. Эти воздействия на практике являются однако часто пренебрежимыми.
Является выгодным, если уравнение теплопроводности в много- или одномерном виде имеет вид
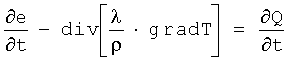 или, соотв.,
или, соотв., 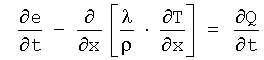 .
.
При этом означают λ - теплопроводность по меньшей мере одного элемента объема, ρ - плотность стали и Q - количество тепла, которое создается в по меньшей мере одном элементе объема за счет внешних воздействий. Созданное в по меньшей мере одном элементе объема за счет внешних воздействий количество тепла не содержит при этом никаких составляющих, которые происходят от фазовых превращений.
Этот подход для уравнения теплопроводности имеет преимуществом, что можно корректно моделировать температурные изменения, вызванные теплопроводностью и фазовыми превращениями.
Для решения уравнения фазового превращения возможны различные образы действий. Например, является возможным, что вычислительная машина в рамках решения уравнения фазового превращения определяет свободные энтальпии Гиббса фаз аустенит, феррит и цементит, на основе свободных энтальпий Гиббса - скорости превращения фаз аустенит, феррит и цементит и на основе скоростей превращения фаз - относительные содержания pA, pF и pZ фаз аустенит, феррит и цементит. Этот образ действий детально описан на качестве примера в DE-B3-10251716.
Альтернативно является также возможным, что вычислительная машина в рамках решения уравнения фазового превращения
- при решении по меньшей мере одной задачи Стефана для по меньшей мере одного элемента объема определяет аустенитную область и распределение концентрации внедренных элементов в аустенитной области по меньшей мере одного элемента объема и
- на основе соотношения аустенитной области и по меньшей мере одного элемента объема определяет в целом относительное содержание фазы аустенит.
Этот образ действий подробно описан в более старшей немецкой заявке на патент заявителя DE 102004005919.5, еще не опубликованной на день подачи настоящей заявки. В подобном случае среднюю концентрацию внедренных элементов в фазе аустенит можно определять путем усреднения распределения концентрации внедренных элементов в аустенитной области по меньшей мере одного элемента объема.
Соответствующий изобретению способ моделирования можно выполнять в автономном режиме ”оф-лайн”. В частности, вследствие избежания ненужных операций деления и возможности предварительного определения температуры и теплопроводности в качестве многомерных полей опорных точек, является однако также возможным, что вычислительная машина выполняет способ моделирования в режиме ”он-лайн” и в реальном времени с прохождением соответствующего действительного объема стали через устройство воздействия для термического воздейстия на действительный объем стали.
Устройство воздействия выполнено, как правило, в виде участка охлаждения для объема стали. Однако было бы также возможным, что устройство воздействия выполнено в виде клети прокатного стана для объема стали.
Возможно, что вычислительная машина выполняет только моделирование, как таковое, но не предпринимает никаких управляющих воздействий. Это может быть, например, целесообразным, чтобы испытывать и оптимизировать способ моделирования. Во многих случаях однако будет так, что вычислительная машина при применении способа моделирования определяет задающие воздействия для нацеленного воздействия на состояние действительного объема стали и передает на устройство воздействия.
Предпочтительным образом к вычислительной машине подводят действительную температуру действительного объема стали, зарегистрированную после воздействия на действительный объем стали. Так как тогда вычислительная машина находится в состоянии, сравнивать действительную температуру с соответствующей температурой, определенной в рамках способа моделирования, и соответственно согласовывать, при необходимости, способ моделирования.
Дальнейшие преимущества и детали следуют из последующего описания примера выполнения в связи с чертежами. При этом в принципиальном представлении показаны на:
ФИГ.1 - схематически вычислительная машина,
ФИГ.2 - диаграмма процесса,
ФИГ.3 - схематически устройство воздействия и вычислительная машина,
ФИГ.4 - схема для определения зависимости между энтальпией и температурой,
ФИГ.5 и 6 - комбинация уравнения теплопроводности с уравнением фазового превращения,
ФИГ.7 и 8 - возможные реализации шага с ФИГ.2 и
ФИГ.9 - следующая диаграмма процесса.
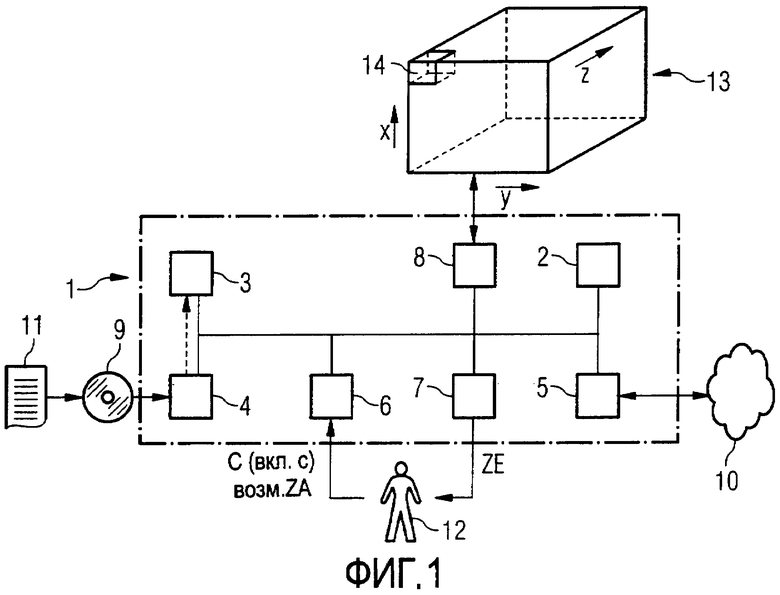
Согласно ФИГ.1 вычислительная машина 1 содержит обычные компоненты 2-8. Прежде всего это процессорный блок 2 и массовый накопитель 3. Массовый накопитель 3 может быть выполнен, например, в виде жесткого диска. Это далее интерфейсы 4 и 5 Интерфейс 4 является интерфейсом для связи выполненного в виде сменной запоминающей среды носителя данных 9 с вычислительной машиной 1. В зависимости от выполнения интерфейса 4 носитель данных 9 может быть, например, выполнен в виде ПЗУ на компакт-диске CD-ROM или как USB-стик. Интерфейс 5 является интерфейсом к сети вычислительных машин 10, например, к сети Интернет или, соответственно, к Всемирной паутине World Wide Web. Следующими компонентами 6-8 вычислительной машины 1 являются устройство ввода 6, устройство вывода 7 и оперативный накопитель 8. Устройство ввода 6 может содержать, например, клавиатуру и ”мышь”. Устройство вывода 7 может содержать устройство визуального отображения (терминал) и печатающее устройство.
На сменной среде 9 запомнена компьютерная программа 11. Компьютерная программа 11 после присоединения сменной среды 9 к интерфейсу 4 считывается вычислительной машиной 1. Считанная компьютерная программа 11 запоминается вычислительной машиной 1 в массовом накопителе 3. При вызове компьютерной программы 11, - например, на основе соответствующих данных ввода пользователя 12 через устройство ввода 6, - вычислительная машина 1 выполняет затем способ моделирования, который в последующем поясняется более подробно.
Посредством способа моделирования должна моделироваться временная характеристика состояния Z объема стали 13. Это происходит за счет того, что объем стали 13 в вычислительной машине 1 - точнее: в его оперативном накопителе 8 - моделируют с помощью множества элементов объема 14. При этом, как правило, объем стали 13 моделируют с помощью множества элементов объема 14, которые граничат друг с другом. В частном случае является однако также возможным, что объем стали 13 моделируют только с помощью одного единственного элемента объема 14.
Если объем стали 13 моделируют с помощью множества граничащих друг с другом элементов объема 14, расположение элементов объема 14 альтернативно может быть одномерным, двухмерным или трехмерным. Самым общим случаем является при этом трехмерное расположение. Двухмерное расположение элементов объема 14 принимают во внимание, например, если должна моделироваться характеристика соответствующего действительного объема стали 13', который выполнен в виде прутка, то есть, например, сортовой заготовки 13' или другого профиля. Так как в этих случаях тепловой поток в направлении прутка является практически пренебрежимым. Одномерное расположение элементов объема 14, например, принимают во внимание, если действительный объем стали 13' имеет форму полосы. Поскольку в этом случае тепловой поток в поперечном направлении полосы и продольном направлении полосы является практически пренебрежимым. Только в направлении толщины полосы появляется достойный упоминания тепловой поток.
Состояние отдельного элемента объема 14 в определенный момент времени t охватывает энтальпию е соответствующего объема стали 13 и относительные содержания рА, pF, pZ фаз аустенит, феррит и цементит в соответствующем элементе объема 14 или, соответственно, характеристические для этого величины е, рА, сА. Соответственно этому состояние Z объема стали 13 в этот момент времени t охватывает совокупность состояний всех элементов объема 14 моделированного объема стали 13.
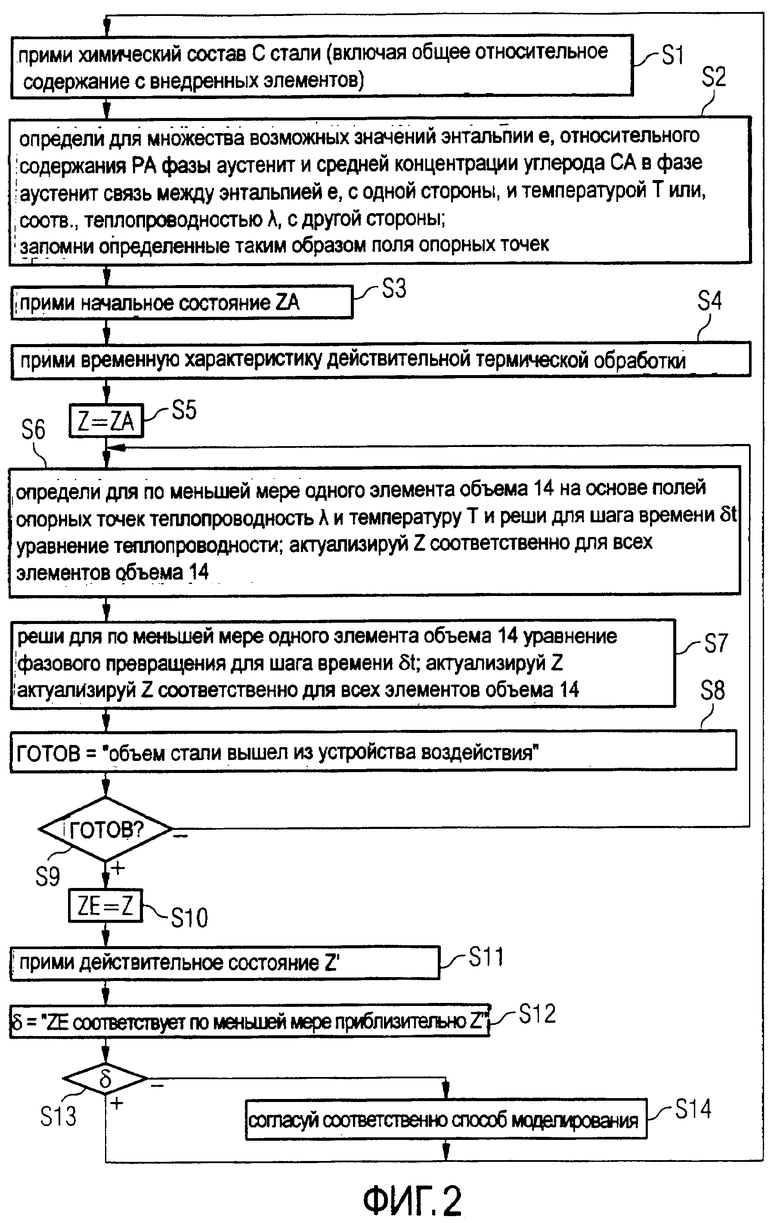
Временная характеристика состояния Z объема стали 13 является зависящей от множества параметров. Одним из параметров является химический состав С стали. Химический состав С содержит между прочим общее относительное содержание с внедренных элементов. Этот состав поэтому подводят к вычислительной машине 1 согласно ФИГ.2 в шаге S1.
Задание химического состава С можно производить, например, с помощью соответствующего ввода пользователя 12. Он может задаваться вычислительной машине 1 однако также - смотри ФИГ.3 - от вышестоящей вычислительной машины процесса 15 через подходящий интерфейс вычислительная машина - вычислительная машина 15'.
Наиболее часто имеющимся в стали внедренным элементом является углерод. Для более краткого изложения поэтому в последующем говорится об углероде, даже если при этом имеются в виду внедренные элементы в общем.
В шаге S2 - то есть еще до решения уравнения теплопроводности и уравнения фазового превращения - вычислительная машина 1 определяет тогда для теплопроводности λ стали и для температуры Т стали два многомерных поля опорных точек. Поля опорных точек имеют поэтому по меньшей мере три входных параметра, а именно энтальпию е соответствующего элемента объема 14 и две величины рА, сА. Одной характеристической величиной является относительное содержание рА, в котором сталь в соответствующем элементе объема 14 присутствует в фазе аустенит. Другой характеристической величиной является локально неизменная внутри соответствующего элемента объема 14 средняя концентрация углерода cA в фазе аустенит соответствующего элемента объема 14.
Общее относительное содержание углерода с стали при данном химическом составе С стали является постоянным по времени и одинаковым для всех элементов объема 14.
На основе зависимости между относительными содержаниями фаз рА, pF, pZ, общим относительным содержанием углерода с и средней концентрацией углерода сА в фазе аустенит поэтому могут быть определены без проблем два других относительных содержания фаз pF, pZ для фаз феррит и цементит в соответствующем элементе объема 14.
Вычислительная машина 1 определяет тем самым в шаге S2 для множества возможных значений энтальпии е, удельного содержания рА фазы аустенит и средней концентрации углерода сА в фазе аустенит соответствующего элемента объема 14 соответствующую температуру Т и соответствующую теплопроводность λ, элемента объема 14. Таким образом получается функциональная звисимость между энтальпией е, с одной стороны, и температурой Т или, соответственно, теплопроводностью λ, с другой стороны. Эти поля опорных точек запоминают. Их можно поэтому позднее очень быстро анализировать в рамках решения уравнения теплопроводности за счет линейной интерполяции или нелинейной интерполяции (например, посредством многомерного В-сплайна).
Предпочтительным образом вычислительная машина 1 при определении зависимости между энтальпией е и температурой Т учитывает среднюю концентрацию углерода сА в фазе аустенит, как таковую, то есть не только для того, чтобы определять удельные содержания pF и pt.
Зависимость между энтальпией е и температурой Т определяют согласно ФИГ.4 тем самым предпочтительно на основе формулы
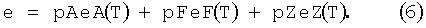
При этом еА, eF и eZ являются функциями, которые соответственно описывают зависимость между энтальпией е и температурой Т в элементах объема 14. eF описывает при этом зависимость для случая, что элемент объема 14 присутствует исключительно в фазе феррит. Аналогично eZ описывает зависимость для случая, что элемент объема 14 присутствует исключительно в фазе цементит. Функции eF и eZ не зависят от средней концентрации углерода сА в фазе аустенит элемента объема 14. Функция еА, напротив, которая описывает зависимость между энтальпией е и температурой Т для случая, что элемент объема 14 имеется в фазе аустенит, зависит, как таковая, от средней концентрации углерода сА в фазе аустенит. Эта зависимость поэтому учитывается в функции еА согласно ФИГ.4.
При желании совершенно точного рассчета, необходимо бы даже подставлять концентрацию углерода сА в фазе аустенит внутри соответствующего элемента объема 14 переменно по месту. Тогда однако для температуры Т было бы невозможно, определять ее заранее в виде поля опорных точек. В этом случае определение температуры Т должно было бы происходить в рамках моделирования временной характеристики состояния Z самого объема стали 13. Этот образ действий потребовал бы также значительных затрат машинного времени. По этой причине концентрацию углерода сА в фазе аустенит устанавливают как локально неизменную внутри соответственно рассматриваемого элемента объема 14.
Определение поля опорных точек для теплопроводности λ происходит согласно ФИГ.4 аналогичным образом на основе уравнения
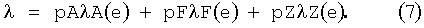
λА, λF и λZ являются при этом функциями, которые описывают соответственно зависимость между энтальпией е и теплопроводностью λ в элементе объема 14 для случая, когда элемент объема 14 имеется исключительно в фазе аустенит, феррит или, соответственно, цементит. Точнее говоря, функция λA также является зависимой от средней концентрации углерода сА в фазе аустенит соответствующего элемента объема 14. При необходимости, поэтому является возможным, соответственно учитывать эту зависимость. Во многих случаях применения влияние средней концентрации углерода сА в фазе аустенит соответствующего элемента объема 14 однако является только малым и в его практических воздействиях им можно пренебречь.
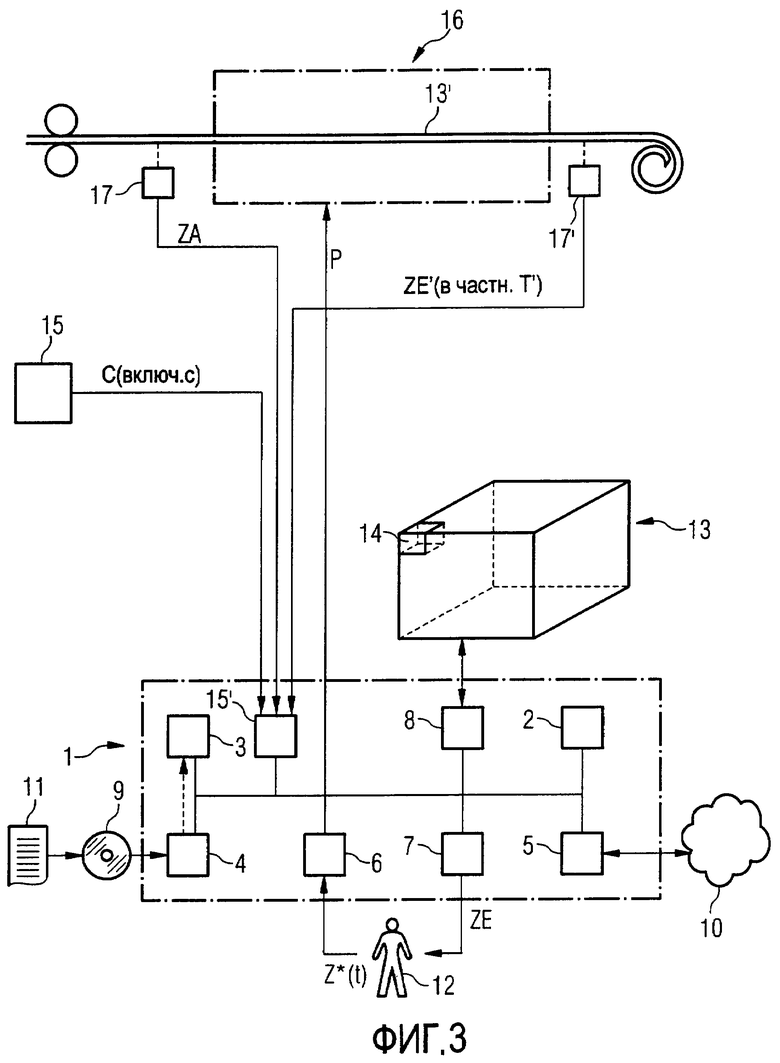
В шаге S3 вычислительная машина 1 тогда принимает начальное состояние ZA объема стали 13. В рамках чисто автономного режима моделирования - смотри ФИГ.1 - например, является возможным, что это начальное состояние ZA задается вычислительной машине 1 пользователем 12 через устройство ввода 6. Если, в противоположность этому, способ моделирования выполняют в режиме он-лайн, - возможно даже в реальном времени - с прохождением соответствующего действительного объема стали 13' через устройство воздействия 16 для воздействия на действительный объем стали 13' (смотри ФИГ.3), задание происходит посредством соответствующего измерительного устройства 17, которое расположено в начале устройства воздействия 16. В обоих случаях однако начальное состояние ZA соответствует состоянию соответствующего действительного объема стали 13' при поступлении в устройство воздействия 16.
В шаге S4 вычислительная машина 1 принимает далее краевые условия. Например, вычислительной машине 1 может задаваться, с какой временной характеристикой действительный объем стали 13' действительно термически обрабатывается при прохождении через устройство воздействия 16. Если устройство воздействия 16, что является обычным случаем, например, выполнено в виде участка охлаждения 16, временная характеристика действительного термического воздействия на объем стали соответствует временной характеристике охлаждения действительного объема стали 13'. Если устройство воздействия 16 (в виде исключения) выполнено в виде группы клетей прокатного стана, термическое воздействие соответствует процессам прокатки, которые предпринимают на действительном объеме стали 13', с прибавлением процесса охлаждения при проходе через группу клетей прокатного стана.
В шагах S5 до S10 вычислительная машина 1 определяет затем временную характеристику состояния Z моделированного объема стали 13.
В идеальном случае это происходит за счет того, что вычислительная машина 1 индивидуально для каждого элемента объема 14 моделированного объема стали 13 решает уравнение теплопроводности и уравнение фазового превращения и тем самым определяет временную характеристику характеристических величин е, рА, сА. В минимальном случае это происходит за счет того, что вычислительная машина 1 решает уравнение теплопроводности и уравнение фазового превращения для одного единственного из элементов объема 14 и перенимает определенное для этого одного элемента объема 14 состояние для всех других элементов объема 14 моделированного объема стали 13. Поэтому также этот названный последним образ действий приводит в результате к тому, что вычислительная машина 1 для каждого элемента объема 14 и каждого момента времени t определяет энтальпию е соответствующего элемента объема 14, относительное содержание фазы pA и концентрацию cA и - таким образом в неявном виде также относительное содержание фаз pF и pZ.
На практике часто выбирают средний путь, при котором уравнение теплопроводности решают индивидуально для каждого элемента объема 14, однако уравнение фазового превращения только для одного единственного элемента объема 14 или только для части элементов объема 14, например, каждого восьмого (8=23) или каждого двадцать седьмого (27=33) элемента объема 14. В любом случае однако вычислительная машина 1 в шаге S5 устанавливает мгновенное состояние Z моделированного объема стали 13, равным подведенному в шаге S3 начальному состоянию ZA объема стали 13. Затем вычислительная машина 1 решает в шаге S6 для временного шага δt для по меньшей мере одного из элементов объема 14 уравнение теплопроводности. Далее вычислительная машина 1 в шаге S7 для того же самого временного шага δt для по меньшей мере одного из элементов объема 14 решает уравнение фазового превращения. При необходимости, определенные результаты перенимаются для других элементов объема 14. На всякий случай следует далее упомянуть, что последовательность шагов S6 и S7 является незначительной.
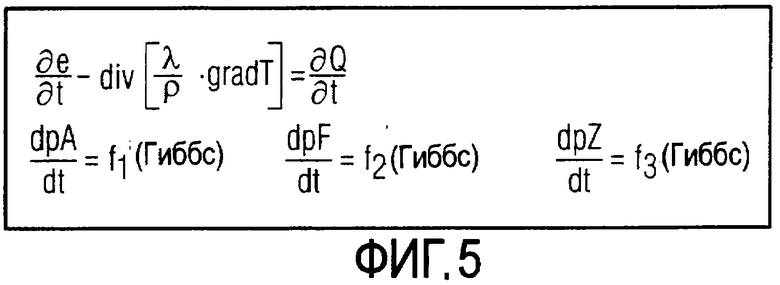
Уравнение теплопроводности - в зависимости от вида моделированного объема стали 13 или, соответственно, 13' - может решаться многомерно или одномерно. Если уравнение теплопроводности решается многомерно, оно имеет согласно ФИГ.5 форму

В этом уравнении теплопроводности t это время, ρ - плотность стали и Q - количество тепла, которое создается в рассматриваемом элементе объема 14 за счет внешних воздействий. Оно не содержит никаких составляющих, которые происходят от фазовых превращений, div и grad являются обычными математическими операторами дивергенция и градиент.
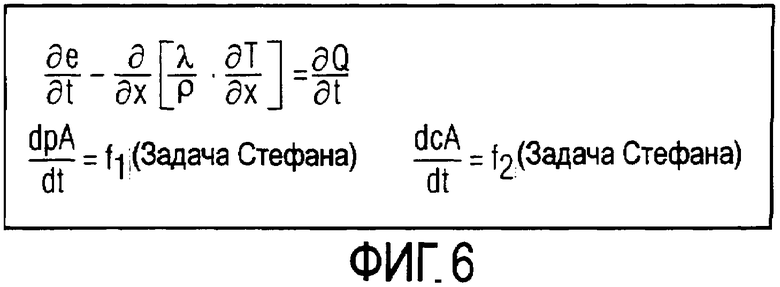
Если уравнение теплопроводности решается одномерно, в уравнении 5 математические операторы дивергенция и градиент заменяются одномерной производной по месту. Х при этом является координатой места одной размерности. Уравнение теплопроводности упрощается поэтому согласно ФИГ.6 до
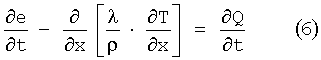
Это упрощение является допустимым, если должна моделироваться временная характеристика стальной полосы.
Так как в таком случае тепловой поток в продольном направлении полосы и в поперечном направлении полосы является пренебрежимым. Только в направлении толщины полосы имеется достойный упоминания тепловой поток.
Независимо от того, решают ли уравнение теплопроводности многомерно или одномерно, вычислительная машина 1 однако определяет для решения уравнения теплопроводности (шаг S6) и уравнения фазового превращения (шаг S7) согласно ФИГ.5 и 6 соответственно получающуюся теплопроводность λ и соответственно получающуюся температуру Т на основе определенных в шаге S2 полей опорных точек. Определение конкретных значений для теплопроводности λ и температуры Т можно при этом, например, производить за счет линейной интерполяции или за счет интерполяции с гладкими кривыми - ключевое слово многомерные сплайны.
В случае, если требуется еще более точное определение температуры Т, возможно учитывать дополнительно также поверхностную энергию. В этом случае состояние элемента объема 14 охватывает также количество n образовавшихся к соответствующему моменту времени t в рассматриваемом элементе объема 14 или, соответственно, разрушившихся перлитных слоев, то есть количество слоев феррит-цементит-феррит-цементит …. Естественно, можно также привлекать для этого другую эквивалентную величину.
Количество n дает в связи с изменением относительного содержания рА фазы аустенит в рассматриваемом элементе объема 14 изменение содержащейся в рассматриваемом элементе объема 14 поверхностной энергии. Энтальпию е в этом случае корректируют на изменение поверхностной энергии, и температуру Т тогда определяют на основе скорректированного значения энтальпии е.
Коррекцию на изменение поверхностной энергии, поскольку поверхностная энергия не зависит от температуры Т, можно быстро и просто учитывать в виде смещения. Альтернативно этот учет можно было бы производить также за счет того, что поле опорных точек для температуры Т в качестве следующей размерности содержит изменение поверхностной энергии или также количество n слоев.
Уравнение фазового превращения может быть в принципе образовано произвольно. Важным является, чтобы вычислительная машина 1 в рамках решения уравнения фазового превращения определяла в явном виде характеристические величины рА, сА и тем самым в неявном виде также то, в каком относительном содержании рА, pF и pZ в рассматриваемом элементе объема 14 сталь присутствует в фазах аустенит, феррит и цементит. Это можно производить, как показано на ФИГ.4, например, за счет того, что вычислительная машина 1 определяет в рамках решения уравнения фазового превращения свободные энтальпии Гиббса фаз аустенит, феррит и цементит. На основе свободных энтальпий тогда вычислительная машина 1 определяет скорости превращения фаз аустенит, феррит и цементит. На основе скоростей превращения вычислительная машина 1, наконец, определяет относительные содержания рА, pF, pZ фаз аустенит, феррит и цементит. Эта реализация схематически представлена на ФИГ.7. Она предусматривает тем самым возможную форму выполнения шага S7 с ФИГ.2.
ФИГ.8 показывает возможную альтернативную реализацию шага S7 с ФИГ.2. Согласно шага ФИГ.7 вычислительная машина 1 в рамках решения уравнения фазового превращения определяет аустенитную область и распределение концентрации углерода в аустенитной области соответствующего элемента объема 14. Определение аустенитной области и распределения концентрации углерода производят при этом при решении по меньшей мере одной задачи Стефана. На основе соотношения аустенитной области и элемента объема 14 в целом вычислительная машина 1 тогда определяет относительное содержание рА фазы аустенит в рассматриваемом элементе объема 14. За счет усреднения распределения концентрации углерода вычислительная машина 1 определяет среднюю концентрацию углерода сА в аустенитной области.
Для полноты при этом следует упомянуть, что уравнение фазового превращения является определяемым независимо от того, является ли уравнение теплопроводности многомерным или одномерным.
Как уже упомянуто, возможно, что вычислительная машина 1 выполняет способ моделирования в режиме он-лайн и в реальном времени с проходом соответствующего действительного объема стали 13' через устройство воздействия 16 для термического воздействия на действительный объем стали 13'. По причинам возможной производительности вычислительной машины поэтому необходимо, чтобы элементы объема 14 имели размер, который является значительно больше, чем действительный размер зерна стали. Это справедливо также тогда, когда вычислительная машина 1 действует только в качестве наблюдателя, то есть не действует сама управляюще на устройство воздействия 16.
После решения уравнений состояния в шагах S6 и S7 вычислительная машина 1 определяет в шаге S8 логическую переменную ГОТОВ. Логическая переменная ГОТОВ принимает значение ”истина”, если объем стали 13 согласно моделированию вышел из устройства воздействия 16. В противном случае, она принимает значение ”ложь”. В зависимости от логической переменной ГОТОВ вычислительная машина 1 проверяет в шаге S9, должна ли она перейти к шагу S10 или должна ли она предпринять дальнейший проход шагов с S6 до S9.
Коль скоро вычислительная машина 1 продолжает шагом S10 дальнейшее выполнение способа моделирования, она устанавливает в шаге S10 конечное состояние ZE моделированного объема стали 13 на определенное последним состояние Z.
Согласно ФИГ.2 после шага S10 выполняют еще шаги S11 до S14. Эти шаги однако являются только необязательными.
В шаге S11 вычислительная машина 1 принимает действительное конечное состояние ZE' действительного объема стали 13'. Например, может - смотри ФИГ.3 - следующее измерительное устройство 17', которое расположено в конце устройства воздействия 16, регистрировать действительную температуру Т' действительного объема стали 13'.
В шаге S12 вычислительная машина 1 определяет логическую переменную δ. Логическая переменная δ принимает значение ”истина”, если определенное в рамках способа моделирования конечное состояние ZE (по меньшей мере приблизительно) совпадает с действительным конечным состоянием ZE'. В противном случае она принимает значение ”ложь”.
Значение логической переменной δ проверяется вычислительной машиной 1 в шаге S13. В зависимости от значения логической переменной δ шаг S14 выполняется или также не выполняется. В рамках выполнения шага S14 вычислительная машина 1 соответственно согласовывает способ моделирования.
Адаптирование способа моделирования согласно шагам S11 до S14 является возможным также тогда, когда способ моделирования выполняют не в режиме он-лайн и/или не в реальном времени. Так как, например, является возможным, хотя и регистрировать действительные начальные состояния ZA' и действительные конечные состояния ZE' в реальном времени, но запоминать их только промежуточно. Тогда способ моделирования может выполняться в другой момент времени в автономном режиме работы.
В рамках предыдущих рассуждений вычислительная машина 1 выполняла чистое моделирования объема стали 13, однако никакого прямого или косвенного управления устройством воздействия 16. Также подобное управление является однако возможным. Это поясняется в последующем в связи с ФИГ.9. Шаги S1, S2 и S11 до S14 при этом на ФИГ.9 не представлены. Они соответствуют таковым с ФИГ.2.
Сначала необходимо, чтобы к вычислительной машине 1 подводилось начальное состояние ZA через измерительное устройство 17, которое расположено перед устройством воздействия 16. В случае, если должна производиться адаптация способа моделирования, далее является необходимым, в шаге S11 также - например, с помощью измерительного устройства 17' - прямо регистрировать действительное конечное состояние ZE' действительного объема стали 13' при выходе из устройства воздействия 16.
Далее согласно ФИГ.8 необходимо, модифицировать шаги S4, S6 и S7 в шаги S4', S6' и S7'. Шаг S4 при этом модифицируют в шаг S4' в том смысле, что в качестве подлежащего соблюдению краевого условия задают желаемую характеристику конечного состояния Z*, например, желаемую характеристику температуры от времени. Шаги S6' и S7' в основном соответствуют шагам S6 и S7. Отличие относительно шагов S6 и S7 состоит в том, что определенный результат дает не непосредственно новое состояние моделированного объема стали, а только предварительное состояние Z'.
Прежде всего, однако, согласно ФИГ.9 после шага S5 и после шага S7' должны вставляться шаги S15 до S19.
В шаге S15 вычислительная машина 1 устанавливает начальное значение для задающего воздействия Р, которым устройство воздействия 16 должно влиять на соответствующий действительный объем стали 13'. С этим значением действительного задающего воздействия Р выполняются шаги S6' и S7'.
После выполнения шага S7' вычислительная машина 1 определяет в шаге S16 логическую переменную ОК. Логическая переменная ОК принимает значение ”истина”, если предварительное состояние Z', определенное в рамках выполнения шагов S6' и S7', совпадает (по меньшей мере в основном) с соответствующим состоянием Z*, желательным для соответствующего временного шага δt. В противном случае логическая переменная ОК принимает значение ”ложь”.
Значение логической переменной ОК проверяют в шаге S17. В зависимости от значения логической переменной ОК выполняют или шаг S18 или шаг S19. В шаге S18 вычислительная машина 1 изменяет задающее воздействие Р, с помощью которого должно оказываться воздействие на соответствующий действительный объем стали 13'. Изменение происходит при этом само собой разумеется с учетом предварительного состояния Z' и желательного в соответствующем временном шаге δt состояния Z*. После этого возвращаются к шагу S6'. Если выполняют шаг S19, вычислительная машина 1 перенимает предварительное состояние Z' в качестве нового состояния Z. Далее она передает задающее воздействие Р на устройство воздействия 16 так, что оно может термически воздействовать на соответствующий действительный объем стали 13' в соответствии с определенным задающим воздействием Р.
Образ действий согласно ФИГ.9 выполняют в режиме он-лайн и в реальном времени с проходом соответствующего действительного объема стали 13' через устройство воздействия 16. В этом случае таким образом устройство воздействия 16 управляется прямо и непосредственно вычислительной машиной 1. Возможным было бы также однако, производить в шаге S19 вместо прямого управления устройством воздействия 16 запоминание соответствующих управляющих воздействий Р. В этом случае вычислительная машина 1 могла бы работать в автономном режиме и/или не в реальном времени и тем не менее управлять устройством воздействия 16, даже если теперь еще только косвенно.
Посредством соответствующего изобретению образа действий - в частности, учета зависимости температуры Т также от относительного содержания углерода сА в аустените - тем самым является возможным значительно более простое и одновременно также лучшее моделирование, чем в уровне техники.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ МОДЕЛИРОВАНИЯ ДЛЯ МЕТАЛЛА | 2003 |
|
RU2317577C2 |
| СПОСОБ ФУНКЦИОНИРОВАНИЯ ОХЛАЖДАЮЩЕГО УЧАСТКА ДЛЯ ОХЛАЖДЕНИЯ ПРОКАТЫВАЕМОГО МАТЕРИАЛА С НЕ СВЯЗАННЫМ С ТЕМПЕРАТУРОЙ ОХЛАЖДЕНИЕМ ДО КОНЕЧНОГО ЗНАЧЕНИЯ ЭНТАЛЬПИИ | 2009 |
|
RU2507017C2 |
| СПОСОБ ЛЕГИРОВАНИЯ СТАЛИ АЛЮМИНИЕМ | 2009 |
|
RU2431696C2 |
| СПОСОБ ТЕРМИЧЕСКОЙ ОБРАБОТКИ ИЗДЕЛИЙ ИЗ СПЛАВОВ НА ОСНОВЕ ЖЕЛЕЗА (ВАРИАНТЫ) | 2010 |
|
RU2447163C1 |
| СПОСОБ ТЕРМИЧЕСКОЙ ОБРАБОТКИ ИЗДЕЛИЙ ИЗ СТАЛИ И СПЛАВОВ | 2009 |
|
RU2413777C1 |
| СПОСОБ УСКОРЕННОЙ ЦЕМЕНТАЦИИ СТАЛЬНЫХ ДЕТАЛЕЙ | 2007 |
|
RU2355816C2 |
| СПОСОБ ПРОИЗВОДСТВА ТЕРМИЧЕСКИ ОБРАБОТАННОЙ ЛИСТОВОЙ СТАЛИ | 2017 |
|
RU2732461C1 |
| СПОСОБ УПРАВЛЕНИЯ ОХЛАЖДАЮЩИМ УСТРОЙСТВОМ В ЛИНИИ ПРОКАТНОГО СТАНА | 2020 |
|
RU2783688C1 |
| СПОСОБ ДИНАМИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРОЦЕССА ПРОИЗВОДСТВА ТЕРМООБРАБОТАННОГО СТАЛЬНОГО ЛИСТА | 2017 |
|
RU2731116C1 |
| СПОСОБ УПРАВЛЕНИЯ ДЛЯ РАСПОЛОЖЕННОЙ ПЕРЕД УЧАСТКОМ ОХЛАЖДЕНИЯ ЧИСТОВОЙ ЛИНИИ КЛЕТЕЙ ДЛЯ ПРОКАТКИ ГОРЯЧЕКАТАНОЙ МЕТАЛЛИЧЕСКОЙ ПОЛОСЫ | 2002 |
|
RU2291750C2 |
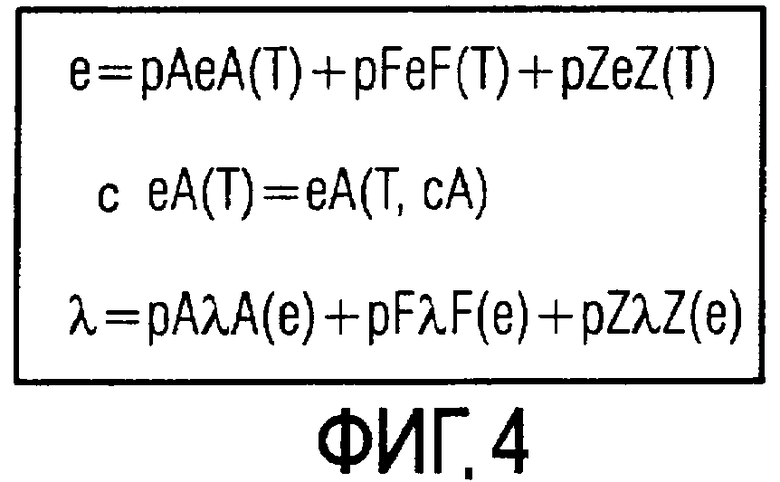



Изобретение относится к моделированию с помощью вычислительной машины параметров состояния (Z) объема стали (13), температура которого подвергается прямому или косвенному воздействию. В вычислительную машину задают химический состав стали, включая общее относительное содержание элементов внедрения. Объем стали (13) моделируют в вычислительной машине (1) с помощью множества элементов объема (14). Для указанных элементов объема для энтальпии (е), относительного содержания фазы аустенита (рА), относительного содержания фазы феррита (pF) и относительного содержания фазы цементита (pZ) определяют в определенный момент времени (t) характеристические величины (е, рА, сА), где (е) - энтальпия, (рА) - относительное содержание фазы аустенита в элементе объема (14), (сА) - локально неизменная внутри соответствующего элемента объема (14) концентрация элементов внедрения в фазе аустенита. Решая уравнение теплопроводности и уравнения фазового превращения определяют для по меньшей мере одного из элементов объема (14) временные характеристики характеристических величин и на их основе (pF) и (pZ). Вычислительная машина рассчитывает и моделирует объем стали (13) по множеству состояний соответствующих элементов объема (14) с получением параметров (Z) объема стали (13). Упрощается процесс моделирования и улучшаются его результаты. 5 н. и 10 з.п. ф-лы, 9 ил.
1. Способ моделирования параметров состояния (Z) объема стали (13) с помощью вычислительной машины, в котором в вычислительную машину задают химический состав стали, включая общее относительное содержание элементов внедрения, моделирование объема стали (13) осуществляют по множеству элементов объема (14), в которых для энтальпии (е), относительного содержания фазы аустенита (рА), относительного содержания фазы феррита (pF) и относительного содержания фазы цементита (pZ) определяют в определенный момент времени (t) характеристические величины (е, рА, сА), где (е) - энтальпия, (рА) - относительное содержание фазы аустенита в элементе объема (14), (сА) - локально неизменная внутри соответствующего элемента объема (14) концентрация элементов внедрения в фазе аустенита, с помощью определенных характеристик путем решения уравнения теплопроводности и уравнения фазового превращения определяют для по меньшей мере одного из элементов объема (14) временные характеристики характеристических величин и на их основе (pF) и (pZ), после чего вычислительная машина рассчитывает и моделирует параметры состояния (Z) по меньшей мере одного из элементов объема (14) и для моделирования объема стали (13) по множеству состояний соответствующих элементов объема (14) перенимает определенные параметры состояния (Z) для элементов объема (14), для которых параметры состояния (Z) не определялись.
2. Способ по п.1, отличающаяся тем, что при решении уравнения теплопроводности и/или уравнения фазового превращения определяют для по меньшей мере одного элемента объема (14) зависимость между энтальпией (е) и температурой стали (Т) и при этом указанная зависимость зависит от относительных содержаний фаз аустенита (рА), феррита (pF) и цементита (pZ) и от концентрации элементов внедрения в фазе аустенита (сА).
3. Способ по п.1 или 2, отличающийся тем, что зависимость между энтальпией (е) и температурой стали (Т) устанавливают по уравнению е=рАеА(Т)+pFeF(T)+pZeZ(T), где рА, pF и pZ - относительные содержания фаз аустенита, феррита и цементита в по меньшей мере одном элементе объема (14), а еА, eF и eZ - функции, описывающие зависимость между энтальпией (е) и температурой стали (Т) в по меньшей мере одном элементе объема (14) при условии, что элемент объема (14) содержится только в фазе аустенита, феррита или цементита, а функция еА учитывает зависимость между энтальпией (е) и температурой стали (Т) в фазе аустенита от концентрации элементов внедрения в фазе аустенита (сА).
4. Способ по п.1, отличающийся тем, что до моделирования параметров (Z) объема стали (13) с использованием вычислительной машины (1) для множества значений характеристических величин (е, рА, сА) определяют зависимость межу энтальпией (е) и температурой стали (Т) и запоминают ее в виде поля опорных точек, а при моделировании параметров (Z) объема стали (13) определяют на основании поля опорных точек температуру стали (Т), имеющуюся в по меньшей мере одном элементе объема (14).
5. Способ по п.4, отличающийся тем, что до моделирования параметров (Z) объема стали (13) с использованием вычислительной машины (1) для множества значений характеристических величин (е, рА, сА) определяют зависимость между энтальпией (е) и теплопроводностью (λ) и запоминают ее в виде поля опорных точек, а при моделировании параметров (Z) объема стали (13) определяют на основании поля опорных точек теплопроводность (λ), имеющуюся в по меньшей мере одном элементе объема (14).
6. Способ по п.1, отличающийся тем, что решают уравнение теплопроводности, которое имеет в много- или, соответственно, одномерном случае форму
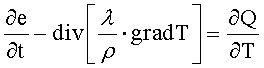 или соответственно,
или соответственно, 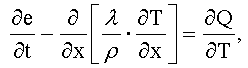
где λ - теплопроводность по меньшей мере одного элемента объема (14), ρ - плотность стали, Q - количество тепла, производимого за счет внешних воздействий в по меньшей мере одном элементе объема (14) и не зависящее от фазовых превращений, х - координата местоположения в пространстве, причем количество тепла (Q) не содержит никаких составляющих, которые происходят от фазовых превращений.
7. Способ по п.1, отличающийся тем, что при решении уравнения фазового превращения с использованием вычислительной машины (1) определяют свободные энергии Гиббса фаз аустенита, феррита и цементита, на основе которых определяют скорости превращения фаз аустенита, феррита и цементита, а на основе скоростей превращения определяют относительные содержания фаз аустенита, феррита и цементита (рА, pF, pZ).
8. Способ по п.1, отличающийся тем, что при решении уравнения фазового превращения с использованием вычислительной машины (1) решают по меньшей мере одну задачу Стефана для по меньшей мере одного элемента объема (14), определяя фазу аустенита и распределение концентрации элементов внедрения в фазе аустенита по меньшей мере одного элемента объема (14), на основе соотношения фазы аустенита и по меньшей мере одного элемента объема (14) определяют в целом относительное содержание фазы аустенита (рА) и путем усреднения распределения концентрации элементов внедрения в фазе аустенита по меньшей мере одного элемента объема (14) определяют среднюю концентрацию (сА) элементов внедрения в фазе аустенита.
9. Способ по п.1, отличающийся тем, что моделирование выполняют в режиме «онлайн» и в реальном времени с прохождением соответствующего действительного объема стали (13') через устройство воздействия (16) для последующего выполнения термического воздействия на действительный объем стали (13').
10. Способ по п.1, отличающийся тем, что при моделировании определяют требуемое задающее воздействие (Р) на действительный объем стали (13'), которое передают на устройство термического воздействия (16) для последующего выполнения термического воздействия на действительный объем стали (13').
11. Способ моделирования по п.9 или 10, отличающийся тем, что регистрируют действительную температуру (Т') действительного объема стали (13') после термического воздействия, подводят температуру к вычислительной машине (1) и осуществляют сравнение действительной температуры (Т') с соответствующей, определенной в рамках способа моделирования температурой (Т) и соответственно корректируют способ моделирования.
12. Носитель данных с запомненной на носителе данных компьютерной программой (11) для осуществления способа моделирования по любому из пп.1-11.
13. Вычислительная машина (1), содержащая массовый накопитель (3) с заложенной в нем компьютерной программой (11) для осуществления способа моделирования по любому из пп.1-11.
14. Устройство термического воздействия (16) на действительную температуру (Т') действительного объема стали (13'), в частности на участке охлаждения, отличающееся тем, что оно содержит вычислительную машину по п.13.
15. Сталь, отличающаяся тем, что она подвергнута термической обработке в устройстве термического воздействия по п.14.
| DE 10251716 В3, 26.08.2004 | |||
| СПОСОБ УПРАВЛЕНИЯ ПРОЦЕССОМ ОХЛАЖДЕНИЯ ПРОКАТА | 2001 |
|
RU2183522C1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ПРОЦЕССА ПРОКАТКИ | 1992 |
|
RU2078626C1 |
| СПОСОБ УПРАВЛЕНИЯ УСЛОВИЯМИ ОХЛАЖДЕНИЯ НАГРЕТОГО ТЕЛА | 1993 |
|
RU2067904C1 |
| Устройство для регулирования температуры полосы в чистовой группе стана горячей прокатки | 1978 |
|
SU768514A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
2011-04-27—Публикация
2006-07-13—Подача