Настоящее изобретение относится к способу моделирования для металла, температура которого непосредственно или косвенно подвергается воздействию исполнительного органа,
причем модели материала задают исходную температуру металла и исходные относительные содержания, в которых металл присутствует по крайней мере в первой или, соответственно, второй фазе,
причем внутри модели материала с учетом исходной температуры, исходных относительных содержаний и регулирующего воздействия для исполнительного органа в реальном времени решают уравнение теплопроводности и уравнение превращения и определяют таким образом ожидаемую температуру металла, а также ожидаемые относительные содержания, в которых металл присутствует по крайней мере в первой или, соответственно, второй фазе, причем исполнительным органом управляют согласно регулирующему воздействию.
Подобные способы известны, например, из статьи "Цифровое моделирование теплопроводности в листовых сталях - математика помогает при управлении участков охлаждения", В.Борхерс и др., опубликованной в Вестнике Фридрих-Александер-университета Эрланген-Нюрнберг, выпуск 102, октябрь 2001, 27-й год выпуска.
Известные способы используют, в частности, для управления исполнительными органами для охладителя в прокатных станах. Исполнительные органы для охладителя могут быть расположены между клетей прокатного стана. Они могут быть также расположены после клетей прокатного стана. Можно представить себе также другие случаи применения, например в рамках вычисления процессов затвердевания при непрерывной разливке или при управлении прокатными станами как таковыми.
Для определения относительного содержания фаз в уровне техники привлекают правило Шайла или подходы Джонсон-Мель-Аврами, или Бримакомбе.
Исходные положения уровня техники на практике не работают безошибочно во всех случаях, в частности они имеют целый ряд систематических недостатков. Во-первых, каждый материал должен отдельно параметрироваться. Интерполяции между различными материалами являются невозможными или по крайней мере возможными только ограниченно. Во-вторых, в способах уровня техники рассматриваются только две фазы. Расширение на большее число фаз, чем две, систематически не является возможным. В-третьих, способы согласно уровню техники дают хорошее совпадение между моделью и реальностью только при полном превращении рассматриваемого металла. В-четвертых, способ согласно уровню техники не дает никакой информации о выделяющейся при фазовом превращении теплоте превращения. Знание теплоты превращения, однако, является обязательным для корректного решения уравнения теплопроводности.
Задачей настоящего изобретения поэтому является создание способа моделирования для металла, который дает лучшие результаты на модели.
Задача решается за счет того, что в рамках уравнения превращения определяют свободные энтальпии Гиббса фаз металла, на основе свободных энтальпий Гиббса определяют скорость превращения металла из первой фазы во вторую фазу и на основе скорости превращения определяют ожидаемые относительные содержания.
В простейшем случае в настоящем изобретении, так же как в уровне техники, рассматривают чисто двухфазную систему, например превращение аустенита в феррит и наоборот. Однако его можно расширить без проблем также на многофазные системы, в частности на систему феррит-аустенит-цементит.
Как правило, относительные содержания добавок не могут рассматриваться независимо друг от друга. Влияние - также связанное - добавок на свободную энтальпию Гиббса является, однако, известным. В качестве примера можно сослаться на специальные статьи "Аппроксимативное термодинамическое решение фазовых данных для сталей", Юрки Миттинен, Кальфад, том 22, №.2, стр.275-300, 1998 и "Регулярная решающая модель для фаз с различными компонентами и подрешетками, подходящая для компьютерных применений", Бо Сундман и Джон Агрен, Journal Phys. Chem. Solids, том 42, стр.297-301. Тем самым для стали является возможным определять свободную энтальпию Гиббса смеси железо-углерод в качестве функции содержания углерода и температуры и учитывать действия добавок, например Ni, Si, P, в качестве функции смеси железо-углерод и температуры. При таком выполнении модели материала, что ей задаются также относительные содержания добавок, свободные энтальпии Гиббса рассматриваемых фаз могут определяться тем самым также для материалов, заданных не явно.
Если определяют удельные, то есть отнесенные к единому количеству металла, свободные энтальпии Гиббса фаз, то скорость превращения можно определять особенно простым образом, а именно на основе разности удельных свободных энтальпий Гиббса.
Альтернативно является возможным определять скорость превращения на основе суммы взвешенных с относительными содержаниями фаз удельных свободных энтальпий Гиббса фаз.
Далее является возможным определять скорость превращения на основе интеграла по месту по удельным свободным энтальпиям Гиббса. Этот вид определения является преимущественным, в частности, в случае зависимости от места свободных энтальпий Гиббса по крайней мере одной из фаз.
Если металл содержит по крайней мере две химически отличные друг от друга компоненты, то свободные энтальпии Гиббса могут привлекаться также для определения распределения компонентов по химическим составам.
Соответствующий изобретению способ моделирования является применимым также тогда, когда по крайней мере одна из фаз соответствует жидкому агрегатному состоянию металла. Возможно, однако, также, что по крайней мере одна фаза (предпочтительным образом все фазы) соответствует (соответствуют) твердому агрегатному состоянию металла.
Возможно, что способ применяется для металла только один раз. Предпочтительно, однако, применять его на множестве локально следующих непосредственно друг за другом участков металла.
Если модели материала задают по крайней мере одну заданную температуру, то возможно, что модель материала автоматически определяет регулирующее воздействие. Заданная температура может при этом быть, в частности, временной характеристикой заданной температуры.
Регулирующее воздействие может быть временной характеристикой регулирующего воздействия. В этом случае, в частности, возможно, что с привлечением характеристики регулирующего воздействия пошагово решают уравнение теплопроводности и превращения и таким образом определяют ожидаемую температурную характеристику металла, а также ожидаемые характеристики относительного содержания фаз. Управление исполнительным звеном происходит в этом случае предпочтительно только после полного решения уравнения теплопроводности и превращения.
Регулирующее воздействие может быть также одиночным значением. В этом случае оно привлекается только для соответственно одного шага. Управление исполнительным органом происходит в этом случае предпочтительно между предыдущим и последующим шагом.
Способ моделирования работает особенно надежно, если исходная температура является фактической температурой, зарегистрированной измерительным органом перед оказанием воздействия на металл посредством исполнительного органа.
Если после воздействия на металл посредством исполнительного органа измерительным органом измеряется конечная температура металла, конечная температура сравнивается с желаемой температурой и модель материала адаптируется на основе сравнения, то модель материала является выполненной в виде самообучающейся модели.
Предпочтительным образом подлежащее решению для внутреннего объема металла 1 уравнение теплопроводности имеет вид
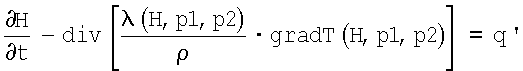
при этом означают: Н - энтальпия, t - время, λ - теплопроводность, р1 и р2 - относительные содержания фаз, ρ - плотность и Т - температура металла, q' является количеством теплоты, которое создается внутри металла за счет внешних воздействий, например деформации при прокатке или индуктивном нагреве. Теплота превращения, возникающая вследствие фазовых превращений, в противоположность этому, уже учтена в левой части уравнения.
Вышестоящее корректное уравнение теплопроводности является применимым всегда, независимо от формы и агрегатного состояния металла. Если металл выполнен в виде металлической полосы с направлением толщины полосы, то является возможным, вместо вышестоящего уравнения решать упрощенное уравнение,
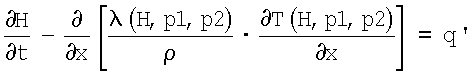
причем х является местом в направлении толщины полосы.
Дальнейшие преимущества и подробности следуют из последующего описания примера выполнения в связи с чертежами. При этом в принципиальном представлении показаны на:
Фиг.1 - установка для температурного воздействия на металл,
Фиг.2 и 3 - модели материала,
Фиг.4 - блок-схема для решения уравнения превращения,
Фиг.5 и 6 - примерные характеристики свободных энтальпий Гиббса и
Фиг.7-9 - другие установки для температурного воздействия на металл.
Согласно Фиг.1 установка для оказания температурного воздействия на металл 1 содержит исполнительный орган 2. Посредством исполнительного органа 2 (как правило, путем охлаждения, в отдельных случаях также путем нагрева) непосредственно или косвенно можно влиять на температуру Т металла 1. Например, можно наносить на металл 1 определенное количество охлаждающей среды, обычным образом воды.
Металл 1 в настоящем случае представляет собой сталь в твердом агрегатном состоянии. Он мог бы, однако, также иметь жидкое агрегатное состояние. Металл 1 мог бы быть также другим металлом, чем сталь, например алюминием или цветным металлом. Согласно Фиг.1 металл 1 выполнен в виде металлической полосы с направлением толщины полосы. Возможными, однако, являются также другие формы металла 1, например, профили в виде прутка (например, проволоки), трубы или U-профили.
Установка управляется управляющей вычислительной машиной 3. В частности, также исполнительный орган 2 управляется согласно регулирующему воздействию S управляющей вычислительной машиной 3. Управляющая вычислительная машина 3 программирована компьютерной программой 4. На основе программирования компьютерной программой 4 управляющая вычислительная машина 3 - дополнительно к управлению установкой - выполняет описанный ниже более подробно способ моделирования для металла 1.
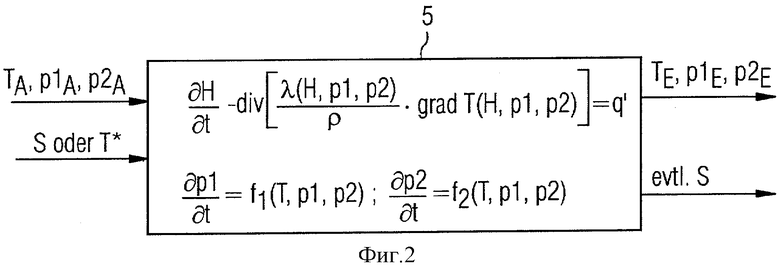
В рамках выполнения способа моделирования согласно Фиг.2 модели материала 5 для металла 1 задают исходную температуру TA металла 1, а также исходные относительные содержания р1A, р2A, в которых металл 1 присутствует в первой или, соответственно, второй фазе. Исходная температура TA может быть оценочным значением или теоретически вычисленным значением. Предпочтительно, однако (смотри Фиг.1), установка имеет измерительный орган 6. Посредством измерительного органа 6 может регистрироваться действительная температура Т металла 1. В настоящем случае такая регистрация действительного значения температуры Т происходит перед оказанием воздействия на металл 1 исполнительным органом 2. Зарегистрированная к этому моменту времени действительная температура Т является исходной температурой TA, которую подводят к модели материала 5.
Исходные относительные содержания р3A, р2A, как правило, являются значениями, определенными на основе вычислений или, соответственно, известными вследствие условий процесса. Например, заранее известно, что перед разливкой металл 1 полностью присутствует в жидкой фазе. Или известно, что материал является аустенитом, если сталь достаточно долго выдерживалась при температуре, выше температуры превращения стали.
Внутри модели материала 5 согласно Фиг.2 с учетом этих исходных значений TA, р1A, р2A, регулирующего воздействия S, а также эффективности исполнительного органа 2 для внутреннего объема металла 1 в реальном времени решают уравнения материала. Уравнения материала охватывают уравнение теплопроводности в виде
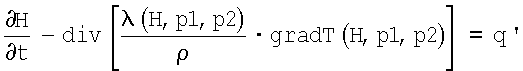
а также уравнение превращения. В уравнениях означают: Н - энтальпия, t - время, λ - теплопроводность, р1 и р2 - относительные содержания фаз, ρ - плотность и Т - температура металла, q' является количеством теплоты, которое создается внутри металла 1 за счет внешних воздействий, например, деформации при прокатке или индуктивном нагреве. Возникающая вследствие фазовых превращений теплота превращения в противоположность этому уже учтена в левой части уравнения. Внутри модели материала 5 тем самым в реальном времени определяют ожидаемую температуру Те металла 1, а также ожидаемые относительные содержания p1E и р2E, в которых металл 1 присутствует в первой или, соответственно, второй фазе.
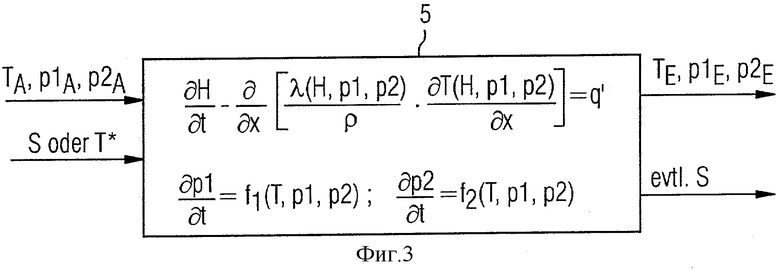
Решение уравнения теплопроводности, а также учет регулирующего воздействия S и эффективности исполнительного органа 2 является для специалистов общеизвестным. На этом в последующем поэтому более подробно не останавливаются. Следует еще только упомянуть, что вышестоящее уравнение теплопроводности является общим уравнением, подлежащим решению не зависимо от агрегатного состояния и формы металла 1. В настоящем случае, в котором металл 1 присутствует в виде металлической полосы с направлением толщины полосы, уравнение теплопроводности согласно Фиг.3 может быть сформулировано одноразмерно, так как градиенты в направлении движения полосы, а также в направлении ширины полосы в основном равны нулю. В этом случае уравнение теплопроводности может быть упрощено к виду
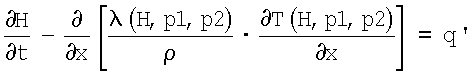
причем х дополнительно является местом в направлении толщины полосы.
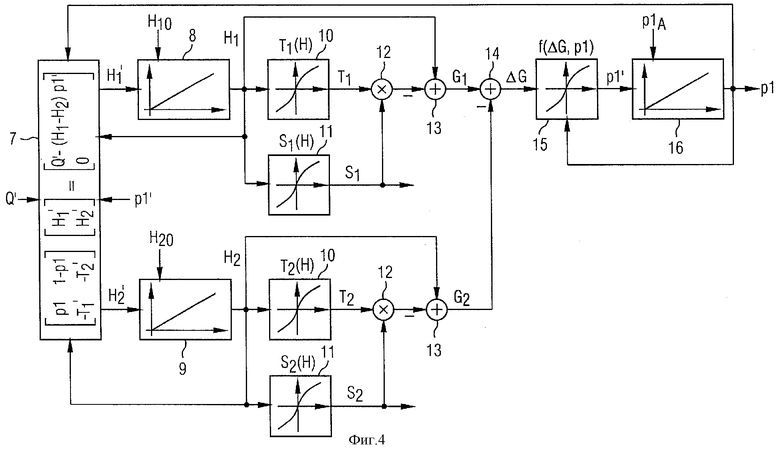
Для решения уравнения превращения применяют способ, который в последующем более подробно поясняется в связи с Фиг.4. В представлении согласно Фиг.4 при этом было сделано упрощающее предположение, что металл 1 может принимать две фазы. Способ является, однако, расширяемым без проблем на металл 1 с более чем двумя фазами.
Согласно Фиг.4 к блоку решения уравнения 7 подводят множество входных величин. Сначала к блоку решения уравнения 7 подводят количество теплоты Q'. Количество теплоты Q' охватывает, во-первых, изменение теплового баланса вследствие теплопроводности, во-вторых, также произведенное внутри металла 1 за счет внешних воздействий количество теплоты q'.
Затем к блоку решения уравнения 7 подводят еще относительное содержание р1, в котором металл 1 присутствует в первой фазе. К блоку решения уравнения 7 подводят также временное изменение р1'. Вследствие обстоятельства, что согласно Фиг.4 рассматривается только двухфазная система, тем самым известным является также относительное содержание р2 второй фазы и ее изменение р2'.
Наконец, к блоку решения уравнения 7 подводят еще энтальпии H1, H2 фаз металла 1. Энтальпии H1, H2 при этом отнесены к единому количеству металла 1, например, один килограмм или один моль.
Блок решения уравнения 7 определяет на основе линейной системы уравнений
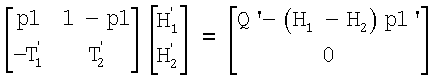
временные изменения H1', H2' энтальпий H1, H2. Эти изменения H1', H2' подводят к интеграторам 8, 9, которые затем определяют энтальпии H1, H2 в качестве выходного сигнала.
Интеграторы 8, 9 подходящим образом инициализированы исходными значениями Н10, Н20. Исходные значения Н10, Н20 при этом не могут задаваться независимо друг от друга. Более того, они должны определяться так, чтобы получающиеся удельные свободные энтальпии Гиббса G1, G2 принимали одинаковое значение при температуре фазового превращения.
В линейной системе уравнений под Т1' и Т2' следует понимать первые производные соответствующих температур Т1, Т2 по энтальпии H1 или, соответственно, H2, то есть производные не по времени.
Вместо вышеназванной линейной системы уравнений можно решать также нелинейную систему уравнений в виде
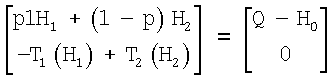
Н0 при этом является подходящим стартовым значением для энтальпии Н системы. Эта система уравнений дает непосредственно энтальпии H1, H2. При этом она, как уже упомянуто, является нелинейной.
Определенную энтальпию H1 подводят к определителю температуры 10. Он определяет на основе энтальпии H1 для рассмотренной фазы ожидаемую температуру Т1. Далее энтальпию H1 подводят к определителю энтропии 11. Он определяет для рассмотренной фазы на основе уравнения
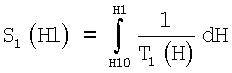
энтропию S1.
Ожидаемую температуру Т1 и определенную энтропию S1 подводят к умножителю 12. Его выходной сигнал - с отрицательным знаком - подводят к сумматору 13, к которому также подводят энтальпию H1. Выходной сигнал сумматора 13 соответствует удельной свободной энтальпии Гиббса G1 рассмотренной фазы.
Аналогичным образом также для второй фазы определяют соответствующую удельную свободную энтальпию Гиббса G2. В сумматоре 14 тогда образуется разность ΔG обоих удельных свободных энтальпий Гиббса G1, G2.
Определенную таким образом разность ΔG удельных свободных энтальпий Гиббса G1, G2 подводят к определителю скорости превращения 15. Он определяет на основе разности ΔG и относительного содержания р1 скорость превращения. Скорость превращения подводят к интегратору 16, к которому дополнительно подводят в качестве исходного значения исходное относительное содержание p1A. Выходной сигнал интегратора 16, то есть определенное ожидаемое относительное содержание p1E, затем подводят к блоку решения уравнения 7 и к определителю скорости превращения 15.
Как видно из Фиг.4, уравнение превращения решается пошагово, причем при каждом шаге к блоку решения уравнения 7 подводят определенные перед этим ожидаемые значения. Подобным образом пошагово решается также уравнение теплопроводности. Результаты решения уравнения теплопроводности и уравнения превращения при этом разумеется согласуют после каждого шага. Способ предпочтительно применяют для каждой опорной точки уравнения теплопроводности. Для экономии времени вычисления, однако, можно уменьшить также затраты при вычислении модели превращения за счет объединения опорных точек при преобразовании фаз. Уравнение теплопроводности, однако, решается всегда - то есть также в этом случае - для каждой опорной точки.
Далее температуры T1, Т2 при корректном вычислении к каждому моменту времени имеют то же самое значение, обозначаемое в последующем так же как ожидаемая температура Те. Возможное отклонение температур T1, T2 друг от друга поэтому является показателем для недостаточно оптимальной конфигурации модели материала 5. Оно может поэтому в рамках программно-технического составления модели материала 5 привлекаться для оптимирования модели материала 5 - в частности, для определителей энтропии и температуры 10, 11.
Посредством способа согласно Фиг.4 таким образом определяют временные зависимости для ожидаемой температуры те и ожидаемых относительных содержаний p1E.p2E.
Регулирующее воздействие S в способе согласно Фиг.4 не должно иметь то же самое значение в любой момент времени. Более того, регулирующее воздействие S может иметь временную характеристику, называемую в последующем характеристикой регулирующего воздействия S. Также актуальное значение регулирующего воздействия S поэтому при каждом шаге актуализируют. Оно при обработке металла 1, эффективной только на поверхности, например, при подаче воды, входит в краевые условия, которые должны учитываться при решении уравнения теплопроводности. В противоположность этому при обработке металла 1, эффективной в объеме, например, в процессе прокатки или индукционном нагреве, регулирующее воздействие S входит в количество теплоты Q'.
При пошаговом решении уравнения теплопроводности и уравнения материала возможны два альтернативных подхода. Во-первых, управление исполнительного органа 2 может производиться согласно заданной характеристике регулирующего воздействия S после определения временных характеристик для ожидаемой температуры Те и ожидаемых относительных содержаний р3E, р2Е. Во-вторых, однако, возможно также привлекать для соответствующего шага только регулирующее воздействие S и управлять исполнительным органом 2 между предыдущим и последующим шагом согласно регулирующему воздействию S.
В обоих случаях возможно задавать модели материала 5 только регулирующее воздействие S. Согласно Фиг.2 и 3, однако, возможно задавать модели материала 5 также заданную температуру Т* - предпочтительно даже временную характеристику заданной температуры Т*. В этом случае возможно, что модель материала 5 самостоятельно определяет регулирующее воздействие S на основе заданной температуры Т*, исходной температуры ТA и эффективности исполнительного органа 2.
После оказания воздействия на металл 1 посредством исполнительного органа 2 - согласно Фиг.1 посредством следующего измерительного органа 6' - снова регистрируют действительную температуру Т металла 1. Эту температуру Т, обозначаемую в последующем как конечная температура, сравнивают согласно Фиг.5 адаптерным органом 5' с ожидаемой температурой Те. На основе сравнения адаптерный орган 5' затем адаптирует модель материала 5. Например, могут варьироваться величины теплоперехода уравнения теплопроводности или величины воздействия для скоростей превращения.
Согласно данному примеру выполнения таким образом определяют удельные свободные энтальпии Гиббса G1, G2 фаз, которые относятся к единому количеству металла 1. Скорость превращения тогда определяют на основе разности ΔG. В простейшем случае скорость превращения получается как произведение постоянной с определенной разностью ΔG. Предпочтительным образом здесь, однако, предусматривают определитель скорости превращения 15, который определяет скорость превращения р1' из разности ΔG и мгновенного относительного содержания фазы p1. Такой определитель скорости превращения 15 может параметрироваться, например, на основе набора данных диаграмм время-температура фазового превращения для различных сталей.
Полностью равноценным было бы далее определять скорость превращения на основе суммы взвешенных с относительными содержаниями р1, р2 фаз удельных свободных энтальпий Гиббса G1, G2. Здесь пользуются тем, что превращение при поддерживаемой постоянной температуре происходит самостоятельно только в направлении уменьшения свободной энтальпии Гиббса G.
Описанный выше в связи с Фиг.4 образ действий является целесообразным, в частности, тогда, когда происходит чистое фазовое превращение одного и того же химического состава, например чистое превращение аустенита в феррит. Он может применяться также тогда, когда происходит чистое превращение из твердой фазы в жидкую фазу или наоборот.
При выше названном описании определения относительных содержаний р1, р2 постоянно используют актуальные мгновенные значения для удельных свободных энтальпий Гиббса G1, G2, для удельных энтропий S1, S2, для удельных энтальпий H1, Н2 и ожидаемые температуры Т1, Т2. Анализ определителей температуры и энтропии 10, 11, однако, предполагает, что функциональные характеристики или, соответственно, зависимости температур T1, T2 и удельных энтропий S1, S2 соответствующих удельных энтальпий H1, H2 являются известными. Поэтому, чтобы иметь возможность хорошо и правильно описывать фазовые превращения, необходимо предоставлять в распоряжение определителя температуры 10 и определителя энтропии 11 лежащие в основе функции, которые зависят от действительно моделируемого металла 1, в частности от его химического состава. Для этого при разработке модели материала 5 предпочтительно сначала определяют удельные свободные энтальпии Гиббса G1, G2 для фаз рассматриваемого вещества в качестве функции температуры. Определение удельной свободной энтальпии Гиббса в качестве функции температуры описано, например, в специальной статье "Термодинамический анализ системы Fe-C", Пьер Густафсон, в журнале Scandinavian Journal of Metallurgy 14(1985), стр.259-267.
На основе определенной таким образом удельной свободной энтальпии Гиббса G1 или, соответственно, G2 в качестве функции соответствующей температуры Т1 или, соответственно, Т2 - то есть функциональных характеристик удельных свободных энтальпий Гиббса G1, G2, - могут быть тогда определены без проблем функциональные характеристики температур T1, T2 или, соответственно, удельных энтропии S1, S2, в качестве функции удельной энтальпии H1, H2. Это определение является специалистам общеизвестным. Относительно подробностей снова делается ссылка на упомянутую выше статью Пера Густафсона.
При определении функциональных характеристик удельных свободных энтальпий Гиббса G1, G2, а также функциональных характеристик температур T1, T2 и удельных энтропий S1, S2 должны, в частности, учитываться также изменения удельных свободных энтальпий Гиббса G1, G2, которые вызваны добавками. Таким образом для подлежащих рассмотрению добавок определяют изменения удельных свободных энтальпий Гиббса G1, G2 в качестве функции от добавленных количеств рассматриваемых добавок. Эти изменения относительно количества рассматриваемой добавки могут быть сильно нелинейными. Они могут быть также зависимыми друг от друга. Как действие, так и взаимные зависимости являются, однако, известными, смотри уже упомянутые работы Ю.Миттинена, а также Б.Сундмана и Дж.Агрена. В результате таким образом определены определитель температуры 10 и определитель энтропии 11 также для неизвестных смесей, если относительные содержания добавок являются известными. Поэтому является возможным моделировать с высокой точностью также неизвестные смеси (в частности, неизвестные составы сталей).
На практике металл 1 имеет часто две химически отличные друг от друга основные компоненты. В случае стали этими основными компонентами являются обычно железо (в качестве основной компоненты с явно больше, чем 50 атомных процентов) и углерод. В этом случае сначала определяют удельную свободную энтальпию Гиббса G в качестве функции (относительного) содержания n одной из обеих компонент и температуры. Затем опять для подлежащих рассмотрению добавок определяют, как изменяется эта функция. Также и здесь справедливо, что изменения могут быть сильно нелинейными. Это справедливо как относительно количеств добавок, так и относительно действия тех же количеств добавок при различных соотношениях смеси железа и углерода. Таким образом вполне возможно, что определенное количество добавок (например, 1% кремния и 2% фосфора) в случае смеси железо-углерод с 1% углерода и 99% железа имеет совершенно другое влияние на удельную свободную энтальпию Гиббса смеси, чем в случае смеси железо-углерод с 4% углерода и 96% железа. Процентные данные относятся при этом к атомным процентам. Также вполне возможно, что, например, двойное количество добавок имеет совершенно другое влияние на удельную свободную энтальпию Гиббса, чем однократное количество добавок. Однако, справедливо и дальше, что влияния добавок являются известными или, соответственно, могут определяться известным образом.
Определенная таким образом характеристика удельной свободной энтальпии Гиббса G смеси железо-углерод может быть привлечена для того, чтобы опредить распределение металла 1 по химическим составам компонентов. Это еще будет более подробно поясняться на основе примерной смеси железо-углерод.
Предположим, что имеется смесь железо-углерод. При этом nа является относительным содержанием железа, nB является относительным содержанием углерода в смеси. Сумма относительных содержаний nА, nB само собой разумеется составляет единицу. Предположим далее, что nа1 является относительным содержанием железа в первом химическом составе, nA2 является относительным содержанием железа во втором химическом составе. Сумма этих относительных содержаний nA1, nA2 соответствует при этом, само собой разумеется, полному относительному содержанию nA железа. Подобным образом в обоих составах имеются также относительные содержания nB1, nB2 углерода. Сумма этих относительных содержаний nB1, nB2 дает при этом снова полное относительное содержание nВ углерода. Cm1=nA1+nB1 и m2=nA2+nB2 вводят относительные содержания для соответствующего состава. При этом свободная энтальпия Гиббса G всей системы получается в виде
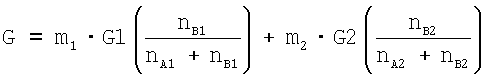
За счет (полного) дифференцирования этого уравнения по nА1 или, соответственно, nB1 и установки производных на нуль получают два уравнения и тем самым два условия для относительных содержаний nA1 и nB1. При этом следует учитывать, что в этом уравнении m1, m2 и аргумент G2 содержатся в неявном виде и nА1 и nВ2 в качестве переменных.
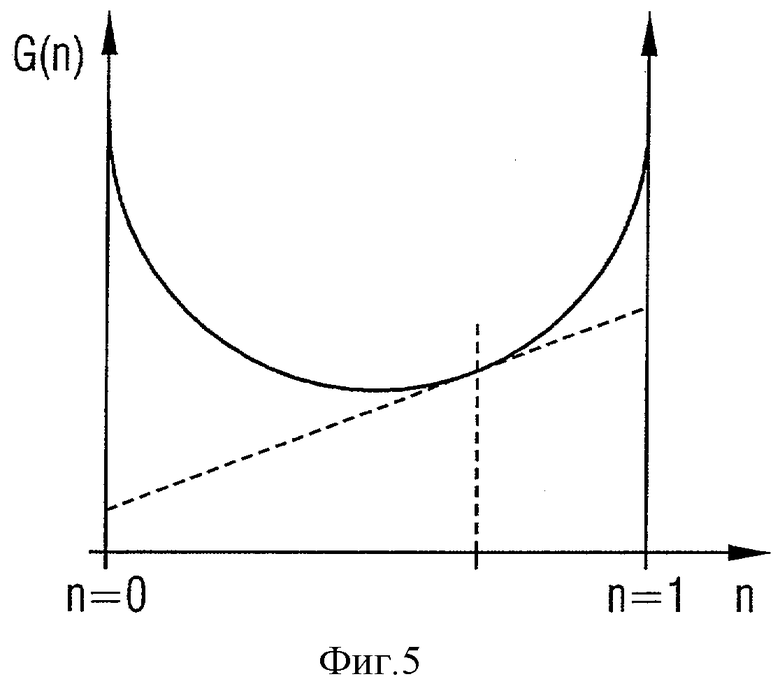
Если свободная энтальпия Гиббса G смеси железо-углерод в качестве функции относительного содержания n углерода имеет выпуклую характеристику, как она представлена, в качестве примера на Фиг.5, то разделение на два химических состава, в которых взвешенная по относительным содержаниям сумма удельных свободных энтальпий Гиббса G1, G2 является меньше, чем свободная энтальпия Гиббса G однородной смешанной системы, не возможно. В этом случае уравнения являются линейно зависимыми. В результате получается однородный химический состав металла 1.
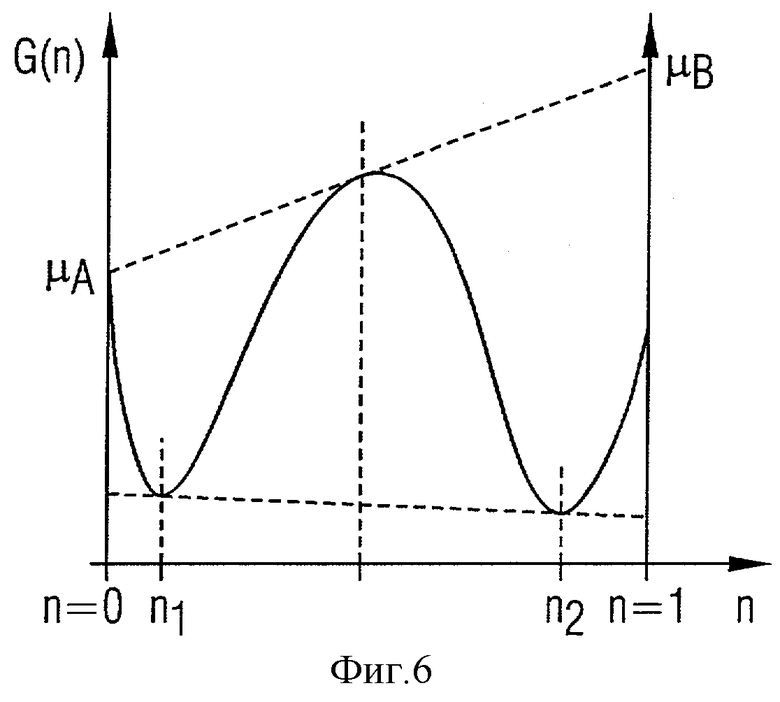
Если наоборот, как представлено в качестве примера на Фиг.6, свободная энтальпия Гиббса G в качестве функции относительного содержания углерода не проходит исключительно выпукло, то подобное разделение на два различных химических состава, в случае которых взвешенная по относительным содержаниям сумма удельных свободных энтальпий Гиббса G1, G2 является меньше, чем свободная энтальпия Гиббса G однородной смеси, возможно. В этом случае уравнения являются линейно независимыми. За счет этого в результате получаются однозначные значения для относительных содержаний nA1, nA2, nB1 и nB2. В этом случае металл 1 распадается на два отличных друг от друга химических состава. Составы имеют соотношения смеси n1 или, соответственно, n2.
Соотношения смеси n1 или, соответственно, n2 определены уравнениями
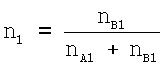
или, соответственно,
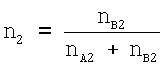
На практике часто должны предприниматься смешанные формы таких образов действия. Так, например, в аустените является растворимым относительно большое количество углерода. В противоположность этому в феррите является растворимым только малое количество углерода. Аустенит распадается поэтому при охлаждении в смесь феррита и перлита, причем перлит является эвтектической смесью, которая состоит из цементита (Fe3С) и феррита и возникла за счет охлаждения насыщенного углеродом аустенита ниже температуры превращения.
Скорость фазового превращения описывается так называемым диффузионным механизмом превращения. При этом различные фазы разделены друг от друга подвижными границами раздела фаз. Внутри каждой фазы имеются подвижные и неподвижные элементы. Неподвижные элементы распределены равномерно. Подвижные элементы в основном распределены в фазе не равномерно. Диффузия подвижных элементов происходит в каждой фазе в направлении отрицательного градиента соответствующего химического потенциала. Скорость диффузии подвижных элементов при этом является конечной. При этом химический потенциал получается путем дифференцирования удельных (то есть отнесенных к единому количеству) свободных энтальпий Гиббса по концентрации подвижных элементов. Точное представление диффузии для одного или нескольких подвижных элементов специалистам известно. На свободных поверхностях раздела фаз для определения скорости, с которой перемещается поверхность раздела фаз, должна образовываться разность удельных свободных энтальпий Гиббса непосредственно перед и непосредственно после поверхности раздела фаз. Эта постановка задачи обозначается специалистами как свободная краевая задача с диффузией или также как задача Стефана и является общеизвестной. Аппроксимативное решение находится, например, в работе Кар, А. и Мацумдер, Дж. "Аналитическое решение задачи Стефана в конечных средах." Quart. Appl. Math., том 52, 1994.
В рамках настоящего изобретения для каждого превращения - как для фазового превращения, как такового, так и для распада химического состава на другие химические составы - может быть определена собственная скорость превращения. В целом следует констатировать, что протекание процесса превращения происходит в любое время в направлении уменьшения свободной энтальпии Гиббса G общей системы. Так выше названное представление модели может быть сформулировано также без явного применения разности удельных свободных энтальпий Гиббса G1, G2 на поверхностях раздела фаз. В частности, с учетом поведения при охлаждении металла 1 тем самым возможным является не только высказывание о фазовом состоянии металла 1, но также и высказывание о его структуре строения и размере зерен.
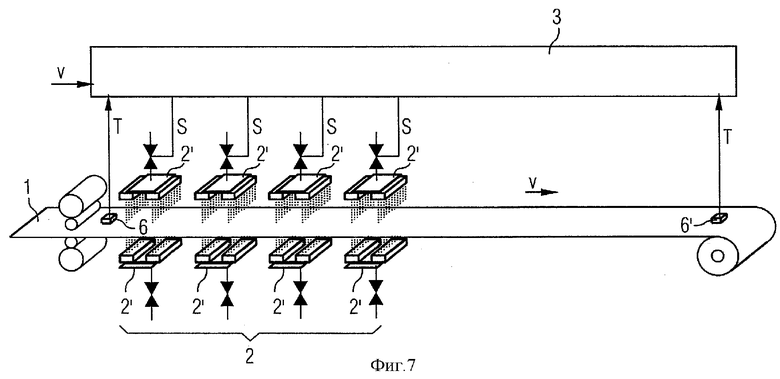
Согласно Фиг.7 установка выполнена в виде охлаждающего устройства для металла 1. Исполнительный орган 2 выполнен в виде органа для регулирования охладителя 2. Он расположен или между клетьми прокатного стана или после клетей прокатного стана. Он может подавать на металл 1 через отдельно управляемые секции 2' определенные количества охладителя, обычным образом воды.
Как уже пояснялось выше в связи с Фиг.1, посредством измерительных органов 6, 6' соответственно регистрируют температуру Т металла 1. Если охлаждающее устройство расположено исключительно после клетей прокатного стана, то измерительный орган 6 расположен после последней клети прокатного стана и перед охлаждающим устройством. С другой стороны, измерительный орган 6 расположен предпочтительно перед клетью или, соответственно, клетьми прокатного стана, расположенными перед охлаждающим устройством, а измерительный орган 6' после клети или, соответственно, клетей прокатного стана, расположенных после охлаждающего устройства.
При работе участка охлаждения во временном такте с решением уравнения теплопроводности и превращения соответственно посредством измерительного органа 6 регистрируют исходную температуру ТA металла 1. Далее к модели материала 5 подводят скорость материала v. За счет этого модель материала 5 является в состоянии, относительно участков металла 1, в которых была зарегистрирована исходная температура ТA, выполнять прослеживание материала и таким образом управлять в реальном времени отдельными секциями 2' исполнительного органа 2. Также регистрация конечной температуры Т посредством дальнейшего измерительного органа 6' в конце участка охлаждения может производиться в реальном времени и присваиваться соответствующему участку металла 1. При форме выполнения согласно Фиг.7 способ моделирования таким образом применяют при множестве расположенных непосредственно последовательно друг за другом участков металла 1.
В примере Фиг.7 направление прохождения материала всегда то же самое. Однако направление прохождения материала может также изменяться. Так, например, в случае толстолистового прокатного стана материал для охлаждения возвращают обратно к клети прокатного стана и подвергают снова операции прокатки с последующей операцией охлаждения.
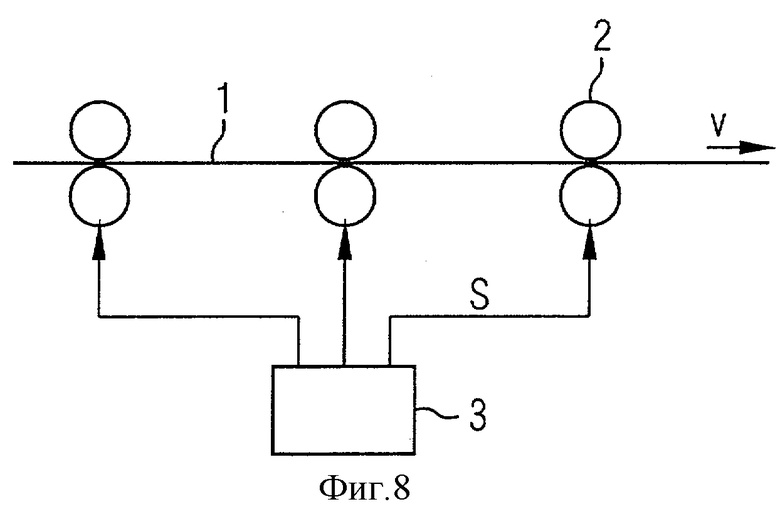
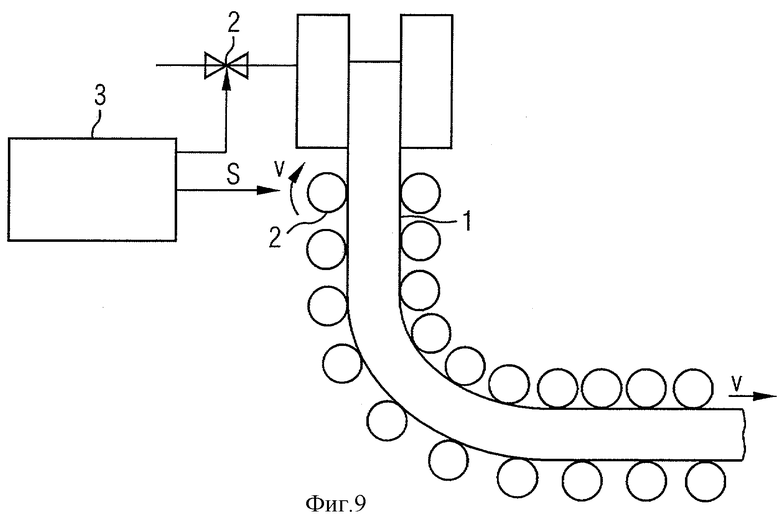
Фиг.8 и 9 показывают дальнейшие возможности применения соответствующего изобретению способа моделирования.
Согласно Фиг.8 установка выполнена в виде группы клетей прокатного стана. Исполнительным органом 2 в данном случае является одна из клетей прокатного стана, соответствующее регулирующее воздействие S скоростью прокатки. Исполнительный орган 2 при известных условиях может быть также комбинацией клети прокатного стана и охлаждающего устройства. В этом случае само собой разумеется также регулирующее воздействие S является комбинированным регулирующим воздействием.
В форме выполнения согласно Фиг.9 установка выполнена в виде установки непрерывной разливки. Исполнительный орган 2 выполнен в виде комбинированного исполнительного органа, посредством которого, с одной стороны, оказывают влияние на охлаждение кристаллизаторов установки непрерывной разливки и, с другой стороны, скорость вытягивания v, с которой отлитую заготовку 1 вытягивают из кристаллизатора.
Преимущества настоящего изобретения являются разнообразными. Во-первых, модель материала 5 настоящего изобретения позволяет получать при полном параметрировании относительно возможных добавок действительные в общем результаты, которые также позволяют производить обработку неизвестных классов материалов и веществ. Далее, - в противоположность к исходным положениям Шейла и Аврами - процесс превращения корректно описывается также для случая неполного превращения. При этом в рамках модели материала 5 - в противоположность к способам уровня техники - корректно определяется и учитывается также возникающая при фазовом превращении теплота превращения. Прежде всего, однако, сложная топология диаграмм состояния и диаграмм время-температура фазового превращения сводится к параметрированию обычных гладких кривых. За счет этого становится вообще возможной техническая обработка чрезвычайно сложной в случае стали зависимости от легирующих элементов. Так как, если давление и температура Т рассматриваемой системы - здесь металла 1 - поддерживаются постоянными, свободная энтальпия Гиббса G системы стремится к своему минимальному значению. Сравнение свободных энтальпий Гиббса G1, G2 различных фаз указывает тем самым направление фазового превращения. При этом еще может быть физически корректно обработан даже чрезвычайно трудный случай металла с добавками и такими соединениями как цементит (Fe3С) в качестве фаз. Наконец, исходные положения являются применимыми не только к температурной обработке, но также к вычислению структуры и зернистости.
Изобретение относится к области электротехнике, в частности к способам моделирования для металла (1), температура (Т) которого непосредственно или косвенно подвергается воздействию по крайней мере одного исполнительного органа (2), который управляется согласно регулирующему воздействию (S). Модели материала (5) задают регулирующее воздействие (S), а также исходные значения (Та, p1A, р2A) для температуры металла (1) и относительных содержаний фаз, в которых металл (1) имеется по крайней мере в первой или, соответственно, второй фазе. Внутри модели материала (5) с учетом этих величин (ТA, p1A, р2A) в реальном времени решают уравнение теплопроводности и уравнение превращения и определяют таким образом ожидаемые значения (Те, р1E, р2E) для этих величин. В рамках уравнения превращения при этом определяют свободные энтальпии Гиббса (G1, G2) фаз металла (1), из этого определяют скорость превращения металла (1) из первой фазы во вторую фазу и из этого определяют ожидаемые относительные содержания (р1E, р2E). Техническим результатом изобретения является улучшение результатов при моделировании, повышение надежности и возможность производить обработку неизвестных классов материалов и веществ. 4 н. и 23 з.п. ф-лы, 9 ил.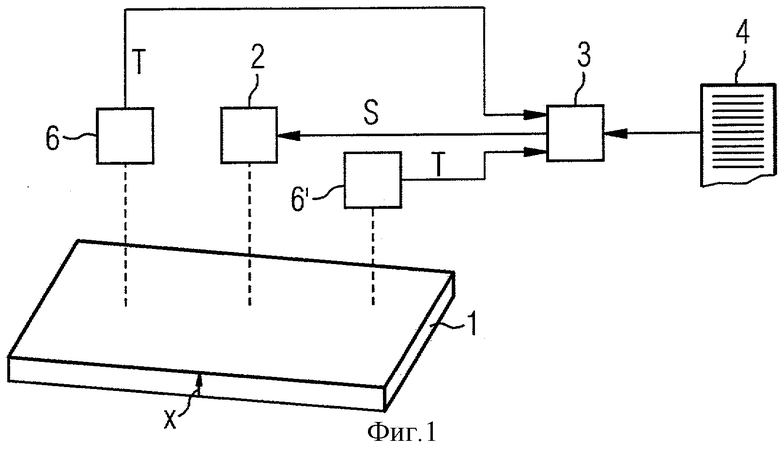
причем исполнительный орган (2) управляют согласно регулирующему воздействию (S),
отличающийся тем, что в рамках уравнения превращения определяют свободные энтальпии Гиббса (G1, G2) фаз металла (1), на основе свободных энтальпий Гиббса (G1, G2) определяют скорость превращения металла (1) из первой фазы во вторую фазу и на основе скорости превращения определяют ожидаемые относительные содержания (р1E, р2E).
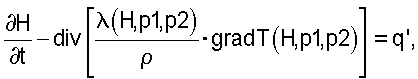
где Н - энтальпия, t - время, λ - теплопроводность, р1 и p2 - относительные содержания фаз, ρ - плотность и Т - температура металла (1), а q' - количество теплоты, которое создается внутри металла (1) за счет внешних воздействий.
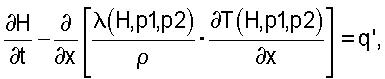
где Н - энтальпия, t - время, x - место в направлении толщины полосы, λ - теплопроводность, р1 и p2 - относительные содержания фаз, ρ - плотность и Т - температура металла (1), а q' количество теплоты, которое создается внутри металла (1) за счет внешних воздействий.
| СПОСОБ УПРАВЛЕНИЯ МЕТАЛЛУРГИЧЕСКОЙ ПЛАВКОЙ | 2001 |
|
RU2180951C1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОЦЕССОМ ПЛАВКИ В ЭЛЕКТРИЧЕСКОЙ ПЕЧИ | 2001 |
|
RU2180923C1 |
| US 6115404 А, 05.09.2000 | |||
| US 6430461 А, 06.08.2002 | |||
| DE 19963185 А, 12.07.2001 | |||
| DE 19740691 А, 18.03.1999. | |||
Авторы
Даты
2008-02-20—Публикация
2003-10-24—Подача