Настоящее изобретение относится в целом к области высокоразрешающего доплеровского анализа радиосигнала. Более точно, изобретение относится к анализу движения воздушных масс при помощи метеорологического радара.
Известно, что точная информация о движении воздушных масс в области, образующей зону впереди траектории полета самолета, имеет особое значение. Такая информация позволяет определять наличие зон турбулентности, которые способны пагубно повлиять на поведение воздушного судна.
Данная информация может быть получена различными способами и, в частности, при помощи метеорологического радара, установленного на воздушном судне, или, в более общем случае, при помощи бортовой радиолокационной станции, которая может представлять собой многоцелевую радиолокационную станцию.
Применяемый в уровне техники метеорологический радар обнаруживает движения влажных воздушных масс, которые отображают излучаемый радиосигнал, и определяет их скорости методом доплеровского анализа, в целом, методом преобразования Фурье. Принцип доплеровского анализа довольно прост и заключается в том, что для получения достаточно точных результатов передают сигнал, позволяющий получать достаточно большое число выборок при заданном расстоянии. В настоящее время метеорологические радары в целом не используют сигналы с большой периодичностью, обнаружение которых основано на относительно небольшом числе выборок (т.е. совпадений), например, в пределах от 8 до 16. В этом случае спектральный анализ методом преобразования Фурье не обеспечивает достаточную точность для того, чтобы точно определять зоны турбулентности. Это еще в большей степени справедливо, когда метеорологический анализ осуществляют при помощи многоцелевой радиолокационной станции, у которой неизбежно ограничено время, отведенное на функцию метеорологического анализа.
Данная проблема разрешающей способности также возникает, когда речь идет о наземных установках, задача которых, в частности, заключается в обнаружении движений воздушных масс в зоне приземления и зонах подхода к взлетно-посадочной полосе. Такое радиооборудование часто осуществляет высокоразрешающий доплеровский анализ, который обычно заключается, в частности, в осуществлении авторегрессивного анализа или даже анализа естественного подпространства.
Более широко распространены методы авторегрессивного анализа принимаемых сигналов. Если доступно лишь небольшое число выборок, данные методы обеспечивают значительно более высокую разрешающую способность, чем в случае использования преобразования Фурье, а также отличаются относительной простотой применения. Принцип их действия заключается в оценке маски (т.е. коэффициентов) подвижного фильтра, соответствующего сигналу, и предполагает определение порядка искомого фильтра. Основным следствием неверного определения порядка фильтра и его коэффициентов является появление ложных целей.
Обычно стандартные методы высокоразрешающего авторегрессивного анализа представляют собой рекуррентные методы, недостатком которых является неустойчивость численных решений, ставящая под угрозу способность обнаруживать цели, в частности, при небольшом числе выборок.
Задача получения стабильных результатов может быть решена при помощи известных из уровня техники методов, таких как методы, разработанные компанией ТАЛЕ (Франция), которые, в частности, заключаются в сочетании решетчатой авторегрессивной фильтрации в виде блоков с использованием алгоритма Бурга или даже алгоритма типа "MUSIC" (многосигнальная классификация) с так называемым методом регуляризации. Помимо функций фильтрации, решетчатый алгоритм Бурга определяет коэффициенты отражения µn, описывающие примененную к сигналу модель идентификации. При определении данных коэффициентов к нему применяют метод регуляризации, одной из задач которого является обеспечение убывания коэффициентов в зависимости от показателя n. Преимущество метода регуляризации состоит в том, что он позволяет определять действующий порядок модели. Вместе с тем, в настоящем уровне техники метод регуляризации обычно применяют эмпирически, что часто приводит к неточному определению порядка модели и в конечном итоге ставит под угрозу разрешающую способность произведенных измерений.
Одной из задач изобретения является повышение точности анализа, который осуществляют известными из уровня техники авторегрессивными методами, в частности, методами с использованием алгоритма Бурга, за счет точного и систематического определения порядка авторегрессивной модели идентификации анализируемого сигнала, при этом данная задача в конечном итоге заключается в повышении стабильности получаемых результатов доплеровского анализа с тем, чтобы иметь возможность с достаточной точностью определять поле радиальных скоростей воздушных масс в соответствующей анализируемой области.
Для этого в изобретении предложен способ высокоразрешающего спектрального анализа, задачей которого является оценка спектральных составляющих принимаемого сигнала на основе модели идентификации, определенной при помощи авторегрессивного фильтра типа решетчатого фильтра Бурга. Данный способ включает следующие основные шаги, на которых:
- осуществляют фильтрацию принимаемого сигнала, сочетая применение алгоритма решетчатой фильтрации и операции регуляризации, которую используют для получения заданного числа наборов коэффициентов отражения µn,
- выбирают оптимальный набор коэффициентов отражения µn,
- определяют порядок М модели идентификации сигнала,
- на основе сглаженных коэффициентов отражения µ'n определяют собственные частоты принимаемых сигналов и порядок М модели.
В предпочтительном варианте осуществления предложенный в изобретении способ также включает дополнительный шаг, на котором путем сглаживания коэффициентов µn оптимального набора получают набор коэффициентов µ'n и который осуществляют между шагом выбора оптимального набора коэффициентов µn и шагом определения порядка модели.
В частном варианте осуществления, особо применимом для анализа движения воздушных масс, предложенный в изобретении способ также включает дополнительный шаг, на котором для каждой группы расстояний выбирают, какая из определенных собственных частот является частотой, соответствующей скорости воздушной массы в соответствующей группе расстояний.
В предпочтительном варианте осуществления данный шаг выбора заключается в том, что для каждой группы расстояний определяют мощность собственных частот принимаемого сигнала в кейпеновском спектре модели.
Преимуществом предложенного в изобретении способа является его применимость для точной и систематической оценки порядка модели идентификации, созданной при помощи алгоритма решетчатой фильтрации, используемого вопреки небольшому числу выборок, доступных для заданной группы (области) расстояний. Знание точного порядка модели облегчает определение ее собственных частот.
Преимуществом данного способа также является то, что в случае применения в метеорологических радарах, он позволяет определять места возникновения внезапных изменений скорости анализируемых воздушных масс. В этом же случае способ также может использоваться для анализа каждой группы расстояний, чтобы с учетом среды, сформированной соседними группами расстояний, определять собственные частоты принимаемого сигнала. Способ также применим для выбора для каждой группы расстояний собственной частоты, которая с наибольшей вероятностью соответствует скорости воздушной массы.
Описание чертежей
Особенности и преимущества предложенного в изобретении способа станут очевидными из следующего далее описания со ссылкой на приложенные чертежи, на которых показано:
на фиг.1 - теоретическая блок-схема последовательности шагов осуществления предложенного в изобретении способа,
на фиг.2 - схематическая иллюстрация принципа работы решетчатого фильтра, в котором применен алгоритм Бурга,
на фиг.3 - иллюстрация, отображающая роль шага сглаживания коэффициентов отражения.
Общее правило применения авторегрессивного фильтра к сигналу заключается в определении модели идентификации, максимально приближенной с учетом соответствующего применения к желательному сигналу, с учетом того, что принимаемый сигнал соответствует желательному сигналу, на который наложен шум. Источники шума в целом имеют различное происхождение, внутреннее по отношению к системе, отвечающей за прием и обработку сигнала (тепловой шум и т.д.), или даже внешнее (радиолокационные помехи и т.д.).
Применительно к общему случаю импульсной радиолокационной станции принятый приемником сигнал подвергают комплексной демодуляции и получают импульсный сигнал с синус-амплитудой (со сдвигом по фазе на 90°) и косинус-амплитудой (совпадающей по фазе), образующими последовательность комплексных выборок, каждая из которых соответствует небольшой части диапазона радиолокационной станции, которую также называют группой расстояний. Анализ принимаемого сигнала в каждой группе расстояний и, в частности, доплеровский анализ предусматривает интегрирование сигналов, которые генерированы несколькими последовательно излучаемыми импульсами. Кроме того, считается, что за время проведения анализа среда, в частности, движущиеся объекты и условия эксплуатации радиолокационной станции остаются преимущественно неизменными. Окно анализа сигнала применительно к группе расстояний состоит, например, из N = от 8 до 16 выборок, накопленных на протяжении последовательности из N излучений или повторяющихся импульсов. В идеале для осуществления анализа принимаемый сигнал y(t) пытаются идентифицировать при помощи сигнала y'(t), состоящего, предпочтительно, из небольшого числа Р комплексных синусоид, то есть моделируют сигнал при помощи следующей зависимости:

в которой Aj означает комплексный коэффициент, B(t) означает комплексную величину шума (теплового шума, радиолокационных помех и т.д.), a fj означает собственные частоты (доплеровские частоты) сигнала.
При работе радара в импульсном режиме осуществляют дискретизацию принимаемого сигнала с частотой, соответствующей периоду следования импульсов или PRI (периоду повторения импульсов), или длительности Т. Следовательно, для каждой группы расстояний сигнал y(t) выражен в виде следующего числового ряда:

Авторегрессивная идентификация заключается в определении оптимального набора р коэффициентов a1, …, ар, чтобы обеспечить минимально возможное отклонение  с точки зрения определенного критерия, которым может являться минимальная энергия (критерий по методу наименьших квадратов), и записать его в виде следующего уравнения:
с точки зрения определенного критерия, которым может являться минимальная энергия (критерий по методу наименьших квадратов), и записать его в виде следующего уравнения:

в котором en означает остаточный член оценки.
Данное уравнение соответствует модели идентификации сигнала уn.
Затем осуществляют спектральный анализ, заключающийся в определении частот fj, что влечет за собой определение значения Р. Анализ частот осуществляют непосредственно по фазам корней комплексного многочлена  .
.
Задачей описанного в заявке способа является получение такого выражения у'n, которое обеспечивает спектральный анализ с оптимальным разрешением, причем данный анализ осуществляют при ограниченном числе N выборок, как правило, в пределах от 8 до 16.
Рассмотрим сначала фиг.1, на которой проиллюстрирован предложенный в изобретении способ.
Как показано на фиг.1, предложенный в изобретении способ включает пять основных шагов. Его применяют к каждой группе расстояний до принимаемого сигнала, чтобы определить спектральный компонент, соответствующий принимаемому сигналу, для соответствующей группы расстояний в зависимости от окружающих групп расстояний.
На первом шаге 11 к выборкам принимаемого сигнала применяют блочный алгоритм решетчатой AR (авторегрессивной) фильтрации с использованием алгоритма Бурга. Алгоритм фильтрации данного типа является общеизвестным и подробно не описан. Вместе с тем, далее рассмотрены некоторые общие данные, относящиеся к нему.
Решетчатая фильтрация заключается в предсказуемой фильтрации принимаемого сигнала путем идентификации данного сигнала при помощи модели.
Принцип действия алгоритма Бурга, проиллюстрированный на фиг.2, основан на суммировании М приблизительно идентичных стадий 21 вычислений, чтобы методом наименьших квадратов определить для каждой стадии n выражение оптимальной линейной оценки сигнала y(t)=у0, принимаемого в момент t, в зависимости от сигналов y(t-T)=y1, y(t-2T)=y2, …, y(t-nT)=yn, принимаемых в тот же момент t, соответствующий заданной группе расстояний во время n предшествующих повторений. Следовательно, n является целым числом, меньшим, чем число стадий М.
Для обозначения выборки принимаемого сигнала, соответствующей заданному повторению, далее в описании для простоты используется выражение y(t), в котором t означает положительное целое число от 1 до N, соответствующее числу повторений, доступных для анализа.
На каждом шаге En 21 для каждого значения t и для заданной группы расстояний вычисляют прямой  и обратный
и обратный  поправочные коэффициенты.
поправочные коэффициенты.
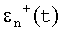 отображает существующее расхождение между y(t) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе n предыдущих выборок.
отображает существующее расхождение между y(t) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе n предыдущих выборок.
 отображает существующее расхождение между y(t-nT) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе n последующих выборок. Следует еще раз указать, что прямая и обратная поправки для шага n и для заданной группы расстояний могут быть выражены в виде следующих общих зависимостей:
отображает существующее расхождение между y(t-nT) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе n последующих выборок. Следует еще раз указать, что прямая и обратная поправки для шага n и для заданной группы расстояний могут быть выражены в виде следующих общих зависимостей:

и

в которых "Р(А|В)" отображает оптимальную линейную оценку А на основании В.
Функции  и
и  в данном случае также принимаются за имеющие неизменный характер и, следовательно, одинаковые статистические значения при t, равном любому целому числу от 1 до N.
в данном случае также принимаются за имеющие неизменный характер и, следовательно, одинаковые статистические значения при t, равном любому целому числу от 1 до N.
На основании прямой и обратной поправок, вычисленных для набора N выборок, на каждом из шагов En определяют коэффициент отражения µn, который применительно к данному шагу связан с моделью идентификации. Данные коэффициенты отражения µn, характеризующие модель идентификации, определяют известным способом на основании прямой и обратной поправок согласно следующим общим зависимостям:

в которых символом * обозначена комплексная единица, a |z| означает абсолютное значение комплексного числа z.
Данным способом решетчатый фильтр, полученный при помощи алгоритма Бурга, можно описать в виде системы, имеющей М стадий:
стадия 0: входной сигнал:
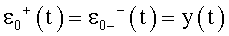 при любом значении t от 1 до N = инициализация алгоритма
при любом значении t от 1 до N = инициализация алгоритма
стадии с 1 до М:
 при любом значении t от n+1 до N
при любом значении t от n+1 до N
 при любом значении t от n+1 до N.
при любом значении t от n+1 до N.
Отфильтрованный выходной сигнал выражен следующим уравнением:
 при любом значении t от М+1 до N.
при любом значении t от М+1 до N.
Отфильтрованный сигнал еМ(t) в конечном итоге представлен как функция обратных поправок, вычисленных на каждом из шагов М.
По построению  образует ортогональный базис векторного пространства {y(t), y(t-1), … y(t-M)}. Коэффициенты отражения -µn представляют собой коэффициенты проекции y(t) на данный базис, а также комплексные коэффициенты корреляции.
образует ортогональный базис векторного пространства {y(t), y(t-1), … y(t-M)}. Коэффициенты отражения -µn представляют собой коэффициенты проекции y(t) на данный базис, а также комплексные коэффициенты корреляции.
Z-преобразование линейного фильтра для перехода от сигнала y(t) к сигналу  обозначено как
обозначено как  .
.
Z-преобразование линейного фильтра для перехода от сигнала y(t) к сигналу  обозначено как
обозначено как  .
.
 и
и  путем перестановки формул решетки доказывают верность следующих зависимостей:
путем перестановки формул решетки доказывают верность следующих зависимостей:
- для n=0:

для n=от 1 до М:
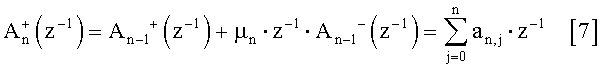

AM +(z-1) является многочленом z-1, представляющим собой z-преобразование фильтра, который таким образом преобразует сигнал y(t) в еМ(t).
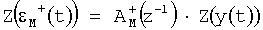 ; причем Z(A) отображает z-преобразование сигнала
; причем Z(A) отображает z-преобразование сигнала
А. Его также можно выразить в виде следующей зависимости:

в которой
- коэффициент а0 равен 1,
- коэффициент аМ равен µМ.
Кроме того, поскольку многочлены  и
и  являются возвратными, коэффициент а0 многочлена 1
являются возвратными, коэффициент а0 многочлена 1  равен µM * коэффициент аМ многочлена
равен µM * коэффициент аМ многочлена  равен 1.
равен 1.
Должным образом определенные члены  образуют семейство отбеливающих фильтров, поскольку создаваемое ими колебание между y(t) и его оптимальной линейной оценкой основано на (y(t-1), …y(t-n)).
образуют семейство отбеливающих фильтров, поскольку создаваемое ими колебание между y(t) и его оптимальной линейной оценкой основано на (y(t-1), …y(t-n)).
Алгоритм Бурга позволяет на практике определять коэффициенты отражения µn на каждом шаге на основе того факта, что данные коэффициенты сводят к минимуму функции Ln(µn), заданные следующей эмпирической зависимостью:
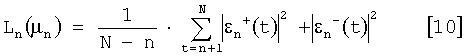
Ln(µn) является функцией µn, которая зависит, в частности, от  и
и 
В таком случае для определения коэффициентов отражения µn для значения µn определяют значение, которое аннулирует производное функции Ln(µn) относительно µn.
Данное условие позволяет вывести µn из следующей зависимости:

В обычных случаях применения решетчатого фильтра искомой является функция фильтрации, а пользователь в большей степени заинтересован в использовании поправок для получения фильтрованного сигнала еt.
Однако задачей предложенного в изобретении способа анализа является определение собственных частот принимаемого сигнала при помощи модели идентификации. Для этого в способе используют, как это проиллюстрировано на фиг.3, значения коэффициентов µn, определенные на каждой стадии. С учетом небольшого числа N доступных выборок, например, от 8 до 16, применение обычного решетчатого авторегрессивного фильтра, проиллюстрированного на фиг.2, в данном случае дает неудовлетворительные результаты. Из практики известно, что при наличии достаточного числа выборок значения коэффициентов µi, получаемые при помощи алгоритма идентификации, преимущественно убывают с рангом соответствующей стадии. С другой стороны, как показывают вычисления, данное убывание не подтверждается при наличии лишь небольшого числа выборок. Вследствие данного неудовлетворительного характера изменения затруднительно определить порядок модели идентификации фильтра, а спектральный анализ сигнала при помощи модели идентификации становится недостаточно точным.
Известен способ решения данной проблемы неудовлетворительной сходимости, в котором для определения коэффициентов µn применяют метод регуляризации по типу метода Тихонова, заключающийся в том, что к числителю и знаменателю дроби, отображающей коэффициенты µn, заданные уравнениями [5] и [12], добавляют поправочные члены. Данные поправочные члены стабилизируют вычисление коэффициентов µn. В таком случае скорректированные коэффициенты µn в целом могут быть представлены в виде следующей зависимости:
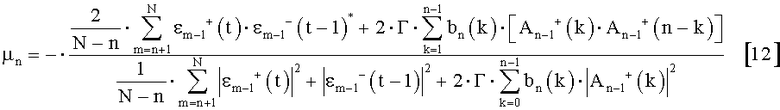
в которой
- bn(k)=(2π)2(k-n)2,
-  означает коэффициент порядка k многочлена
означает коэффициент порядка k многочлена  , заданного зависимостью [7].
, заданного зависимостью [7].
Коэффициент Г, входящий в числитель и знаменатель, называют коэффициентом регуляризации. Значение Г должно быть определено таким образом, чтобы оптимизировать данную регуляризацию.
С теоретической точки зрения регуляризация заключается в ограничении полюсов функции  таким образом, чтобы они располагались ближе к нолю в комплексной плоскости, вследствие чего обеспечивается более высокая стабильность передаточной функции. Полюса оказывают меньшее влияние на спектр (абсолютное значение
таким образом, чтобы они располагались ближе к нолю в комплексной плоскости, вследствие чего обеспечивается более высокая стабильность передаточной функции. Полюса оказывают меньшее влияние на спектр (абсолютное значение  , ограниченное единичной окружностью), в результате чего менее заметны максимальные значения. Это отражено в последовательности абсолютных значений коэффициентов отражения µn в виде повторного возникновения убывания в зависимости от порядка n стадии.
, ограниченное единичной окружностью), в результате чего менее заметны максимальные значения. Это отражено в последовательности абсолютных значений коэффициентов отражения µn в виде повторного возникновения убывания в зависимости от порядка n стадии.
Основная проблема, связанная с регуляризацией, состоит в оценке значения, которое должно быть присвоено Г. На практике чрезмерно жесткая регуляризация стабилизирует коэффициенты µn, но отдаляет результат, получаемый путем фильтрации, от точной теоретической идентификации, в частности, за пределы досягаемости. При слишком высоком коэффициенте регуляризации происходит распределение полюсов идентифицированной передаточной  в виде правильной звезды вокруг ноля комплексной плоскости. Данная правильность отражает потерю информации, поскольку считается, что положение полюсов отражает рабочие частоты синусоид, содержащихся в сигнале. С другой стороны, слишком низкий коэффициент регуляризации допускает чрезмерное колебание коэффициентов отражения µn и, следовательно, не выполняет требуемую функцию.
в виде правильной звезды вокруг ноля комплексной плоскости. Данная правильность отражает потерю информации, поскольку считается, что положение полюсов отражает рабочие частоты синусоид, содержащихся в сигнале. С другой стороны, слишком низкий коэффициент регуляризации допускает чрезмерное колебание коэффициентов отражения µn и, следовательно, не выполняет требуемую функцию.
Из литературы известны различные предложения по оптимизации коэффициента регуляризации. Особо следует отметить байесовский подход, соответствие данным, средний уровень риска, перекрестную проверку результата на достоверность. Тем не менее, данные предложения имеют скорее теоретическое, чем практическое значение, и на существующем уровне техники коэффициент регуляризации обычно определяют эмпирически по результатам определенного числа испытаний, при этом его часто требуется корректировать, а оптимальное значение данного коэффициента зависит, в частности, от мощности входного сигнала y(t).
Таким образом, проблема оценки значения, присваиваемого Г, не имеет эффективного решения на существующем уровне техники.
В настоящем изобретении предложен успешный способ определения оптимального коэффициента регуляризации. В данном способе для обработки, которую осуществляют на шаге 11 фильтрации, и определения оптимального набора коэффициентов отражения µn на последующем шаге 12 используется алгоритм решетчатой фильтрации Бурга. Способ основан на проведении экспериментов с целью формирования нового подхода к решению поставленной задачи.
Как показывает изучение зависимости [13], отображающей регуляризованные коэффициенты отражения, она обеспечивает получение результатов в виде безразмерных величин лишь при условии равномерности коэффициента Г при заданной мощности. На практике одна половина выражений числителя и знаменателя пропорциональна мощности входного сигнала Р0=E|y(t)|2, тогда как другая половина представляет собой абстрактную сущность, зависящую лишь от коэффициента передаточной функции  . Именно поэтому предложенный в изобретении способ изначально заключается в том, что выбирают коэффициент Г, который выражен в форме следующего уравнения:
. Именно поэтому предложенный в изобретении способ изначально заключается в том, что выбирают коэффициент Г, который выражен в форме следующего уравнения:

в котором q означает безразмерный коэффициент менее 1, корректируемый на основании данных (т.е. сигнала, принятого в соответствующей группе расстояний) и зависящий лишь от отношения сигнал-шум. Как правило, значения q составляют порядка 10-4.
Таким образом, при ставших равномерными формулах регуляризованного алгоритма Бурга коэффициент отражения уже не зависит от единиц измерения, а полученный спектр не меняется при умножении входного сигнала на постоянную величину. Оценка частот остается без изменений.
Следует отметить, что значение, присвоенное коэффициенту q, значительно сказывается на спектре модели. Так, при коэффициенте q порядка 1 получают равномерный спектр и последовательность Sµ практически идентичных нулевых коэффициентов отражения. С другой стороны, при уменьшении q коэффициенты отражения µn увеличиваются по абсолютной величине независимо от значения показателя n.
При q ниже определенного порогового уровня влияние регуляризации полностью прекращается, а коэффициенты с высоким показателем n возвращаются к значениям, близким к 1, случайно переходя от одного показателя к другому, в частности, что касается показателей, превышающих действующий порядок Р искомой модели идентификации.
Наконец, для промежуточных значений q восстанавливается ожидаемый характер изменения последовательности Sµ, и в таком случае данная последовательность выявляет действующий порядок модели.
Если выражение Г определено в соответствии с зависимостью [13], предложенный в изобретении способ оценки Г заключается в том, что вычисляют набор коэффициентов µn для различных значений q. Различные наборы коэффициентов вычисляют, применяя регуляризованный алгоритм решетчатой фильтрации столько же раз, сколько было сохранено значений q.
Осуществление предложенного в изобретении способа оценки Г продолжается на шаге 12, на котором анализируют набор (или наборы) коэффициентов µn, полученных на шаге 11. Данный анализ осуществляют путем вычисления для каждого значения q величины V(q), заданной следующей зависимостью:

в которой 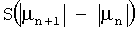 имеет значение
имеет значение  , если разность
, если разность  положительна, и 0, если она отрицательна.
положительна, и 0, если она отрицательна.
Значение V(q) называют полной положительной остаточной вариацией последнего элемента последовательности Sµ коэффициентов отражения, вычисленной для соответствующего значения q. Последний элемент последовательности образован коэффициентами µn с положительным целочисленным показателем n в пределах от положительного целого числа р менее М-1 до числа М-1 шагов.
Показатель р начала последнего элемента выбирают таким образом, чтобы он превышал ожидаемое при спектральном анализе число частот. Так, в случае спектрального анализа, осуществляемого метеорологическим радаром, ожидаемое число частот составляет порядка 3 или 4, при этом каждая частота способна, в частности, соответствовать определенному перемещению воздушной массы. В таком случае ранг р начала последнего элемента будет, например, приравнен к 5.
Следует отметить, что при высоком значении q (то есть близком к 1) V(q) стремится приблизительно к идеальному значению V(q)=0. На практике, как указано ранее, при высоком значении q коэффициенты µn убывают по абсолютной величине с увеличением n. Напротив, при чрезмерно высоком значении q происходит сжатие спектра модели. С другой стороны, при уменьшении q начинает расти V(q), что делает невозможным далее обеспечивать регуляризацию. Таким образом, чтобы осуществить практичный выбор значения q, для V(q) устанавливают пороговую величину, которая не должна быть превзойдена.
Далее осуществление способа оценки Г продолжают путем сравнения каждого значения V(q) с установленной пороговой величиной и сохранения наименьшего значения q, для которого значение V(q) остается меньшим, чем пороговая величина S1, предпочтительно, имеющая низкое значение.
Должным образом сохраненное значение q позволяет определять оптимальное значение G и соответствующий набор коэффициентов µn.
В таком случае способ определения соответствующего значения Г может быть суммарно описан следующей последовательностью операций, которая включает:
- определение набора коэффициентов отражения µn для каждого значения измеренного значения q,
- вычисление значения положительной вариации V(q) для каждого набора коэффициентов,
- сравнение каждого вычисленного значения V(q) с установленной пороговой величиной S1,
- выбор наименьшей величины q, для которой значение V(q) остается меньше, чем пороговая величина S1.
Например, можно рассмотреть случай регуляризованного фильтра Бурга, включающего 12 стадий вычислений и обеспечивающего получение набора из 12 коэффициентов отражения µ1-µ12. В соответствии с изобретением оптимальный коэффициент Г может быть оценен путем выбора для q четырех значений 10-2, 10-3, 10-4 и 10-5 и вычисления наборов коэффициентов µ1-µ12, соответствующих каждому из выбранных значений. Затем вычисляют положительные вариации V(10-2), V(10-3), V(10-4) и V(10-5) и сравнивают каждую вычисленную положительную вариацию с установленной пороговой величиной S1. В случае применения 12-стадийного фильтра и при вычислении V(q) с использованием показателя р, равного 5, пороговая величина S1, как правило, составляет порядка 0,15.
Тем не менее, при небольшом числе доступных выборок сигнала для каждой группы расстояний набор оптимальных коэффициентов, определенный описанным выше способом, отличается некоторой неточностью самих коэффициентов, которую, возможно, требуется исправить. Для этого предложенный в изобретении способ может включать шаг сглаживания данных коэффициентов, что позволяет успешно использовать среду, сформированную соседними группами расстояний. Данный промежуточный шаг, вводимый между шагами 12 и 13, обеспечивает эффективный вариант осуществления способа, предложенного в изобретении. Промежуточный шаг сглаживания, обозначенный на фиг.1 пунктирными линиями, более подробно описан далее.
Как показано на фиг.1, в наиболее общем варианте осуществления предложенный в изобретении способ также включает следующий за шагами 11 и 12 шаг 13, на котором определяют действующий порядок модели идентификации, определенной на шагах 11 и 12. Данный действующий порядок соответствует числу Р коэффициентов отражения µn, необходимых для исчерпывающей характеристики передаточной функции A(z-1), описывающей модель идентификации.
Кульминацией случая использования обычного решетчатого фильтра является передаточная функция, представленная в виде многочлена z-1, порядок которого соответствует общему числу М коэффициентов отражения, определенных фильтром. В таком случае сложность заключается в определении или вернее оценке действительного порядка Р модели идентификации.
На практике, как показывают известные теоретические результаты применения алгоритма Бурга к большому числу выборок, при ранге n, меньшем, чем значение Р, которое соответствует действующему порядку модели, коэффициенты отражения имеют абсолютное значение, близкое к 1, а затем убывают при ранге, большем, чем значение Р. С другой стороны, при небольшом числе доступных выборок сигнала, как это, в частности, имеет место в случае метеорологических радаров, данная особенность обычно не подтверждается ввиду неустойчивости численного решения, которое в этом случае влияет на расчеты коэффициентов µn. В таком случае известные из уровня техники обычные способы оценки порядка модели, такие как информационный критерий AKAIKE, MDL test, проверка χ2, которые оперируют с мощностями  последовательных остатков решетчатого фильтра, не эффективны при их применении к результатам алгоритма Бурга и не регуляризованы, когда их применяют к небольшому числу выборок. Кроме того, если регуляризация осуществлена не оптимально, эти же способы остаются, как правило, неэффективными. И даже когда осуществлена оптимальная регуляризация, данные способы остаются неудовлетворительными, допуская при оценке порядка модели ошибку, например, равную 1, для моделей, у которых действующий порядок равен 4. Таким образом, проблема не имеет эффективного решения на существующем уровне техники.
последовательных остатков решетчатого фильтра, не эффективны при их применении к результатам алгоритма Бурга и не регуляризованы, когда их применяют к небольшому числу выборок. Кроме того, если регуляризация осуществлена не оптимально, эти же способы остаются, как правило, неэффективными. И даже когда осуществлена оптимальная регуляризация, данные способы остаются неудовлетворительными, допуская при оценке порядка модели ошибку, например, равную 1, для моделей, у которых действующий порядок равен 4. Таким образом, проблема не имеет эффективного решения на существующем уровне техники.
Для ее решения на шаге 13 предложенного в изобретении способа успешно применяется оригинальный метод, включающий наблюдение за оптимальными коэффициентами отражения, определенными на шагах 11 и 12. Поскольку данные коэффициенты являются производными оптимально регуляризованного фильтра, они представлены в виде последовательности коэффициентов µn, абсолютное значение которых близко 1 при значениях n, меньших, чем значение Р, которое отображает порядок модели, и абсолютное значение которых является низким и убывающим при значениях n, больших, чем значение Р. Данный метод, используемый в предложенном в изобретении способе, позволяет описанным ранее эффективным способом оценивать порядок модели по коэффициентам µn, полученным при помощи регуляризованного фильтра Бурга.
В соответствии с изобретением коэффициенты µn наблюдают на шаге 13, используя испытующую функцию G(µn), которая гарантирует контраст, позволяющий систематически обеспечивать значительный интервал между значащими коэффициентами µn c абсолютным значением, близким к 1, и коэффициентами µn с низким абсолютным значением. Таким образом, функция G преобразует последовательность абсолютных значений коэффициентов отражения (|µ1|, |µ2|, |µ3|, …, |µM|) в последовательность высококонтрастных коэффициентов (ξ1, ξ2, ξ3, …, ξM). Затем коэффициенты ξn сравнивают в порядке убывания с установленной пороговой величиной S2. Следовательно, операция определения порядка модели в таком случае заключается в сравнении коэффициентов ξn c пороговой величиной S2 в порядке убывания показателей, начиная с ξM, до тех пор, пока не будет обнаружен первый коэффициент ξK, значение которого превышает S2. Показатель Р, для которого обеспечено данное условие, используют для оценки действующего порядка модели.
Испытующая функция G может быть задана различными способами при условии, что она гарантирует удовлетворительный контраст, позволяющий систематически определять порядок Р путем простого сравнения с пороговой величиной S2. G(µn) может быть задана, например, следующей зависимостью:

в которой оператор artanh соответствует функции "независимой переменной гиперболического тангенса".
Пороговую величину S2 определяют в соответствии с порядком М примененного решетчатого фильтра. Так, при М=12 может быть выбрана пороговая величина S2, как правило, равная 0,3.
После осуществления шага 13 предложенный в изобретении способ может затем быть применен для определения выражения передаточной функции A(z-1), т.е. порядка Р, характеризующего модель идентификации. Данная функция в целом выражена следующим уравнением:

в котором Р соответствует оценке действующего порядка соответствующим образом определенной модели.
Здесь следует отметить, что если исходить из того, что z=еiθ, то выражение  отображает спектр сигнала y(t) таким образом, что вычисление корней многочлена A(z-1) позволяет определить собственные частоты сигнала, выведенные из независимых переменных корней A(z-1).
отображает спектр сигнала y(t) таким образом, что вычисление корней многочлена A(z-1) позволяет определить собственные частоты сигнала, выведенные из независимых переменных корней A(z-1).
Таким образом, предложенный в изобретении способ включает шаг 14, на котором вычисляют корни многочлена A(z-1) и спектральные составляющие сигнала y(t).
Корни A(z-1) могут быть вычислены различными способами с учетом того, что не существует метода расчета, применимого для вычисления корней данного многочлена. В связи с этим, вне данного порядка обычно используют численный расчет методом последовательных приближений.
Вместе с тем, в том случае, когда корни принадлежат комплексной плоскости, расчет методом последовательных приближений затруднен ввиду возможной дисперсии корней.
Для преодоления данного затруднения в предложенном в изобретении способе эффективно используется замена многочлена A(z-1) многочленом A'(z-1), независимые переменные у корней которого очень близки независимым переменным корней многочлена A(z-1), но расположены на единичной окружности. Как показывают общеизвестные расчеты, которые здесь не приведены, такой многочлен может быть вычислен путем построения многочлена A'(z-1), выраженного следующей зависимостью:
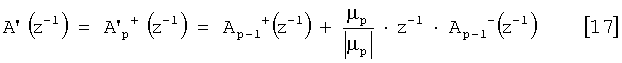
Как видно, коэффициент z-p, появляющийся, когда сформулирован многочлен из уравнения [17], преимущественно отображает абсолютное значение, равное 1, что упрощает вычисление корней.
Поиск корней многочлена A'(z-1) преимущественно проще, чем поиск корней многочлена A(z-1).
Должным образом сформулированный многочлен A'(z1 -1) также может быть обработан при помощи инструмента преобразования по типу трансформанты Кэли с тем, чтобы получить рациональную функцию с действительными значениями Q(z-1), отражающими A'(z-1), корни которого, равные A'(z-1) и расположенные на отрезке прямой между -π и +π, легко вычислить, в частности, методом дихотомии.
Таким образом, при наличии средства доступа к использованию многочлена A'(z-1), корни которого расположены на единичной окружности, и к преобразованию Кэли, можно на основе модели идентификации, созданной после осуществления шагов 11-13, успешно определять собственные частоты анализируемого сигнала.
Так, последовательность шагов с 11 по 14 предложенного в изобретении способа, проиллюстрированная на фиг.1, обеспечивает способ анализа принимаемого сигнала, в котором сигнал сопоставляют с моделью и вычисляют спектральные составляющие собственных частот такой модели. Данный способ может быть успешно применен для осуществления спектрального анализа на основе относительного небольшого числа N выборок сигнала, разрешающая способность которого превышает разрешающую способность, ожидаемую при обычной доплеровской фильтрации по типу быстрого преобразования Фурье.
Предложенный в изобретении способ также включает метод вычисления коэффициента регуляризации Г и метод определения действующего порядка модели. Способ дополнительно включает метод подстановки, который используют для облегчения поиска отображающих собственные частоты модели независимых переменных корней многочлена A(z-1).
Таким образом, в предложенном в изобретении способе для каждой группы Р расстояний получают собственные частоты, соответствующие Р корням многочлена A(z-1) и характеризующие спектр принимаемого сигнала.
Описанный выше способ спектрального анализа, предложенный в изобретении, разумеется, может быть осуществлен как таковой для определения собственной частоты или частот принимаемого сигнала для каждой группы расстояний. Затем для сохранения наиболее значимой частоты может быть осуществлена дополнительная обработка. После этого каждую частоту можно рассматривать как отображающую обнаруженный объект и осуществлять по отдельности обработку каждой из собственных частот.
Применительно к метеорологическому радару, высокоразрешающий доплеровский анализ имеет целью формирование изображения поля радиальных скоростей атмосферных масс, которое выявляет районы возмущения. Информация, почерпнутая из сигнала, являющегося производным заданной группы скоростей, в значительной степени подвержена влиянию шумов, главным образом, вследствие расширения спектра, связанного с наблюдаемым метеорологическим явлением (турбулентной воздушной массой), неточности статистических результатов, связанной с небольшим числом выборок, доступным для каждой группы, наличия какого-либо отражения от наземных предметов и собственного шума радара. Данное ухудшение качества сигнала обычно проявляется при определении нескольких собственных частот для каждой группы расстояний, причем число собственных частот, определенных таким способом, необязательно одинаково для одной группы расстояний и другой группы вблизи первой группы. Вместе с тем, моделирование принимаемого сигнала путем сбора четко разнесенных собственных частот не имеет большого смысла. Действительным спектром является широкий спектр, образованный набором очень близких частот, сгруппированных в пучки, имеющие основную центральную частоту, которая соответствует максимальной частоте. Особо важно определить именно эту основную частоту, поскольку именно она фактически отображает доплеровскую частоту, а именно скорость соответствующей атмосферной массы. Для этого предложенный в изобретении способ может быть дополнен, в частности, применительно к метеорологическому радару дополнительным шагом 16, на котором на основании собственных частот определяют основную частоту, которая фактически соответствует скорости атмосферной массы.
В соответствии с изобретением поиск данной частоты осуществляют путем вычисления максимального уровня на протяжении кейпеновского спектра сигнала. В данном случае следует отметить, что кейпеновский спектр принимаемого сигнала для заданной группы расстояний выражается в виде следующего уравнения:

при этом Р≤R≤М, где  отображает функцию
отображает функцию  , заданную зависимостью [7], когда z=еiθ. Следует напомнить, что θ выражается в виде θ=2р·fj·Т, где fj означает собственную частоту сигнала, пропорциональную скорости воздушной массы для соответствующей группы i расстояний.
, заданную зависимостью [7], когда z=еiθ. Следует напомнить, что θ выражается в виде θ=2р·fj·Т, где fj означает собственную частоту сигнала, пропорциональную скорости воздушной массы для соответствующей группы i расстояний.
Согласно изобретению для всех значений θ, соответствующих собственным частотам, вычисляют S(θ). Данные значения затем сравнивают, чтобы определить частоту, обеспечивающую максимальное значение.
С учетом того, что, как было указано ранее, спектр принимаемого сигнала представляет собой широкий спектр с основной центральной частотой, которая соответствует максимальной частоте, данную конкретную собственную частоту выбирают таким образом, чтобы она отображала значение поля скоростей для соответствующей группы расстояний.
Следует отметить, что коэффициенты σn вычисляют методом следующих рекуррентных соотношений:
- 
- 
Таким образом, вслед за шагом 16 осуществляют спектральный анализ предложенным в изобретении способом, после чего для каждой группы расстояний остается лишь единственная собственная частота, которая в случае применения в целях метеорологического анализа соответствует значению поля скоростей для соответствующей группы расстояний.
Предложенный в изобретении способ, который описан выше, имеет ряд преимуществ, позволяющих эффективно, действенно и методично осуществлять высокоразрешающий спектральный анализ путем обработки с использованием алгоритма решетчатой фильтрации и, в частности, алгоритма Бурга. Вместе с тем, существует возможность дальнейшего повышения эффективности предложенного в изобретении способа за счет осуществления дополнительно обработки оптимального набора коэффициентов µn после выполнения шага 12. Данная возможность, в частности, осуществима, когда сигнал y(t), принимаемый в заданной группе расстояний, не является полностью независимым от сигнала, принимаемого в удаленных соседних группах. В таких условиях может быть успешно реализован один из вариантов осуществления предложенного в изобретении способа. В данном варианте осуществления между шагами 12 и 13 исходного способа выполняют промежуточный шаг 15, на котором для каждой группы расстояний сглаживают вычисленный после выполнения шага 12 оптимальный набор коэффициентов µn в зависимости от наборов коэффициентов соседних групп. Принцип данного сглаживания проиллюстрирован на фиг.3, на которой схематически представлено возможное изменение собственной частоты принимаемого сигнала, соответствующей, например, воздушной массе, в зависимости от групп проходимого расстояния. В данном примере рассматриваемая воздушная масса имеет поле скоростей или поле частот с двумя зонами 31 и 32, в которых изменения собственной частоты относительно малы. Собственная частота в данных зонах в зависимости от соответствующей группы расстояний принимает значение, которое колеблется вокруг среднего значения, частоты F1 для зоны 31 и частоты F2 для зоны 32.
Поле скоростей, соответствующее примеру, проиллюстрированному на фиг.3, также включает определенное число групп расстояний, образующих переходную зону 33, в которой соответствующая собственная частота значительно меняется.
В действительности данная переходная зона может, например, соответствовать зоне турбулентности, положение и размеры которой полезно определить. Задача сглаживания согласно предложенному в изобретении способу заключается в том, чтобы уменьшить несоразмерность коэффициентов отражения, относящихся к группам расстояний, расположенным в одной и той же зоне 31 и 32, не размывая контуров каждой зоны, которые обозначают положение зон турбулентности.
В соответствии с изобретением операция сглаживания заключается в том, что к каждому из коэффициентов µn из оптимального набора применяют гауссову анизотропную и нелинейную фильтрацию, для чего в каждой группе расстояний каждый коэффициент µn из оптимального набора коэффициентов заменяют коэффициентом µ'n, значение которого является результатом линейного комбинирования коэффициентов µn соседних групп расстояний. Данное линейное комбинирование осуществляют в диапазоне групп расстояний с центром в группе r и полушириной L (для L, например, может быть установлено значение 10), в результате чего окно показателей групп расстояний располагается между положением sup(0, r-L) и inf(Lmax, r+L), причем Lmax означает максимальное число доступных групп расстояний. Данное линейное комбинирование представлено в виде суммы взвешенных по весу коэффициентов µn, форма которого отражает закон Гаусса и которое для рассматриваемой группы i выражено в виде следующего уравнения:

где σ означает регулируемый параметр типа изменения, который регулирует гауссову ширину, a d(r, i) означает криволинейное расстояние, разделяющее эталонную группу расстояний r, для которой вычислен коэффициент µ'n, и рассматриваемую соседнюю группу расстояний i. Расстояние d(r, i) является криволинейным настолько, насколько оно является суммой расстояний между соседними группами r и i.
d(r, i) = сумме расстояний d(j, j+1) от r до i-1, если i>r, и сумме расстояний d(j, j+1) от i до r-1, если i<r.
В соответствии с изобретением данное первичное расстояние d(j, j+1), которое будет обозначено просто как d, выражено следующей зависимостью:

Δх означает количество, пропорциональное расстоянию, разделяющему две соседние группы расстояний, следовательно, пропорциональное ширине группы расстояний. Δх задано следующей зависимостью:
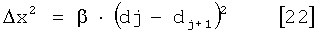
в которой β означает регулируемый положительный коэффициент масштабирования, (di-dr) означает радиальное расстояние между двумя группами i и r.
Δy означает спектральное расстояние, которое при помощи коэффициентов µn соответствующих групп s j и k=j+1 задано следующей зависимостью:

при 
Puj и Puk в данном случае означают мощность сигнала, принимаемого, соответственно, в группе j и группе k, причем каждая групп расстояний j условно обозначена вектором с М+1 компонентов (Puj, µ1,j, µ2,j, …, µM,j).
Мощности Puj и Puk также заданы следующей зависимостью:

в которой y(t) в данном случае означает сигнал, принимаемый в соответствующей группе расстояний.
Δy означает геодезическое расстояние между спектрами согласно геометрической теории Ченцова, установленное при помощи алгоритма Бурга, исходя из гауссова входного сигнала (риманова геометрия информации о сложном разбросе параметров Рu и µ в сочетании с информационной матрицей Фишера для метрического тензора).
После осуществления сглаживания на шаге 15 получают новый набор коэффициентов µ'n, выбранных из оптимального набора коэффициентов µn, используемого на шагах 13, 14, и последующем шаге 16.
Следует отметить, что в предложенном в изобретении способе сглаживания в качестве критерия преимущественно используется тот факт, что, чем более удалена группа расстояний i географически или спектрально от рассматриваемой группы r, тем меньше соответствующий коэффициент отражения µi влияет на значение сглаженного коэффициента µr.
Нелинейный и анизотропный характер осуществляемого сглаживания связан с применением закона взвешивания, который для показателей r и i зависит от общего криволинейного расстояния между r и i.
Применяемый закон взвешивания Wi,r коэффициентов позволяет успешно осуществлять сглаживание коэффициентов µ. Так, для групп расстояний, расположенных в зоне, в которой скорость атмосферной массы приблизительно постоянна, общее криволинейное расстояние, включающее спектральное расстояние между двумя группами, относительно мало, а сглаженное значение коэффициента отражения µn заданной группы расстояний r, относящейся к данной зоне, представляет собой результат усреднения значений коэффициентов µi из набора окружающих групп. Напротив, в зоне 35 вблизи переходной зоны 33 сглаженное значение коэффициента отражения группы r представляет собой просто результат усреднения значений коэффициентов µi групп расстояний, близких географически, но расположенных на другой стороне переходной зоны, т.е. удаленных спектрально, и является очень небольшим.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ЧАСТОТНОГО АНАЛИЗА ДАННЫХ | 2009 |
|
RU2503938C2 |
| Способ улучшения речевого сигнала с низкой задержкой, вычислительное устройство и считываемый компьютером носитель, реализующий упомянутый способ | 2023 |
|
RU2802279C1 |
| СПОСОБ ОДНОПОЗИЦИОННОГО ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ДКМВ ПЕРЕДАТЧИКОВ | 2004 |
|
RU2285934C2 |
| СПОСОБЫ СИНТЕЗА И КОДИРОВАНИЯ РЕЧИ | 2010 |
|
RU2557469C2 |
| ИЗМЕНЕНИЕ ФОРМЫ ШУМА ОКРУГЛЕНИЯ ДЛЯ ОСНОВАННЫХ НА ЦЕЛОЧИСЛЕННОМ ПРЕОБРАЗОВАНИИ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ АУДИО И ВИДЕОСИГНАЛА | 2008 |
|
RU2530926C2 |
| СПОСОБ ОБНАРУЖЕНИЯ И АВТОСОПРОВОЖДЕНИЯ ОБЪЕКТОВ ЦЕЛЕУКАЗАНИЯ ОПТИКО-ЭЛЕКТРОННОЙ СИСТЕМОЙ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2020 |
|
RU2748763C1 |
| Способ регуляризованного обнаружения полезных сигналов загоризонтной радиолокации при нестационарном ионосферно-пространственном распространении радиоволн | 2023 |
|
RU2817867C1 |
| СПОСОБ ПОДАВЛЕНИЯ ОШИБОК МНОГОЛУЧЕВОСТИ В ПРИЕМНИКЕ СПУТНИКОВОЙ НАВИГАЦИИ | 2010 |
|
RU2432585C1 |
| Способ оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763125C1 |
| УСТРОЙСТВО И СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОЛОГИЧЕСКИХ ГРАНИЦ | 2011 |
|
RU2600493C2 |


Изобретение относится к области анализа движения воздушных масс при помощи метеорологического радара. Предлагается способ спектрального анализа дистанционно дискретизированного периодического радиосигнала с использованием алгоритма решетчатой авторегрессивной фильтрации Бурга, при помощи которого для каждой группы расстояний путем определения оптимального набора коэффициентов отражения µn сигнала определяют собственные частоты принимаемого сигнала. Коэффициенты отражения являются объектом регуляризации, имеющей целью ограничить неустойчивость численного решения расчетов. Регуляризованные коэффициенты применяют для оценки действующего порядка модели идентификации решетчатого фильтра и для определения собственных частот сигнала путем вычисления независимых переменных комплексных корней многочлена, отображающего передаточную функцию решетчатого фильтра. Для каждой группы расстояний определяют, какая из собственных частот является для данной группы доплеровской частотой воздушной массы. Способ дополнен пространственным сглаживанием коэффициентов отражения перед определением действующего порядка модели и поиском корней многочлена. Предложенный способ применим для высокоразрешающего спектрального анализа, когда его необходимо осуществлять на основе небольшого числа выборок сигнала. Достигаемый технический результат - повышение точности спектрального анализа. 10 з.п. ф-лы, 3 ил.
1. Способ высокоразрешающего спектрального анализа дистанционно дискретизированного периодического радиолокационного сигнала, где каждая выборка соответствует небольшой части диапазона радиолокатора, называемой группой расстояний, позволяющий на основании модели авторегрессивной идентификации определять собственные частоты принимаемого сигнала для каждой группы расстояний, отличающийся тем, что в нем осуществляют по меньшей мере:
шаг (11) фильтрации, на котором применяют авторегрессивный алгоритм решетчатой фильтрации, включающий М стадий вычисления набора М коэффициентов отражения µn, характеризующих принимаемый сигнал, которые осуществляют на основании N выборок сигнала, при этом алгоритм фильтрации сочетают с операцией регуляризации вычисленного коэффициента, в результате чего получают выражение коэффициентов отражения, зависящих от коэффициента регуляризации Г, причем алгоритм решетчатой фильтрации применяют на шаге фильтрации к различным выбранным значениям Г, чтобы получить несколько наборов коэффициентов µn, каждый из которых соответствует одному из выбранных значений Г;
шаг (12), на котором на основании наборов коэффициентов, определенных на шаге фильтрации, определяют оптимальный набор коэффициентов отражения;
шаг (13), на котором на основании оптимального набора М коэффициентов µn путем анализа коэффициентов µn при помощи функции контраста G(µn) определяют действующий порядок Р модели идентификации фильтра;
шаг (14), на котором на основании многочлена A(z-1), характеризующего передаточную функцию фильтра, полученного при помощи алгоритма фильтрации, определяют собственные частоты модели идентификации.
2. Способ по п.1, в котором на шаге фильтрации применяют решетчатый алгоритм Бурга.
3. Способ по п.1, в котором коэффициент регуляризации Г выражен в виде уравнения:
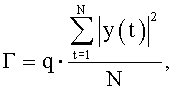
в котором y(t) означает принимаемый сигнал для заданной группы расстояний, N означает число выборок, а q означает регулируемый положительный безразмерный коэффициент менее 1, зависящий лишь от отношения сигнал-шум.
4. Способ по п.1, в котором для определения оптимального набора коэффициентов отражения для каждого набора осуществляют анализ значения величины V(q), заданной следующей зависимостью:

в которой 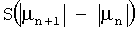 равно
равно  если разность
если разность 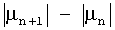 является положительной, и равно 0, если она отрицательна, µn+1 и µn соответствуют коэффициентам отражения, вычисленным на стадиях n и n+1, причем показатели n коэффициентов находятся между положительным целым числом р, меньшим, чем М-1, и числом М-1, при этом М означает общее число стадий фильтра, а р выбирают таким образом, чтобы оно было больше, чем число ожидаемых при спектральном анализе частот.
является положительной, и равно 0, если она отрицательна, µn+1 и µn соответствуют коэффициентам отражения, вычисленным на стадиях n и n+1, причем показатели n коэффициентов находятся между положительным целым числом р, меньшим, чем М-1, и числом М-1, при этом М означает общее число стадий фильтра, а р выбирают таким образом, чтобы оно было больше, чем число ожидаемых при спектральном анализе частот.
5. Способ по п.1, в котором функция контраста G(µn) выражена в виде следующего уравнения:

где оператор artanh соответствует функции обратного гиперболического тангенса.
6. Способ по п.1, в котором на шаге определения собственных частот модели идентификации вычисляют корни многочлена A'(z-1), выраженного в виде уравнения:
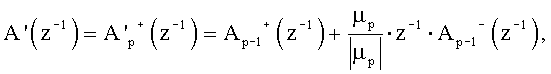
в котором Р соответствует оценке действующего порядка модели.
7. Способ по п.1, дополнительно включающий шаг (16), на котором для каждой группы расстояний определяют, какая из ранее определенных собственных частот является основной частотой, соответствующей значению поля скоростей в рассматриваемой группе расстояний.
8. Способ по п.7, в котором для определения основной частоты осуществляют поиск собственной частоты fj с максимальным значением в кейпеновском спектре, заданным уравнением:

при этом Р≤R≤М,
где 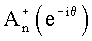 отображает функцию
отображает функцию  для z=еiθ при θ=2π·fj·Т и
для z=еiθ при θ=2π·fj·Т и
где коэффициенты  вычисляют методом следующих рекуррентных соотношений:
вычисляют методом следующих рекуррентных соотношений:
σ0=1

где fj означает собственную частоту сигнала, пропорциональную скорости воздушных масс для соответствующей группы i расстояний, a  соответствует Z-преобразованию линейного фильтра для перехода от полученного сигнала y(t) к сигналу εn +(t), отображающему существующее расхождение между y(t) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе предыдущих выборок.
соответствует Z-преобразованию линейного фильтра для перехода от полученного сигнала y(t) к сигналу εn +(t), отображающему существующее расхождение между y(t) и его выраженным методом наименьших квадратов оптимальным прогнозом, полученным на основе предыдущих выборок.
9. Способ по п.1, дополнительно включающий промежуточный шаг (15) сглаживания коэффициентов отражения, образующих оптимальный набор, для чего осуществляют гауссову анизотропную и нелинейную фильтрацию с целью замены каждого коэффициента µn из оптимального набора коэффициентов коэффициентом µ'n, значение которого является результатом линейного комбинирования коэффициентов µn соседних групп расстояний.
10. Способ по п.9 в котором линейное комбинирование представлено в виде суммы взвешенных по весу коэффициентов µn смежных груп, форма которого отражает закон Гаусса и которое для рассматриваемой группы i выражено в виде уравнения:

где σ означает регулируемый параметр дисперсионного типа, который регулирует гауссову ширину, a d(r, i) означает криволинейное расстояние, разделяющее эталонную группу расстояний r, для которой вычислен коэффициент µ'n, и рассматриваемую соседнюю группу расстояний i.
11. Способ по п.10, в котором расстояние d(r, i) выражено уравнением:
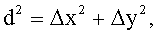
в котором Δх и Δy заданы следующими зависимостями:

где β означает регулируемый положительный коэффициент масштабирования, (di-dj+1) означает радиальное расстояние между двумя смежными группами i и j+1,
и

при

где Puj и Puj+1 означают мощность сигнала, принимаемого соответственно в группе j и группе j+1, а М - число коэффициентов отражения µn, характеризующих полученный сигнал, и n - индекс соответствующего коэффициента отражения µ.
| СПОСОБ И СИСТЕМА ИЗМЕРЕНИЯ РАДИОЛОКАЦИОННОЙ ОТРАЖАТЕЛЬНОЙ СПОСОБНОСТИ И ДОПЛЕРОВСКОГО СДВИГА ПОСРЕДСТВОМ ИМПУЛЬСНОГО РАДИОЛОКАТОРА | 1999 |
|
RU2249230C2 |
| Способ дистанционного зондирования атмосферы и подстилающей поверхности Земли | 1983 |
|
SU1111582A1 |
| СПОСОБ РАДИОАКУСТИЧЕСКОГО ЗОНДИРОВАНИЯ АТМОСФЕРЫ | 2000 |
|
RU2196345C2 |
| СПОСОБ ИЗМЕРЕНИЯ ПОЛНОГО ВЕРТИКАЛЬНОГО ОСЛАБЛЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В АТМОСФЕРЕ | 1985 |
|
SU1394936A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ИОНОСФЕРЫ ЗЕМЛИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2177161C1 |
| US 5724125 A, 03.03.1998 | |||
| WO 2005040853 A, 06.05.2005 | |||
| EP 1608995 A2, 28.12.2005 | |||
| US 5442359 A, 15.08.1995. | |||
Авторы
Даты
2011-06-20—Публикация
2006-09-06—Подача