Текст описания приведен в факсимильном виде.





















Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических операций умножения аргументов множимого [mj]f(2n) и множителя [ni]f(2n) в позиционном формате. Техническим результатом является упрощение структуры умножителя и повышение быстродействия. В одном варианте устройство содержит две логические структуры, каждая из которых состоит из j логических элементов И, логическую структуру, состоящую из j+2 логических элементов И, логическую структуру, состоящую из j+2 логических элементов ИЛИ. 4 н.п. ф-лы.
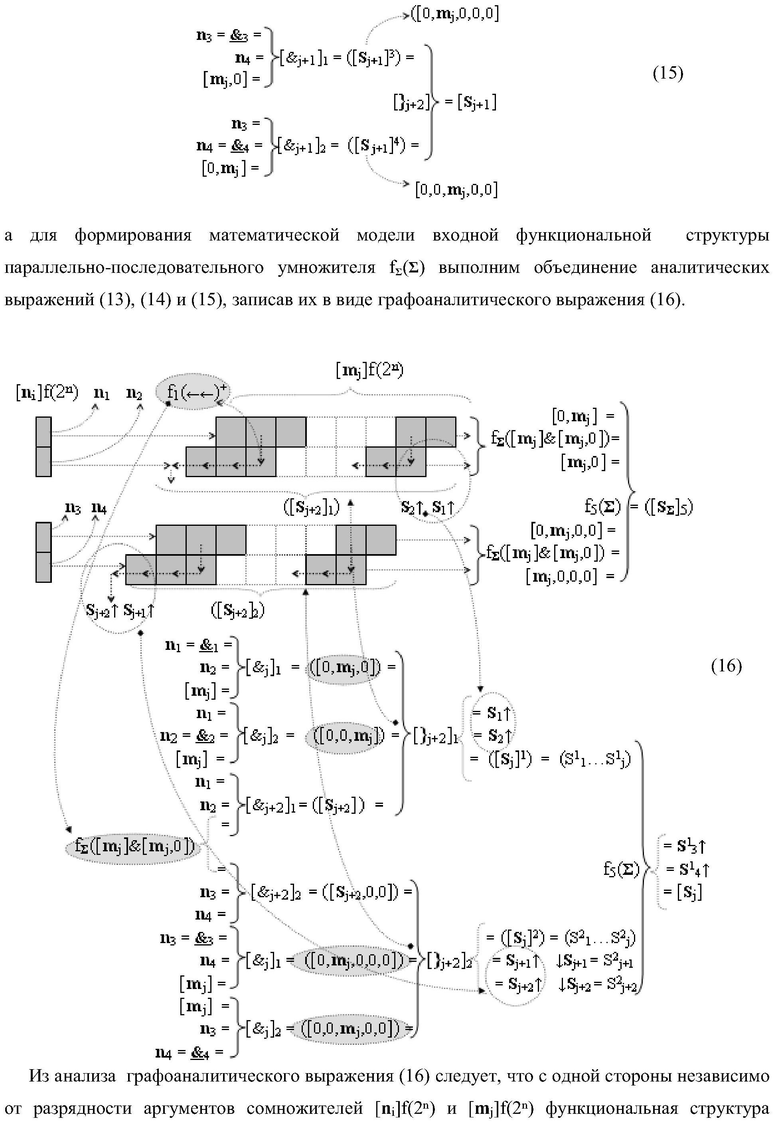
1. Функциональная входная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [mj]f(2n) и множителя [ni]f(2n), которая включает сумматор для формирования промежуточной суммы [Sj+2]0 и линейные логические структуры f1([&j])-И и f2([&j])-И из «j» логических функций f(&)-И для формирования двух условно «i+1» и «i» частичных произведений, в которых первые функциональные входные связи являются функциональными входными связями входной структуры для приема аргумента ni и ni+1 множителя [ni]f(2n), а вторые функциональные входные связи являются функциональными входными связями входной структуры для приема соответствующего аргумента [mj] множимого [mj]f(2n), отличающаяся тем, что во входную структуру дополнительно введена линейная логическая структура f([&j+2])-И из «j+2» логических функций f(&)-И и линейная логическая структура f([}j+2])-ИЛИ из «j+2» логических функций f(})-ИЛИ для формирования результирующей суммы [Sj+2](i+1&i) двух условно «i+1» и «i» последовательных частичных произведений, при этом функциональные связи во входной структуре параллельно-последовательного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
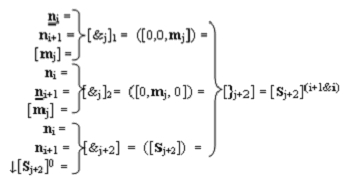
где 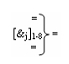 - линейная логическая структура f1-8([&j])-И, которая включает «j» логических функций f(&)-И
- линейная логическая структура f1-8([&j])-И, которая включает «j» логических функций f(&)-И 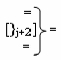 - линейная логическая структура f([}j+2])-ИЛИ, которая включает «j+2» логических функций f(})-ИЛИ.
- линейная логическая структура f([}j+2])-ИЛИ, которая включает «j+2» логических функций f(})-ИЛИ.
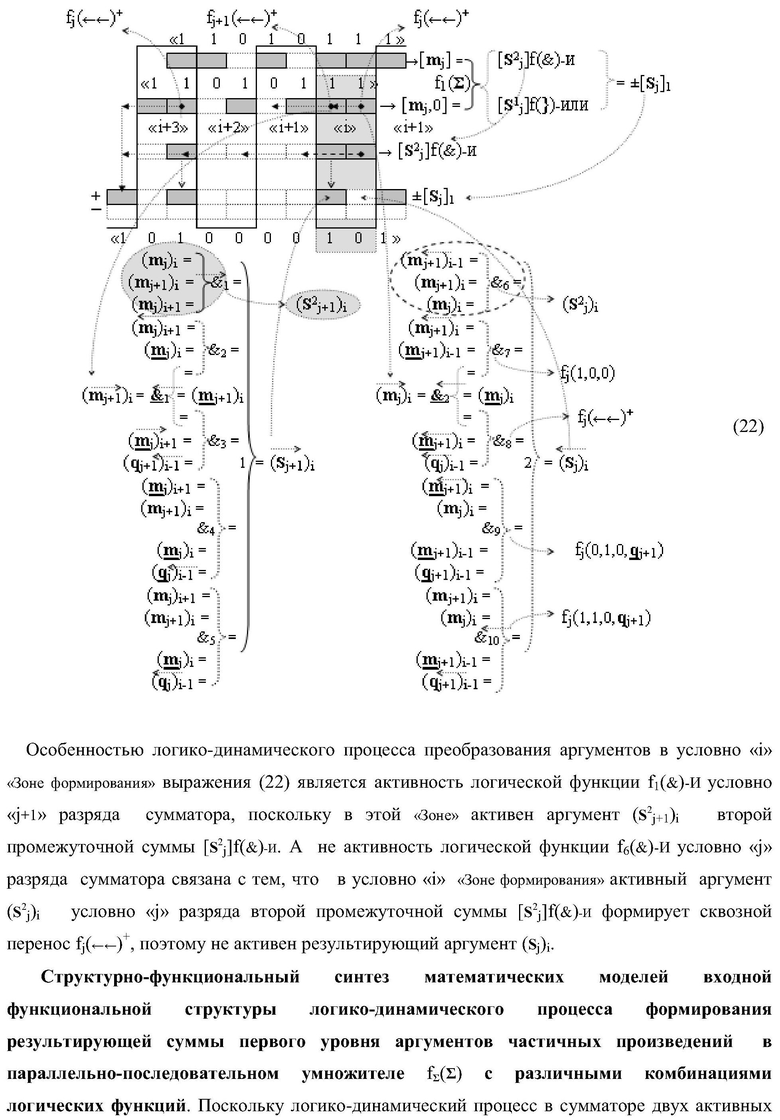
2. Функциональная входная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [mj]f(2n) и множителя [ni]f(2n), которая включает сумматор для формирования промежуточной суммы [Sj+2]0, отличающаяся тем, что во входную структуру дополнительно введены линейные логические структуры f1([&
j])-И-НЕ, f2([&
j])-И-НЕ из «j» логических функций f(&)-И-НЕ, f1([&
j+2])-И-НЕ из «j+2» логических функций f(&)-И-НЕ и линейная логическая структура f1([&
j+2])-И-НЕ из «j+2» логических функций f(&)-И-НЕ для формирования результирующей суммы [Sj+2](i+1&i) двух условно «i+1» и «i» последовательных частичных произведений, при этом функциональные связи во входной структуре параллельно-последовательного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
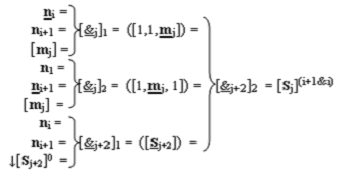
где 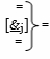 - линейная логическая структура f([&
j])-И-НЕ, которая включает «j» логических функций f(&)-И-НЕ.
- линейная логическая структура f([&
j])-И-НЕ, которая включает «j» логических функций f(&)-И-НЕ.
3. Функциональная входная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [mj]f(2n) и множителя [ni]f(2n), которая включает сумматор для формирования промежуточной суммы [S
j+2]0 с измененным уровнем аналогового сигнала, отличающаяся тем, что во входную структуру дополнительно введены линейные логические структуры f1([}j])-ИЛИ, f2([}j])-ИЛИ из «j» логических функций f(})-ИЛИ, линейная логическая структура f1([}j+2])-ИЛИ из «j+2» логических функций f(})-ИЛИ и линейная логическая структура f1([&
j+2])-И-НЕ из «j+2» логических функций f(&)-И-НЕ для формирования результирующей суммы [Sj+2](i+1&i) двух условно «i+1» и «i» последовательных частичных произведений, при этом функциональные связи во входной структуре параллельно-последовательного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
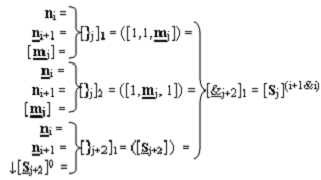
4. Функциональная входная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [mj]f(2n) и множителя [ni]f(2n), которая включает сумматор для формирования промежуточной суммы [S
j+2]0 с измененным уровнем аналогового сигнала, отличающаяся тем, что во входную структуру дополнительно введены линейные логические структуры f1([}&
j])-ИЛИ-НЕ, f2([}&
j])-ИЛИ-НЕ из «j» логических функций f(}&)-ИЛИ-НЕ, линейная логическая структура f([}&
j+2])-ИЛИ-НЕ из «j+2» логических функций f(}&)-ИЛИ-НЕ и линейная логическая структура f([}j+2])-ИЛИ из «j+2» логических функций f(})-ИЛИ для формирования результирующей суммы [Sj+2](i+1&i) двух условно «i+1» и «i» последовательных частичных произведений, при этом функциональные связи во входной структуре параллельно-последовательного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
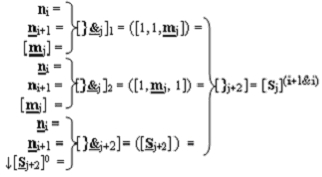
где 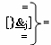 - линейная логическая структура f1,2([}&
j])-ИЛИ-НЕ, которая включает «j» логических функций f(}&)-ИЛИ-НЕ.
- линейная логическая структура f1,2([}&
j])-ИЛИ-НЕ, которая включает «j» логических функций f(}&)-ИЛИ-НЕ.
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ ФОРМАТА ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2378684C1 |
| ОДНОТАКТНЫЙ УМНОЖИТЕЛЬ ДВОИЧНЫХ ЧИСЕЛ | 1988 |
|
RU2012039C1 |
| JP 2000172487 A, 23.06.2000 | |||
| JP 10307706 A, 17.11.1998 | |||
| JP 4216126 A, 06.08.1992. | |||
Авторы
Даты
2011-06-27—Публикация
2010-03-04—Подача