Текст описания приведен в факсимильном виде.




















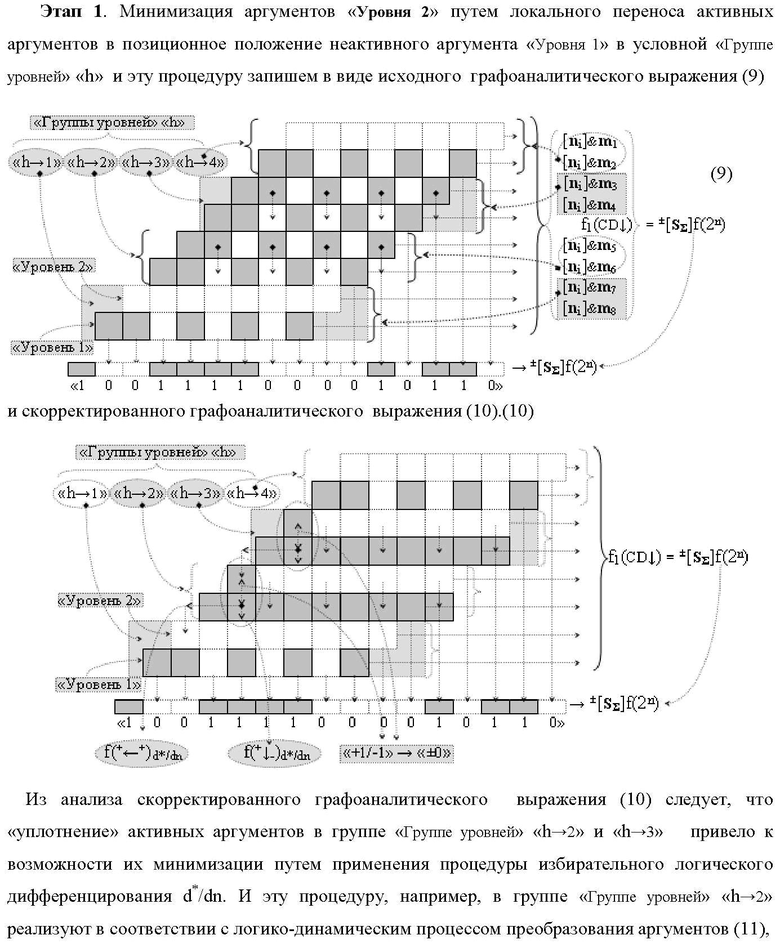




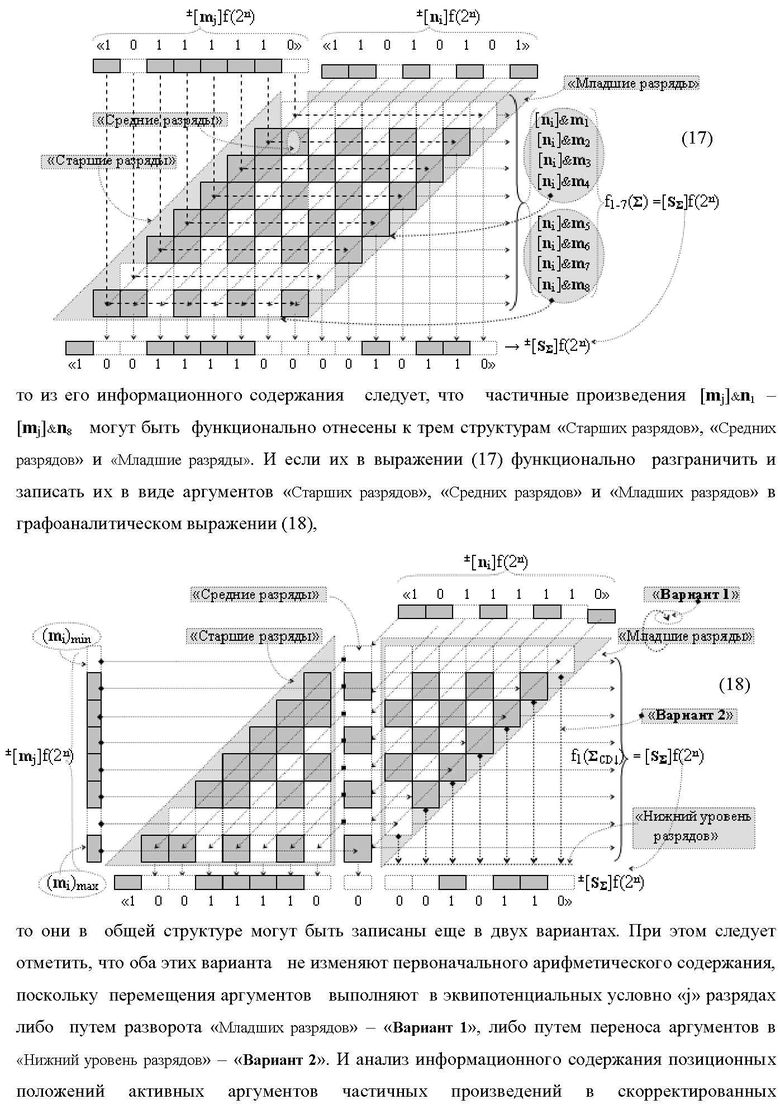









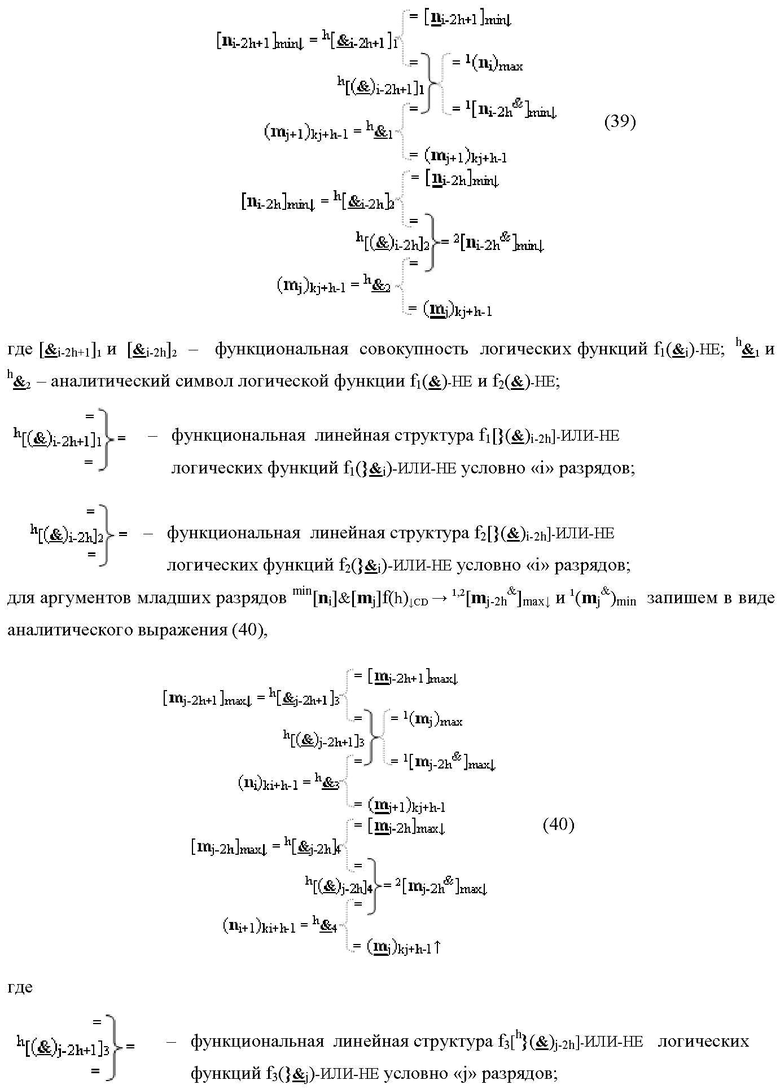

Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических операций умножения аргументов ±[mj]f(2n) и ±[ni]f(2n) - «Дополнительный код». Техническим результатом является повышение быстродействия процесса преобразования аргументов частичных произведений в функциональных структурах умножителя. В одном из вариантов структура реализована с использованием логических элементов И. 4 н.п. ф-лы.
1. Способ формирования аналоговых сигналов аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы ±[S
Σ]f(2n - «Дополнительный код», который включает активизацию упорядоченной последовательности аналоговых сигналов частичных произведений младших разрядов min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min группы «h» первых и вторых уровней и активизацию аналоговых сигналов частичных произведений средних разрядов
0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) и частичных произведений старших разрядов
max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓ в соответствии с логико-динамическим процессом преобразования аргументов аналоговых сигналов, который в «логическом информационном пространстве» соответствует графоаналитическому выражению вида
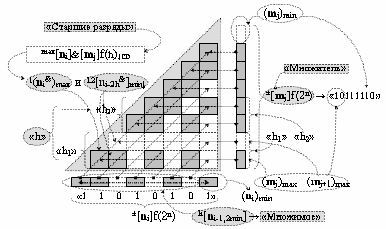
где в каждой «h» группе выполняют одновременный анализ на логическом уровне активности как аргументов аналоговых сигналов сомножителя h[n
i-1min] → «Множимое» и h[n
i-2min] → «Множимое», в котором в зависимости от уровня в группе «h» исключают один и два аргумента аналоговых сигналов младшего разряда (n
i)min, а оставшуюся структуру аргументов h[n
i-1min] → «Множимое» и h[n
i-2min] → «Множимое» сдвигают в позицию младших разрядов в соответствии с количеством исключенных разрядов, так и двух последовательных аргументов аналоговых сигналов (m
j)max и (m
j+1)max условно «j» разрядов сомножителя ±[m
j]f(2n) той же группы «h» и активизируют аргументы аналоговых сигналов частичных произведений старших разрядов max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓, при этом аргументы аналоговых сигналов частичных произведений средних разрядов
0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) активизируют в соответствие с логико-динамическим процессом преобразования аргументов аналоговых, который в «логическом информационном пространстве» соответствует графоаналитическому выражению вида
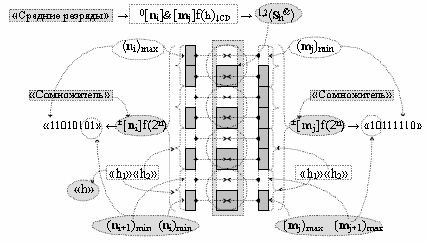
где в каждой «h» группе выполняют одновременный анализ на логическом уровне активности как аргументов аналоговых сигналов (n
i)min и (m
j)max условно «i» и «j» разрядов, так и аргументов аналоговых сигналов (n
i+1)min и (m
j+1)max условно «i+1» и «j+1» разрядов той же группы «h» сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) и активизируют аргументы аналоговых сигналов частичных произведений средних разрядов 0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &), отличающийся тем, что активизацию аргументов аналоговых сигналов частичных произведений младших разрядов
min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min группы «h» первых и вторых уровней выполняют в соответствии с логико-динамическим процессом преобразования аргументов аналоговых сигналов, который в «логическом информационном пространстве» соответствует графоаналитическому выражению вида
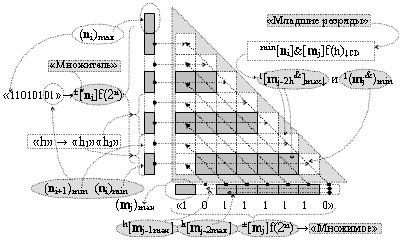
где также в каждой «h» группе выполняют одновременный анализ на логическом уровне активности как аргументов аналоговых сигналов сомножителя h[m
j-1max] и h[m
j-2max] → «Множимое», так и двух последовательных аргументов аналоговых сигналов (n
i)min и (n
i+1)min условно «i» разрядов сомножителя ±[n
i]f(2n) той же группы «h» и активизируют аргументы аналоговых сигналов частичных произведений младших разрядов min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min, после чего выполняют объединение с процедурой формирования частичных произведений аналоговых сигналов средних разрядов 0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) и старших разрядов max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓ в соответствии с логико-динамическим процессом преобразования аргументов аналоговых сигналов, который в «логическом информационном пространстве» соответствует графоаналитическому выражению вида

2. Способ формирования аналоговых сигналов аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы в формате ±[S
Σ]f(2n) - «Дополнительный код», который включает одновременный анализ структуры аргументов аналоговых сигналов множимых [n
i-2h+1] и [n
i-2h] сомножителя ±[n
i]f(2n), где «h» - число первых и вторых уровней в структуре частичных произведений max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓ старших разрядов и соответствующих аргументов множителей (m
j+1)kj+h-1 и (m
j)kj+h-1 сомножителя ±[m
j]f(2n), и этот анализ выполняют посредством функциональной линейной структуры первого уровня f1[&i-2h+1]-И и функциональной линейной структуры f2[&i-2h]-И второго уровня с логическими функциями f1(h&i)-И и f2(h&i)-И условно «i» разрядов в соответствии с математическими моделями вида

и в соответствии с графоаналитическим выражением вида
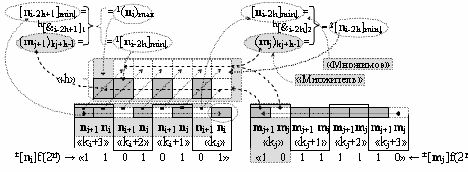
и формируют аргумент аналогового сигнала 1(n
i)max старшего разряда и аргументы аналогового сигнала младших разрядов 1[n
i-2h]min↓ первого уровня и аргументы аналоговых сигналов 2[n
i-2h]min↓ второго уровня частичных произведений с удаленными (↓2h min) аргументами младших разрядов структуры сомножителя ±[n
i]f(2n), при этом включает одновременный анализ аргументов (m
j+1)kj+h-1, (n
i)ki+h-1 и (m
j)kj+h-1, (n
i+1)ki+h-1 посредством логической функции f1(h&)-И и логической функции f2(h&)-И в соответствии с математическими моделями вида

и в соответствии с графоаналитическим выражением вида
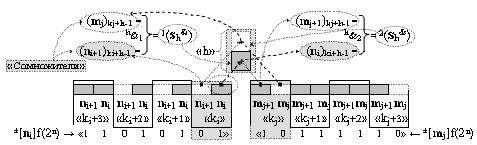
и формируют аргументы аналоговых сигналов 1(S
h &) и 2(S
h &) соответственно первого и второго уровня в группе «h» частичных произведений средних разрядов
0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &), отличающийся тем, что одновременный анализ при активизации аргументов аналоговых сигналов частичных произведений
min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min младших разрядов группы первых и вторых уровней «h» выполняют структуры аргументов аналоговых сигналов множимых [m
j-2h+1] и [m
j-2h] сомножителя ±[m
j]f(2n) и соответствующих аргументов множителей (n
i)kj+h-1 и (n
i+1)kj+h-1 сомножителя ±[n
i]f(2n), и его выполняют посредством функциональной линейной структуры f4[h&j-2h+1]-И логических функций f3(h&j)-И и посредством функциональной линейной структуры f4[h&j-2h]-И логических функций f6(h&j)-И условно «j» разрядов в соответствии с математическими моделями вида
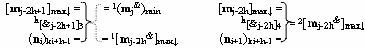
и в соответствии с графоаналитическим выражением вида
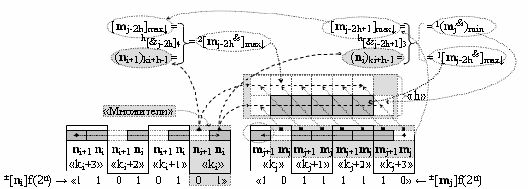
и активизируют аргумент аналогового сигнала 1(m
j &)min младшего разряда и структуру аргументов 1[m
j-2h &]max↓ первого уровня и структуру аргументов 2[m
j-2h &]max↓ второго уровня соответственно, при этом функциональные структуры, активизирующие результирующие аргументы частичных произведений max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓ старших разрядов, 0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) средних разрядов и младших разрядов min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min группы первых и вторых уровней «h» объединяют в соответствии с математической моделью вида
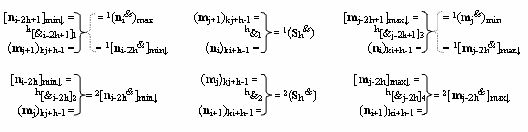
посредством которой и формируют аналоговые сигналы аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы в формате ±[S
Σ]f(2n) - «Дополнительный код».
3. Функциональная структура формирования аналоговых сигналов аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы в формате ±[S
Σ]f(2n) - «Дополнительный код», включающая функциональную линейную структуру f1[&i-2h]-И и функциональную линейную структуру f2[&i-2h]-И условно «i» разрядов, где «h» - группа первых и вторых уровней частичных произведений и выполненную в соответствии с математической моделью вида
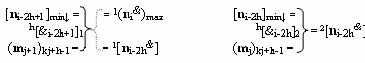
в которых первые функциональные связи являются функциональными связями структуры для приема аргументов множимых [n
i-2h+1]min↓ и [n
i-2h]min↓ сомножителя ±[n
i]f(2n), вторые функциональные связи являются функциональными входными связями структуры для приема аргумента множителя (m
j+1)kj+h-1 и множителя (m
j)kj+h-1 сомножителя ±[m
j]f(2n), а функциональные выходные связи, формирующие частичное произведение 1(n
i &)max старшего разряда и структуру аргументов 1[n
i-2h &]min↓ условно «i» разрядов первого уровня и структуру аргументов 2[n
i-2h &]min↓ условно «i» разрядов второго уровня являются функциональными выходными связями структуры, включающая функциональные структуры с логическими функциями f1(h&)-И и f2(h&)-И средних разрядов, выполненные в соответствии с математическими моделями вида
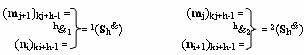
в которых первые функциональные связи являются функциональными связями структуры для приема аргумента (m
j+1)kj+h-1 условно «j+1» разряда и аргумента (m
j)kj+h-1 условно «j» разряда, вторые функциональные связи являются функциональными входными связями структуры для приема аргумента (n
i)ki+h-1 условно «i» разряда и аргумента (n
i+1)ki+h-1 условно «i+1» разряда сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) соответственно, а функциональные выходные связи, формирующие аргумент 1(S
h &) и 2(S
h &) частичного произведения средних разрядов, являются функциональными входными связями структуры и включающая функциональные линейные структуры f3[h&j-2h+1]-И и f4[h&j-2h]-И условно «j» разрядов, активизирующие аргументы младших разрядов частичных произведений, отличающаяся тем, что функциональные связи функциональных линейных структур f3[h&j-2h+1]-И и f4[h&j-2h]-И условно «j» разрядов выполнены в соответствии с аналитическими выражениями вида

и в соответствии с математической моделью вида

посредством которой и формируют аналоговые сигналы аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы в формате ±[S
Σ]f(2n) - «Дополнительный код».
4. Функциональная структура формирования аналоговых сигналов аргументов частичных произведений [n
i]&[m
j]f(h)↓CD сомножителей ±[n
i]f(2n) и ±[m
j]f(2n) - «Дополнительный код» в пирамидальном умножителе fΣ(↓CD
Σ) для последующего логического дешифрирования f1(CD↓) и формирования результирующей суммы в формате ±[S
Σ]f(2n) - «Дополнительный код», отличающаяся тем, что функциональная структура выполнена в виде функциональных структур активизации аргументов частичных произведений первого и второго уровня «Группы уровней» «h» старших разрядов max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓, средних разрядов 0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) и младших разрядов min[n
i]&[m
j]f(h)↓CD → 1[m
j-2h &]max↓ и 1(m
j &)min, при этом в функциональную структуру активизации аргументов частичных произведений «Группы уровней» «h» старших разрядов max[n
i]&[m
j]f(h)↓CD → 1(n
i &)max и 1,2[n
i-2h &]min↓ введены функциональная совокупность [
&
i-2h+1]1 и [
&
i-2h]2 логических функций f1(
&
i)-НЕ, логические функции f1(h
&
)-НЕ и f2(h
&
)-НЕ и функциональная линейная структура f1[}(
&
)i-2h]-ИЛИ-НЕ, а функциональные связи выполнены в соответствии с математической моделью вида

где [
&
i-2h+1]1 и [
&
i-2h]2 - функциональная совокупность логических функций f1(
&
i)-НЕ; h
&
1 и h
&
2 - аналитический символ логической функции f1(h
&
)-НЕ и f2(h
&
)-НЕ; «h» - «Группа уровней» первых и вторых в пирамидальной структуре умножителя fΣ(↓CD
Σ);
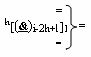 - функциональная линейная структура f1[}(
&
)i-2h]-ИЛИ-НЕ
- функциональная линейная структура f1[}(
&
)i-2h]-ИЛИ-НЕ
логических функций f1(}&
i)-ИЛИ-НЕ условно «i» разрядов;
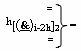 - функциональная линейная структура f2[}(
&
)i-2h]-ИЛИ-НЕ
- функциональная линейная структура f2[}(
&
)i-2h]-ИЛИ-НЕ
логических функций f2(}&
i)-ИЛИ-НЕ условно «i» разрядов;
и в функциональную структуру активизации аргументов частичных произведений «Группы уровней» «h» средних разрядов 0[n
i]&[m
j]f(h)↓CD → 1,2(S
h &) введены логические функции f1(h
}&
)-ИЛИ-НЕ и f2(h
}&
)-ИЛИ-НЕ, а функциональные связи выполнены в соответствии с математическими моделями вида
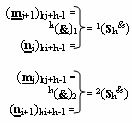
где
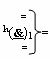 и
и  - логическая функция f1(h
}&
)-ИЛИ-НЕ и f2(h
}&
)-ИЛИ-НЕ;
- логическая функция f1(h
}&
)-ИЛИ-НЕ и f2(h
}&
)-ИЛИ-НЕ;
а в функциональную структуру активизации аргументов частичных произведений «Группы уровней» «h» младших разрядов min[n
i]&[m
j]f(h)↓CD → 1,2[m
j-2h &]max↓ и 1(m
j &)min введены функциональная совокупность h[
&
j-2h+1]3 и h[
&
j-2h]4 логических функций f3(h
&
j)-НЕ и f4(h
&
j)-НЕ, логические функции f3(h
&
)-НЕ и f4(h
&
)-НЕ, а также функциональная линейная структура f3[h
}(
&
)j-2h]-ИЛИ-НЕ, функциональная линейная структура f4[h
}(
&
)j-2h]-ИЛИ-НЕ и функциональная линейная структура
f2[h
}
j-2h]-ИЛИ условно «j» разрядов, а функциональные связи выполнены в соответствии с математической моделью вида

где h[
&
j-2h+1]3 и h[
&
j-2h]4 - функциональная совокупность логических функций f3(h
&
j)-НЕ и f4(h
&
j)-НЕ; h
&
3 и h
&
4 - аналитический символ логической функции f3(h
&
)-НЕ и f4(h
&
)-НЕ;
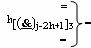 - функциональная линейная структура f3[h
}(
&
)j-2h]-ИЛИ-НЕ логических
- функциональная линейная структура f3[h
}(
&
)j-2h]-ИЛИ-НЕ логических
функций f3(}&
j)-ИЛИ-НЕ условно «j» разрядов;
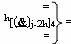 - функциональная линейная структура f4[h
}(
&
)j-2h]-ИЛИ-НЕ логических
- функциональная линейная структура f4[h
}(
&
)j-2h]-ИЛИ-НЕ логических
функций f4(h
}&
j)-ИЛИ-НЕ условно «j» разрядов.
| УЭЙКЕРЛИ ДЖ | |||
| Проектирование цифровых устройств, т.1 | |||
| - М.: ПОСТМАРКЕТ, 2002, с.518-521, рис.5.98 | |||
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА УМНОЖИТЕЛЯ, В КОТОРОМ ВХОДНЫЕ АРГУМЕНТЫ ИМЕЮТ ФОРМАТ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(2), А ВЫХОДНЫЕ АРГУМЕНТЫ СФОРМИРОВАНЫ В ФОРМАТЕ ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2373563C9 |
| JP 7141148 A, 02.06.1995 | |||
| JP 56094435 A, 30.07.1981. | |||
Авторы
Даты
2013-01-27—Публикация
2011-06-08—Подача