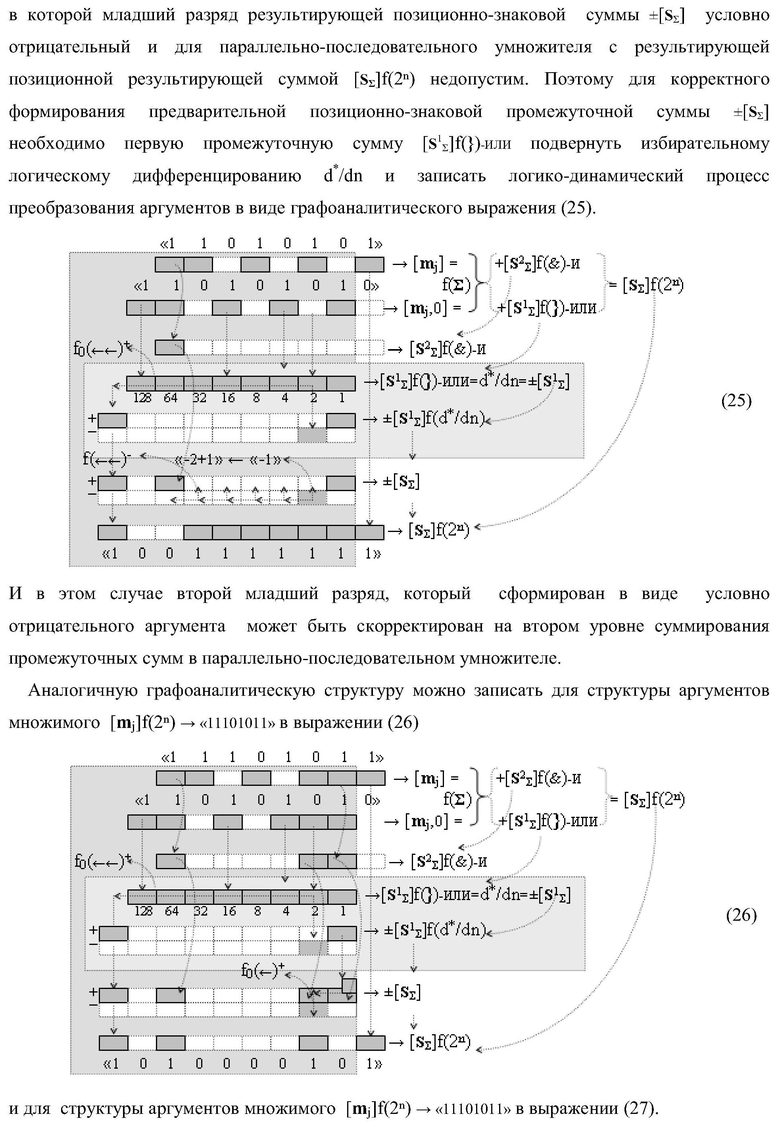
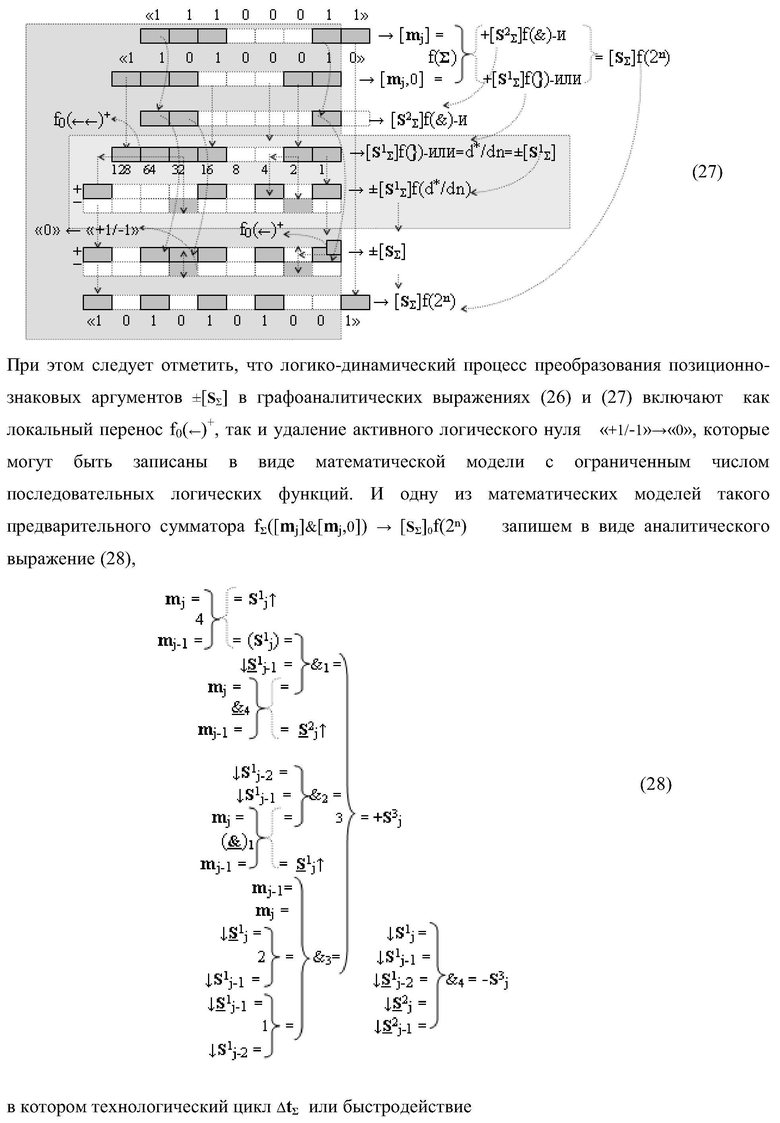
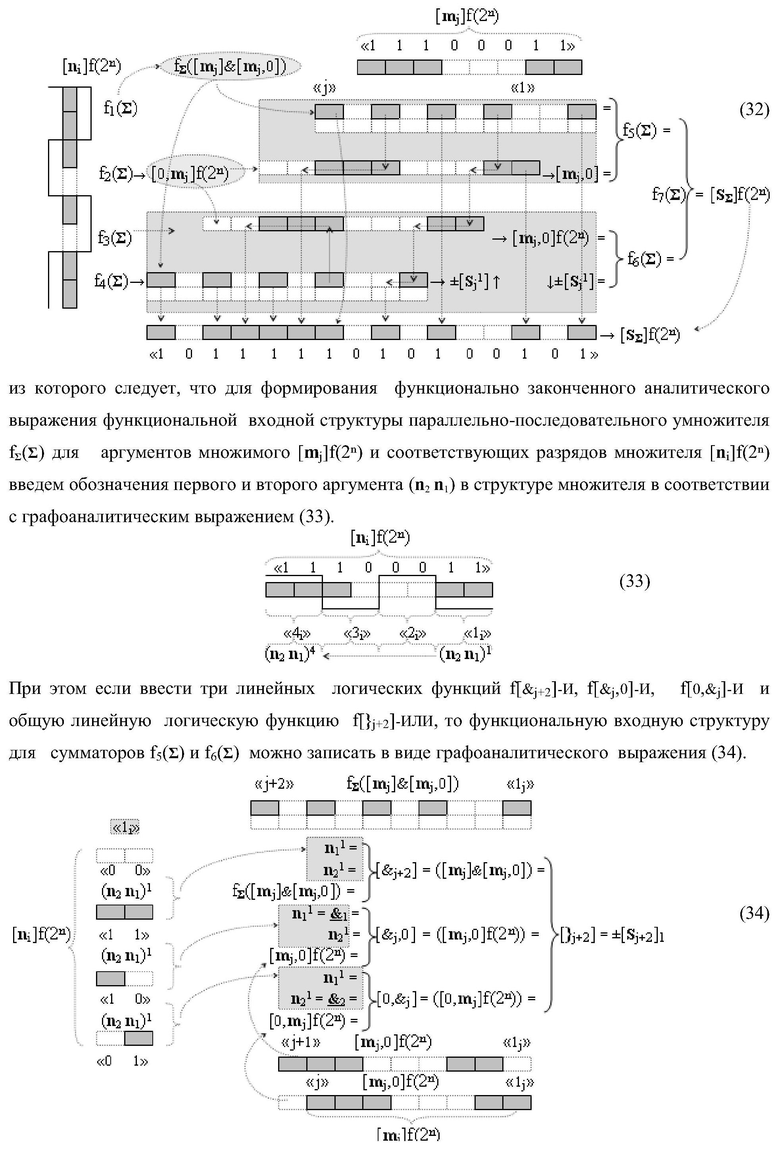
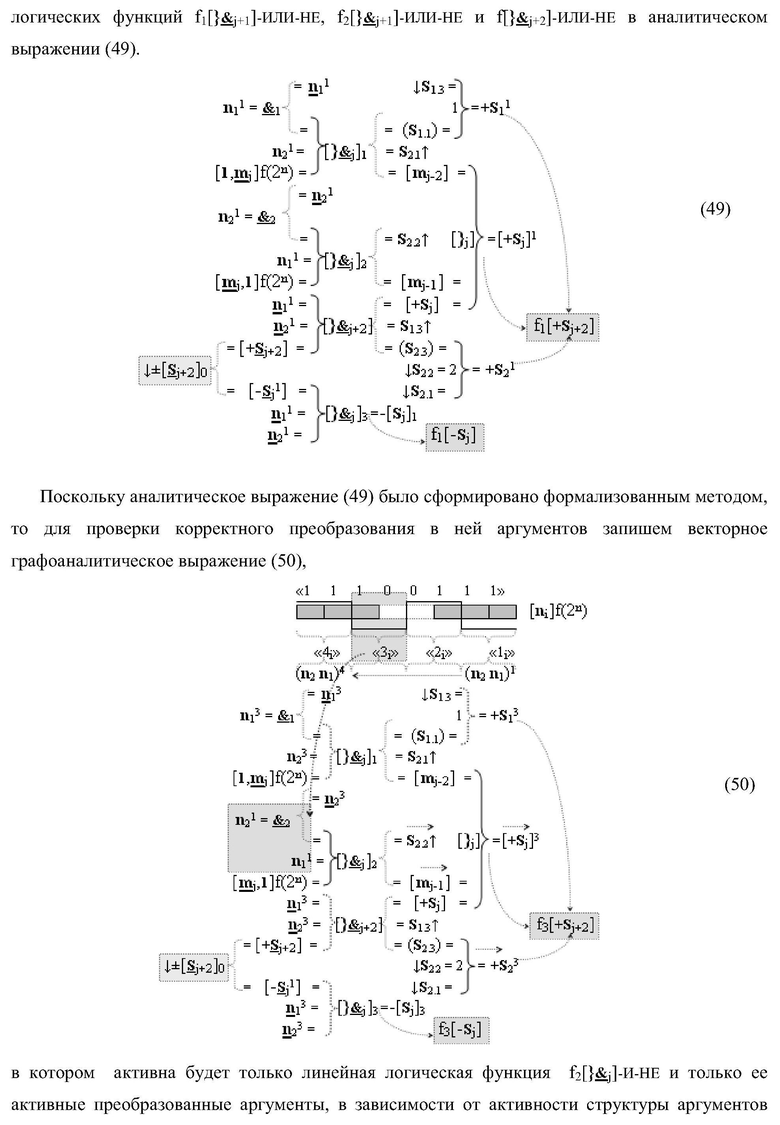
Текст описания приведен в факсимильном виде.





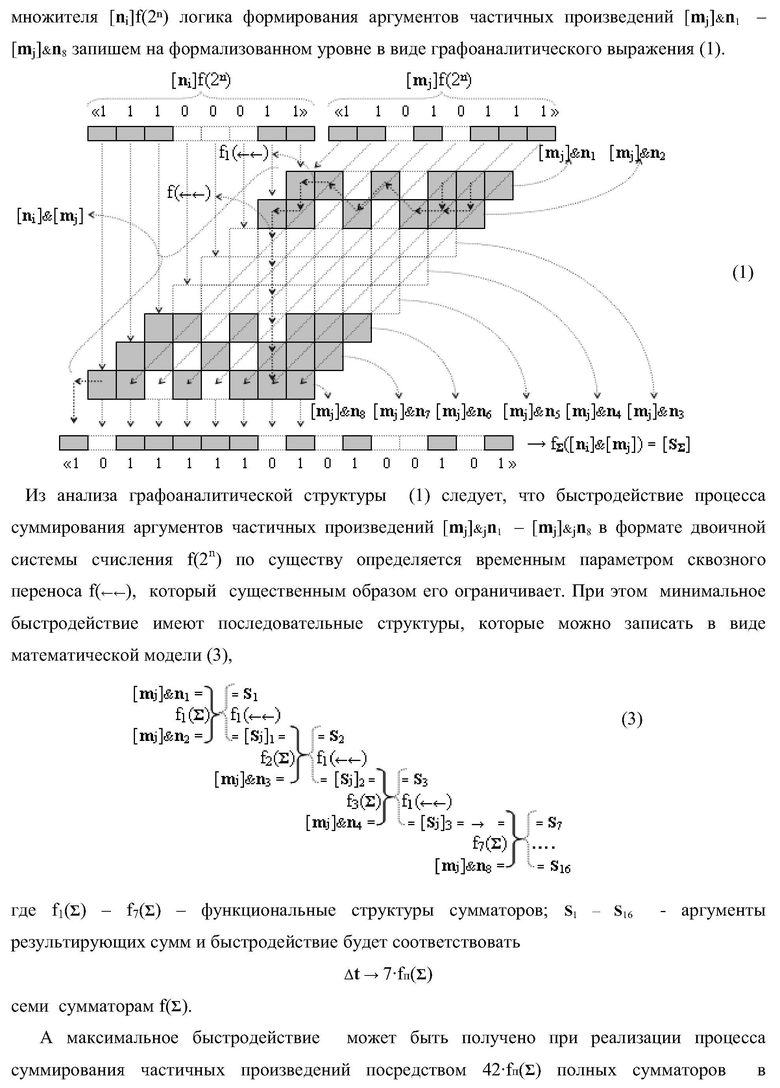






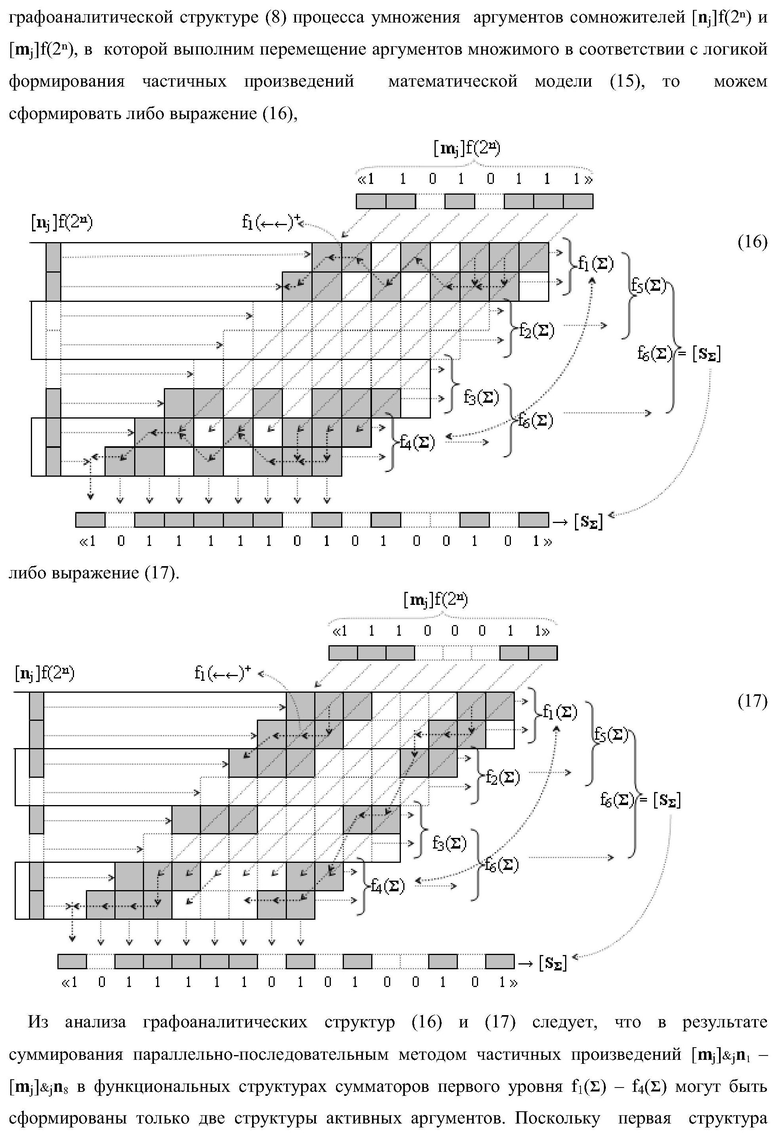


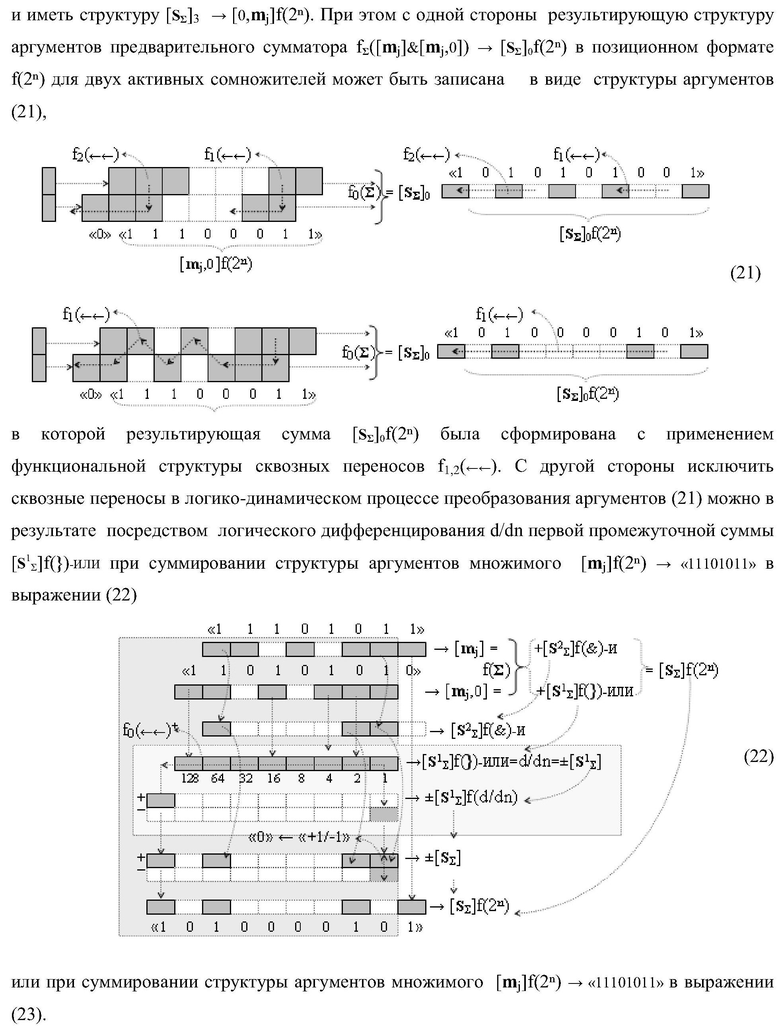
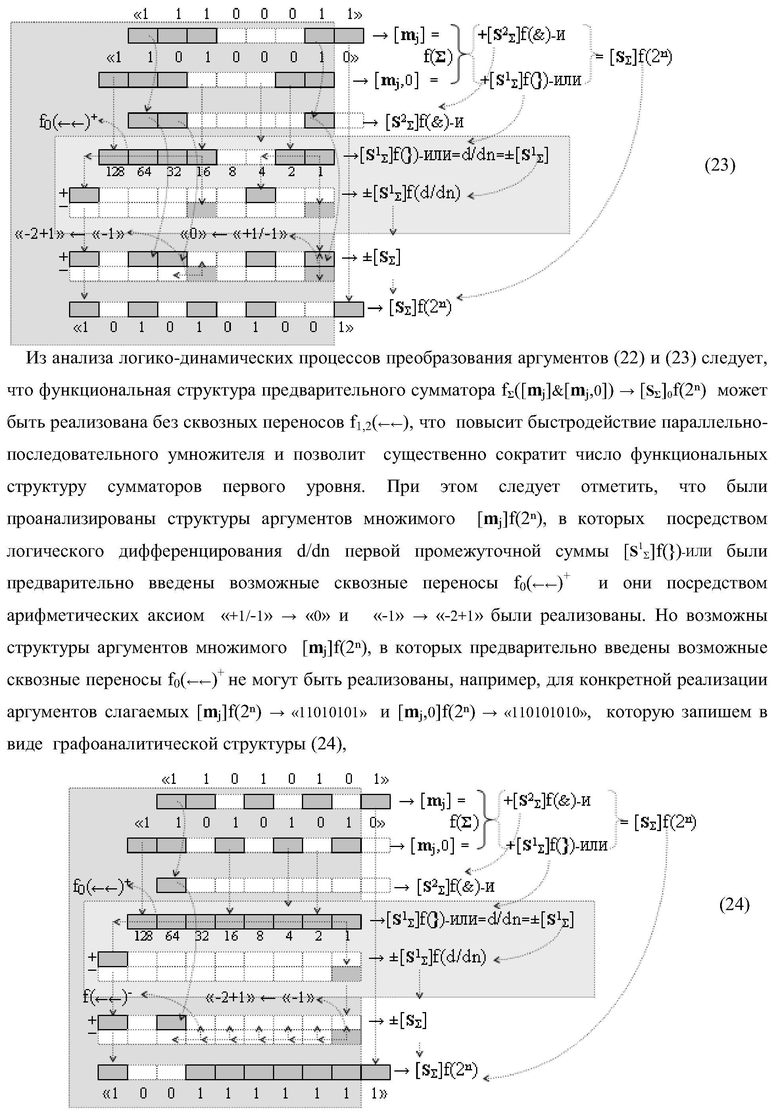












Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройствах для выполнении арифметических операций умножения аргументов множимого [mj]f(2n) и множителя [ni]f(2n) в позиционном формате. Техническим результатом является упрощение функциональной структуры параллельно-последовательного умножителя и повышение его быстродействия. Структура умножителя в первом варианте реализации содержит четыре сумматора, линейные логические функции И, а также три линейные логические ИЛИ для формирования промежуточных сумм частичных произведений первого уровня суммирования, причем функциональные структуры сумматоров выполнены с возможностью приема позиционно-знаковых аргументов промежуточных сумм частичных произведений. 4 н.п. ф-лы.
1. Функциональная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [m
j]f(2n) и множителя [n
i]f(2n) с минимизированной процедурой формирования первого уровня промежуточных сумм f1..k[S
j+2] частичных произведений, где «k» - число промежуточных сумм первого уровня, которая содержит линейные логические функции fk[&j,0]-И и fk[0,&j]-И, в которых функциональные входные связи являются функциональной входной связью структуры умножителя для приема соответствующих аргументов множимого [m
j]f(2n), а вторые функциональные связи является функциональной входной связью функциональной структуры умножителя для приема одного из аргументов n
1 - n
2k множителя [n
i]f(2n), структура умножителя также содержит сумматоры fΣ([m
j]&[m
j,0]), f2(±Σ) и сумматор f1(±Σ), в котором функциональные выходные связи являются первыми функциональными входными связями сумматора f3(±Σ), отличающаяся тем, что дополнительно введены логические функции f1[
&
]-НЕ и f2[
&
]-НЕ, линейные логические функции f[&j+2]-И и f[&j]-И, а также логические функции f1(})-ИЛИ, f2(})-ИЛИ и линейные логические функции f[}
j]-ИЛИ для формирования промежуточных сумм f1..k[S
j+2] частичных произведений первого уровня суммирования, а функциональные структуры сумматоров f1(±Σ) - f3(±Σ) выполнены с возможностью приема позиционно-знаковых аргументов промежуточных сумм частичных произведений, при этом функциональные связи в функциональной структуре, например, восьмиразрядного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
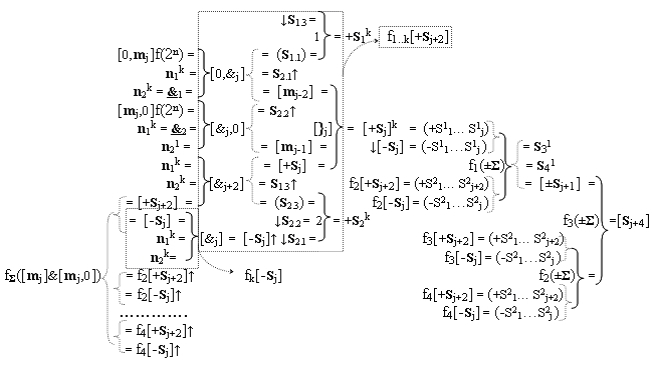
где n
1 k и n
2 k - первый и второй аргументы множителя [n
i]f(2n);
&
1 и
&
2 - логические функции f1(
&
)-НЕ и f2(
&
)-НЕ;
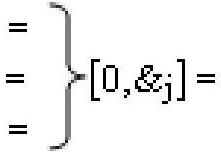 ,
,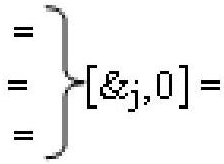 и
и 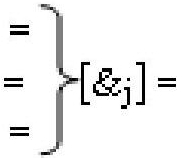 - линейные последовательности f[0,&j]-И, f[&j,0]-
- линейные последовательности f[0,&j]-И, f[&j,0]-
И и f[&j]-И из «j» логических функций f[&]-И;
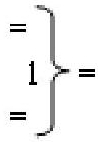 ,
, 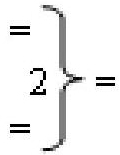 - логические функции f1(})-ИЛИ и f2(})-ИЛИ;
- логические функции f1(})-ИЛИ и f2(})-ИЛИ;
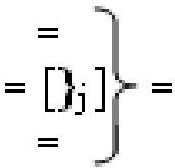 - линейная последовательность f[}
j]-ИЛИ из «j» логических функций f[}]-ИЛИ.
- линейная последовательность f[}
j]-ИЛИ из «j» логических функций f[}]-ИЛИ.
2. Функциональная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [m
j]f(2n) и множителя [n
i]f(2n) с минимизированной процедурой формирования первого уровня промежуточных сумм f1..k[S
j+2] частичных произведений, где «k» - число промежуточных сумм первого уровня, которая содержит линейные логические функции fk[&j,0]-И и сумматоры fΣ([m
j]&[m
j,0]), f2(±Σ) и сумматор f1(±Σ), в котором функциональные выходные связи являются первыми функциональными входными связями сумматора f3(±Σ), отличающаяся тем, что дополнительно введены логические функции f1[
&
]-НЕ и f2[
&
]-НЕ, линейные логические функции f[1,&
j]-И-НЕ, f[&
j,1]-И-НЕ и f[&
j+2]-И-НЕ, а также логические функции f1(&)-И-НЕ, f2(&)-И-НЕ и линейные логические функции f[&
j]-И-НЕ для формирования промежуточных сумм f1..k[S
j+2] частичных произведений первого уровня суммирования, а функциональные структуры сумматоров f1(±Σ) - f3(±Σ) выполнены с возможностью приема позиционно-знаковых аргументов промежуточных сумм частичных произведений, при этом функциональные связи в функциональной структуре, например, восьмиразрядного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида
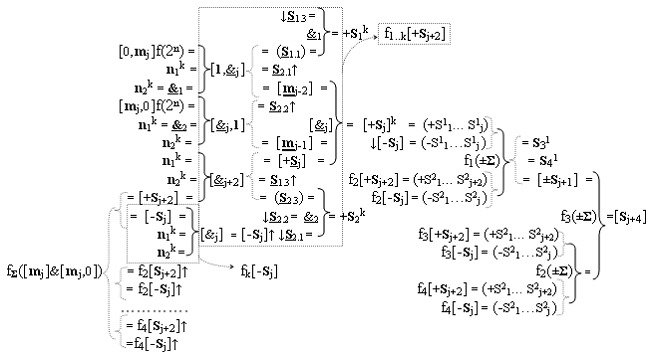
где 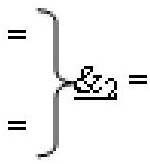 и
и 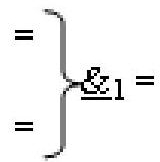 - логические функции f1(&)-И-НЕ и f2(&)-И-НЕ;
- логические функции f1(&)-И-НЕ и f2(&)-И-НЕ;
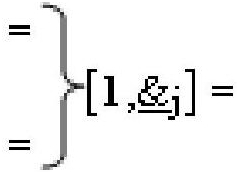 ,
, 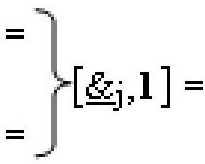 и
и 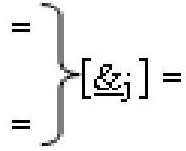 - линейные последовательности
- линейные последовательности
f[1,&
j]-И-НЕ, f[&
j,1]-И-НЕ и f[&
j]-И-НЕ из «j» логических функций f[&]-И-НЕ.
3. Функциональная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [m
j]f(2n) и множителя [n
i]f(2n) с минимизированной процедурой формирования первого уровня промежуточных сумм f1..k[S
j+2] частичных произведений, где «k» - число промежуточных сумм первого уровня, которая содержит сумматоры fΣ([m
j]&[m
j,0]), f2(±Σ) и сумматор f1(±Σ), в котором функциональные выходные связи являются первыми функциональными входными связями сумматора f3(±Σ), отличающаяся тем, что дополнительно введены логические функции f1[
&
]-НЕ и f2[
&
]-НЕ, линейные логические функции f[1,&
j]-И-НЕ, f1[}
j+1]-ИЛИ, f1[}
j+1]-ИЛИ, f[}
j+2]-ИЛИ и f[}&
j]-ИЛИ-НЕ, а также логические функции f1(&)-И-НЕ, f2(&)-И-НЕ и линейные логические функции f[&
j]-И-НЕ для формирования промежуточных сумм f1..k[S
j+2] частичных произведений первого уровня суммирования, а функциональные структуры сумматоров f1(±Σ) - f3(±Σ) выполнены с возможностью приема позиционно-знаковых аргументов промежуточных сумм частичных произведений, при этом функциональные связи в функциональной структуре, например, восьмиразрядного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида

где 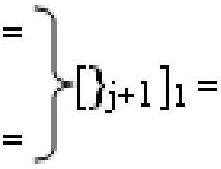 и
и 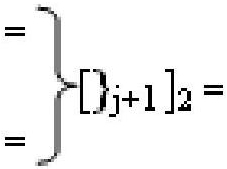 - линейная последовательность f1[}
j]-ИЛИ и f2[}
j]-ИЛИ
- линейная последовательность f1[}
j]-ИЛИ и f2[}
j]-ИЛИ
из «j+1» логических функций f[}]-ИЛИ;
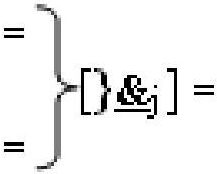 - линейная последовательность f[}&
j]-ИЛИ-НЕ из «j» логических
- линейная последовательность f[}&
j]-ИЛИ-НЕ из «j» логических
функций f(}&)-ИЛИ-НЕ.
4. Функциональная структура параллельно-последовательного умножителя fΣ(Σ) в позиционном формате множимого [m
j]f(2n) и множителя [n
i]f(2n) с минимизированной процедурой формирования первого уровня промежуточных сумм f1..k[S
j+2] частичных произведений, где «k» - число промежуточных сумм первого уровня, которая содержит сумматоры fΣ([m
j]&[m
j,0]), f2(±Σ) и сумматор f1(±Σ), в котором функциональные выходные связи являются первыми функциональными входными связями сумматора f3(±Σ), отличающаяся тем, что дополнительно введены логические функции f1[
&
]-НЕ и f2[
&
]-НЕ, линейные логические функции f1[},
&
j+1]-ИЛИ-НЕ, f2[}&
j+1]-ИЛИ-НЕ, f[}&
j+12]-ИЛИ и f[}&
j]-ИЛИ-НЕ, а также логические функции f1(})-ИЛИ, f2(})-ИЛИ и линейные логические функции f[}
j]-ИЛИ для формирования промежуточных сумм f1..k[S
j+2] частичных произведений первого уровня суммирования, а функциональные структуры сумматоров f1(±Σ) - f3(±Σ) выполнены с возможностью приема позиционно-знаковых аргументов промежуточных сумм частичных произведений, при этом функциональные связи в функциональной структуре, например, восьмиразрядного умножителя fΣ(Σ) выполнены в соответствии с математической моделью вида

| ДЖ.УЭЙКЕРЛИ | |||
| Проектирование цифровых устройств | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| - М.: Постмаркет, 2002, всего с.1018, см | |||
| Устройство для очищения сточных вод | 1916 |
|
SU519A1 |
| Прибор для автоматической записи пройденного пути | 1928 |
|
SU11698A1 |
| ФУНКЦИОНАЛЬНАЯ ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ ФОРМАТА ПОЗИЦИОННО-ЗНАКОВОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+/-) | 2008 |
|
RU2378684C1 |
| US 5986587 A, 16.11.1999 | |||
| US 5907499 A, 25.05.1999. | |||
Авторы
Даты
2011-06-27—Публикация
2010-03-22—Подача