Изобретение относится к средствам коррекции навигационных систем подвижных (в частности, морских) объектов, нуждающихся в непрерывном или дискретном определении местоположения и пространственной ориентации (углы курса, крена и дифферента) в масштабе реального времени. В проведении коррекции нуждаются гироскопические системы (инерциальные навигационные системы и др.), а также измерители скорости (лаги) и курса (компасы, гирогоризонткомпасы), способные вырабатывать текущие значения параметров движения объекта в автономном режиме функционирования. Необходимость коррекции показаний этих систем вызывается снижением во времени точности выработки ими навигационных параметров в процессе автономного функционирования.
В настоящее время алгоритмы определения по спутникам местоположения и вектора скорости подвижного объекта основаны на измерениях дальности и скорости ее изменения от объекта до четырех и более среднеорбитных навигационных спутников, причем положение и скорость объекта определяются путем линеаризации измерений относительно расчетной траектории движения. Для определения скорости объекта по измерениям дальности до четырех и более среднеорбитных спутников к настоящему времени разработаны различные алгоритмы обработки измерительной информации [1-5].
Известные способы определения курса объекта с помощью спутников требуют либо пространственного разнесения по объекту нескольких антенн, либо вращения (с относительно большим радиусом) в горизонтальной плоскости одной антенны, либо, наконец, автоматического пеленгования спутников по азимуту и высоте с одновременным использованием данных автономных навигационных средств объекта об углах качки и курса объекта [6]. Реализация этих способов в реальных условиях встречает серьезные трудности.
Известна корректируемая система инерциальной навигации и стабилизации (СИНС) Ладога-М [7], принятая за прототип. В системе реализован классический способ и алгоритм функционирования инерциальной навигационной системы (ИНС) полуаналитического типа с коррекцией по сигналам спутниковой навигационной системы (СНС).
На фиг.1 представлена структура СИНС. В состав системы входят гироприбор (ГП) - 1, прибор термостабилизации (ТС) - 2, усилитель мощности термостабилизации (УМТ) - 3, прибор цифровой (ПЦ) - 4, прибор управления (ПУ) - 5, ЭВМ «Багет-41» - Б-41 - 6.
Система функционирует следующим образом: Из ГП В ПЦ через аналого-цифровые преобразователи поступают три составляющие ускорения (ωx, ωy, ωz), углы качки (Qк, ψк) и азимутальный угол A, а из прибора ПЦ в гироприбор ГП подаются сигналы (Ωx, Ωy, Ωz). Коррекция СИНС осуществляется путем выработки корректирующей информации (НД) алгоритмами ЭВМ Б-41 по данным ПЦ, НД и приемной аппаратуры СНС, вырабатывающей информацию о координатах Фc, λc; скорости Vc и путевом угле К. Управление функционированием СИНС осуществляется по каналам «команды, сигналы».
В систему поступает следующая информация:
- скорость от лага Vл;
- грубый курс от гирокомпаса K0;
- координаты φc, λc, скорость Vc и путевой угол К от приемника СНС.
Система имеет два рабочих режима:
- корректирующий режим (КР);
- автономный режим (АР).
В каждом запуске системы производится калибровка, которая продолжается 6-8 часов. Калибровка требует поступления внешних позиционных скоростных данных. Для КР используется информация от приемника СНС и лага, а в АР - только от лага.
Описанной структуре системы соответствует способ, представляющий собой совокупность следующих приемов:
- измеряют три составляющие ускорения;
- принимают данные об углах качки и азимутальном угле (A);
- принимают информацию о координатах, скорости и путевом угле от приемника СНС;
- осуществляют начальную выставку и калибровку системы.
Процесс калибровки состоит в том, чтобы по внешним данным о координатах и скорости вычислить и скорректировать ошибки и воздействия, снижающие точность функционирования. Поскольку процесс выставки продолжается 6-8 часов, оперативная коррекция параметров ориентации изложенным способом не представляется возможной.
Кроме того, в современных условиях функционирования СНС ГЛОНАС из-за ее недостаточной доступности и целостности система коррекции не обеспечивает нормальную работу СИНС «Ладога-М», а необходимость длительного сеанса обсервации по сигналам СНС ведет к опасности быть обнаруженным средствами наблюдения противника. Сокращение же длительности сеанса обсервации приводит к снижению точности выработки навигационных данных.
Для устранения недостатков аналогов и прототипа в части обеспечения коррекции параметров ориентации объекта предлагается новый способ определения местоположения объекта и параметров его движения по измеренным дальностям «объект-спутник». Суть способа (в отличие от традиционного подхода) в измерении дальностей до навигационных спутников в три близких момента времени. В основе этого способа лежит решение навигационной задачи методом Гаусса - методом преобразования совокупности угловых координат спутника к его радиусам - векторам в инерциальной системе координат. Реализация способа возможна и при ограниченном числе используемых спутников - от одного до трех, что особенно актуально в условиях помех, в горных районах, в городах с высотными зданиями и т.п.
Для решения этой задачи исходим из того, что в моменты времени t1, t, t2 инерциальные Декартовы координаты навигационного спутника известны достаточно точно, обозначим их через (x1, y1, z1), (x, y, z), (x2, y2, z2), а расчетные координаты объекта в той же системе координат - через (X1, Y1, Z1), (X, Y, Z), (X2, Y2, Z2).
Вырабатываемые по спутникам поправки к координатам объекта в эти же три момента времени обозначим через
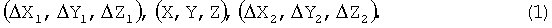
Требуется вначале найти поправки к координатам объекта по измерениям дальностей ρi (i=1÷3) до трех навигационных спутников в три момента времени t1, t, t2.
Сущность подхода Гаусса заключается в следующем.
Обозначим через 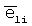 ,
, 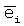 ,
, 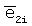 направляющие косинусы с объекта на навигационный спутник в моменты t1, t, t2.
направляющие косинусы с объекта на навигационный спутник в моменты t1, t, t2.
Условия нахождения трех геоцентрических положений навигационного спутника в плоскости, проходящей через центр Земли, позволяют составить уравнения [8]:
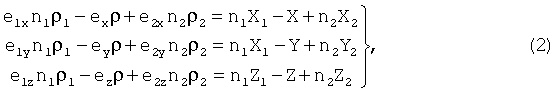
где ρ1, ρ, ρ2 - дальности «объект - спутник»;
n1 и n2 - отношения площадей треугольников, заключенных между радиусами - векторами спутника 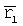 ,
, 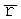 ,
, 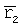 в три момента времени.
в три момента времени.
n1 и n2 определяются по соотношениям [8]:
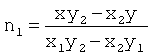 ,
, 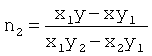 .
.
Для получения системы уравнений, определяющих поправки к местоположению объекта, необходимо систему уравнений (2) линеаризовать относительно этих поправок. При этом направляющие косинусы «спутник - объект» будут:

где символ νc обозначает координаты xc, yc, zc спутника, a V - координаты объектах X, Y, Z.
ev можно представить в виде:
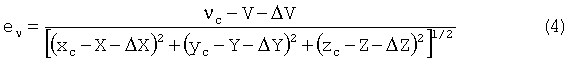
Линеаризуя (4) относительно поправок ΔV, ΔX, ΔY, ΔZ, будем иметь:
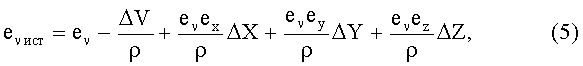
где ev - расчетные значения компонент направляющих косинусов;
ρ - расчетное значение дальности «объект - спутник»;
ΔX, ΔY, ΔZ - искомые поправки к координатам объекта в инерциальной системе координат;
ev ист - истинное значение компоненты направляющих косинусов.
Подставляя (5) в систему уравнений (2), получим систему уравнений для трех наблюдаемых спутников в три близких момента времени:
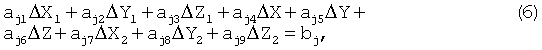
где j=1÷9.
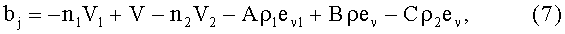
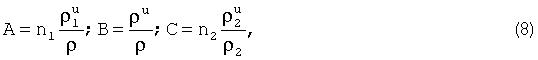
где ρu - измеренные значения дальностей.
Коэффициенты aj1, …, aj9 зависят только от значений A, B, C и расчетных значений дальностей и направляющих косинусов.
Благодаря тому, что в выражениях (6), (7) ρu игр расчетное входит как отношение ρu/ρ, систематическая погрешность в ρu значительно подавляется.
Коэффициенты aji легко выводятся и в целях сокращения записи не приводятся.
Непосредственное решение системы (6), состоящей из девяти уравнений и девяти неизвестных, позволит определить искомые поправки к инерциальным координатам положения объекта, однако для неподвижного объекта число неизвестных можно уменьшить до трех.
Поэтому будем искать поправки к широте, долготе и высоте объекта.
Местоположение неподвижного на Земном эллипсоиде объекта в инерциальной системе координат определяется из соотношений [9]:



где
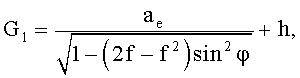
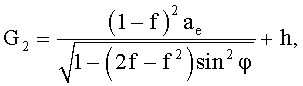
Θ=Θg0+Ω(t-t0)+λE.
φ - широта;
λE - восточная долгота;
ae - большая полуось эллипсоида вращения модели фигуры Земли;
f - сжатие, равное разности большой a и малой b полуосей эллипсоида вращения модели фигуры Земли, деленной на большую полуось: 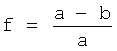 ;
;
Θg0 - гринвичское звездное время для Oh UT (всемирного времени) как функция юлианской даты;
Ω - угловая скорость вращения Земли;
h - геодезическая высота над поверхностью эллипсоида.
Из соотношений (9)-(11) определим зависимость поправок к прямоугольным инерциальным координатам потребителя от поправок к широте, долготе и высоте.
Для этого линеаризуем соотношения (9), (10), (11) относительно поправок к расчетным координатам объекта. В результате получаем:


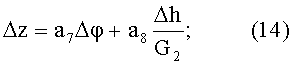
где
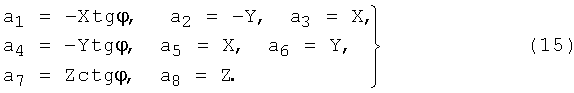
С учетом соотношений (12), (13), (14), (15) систему линейных уравнений (6) можно привести к виду:

Запишем ее в матричном виде:

Исходя из принципа метода наименьших квадратов [10] решение системы (17) получим в виде:
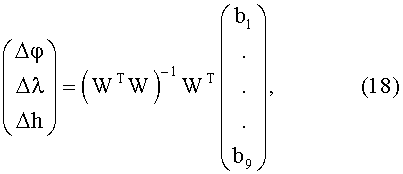
где матрица 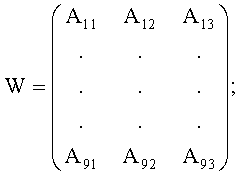
WT - транспонированная матрица W;
(WTW)-1 - обращенная матрица произведении WTW.
Для исследования точностных характеристик определения местоположения объекта по измерениям дальностей до трех среднеорбитных спутников было проведено моделирование решения навигационной задачи рассмотренным методом. Предполагалось, что спутники расположены в трех равномерно разнесенных по экватору плоскостях. Для демонстрации возможностей рассматриваемого метода решения навигационной задачи оптимизация расположения спутников не использовалась. Измерения производились в момент видимости трех спутников в каждой из плоскостей. В начальный момент погрешности эфемерид спутников составляли вдоль орбиты 3 м, по радиусу вектору - 5 м, по трансверсали - 1 м.
Расчетное местоположение объекта полагалось с координатами φc=60°, λc=30°, «истинное» местоположение - φu=60°+60', λu=30°+120', h=0, что соответствует начальной погрешности места в 124,45 км. Из системы (18) определялись искомые поправки Δφ, Δλ, Δh/G и их погрешности относительно «истинного» местоположения, Δξ - северная и Δη - восточная погрешности определения местоположения 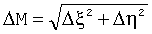 . Измерения проводились в моменты t0, t+1m, t0+2m.
. Измерения проводились в моменты t0, t+1m, t0+2m.
В табл.1 приводятся результаты моделирования при различных значениях систематических погрешностей в измеренных дальностях, вызванных в основном расхождением шкал времени наземного объекта и спутников, по измерениям до трех спутников в указанные выше моменты.
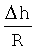
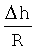
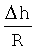
Анализ данных табл.1 показывает, что при систематических погрешностях в измеренных дальностях до 500 м можно получить приемлемое определение местоположения объекта, для чего необходимо провести не менее трех итераций. Однако высота объекта над геоидом определяется неадекватно, что не отражается на определении поправок к широте и долготе.
В табл.2 приводятся результаты моделирования определения местоположения объекта по одному спутнику при тех же условиях, что и в табл.1.
по одному спутнику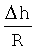
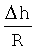
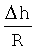
Анализ данных табл.2 показывает, что при систематических погрешностях в дальностях порядка 10 м можно получить приемлемый результат, при больших погрешностях результат ухудшается и может быть использован для приблизительного улучшения местоположения.
В табл.3 приведены результаты моделирования определения местоположения объекта по двум спутникам при тех же условиях. Анализ данных табл.3 показывает, что при систематических погрешностях в дальностях менее 500 м можно получить приемлемый результат, а при систематической погрешности 10000 м происходит расхождение процесса итераций.
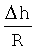
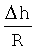
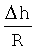
Обратимся теперь к параметрам скорости и курса.
Допустим, что на подвижном объекте имеются приборы, способные измерять продольную Vy и поперечную Vx составляющие вектора скорости
относительно водной среды, а также система курсоуказания, измеряющая курс объекта K.
Положим, что ΔVy, ΔVx, ΔK - систематические погрешности продольной и поперечной скоростей объекта и системы курсоуказания. Тогда измеренные значения 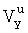 ,
, 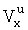 , Ku будут:
, Ku будут:
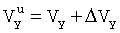 ,
,

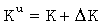 ,
,
где Vy, Vx, K - будем считать точными значениями параметров без учета случайных погрешностей, которые при оценке возможностей метода не рассматриваются.
Расчетные значения северной 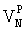 и восточной
и восточной 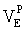 составляющих скорости объекта определим из соотношений [11]:
составляющих скорости объекта определим из соотношений [11]:

Тогда расчетная скорость движения объекта по широте 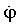 и долготе
и долготе 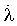 могут быть опредены из соотношений [11]:
могут быть опредены из соотношений [11]:

где M и N - главные радиусы кривизны реффенц-эллипсоида.
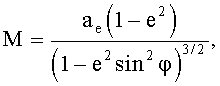
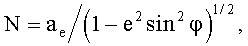
где ae - большая полуось эллипсоида вращения модели фигуры Земли,
φ, λ - геодезические координаты объекта,
e2 - квадрат эксцентриситета,
h - высота объекта над поверхностью эллипсоида, которая в данной работе считается постоянной.
Значения расчетных координат объекта - широты φ и долготы λ, скорости их изменения 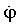 ,
, 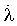 в зависимости от времени можно представить в виде:
в зависимости от времени можно представить в виде:

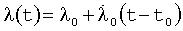 ,
,
а с учетом искомых поправок Δφ0, 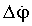 , Δλ0,
, Δλ0, 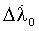 откорректированные значения φ(t), λ(t) моменты измерения дальностей «объект - спутник» будут:
откорректированные значения φ(t), λ(t) моменты измерения дальностей «объект - спутник» будут:

Учитывая зависимости ΔX, ΔY, ΔZ от Δφ(t), Δλ(t), Δh, приведенные в (12), и подставляя их в (6), получим систему уравнений в виде:
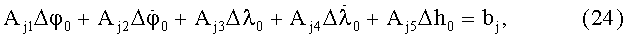
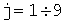
где Aj1…Aj5, как и в (6), являются функциями координат спутников, расчетных координат объекта и измеренных и расчетных дальностей «объект - спутник».
Запишем (24) в матричном виде:

Решение системы (25) методом наименьших квадратов имеет вид [12]:

где матрица W имеет вид:

WT - транспонированная матрица W;
(WTW)-1 - обратная матрица.
Решая систему (26) методом последовательных приближений, определим Δφ0, Δλ0, 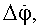
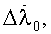 Δh0, а из соотношений (21) с уточненными φ0, λ0,
Δh0, а из соотношений (21) с уточненными φ0, λ0, 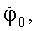
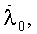 h0 получим значения VN,VE;
h0 получим значения VN,VE;

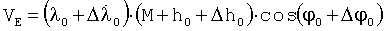 .
.
Систематическую поправку курса определим следующим образом.
Расчетное значение путевого угла имеет вид:

а уточненное значение путевого угла:

Вычитая из (11) (29), получим приближенное значение систематической поправки курса:
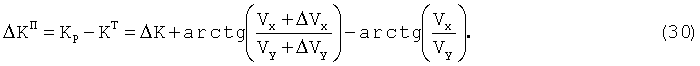
Поскольку ΔVy, ΔVx неизвестны, то с учетом того, что составляющие путевой скорости VN и VE, определенные по спутникам, достаточно точны, с учетом равенства (29) систематическую поправку курса ΔKП можно определить из соотношения:
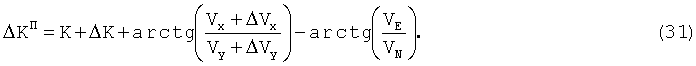
Из (30) видно, что ΔKП зависит от разности:
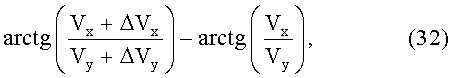
т.е. от величины систематических погрешностей ΔVx, ΔVy.
С учетом (32) погрешность определения курса ΔKП будет:

Вычитаемым членом в (33) можно пренебречь. В результате систематическая погрешность курса ΔKП в (31) определится с погрешностью:

Откуда видно, что чем больше скорость Vy, тем точнее можно определить курс подвижного объекта.
Поскольку измеренное значение курса

то уточненное значение курса Ky будет определяться с погрешностью:

Из соотношений (20), решенных относительно Vx, Vy с учетом исключения систематической погрешности курса ΔKП и полученных по спутникам относительно точных значений VE, VN получим уточненные значения 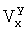 ,
, 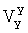 .
.

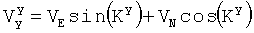 .
.
Определение ΔKП, 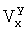 ,
, 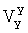 производится после уточнения VE, VN (27).
производится после уточнения VE, VN (27).
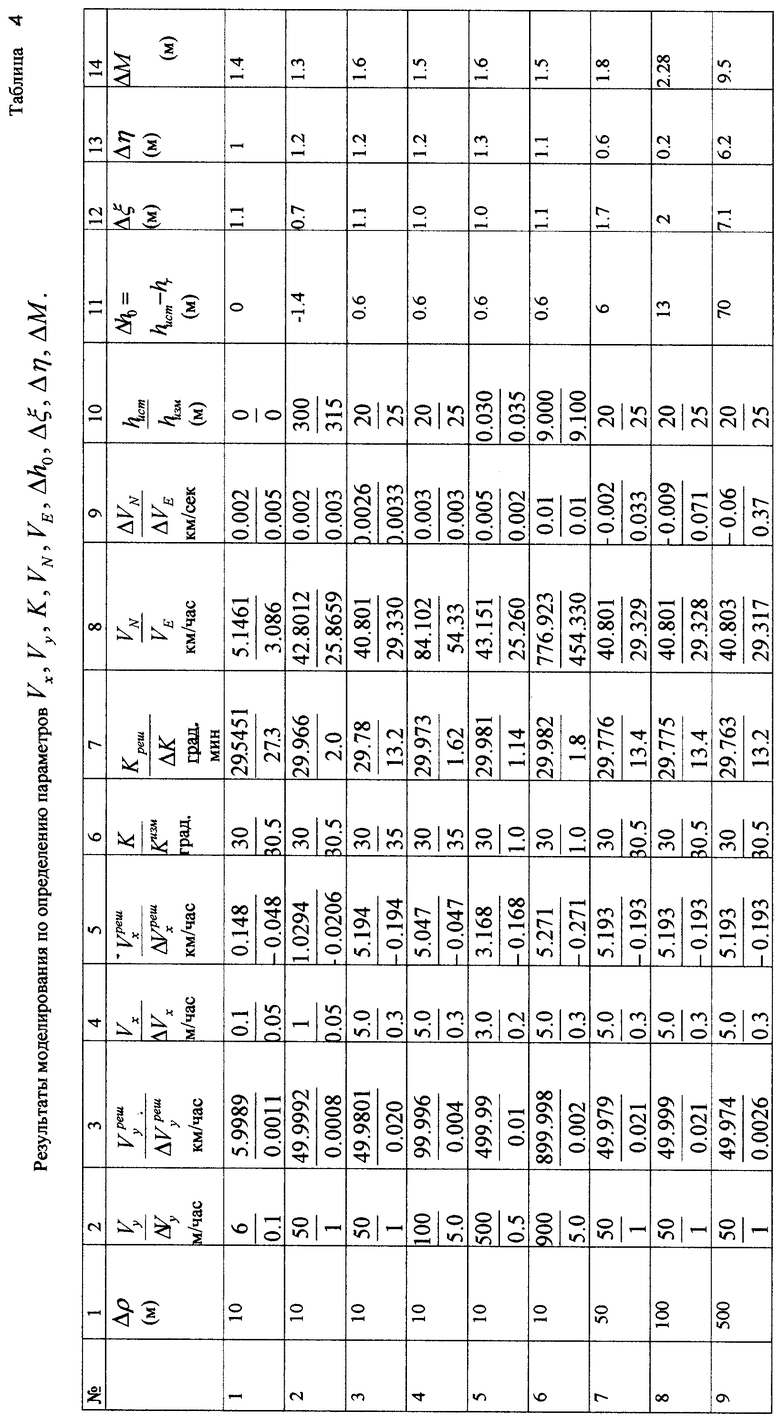
Для определения точностных характеристик навигационных параметров подвижного объекта по результатам измерения дальностей до трех среднеорбитных спутников было проведено моделирование решения навигационной задачи (табл.4). Предполагалось, что спутники расположены в трех равномерно разнесенных по экватору плоскостях, при этом оптимизация расположения спутников не использовалась.
Измерения производились в моменты видимости трех спутников в каждой из плоскостей.
В начальный момент погрешности эфемерид спутников приняты равными: вдоль орбиты 3 м, в направлении радиуса вектора спутника и трансверсали 5 м и 1 м соответственно.
Расчетное местоположение объекта полагалось с координатами φc=60°, λc=30°, истинное местоположение φu=60°+60', λu=30°+120'. Решая систему (25), определим искомые поправки Δφ0, 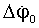 , Δλ0,
, Δλ0, 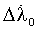 , Δh0.
, Δh0.
Уточнив с учетом поправок местоположения объекта в начальный момент времени t1, определим составляющие погрешности относительно истинного местоположения северную, восточную и суммарную погрешность: Δξ, Δη, 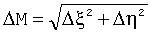 .
.
Как показало моделирование, измерения можно проводить с интервалом в одну секунду, т.е. в моменты t0, t0+1s, t0+2s.
Учитывая малый интервал измерений, вполне возможно в первый момент наблюдения выбранных навигационных спутников измерить непосредственно псевдодальности, а в следующие моменты дельтапсевдодальности, которые представляют приращения дальностей в последующие моменты измерений [11]. Как показано в [11], среднеквадратическая погрешность измерения приращения дальности доплеровским методом не зависит от длительности интервала интегрирования и от разбиения этого интервала на части и составляет 2 см.
В столбцах 1÷14 таблицы 1 приняты следующие обозначения:
- Δρ - систематическая погрешность измерения дальности,
- Vy - истинное значение скорости продольного движения объекта, ΔVy - систематическая погрешность измерения,
- 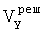 - значение продольной скорости объекта, определенной в результате моделирования,
- значение продольной скорости объекта, определенной в результате моделирования, 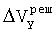 - погрешность определения
- погрешность определения 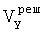 ,
,
- Vx - значение поперечной скорости объекта, систематическая погрешность измерителя ΔVx,
- 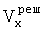 - значение поперечной скорости, определенной в результате моделирования,
- значение поперечной скорости, определенной в результате моделирования, 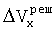 - погрешность определения Vx,
- погрешность определения Vx,
- истинное значение курса K, измеренное значение курса Kизм,
- Kреш - значение курса, определенное в результате моделирования, ΔK - погрешность определения курса,
- VN - северная составляющая скорости движения объекта, VE - восточная составляющая скорости движения объекта, определенные в результате моделирования,
- погрешности определения ΔVN и ΔVE,
- hист - истинное значение высоты объекта над земным эллипсоидом, hизм - измеренное (расчетное) значение высоты,
- Δh0 - разность между истинной высотой hист и высотой, полученной в результате моделирования hr,
- Δξ, Δη, ΔM - соответственно погрешности по широте, долготе и суммарная погрешность местоположения объекта.
Анализ таблицы 1 показывает, что продольная скорость объекта определяется с погрешностью порядка нескольких метров в час, а поперечная - около десяти метров в час, при этом северная и восточная составляющие путевой скорости объекта определяются с точностью долей сантиметра в секунду. Систематическая составляющая погрешности курса объекта определяется тем точнее, чем больше продольная скорость объекта. При увеличении систематических погрешностей измерения дальностей точность определяемых параметров ухудшается.
Литература
1. Дубинко Ю.С., Никитин О.В. Управляющий комплекс подвижных объектов на базе спутниковых навигационных приемников. Навигация и гидрография. - 2006. - №22. - С.16-21.
2. Marvin, Mag Measuring Velosity Using // GPS World September 1992. - P.58-65.
3. Salman Syed, Elizabeth Cannon, Map-Aided GPS Navigation // GPS World November 2005. - P.39-44.
4. Sequential Piecewise Recursive Filter for GPS Low-Dynamics Navigation. T.N. UPADHYAY, J.N. DAHOULSKIS // IEEE TRANSACTION AEROSPACE AND ELECTRONIC SYSTEMS. Vol. AES - 16, №4 JULY 1980. P.481-491.
5. Резниченко В.И., Левит Г.А. Определение скорости по сигналам спутниковых навигационных систем. СПб.: ГНИНГИ МО РФ. - 2004. - 83 с.
6. Резниченко В.И., Мониев А.А. Определение курса корабля по сигналам спутниковых навигационных систем. - СПб.: ГНИНГИ МО РФ. - 2000. - 73 с.
7. Пешехонов В.Г. и др. Единая система инерциальной навигации и стабилизации «Ладога-М». Морская радиоэлектроника. 2003. - В.1(4). - С.26-30.
8. Эскобал П. Методы определения орбит. М.: Мир, 1970. - 471 с.
9. Стренг Г. Линейная алгебра и ее применение. М.: МИР. 1980. - 454 с.
10. С.П.Дмитриев. Высокоточная морская навигация. - СПб.: Судостроение. - 1991. - 222 с.
11. Бортовые устройства спутниковой радионавигации. Сборник статей под редакцией проф. B.C.Шебшаевича. - М.: Транспорт. - 1988. - 200 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА НАВИГАЦИИ, ОРИЕНТАЦИИ И СТАБИЛИЗАЦИИ | 2008 |
|
RU2375679C2 |
| СПОСОБ СПУТНИКОВОЙ КОРРЕКЦИИ ГИРОСКОПИЧЕСКИХ НАВИГАЦИОННЫХ СИСТЕМ МОРСКИХ ОБЪЕКТОВ | 2008 |
|
RU2428659C2 |
| СПОСОБ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ И ЕЁ КОРРЕКЦИИ ПО НЕПОДВИЖНОМУ НАЗЕМНОМУ ОРИЕНТИРУ С ИЗВЕСТНЫМИ ГЕОГРАФИЧЕСКИМИ КООРДИНАТАМИ | 2019 |
|
RU2713582C1 |
| КОРРЕКТИРУЕМАЯ СИСТЕМА ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ И СТАБИЛИЗАЦИИ | 2006 |
|
RU2319930C2 |
| СПОСОБ СПУТНИКОВОЙ КОРРЕКЦИИ АВТОНОМНЫХ СРЕДСТВ НАВИГАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ | 2012 |
|
RU2506542C1 |
| СПОСОБ КОРРЕКЦИИ ДАТЧИКА ПРОЙДЕННОЙ ДИСТАНЦИИ | 2003 |
|
RU2243505C1 |
| СПОСОБ ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ ИНФОРМАЦИИ И ЕЁ КОРРЕКЦИИ ПО ИЗМЕРЕНИЯМ ДОПЛЕРОВСКОГО ИЗМЕРИТЕЛЯ СКОРОСТИ | 2015 |
|
RU2614192C1 |
| СПОСОБ АВТОНОМНОГО МГНОВЕННОГО ОПРЕДЕЛЕНИЯ ПОЛЬЗОВАТЕЛЯМИ-АБОНЕНТАМИ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ, СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ, УГЛОВОЙ ОРИЕНТАЦИИ В ПРОСТРАНСТВЕ И ПЕЛЕНГА ПО ФАЗЕ НЕСУЩЕЙ РАДИОСИГНАЛОВ НАЗЕМНЫХ РАДИОМАЯКОВ, РЕТРАНСЛИРУЕМЫХ СПУТНИКАМИ | 2004 |
|
RU2286584C2 |
| ЗАЩИЩЕННЫЙ СПОСОБ ОПТИМАЛЬНОЙ ПРИВЯЗКИ К ПОДВИЖНОЙ НАЗЕМНОЙ ЦЕЛИ | 2019 |
|
RU2713584C1 |
| СПОСОБ ФОРМИРОВАНИЯ БАРОИНЕРЦИАЛЬНОЙ ВЫСОТЫ И ВЕРТИКАЛЬНОЙ СКОРОСТИ | 2019 |
|
RU2713583C1 |
Изобретение относится к измерительной технике и может быть использовано для коррекции показаний автономных навигационных систем подвижных объектов. Технический результат - расширение функциональных возможностей. Для достижения данного результата выработка спутниковой системой навигационных параметров коррекции базируется на измерениях дальности от объекта до навигационных спутников в три близких (около 1 сек) момента времени с возможностью использования только одного спутника для коррекции автономных средств навигации подвижных объектов. 1 ил., 4 табл.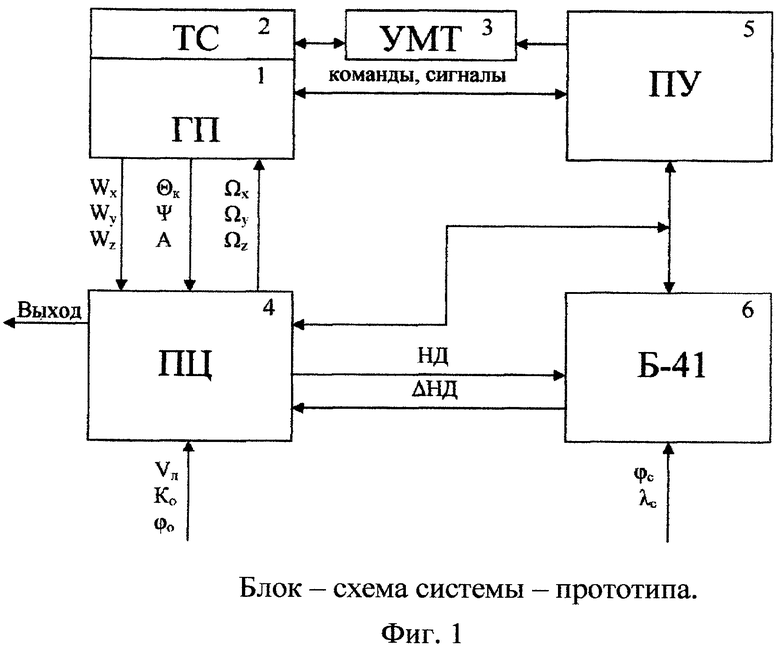
Способ спутниковой коррекции автономных средств навигации подвижных объектов, включающий автономные средства измерения местоположения, скорости и курса объекта и приемник спутниковой навигационной системы, отличающийся тем, что выработка спутниковой системой навигационных параметров коррекции базируется на измерениях дальности от объекта до навигационных спутников в три близких (около 1 с) момента времени с возможностью использования только одного спутника для коррекции автономных средств навигации подвижных объектов.
| Единая система инерциальной навигации и стабилизации «Ладога-М» / ПЕШЕХОНОВ В.Г | |||
| и др | |||
| Морская радиоэлектроника | |||
| Способ и приспособление для нагревания хлебопекарных камер | 1923 |
|
SU2003A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Прибор для получения стереоскопических впечатлений от двух изображений различного масштаба | 1917 |
|
SU26A1 |
| ОПРЕДЕЛЕНИЕ МЕСТОПОЛОЖЕНИЯ С ПОМОЩЬЮ ОДНОГО СПУТНИКА НА НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЕ | 1997 |
|
RU2241239C2 |
| ГИРОСКОПИЧЕСКАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ПОДВИЖНЫХ ОБЪЕКТОВ | 2006 |
|
RU2308681C1 |
| ОЦЕНКА НЕОДНОЗНАЧНОСТИ СИГНАЛОВ GNSS ДЛЯ ТРЕХ ИЛИ БОЛЕЕ НЕСУЩИХ | 2004 |
|
RU2374660C2 |
| US 5570097 A, 29.10.1996. | |||
Авторы
Даты
2012-04-20—Публикация
2010-06-10—Подача