Текст описания приведен в факсимильном виде.
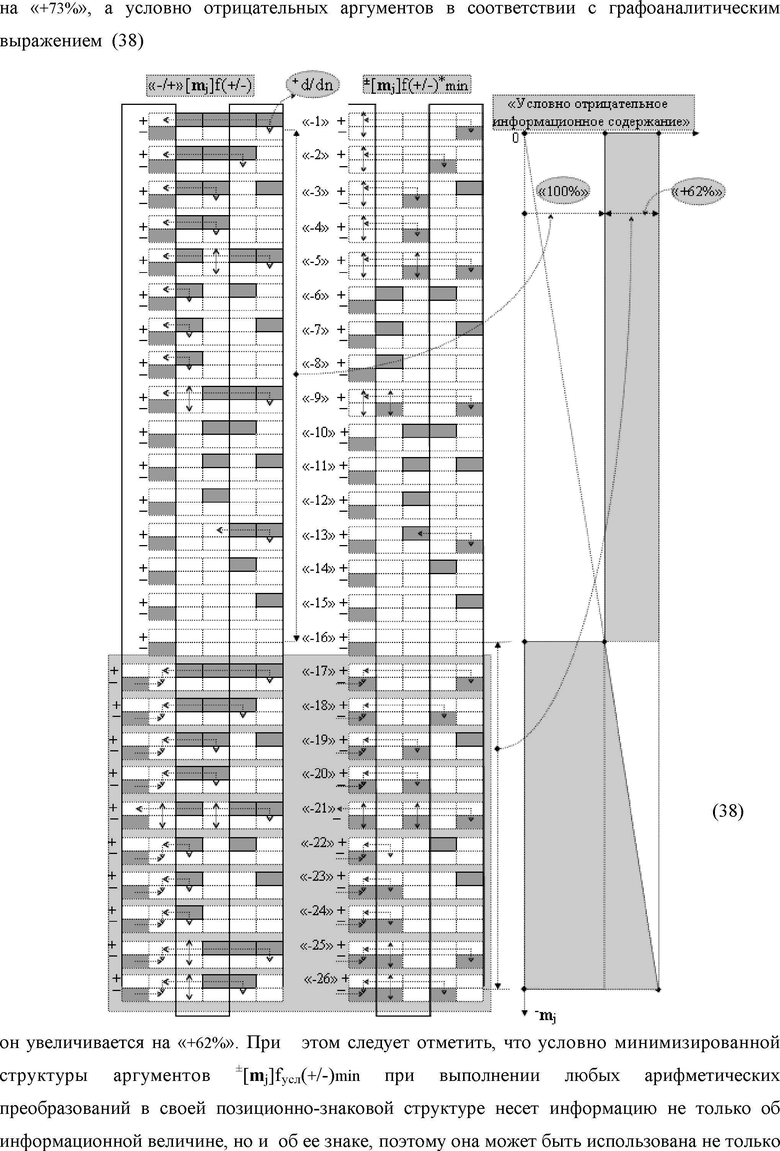
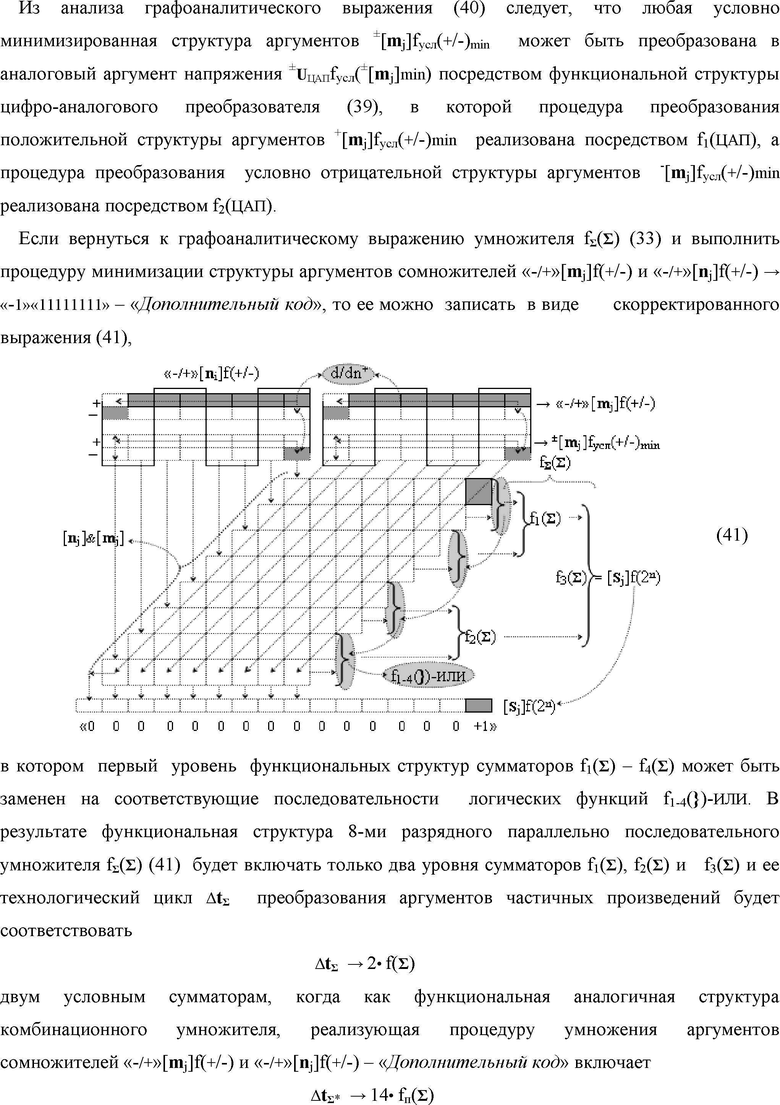
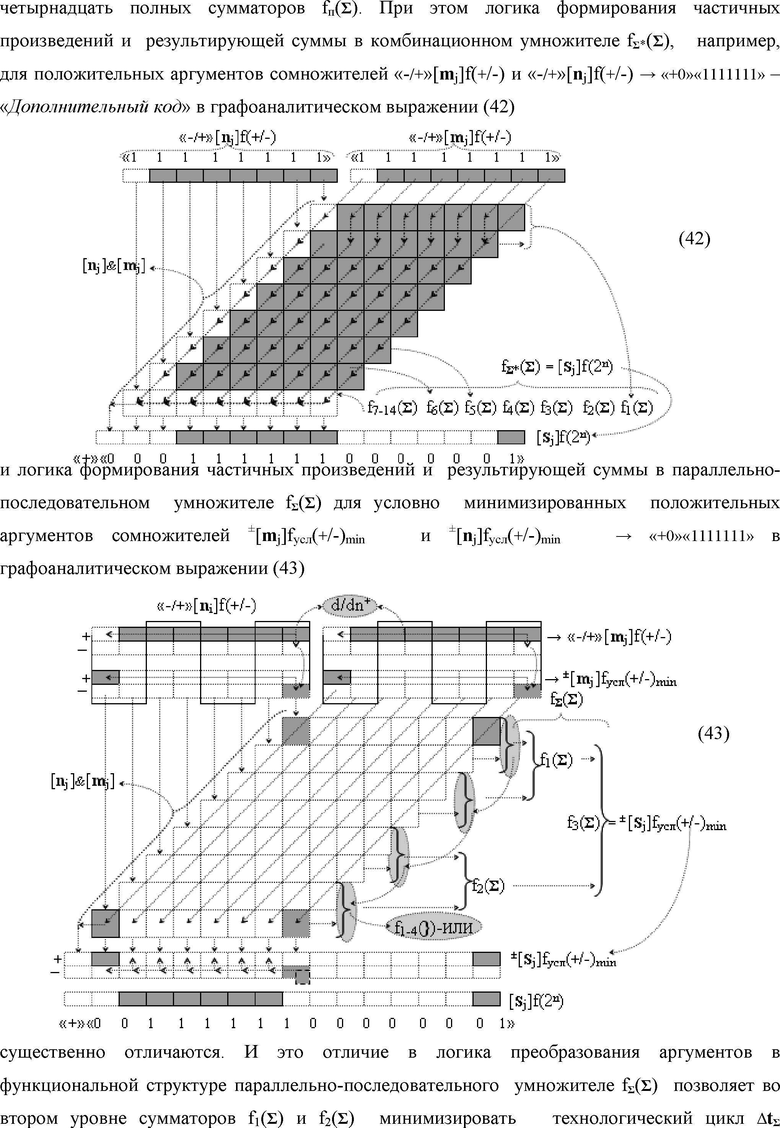
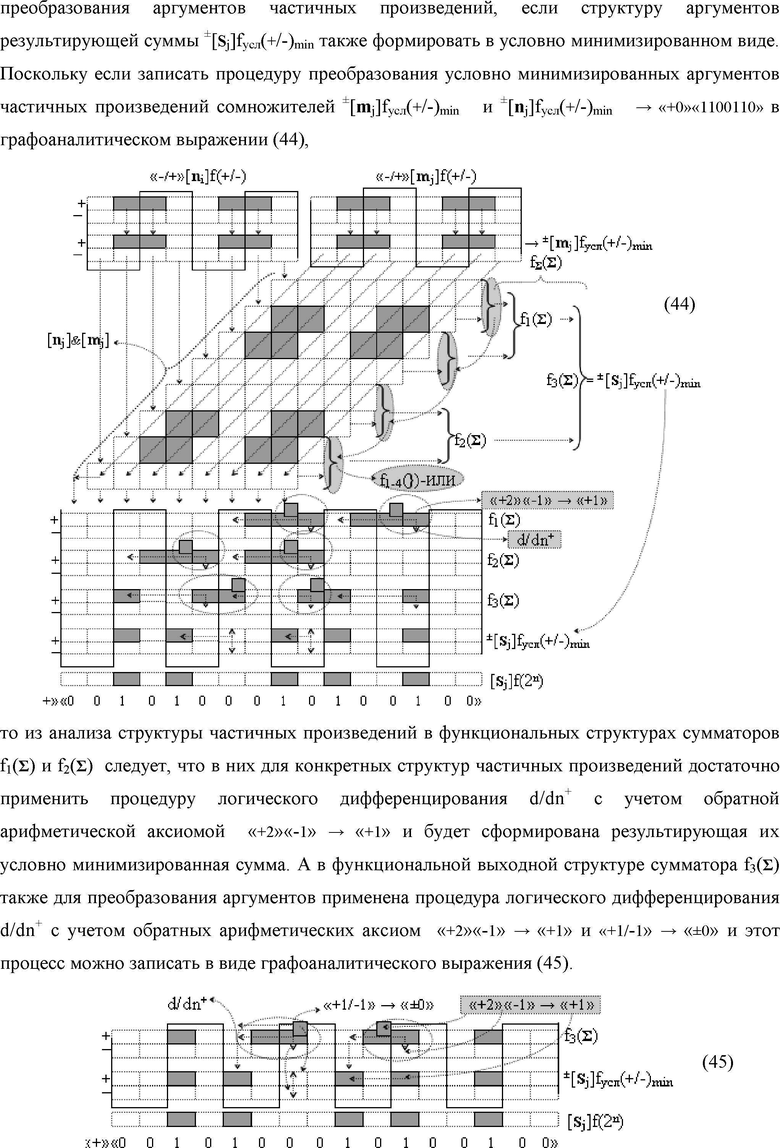
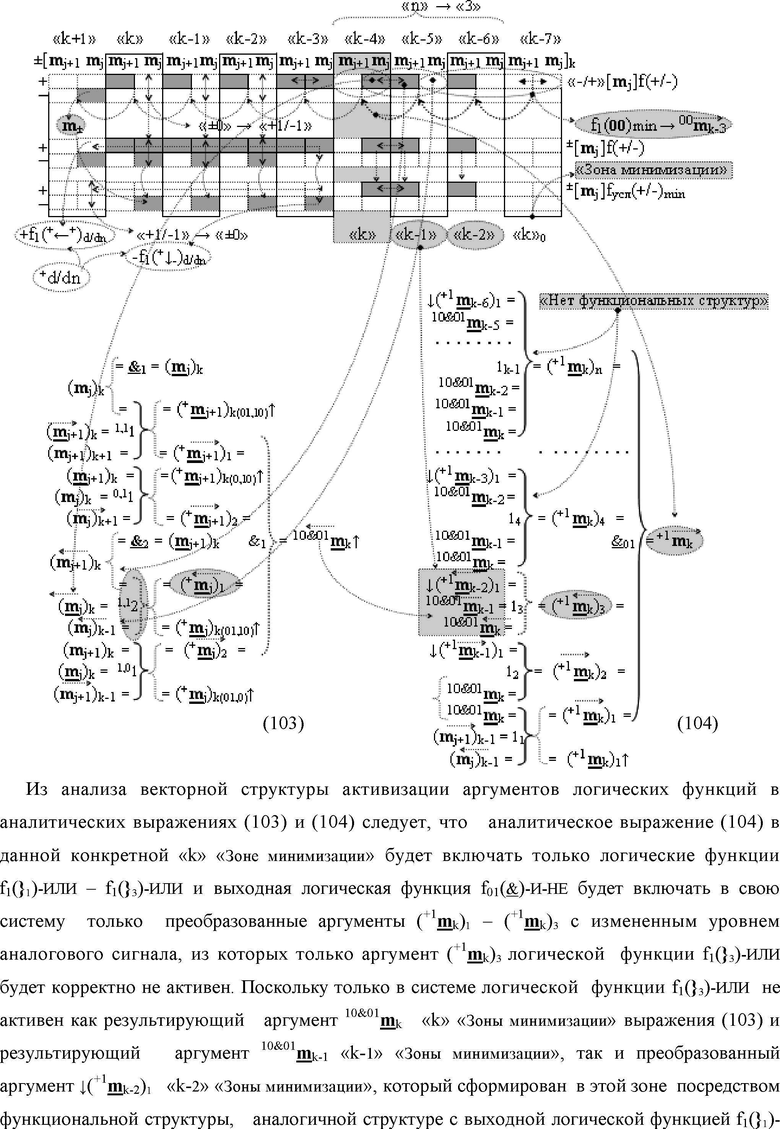
Изобретения относятся к вычислительной технике и могут быть использованы в системах контроля и управления в совокупности с арифметическими устройствами, которые реализуют различные арифметические процедуры над аргументами, представленными в позиционно-знаковой структуре «Дополнительный код». Техническим результатом является расширение диапазона и увеличение быстродействия преобразования. В одном из вариантов функциональная структура реализована с использованием логических элементов И, ИЛИ, НЕ. 5 н.п. ф-лы.
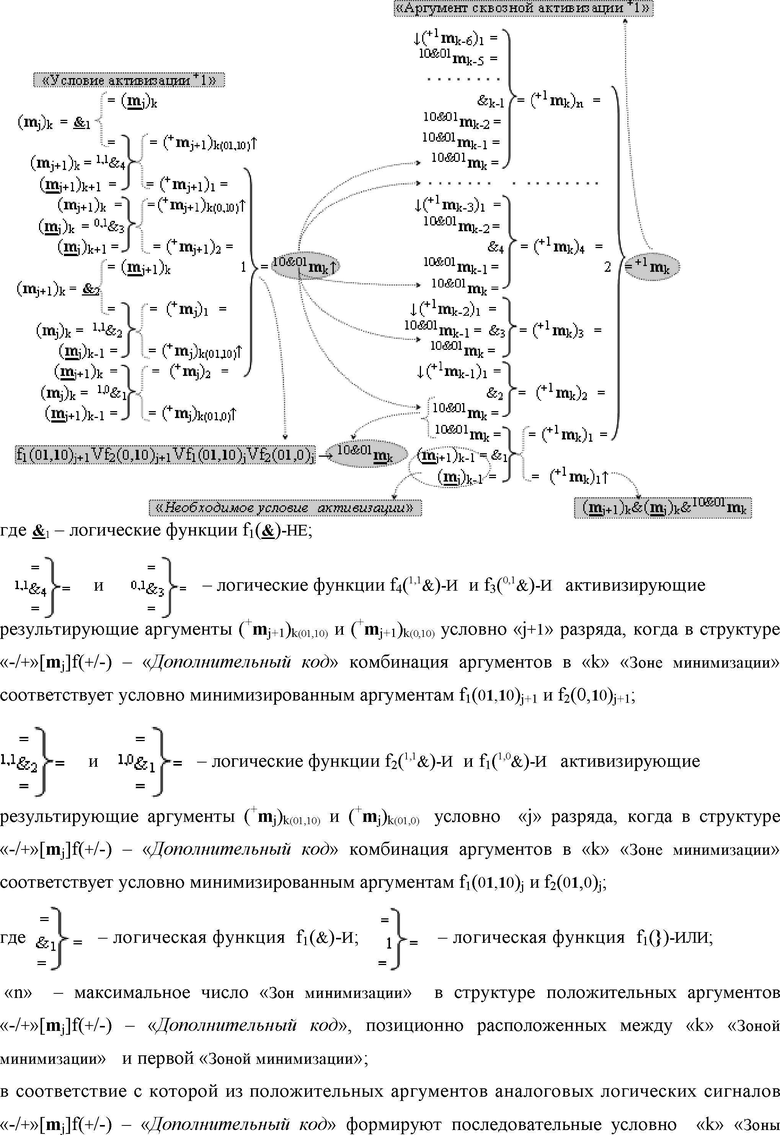
1. Способ формирования в
«k» «Зоне минимизации» результирующего аргумента
+1
m
k
сквозной активизации f1(00)min → +1
m
k для преобразования в соответствии с арифметическими аксиомами троичной системы счисления
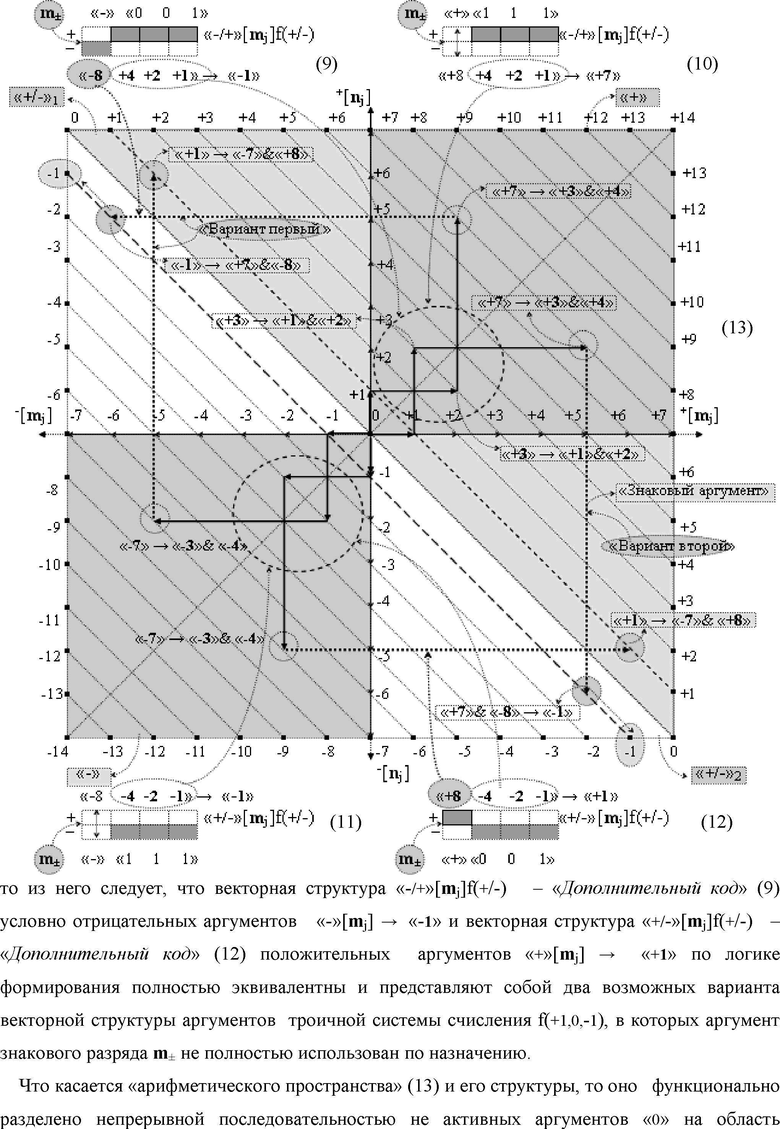
f(+1,0,-1) структуры аргументов аналоговых сигналов
«-/+»[m
j]f(+/-) - «Дополнительный код» в структуру условно минимизированных позиционно- знаковых аргументов аналоговых сигналов
±[m
j]fусл(+/-)min, отличающийся тем, что из положительных аргументов аналоговых логических сигналов «-/+»[m
j]f(+/-) - «Дополнительный код» формируют последовательные условно «k» «Зоны минимизации» с аргументами (m
j+1)k и (m
j)k условно «j+1» и «j» разрядов и выполняют логический анализ их активности как в «k» «Зоне минимизации», так и предыдущих «Зонах минимизации» посредством функциональной структуры f1(00)min сквозной активизации с формированием результирующего аргумента +1
m
k в «k» «Зоне минимизации», который активизируют, когда одновременно активен аргумент (
m
j+1)k&(
m
j)k условно «j+1» и «j» разрядов «Необходимого условия активизации» функциональной структуры f&(00)k → (
m
j+1)k&(
m
j)k в любой предыдущей «Зоне минимизации» и также активны аргументы «Условие активизации +1» структур аргументов f1(01,10)j+1 и f2(0,10)j+1 условно «j+1» разряда или структуры аргументов f1(01,10)j и f2(01,0)j условно «j» разряда, которые объединяет функциональная структура f1(01,10)j+1Vf2(0,10)j+1Vf1(01,10)jVf2(01,0)j → 10&01
m
k в каждой предыдущей «Зоне минимизации», где V - логическая функция объединения; 10&01
m
k - аргумент «Условия активизации +1», при этом процесс активизации аргумента +1
m
k функциональной структуры f1(00)min в «Зонах минимизации» выполняют в соответствии с логико-динамическим процессом вида
2. Способ формирования в
«k» «Зоне минимизации» результирующего аргумента
+1
m
k сквозной активизации f1(00)min → +1
m
k для преобразования в соответствии с арифметическими аксиомами троичной системы счисления
f(+1,0,-1) структуры аргументов аналоговых сигналов
«-/+»[m
j]f(+/-) - «Дополнительный код» в структуру условно минимизированных позиционно-знаковых аргументов аналоговых сигналов
±[m
j]fусл(+/-)min, отличающийся тем, что результирующий «Аргумент сквозной активизации +1»
+1
m
k формируют в соответствии с математической моделью вида
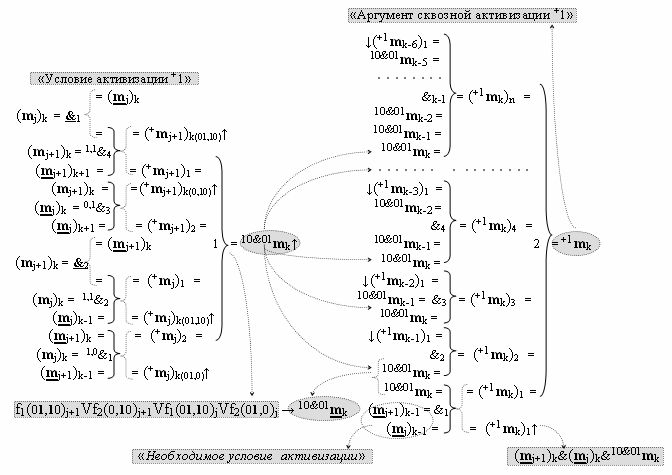
где
&
1 - логические функции f1(
&
)-НЕ;
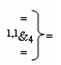и 
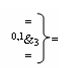- логические функции f4(1,1&)-И и f3(0,1&)-И активизирующие результирующие аргументы (+
m
j+1)k(01,10) и (+
m
j+1)k(0,10) условно «j+1» разряда, когда в структуре «-/+»[m
j]f(+/-) - «Дополнительный код» комбинация аргументов в «k» «Зоне минимизации» соответствует условно минимизированным аргументам f1(01,10)j+1 и f2(0,10)j+1;
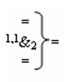и 
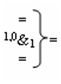- логические функции f2(1,1&)-И и f1(1,0&)-И активизирующие результирующие аргументы (+
m
j)k(01,10) и (+
m
j)k(01,0) условно «j» разряда, когда в структуре «-/+»[m
j]f(+/-) - «Дополнительный код» комбинация аргументов в «k» «Зоне минимизации» соответствует условно минимизированным аргументам f1(01,10)j и f2(01,0)j;
где
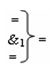- логическая функция f1(&)-И;
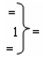- логическая функция f1(})-ИЛИ;
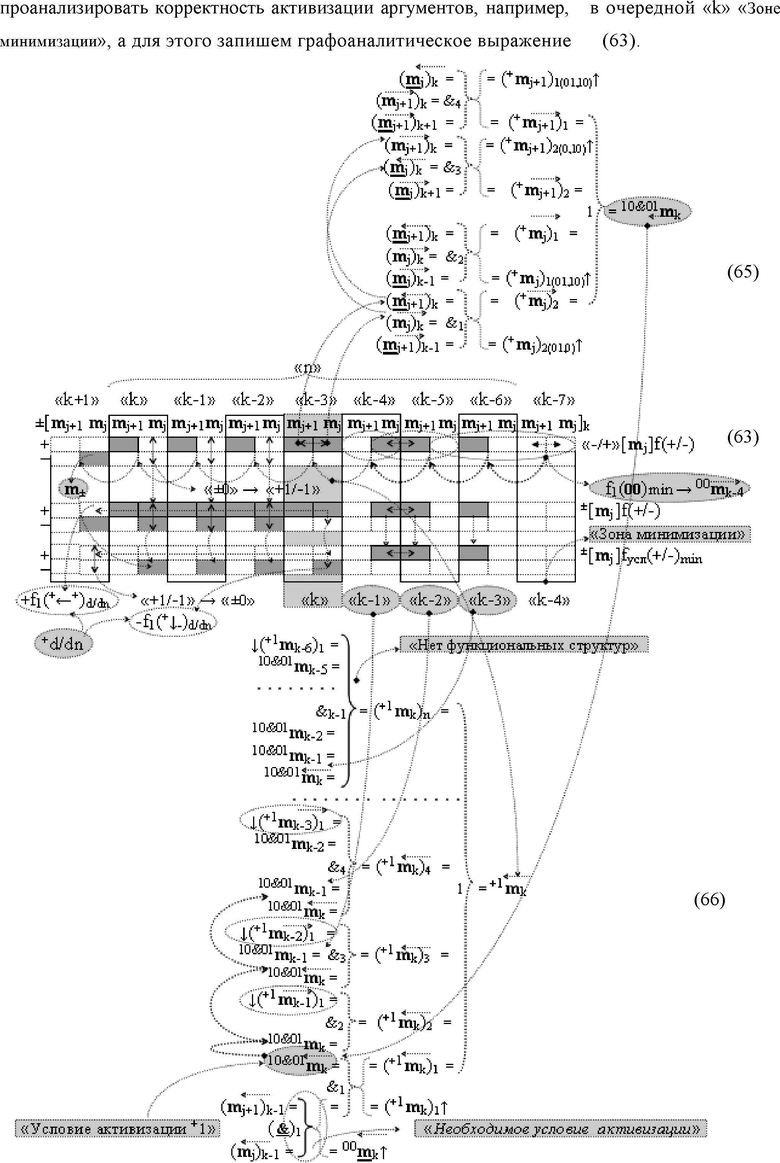
«n» - максимальное число «Зон минимизации» в структуре положительных аргументов «-/+»[m
j]f(+/-) - «Дополнительный код», позиционно расположенных между «k» «Зоной минимизации» и первой «Зоной минимизации»;
в соответствии с которой из положительных аргументов аналоговых логических сигналов «-/+»[m
j]f(+/-) - «Дополнительный код» формируют последовательные условно «k» «Зоны минимизации» с аргументами (m
j+1)k и (m
j)k условно «j+1» и «j» разрядов и выполняют логический анализ их активности в «k» «Зоне минимизации» посредством функциональной структуры f1(01,10)j+1Vf2(0,10)j+1Vf1(01,10)jVf2(01,0)j → 10&01
m
k с выходной логической функцией f1(})-ИЛИ, при этом преобразованный аргумент 10&01
m
k активизируют, если в «k» «Зоне минимизации» активизирован будет один из результирующих аргументов (+
m
j+1)1, (+
m
j+1)2, (+
m
j)1 и (+
m
j)1 логических функций f4(1,1&)-И, f3(0,1&)-И, f2(1,1&)-И и f1(1,0&)-И, соответствующих либо когда в структуре «-/+»[m
j]f(+/-) - «Дополнительный код» комбинация аргументов в «k» «Зоне минимизации» соответствует условно минимизированным аргументам f1(01,10)j+1 и f2(0,10)j+1, либо когда в структуре «-/+»[m
j]f(+/-) - «Дополнительный код» комбинация аргументов в «k» «Зоне минимизации» соответствует условно минимизированным аргументам f1(01,10)j и f2(01,0)j, а «Аргумент сквозной активизации +1» +1
m
k выходной логической функции f2(})-ИЛИ активизируют, когда в ее системе активен либо аргумент (
m
j+1)k&(
m
j)k&10&01
m
k → (+1
m
k)1 «Необходимого условия активизации»&«Условия активизации +1» логической функции f1(&)-И, либо активен любой аргумент (+1
m
k)2 - (+1
m
k)n логических функций f2(&)-И - fk-1(&)-И в любой предыдущей «Зоне минимизации», которые активизируют при условии, что в их системах одновременно активны все аргументы 10&01
m
k - 10&01
m
k-5 «Условие активизации +1» всех предыдущих «Зон минимизации».
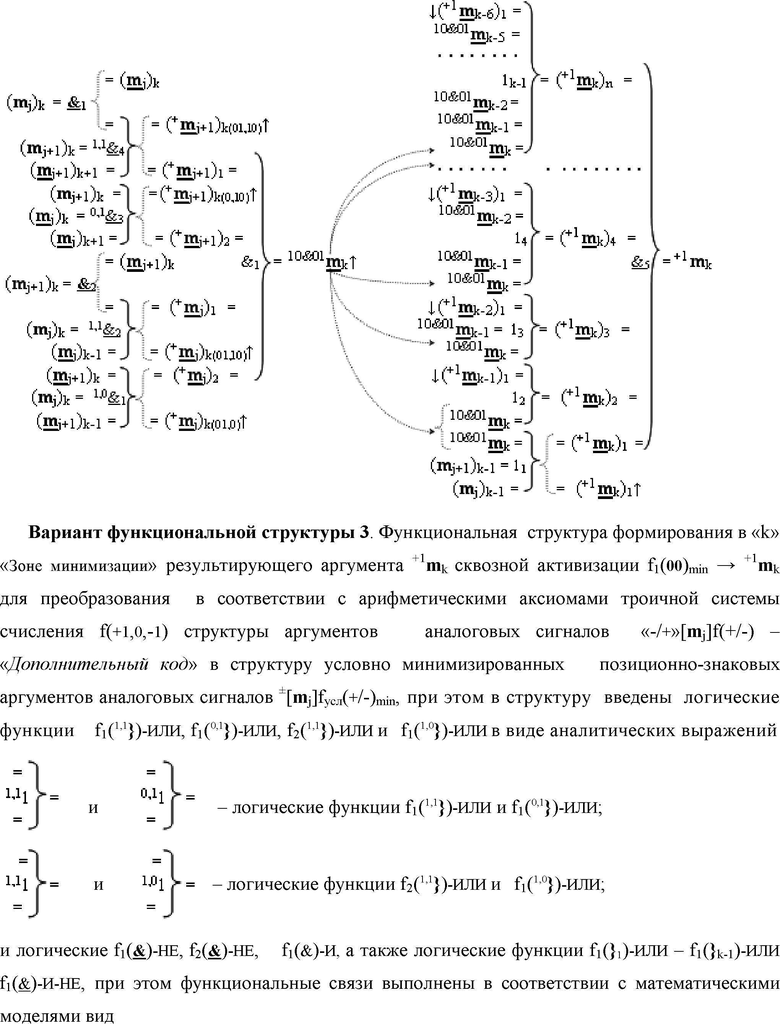
3. Функциональная структура формирования в
«k» «Зоне минимизации» результирующего аргумента
+1
m
k сквозной активизации f1(00)min → +1
m
k для преобразования в соответствии с арифметическими аксиомами троичной системы счисления
f(+1,0,-1) структуры аргументов аналоговых сигналов «-/+»[m
j]f(+/-) - «Дополнительный код» в структуру условно минимизированных позиционно-знаковых аргументов аналоговых сигналов
±[m
j]fусл(+/-)min, отличающаяся тем, что в структуру введены логические функции f1(1,0&)-И, f2(1,1&)-И, f3(0,1&)-И, f4(1,1&)-И в виде аналитических выражени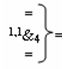й
и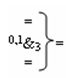 
- логические функции f4(1,1&)-И и f3(0,1&)-И;
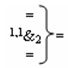и 
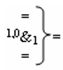- логические функции f2(1,1&)-И и f1(1,0&)-И,
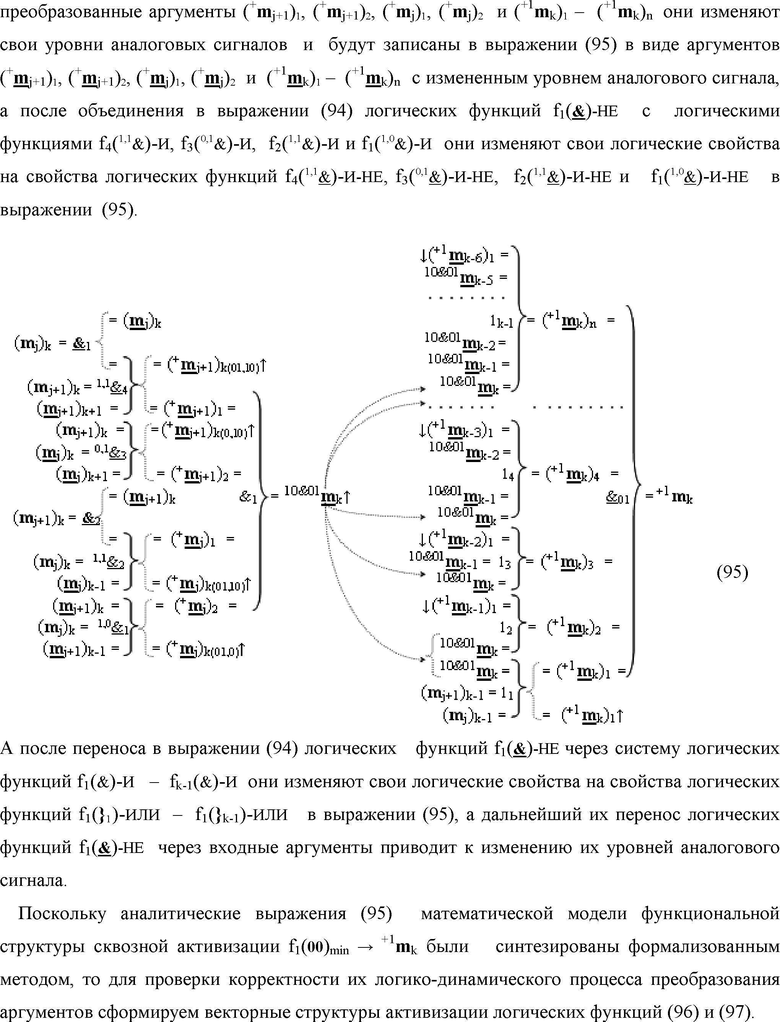
а также логические f1(
&
)-НЕ, f2(
&
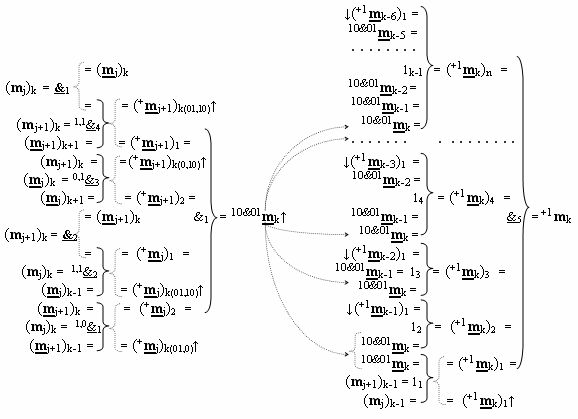
)-НЕ, f1(})-ИЛИ, f1(&)-И - fk-1(&)-И и f2(})-ИЛИ, при этом функциональные связи выполнены в соответствии с математическими моделями вида
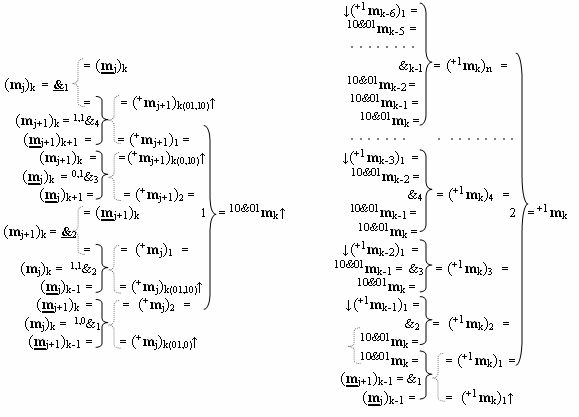
4. Функциональная структура формирования в
«k» «Зоне минимизации» результирующего аргумента
+1
m
k сквозной активизации f1(00)min → +1
m
k для преобразования в соответствии с арифметическими аксиомами троичной системы счисления
f(+1,0,-1) структуры аргументов аналоговых сигналов «-/+»[m
j]f(+/-) - «Дополнительный код» в структуру условно минимизированных позиционно-знаковых аргументов аналоговых сигналов
±[m
j]fусл(+/-)min, отличающаяся тем, что в структуру введены логические функции f1(1,0
&)-И-НЕ, f2(1,1
&)-И-НЕ, f3(0,1
&)-И-НЕ и в виде аналитических выражений
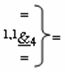и 
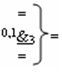- логические функции f4(1,1
&)-И-НЕ и f3(0,1
&)-И-НЕ;
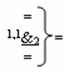и 
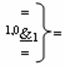- логические функции f2(1,1
&)-И-НЕ и f1(1,0
&)-И-НЕ,
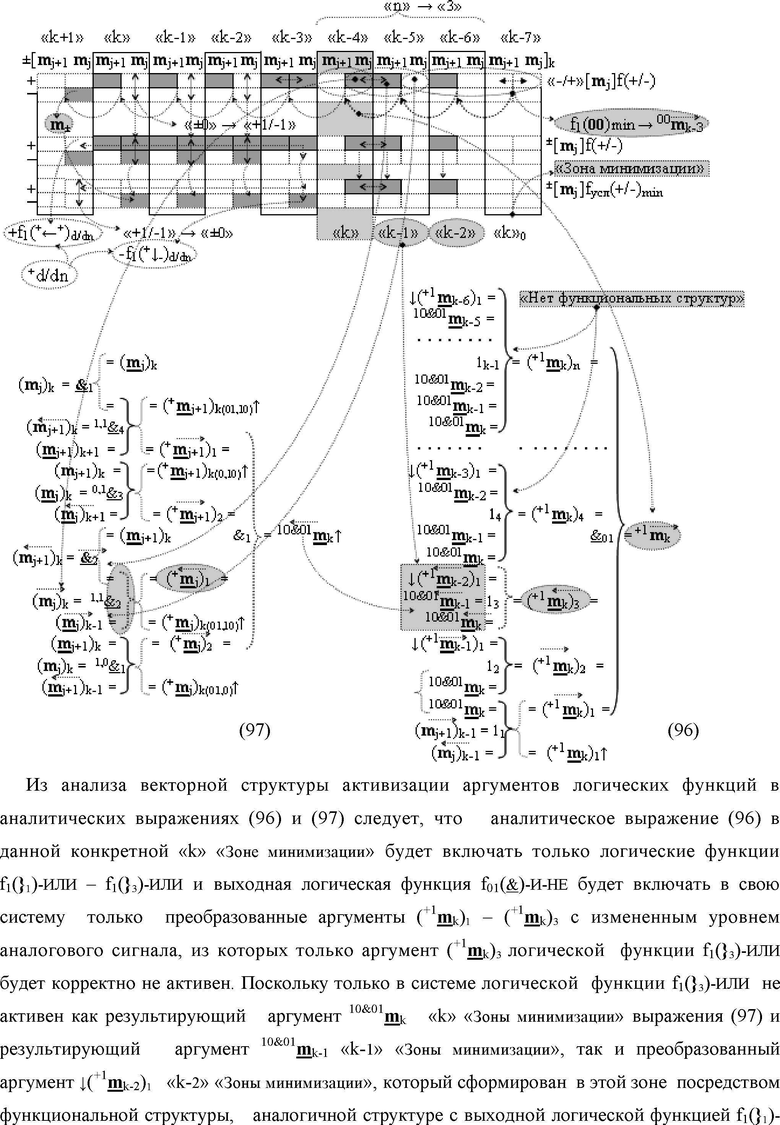
и логические f1(
&
)-НЕ, f2(
&
)-НЕ, f1(&)-И, а также логические функции f1(}
1)-ИЛИ - f1(}
k-1)-ИЛИ и логическая функция f5(&)-И-НЕ, при этом функциональные связи выполнены в соответствии с математическими моделями вида
5. Функциональная структура формирования в
«k» «Зоне минимизации» результирующего аргумента
+1
m
k сквозной активизации f1(00)min → +1
m
k для преобразования в соответствии с арифметическими аксиомами троичной системы счисления
f(+1,0,-1) структуры аргументов аналоговых сигналов «-/+»[m
j]f(+/-) - «Дополнительный код» в структуру условно минимизированных позиционно-знаковых аргументов аналоговых сигналов
±[m
j]fусл(+/-)min, отличающаяся тем, что в структуру введены логические функции f1(1,1
})-ИЛИ, f1(0,1
})-ИЛИ, f2(1,1
})-ИЛИ и f1(1,0
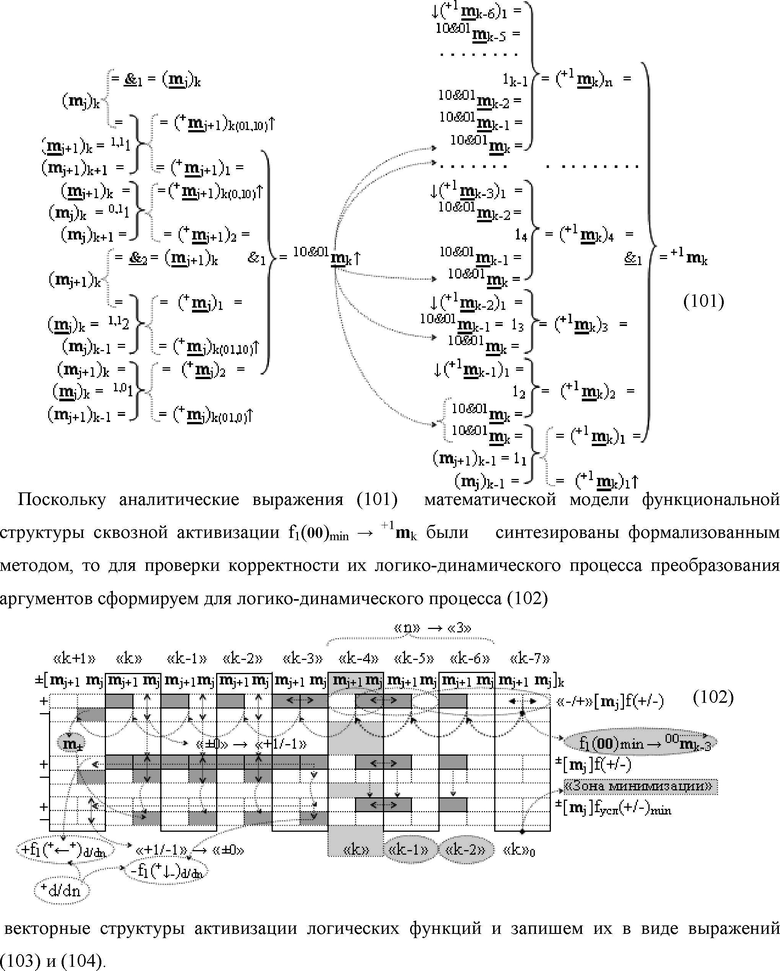
})-ИЛИ в виде аналитических выражений
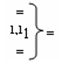и 
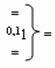- логические функции f1(1,1
})-ИЛИ и f1(0,1
})-ИЛИ;
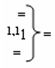и 
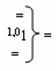- логические функции f2(1,1
})-ИЛИ и f1(1,0
})-ИЛИ;
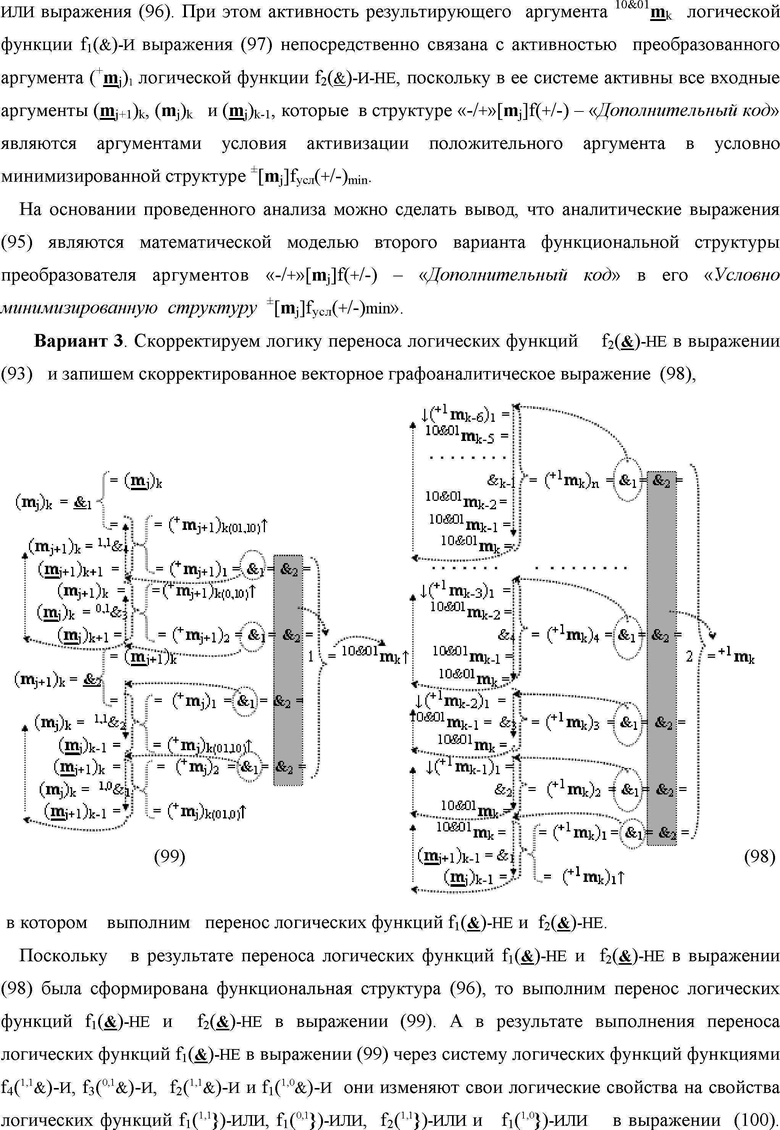
и логические f1(
&
)-НЕ, f2(
&
)-НЕ, f1(&)-И, а также логические функции f1(}
1)-ИЛИ - f1(}
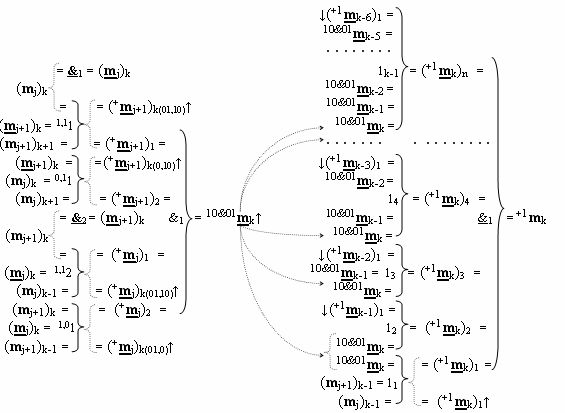
k-1)-ИЛИ f1(&)-И-НЕ, при этом функциональные связи выполнены в соответствии с математическими моделями вида
