ГЕНЕРАТОР НЕЛИНЕЙНЫХ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Российский патент 2015 года по МПК G06F7/58 

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах для формирования кодовых последовательностей.

Известен генератор нелинейных последовательностей, приведенный в [1], содержащий регистр сдвига из последовательно соединенных триггеров, сумматор по модулю два, второй, третий и четвертый триггеры, сумматор по модулю два, с первого по девятый элементы «И», четыре сумматора по модулю два. Указанный генератор реализован на основе известной схемы генератора линейной М-последовательности [1, к. 1, с. 22-27].

Известен генератор псевдослучайных последовательностей, приведенный в книге [2] на с. 147, (генератор М-последовательностей), выбранный в качестве прототипа, содержащий генератор тактовых импульсов, регистр сдвига с синхровходом, с последовательным входом и с выходом на h разрядов, h умножителей и сумматор по модулю два на h входов.

Устройство-прототип имеет следующие функциональные связи.

Выход генератора тактовых импульсов соединен с синхровходом регистра сдвига, а h разрядов с выхода регистра сдвига через h умножителей соединены с h входами сумматора по модулю два, выход которого соединен с последовательным входом регистра сдвига, h разрядов, снимаемых с выхода регистра сдвига, являются выходом устройства.

Работает устройство-прототип следующим образом. С генератора тактовых импульсов импульсы поступают на синхровход регистра сдвига, h разрядов выхода регистра сдвига поступают на выход устройства, а также через h умножителей поступают на h входов сумматора по модулю два, с выхода которого сигнал поступает на последовательный вход регистра сдвига.

При фиксированной разрядности h сдвигового регистра устройство позволяет формировать за счет применения h умножителей возможное количество (объем) различающихся М-последовательностей с периодом N=2^h-1 (под различающимися М-последовательностями понимаются последовательности, каждую из которых нельзя было бы представить в виде циклического сдвига любой другой), определяемое по формуле вида [3, с. 33.]

,

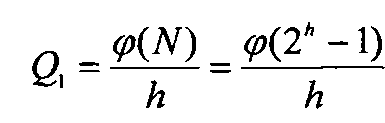где φ(N) - функция Эйлера (при h=10, Q₁=60).

Известные свойства М-последовательностей показывают, что, несмотря на достаточно большой период и хорошие статистические качества, последовательности этого класса имеют простое аналитическое строение. Данный недостаток является следствием того, что М-последовательности формируются (в том числе и в устройстве - прототипе) на основе класса невырожденных двоичных матриц, связанных с классом примитивных полиномов над полем GF(2) и их схемная реализация сводится к применению одного типа линейных операций «сложение по модулю два».

Техническим результатом предлагаемого устройства является расширение функциональных возможностей за счет расширения класса формируемых последовательностей, путем добавления на h-разрядный выход устройства-прототипа модуля, содержащего h/3 нелинейных преобразователей, каждый из которых имеет три двоичных входа и двухбитовый выход, а также блока из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом.

На выходе модуля можно получать последовательности двоичных n-разрядных чисел, n=(2/3)·h, hmod3=0, с периодом N=2^h-1 из класса нелинейных периодических последовательностей или последовательности двоичных h-разрядных чисел с периодом N=2^h-1 из класса М-последовательностей.

Добавленный модуль, содержащий h/3 нелинейных преобразователей, функционально реализует нелинейную функцию аналитического усложнения поступающей на его вход М-последовательности.

На выходе модуля получаем двоичное псевдослучайное число, характер которого зависит от значения на общем управляющем входе блока из h мультиплексоров. Либо это h-разрядное число, формируемое генератором М-последовательности, либо n-разрядное число, снимаемое с генератора нелинейных псевдослучайных последовательностей, n=(2/3)·h, при условии, что hmod3=0.

Нелинейная функция усложнения описывается следующим образом. Рассмотрим преобразование, представляемое в виде отображения (1), где GF(2)ⁿ множество n-разрядных двоичных векторов над полем GF(2)={0, 1}.

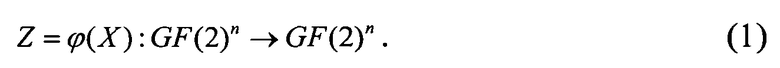
Примем ограничение: отображение (1) является биективным преобразованием (биекцией), n - четное. Всего имеется 2ⁿ! различных биекций [4].

Определим линейное преобразование вектора Х в виде:

где А - двоичная невырожденная матрица размера n и равенство понимается по модулю 2. Число линейных невырожденных преобразований, выполняемых по формуле (2), определяется числом невырожденных матриц по соотношению [5]:

Далее будем рассматривать невырожденные преобразования и ограничимся рассмотрением преобразований над двумя переменными.

Разобьем вектор X на непересекающиеся пары переменных (x_2i-1, x_2i), 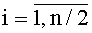$$i=\overline{\mathrm{1,}n/2}$$ . Линейному преобразованию над двумя переменными (x_2i-1, x_2i), выполняемому по формуле (2), поставим в соответствие линейный операционный преобразователь (ОП_L) от двух переменных, имеющий двухбитовый выход.

Отображению (1) при n=2 соответствует 2²!=24 биекции, что больше числа (определяемого по формуле (3)) линейных преобразований, представляемых невырожденными матрицами размера 2.

Рассмотрим аффинные преобразования, представляемые по формуле:

где вектор В∈GF(2)ⁿ, символ ⊕ - обозначение операции суммирования по модулю 2. Число аффинных преобразований определяется формулой:

Аффинному преобразованию над парой переменных (x_2i-1, x_2i), осуществляемому по формуле (4), ставим в соответствие операционный преобразователь (ОП_aff). В этом случае, как следует из (5), число различных ОП_aff равно 24. Множество всех этих ОП_aff обозначим символом П_aff.

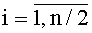
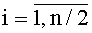
Операционные преобразователи ОП_L и ОП_aff будем называть эквивалентными, если для вектора (x_2i-1, x_2i), $$i=\overline{\mathrm{1,}n/2}$$ , биективные преобразования вектора (x_2i-1, x_2i) в вектор (z_2i-1, z_2i), $$i=\overline{\mathrm{1,}n/2}$$ , выполняемые в ОП_L, и ОП_aff, удовлетворяют условию Z_L=Z_aff.

Обозначим символом П_L={ОП_Li}, $$i=\overline{\mathrm{1,24}}$$ , множество ОП_L, эквивалентных ОП_aff∈П_aff. Введем в рассмотрение систему - транспонированный кортеж вида

где m=n/2, g_i - некоторое линейное биективное преобразование над вектором (x_2i-1, x_2i), 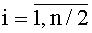$$i=\overline{\mathrm{1,}n/2}$$ , выполняемое по формуле (2) соответствующим линейным операционным преобразователем ОП_L.

Вследствие биективности преобразований g_i, 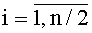$$i=\overline{\mathrm{1,}n/2}$$ , система (6) описывает выполнение биективного преобразования вектора Х=(х₁, х₂, …, x_n) в вектор Z=(z₁, z₂, …, z_n). Систему (6) будем рассматривать как модель функции усложнения, реализующей отображение (1).

Обозначим символом M_L={A_i}, множество невырожденных матриц A_i, размера 3 вида:

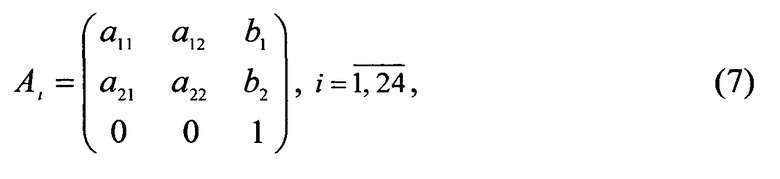
элементы а₁₁, а₁₂, b₁, а₂₁, а₂₂ и b₂ принимают значения 0 или 1. Введем следующее подмножество M_B множества M_L: M_B={A₁₄, А₁₉, А₇}, где 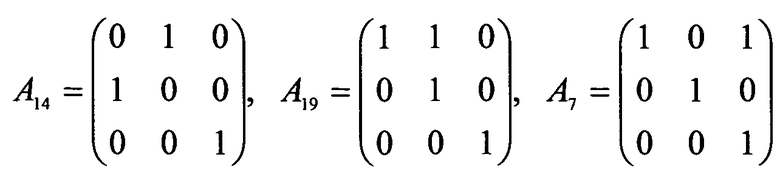(значения индекса i из интервала [1, 24] присвоены этим трем матрицам произвольно). Множество M_B является базисом, порождающим множество M_L.

Путем композиции (произведения) базисных матриц построим в соответствии с [6] все остальные матрицы множества M_L. В таблице 1 дано представление множества матриц M_L в базисе M_B.

Матрицы, представленные в таблице 1, однозначно соответствуют 24-м аффинным преобразованиям вида:

т.е. реализуют все биективные преобразования от двух переменных и ОП_Li∈П_L можно задать матрицей A_i∈M_L, где в качестве входного вектора используем расширение вектора (x_2i-1, x_2i), представляемое вектором (x_2i-1, x_2i, 1).

Отсюда следует, что ОП_Li∈П_L можно задать 1) матрицей A_i∈M_L, где в качестве входного вектора используется расширение вектора (x_2i-1, x_2i), представляемое вектором (x_2i-1, x_2i, 1) или 2) по формуле (8), на основе значений а₁₁, а₁₂, b₁, а₂₁, а₂₂ и b₂, заданных по матрицам вида (7), представленным в таблице 1.

Представим нелинейную модель функции усложнения на основе системы ОП_Li∈П_L.

Рассмотрим преобразование двоичной последовательности, представляемое в виде отображения

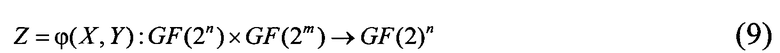
пространства GF(2)^g h-мерных, h=n+m, nmod2=0, векторов V=(X, Y)=(x₁, x₂, …, x_n, y₁, y₂, …, y_m) в пространство GF(2)ⁿ и-мерных векторов Z=(z₁, z₂, …, z_n) над полем GF(2). В преобразовании (9) вектор V рассматривается как конкатенация векторов Х=(х₁, x₂, …, x_n) и Y=(y₁, y₂, …, y_m), m=n/2, где вектор Х - преобразуемый, а вектор Y - управляющий.

Отображение (9) зависит от управляющего вектора Y. Известно [4], что при таком способе преобразования нелинейность последовательности векторов Z в (9) проявляется ввиду существования этой зависимости.

Пусть периодическая последовательность векторов V=(Х, Y)=(x₁, x₂, …, x_n, y₁, y₂, …, y_m) в (9) формируется генератором псевдослучайных М-последовательностей с периодом L=2^h-1, основанном на линейном регистре сдвига, длина которого, h, отвечает условию (10)

где nmod2=0, m=n/2, hmod3=0.

Будем рассматривать эту М-последовательность как последовательность векторов Х=(х₁, x₂, …, x_h) размера h. Разобьем вектор X на непересекающиеся триграммы переменных (x_3i-2, x_3i-1, x_3i), где i=1, …, n/2. В каждой триграмме переменную x_3i будем рассматривать как управляющую переменную y_i из управляющего вектора Y=(y₁, y₂, …, y_m), m=n/2. Период последовательности векторов Z=(z₁, z₂, …, z_n) в этом случае равен L=2^h-1.

Преобразование (9) при данных ограничениях является моделью рассматриваемой нелинейной функции усложнения. При фиксированном управляющем векторе Y отображение (9) выполняет биективное преобразование [4].

Структурное представление нелинейной векторной функции усложнения. Введем операционный преобразователь ОП_н от 3-х переменных, имеющий 2-битовый выход. В качестве входного вектора элемента ОП_н используем вектор (x_3i-2, x_3i-1, x_3i), i=1, …, n/2. ОП_н осуществляет нелинейное преобразование вектора (x_3i-2, x_3i-1, x_3i) в вектор (z_2i-1, z_2i), где i=1, 2, …, n/2. В каждой триграмме (x_3i-2, x_3i-1, x_3i), i=1, …, n/2 переменная x _3i является управляющей. ОП_н представим как пару ОП_Li∈П_L. В ОП_н один ОП_Li∈П_L выполняет преобразование над вектором (x_3i-2, x_3i-1, 1) при x _3i=0, а второй ОП_Li∈П_L выполняет преобразование над вектором (x_3i-2, x_3i-1, 1) при x_3i=1. Нелинейность преобразования в ОП_н реализуется ввиду зависимости операции, выполняемой в ОП_н, от управляющего бита. Объединение ОП_н рассматривается как реализация отображения (9).

Предложена модель представления ПСП, основанная на применении нелинейной функции усложнения, представляемой в виде системы линейных биективных преобразований, выполняемых над двумя двоичными переменными. Модель отличается тем, что алгоритмические возможности функции усложнения максимально расширены за счет сведения аффинного преобразования к линейному преобразованию вида (2), представляемому невырожденными двоичными матрицами вида (7), которые реализуют максимальное число биективных преобразований от двух переменных.

Предлагаемое устройство позволяет увеличить объем формируемых последовательностей с периодом N=2^h-1 до величины Q=(n/2)!, n=(2/3)·h. Например, для h=48 Q=16!+20,9·10¹².

Величину ансамбля Q при фиксированной входной М-последовательности можно менять следующим образом.

1) применяя в блоках ОП_н различные сочетания блоков ОП_Li∈П_L. Максимальное число сочетаний (и соответственно максимальное число различающихся ОП_н) равно величине 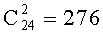$$C_{24}^2=276$$ .

2) путем перестановки блоков ОП_н (при этом можно учитывать, что максимальное число различающихся ОП_н, равное величине 276, достигается при h=828, что следует из (10)).

В этом случае максимальная величина ансамбля Q, получаемая путем перестановки различных блоков ОП_н (при h=828), определяется величиной Q=276!.

Технический результат в генераторе нелинейных псевдослучайных последовательностей, содержащем генератор тактовых импульсов, регистр сдвига на h разрядов с синхровходом и с последовательным входом, h умножителей, каждый из которых на два входа и один выход, и сумматор по модулю два на h входов, достигается тем, что в него введены h/3 однотипных нелинейных преобразователей с тремя входами данных и двумя выходами каждый, hmod3=0, и блок из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом, каждый из нелинейных преобразователей содержит инвертор, четыре функциональных преобразователя и четыре конъюнктора на два входа каждый, из которых первый и второй входят в первую группу конъюнкторов, а третий и четвертый - во вторую группу конъюнкторов, и два дизъюнктора на два входа каждый, каждый функциональный преобразователь имеет три входа задания преобразования, вход инициализации, два входа данных и выход, содержит параллельный регистр на три разряда с входом инициализации, два двухвходовых сумматора по модулю два и трехвходовый сумматор по модулю два, причем генератор тактовых импульсов соединен с синхровходом регистра сдвига, каждый из выходов которого соединен с первым входом умножителя соответственно, второй вход которого является входом для подачи заданных констант, принимающих значения «0» или «1», выходы каждого из h умножителей соединены с входами сумматора по модулю два соответственно, выход которого соединен с последовательным входом регистра сдвига, выходы которого под номерами (3i-2), (3i-1) и 3i соединены с входами данных i-го нелинейного преобразователя соответственно, а также с первыми входами данных блока мультиплексоров под номерами (3i-2), (3i-1) и 3i, 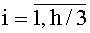$$i=\overline{\mathrm{1,}h/3}$$ , соответственно, выходы данных каждого из n/2 нелинейных преобразователей соединены со вторыми входами данных блока мультиплексоров под номерами с 1 по n соответственно, на вторые входы данных блока мультиплексоров под номерами с (n+1) по h являются входами для подачи значений «0», n=2h/3 соответственно, общий управляющий вход блока мультиплексоров является входом конфигурации, а h выходов блока мультиплексоров являются выходами генератора; первый вход данных нелинейного преобразователя соединен с первым входом данных каждого из четырех функциональных преобразователей, второй вход данных нелинейного преобразователя соединен со вторым входом каждого из четырех функциональных преобразователей, третий вход данных нелинейного преобразователя соединен с входом первого конъюнктора на два входа первой группы, с входом четвертого конъюнктора на два входа второй группы и с входом инвертора, выход инвертора соединен с входом второго конъюнктора на два входа первой группы и с входом третьего конъюнктора на два входа второй группы; выходы конъюнкторов на два входа первой группы соединены с входами первого дизъюнктора на два входа соответственно, выход которого соединен с первым выходом нелинейного преобразователя, а выходы конъюнкторов на два входа второй группы соединены с входами второго дизъюнктора на два входа соответственно, выход которого соединен со вторым выходом нелинейного преобразователя; входы задания преобразования и вход инициализации функционального преобразователя соединены с входами данных и инициализации параллельного регистра на три разряда с входом инициализации соответственно, первый выход данных параллельного регистра на три разряда соединен с входом первого двухвходового сумматора по модулю два, второй выход данных параллельного регистра на три разряда соединен с входом второго двухвходового сумматора по модулю два, третий выход данных параллельного регистра на три разряда соединен с входом трехвходового сумматора по модулю два, два входа которого соединены с выходами сумматоров по модулю два соответственно, а выход трехвходового сумматора соединен с выходом функционального преобразователя; вход первого двухвходового сумматора по модулю два соединен с первым входом данных функционального преобразователя, а вход второго двухвходового сумматора по модулю два соединен со вторым входом данных функционального преобразователя.

Схема генератора нелинейных псевдослучайных последовательностей приведена на фиг. 1, блока нелинейного преобразователя приведена на фиг. 2, а схема блока функционального преобразователя - на фиг. 3.

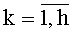
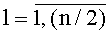
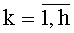
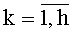
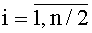
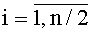
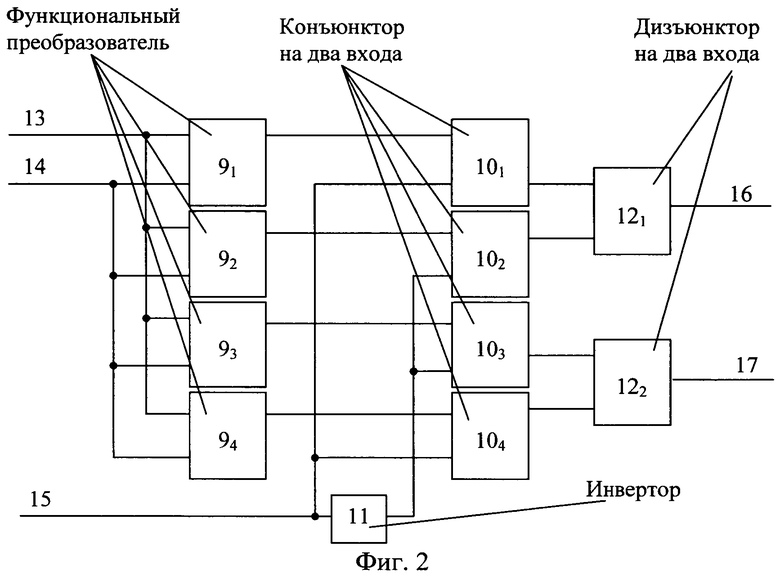
Генератор нелинейных псевдослучайных последовательностей (фиг. 1) содержит генератор 1 тактовых импульсов, регистр 2 сдвига на h разрядов с синхровходом и с последовательным входом, умножители 3_k, $$k=\overline{\mathrm{1,}h}$$ , каждый из которых на два входа и один выход, и сумматор 4 по модулю два на h входов, нелинейные преобразователи 5_l с тремя входами данных и двумя выходами каждый, $$l=\overline{\mathrm{1,}(n/2)}$$ , n=(2/3)·h, блок 6 мультиплексоров с двумя входами данных каждый и с общим управляющим входом 7, выход блока 6 мультиплексоров является h-разрядным выходом 8 генератора нелинейных псевдослучайных последовательностей, причем генератор 1 тактовых импульсов соединен с синхровходом регистра 2 сдвига, k-й выход которого соединен с входом умножителя 3_k, на второй вход каждого из которых - 27_k, $$k=\overline{\mathrm{1,}h}$$ , подаются константы, «0» или «1», соответствующие коэффициентам примитивного неприводимого полинома [7], образующего М-последовательность для генератора, приведенного в книге [2] на с. 147, фиг. 4.2.3, выход каждого из умножителей 3_k, $$k=\overline{\mathrm{1,}h}$$ , соединен с k-м входом сумматора 4 по модулю два, выход которого соединен с последовательным входом регистра 2 сдвига, выходы которого с (3i-2)-го по 3i-й соединены с входами данных под номерами 13, 14 и 15 соответственно нелинейного преобразователя 5_i, $$i=\overline{\mathrm{1,}n/2}$$ , представленного на фиг. 2, и с первыми входами данных блока 6 мультиплексоров под номерами с (3i-2) по 3i, выходы данных каждого из нелинейных преобразователей 5_i, $$i=\overline{\mathrm{1,}n/2}$$ , под номерами 16 и 17, представленные на фиг. 2, соединены со вторыми входами данных блока 6 мультиплексоров под номерами с 1 по n, вторые входы 28 данных блока 6 мультиплексоров под номерами с (n+1) по h являются входами для подачи значение «0», n=2h/3, управляющий вход 7 блока 6 мультиплексоров является входом конфигурации, а выход 8 блока 6 мультиплексоров является h-разрядным выходом генератора нелинейных псевдослучайных последовательностей.

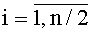
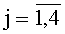
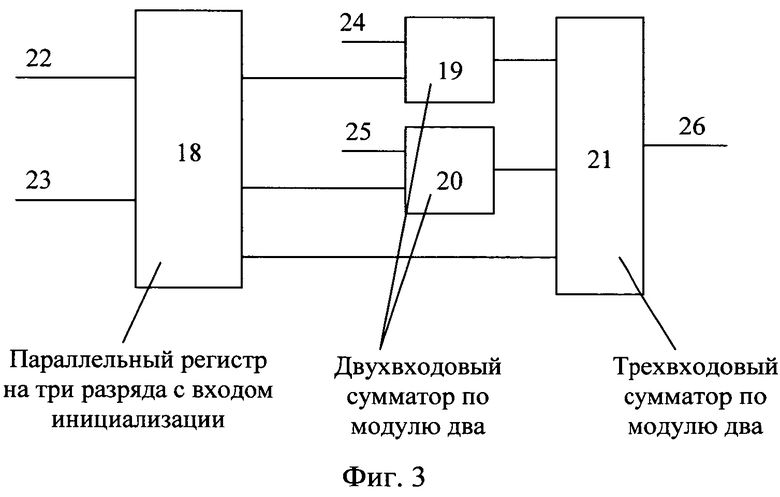
На фиг. 2 представлен нелинейный преобразователь 5_i, $$i=\overline{\mathrm{1,}n/2}$$ , n/2=h/3, который включает четыре функциональных преобразователя 9₁-9₄, четыре конъюнктора 10₁-10₄ на два входа, из которых 10₁ и 10₂ входят в первую группу, 10₃ и 10₄ - во вторую группу, инвертор 11, два дизъюнктора 12₁ и 12₂ на два входа, три входа данных - 13, 14 и 15, а также два выхода 16 и 17, при этом вход 13 нелинейного преобразователя является первым входом 24 каждого из функциональных преобразователей 9₁-9₄, представленных на фиг. 3, вход 14 нелинейного преобразователя является вторым входом 25 каждого из функциональных преобразователей 9₁-9₄ (см. фиг. 3), выход 26 каждого из функциональных преобразователей 9_j (см. фиг. 3) соединен со входом конъюнктора 10_j на два входа соответственно, $$j=\overline{\mathrm{1,4}}$$ , вход 15 нелинейного преобразователя соединен с входами конъюнкторов 10₁ и 10₄ на два входа и входом инвертора 11 соответственно, выход инвертора 11 соединен с входами конъюнкторов 10₂ и 10₃ на два входа соответственно, выходы конъюнкторов 10₁ и 10₂ на два входа соединены с входами дизъюнктора 12₁ на два входа соответственно, выходы конъюнкторов 10₃ и 10₄ на два входа соединены с входами дизъюнктора 12₂ на два входа соответственно, выходы дизъюнкторов 12₁ и 12₂ являются выходами 16 и 17 нелинейного преобразователя соответственно.

На фиг. 3 представлен функциональный преобразователь 9_j, 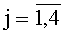$$j=\overline{\mathrm{1,4}}$$ , который содержит параллельный регистр 18 на три разряда с входом инициализации, двухвходовые сумматоры 19 и 20 по модулю два, трехвходовый сумматор 21 по модулю два, вход 22 задания преобразования, вход 23 инициализации, входы 24 и 25 данных и выход 26, при этом вход задания преобразования 22 соединен с входом данных параллельного регистра 18 на три разряда с входом инициализации, вход 23 инициализации соединен с входом инициализации параллельного регистра 18 на три разряда с входом инициализации, первый выход параллельного регистра 18 на три разряда с входом инициализации соединен с входом двухвходового сумматора 19 по модулю два, второй выход параллельного регистра 18 на три разряда с входом инициализации соединен с входом двухвходового сумматора 20 по модулю два, третий выход параллельного регистра 18 на три разряда с входом инициализации соединен с входом трехвходового сумматора 21 по модулю два, входы которого соединены с выходами двухвходовых сумматоров 19 и 20 по модулю два, выход трехвходового сумматора 21 по модулю два является выходом 26 функционального преобразователя, входы данных 24 и 25 функционального преобразователя соединены с входами двухвходовых сумматоров 19 и 20 по модулю два соответственно.

Все блоки, приведенные на фиг. 1, фиг. 2 и фиг. 3, имеют стандартную и опубликованную в литературе реализацию, а также имеют входы электропитания, которые не изображены на фиг. 1, фиг. 2 и фиг. 3.

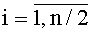
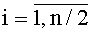
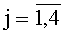
Рассмотрим генератор нелинейных псевдослучайных последовательностей в работе. В предлагаемом генераторе, как и в [1], вычисление элементов псевдослучайных последовательностей производится на основе генератора М-последовательности. По сравнению с прототипом ([2] на с. 147), в устройство введены: n/2=h/3 однотипных нелинейных преобразователя 5_i, $$i=\overline{\mathrm{1,}n/2}$$ , с тремя входами данных и двумя выходами, n=(2/3)·h, hmod3=0, и блок 6 мультиплексоров с общим управляющим входом 7, выход 8 блока 6 является h-разрядным выходом генератора нелинейных псевдослучайных последовательностей; каждый из нелинейных преобразователей 5_i, $$i=\overline{\mathrm{1,}n/2}$$ , включает по четыре функциональных преобразователя 9₁-9₄, четыре конъюнктора 10₁-10₄ на два входа, из которых 10₁ и 10₂ входят в первую группу, а 10₃ и 10₄ - во вторую группу, инвертор 11, два дизъюнктора 12₁ и 12₂ на два входа, каждый функциональный преобразователь 9_j, $$j=\overline{\mathrm{1,4}}$$ , включает параллельный регистр 18 на три разряда с входом инициализации, двухвходовые сумматоры 19 и 20 по модулю два, трехвходовый сумматор 21 по модулю два.

Сущность изобретения в том, что предлагаемый генератор реализует процедуру последовательного вычисления элементов псевдослучайных последовательностей согласно формуле

где z₁ и z₂ вычисляются согласно (8) на основе значений a₁₁, а₁₂, b₁, а₂₁, а₂₂ и b₂, заданных по матрицам (7) при инициализации функциональных преобразователей, а значения (x₁=x _3i-2, x₂=x _3i-1, y_i=x_3i), $$i=\overline{\mathrm{1,}(n/2)}$$ , поступают с выхода генератора М-последовательности (прототипа), приведенного в книге [2] на с. 147, фиг. 4.2.3.

Техническая реализация процедуры (11) в виде блока нелинейного преобразователя, позволяет увеличить объем формируемых последовательностей с периодом N=2^h-1 до величины Q=(n/2)!, n=(2/3)·h, где возможная максимальная величина - Q, получаемая путем перестановки различных блоков ОП_н, определяется как Q=276! при h=828 (n=552).

При этом блок нелинейного преобразователя позволяет получить последовательность с периодом N=2^h-1 согласно формуле вида (11).

Технический результат выражен в увеличении объема формируемых последовательностей путем применения нелинейного преобразователя.

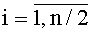
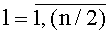
Значения элементов М-последовательности, h-разрядные числа X, формируемые по синхросигналу, подаваемому с генератора 1 тактовых импульсов на синхровход регистра 2 сдвига, поступают с выходов регистра 2 сдвига на входы данных нелинейных преобразователей 5_i, $$i=\overline{\mathrm{1,}n/2}$$ . По синхросигналу, поступающему с генератора 1 тактовых импульсов, значения Х={{x_2l-1, x_2l, y_l}}, поступают на входы 13, 14 и 15 данных каждого из нелинейных преобразователей 5_l, с выходов 16 и 17 каждого из которых снимаются значения Z={(z_2l-1, z_2l)}, соответственно, $$l=\overline{\mathrm{1,}(n/2)}$$ (фиг. 2). Выходы 16 и 17 каждого из нелинейных преобразователей 5_l, $$l=\overline{\mathrm{1,}(n/2)}$$ , общее количество которых равно n, соединены с вторыми входами данных блока 6 мультиплексоров под номерами с 1 по n, n=2h/3, на вторые входы 28 данных блока 6 мультиплексоров под номерами с (n+1) по h подано значение «0», с первыми входами данных блока 6 мультиплексоров соединены выходы данных регистра 2 сдвига, общий вход 7 блока 6 мультиплексоров является входом конфигурации, а выход 8 блока 6 мультиплексоров является выходом генератора нелинейных псевдослучайных последовательностей.

При подаче напряжения питания происходит инициализация генератора нелинейных псевдослучайных последовательностей.

На этапе инициализации на вход 23 (фиг. 2) инициализации параллельного регистра 18 на три разряда с входом инициализации поступает сигнал (значение «1»), согласно которому в регистр 18 на три разряда с входом инициализации заносится информация о выполняемом преобразовании согласно формуле (7): на вход 22 задания преобразования функциональных преобразователей 9₁ и 9₃ каждого из нелинейных преобразователей 5_l, $$l=\overline{\mathrm{1,}(n/2)}$$ , поступают значения а₁₁, а₂₁ и b₁ на первый, второй и третий разряды параллельного регистра 18 на три разряда с входом инициализации соответственно, а на вход 22 задания преобразования функциональных преобразователей 9₂ и 9₄ каждого из нелинейных преобразователей 5_l, $$l=\overline{\mathrm{1,}(n/2)}$$ , поступают значения а₂₁, а₂₂ и b₂ на первый, второй и третий разряды параллельного регистра 18 на три разряда с входом инициализации соответственно. При этом в каждый из нелинейных преобразователей 5_l, $$l=\overline{\mathrm{1,}(n/2)}$$ , заносятся свои значения а₁₁, а₁₂, b₁, а₂₁, а₂₂ и b₂, задающие одно из аффинных преобразований (биекций) вида (7).

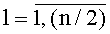
Если на выходе 8 генератора требуется получить значения М-последовательности, то на вход 7 конфигурации генератора псевдослучайных чисел требуется подать значение «0», если же на выходе 8 генератора требуется получить значения нелинейной последовательности, то на вход 7 конфигурации требуется подать значение «1».

На этапе функционирования, с генератора 1 тактовых импульсов поступает синхросигнал на синхровход регистра 2 сдвига. В данной связи в регистра 2 сдвига производится логический сдвиг двоичных значений его разрядов, а значение, формируемое на его последовательном входе при использовании умножителей 3₁, …, 3_h и сумматора 4 по модулю два, заносится в младший разряд регистра 2 сдвига, n двоичных значений из регистра 2 сдвига поступают на входы нелинейных преобразователей 5l, n=(2/3)·h, hmod3=0, причем значения (x_2l-1, x_2l, y_l) поступают на входы 13, 14 и 15 данных нелинейного преобразователя 5_l, 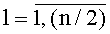$$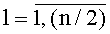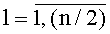l=\overline{\mathrm{1,}(n/2)}$$ , внутри которого значения с входов 13 и 14 данных поступают на входы 24 и 25 данных каждого из функциональных преобразователей 9₁, …, 9₄ соответственно, а с входа данных 15 - на входы конъюнкторов 10₁ и 10₄ на два входа и инвертора 11, с выхода которого значения поступают на входы конъюнкторов 10₂ и 10₃ на два входа; внутри каждого из функциональных преобразователей 9₁, …, 9₄ значения, поступившие на входы 24 и 25 данных поступают на один из входов двухвходовых сумматоров 19 и 20 по модулю два, значения с выходов двухвходовых сумматоров 19 и 20 поступают на два входа трехвходового сумматора 21 по модулю два, значение с выхода которого поступает на выход 26 каждого из функциональных преобразователей 9₁, …, 9₄; значения с выходов функциональных преобразователей 9₁, …, 9₄ поступают на входы конъюнкторов 10₁, …, 10₄ соответственно, значения с выходов конъюнкторов 10₁ и 10₂ поступают на входы дизъюнктора 12₁ на два входа, а значения с выходов конъюнкторов 10₃ и 10₄ поступают на входы дизъюнктора 12₂ на два входа, с выходов дизъюнкторов 12₁ и 12₂ на два входа, которые являются выходами 16 и 17 нелинейного преобразователя 5_l, снимаются значения (z_2l-1, z_2l), $$l=\overline{\mathrm{1,}(n/2)}$$ , поступающие на вторые входы данных блока 6 мультиплексоров под номерами с 1 по n, на вторые входы 28 данных блока 6 мультиплексоров под номерами с (n+1) по h подано значение «0», на первый вход блока 6 мультиплексоров поступают данные с h-разрядного регистра 2 сдвига, значение на общем управляющем входе 7 блока 6 мультиплексоров позволяет выбрать, какая из последовательностей, линейная или нелинейная, поступит на выход 8 блока 6 мультиплексоров. Выход 8 является h-разрядным выходом генератора нелинейных псевдослучайных последовательностей, на который поступают h значений из регистра 2 сдвига (М-последовательность) при подаче на управляющий вход 7 значения «0», тогда как при подаче на вход 7 значения «1», на n разрядов h-разрядного выхода 8 поступают значения, снимаемые с n/2 нелинейных преобразователей 5_l, $$l=\overline{\mathrm{1,}(n/2)}$$ , n=2h/3.

Таким образом, введение в генератор нелинейных псевдослучайных последовательностей h/3 однотипных нелинейных преобразователей с тремя входами данных и двумя выходами каждый, а также блока из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом, позволяет увеличить объем формируемых максимальных периодических последовательностей до величины Q=(n/2)!, n=(2/3)·h, hmod3=0, где h - количество двоичных разрядов чисел, снимаемых с выхода регистра сдвига, целое положительное число.

Источники информации

1. Пат. 1413616 SU, МПК⁴ G06F 1/02. Генератор нелинейных последовательностей / П.Г. Тараненко, Ю.И. Лютынский, А.В. Астанин и др. №4183715/24-24; заявл. 19.01.1987; опубл. 30.07.1988, Бюл. №28. 3 с.: ил.

2. Шумоподобные сигналы в системах передачи информации / В.Б. Пестряков, В.П. Афанасьев, В.Л. Гурвич и др. - М.: Сов. радио, 1973. - 424 с.

3. Свердлик М.Б. Оптимальные системы и сигналы. - М.: Сов. радио, 1975. - 200 с.

4. Молдовян Н.А., Молдовян А.А., Еремеев М. А. Криптография: от примитивов к синтезу алгоритмов. - СПб.: БХВ-Петербург, 2004. - 448 с.

5. Gunter, W. Linear transformations and exact minimization of BDDs / W. Gunter, R. Drechsler // IEEE Great Lakes Symposium on VLSI, Lafayette. - 1998. - P. 325-330.

6. Колпаков А.В. Методы и алгоритмы линейных и аффинных преобразований для модели бинарных диаграмм решений. Дисс. … канд. техн. наук: 05.13.18. - Казань, 2004.

7. Бухштаб А.А. Теория чисел / А.А. Бухштаб. - М.: Просвещение, 1966. - 384 с.

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах для формирования кодовых последовательностей. Технический результат заключается в расширении функциональных возможностей за счет расширения класса формируемых последовательностей путем добавления на h-разрядный выход устройства-прототипа модуля, содержащего h/3 нелинейных преобразователей, каждый из которых имеет три двоичных входа и двухбитовый вход, а также блока из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом. Технический результат достигается за счет того, что в генератор нелинейных псевдослучайных последовательностей введены h/3 однотипных нелинейных преобразователя с тремя входами данных и двумя выходами, hmod3=0, и блок из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом, каждый из нелинейных преобразователей содержит инвертор, четыре функциональных преобразователя и четыре конъюнктора на два входа и два дизъюнктора на два входа. 3 ил., 1 табл.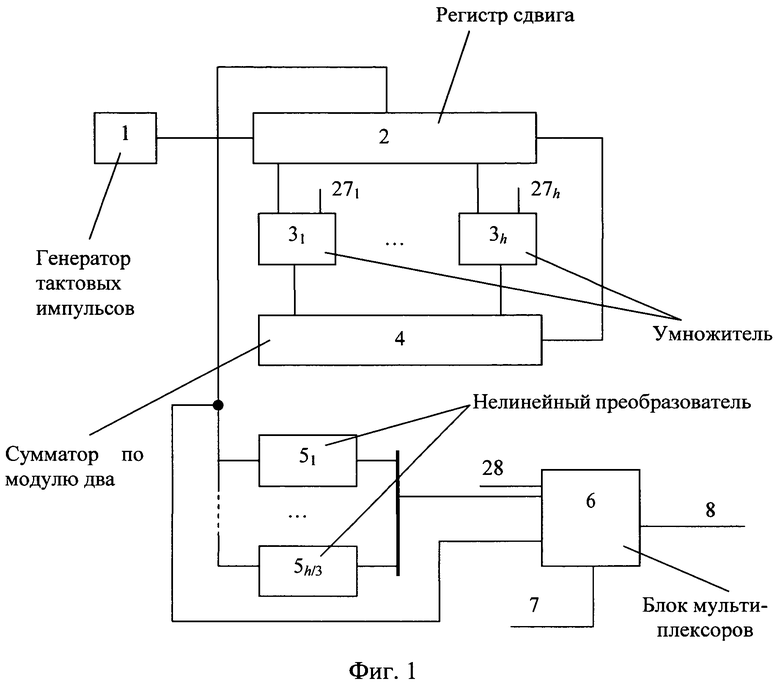

Генератор нелинейных псевдослучайных последовательностей, содержащий генератор тактовых импульсов, регистр сдвига на h разрядов с синхровходом и с последовательным входом, h умножителей, каждый из которых на два входа и один выход, и сумматор по модулю два на h входов, отличающийся тем, что в него введены h/3 однотипных нелинейных преобразователей с тремя входами данных и двумя выходами каждый, hmod3=0, и блок из h мультиплексоров с двумя входами данных каждый и с общим управляющим входом, каждый из нелинейных преобразователей содержит инвертор, четыре функциональных преобразователя и четыре конъюнктора на два входа каждый, из которых первый и второй входят в первую группу конъюнкторов, а третий и четвертый - во вторую группу конъюнкторов, и два дизъюнктора на два входа каждый, каждый функциональный преобразователь имеет три входа задания преобразования, вход инициализации, два входа данных и выход, содержит параллельный регистр на три разряда с входом инициализации, два двухвходовых сумматора по модулю два и трехвходовый сумматор по модулю два, причем генератор тактовых импульсов соединен с синхровходом регистра сдвига, каждый из выходов которого соединен с первым входом умножителя соответственно, второй вход которого является входом для подачи заданных констант, принимающих значения «0» или «1», выходы каждого из h умножителей соединены с входами сумматора по модулю два соответственно, выход которого соединен с последовательным входом регистра сдвига, выходы которого под номерами (3i-2), (3i-1) и 3i соединены с входами данных i-го нелинейного преобразователя соответственно, а также с первыми входами данных блока мультиплексоров под номерами (3i-2), (3i-1) и 3i, 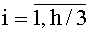, соответственно, выходы данных каждого из n/2 нелинейных преобразователей соединены со вторыми входами данных блока мультиплексоров под номерами с 1 по n соответственно, на вторые входы данных блока мультиплексоров под номерами с (n+1) по h являются входами для подачи значений «0», n=2h/3 соответственно, общий управляющий вход блока мультиплексоров является входом конфигурации, a h выходов блока мультиплексоров являются выходами генератора; первый вход данных нелинейного преобразователя соединен с первым входом данных каждого из четырех функциональных преобразователей, второй вход данных нелинейного преобразователя соединен со вторым входом каждого из четырех функциональных преобразователей, третий вход данных нелинейного преобразователя соединен с входом первого конъюнктора на два входа первой группы, с входом четвертого конъюнктора на два входа второй группы и с входом инвертора, выход инвертора соединен с входом второго конъюнктора на два входа первой группы и с входом третьего конъюнктора на два входа второй группы; выходы конъюнкторов на два входа первой группы соединены с входами первого дизъюнктора на два входа соответственно, выход которого соединен с первым выходом нелинейного преобразователя, а выходы конъюнкторов на два входа второй группы соединены с входами второго дизъюнктора на два входа соответственно, выход которого соединен со вторым выходом нелинейного преобразователя; входы задания преобразования и вход инициализации функционального преобразователя соединены с входами данных и инициализации параллельного регистра на три разряда с входом инициализации соответственно, первый выход данных параллельного регистра на три разряда соединен с входом первого двухвходового сумматора по модулю два, второй выход данных параллельного регистра на три разряда соединен с входом второго двухвходового сумматора по модулю два, третий выход данных параллельного регистра на три разряда соединен с входом трехвходового сумматора по модулю два, два входа которого соединены с выходами сумматоров по модулю два соответственно, а выход трехвходового сумматора соединен с выходом функционального преобразователя; вход первого двухвходового сумматора по модулю два соединен с первым входом данных функционального преобразователя, а вход второго двухвходового сумматора по модулю два соединен со вторым входом данных функционального преобразователя.