Изобретение относится к области машиностроения и может использоваться для соединения звеньев механизмов и деталей машин.
Известно, что любая механическая система (механизм, машина) состоит из звеньев и соединений звеньев. Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой [1, с. 20, 5-й абзац сверху].
Известна двухподвижная цилиндрическая кинематическая пара [1, стр. 57, рис. 95], образованная связью двух звеньев - прямого кругового цилиндра [2, стр. 188, рис. 2.49] и желоба, входящих в контакт по поверхности. Такая пара позволяет воспроизводить независимые вращательное и поступательное движения (движения ВП) относительно одной общей оси декартовой системы координат.
Недостатком этой пары является невозможность воспроизведения указанных независимых движений относительно двух осей координат.
Наиболее близкой к заявляемой кинематической паре является удерживающая трехподвижная кинематическая пара [3], принимаемая за прототип. Эта пара образуется двумя звеньями - прямым круговым цилиндром и двойным корсетом, при этом поверхности звеньев имеют разную кривизну. Контакт звеньев пары обеспечивается в двух точках, при этом радиус кривизны образующей вогнутой поверхности корсета на всем возможном участке ее соприкосновения с цилиндром обеспечивается меньшим, чем удвоенный радиус цилиндра. Пара позволяет воспроизводить вращательное и поступательное движения (ВП) относительно одной общей оси и вращательное движение (В) относительно второй оси декартовых координат. Относительно третьей оси никаких движений нет. Таким образом, пара имеет комплекс движений ВПВ.
В технике могут возникать ситуации, требующие воспроизведения звеньями гарантированно двух независимых движений - поступательного и вращательного относительно разных осей декартовой системы координат (движений ПВ). В связи с этим недостатком прототипа является наличие дополнительного вращательного движения вокруг продольной оси цилиндра, соединяющей центры его оснований.
Задачей изобретения является создание двухподвижной кинематической пары, воспроизводящей комплекс двух независимых движений - поступательного и вращательного относительно двух из осей декартовой системы координат (движений ПВ) путем устранения вращательного движения вокруг продольной оси цилиндра.
Сущность заявляемого устройства заключается в том, что предлагается двухподвижная кинематическая пара, включающая два звена - цилиндр и двойной корсет, поверхности которых имеют разную кривизну и входят между собой в точечный контакт, при этом цилиндр выполнен прямым эллиптическим, удерживающимся двойным корсетом, при этом радиус кривизны образующей вогнутой поверхности корсета обеспечивается большим длины малой полуоси эллипса основания цилиндра, при этом кинематическая пара исполнена двухподвижной, воспроизводящей независимые поступательное и вращательное движения относительно двух из осей декартовых координат.
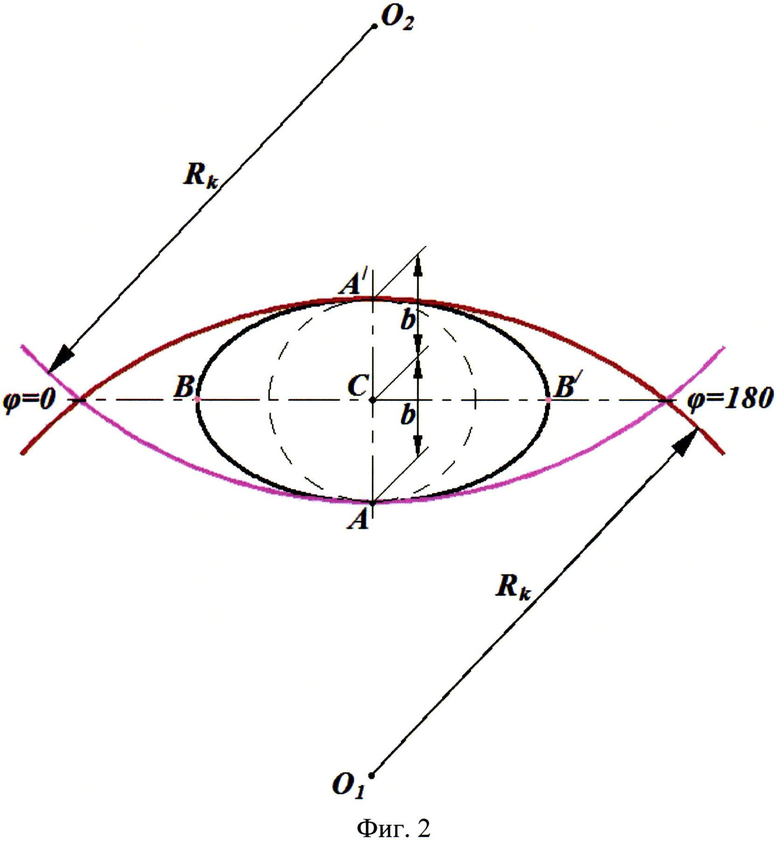
На фиг. 1 показан общий вид двухподвижной кинематической пары. На фиг. 2 изображена геометрия двухподвижной кинематической пары.
Пара включает два звена - корсет 1, выполненный двойным, и цилиндр 2, выполненный прямым эллиптическим. Корсет 1 контактирует с поверхностью цилиндра 2 в двух точках (точках А и A/

Положение центра кривизны образующей вогнутой поверхности корсета (точки О1 и О2) зависит от величины эксцентриситета эллипса e [4] основания цилиндра, который определяет «вытянутость» эллипса в направлении его большой оси и изменяется в интервале 0≤е<1. При e=0 эллипс вырождается в окружность. Чем эксцентриситет ближе к единице, тем эллипс более «вытянут». Поэтому при меньшем эксцентриситете радиус также может быть меньшим. При большем эксцентриситете радиус Rk, как и расстояние O1O2, должен быть большим. Но при любом значении эксцентриситета е радиус Rk обязательно должен быть больше длины малой полуоси эллипса b.
Относительный поворот звеньев пары вокруг точек A(A/) и C невозможен в силу исполнения цилиндра прямым эллиптическим. Любой отрезок, соединяющий точку A(A/) с любой из точек, лежащих на дуге эллипса BA/B/(B/AB), всегда будет больше длины малой оси эллипса 2b. Только в точках А и A/ эти отрезки будут равны, то есть AA/=A/A=2b. Аналогично для точки C: любой отрезок, соединяющий точку C (центр эллипса) с любой из точек, принадлежащих эллипсу, будет всегда больше длины малой полуоси эллипса b. Только в точках А и A/ эти отрезки оказываются равными, когда CA=CA/=b. Корсет 1 выполняется с вогнутой поверхностью по дуге окружности относительно точек O1 и O2 (фиг. 2).
Двухподвижная кинематическая пара работает следующим образом. Задавая движение прямому эллиптическому цилиндру 2, удерживаемому корсетом 1, выполненным двойным, относительно оси x будет обеспечено только поступательное движение, а относительно оси z - только вращательное. Запрещенными движениями в этой паре оказываются вращательное движение вокруг оси x, оба движения (вращательное и поступательное) относительно оси y и поступательное движение вдоль оси z. Таким образом, двухподвижная кинематическая пара обеспечивает независимые поступательное и вращательное движения относительно двух из осей декартовой системы координат (движения ПВ).
Источники информации
1. Артоболевский И.И. Теория механизмов. Изд-во «Наука», Гл. ред. физ.-мат. лит., 1965, 776 с.
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - 13-е изд., исправленное. Изд-во «Наука», Гл. ред. физ.-мат. лит., 1986, 544 с.
3. Пат. №2502898 С1 Российская Федерация, МПК F16C 29/02, F16H 25/00, F16S 5/00. Удерживающая трехподвижная кинематическая пара / Дворников Л.Т., Фомин А.С., Живаго Э.Я.; заявитель и патентообладатель ФГБОУ ВПО «Сибирский государственный индустриальный университет». - №2012122955/11,; заяв. 04.06.2012; опубл. 27.12.2013, Бюл. №36 - 5 с.; 2 ил.
4. Википедия: [Электронный ресурс]. URL: http://ru.wikipedia.org/wiki/Эллипс (Дата обращения: 16.01.2014).
| название | год | авторы | номер документа |
|---|---|---|---|
| ДВУХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2013 |
|
RU2534095C1 |
| УДЕРЖИВАЮЩАЯ ТРЕХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2012 |
|
RU2502898C1 |
| ТРЕХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2013 |
|
RU2578809C2 |
| ТРЕХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2012 |
|
RU2520624C2 |
| Трехзвенное кинематическое соединение с тремя относительными движениями | 2015 |
|
RU2610239C1 |
| ОДНОКОНТАКТНАЯ ДВУХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2018 |
|
RU2681467C1 |
| ТРЕХКОНТАКТНАЯ ДВУХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2003 |
|
RU2241880C1 |
| УРАВНОВЕШЕННЫЙ САМОУСТАНАВЛИВАЮЩИЙСЯ ПЛАНЕТАРНЫЙ МЕХАНИЗМ | 2009 |
|
RU2397384C1 |
| МЕХАНИЗМ ДЛЯ ВОСПРОИЗВЕДЕНИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ | 2005 |
|
RU2309051C2 |
| МЕХАНИЗМ ДЛЯ ВЫЧЕРЧИВАНИЯ ПРОСТРАНСТВЕННЫХ КРИВЫХ | 2017 |
|
RU2668414C1 |
Изобретение относится к области машиностроения и может использоваться для соединения звеньев механизмов и деталей машин. Двухподвижная кинематическая пара включает два звена - цилиндр (2) и двойной корсет (1), поверхности которых имеют разную кривизну и входят между собой в точечный контакт. Цилиндр (2) выполнен прямым эллиптическим, удерживающимся двойным корсетом (1). Радиус кривизны образующей вогнутой поверхности корсета (1) обеспечивается большим длины малой полуоси эллипса основания цилиндра (2). Кинематическая пара исполнена двухподвижной, воспроизводящей независимые поступательное и вращательное движения относительно двух из осей декартовых координат. Технический результат: создание двухподвижной кинематической пары, воспроизводящей комплекс двух независимых движений - поступательного и вращательного относительно двух из осей декартовой системы координат (движений ПВ) путем устранения вращательного движения вокруг продольной оси цилиндра. 2 ил.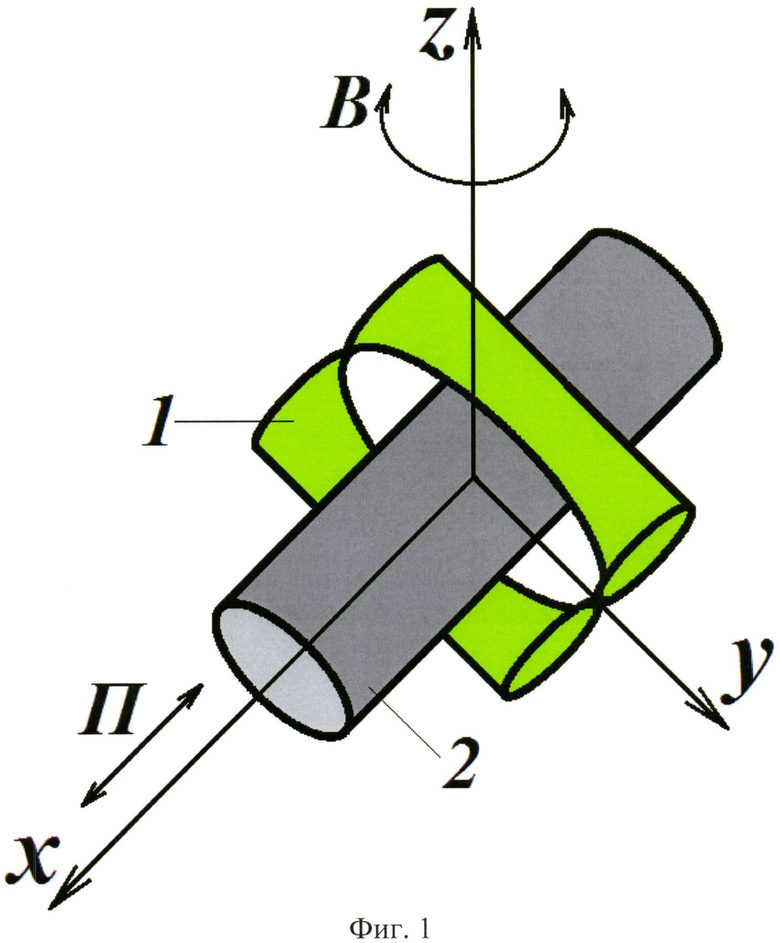
Двухподвижная кинематическая пара, включающая два звена - цилиндр и двойной корсет, поверхности которых имеют разную кривизну и входят между собой в точечный контакт, отличающаяся тем, что цилиндр выполнен прямым эллиптическим, удерживающимся двойным корсетом, при этом радиус кривизны образующей вогнутой поверхности корсета обеспечивается большим длины малой полуоси эллипса основания цилиндра, при этом кинематическая пара исполнена двухподвижной, воспроизводящей независимые поступательное и вращательное движения относительно двух из осей декартовых координат.
| УДЕРЖИВАЮЩАЯ ТРЕХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2012 |
|
RU2502898C1 |
| ТРЕХКОНТАКТНАЯ ДВУХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 2003 |
|
RU2241880C1 |
| ПРОСТРАНСТВЕННЫЙ КРИВОШИПНО-ШАТУННЫЙ МЕХАНИЗМ ВТОРОГО СЕМЕЙСТВА | 2010 |
|
RU2422703C1 |
| ДВУХКОНТАКТНАЯ ДВУХПОДВИЖНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 1998 |
|
RU2137964C1 |
| JP 2011163504 A, 25.08.2011. | |||
Авторы
Даты
2015-10-10—Публикация
2014-02-28—Подача