Изобретение относится к теории автоматического управления и может быть использовано для получения моделей сложных объектов, описываемых дифференциальными уравнениями в частных производных, процесс получения математических моделей которых затруднен вследствие неполной информации, сложных эксплуатационных режимов и структурных особенностей объекта.
Известна система идентификации параметров нестационарного объекта с переменным запаздыванием [патент на изобретение РФ 2027214].
Изобретение относится к системам идентификации переменных параметров динамических объектов, в том числе и переменного запаздывания, зависящего от времени. Способ определения переменного запаздывания основан на подстройке параметров системы по сигналу 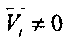 , означающему наличие отклонений параметров объекта и модели. При
, означающему наличие отклонений параметров объекта и модели. При 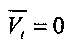 параметры объекта и модели равны. Лежащее в основе изобретения представление x(t-τ) в ряд Тейлора в точке t обладает очень низкой точностью и существенно зависит от числа членов разложения, к тому же автор ограничивается двумя членами разложения. Следует отметить, ведение дифференциаторов еще более усугубляет положение, так как вносит в систему импульсные воздействия, что вряд ли может гарантировать высокое качество идентификации.
параметры объекта и модели равны. Лежащее в основе изобретения представление x(t-τ) в ряд Тейлора в точке t обладает очень низкой точностью и существенно зависит от числа членов разложения, к тому же автор ограничивается двумя членами разложения. Следует отметить, ведение дифференциаторов еще более усугубляет положение, так как вносит в систему импульсные воздействия, что вряд ли может гарантировать высокое качество идентификации.
Наиболее близким к предлагаемому решению, принятым за прототип, является способ активной идентификации линейных объектов управления [патент на изобретение РФ №2306592] путем анализа входного и выходного сигналов, заключающийся в том, что испытательные гармоники подаются на вход объекта последовательно во времени, при этом каждой гармонике, действующей в течение рабочего интервала, предшествует интервал (интервал - пауза), на котором испытательный сигнал отсутствует, паузы и рабочие интервалы позволяют оценить влияние реализовавшегося внешнего возмущения на ошибку идентификации и уменьшить это влияние путем увеличения времени идентификации.
С существенными признаками предложенного способа совпадает следующая совокупность признаков прототипа: сбор статистических данных о входных и выходных переменных объекта.
Недостатком прототипа является снижение точности получаемой математической модели для объектов, описываемых дифференциальными уравнениями в частных производных, вследствие того, что он позволяет получить модели только в форме передаточных функций целого порядка, которые обладают более низким уровнем адекватности объекту по сравнению с указанными уравнениями или передаточными функциями дробного порядка.
Этот недостаток связан с тем, что прототип использует математическое описание динамики в полных производных, в то время как многие процессы, например теплотехнические, более точно описываются моделью дифференциальных уравнений в частных производных. Для повышения точности описания объектов, описываемых дифференциальными уравнениями в частных производных, необходим переход к математическим моделям дробного порядка.
В основу изобретения положена задача повышения точности математической модели сложного объекта, описываемого дифференциальными уравнениями в частных производных.
Поставленная задача решается тем, что способ идентификации сложного теплового объекта управления включает процедуру сбора статистических данных в режиме его номинального функционирования и использует их в качестве обучающей выборки динамической нейронной сети с элементами дробного запаздывания в ветви обратной связи, причем после завершения обучения на вход нейронной сети, как на "черный ящик", подается типовое ступенчатое воздействие, а полученная реакция на выходе нейронной сети с помощью модифицированного метода Симою аппроксимируется в форме передаточной функции дробного порядка.
Заявляемый способ позволяет получать математические модели объектов в форме передаточных функций дробного порядка, что повышает точность моделирования процессов, описываемых дифференциальными уравнениями в частных производных. Кроме того, полученная модель в форме передаточных функций дробного порядка позволяет применить методы теории автоматического управления для решения задачи анализа и синтеза систем управления, что затруднительно при использовании моделей в форме дифференциальных уравнений в частных производных. В предлагаемом способе впервые применяется модификация нейронных сетей путем введения звена дробного запаздывания и модификация метода идентификации Симою для получения возможности идентифицировать процессы дробного порядка [Karikov, Е.В. Construction of a Dynamic Neural Network Model as a Stage of Grate Cooler Automation. / E.B. Karikov, V.G. Rubanov, V.K. Klassen // World Applied Sciences Journal. - 2013. - 25 (2). - Pp.: 227-232].
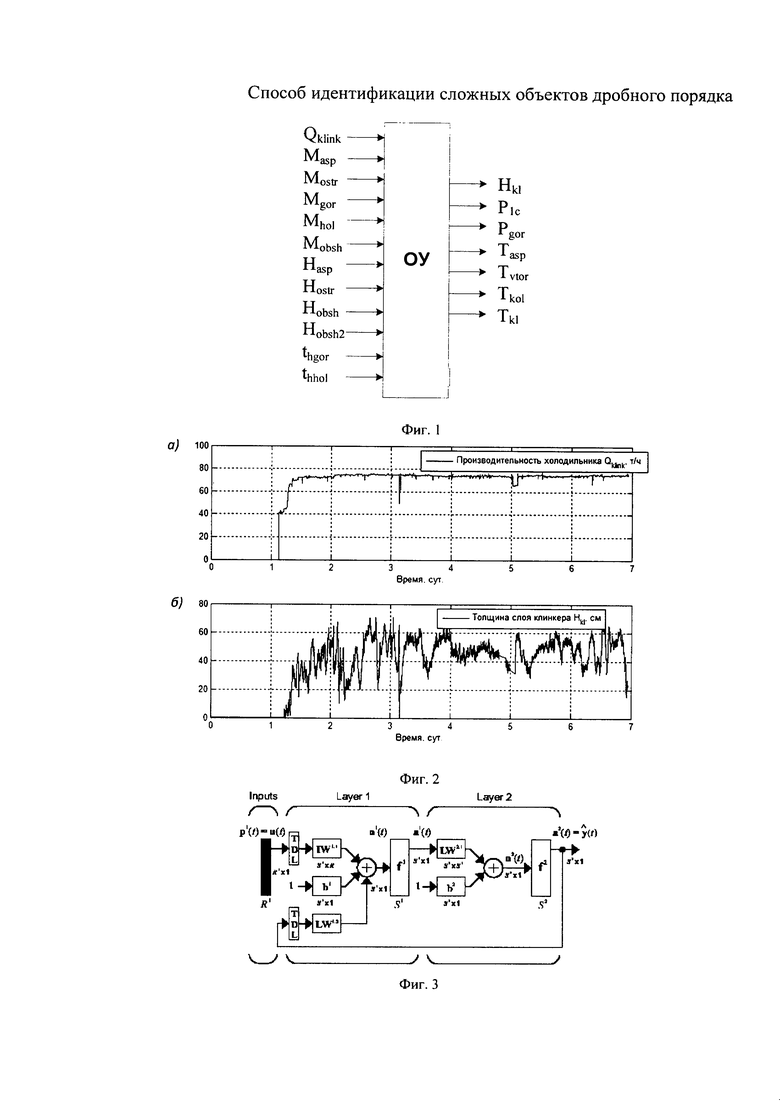
Изобретение поясняется на примере построения модели колосникового холодильника цементного клинкера "Волга-75". На фиг. 1 представлен объект управления в виде «черного ящика», на фиг. 2 показан фрагмент реальных изменений во времени одной из входных и одной из выходных переменных в режиме нормального функционирования колосникового холодильника «Волга-75», на фиг. 3 изображена структура нейронной сети (NARX), где IW - матрица весов входа; LW - матрица весов нейронов промежуточного слоя; р - вектор входов; y - выход сети; TDL (Tapped Delay Line) - линии задержки, определенные вектором L=(lin; lout), где lin, lout - длины входной и выходной линий соответственно.
Процесс идентификации объекта состоит из 3-х этапов:
1. Анализ объекта исследования и сбор информации о входных и выходных переменных. На данном этапе проводится определение входных и выходных переменных объекта, характер изменений которых записывается при сборе статистических данных в режиме его нормального функционирования.
2. Построение модели в форме динамических нейронных сетей, где в качестве структуры нейронной сети предложено использовать нелинейную авторегрессионную сеть с экзогенными входами (NARX-сеть), при этом обучение нейронной сети осуществляется путем серии экспериментов с сигналами, записанными в процессе функционирования объекта (1-й этап), в результате чего устанавливаются параметры сети. Для объектов исследования, описываемых уравнениями в частных производных, используется NARX-сеть с добавлением звеньев дробного запаздывания.
3. Получение результирующей математической модели в форме передаточной функции по каналам управления объекта осуществляется путем анализа отклика нейронной сети на стандартные входные воздействия. Наиболее простым и эффективным является подача на входы сети функции Хевисайда и аппроксимации отклика с помощью метода Симою (в случае идентификации объекта целого порядка) или модифицированного метода Симою (для объекта дробного порядка).
Проиллюстрируем суть способа на примере построения модели колосникового холодильника цементного клинкера "Волга-75". В соответствии с первым этапом осуществляется запись реализации входных и выходных переменных объекта. Фрагмент реальных изменений во времени входных и выходных переменных в режиме нормального функционирования объекта (колосникового холодильника) приведен на фиг. 2.
Второй этап получения модели в форме нейронной сети начинается с выбора структуры в классе NARX-сети, которая относится к классу рекуррентных нейронных сетей. Наличие обратных связей позволяет NARX-сети принимать решения, основываясь не только на входных данных, но и с учетом предыстории состояний динамического объекта.
В общем случае модель нелинейной авторегрессии с внешними входами описывается рекуррентным уравнением:
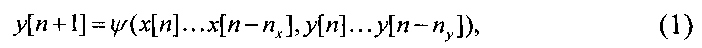
где х[n] - входной сигнал; y[n] - выходной сигнал; ψ - некоторое нелинейное преобразование; nx и ny - максимальное число задержек по входному и выходному сигналам соответственно. Архитектура используемой в работе NARX-сети представлена на фиг. 3.
Моделирование объектов, содержащих дробно-иррациональные интегро-дифференциальные преобразования требует применения модифицированных структур нейронных сетей.
Покажем подход к такой модификации на примере NARX-сети (фиг. 3). Данная сеть реализует рекуррентное соотношение (1) за счет использования элементов запаздывания сигнала. Для иллюстрации принципа работы рекуррентной нейронной сети воспользуемся дискретным представлением исследуемой системы в форме пространства состояний:
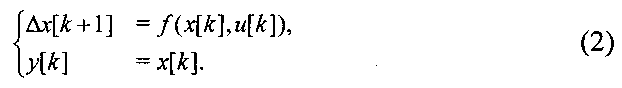
Принимая во внимание, что Δх[k+1]=х[k+1]-х[k], для момента времени к при шаге дискретизации Т, получим:
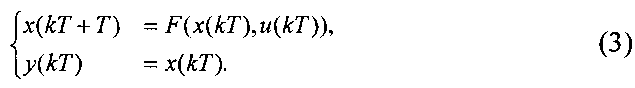
Из систем уравнений (2) и (3) видно, что NARX-сеть реализует уравнение состояния дискретной формы.
Выразим конечную разность через Z-преобразование:
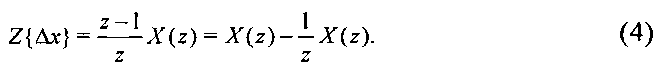
Перейдем к конечной разности дробного порядка:
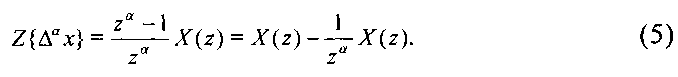
С другой стороны, конечную разность можно вычислить по формуле:

Таким образом, используя соотношения (5) и (6), можно получить формулу для описания звена запаздывания дробного порядка:
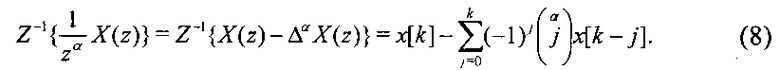
Применяя в структуре нейронной сети звенья запаздывания дробного порядка, получим возможность моделировать динамические объекты дробного порядка.
В ходе обучения нейронных сетей получены следующие результаты:
1. Для модели движения клинкера по колосниковой решетке наименьшее СКО (41.83) соответствует сети с 15 нейронами в скрытом слое и одинарной задержкой сигнала обратной связи.
2. Для модели движения воздуха в колосниковом холодильнике наименьшее СКО (123) отвечает сети с 15 нейронами в скрытом слое и одинарной задержкой сигнала обратной связи.
3. Для модели теплообмена между воздухом и клинкером наименьшее СКО (444) получено для сети с 15 нейронами в скрытом слое и одинарной дробной задержкой сигнала обратной связи порядка 1/2.
Третий этап идентификации состоит в получении результирующей модели объекта в форме передаточной функции дробного порядка путем применения модифицированного авторами метода Симою для аппроксимации кривой разгона объекта дробного порядка.
Исследуемый объект может быть описан линейным дифференциальным уравнением дробного порядка с постоянными коэффициентами:
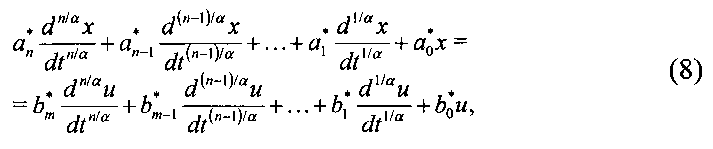
где 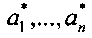 ;
;  - постоянные коэффициенты, x - отклонение регулируемой величины, u - входное воздействие, α∈N - общая кратность порядков дробных операций.
- постоянные коэффициенты, x - отклонение регулируемой величины, u - входное воздействие, α∈N - общая кратность порядков дробных операций.
Приведем уравнение (8) к следующему виду, разделив на 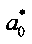 и вынося
и вынося 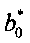 за скобки:
за скобки:
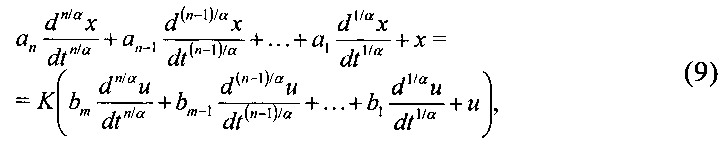
где a 1,…,a n; b1,…,bm - постоянные коэффициенты, K - коэффициент преобразования системы, определяемый по формуле:
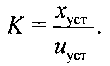
Передаточная функция объекта W(s)=X(s)/U(s), описываемого уравнением (9), может быть представлена в следующем виде:
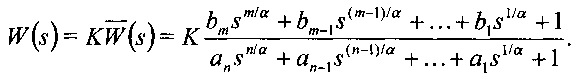
В дальнейшем будем рассматривать нормированную передаточную функцию 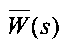 . Введем переменную
. Введем переменную 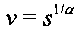 , тогда передаточная функция объекта будет выглядеть следующим образом:
, тогда передаточная функция объекта будет выглядеть следующим образом:
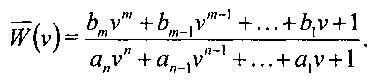
Инверсная передаточная функция объекта будет
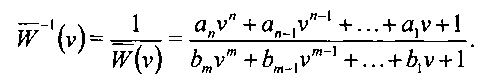
Разложение инверсной функции 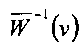 в ряд Тейлора в окрестности точки ν=0 имеет вид:
в ряд Тейлора в окрестности точки ν=0 имеет вид:
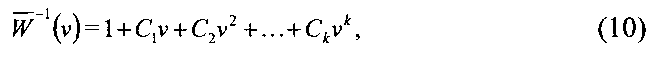
где коэффициенты разложения Ck называются согласно методу Симою площадями. Приравнивая выражение для передаточной функции 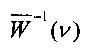 и разложение (10), после приведения подобных получим линейную систему уравнений путем приравнивания коэффициентов при одинаковых степенях ν.
и разложение (10), после приведения подобных получим линейную систему уравнений путем приравнивания коэффициентов при одинаковых степенях ν.

где неизвестные коэффициенты Ck определяются на основании системы уравнений:
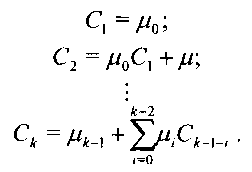
Далее, подставляя значения коэффициентов Ck в систему (11), находим искомые параметры передаточной функции a 1,…,a n; b1,…,bm. Здесь моменты µk находятся из уравнений связи производной k-го порядка изображения Ф(s) и оригинала ϕ(t) в форме:
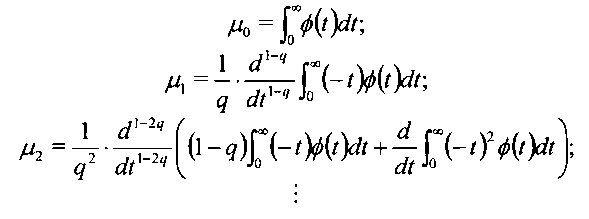
Таким образом, предлагаемый способ позволяет получить математическую модель сложного теплового объекта управления в форме передаточных функций дробного порядка.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЕМКОСТНЫМИ СОСТАВЛЯЮЩИМИ ОБЪЕКТА | 2009 |
|
RU2442206C2 |
| СИСТЕМА СВЯЗИ УПРАВЛЕНИЯ УДАЛЁННЫМИ ОБЪЕКТАМИ | 2015 |
|
RU2666105C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1995 |
|
RU2097818C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ | 1994 |
|
RU2079870C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189621C1 |
| Способ управления химико-технологической системой | 2023 |
|
RU2813658C1 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ДВУХЭТАПНЫМ ИДЕНТИФИКАТОРОМ И НЕЯВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ | 2002 |
|
RU2231819C2 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДИНАМИЧЕСКОЙ ХАРАКТЕРИСТИКОЙ ВЫХОДНОГО ПАРАМЕТРА | 2005 |
|
RU2292575C2 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ВНУТРЕННЕЙ ЕМКОСТНОЙ ЭНЕРГИЕЙ ОБЪЕКТА С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ | 2010 |
|
RU2474857C2 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ИНТЕГРАЛУ КОМПЕНСИРУЮЩЕГО ВОЗДЕЙСТВИЯ | 2003 |
|
RU2285281C2 |
Изобретение относится к теории автоматического управления и может быть использовано для получения моделей сложных объектов, описываемых дифференциальными уравнениями в частных производных, процесс получения математических моделей которых затруднен вследствие неполной информации, сложных эксплуатационных режимов и структурных особенностей объекта. Техническим результатом является повышение точности создания математической модели сложного объекта, описываемого дифференциальными уравнениями в частных производных. Способ содержит сбор статистических данных в режиме номинального функционирования объекта и использование их в качестве обучающей выборки динамической нейронной сети с элементами дробного запаздывания в ветви обратной связи, причем после завершения обучения на вход нейронной сети, как на "черный ящик", подается типовое ступенчатое воздействие, а полученная реакция на выходе нейронной сети с помощью модифицированного метода Симою аппроксимируется в форме передаточной функции дробного порядка. 3 ил.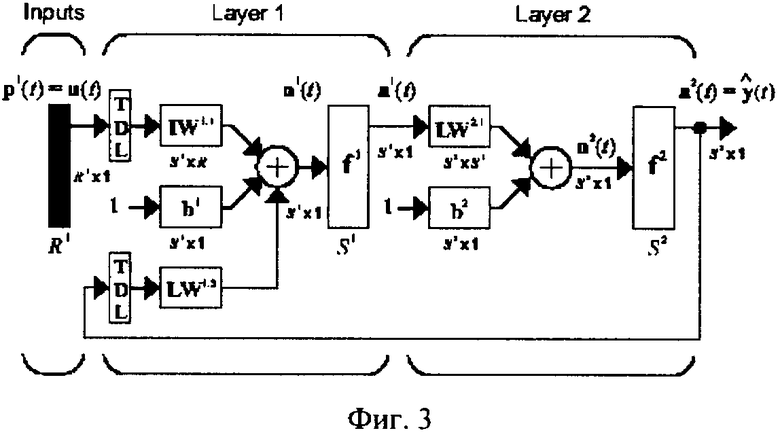
Способ идентификации сложного теплового объекта управления, включающий процедуру сбора статистических данных в режиме его номинального функционирования, отличающийся тем, что статистические данные о входных и выходных переменных объекта управления используются в качестве обучающей выборки динамической нейронной сети с элементами дробного запаздывания в ветви обратной связи, причем после завершения обучения на вход нейронной сети, как на "черный ящик", подается типовое ступенчатое воздействие, а полученная реакция на выходе нейронной сети с помощью модифицированного метода Симою аппроксимируется в форме передаточной функции дробного порядка объекта управления.
| СПОСОБ АКТИВНОЙ ИДЕНТИФИКАЦИИ ЛИНЕЙНЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ | 2006 |
|
RU2306592C1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ НЕСТАЦИОНАРНОГО ОБЪЕКТА С ПЕРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ | 1990 |
|
RU2027214C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2002 |
|
RU2233480C1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ОБЪЕКТОВ УПРАВЛЕНИЯ | 2012 |
|
RU2486563C1 |
| US 2002133243 A1, 19.09.2002. | |||
Авторы
Даты
2016-07-20—Публикация
2015-04-23—Подача