Группа изобретений относится к цифровой вычислительной технике, в частности к недвоичной технике, и предназначена для создания реализуемых в среде полупроводниковой интегральной электроники троичных полных последовательных сумматоров.
Известной успешной реализацией недвоичных цифровых устройств являются троичные ЦВМ "Сетунь" и "Сетунь 70" [1, 2]. Логические элементы этих ЦВМ выполнены на основе электромагнитной техники [8, 9], имеют малое быстродействие, большие потребляемую мощность и размеры. Устройства на таких элементах не могут быть реализованы в среде полупроводниковой интегральной электроники.
Известен функциональный аналог элементов ЦВМ "Сетунь" - "Пороговый Элемент Троичной Логики" (ПЭТЛ), реализуемый в среде интегральной электроники [3]. На ПЭТЛ, используя ПЭТЛ-схемотехнику [7], можно создавать троичные цифровые устройства. Ассортимент средств, которыми в настоящее время располагает ПЭТЛ-схемотехника, недостаточен для создания всего спектра троичных устройств. В частности, в нем отсутствуют троичные полные последовательные сумматоры.
Задача, решаемая заявляемой группой изобретений, направлена на пополнение ассортимента средств ПЭТЛ-схемотехники полными сумматорами, благодаря чему поддерживается создание более широкого набора логических и операционных устройств, работающих в симметричной троичной системе с цифрами -1, 0, +1.
Наиболее близкими техническими решениями к заявляемой группе изобретений являются группы изобретений: "Пороговый Элемент Троичной Логики и устройства на его основе" [3], "Узел Троичной схемотехники и дешифраторы-переключатели на его основе" [4], "Троичный D-триггер (варианты)" [5], «Троичный Т-триггер» и Троичный реверсивный счетчик на его основе» [6].
Известные группы изобретений поддерживают реализацию ограниченного числа троичных устройств:
Комбинационные схемы: троичная схема "И", троичный полусумматор, троичные дешифраторы и троичные переключатели.
Схемы с памятью: четыре варианта Троичных D и Т-триггеров, Троичный реверсивный счетчик.
Реализацию троичных полных последовательных сумматоров известные группы изобретений не раскрывают.
Раскрытие изобретения
Первым аспектом изобретения является Троичный Полный Последовательный 2-входовый Сумматор (ТППС-2), состоящий из двух Троичных Полусумматоров (ТПС1, ТПС2) и Троичного D-Триггера (TDT).
Входы A и В ТПС1 являются входами первого и второго слагаемых ТППС-2, вход С TDT является входом Син ТППС-2, а выход С ТПС2 является выходом СУММА ТППС-2.
Выход С ТПС1 соединен с входом В ТПС2, выходы П ТПС1 и ТПС2 соединены с входом D TDT, выход Q TDT соединен с входом А ТПС2.
Вторым аспектом изобретения является Троичный Полный Последовательный 3-входовый Сумматор (ТППС-3), состоящий из трех Троичных Полусумматоров (ТПС1, ТПС2, ТПСЗ) и Троичного D-Триггера (TDT).
Входы А и В ТПС1 являются входами первого и второго слагаемых ТППС-3, вход А ТПС2 является входом третьего слагаемого ТППС-3, вход С TDT является входом Син ТППС-3, а выход С ТПС3 является выходом СУММА ТППС-3.
Выход С ТПС1 соединен с входом А ТПС3, выход С ТПС2 соединен с входом В ТПС3, выходы П ТПС1, ТПС2 и ТПС3 соединены с входом D TDT, выход Q TDT соединен с входом В ТПС2.
На Фиг. 1 изображен Троичный Полный Последовательный 2-входовый Сумматор, на Фиг. 2 изображен Троичный Полный Последовательный 3-входовый Сумматор, на Фиг. 3 изображен Троичный полусумматор.
Троичный Полный Последовательный Сумматор (ТППС) выполнен на основе ПЭТЛ-схемотехники - совокупности элементов, узлов, правил их соединения, приемов, типовых решений и изобразительных средств, поддерживающих создание цифровых устройств, работающих в троичной системе с цифрами +1, 0, -1.
ПЭТЛ-схемотехника появилась недавно и во многом отличается от других интегральных схемотехник. Она описана в [3, 4, 5, 6, 7, 8]. Краткие сведения приведены ниже
1. Троичным значениям (тритам) +1, 0, -1 на физическом уровне соответствуют дискретные токи +Iф, 0, -Iф.
2. Пороговый Элемент Троичной Логики (ПЭТЛ) - имеет 1 вход и набор из 4-х выходов: +R, +L, -L, -R.
3. Узел Троичной Схемотехники (УТС) имеет 1 вход и набор из 8-ми выходов: M1, М2, М3, М4, М5, М6, М7, М8.
4. На входах ПЭТЛ и УТС происходит алгебраическое сложение дискретных токов +Iф, и -Iф и формируется трит X. Если число +IФ больше числа -Iф - Х=+1, если число +Iф меньше числа -Iф - Х=-1, если число +Iф равно числу -Iф - Х=0.
5. ПЭТЛ и УТС могут иметь более одного набора выходов. Значения на одноименных выходах тождественны.
Значениям X соответствуют значения пар их двузначных компонент на выходах. Это соответствие приведено в Таблице 1. Пары нумеруются римскими цифрами, варианты пар - арабскими.

Хотя в таблице фигурируют триты, сами по себе компоненты двоичны: компоненты в строке I имеют значения +1 или 0; компоненты в строке II - -1 или 0.
Терминология ПЭТЛ-схемотехники не устоялась. Используются сопоставимые термины из двоичных схемотехник и из лексикона "Сетуней". Следует руководствоваться таблицами истинности и сопроводительным текстом.
Алгебраическое сложение тритов на входах и объединение (сборка) выходов являются приемами ПЭТЛ-схемотехники. Например, объединяя +R и -R, на выходе получим повторение трита X на входе, объединяя +L и -L - его нециклическую инверсию НЕ X, объединяя +R и +L или -R и -L - постоянные значения +1 или -1. Практикуется объединение выходов разных ПЭТЛ и УТС.
Сборки изображаются вертикальными линиями, нижние концы которых помечены буквами, а верхние (необязательно) - либо наименованием элемента, ко входу которого сборка подключена, либо названием сигнала. Как правило, слева от сборки - элементы, выходы которых к ней подключены, справа - элемент, на входе которого формируется троичное значение X.
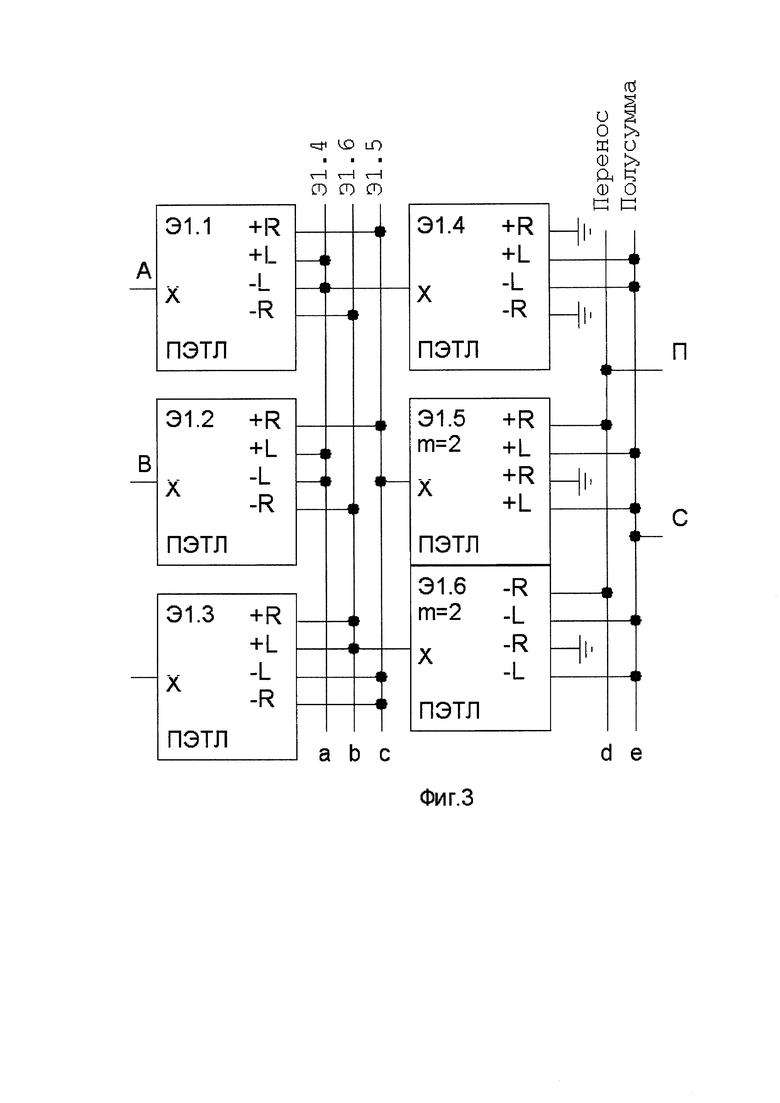
Возможны элементы с половинным числом выходов: либо только положительными (+R, +L), либо только отрицательными (-L, -R). Если у ПЭТЛ или УТС более одного набора выходов, их число m указывают под номером элемента. На Фиг. 3 у ПЭТЛ Э1.5 два набора положительных выходов, а у ПЭТЛ Э1.6 два набора отрицательных.
Неиспользуемые выходы соединяют с землей.
Крупные узлы устройств изображают без подробностей в виде прямоугольников. Для них справедливо все, относящееся к ПЭТЛ: на входах суммируются триты; может быть несколько наборов выходов. На Фиг. 1 и Фиг. 2 таким образом изображены Троичные Полусумматоры ТПС1, ТПС2 и ТПС3 и Троичные D-Триггеры TDT.
Троичный D-триггер [5] TDT запоминает значение трита на входе данных D, в момент, когда значение на управляющем входе С изменяется (т.е по фронту сигнала). Сохраненный трит доступен на выходе Q TDT.
Проиллюстрируем использование ПЭТЛ-схемотехники на примере Троичного полусумматора [3] (Фиг. 3), реализованного на 6 ПЭТЛ Э1.1-Э1.6. Он выполняет сложение двух тритов, поступающих на входы А и В, и формирует на выходах триты Полусумма (С) и Перенос (П) в соответствии с Таблицей 2, в которой представлены все 9 возможных сочетаний значений А и В.
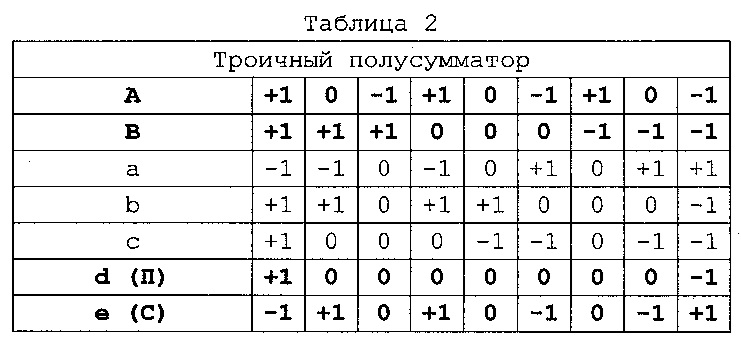
Помимо тритов на входах и выходах Троичного полусумматора в Таблице 2 приводятся триты на сборках a, b, c, d, e. Алгоритм заполнения ячеек таблицы следующий:
1. Берем триты А и В из столбца с заполняемой ячейкой;
2. Из Таблицы 1 берем значения X на выходах ПЭТЛ, подключенных к сборке ячейки, соответствующие выбранным А и В;
3. Определяем согласно п. 4 выше значение X на сборке и заносим его в ячейку;
4. Переходим к другой ячейке (одной сборке соответствуют 9 ячеек) и берем другие триты А и В.
5. По завершении переходим к ячейкам других сборок.
Два варианта Троичных Полных Последовательных Сумматоров ТППС-2 и ТППС-3, различающихся числом входов, изображены соответственно на Фиг. 1 и Фиг. 2. В каждом из них используются троичные полусумматоры ТПС и троичный D-триггер TDT. Слагаемые Сл последовательно, трит за тритом, начиная с младших, подаются на входы ТППС. На выходе СУММА последовательно формируется триты суммы. Работа синхронизируется фронтом сигнала на входе Син.
Функционирование ТППС описано ниже с помощью таблиц истинности. Содержимое таблиц интерпретируют не только как наборы тритов, но и как целые троичные числа (младшие разряды справа). По вертикали таблицы разделены на зоны, число которых равно числу полусумматоров. 1-й столбец показывает разделение на зоны, 2-й - названия сигналов на выводах ТПС, 3-й - сборки, 4-й и 5-й - слагаемые и суммы. Последние даются как в троичном, так и в десятичном представлениях. В нижней строке приведены десятичные веса троичных разрядов.
В обоих вариантах ТППС реализован единый замысел. Триты Полусумм, сформированные на полусумматорах из тритов слагаемых, суммируются с объединенным тритом Переносов, задержанным на такт.
ТППС-2 (Фиг. 1) имеет два входа и содержит полусумматоры ТПС1 и ТПС2. Триты слагаемых Сл1 и Сл2 подаются на входы А1 и В1 ТПС1. С его выхода С1 трит Полусумма поступает на вход В2 ТПС2. Триты переносов П1 и П2 объединяются на входе D-триггера TDT и с его выхода Q, задержанные на такт (Псдв), поступают на вход А2 ТПС2. На выходе С2 ТПС2 формируется трит СУММА.
В Таблице 3 работа ТППС-2 иллюстрируется на примере сложения 9-разрядных целых чисел Сл1 и Сл2 (6056+9464). В результате получается 10-разрядная СУММА 15520.

ТППС-3 (Фиг. 2) имеет три входа и содержит полусумматоры ТПС1, ТПС2 и ТПС3. Триты слагаемых Сл1, Сл2 и Сл3 подаются на входы A1, В1 ТПС1 и вход А2 ТПС2. Триты полусумм с выхода С1 ТПС1 поступают на вход A3 ТПС3, а с выхода С2 ТПС2 на вход В3 ТПС3. Триты переносов П1, П2 и П3 объединяются на входе D-триггера TDT и с его выхода Q, задержанные на такт (Псдв), поступают на вход В2 ТПС2. На выходе С3 ТПС3 формируется трит СУММА.
В Таблице 4 работа ТППС-3 иллюстрируется на примере сложения 9-разрядных целых чисел Сл1, Сл2 и Сл3 (6056+9464+4921). В результате получается 10-разрядная СУММА 20441.
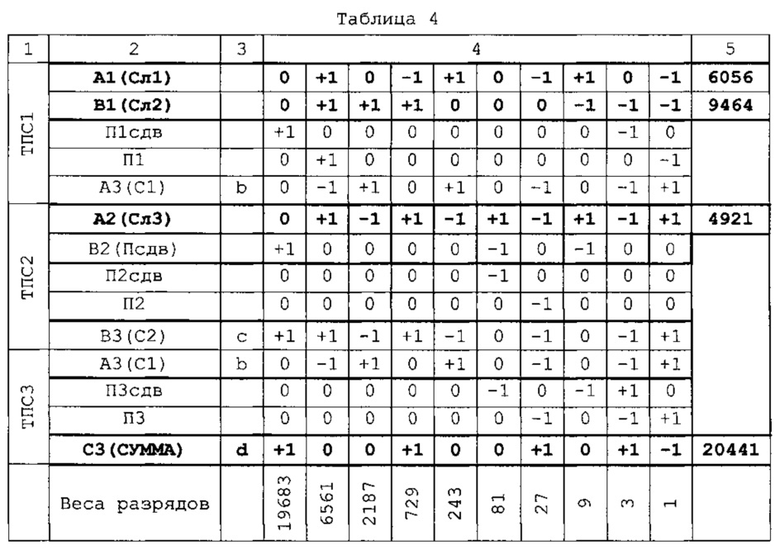
ТППС не комбинационная схема, а устройство с памятью. Текущее значение трита СУММА зависит не только от текущих значений слагаемых, но и от предшествующих. Поэтому ячейки таблиц заполняют не в произвольном порядке, а начиная с младших разрядов. Триты П1, П2 и П3 текущего разряда помещают в ячейки П1сдв, П2сдв и П3сдв следующего разряда и используют для формировании объединенного трита Переносов Псдв=(П1+П2+П3)сдв.
Литература
1. Брусенцов Н.П., Маслов С.П., Розин В.П., Тишулина A.M. Малая цифровая вычислительная машина "Сетунь". - М.: Изд-во Московского университета, 1965. 145 с.
2. Брусенцов Н.П., Жоголев Е.А., Маслов С.П., Рамиль Альварес X. Опыт создания троичных цифровых машин. // Компьютеры в Европе. Прошлое, настоящее и будущее. - Киев: Феникс, 1998. С. 67-71.
3. Маслов С.П. Пороговый элемент троичной логики и устройства на его основе. Патент на изобретение RU №2394366 С1. Зарегистрирован: 10.07.2010
4. Маслов С.П. Узел троичной схемотехники и дешифраторы - переключатели на его основе. Патент на изобретение RU №2461122 С1. Зарегистрирован: 10.09.2012
5. Маслов С.П. Троичный D-триггер (варианты). Патент на изобретение RU №2510129 С1. Зарегистрирован: 20.03.2014
6. Маслов С.П. Троичный Т-триггер и Троичный реверсивный счетчик на его основе. Патент на изобретение RU №2562370 С2. Зарегистрирован: 11.08.2015
7. Маслов С.П. Об одной возможности реализации троичных цифровых устройств. Тематический сборник №12 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2011. С. 222-227.
8. Маслов С.П. Троичная схемотехника. Тематический сборник №13 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2012. С. 152-158.
9. Брусенцов Н.П. Пороговая реализация трехзначной логики электромагнитными средствами. // Вычислительная техника и вопросы кибернетики. Вып. 9. - М.: Изд-во Моск. ун-та, 1972. С. 3-35.
10. Брусенцов Н.П. Электромагнитные цифровые устройства с однопроводной передачей трехзначных сигналов. - В кн.: Магнитные элементы автоматики и вычислительной техники. XIV Всесоюзное совещание (Москва, сентябрь 1972 г.). М., "Наука", 1972, с. 242-244.
| название | год | авторы | номер документа |
|---|---|---|---|
| ТРОИЧНОЕ МНОЖИТЕЛЬНОЕ УСТРОЙСТВО | 2017 |
|
RU2642408C1 |
| УСТРОЙСТВО ТРОИЧНОГО СЛОЖЕНИЯ И ВЫЧИТАНИЯ | 2017 |
|
RU2645279C1 |
| ТРОИЧНЫЙ Т-ТРИГГЕР И ТРОИЧНЫЙ РЕВЕРСИВНЫЙ СЧЕТЧИК НА ЕГО ОСНОВЕ | 2014 |
|
RU2562370C2 |
| ТРОИЧНЫЙ ПОРАЗРЯДНЫЙ УМНОЖИТЕЛЬ | 2016 |
|
RU2631166C1 |
| ТРОИЧНЫЙ РЕВЕРСИВНЫЙ РЕГИСТР СДВИГА | 2015 |
|
RU2585263C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2016 |
|
RU2618901C1 |
| УСТРОЙСТВО ТРОИЧНОЙ СХЕМОТЕХНИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2017 |
|
RU2648565C1 |
| ТРОИЧНЫЙ D-ТРИГГЕР (ВАРИАНТЫ) | 2012 |
|
RU2510129C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
| УЗЕЛ ТРОИЧНОЙ СХЕМОТЕХНИКИ И ДЕШИФРАТОРЫ-ПЕРЕКЛЮЧАТЕЛИ НА ЕГО ОСНОВЕ | 2011 |
|
RU2461122C1 |


Группа изобретений относится к устройствам цифровой вычислительной техники, в частности к недвоичной схемотехнике, и предназначена для создания цифровых устройств троичной логики. Техническим результатом является реализация троичных полных последовательных сумматоров. В одном из вариантов троичный полный сумматор на два входа содержит два троичных полусумматора и троичный D-триггер. 2 н.п. ф-лы, 3 ил., 4 табл.
1. Троичный Полный Последовательный 2-входовый Сумматор (ТППС-2), состоящий из двух Троичных Полусумматоров (ТПС) и Троичного D-Триггера (ТDТ), причем А и В входы первого ТПС являются соответственно входами первого и второго слагаемых ТППС-2, причем выход С второго ТПС через сборку d соединен с выходам СУММА ТППС-2, причем вход С TDT является входом Син ТППС-2, причем выход С первого ТПС через сборку b соединен с входом В второго ТПС, причем выходы П первого и второго ТПС через сборку а соединены с входом D TDT, причем выход Q TDT через сборку с соединен с входом А второго ТПС.
2. Троичный Полный Последовательный 3-входовый Сумматор (ТППС-3), состоящий из трех Троичных Полусумматоров (ТПС) и Троичного D-Триггера (TDT), причем А и В входы первого ТПС являются соответственно входами первого и второго слагаемых ТППС-3, а вход А второго ТПС является входом третьего слагаемого ТППС-3, причем выход С третьего ТПС через сборку d соединен с выходам СУММА ТППС-3, причем вход С TDT является входом Син ТППС-3, причем выход С первого ТПС через сборку b соединен с входом А третьего ТПС, причем выход С второго ТПС через сборку с соединен с входом В третьего ТПС, причем выходы П первого, второго и третьего ТПС через сборку а соединены с входом D TDT, причем выход Q TDT соединен с входом В второго ТПС.
| Троичный сумматор | 1972 |
|
SU455339A1 |
| Троичный сумматор | 1983 |
|
SU1137461A1 |
| САМОСИНХРОННЫЙ ОДНОЗАРЯДНЫЙ ТРОИЧНЫЙ СУММАТОР | 2014 |
|
RU2574818C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
| US 8482312 B1, 09.07.2013 | |||
| US 7274211 B1, 25.09.2007. | |||
Авторы
Даты
2017-04-18—Публикация
2016-04-22—Подача