Изобретение относится к цифровой вычислительной технике, в частности к недвоичной технике, и предназначено для создания троичных цифровых устройств, реализуемых в среде полупроводниковой интегральной электроники.
Известной успешной реализацией недвоичных цифровых устройств являются троичные ЦВМ "Сетунь" и "Сетунь-70" [1, 2]. Логические элементы этих ЦВМ, основанные на Троичной Пороговой Логике [9], изготавливаются средствами электромагнитной техники [9], имеют низкое быстродействие, большие потребляемую мощность и размеры. Элементы ЦВМ "Сетунь" не реализуются в среде полупроводниковой интегральной электроники.
Известен функциональный аналог элементов ЦВМ "Сетунь" "Пороговый Элемент Троичной Логики" (ПЭТЛ) [3]. ПЭТЛ реализуется в среде полупроводниковой интегральной электроники.
На ПЭТЛ можно создавать троичные цифровые устройства используя ПЭТЛ-схемотехнику [3, 4, 5, 6, 7, 8, 9], Арсенал ПЭТЛ-схемотехники располагает набором типовых решений и узлов. Однако в нем отсутствуют средства разработки троичных множительных устройств.
Целью изобретения является создание на ПЭТЛ троичного поразрядного умножителя - устройства, реализующего таблицу троичного умножения [1.С.16].
В результате ассортимент средств ПЭТЛ-схемотехники пополнится новым компонентом, вследствие чего расширится круг создаваемых троичных устройств.
Наиболее близким техническим решением к заявляемому изобретению является троичный полусумматор, входящий в состав группы изобретений: "Пороговый Элемент Троичной Логики и устройства на его основе" [3]. Троичный полусумматор не реализует таблицу троичного умножения
Раскрытие изобретения
Троичный Поразрядный Умножитель (ТПУ) содержит 7 Пороговых Элементов Троичной Логики (ПЭТЛ): Э1.1-Э1.7.
Входы Э1.1 и Э1.2 являются входами А и В ТПУ.
Выходы +R Э1.1 и Э1.2 и выходы -R, -L Э1.3 через сборку а подключены к входу Э1.5, выходы -L Э1.1 и Э1.2 и выходы +L, +R Э1.3 через сборку b подключены к входу Э1.4, выход +L Э1.1 и выход -R Э1.2 через сборку с подключены к входу Э1.6, выход +L Э1.2 и выход -R Э1.1 через сборку d подключены к входу Э1.7.
Выходы +R Э1.4, Э1.5 и выходы -R Э1.6, Э1.7 через сборку е подключены к выходу Р ТПУ, выходы +L Э1.4, Э1.5 и выходы -L Э1.6, Э1.7 через сборку f подключены к выходу НЕ Р ТПУ.
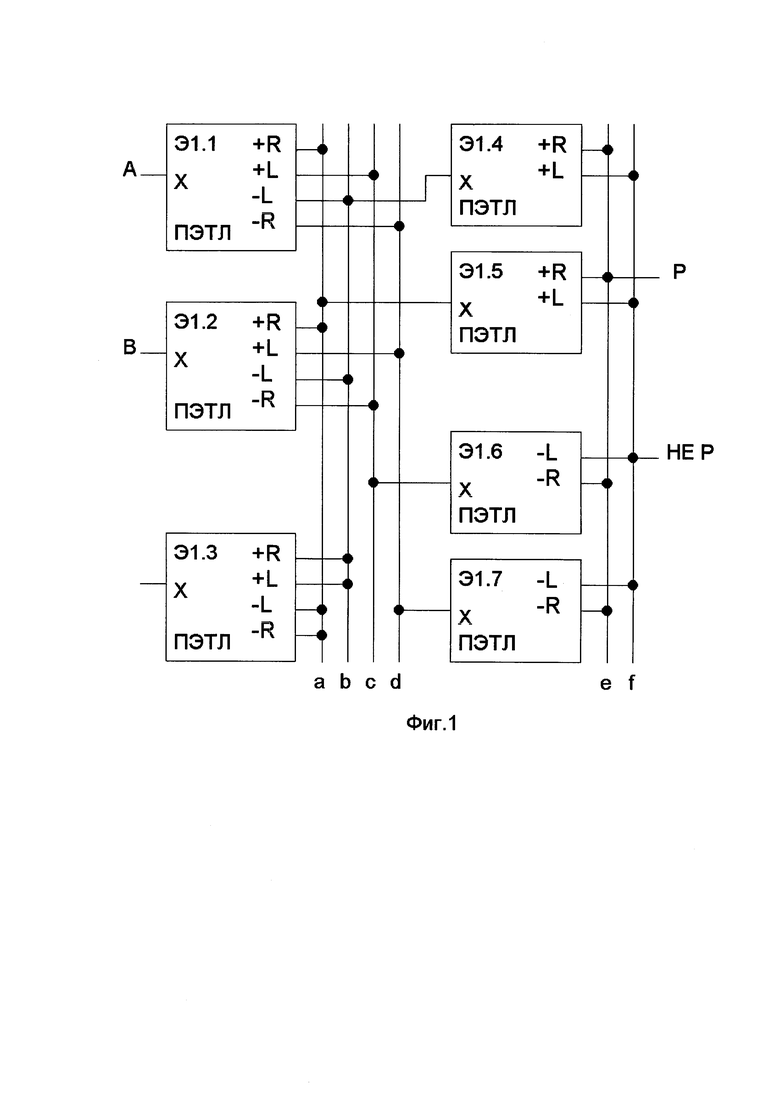
На Фиг. 1 изображен Троичный Поразрядный Умножитель (ТПУ).
Проектирование устройств на Пороговых Элементах Троичной Логики (ПЭТЛ) базируется на ПЭТЛ-схемотехнике - наборе элементов, узлов, правил их соединения, приемов, типовых решений и изобразительных средств, поддерживающих создание устройств, работающих в троичной системе с цифрами +1,0,-1.
ПЭТЛ-схемотехника отличается от других схемотехник. Она описана в [3, 4, 5, 6, 7, 8]. Краткие сведения приведены ниже:
1. Троичные значения (триты) +1,0,-1 на физическом уровне представлены дискретными токами +Iф, I0=0,-Iф.
2. ПЭТЛ имеет 1 вход и группу из 4-х выходов: +R, +L, -L, -R.
3. На входе ПЭТЛ происходит алгебраическое сложение разнополярных дискретных токов +Iф, и -Iф и формируется трит X. Если число +Iф больше числа -Iф - Х=+1, если число +IФ меньше числа -Iф - Х=-1, если число +Iф равно числу -Iф - Х=0.
4. ПЭТЛ может иметь более одной группы выходов. Значения на одноименных выходах групп тождественны.
Значению X на входе ПЭТЛ соответствуют двузначные компоненты на выходах: +R, -R и +L, -L. Соответствие приведено в Таблице 1 в тритах и в токах +Iф, I0=0, -Iф. Пары пронумерованы римскими цифрами, варианты пар - арабскими.

Алгебраическое сложение разнополярных токов +Iф и -Iф, на входах элементов и объединение (сборка) выходов - приемы ПЭТЛ-схемотехники. Так, объединяя +R и -R, получим повторение X, объединяя +L и -L - его нециклическую инверсию НЕ X, объединяя +R и +L или -R и -L - постоянные значения +1 или -1. Практикуется объединение выходов нескольких разных ПЭТЛ.
Проиллюстрируем применение ПЭТЛ-схемотехники для описания функционирования Троичного Поразрядного Умножителя (ТПУ), показанного на Фиг. 1. На входы А и В ТПУ последовательно поступают триты-сомножители F1 и F2, а на выходе формируется трит-произведение Р в соответствии с Таблицей 2. Устройство реализовано на 7 ПЭТЛ. ПЭТЛ Э1.1-Э1.3 имеют полные наборы выходов, Э1.4, Э1.5 только +R, +L, а Э1.6, Э1.7 только -R, -L.
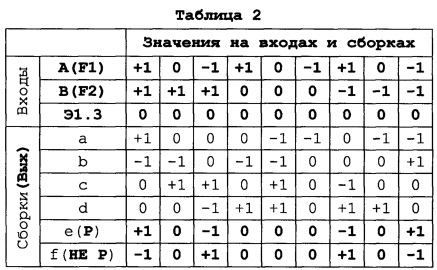
Сборки на Фиг. 1 изображаются вертикальными линиями и помечены буквами а, b, с, d, е, f. Сборкам соответствуют строки в Таблице 2. Слева от сборки - ПЭТЛ, выходы которых на ней объединяются, справа - ПЭТЛ, на входе которого формируется трит X.
В строках А и В все возможные сочетания F1 и F2.
Алгоритм заполнения ячеек таблицы следующий:
1. Берем триты F1 и F2 из столбца с заполняемой ячейкой.
2. По Таблице 1 определяем триты на выходах ПЭТЛ, подключенных к сборке этой ячейки, соответствующие выбранным F1 и F2.
3. Вычисляем (см. выше п. 3) трит X на сборке и заносим его в ячейку.
4. Переходим к следующей ячейке и берем другие триты F1 и F2.
5. Завершив заполнение одной строки, переходим к следующей.
В ячейках строки f формируются значения, инверсные значениям ячеек строки е (НЕ Р). В троичной технике инверсные выходы часто используют при соединении с другими устройствами.
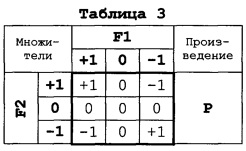
Корректность функционирования ТПУ подтверждает таблица троичного умножения [1, С.16] (Таблица 3), содержимое которой совпадает с содержимым строк F1, F2 и Р Таблицы 2.
В качестве примера, иллюстрирующего формирование Таблицы 2, детально опишем процесс заполнения ячеек строки а:
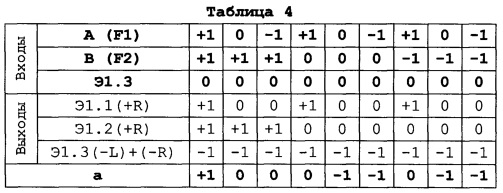
В Таблице 4 строки Входы заимствованы из Таблицы 2. В строках Выходы детально расписана ситуация на каждом из выходов, объединяющихся на сборке a: +R от Э1.1; +R от Э1.2; -L, -R от Э1.3. Известно (см. выше), что объединяя+R, +L или -R, -L получим+1 или -1 при любом X. Поэтому строка Э1.3 заполнена -1.
В ПЭТЛ-схемотехнике объединенные выходы +R, +L или -R, -L подключают к входам ПЭТЛ для привязки их к +1 или -1. Специальная привязка к 0 не требуется - неподключенный вход (I0=0) означает Х=0.
Трит в ячейке строки а определяется числом +1 и -1 в ячейках трех строк над ней. Если поровну, то 0, иначе - каких больше: +1 или -1.
Сборка а подключена к входу ПЭТЛ Э1.4. На него поступят четыре 0, четыре -1 и единственная +1. На выходе +R ПЭТЛ Э1.4 и на сборке е(Р) сформируется +1.
Литература
1. Брусенцов Н.П., Маслов С.П., Розин В.П., Тишулина A.M. Малая цифровая вычислительная машина "Сетунь". - М.: Изд-во Московского университета, 1965. 145 с.
2. Брусенцов Н.П., Жоголев Е.А., Маслов С.П., Рамиль Альварес X. Опыт создания троичных цифровых машин. // Компьютеры в Европе. Прошлое, настоящее и будущее. - Киев: Феникс, 1998. С. 67-71.
3. Маслов С.П. Пороговый элемент троичной логики и устройства на его основе. Патент РФ на изобретение RU №2394366 С1. Зарегистрирован: 10.07.2010.
4. Маслов С.П. Узел троичной схемотехники и дешифраторы - переключатели на его основе. Патент РФ на изобретение RU №2461122 С1. Зарегистрирован: 10.09.2012.
5. Маслов С.П. Троичный D-триггер (варианты). Патент РФ на изобретение RU №2510129 С1. Зарегистрирован: 20.03.2014.
6. Маслов С.П. Троичный Т-триггер и Троичный реверсивный счетчик на его основе. Патент РФ на изобретение RU №2562370 С1. Зарегистрирован: 11.08.2015.
7. Маслов С.П. Троичный реверсивный регистр сдвига. Патент РФ на изобретение RU №2585263 С1. Зарегистрирован: 27.05.2016.
8. Маслов С.П. Об одной возможности реализации троичных цифровых устройств. Тематический сборник №12 "Программные системы и инструменты". М.: Изд-во факультета ВМиК МГУ, 2011. С. 222-227.
9. Маслов С.П. Троичная схемотехника. Тематический сборник №13 "Программные системы и инструменты". М.: Изд-во факультета ВМиК МГУ, 2012. С. 152-158.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ТРОИЧНОГО СЛОЖЕНИЯ И ВЫЧИТАНИЯ | 2017 |
|
RU2645279C1 |
| ТРОИЧНЫЙ РЕВЕРСИВНЫЙ РЕГИСТР СДВИГА | 2015 |
|
RU2585263C1 |
| ТРОИЧНЫЙ ПОЛНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ СУММАТОР (ВАРИАНТЫ) | 2016 |
|
RU2616887C1 |
| ТРОИЧНЫЙ D-ТРИГГЕР (ВАРИАНТЫ) | 2012 |
|
RU2510129C1 |
| ТРОИЧНОЕ МНОЖИТЕЛЬНОЕ УСТРОЙСТВО | 2017 |
|
RU2642408C1 |
| ТРОИЧНЫЙ Т-ТРИГГЕР И ТРОИЧНЫЙ РЕВЕРСИВНЫЙ СЧЕТЧИК НА ЕГО ОСНОВЕ | 2014 |
|
RU2562370C2 |
| УЗЕЛ ТРОИЧНОЙ СХЕМОТЕХНИКИ И ДЕШИФРАТОРЫ-ПЕРЕКЛЮЧАТЕЛИ НА ЕГО ОСНОВЕ | 2011 |
|
RU2461122C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2016 |
|
RU2618901C1 |
| УСТРОЙСТВО ТРОИЧНОЙ СХЕМОТЕХНИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2017 |
|
RU2648565C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
Изобретение относится к устройствам цифровой вычислительной техники и предназначено для создания устройств троичной арифметики схемотехники. Технический результат заключается в расширении арсенала средств. Устройство содержит пороговые элементы троичной логики, связанные между собой сборками. 1 ил., 4 табл.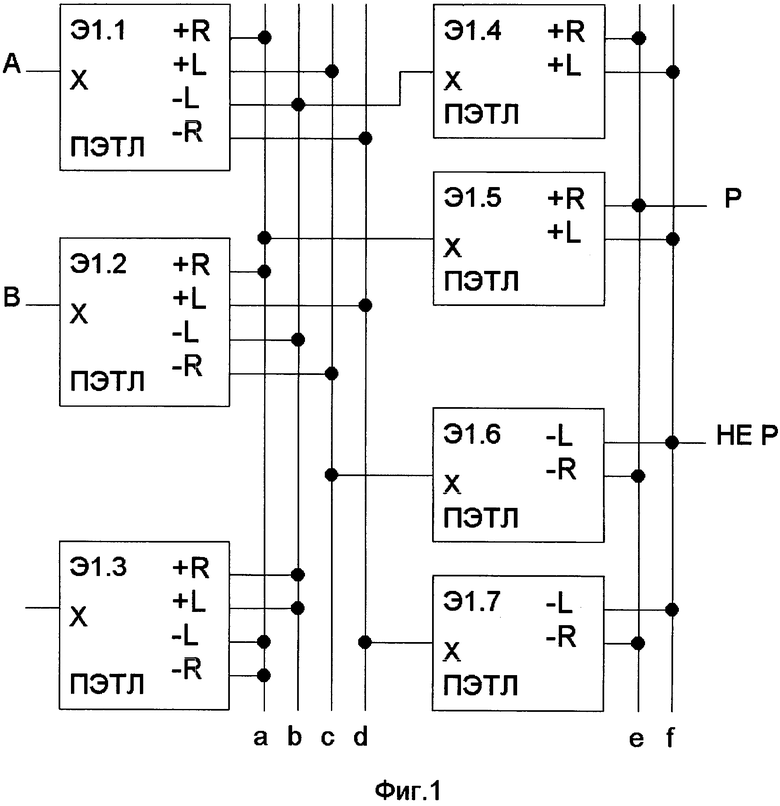
Троичный поразрядный умножитель (ТПУ) содержит семь пороговых элементов троичной логики (ПЭТЛ), причем первый, второй и третий ПЭТЛ имеют положительные и отрицательные R- и L-выходы, четвертый и пятый ПЭТЛ имеют только положительные R- и L-выходы, шестой и седьмой ПЭТЛ имеют только отрицательные R- и L-выходы, причем вход первого ПЭТЛ является А-входом ТПУ, причем вход второго ПЭТЛ является В-входом ТПУ, причем положительные R-выходы первого и второго ПЭТЛ и отрицательные R- и L-выходы третьего ПЭТЛ через сборку а подключены к входу пятого ПЭТЛ, причем отрицательные L- выходы первого и второго ПЭТЛ и положительные R- и L-выходы третьего ПЭТЛ через сборку b подключены к входу четвертого ПЭТЛ, причем положительный L- выход первого ПЭТЛ и отрицательный R-выход второго ПЭТЛ через сборку с подключены к входу шестого ПЭТЛ, причем положительный L-выход второго ПЭТЛ и отрицательный R- выход первого ПЭТЛ через сборку d подключены к входу седьмого ПЭТЛ, причем положительные R-выходы четвертого и пятого ПЭТЛ и отрицательные R-выходы шестого и седьмого ПЭТЛ через сборку е подключены к выходу Р ТПУ, причем положительные L- выходы четвертого и пятого ПЭТЛ и отрицательные L-выходы шестого и седьмого ПЭТЛ через сборку f подключены к выходу НЕ Р ТПУ.
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
| Трехфазный умножитель частоты | 1990 |
|
SU1742959A1 |
| Умножитель частоты | 1990 |
|
SU1797113A1 |
| US 5610537 A, 11.03.1997. | |||
Авторы
Даты
2017-09-19—Публикация
2016-07-15—Подача