Изобретение относится к цифровой вычислительной технике, в частности к недвоичной технике, и предназначено для создания реализуемого в среде полупроводниковой интегральной электроники устройства троичного сложения и вычитания.
Известной успешной реализацией недвоичных цифровых устройств являются троичные ЦВМ "Сетунь" и "Сетунь 70" [1, 2]. Логические элементы этих ЦВМ выполнены на основе электромагнитной техники [8, 9, 10], имеют малое быстродействие, большие потребляемую мощность и размеры. Устройства на таких элементах не могут быть реализованы в среде современной полупроводниковой интегральной электроники.
Известен функциональный аналог элементов ЦВМ "Сетунь" "Пороговый Элемент Троичной Логики" (ПЭТЛ), реализуемый в среде полупроводниковой интегральной электроники [3]. На ПЭТЛ, используя ПЭТЛ-схемотехнику [7, 8], можно создавать троичные цифровые устройства. Ассортимент средств, которыми в настоящее время располагает ПЭТЛ-схемотехника, недостаточен для создания всего спектра троичных устройств. В частности, в нем отсутствует устройство троичного сложения и вычитания.
Изобретение преследует две цели: пополнить ассортимент средств ПЭТЛ-схемотехники и на конкретном примере продемонстрировать такие особенности троичной системы с цифрами -1, 0, +1, которые выгодно отличают ее от традиционной двоичной. Тем самым поддерживается реализация более широкого набора троичных логических и операционных устройств и стимулируется интерес к использованию троичной системы в вычислительной технике.
Наиболее близкими техническими решениями к изобретению являются группы изобретений: "Пороговый Элемент Троичной Логики и устройства на его основе" [3], "Узел Троичной схемотехники и дешифраторы-переключатели на его основе" [4], "Троичный D-триггер (варианты)" [5], "Троичный Т-триггер" и "Троичный реверсивный счетчик" [6].
Известные группы изобретений поддерживают реализацию ограниченного числа троичных устройств:
Комбинационные схемы: троичная схема "И", троичный полусумматор, троичные дешифраторы и троичные переключатели.
Схемы с памятью: четыре варианта троичных D-триггеров, Т-триггер и троичный реверсивный счетчик.
Реализацию устройства троичного сложения и вычитания известные группы изобретений не раскрывают.
Раскрытие изобретения
Устройство троичного сложения и вычитания (УТСВ) состоит из 10 Пороговых Элементов Троичной Логики (ПЭТЛ), Узла Троичной Схемотехники (УТС) и Троичного Полного Последовательного Сумматора (ТППС).
Входы первого и второго ПЭТЛ являются входами первого и второго операндов УТСВ, вход УТС является входом РР УТСВ, а вход Ссин ТППС является входом Ссин УТСВ, выход СУММА ТППС является выходом СУММА/РАЗНОСТЬ УТСВ.
Выход +R первого ПЭТЛ и восьмой выход УТС соединены с входом пятого ПЭТЛ, выход +L первого ПЭТЛ и седьмой выход УТС соединены с входом третьего ПЭТЛ, выход -L первого ПЭТЛ и второй выход УТС соединены с входом четвертого ПЭТЛ, выход -R первого ПЭТЛ и первый выход УТС соединены с входом шестого ПЭТЛ.
Выход +R второго ПЭТЛ и четвертый выход УТС соединены с входом девятого ПЭТЛ, выход +L второго ПЭТЛ и третий выход УТС соединены с входом седьмого ПЭТЛ, выход -L второго ПЭТЛ и шестой выход УТС соединены с входом восьмого ПЭТЛ, выход -R второго ПЭТЛ и пятый выход УТС соединены с входом десятого ПЭТЛ.
Выходы +R третьего и пятого ПЭТЛ и выходы -R четвертого и шестого ПЭТЛ соединены с входом Сл1 ТППС, выходы +R седьмого и девятого ПЭТЛ и выходы -R восьмого и десятого ПЭТЛ соединены с входом Сл2 ТППС.
Все неиспользованные выходы ПЭТЛ соединены с земляной шиной.
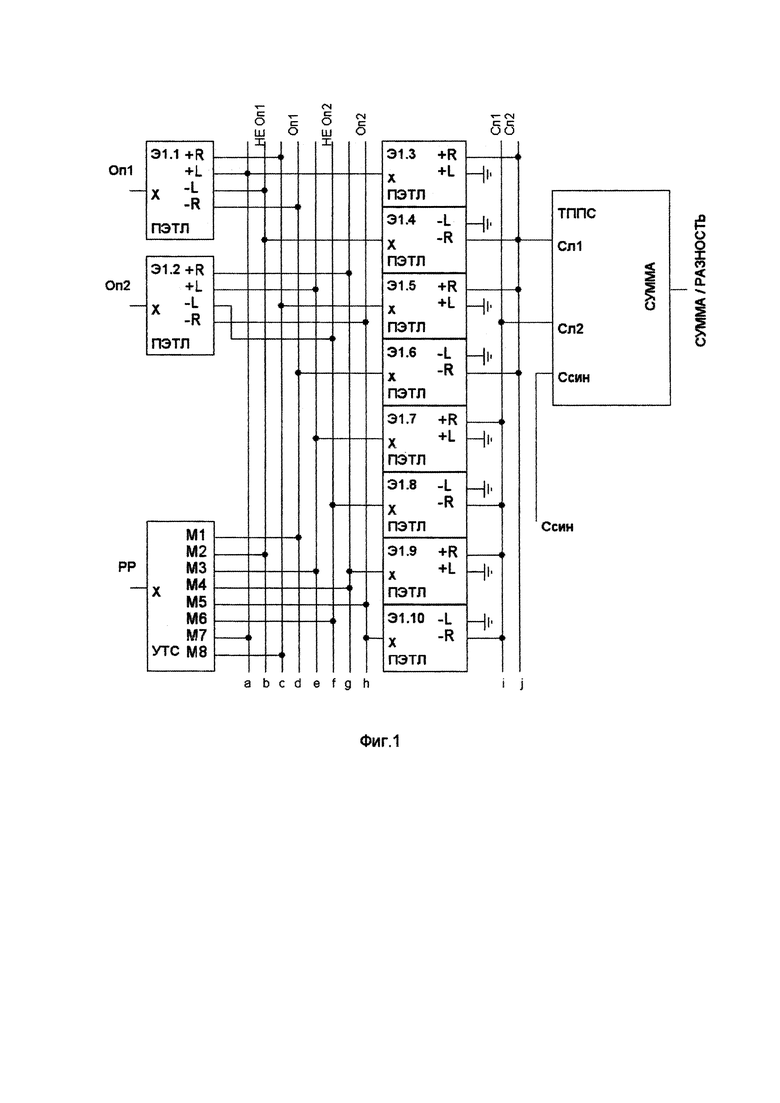
На Фиг. 1 изображено устройство троичного сложения и вычитания.
Устройство Троичного Сложения и Вычитания (УТСВ) выполнено на основе ПЭТЛ-схемотехники - совокупности элементов, узлов, правил их соединения, приемов, типовых решений и изобразительных средств, поддерживающих создание цифровых устройств, работающих в троичной системе с цифрами +1, 0, -1.
ПЭТЛ-схемотехника появилась недавно и отличается от других интегральных схемотехник. Она описана в [3, 4, 5, 6, 7, 8]. Краткие сведения приведены ниже:
1. Троичным значениям (тритам) +1, 0, -1 на физическом уровне соответствуют дискретные токи +Iф, 0, -Iф.
2. Пороговый Элемент Троичной Логики (ПЭТЛ) имеет 1 вход и группу из 4-х выходов: +R, +L, -L, -R.
3. Узел Троичной Схемотехники (УТС) имеет 1 вход и группу из 8-ми выходов: M1, М2, М3, М4, М5, М6, М7, М8.
4. На входах ПЭТЛ и УТС происходит алгебраическое сложение дискретных токов +Iф, и -Iф и формируется трит X. Если число +Iф больше числа -Iф - Х=+1, если число +Iф меньше числа -Iф - Х=-1, если число +Iф равно числу -Iф - Х=0.
5. ПЭТЛ и УТС могут иметь более одной группы выходов. Значения на одноименных выходах тождественны.
Значениям трита X соответствуют значения пар его двузначных компонент на выходах. Это соответствие приведено в таблице 1. Пары нумеруются римскими цифрами, варианты пар - арабскими.

Двузначные компоненты двоичны: компоненты в строке I имеют значения +1 или 0; компоненты в строке II - -1 или 0.
Терминология ПЭТЛ-схемотехники не устоялась. Используются сопоставимые термины из двоичных схемотехник и из лексикона "Сетуней". Следует руководствоваться таблицами истинности и сопроводительным текстом.
Сложение дискретных токов на входах элементов и объединение (сборка) выходов являются приемами ПЭТЛ-схемотехники. Например, объединяя +R и -R, на выходе получим повторение входного трита X, объединяя +L и -L - его нециклическую инверсию НЕ X, объединяя +R и +L или -R и -L - постоянные значения трита +1 или -1. Практикуется объединение выходов разных ПЭТЛ и УТС.
Сборки изображаются вертикальными линиями, нижние концы которых помечены буквами, а верхние (необязательно) - либо наименованием элемента, ко входу которого сборка подключена, либо названием сигнала. Как правило, слева от сборки - элементы, выходы которых к ней подключены, справа - элемент, на входе которого формируется трит X.
Если у ПЭТЛ или УТС более одной группы выходов, их число m указывают под номером элемента.
Возможны ПЭТЛ с половинным числом выходов: либо только положительные (+R, +L), либо только отрицательные (-L, -R). На фиг. 1 у ПЭТЛ Э1.3, Э1.5, Э1.7, Э1.9 только положительные выходы, у ПЭТЛ, Э1.4, Э1.6, Э1.8, Э1.10 - только отрицательные.
Неиспользуемые выходы соединяют с землей.
Крупные узлы изображают без подробностей в виде прямоугольников. Для них справедливо все, относящееся к ПЭТЛ: на входах суммируются триты; может быть несколько групп выходов. На фиг. 1 таким образом изображен Троичный Полный Последовательный Сумматор (ТППС). ТППС осуществляет суммирование двух чисел, которые последовательно, трит за тритом, поступают на входы Сл1 и Сл2. На выходе СУММА последовательно формируется триты суммы. Работа ТППС тактируется фронтом (переходом от +1 к -1) сигнала на входе Ссин.
Использование ПЭТЛ-схемотехники проиллюстрируем на примере троичного дешифратора, который входит в состав УТСВ. Дешифратор выполнен на одном УТС. (На фиг. 1 он изображен внизу слева). В зависимости от значения трита РР на входе дешифратора на четырех парах сборок a,b; c,d; g,h и e,f формируются триты, приведенные в таблице 2.
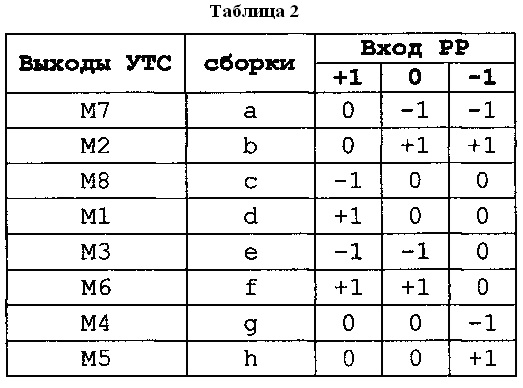
Алгоритм заполнения ячеек таблицы следующий:
1. Берут трит РР из столбца с заполняемой ячейкой.
2. Из таблицы 1 берут трит(ы) на выходах УТС, подсоединенного(ых) к сборке заполняемой ячейки.
3. Определяют трит на сборке и заносят его в ячейку.
4. Переходят к другой ячейке этой сборки и выполняют пп. 2 и 3.
5. Переходят к другой сборке и выполняют пп. 1-3.
Примечание: в данном случае к каждой сборке подключен один выход и в ячейку просто заносят трит из таблицы 1. Возможна ситуация, когда к сборке подключено несколько выходов. Тогда в ячейку заносится трит, полученный в результате алгебраического сложения нескольких тритов из таблицы 1.
Работа устройства в качестве дешифратора, управляющего коммутатором, будет описана далее.
Устройство Троичного Сложения и Вычитания (УТСВ) оперирует с числами в троичном коде с цифрами +1, 0 и -1. Оно имеет входы Oп1 И Oп2, тактирующий вход С и выход СУММА/РАЗНОСТЬ. На входы УТСВ последовательно поразрядно поступают операнды Оп1 и Оп2, над которыми могут выполняться следующие действия:
Сложение: Оп1 + Оп2
Вычитание-1: Оп1 - Оп2
Вычитание-2: Оп2 - Оп1
УТСВ состоит из двух узлов: входного коммутатора, реализованного на 10-ти ПЭТЛ, управляемого дешифратором на УТС (на фиг. 1 слева) и сумматора ТППС (на фиг. 1 справа). Действия УТСВ задаются тритом РР (Режим Работы) согласно таблице 3.

Функционирование УТСВ основывается на особенностях Троичной Симметричной Системы (ТС) и ПЭТЛ-схемотехники.
ТС присущи два ценных свойства: естественность представления относительных чисел и отсутствие проблемы округления.
В ТС нет специального разряда знака числа и не надо вводить дополнительный (или обратный) код для выполнения операций с относительными числами. Знак числа определяется знаком старшей значащей цифры. Чтобы изменить знак числа достаточно выполнить поразрядно нециклическую инверсию - поменять все +1 на -1 и все -1 на +1.
Проблема округления в ТС решается наилучшим образом: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов [1, с. 15].
В ПЭТЛ-схемотехнике нециклическая инверсия легко реализуется на ПЭТЛ. Объединяя выходы +R и –R, получаем повторение входного трита X, объединяя +L и –L, - его нециклическую инверсию НЕ X.
Операнды Oп1 и Оп2 на ПЭТЛ Э1.1 и Э1.2 разделяются на 4 пары двузначных компонент: две на выходах +R, -R и две на выходах +L, -L. Компоненты поступают на 4 пары сборок: a,b; c,d; e,f и g,h (фиг. 1). Сборки подключены к входам 4-х пар ПЭТЛ, на которых формируются двузначные компоненты тритов Oп1 и Оп2: прямые на входах Э1.5, Э1.6 и Э1.9, Э1.10; инвертированные на входах Э1.3, Э1.4 и Э1.7, Э1.8.
Для каждого значения трита РР существуют одна или две пары сборок, на которых дешифратор установил 0. Триты со входов ПЭТЛ, подключенных к этим сборкам, передаются на их выходы. На остальных сборках при этом дешифратор установил +1 или -1. Значение +1 для входов ПЭТЛ, куда поступают -R - запирающее, значение -1 запирающее для входов ПЭТЛ, куда поступают +R. На выходах запертых ПЭТЛ остается 0. В итоге на сборках i и j формируются парные комбинации тритов Оп1, Оп2, НЕ Оп1 и НЕ Оп2.
Таблицы 4 и 5 иллюстрируют работу УТСВ для всех вариантов комбинаций значений тритов Оп1, Оп2 и РР на входах. Кроме сборок а, b, с, d, е, f, g и h в таблицах фигурируют сборки j, i и входы ТППС Сл1 и Сл2.
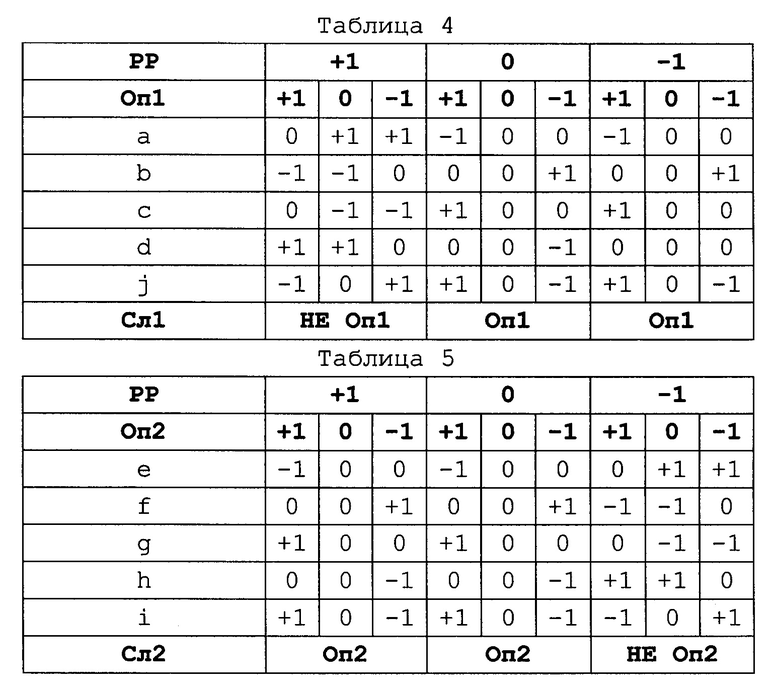
Триты операндов последовательно, начиная с младшего разряда, поступают на входы Оп1 и Оп2 УТСВ. В входном коммутаторе происходит их коммутация и на входах Сл1 и Сл2 ТППС формируются парные комбинации прямых и инверсных тритов Оп1 и Оп2. Если РР=0, оба операнда не инвертированы и на выходе СУММА ТППС формируются триты суммы. Если РР#0, один операнд не инвертирован, а другой инвертирован и на выходе СУММА ТППС формируются триты разностей. Выход СУММА ТППС является выходом СУММА/РАЗНОСТЬ УТСВ. Работа УТСВ синхронизируется фронтом сигнала на входе Син.
Источники информации
1. Брусенцов Н.П., Маслов С.П., Розин В.П., Тишулина A.M. Малая цифровая вычислительная машина "Сетунь". - М.: Изд-во Московского университета, 1965, 145 с.
2. Брусенцов Н.П., Жоголев Е.А., Маслов С.П., Рамиль Альварес X. Опыт создания троичных цифровых машин. // Компьютеры в Европе. Прошлое, настоящее и будущее. - Киев: Феникс, 1998, с. 67-71.
3. Маслов С.П. Пороговый элемент троичной логики и устройства на его основе. Патент РФ на изобретение RU №2394366 С1. Зарегистрирован: 10.07.2010.
4. Маслов С.П. Узел троичной схемотехники и дешифраторы - переключатели на его основе. Патент РФ на изобретение RU №2461122 C1. Зарегистрирован: 10.09.2012.
5. Маслов С.П. Троичный D-триггер (варианты). Патент РФ на изобретение RU №2510129 C1. Зарегистрирован: 20.03.2014.
6. Маслов С.П. Троичный Т-триггер и Троичный реверсивный счетчик на его основе. Патент РФ на изобретение RU №2562370 С2. Зарегистрирован: 11.08.2015.
7. Маслов С.П. Об одной возможности реализации троичных цифровых устройств. Тематический сборник №12 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2011, с. 222-227.
8. Маслов С.П. Троичная схемотехника. Тематический сборник №13 "Программные системы и инструменты", М.: Изд-во факультета ВМиК МГУ, 2012, с. 152-158.
9. Брусенцов Н.П. Пороговая реализация трехзначной логики электромагнитными средствами. // Вычислительная техника и вопросы кибернетики. Вып. 9. - М.: Изд-во Моск. ун-та, 1972, с. 3-35.
10. Брусенцов Н.П. Электромагнитные цифровые устройства с однопроводной передачей трехзначных сигналов. - В кн.: Магнитные элементы автоматики и вычислительной техники. XIV Всесоюзное совещание (Москва, сентябрь 1972 г.). М.: Наука, 1972, с. 242-244.
| название | год | авторы | номер документа |
|---|---|---|---|
| ТРОИЧНЫЙ ПОЛНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ СУММАТОР (ВАРИАНТЫ) | 2016 |
|
RU2616887C1 |
| ТРОИЧНОЕ МНОЖИТЕЛЬНОЕ УСТРОЙСТВО | 2017 |
|
RU2642408C1 |
| ТРОИЧНЫЙ РЕВЕРСИВНЫЙ РЕГИСТР СДВИГА | 2015 |
|
RU2585263C1 |
| ТРОИЧНЫЙ Т-ТРИГГЕР И ТРОИЧНЫЙ РЕВЕРСИВНЫЙ СЧЕТЧИК НА ЕГО ОСНОВЕ | 2014 |
|
RU2562370C2 |
| УСТРОЙСТВО ТРОИЧНОЙ СХЕМОТЕХНИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2017 |
|
RU2648565C1 |
| ТРОИЧНЫЙ ПОРАЗРЯДНЫЙ УМНОЖИТЕЛЬ | 2016 |
|
RU2631166C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2016 |
|
RU2618901C1 |
| ТРОИЧНЫЙ D-ТРИГГЕР (ВАРИАНТЫ) | 2012 |
|
RU2510129C1 |
| УЗЕЛ ТРОИЧНОЙ СХЕМОТЕХНИКИ И ДЕШИФРАТОРЫ-ПЕРЕКЛЮЧАТЕЛИ НА ЕГО ОСНОВЕ | 2011 |
|
RU2461122C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
Изобретение относится к устройствам цифровой вычислительной техники, в частности к недвоичной схемотехнике, и предназначено для создания устройств троичной арифметики. Техническим результатом является реализация устройства троичного сложения и вычитания. Устройство содержит 10 пороговых элементов троичной логики, узел троичной схемотехники и троичный полный последовательный сумматор. 1 ил., 5 табл.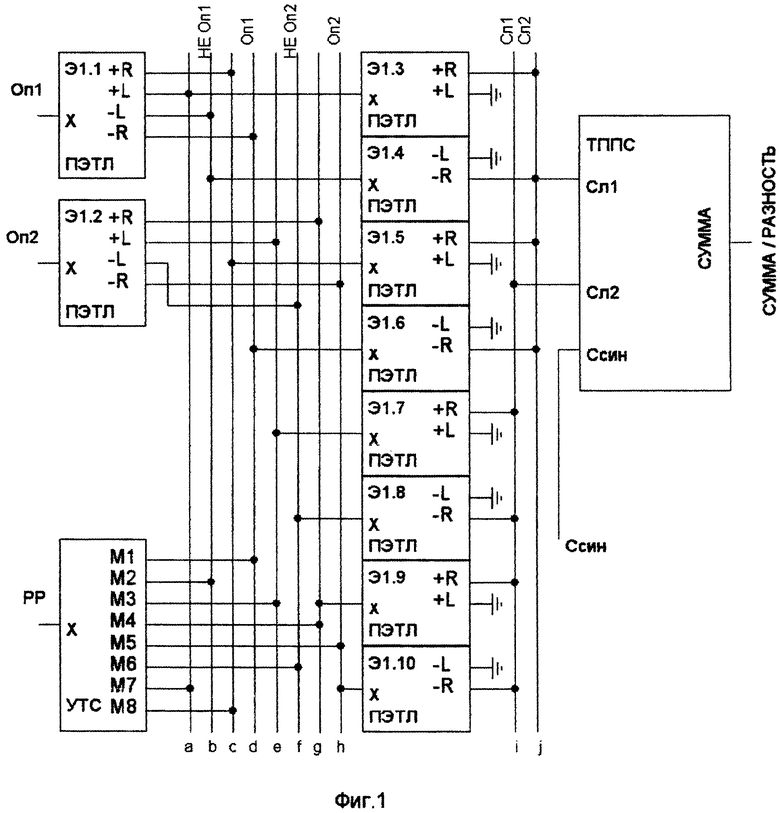
Устройство троичного сложения и вычитания (УТСВ), состоящее из десяти Пороговых Элементов Троичной Логики (ПЭТЛ), Узла Троичной Схемотехники (УТС) и Троичного Полного Последовательного Сумматора (ТППС), причем входы первого и второго ПЭТЛ являются соответственно входами первого и второго операндов УТСВ, вход УТС является входом РР УТСВ, вход Син ТППС является входом Ссин УТСВ, причем выход СУММА ТППС является выходом СУММА/РАЗНОСТЬ УТСВ, причем положительный R выход первого ПЭТЛ и восьмой выход УТС через сборку с соединены с входом пятого ПЭТЛ, причем положительный L выход первого ПЭТЛ и седьмой выход УТС через сборку а соединены с входом третьего ПЭТЛ, причем отрицательный L выход первого ПЭТЛ и второй выход УТС через сборку b соединены с входом четвертого ПЭТЛ, причем отрицательный R выход первого ПЭТЛ и первый выход УТС через сборку d соединены с входом шестого ПЭТЛ, причем положительный R выход второго ПЭТЛ и четвертый выход УТС через сборку g соединены с входом девятого ПЭТЛ, причем положительный L выход второго ПЭТЛ и третий выход УТС через сборку е соединены с входом седьмого ПЭТЛ, причем отрицательный L выход второго ПЭТЛ и шестой выход УТС через сборку f соединены с входом восьмого ПЭТЛ, причем отрицательный R выход второго ПЭТЛ и пятый выход УТС через сборку h соединены с входом десятого ПЭТЛ, причем положительные R выходы третьего и пятого ПЭТЛ и отрицательные R выходы четвертого и шестого ПЭТЛ через сборку j соединены с входом Сл1 ТППС, причем положительные R выходы седьмого и девятого ПЭТЛ и отрицательные R выходы восьмого и десятого ПЭТЛ через сборку i соединены с входом Сл2 ТППС, причем положительные L выходы третьего, пятого, седьмого и девятого ПЭТЛ и отрицательные L выходы четвертого, шестого, восьмого и десятого ПЭТЛ соединены с земляной шиной.
| Троичный сумматор | 1972 |
|
SU455339A1 |
| Троичный сумматор | 1983 |
|
SU1137461A1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
| УЗЕЛ ТРОИЧНОЙ СХЕМОТЕХНИКИ И ДЕШИФРАТОРЫ-ПЕРЕКЛЮЧАТЕЛИ НА ЕГО ОСНОВЕ | 2011 |
|
RU2461122C1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| US 7274211 B1, 25.09.2007. | |||
Авторы
Даты
2018-02-19—Публикация
2017-03-22—Подача