Изобретение относится к цифровой вычислительной технике, в частности к недвоичной технике, и предназначено для создания троичных цифровых устройств, реализуемых в среде полупроводниковой интегральной электроники.
Известной успешной реализацией недвоичных цифровых устройств являются троичные ЦВМ "Сетунь" [1] и "Сетунь-70" [2]. Логические элементы этих ЦВМ, основанные на Троичной Пороговой Логике [3], изготавливаются средствами электромагнитной техники, имеют низкое быстродействие, большие потребляемую мощность и размеры. Элементы ЦВМ "Сетунь" не реализуются в среде полупроводниковой интегральной электроники.
Известен функциональный аналог элемента ЦВМ "Сетунь" Пороговый Элемент Троичной Логики (ПЭТЛ) [4]. ПЭТЛ реализуется в среде полупроводниковой интегральной электроники.
На ПЭТЛ можно создавать троичные устройства, используя ПЭТЛ-схемотехнику [11]. Арсенал ПЭТЛ-схемотехники располагает постоянно расширяющимся ассортиментом типовых решений и узлов [4, 5, 6, 7, 8]. Троичное множительное устройство в нем отсутствует.
Целью изобретения является создание на ПЭТЛ троичного множительного устройства, аппаратно осуществляющего умножение троичных многозначных чисел.
Техническим результатом изобретения является пополнение ассортимента схемотехнических средств, используемых для создании устройств на основе симметричной троичной системы с цифрами +1, 0, -1 в среде интегральной полупроводниковой электроники.
Наиболее близким техническим решением к заявляемому изобретению является троичное устройство умножения, использованное в ЦВМ "Сетунь" [1. с. 64]. Однако это устройство не реализуется в среде современной интегральной электроники.
Раскрытие изобретения
Троичное Множительное Устройство (ТМУ) состоит из K=k/3 Секций Множительного Устройства (СМУ) (k - разрядность операндов) и n Троичных Полных Последовательных Сумматоров (ТППС), образующих несколько ступеней (n=N1+N2+…+1, где N1=K/3 - число ТППС в 1-й ступени, N2=N1/3 - число ТППС во 2-й ступени… и т.д).
Выводы Твх, M1, С и М2вх 1-й СМУ являются выводами соответственно НАЧ, МНОЖИТЕЛЬ, ТАКТ и МНОЖИМОЕ ТМУ, выводы Твых и М2вых m-й СМУ соединяются соответственно с выводами Твх и М2вх (m+1)-й СМУ (m=1, 2, … (K-1)), выводы Твых и М2вых K-й СМУ соединяются с землей.
Выводы Пр СМУ в произвольном порядке соединяются с выводами Сл1,Сл2,Сл3 1-й ступени ТППС, выводы СУММА 1-й ступени ТППС в произвольном порядке соединяются с выводами Сл1,Сл2,Сл3 2-й ступени ТППС,… и т.д., выводы СУММА предпоследней ступени ТППС в произвольном порядке соединяются с выводами Сл1,Сл2,Сл3 последней ступени ТППС, вывод СУММА единственного ТППС в последней ступени является выводом ПРОИЗВЕДЕНИЕ ТМУ.
СМУ состоит из 2-х Троичных Реверсивных Регистров Сдвига (ТРРС), 3-х троичных D-триггеров (Т1,Т2,Т3), 3-х Троичных Поразрядных Умножителей (ТПУ1,ТПУ2,ТПУ3) и одного ТППС.
Выводы Iпр 1-го и 2-го ТРРС являются соответственно выводами Твх и М2вх СМУ, выводы Опр 1-го и 2-го ТРРС являются соответственно выводами Твых и М2вых СМУ, выводы Q1,Q2,Q3 1-го ТРРС соединены соответственно с выводами С D-триггеров Т1,Т2,Т3 на выводы РР обоих ТРРС подается -1.
Выводы Q1,Q2,Q3 D-триггеров Т1,Т2,Т3 соединены соответственно с выводами А ТПУ1,ТПУ2,ТПУ3 выводы Q1,Q2,Q3 2-го ТРРС соединены соответственно с выводами В ТПУ1,ТПУ2,ТПУ3 выводы П ТПУ1,ТПУ2,ТПУ3 соединены соответственно с выводами Сл1,Сл2,Сл3 ТППС, вывод СУММА ТППС является выводом Пр СМУ.
На Фиг. 1 изображено Троичное Множительное Устройство, на Фиг. 2 Секция Множительного Устройства, на Фиг. 3 Троичный Поразрядный Умножитель.
Разработка устройств на Пороговых Элементах Троичной Логики (ПЭТЛ) базируется на ПЭТЛ-схемотехнике - наборе элементов, узлов, правил их соединения, приемов, типовых решений и изобразительных средств, поддерживающих создание устройств, работающих в троичной системе с цифрами +1, 0, -1.
ПЭТЛ-схемотехника описана в Патентах РФ [4, 5, 6, 7, 8, 9] и других материалах [10, 11]. Краткие сведения приведены ниже:
1. Троичные значения (триты) +1, 0, -1 на физическом уровне представлены дискретными разнополярными токами +Iф, I0=0, -Iф.
2. ПЭТЛ имеет один вход X и одну или несколько групп выходов. В каждой группе четыре выхода: +R, +L, -L, -R. Значения на одноименных выходах во всех группах тождественны.
3. На входе X ПЭТЛ происходит алгебраическое сложение разнополярных дискретных токов +Iф и -Iф и формируется трит X. Если число +Iф больше числа -Iф-Х=+1, если число +Iф меньше числа -Iф-Х=-1, если число +Iф равно числу -Iф-Х=0.
4. Значению X на входе ПЭТЛ соответствуют значения пар +R, -R и +L ,-L. Соответствие приведено в Таблице 1 в тритах и в токах +Iф, I0=0, -Iф. Пары пронумерованы римскими цифрами, варианты пар - арабскими.

Проектирование устройств на основе ПЭТЛ-схемотехники имеет особенности:
1. У ПЭТЛ низкие входные и высокие выходные сопротивления. Входные, выходные и межэлементные сигналы являются дискретными токами, а не дискретными напряжениями (как в традиционных схемотехниках). Включать входы ПЭТЛ в параллель нельзя. Незанятые выходы нужно нагружать, подключая их к земле.
2. Включать в параллель входы нельзя, а выходы - можно и нужно. Таким путем реализуется троичная пороговая логика [3], на которой зиждется ПЭТЛ-схемотехника. Объединение (сборка) выходов ПЭТЛ, наряду с суммированием дискретных токов +Iф и -Iф, на входах - ее приемы. Например, объединяя +R и -R, получим на сборке повторение X, объединяя +L и -L - его нециклическую инверсию НЕ(Х). Реализация более сложных функций достигается объединением выходов разных ПЭТЛ.
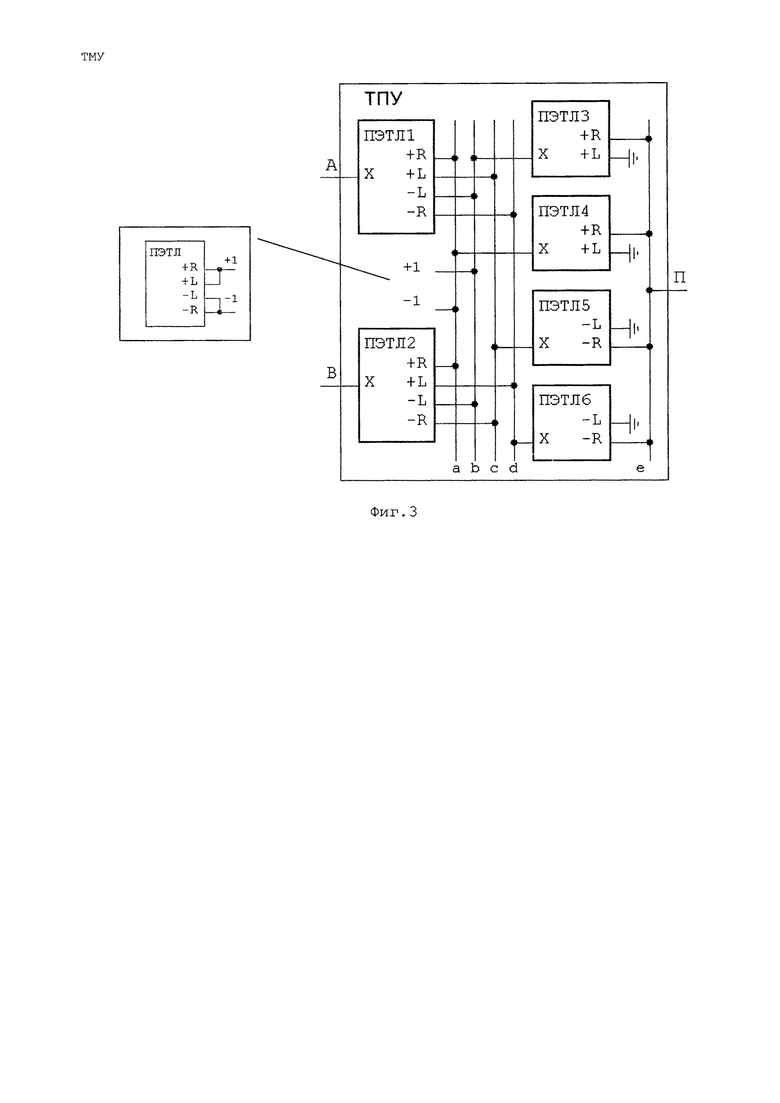
3. Объединяя выходы +R и +L или -R и -L, получим постоянные значения +1 или -1 при любом X на входе (т.е. можно использовать оставшиеся незанятыми пары выходов). Такое включение применяют для формирования положительного или отрицательного порога (постоянного тока +Iф или -Iф). Чтобы не загромождать рисунка ПЭТЛ-формирователь не изображают, а в соответствующем месте схемы ставят +1 или -1 (см. выноску на Фиг. 3). Если нужно задать 0 (Iф=0), вход ПЭТЛ оставляют свободным.
4. Запрет на объединение входов требует, чтобы подача одинаковых сигналов на несколько входов осуществлялась по нескольким проводам (соединениям) от ПЭТЛ с несколькими группами выходов. Чтобы не загромождать рисунка сам ПЭТЛ при этом не изображают, разводку обозначают толстыми линиями (шинами), а названия сигналов помещают в рамку (см. выноску на Фиг. 2).
5. Терминология ПЭТЛ-схемотехники не устоялась. Используются термины из двоичной техники и из лексикона "Сетуней". Для исключения двусмысленностей необходимо руководствоваться таблицами истинности.
Проиллюстрируем сказанное на примере Троичного Поразрядного Умножителя (ТПУ), аппаратно реализующего таблицу троичного умножения (+1*+1=+1; -1*-1=+1; +1*-1=-1; +1*0=0 и т.д.).
ТПУ входят в состав СМУ.
На входы А и В ТПУ (Фиг. 3) поступают триты-сомножители, а на выходе П, в соответствии с Таблицей 2 формируется поразрядное произведение А на В.
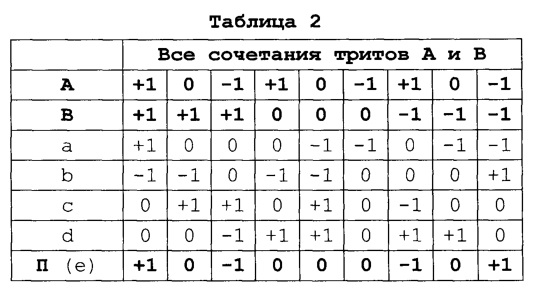
ТПУ содержит 6 ПЭТЛ. У ПЭТЛ 1, 2 полные наборы выходов, у ПЭТЛ 3, 4 только +R, +L выходы, а у ПЭТЛ 5, 6 только -R, -L выходы.
Сборки изображаются вертикальными линиями и помечены буквами a, b, c, d, e. Слева - ПЭТЛ, выходы которых объединяются на сборках, справа - вход ПЭТЛ либо выход устройства (вход следующего), на котором формируется трит X (см. Таблицу 1). К сборкам а и b, помимо выходов ПЭТЛ, постоянно подключены -1 и +1 (пороговые токи -Iф и +Iф). На сборке е (выход ТПУ) объединены выходы ПЭТЛ 3, 4, 5, 6. На нем формируется трит П.
Алгоритм заполнения ячеек таблицы следующий:
1. Берем триты А и В из столбца с заполняемой ячейкой;
2. По Таблице 1 определяем триты на выходах ПЭТЛ, подключенных к сборке этой ячейки, соответствующие выбранным А и В;
3. Определяем (см. пп. 3, 4 стр. 3) трит X на сборке и заносим его в ячейку;
4. Для следующей ячейки строки берем А и В из другого столбца;
5. Заполнив строку переходим к следующей.
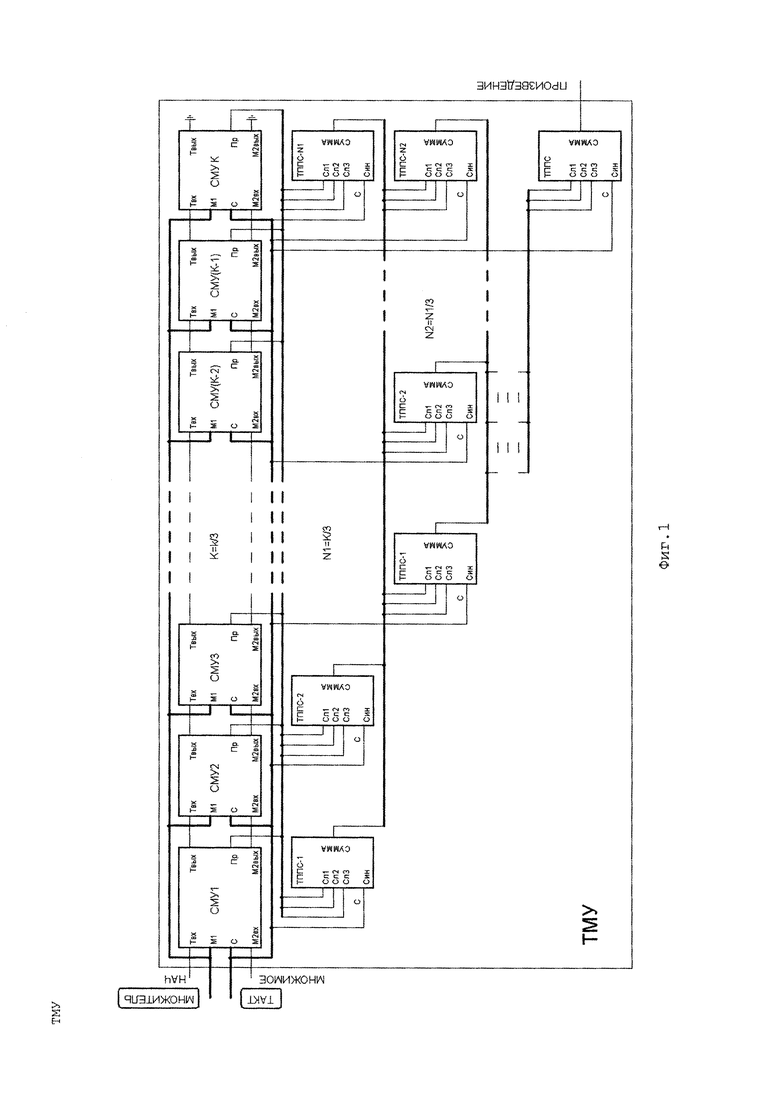
Троичное Множительное Устройство (ТМУ) изображено на Фиг. 1. Оно состоит из модулей двух типов: Секций Множительного Устройства (СМУ) и Троичных Полных Последовательных 3-входовых Сумматоров (ТППС).
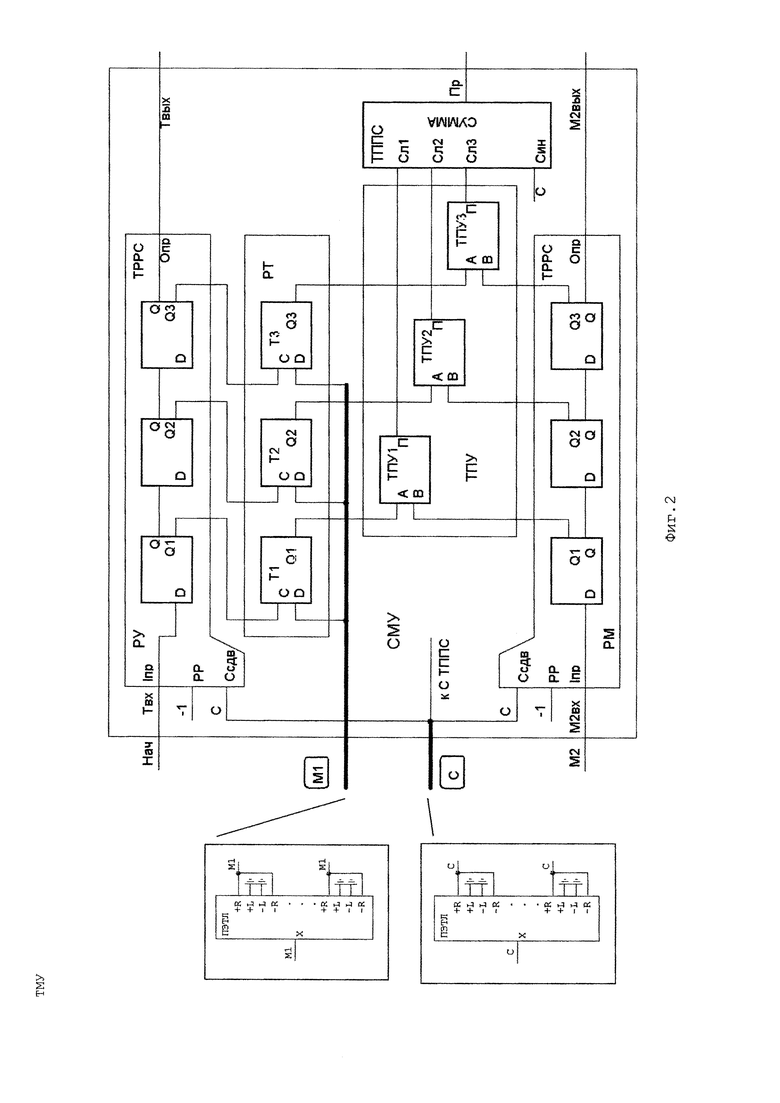
СМУ является "минимальным" троичным множительным устройством. Оно производит умножение 3-тритных чисел M10 и М2. Числа поступают на входы M1 и М2, а с выхода Пр выдается 6-тритное произведение. Работа тактируется фронтом (переходом от -1 к +1) сигнала на входе С и длится 6 тактов.
СМУ (Фиг. 2) состоит из следующих частей:
Регистр Управления (РУ), Регистр Триггеров (РТ), блок Поразрядных Умножителей (ТПУ), Регистр Множимого М2 (РМ) и Сумматор (ТППС).
Использованы типовые узлы ПЭТЛ-схемотехники:
РУ и РМ - Троичные Реверсивные Регистры Сдвига ТРРС [8]. Режим Работы ТРРС задается входом PP. При РР=-1 - сдвиг слева направо по фронту на С.
РТ - D-триггеры [6]. Запись трита с D-входа по фронту на С.
ТПУ - Реализуют троичную таблицу умножения (см. выше).
ТППС - Сумматор с 3-мя входами [9]. Тактируется фронтом на С.
Трит суммы выдается одновременно с поступлением слагаемых, трит переноса в следующем такте.
На вход Твх РУ поступает серия Нач, состоящая из +1 и пяти -1. Она сдвигается слева направо и последовательно выдается на выходы Q1, Q2, Q3 РУ.
Триты множителя M1 в параллель поступают на D-входы триггеров Т1, Т2, Т3. На их С-входы последовательно поступают фронты (переходы от -1 к +1) с выходов Q1, Q2, Q3 РУ. Они инициируют запись в триггеры текущих тритов множителя M1. Записанные триты последовательно появляются на выходах Q1, Q2, Q3 РТ и остаются там до окончания сеанса.
Одновременно триты множимого М2 поступают на вход М2Вх РМ и сдвигаются слева направо. За 6 тактов множимое заходит в РМ и покидает его. При сдвиге триты множимого последовательно, со сдвигом на такт, выдаются по выходам Q1, Q2, Q3 РМ.
Выходы Q1,Q2,Q3 РТ и РМ попарно поступают на входы А и В ТПУ1, ТПУ2, ТПУ3. На их выходах П последовательно формируются произведения множимого на разряды множителя.
Выходы П ТПУ соединены со входами Сл1, Сл2, Сл3 сумматора ТППС. На его выходе СУММА последовательно формируются триты произведения Пр=М1*М2.
Сказанное иллюстрируется в Таблице 3 на примере умножения двух 3-тритных чисел: M1 -1-1 0 (-12) и М2+1+1 0 (+12).
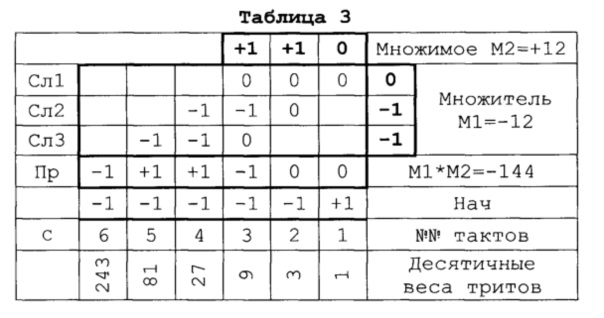
Младшие триты М2 и Пр расположены справа, младшие триты M1 - сверху. В нижней строке даны десятичные веса тритов. В строке над ней показан порядок поступления фронтов синхросерии С.
Сеанс начинается с подачи +1 на вход Нач и синхросерии на С. Одновременно триты множителя (-1-1 0) и множимого (+1+1 0) подаются на входы M1 и М2. Триты множителя, запоминаются в триггерах Т1, Т2, Т3 и выдаются по выходам Q1, Q2, Q3 РТ. Триты множимого сдвигается слева направо и выдаются по выходам Q1, Q2, Q3 РМ. Выходы Q РТ и РМ соединены с входами А и В ТПУ. На входах А ТПУ постоянно стоят триты множителя, а на входы В поступают, со сдвигом на такт, триты множимого. В ТПУ формируются поразрядные произведения множимого на множитель (ПМ). ПМ суммируются в ТППС, на его выходе СУММА (выход Пр СМУ) формируется произведение Пр=М1*М2 (-1+1+1-1 0 0).
Троичное Множительное Устройство (ТМУ) изображено на Фиг. 1. Чтобы не загромождать рисунка соединения из нескольких проводов показаны жирными линиями (шинами). Если это входы, их названия (МНОЖИТЕЛЬ и ТАКТ) помещены в рамки.
ТМУ выполняет умножение k-тритных чисел: МНОЖИТЕЛЯ и МНОЖИМОГО. Числа последовательно, младшими тритами вперед, поступают на входы ТМУ, а с его выхода ПРОИЗВЕДЕНИЕ выдается 2*k-тритное число. Процесс тактируется фронтами сигнала ТАКТ, длится 2*k тактов и начинается с подачи на вход НАЧ серии, состоящей из +1 и последовательности -1, число которых (2*k-1).
ТМУ состоит из модулей СМУ и ТППС, число которых определяется длиной операндов k.
Включенные цепочкой 3-тритные регистры РУ и РМ в СМУ образуют k-тритные регистры в ТМУ: регистр, управляющий записью множителя в триггеры, и регистр сдвига множимого.
Тройки триггеров-защелок Т1, Т2, Т3 и тройки ТПУ1, ТПУ2, ТПУ3 в СМУ образуют k-тритный регистр множителя и k-разрядный блок Поразрядных Умножителей в ТМУ.
ТМУ функционирует сходным с СМУ образом. Сумматор поразрядных произведений k-входовый, состоит из ТППС с 3-мя входами и имеет многоступенную структуру. Нулевую ступень образуют N0=K=k/3 ТППС в СМУ. Их выходы подключены к входам N1=N0/3 ТППС 1-й ступени. Выходы ТППС 1-й ступени подключены к входам N2=N1/3 ТППС 2-й ступени и т.д. В последней ступени единственный ТППС, на его выходе СУММА формируется ПРОИЗВЕДЕНИЕ.
Если числа k,K,N1,N2… не делятся нацело, их округляют до ближайшего сверху целого, кратного 3.
ТМУ аппаратно реализует умножение k-тритных чисел "столбиком".
Вследствие коммутативности сложения выходы ТППС в сумматоре поразрядных произведений могут соединяться со входами ТППС следующих ступеней в произвольном порядке.
Достоинства троичной симметричной системы с цифрами -1, 0, +1 проявляются в следующем:
1. Умножение чисел со знаком происходит без специальных манипуляций с разрядом знака.
2. При вычислении поразрядного произведения (ПМ) множимого М2 на трит множителя (ТМ1) не возникает переносов. Если ТМ1=0, ПМ состоит из нулей; если ТМ1=+1, ПМ=М2; если ТМ1=-1, ПМ=НЕ(М2) (нециклическая инверсия, все +1 заменены на -1 и все -1 на +1).
Литература
1. Брусенцов Н.П., Маслов С.П., Розин В.П., Тишулина A.M. Малая цифровая вычислительная машина "Сетунь". - М.: Изд-во МГУ, 1965. 145 с.
2. Брусенцов Н.П., Жоголев Е.А., Маслов С.П.
Общая характеристика малой цифровой машины "Сетунь-70".
В сб.: Вычислительная техника и вопросы кибернетики. Вып. 10. Л., Изд-во ЛГУ, 1974, с. 3-21.
3. Брусенцов Н.П. Пороговая реализация трехзначной логики электромагнитными средствами // Вычислительная техника и вопросы кибернетики. Вып. 9. - М.: Изд-во Моск. ун-та, 1972. С. 3-35.
4. Маслов С.П. Патент РФ №2394366 С1 на группу изобретений "Пороговый элемент троичной логики и устройства на его основе". Зарегистрирован 10.07.2010.
5. Маслов С.П.. Патент РФ №2461122 С1 на группу изобретений "Узел троичной схемотехники и дешифраторы - переключатели на его основе". Зарегистрирован 10.09.2012.
6. Маслов С.П. Патент РФ №2510129 С1 на группу изобретений "Троичный D-триггер (варианты)". Зарегистрирован 20.03.2014.
7. Маслов С.П. Патент РФ №2562370 С1 на группу изобретений "Троичный Т-триггер и Троичный реверсивный счетчик на его основе". Зарегистрирован 11.08.2015.
8. Маслов С.П. Патент РФ №2585263 С1 на изобретение "Троичный реверсивный регистр сдвига". Зарегистрирован 27.05.2016.
9. Маслов С.П. Патент РФ №2616887 С1 на изобретение "Троичный полный последовательный сумматор". Зарегистрирован 18.04.2017.
10. Маслов С.П. Об одной возможности реализации троичных цифровых устройств. Тематический сборник №12 "Программные системы и инструменты". М.: Изд-во факультета ВМиК МГУ, 2011.
11. Маслов С.П. Троичная схемотехника. Тематический сборник №13. "Программные системы и инструменты". М.: Изд-во факультета ВМиК МГУ, 2012. С. 152-158.
| название | год | авторы | номер документа |
|---|---|---|---|
| ТРОИЧНЫЙ ПОЛНЫЙ ПОСЛЕДОВАТЕЛЬНЫЙ СУММАТОР (ВАРИАНТЫ) | 2016 |
|
RU2616887C1 |
| УСТРОЙСТВО ТРОИЧНОГО СЛОЖЕНИЯ И ВЫЧИТАНИЯ | 2017 |
|
RU2645279C1 |
| ТРОИЧНЫЙ РЕВЕРСИВНЫЙ РЕГИСТР СДВИГА | 2015 |
|
RU2585263C1 |
| ТРОИЧНЫЙ ПОРАЗРЯДНЫЙ УМНОЖИТЕЛЬ | 2016 |
|
RU2631166C1 |
| ТРОИЧНЫЙ Т-ТРИГГЕР И ТРОИЧНЫЙ РЕВЕРСИВНЫЙ СЧЕТЧИК НА ЕГО ОСНОВЕ | 2014 |
|
RU2562370C2 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2016 |
|
RU2618901C1 |
| УСТРОЙСТВО ТРОИЧНОЙ СХЕМОТЕХНИКИ НА ТОКОВЫХ ЗЕРКАЛАХ | 2017 |
|
RU2648565C1 |
| ПОРОГОВЫЙ ЭЛЕМЕНТ ТРОИЧНОЙ ЛОГИКИ И УСТРОЙСТВА НА ЕГО ОСНОВЕ | 2009 |
|
RU2394366C1 |
| ТРОИЧНЫЙ D-ТРИГГЕР (ВАРИАНТЫ) | 2012 |
|
RU2510129C1 |
| УЗЕЛ ТРОИЧНОЙ СХЕМОТЕХНИКИ И ДЕШИФРАТОРЫ-ПЕРЕКЛЮЧАТЕЛИ НА ЕГО ОСНОВЕ | 2011 |
|
RU2461122C1 |
Изобретение относится к устройствам цифровой вычислительной техники, в частности к недвоичной схемотехнике, и предназначено для создания троичного множительного устройства. Технический результат заключается в расширении арсенала средств. Устройство содержит типовые узлы: троичные регистры сдвига, троичные сумматоры, троичные D-триггеры и троичные поразрядные умножители. 3 ил., 3 табл.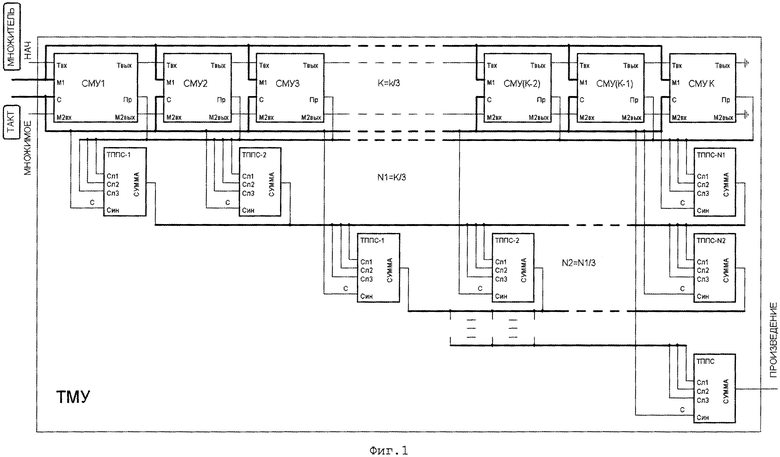
Троичное k-разрядное Множительное Устройство (ТМУ), состоящее из K Секций Множительного Устройства (СМУ), причем K=k/3, и n Троичных Полных Последовательных трехвходовых Сумматоров (ТППС), причем n ТППС образуют ступени, причем n=N1+N2+…+1, причем в первой ступени N1=K/3 ТППС, причем во второй ступени N2=N1/3 ТППС… и т.д., причем, если числа k, K, N1, N2… не делятся нацело, их округляют до ближайшего сверху целого, кратного 3, причем, если в ступени два или три ТППС, то ступень является предпоследней, причем в последней ступени один ТППС, причем выводы Твх, M1, С и М2вх первой СМУ, являются выводами соответственно НАЧ, МНОЖИТЕЛЬ, ТАКТ и МНОЖИМОЕ ТМУ, причем вывод МНОЖИТЕЛЬ содержит k соединений, причем вывод ТАКТ содержит k+n соединений, причем выводы Твых и М2вых m-й СМУ соединяются соответственно с выводами Твх и М2вх (m+1)-й СМУ, причем m=1, 2…(K-1), причем выводы Твых и М2вых K-й СМУ соединяются с землей, причем выводы Пр СМУ в произвольном порядке соединяются с выводами Сл1, Сл2, Сл3 первой ступени В ТППС, причем выводы СУММА у ТППС первой ступени в произвольном порядке соединяются с выводами Сл1, Сл2, Сл3 у ТППС второй ступени… и т.д., причем выводы СУММА предпоследней ступени ТППС в произвольном порядке соединяются с выводами Сл1, Сл2, Сл3 ТППС последней ступени, причем вывод СУММА ТППС последней ступени является выводом ПРОИЗВЕДЕНИЕ ТМУ, причем СМУ состоит из двух Троичных Реверсивных Регистров Сдвига (ТРРС), трех Троичных D-триггеров (Т1, Т2, Т3), трех Троичных Поразрядных Умножителей (ТПУ1, ТПУ2, ТПУ3) и Троичного Полного Последовательного 3-входового Сумматора (ТППС), причем выводы Iпр первого и второго ТРРС являются соответственно выводами Твх и М2вх СМУ, причем выводы Опр первого и второго ТРРС являются соответственно выводами Твых и М2вых СМУ, причем выводы Q1, Q2, Q3 первого ТРРС соединены соответственно с выводами С D-триггеров Т1, Т2, Т3, причем выводы Q1, Q2, Q3 D-триггеров Т1, Т2, Т3 соединены соответственно с выводами А ТПУ1, ТПУ2, ТПУ3, причем выводы Q1, Q2, Q3 второго ТРРС соединены соответственно с выводами В ТПУ1, ТПУ2, ТПУ3, причем выводы П ТПУ1, ТПУ2, ТПУ3 соединены соответственно с выводами Сл1, Сл2, Сл3 ТППС, причем вывод СУММА ТППС является выводом Пр СМУ, причем на выводы РР обоих ТРРС подается -1, причем вывод M1 СМУ содержит три соединения, причем вывод С СМУ содержит три соединения.
| ТРОИЧНЫЙ РЕВЕРСИВНЫЙ РЕГИСТР СДВИГА | 2015 |
|
RU2585263C1 |
| Троичный логический элемент | 1974 |
|
SU516195A1 |
| ТРОИЧНОЕ СЧЕТНОЕ УСТРОЙСТВО | 2002 |
|
RU2231921C2 |
| US 20110293062 A1, 01.12.2011. | |||
Авторы
Даты
2018-01-24—Публикация
2017-05-03—Подача