Область техники, к которой относится изобретение
Настоящее изобретение относится, в общем, к области искусственного интеллекта, и в частности, к рекуррентным нейронным сетям (РНС, RNC), более конкретно, к новым методам байесовского разреживания для рекуррентных архитектур с гейтами.
Предшествующий уровень техники
1. Введение
Рекуррентные нейронные сети (РНС) входят в число наиболее мощных моделей для обработки естественного языка, распознавания речи, вопросно-ответных систем и других задач с последовательными данными ([3], [1], [8], [27], [23]). Для таких сложных задач, как машинный перевод или распознавание речи [1], в современных архитектурах РНС задействовано огромное количество параметров. Чтобы использовать эти модели на портативных устройствах с ограниченной памятью, например, смартфонах, желательно осуществлять сжатие модели. Высокие уровни сжатия также могут ускорить работу РНС. Кроме того, сжатие обеспечивает регуляризацию РНС и позволяет избежать переобучения.
Уменьшение размера РНС является важной и быстро развивающейся областью исследований. Существует множество методов сжатия РНС, основанных на специальных представлениях матриц весов ([25], [16]) или на разреживании методом прунинга [20], при котором веса РНС отсекаются по некоторому порогу. Narang и др. [20] выбирают такой порог, используя несколько гиперпараметров, которые управляют частотой, скоростью и продолжительностью удаления весов. Wen и др. [2] предложили отсекать веса в моделях РНС с долгой краткосрочной памятью (LSTM) группами, соответствующими каждому нейрону, что позволило ускорить проход вперед по сети.
Настоящее изобретение акцентировано на сжатии РНС посредством разреживания. Большинство методов, входящих в эту группу, являются эвристическими и требуют продолжительной настройки гиперпараметров.
В недавней работе Molchanov и др. [18] предложили теоретически обоснованный метод для разреживания полносвязных и сверточных сетей, основанный на вариационном дропауте. В [18] предложена вероятностная модель, в которой параметры, регулирующие разреженность, настраиваются автоматически во время обучения нейронной сети. Эта модель, названная "разреживающий вариационный дропаут" (Sparse Variational Dropout, далее SparseVD), позволяет получать чрезвычайно разреженные решения без значительного снижения качества работы итоговой модели. В [4] представлено развитие этого метода, позволяющее удалять группы весов из модели байесовским методом. Однако до настоящего времени еще не производилось исследования этих методов применительно к РНС.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Согласно настоящему изобретению предложен новый метод байесовского разреживания для рекуррентных архитектур с гейтами, в котором учитываются их рекуррентные особенности и механизм с гейтами. В данном изобретении удаляются нейроны из ассоциированной модели и гейты делаются константными, что обеспечивает не только сжатие сети, но и значительное ускорение прохода вперед. На дискриминативных задачах изобретение обеспечивает максимальное сжатие моделей РНС с долгой краткосрочной памятью (LSTM), так что сохраняется лишь небольшое количество входных и скрытых нейронов при незначительном снижении качества. Такую малую модель легко интерпретировать. Изобретение также было протестировано на задачах моделирования языка, где оно также обеспечило двукратное сжатие соответствующей модели лишь с небольшим снижением качества.
В предложенном решении сначала к рекуррентным нейронным сетям применяют SparseVD. Для учета специфики РНС авторы изобретения берут за основу некоторые аналитические выводы работы [6], в которой предлагается метод применения бинарного дропаута в РНС обоснованный с байесовской точки зрения. Однако применение SparseVD не обязательно приводит к групповой разреженности, при которой из модели удаляются не отдельные веса, а целые группы весов. В ряде недавних работ [14], [4] были предложены методы группового разреживания для полносвязных и сверточных сетей. Основываясь на них, авторы настоящего изобретения предлагают новый подход к групповому разреживанию рекуррентных архитектур с гейтами. Основная идея этого подхода состоит в том, что в модель вводится три уровня шума, и нижние уровни помогают верхним удалить группы весов из модели.
Согласно одному аспекту изобретения предложен компьютерно-реализуемый способ сжатия рекуррентной нейронной сети (РНС). Способ содержит выполнение разреживания в отношении весов РНС, причем разреживание содержит этапы, на которых: i) выполняют оптимизацию для получения апостериорного распределения весов, которое аппроксимируется вторым распределением, причем при оптимизации используют априорное распределение весов, представляющее собой первое распределение, и при оптимизации используется генерация весов из аппроксимированного апостериорного распределения, и ii) идентифицируют веса и/или одну или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС идентифицированные веса и/или удаляют из РНС идентифицированные группы весов. Первое распределение предпочтительно является полностью факторизованным лог-равномерным распределением, а второе распределение - полностью факторизованным нормальным распределением. Способ дополнительно включает в себя следующие этапы, на которых: вводят первые мультипликативные переменные для элементов набора возможных элементов (также именуемых в данном описании как словарь) входных последовательностей РНС; и выполняют разреживание в отношении первых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и на этапе ii) идентифицируют первые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС элементы упомянутой группы, которые ассоциированы с идентифицированными первыми мультипликативными переменными. Способ дополнительно включает в себя следующие операции: вводят вторые мультипликативные переменные для входных и скрытых нейронов РНС; и выполняют разреживание в отношении вторых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и на этапе ii) идентифицируют вторые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС входные и скрытые нейроны, ассоциированные с идентифицированными вторыми мультипликативными переменными.
Согласно предпочтительному варианту изобретения РНС имеет архитектуру с гейтами, и способ дополнительно включает в себя следующие операции: вводят третьи мультипликативные переменные для преактиваций гейтов РНС; и выполняют разреживание в отношении третьих мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и на этапе ii) делают гейт константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше заданного порога.
Согласно предпочтительному варианту изобретения архитектура с гейтами реализована в виде слоя LSTM сети РНС. Согласно предпочтительному варианту осуществления при введении третьих мультипликативных переменных дополнительно вводят третью мультипликативную переменную для преактивации информационного потока в слое LSTM, и на этапе ii) дополнительно делают информационный поток константным, если третья мультипликативная переменная, ассоциированная с данным информационным потоком, имеет ассоциированное значение меньше заданного порога.
Ассоциированное значение предпочтительно представляет собой отношение квадрата среднего к дисперсии. Заданный порог предпочтительно равен 0,05. Элементами упомянутого набора могут быть слова.
Данный способ применим для классификации текста или моделирования языка.
Согласно другому аспекту изобретения предложено устройство для сжатия РНС с архитектурой с гейтами. Устройство содержит: один или более процессоров, и один или более машиночитаемых носителей данных, на которых хранятся машиноисполняемые команды. Машиноисполняемые команды при их исполнении одним или несколькими процессорами предписывают одному или более процессорам: выполнять разреживание в отношении весов РНС, причем разреживание содержит: i) выполнение оптимизации для получения апостериорного распределения весов, которое аппроксимируется полностью факторизованным нормальным распределением, причем при оптимизации используют априорное распределение весов, представляющее собой факторизованное лог-равномерное распределение, и при оптимизации генерируют веса из аппроксимированного апостериорного распределения, и ii) идентификацию весов и/или одной или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаление из РНС идентифицированных весов и/или удаление из РНС идентифицированных групп весов; вводить первые мультипликативные переменные для элементов входного набора возможных элементов входных последовательностей РНС; выполнять разреживание в отношении первых мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и операция ii) содержит идентификацию первых мультипликативных переменных, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаление из РНС элементов упомянутого набора, которые ассоциированы с идентифицированными первыми мультипликативными переменными; вводить вторые мультипликативные переменные для входных и скрытых нейронов РНС; и выполнять разреживание в отношении вторых мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и операция ii) содержит идентификацию вторых мультипликативных переменных, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаление из РНС входных и скрытых нейронов, ассоциированных с идентифицированными вторыми мультипликативными переменными; вводить третьи мультипликативные переменные для преактиваций гейтов РНС; и выполнять разреживание в отношении третьих мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и в операции ii) гейт делается константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше заданного порога.
Согласно еще одному аспекту изобретения предложен один или несколько машиночитаемых носителей данных, на которых хранятся машиноисполняемые команды. Машиноисполняемые команды при их исполнении одним или более процессорами вычислительного устройства предписывают одному или более процессорам выполнять операции для сжатия РНС с архитектурой с гейтами, которая реализована в виде слоя LSTM сети РНС. Упомянутые операции включают в себя следующее: выполняют разреживание в отношении весов РНС, содержащее этапы, на которых: i) выполняют оптимизацию для получения апостериорного распределения весов, которое аппроксимируется полностью факторизованным нормальным распределением, причем при оптимизации используют априорное распределение весов, представляющее собой полностью факторизованное лог-равномерное распределение, и при оптимизации генерируют веса из аппроксимированного апостериорного распределения, и ii) идентифицируют веса и/или одну или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС идентифицированные веса и/или удаляют из РНС идентифицированные группы весов; вводят первые мультипликативные переменные для элементов входного набора возможных элементов входных последовательностей РНС; выполняют разреживание в отношении первых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и на этапе ii) идентифицируют первые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС элементы упомянутого набора, которые ассоциированы с идентифицированными первыми мультипликативными переменными; вводят вторые мультипликативные переменные для входных и скрытых нейронов РНС; и выполняют разреживание в отношении вторых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и на этапе ii) идентифицируют вторые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС входные и скрытые нейроны, ассоциированные с идентифицированными вторыми мультипликативными переменными; вводят третьи мультипликативные переменные для преактиваций гейтов и информационного потока в слое LSTM сети РНС; и выполняют разреживание в отношении третьих мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и на этапе ii) делают гейт константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше заданного порога, и делают информационный поток константным, если третья мультипликативная переменная, ассоциированная с данным информационным потоком, имеет ассоциированное значение меньше заданного порога.
Изобретательский вклад состоит в следующем: (i) SparseVD и его групповые модификации адаптированы к РНС и при этом объясняют специфику полученной модели, и (ii) модель обобщается посредством введения мультипликативных весов для слов для целенаправленного разреживания словаря, а также посредством введения мультипликативных весов для преактиваций гейтов и информационного потока, чтобы целенаправленно сделать гейт и составляющие информационного потока константными. Результаты показывают, что разреживающий вариационный дропаут обеспечивает очень высокий уровень разреженности в рекуррентных моделях без существенного снижения качества. Модели с дополнительным разреживанием словаря повышают степень сжатия в задачах классификации текста, но не улучшают также сильно результаты в задачах моделирования языка. В задачах классификации обеспечивается сжатие словаря в десятки раз и выбор слов можно интерпретировать.
Краткое описание чертежей
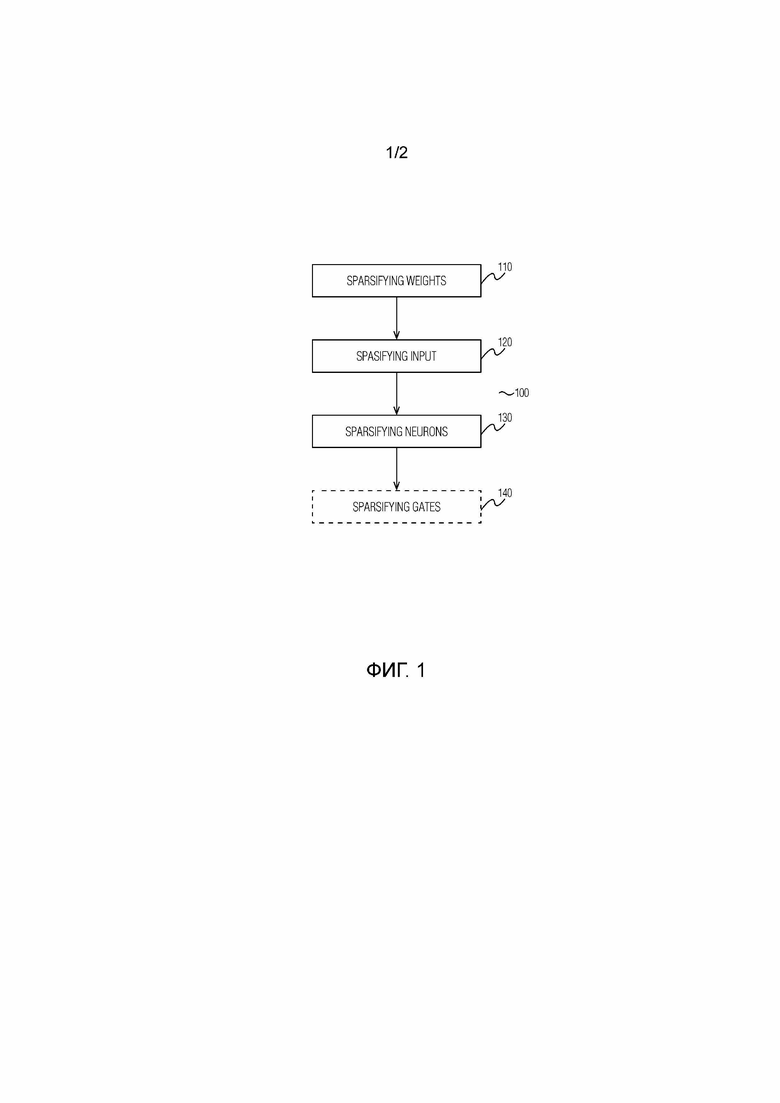
Фиг.1 - блок-схема последовательности операций способа сжатия рекуррентной нейронной сети согласно варианту осуществления настоящего изобретения;
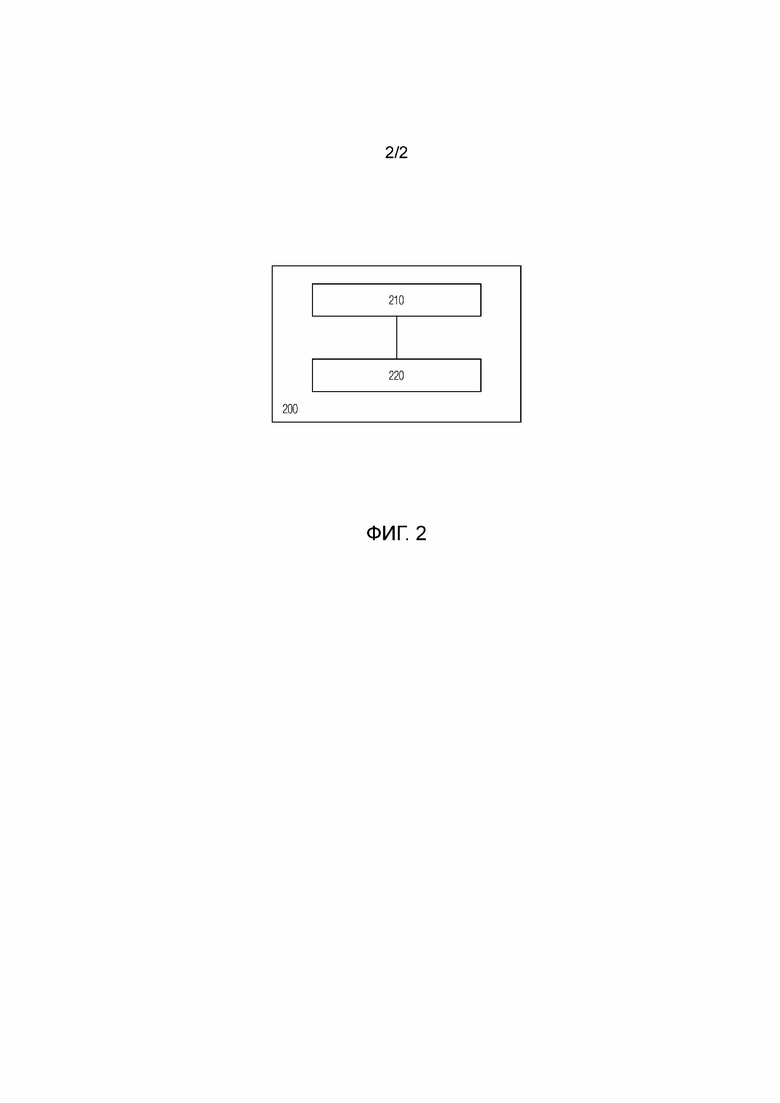
Фиг.2 - высокоуровневая блок-схема вычислительного устройства, в котором могут быть реализованы аспекты настоящего изобретения.
Подробное описание
Далее будут описаны аспекты, положенные в основу предложенного подхода, в том числе методы байесовского разреживания для сетей прямого распространения, а затем будет раскрыт сам подход.
2. Предисловие
2.1. Байесовские нейронные сети
Рассмотрим нейронную сеть с весами ω, моделирующую зависимость целевых переменных y={y1, …, ye} от соответствующих входных объектов X={x1, …, xe}. В байесовской нейронной сети веса ω рассматриваются как случайные переменные. При априорном распределении p(ω) осуществляется поиск апостериорного распределения p(ω|X,y), которое позволит найти ожидаемое целевое значение в процессе логического вывода. В случае нейронных сетей истинное апостериорное распределение обычно найти невозможно, но его можно аппроксимировать некоторым параметрическим распределением 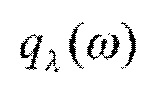 . Качество этой аппроксимации измеряется KL-дивергенцией
. Качество этой аппроксимации измеряется KL-дивергенцией 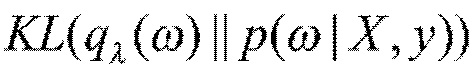 . Оптимальный параметр λ можно найти путем максимизации вариационной нижней оценки по λ:
. Оптимальный параметр λ можно найти путем максимизации вариационной нижней оценки по λ:
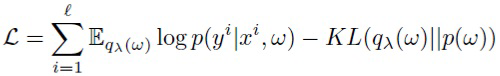 (1)
(1)
Ожидаемое значение логарифма правдоподобия в (1) обычно аппроксимируют путем генерации по методу Монте-Карло (МК). Чтобы получить несмещенную оценку MК, осуществляют параметризацию весов детерминированной функцией: ω=g(λ, ξ), где ξ сэмплируется из некоторого непараметрического распределения (трюк репараметризации [12]). Слагаемое KL-дивергенции в (1) действует как регуляризатор и обычно вычисляется или аппроксимируется аналитически.
Следует подчеркнуть, что основным преимуществом методов байесовского разрежения является то, что они имеют небольшое количество гиперпараметров по сравнению с методами, основанными на прунинге. Кроме того, они обеспечивают более высокий уровень разреженности ([18], [14], [4]).
2.2. Разреживающий вариационный дропаут
Дропаут ([24]) - это стандартный метод регуляризации нейронных сетей. Он подразумевает умножение входов каждого слоя на случайно генерируемый вектор шума. Обычно элементы этого вектора генерируются из распределения Бернулли или нормального распределения с параметрами, настраиваемыми с помощью кросс-валидации. В работе Kingma и др. ([13]) описана интерпретация гауссовского дропаута с байесовской точки зрения, которая позволяет настраивать параметры дропаута автоматически во время обучения модели. Позже эта модель была расширена на разреживание полносвязных и сверточных нейронных сетей и названа разреживающим вариационным дропаутом (SparseVD) ([18]).
Рассмотрим один полносвязный слой нейронной сети прямого распространения с входом размера n, выходом размера m и матрицей весов W. Согласно Kingma и др. ([13]), в SparseVD априорное распределение на весах является полностью факторизованным лог-равномерным распределением 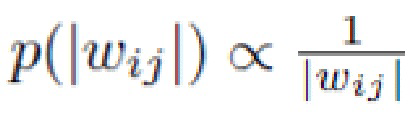 и поиск апостериорного распределения осуществляется в виде полностью факторизованного нормального распределения:
и поиск апостериорного распределения осуществляется в виде полностью факторизованного нормального распределения:
 (2)
(2)
Применение такой формы апостериорного распределения равносильно наложению мультипликативного ([13]) или аддитивного ([18]) нормального шума на веса следующим образом:
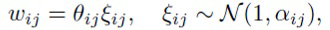 (3)
(3)
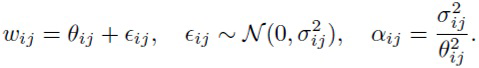 (4)
(4)
Представление (4) называется аддитивной репараметризацией ([18]). Она уменьшает дисперсию градиентов 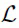 по θij. Кроме того, поскольку сумма нормальных распределений есть нормальное распределение с вычисляемыми параметрами, шум можно накладывать на преактивацию (входной вектор, умноженный на весовую матрицу W), а не на W. Этот прием называется трюком локальной репараметризации ([26], [13]), и он еще сильнее уменьшает дисперсию градиентов, а также повышает эффективность обучения.
по θij. Кроме того, поскольку сумма нормальных распределений есть нормальное распределение с вычисляемыми параметрами, шум можно накладывать на преактивацию (входной вектор, умноженный на весовую матрицу W), а не на W. Этот прием называется трюком локальной репараметризации ([26], [13]), и он еще сильнее уменьшает дисперсию градиентов, а также повышает эффективность обучения.
В SparseVD оптимизация вариационной нижней оценки (1) проводится по {Θ, log σ}. KL-дивергенция факторизуется по отдельным весам, и ее слагаемые зависят только от αij в силу специального выбора априорного распределения ([13]):
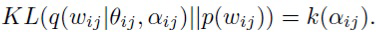 (5)
(5)
Каждое слагаемое можно аппроксимировать следующим образом ([18]):
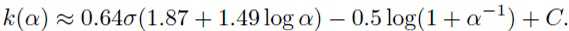 (6)
(6)
Слагаемое KL-дивергенции обеспечивает большие значения αij. Если αij → ∞ для веса wij, то апостериорное распределение этого веса является нормальным распределением с большой дисперсией, и для модели выгодно установить θij=0 и σij=αijθ2=0, чтобы избежать ошибок предсказания. В результате, апостериорное распределение wij приближается к центрированной в нуле дельта-функции, и данный вес не влияет на выход сети и может быть проигнорирован.
2.3. Разреживающий вариационный дропаут для группового разреживания
В (4) модель SparseVD была расширена, чтобы достичь группового разреживания. Под групповым разреживанием понимается, что веса делятся на несколько групп, и вместо отдельных весов удаляются эти группы. В качестве примера рассмотрим группы весов, соответствующие одному входному нейрону в полносвязном слое, и пронумеруем эти группы 1 … n.
Для достижения групповой разреженности авторы изобретения предлагают ввести дополнительные мультипликативные веса zi для каждой группы и настраивать эти веса в следующем виде:
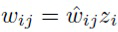
В полносвязном слое это эквивалентно наложению мультипликативных переменных на вход слоя. Поскольку главной задачей является обеспечение zi=0 и удаление нейрона из модели, используется та же пара априорного и апостериорного распределений для zi, что и в SparseVD:
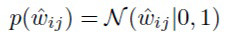
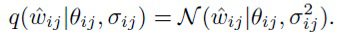
Для отдельных весов 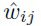 авторы изобретения используют стандартное нормальное априорное распределение и нормальное аппроксимированное апостериорное распределение с обучаемыми средним и дисперсией:
авторы изобретения используют стандартное нормальное априорное распределение и нормальное аппроксимированное апостериорное распределение с обучаемыми средним и дисперсией:
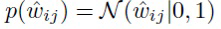
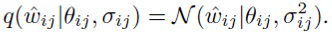
В этой модели априорное распределение на отдельные веса обеспечивает θij → 0, и это помогает приблизить групповые средние 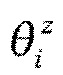 к нулю.
к нулю.
3. Предлагаемый метод
В данном разделе описан основной подход к байесовскому разреживанию рекуррентных нейронных сетей, а затем вводится метод группового байесовского разреживания рекуррентных сетей с долгой краткосрочной памятью (LSTM). В данном контексте LSTM рассматривается в силу того, что в настоящее время она является одной из наиболее популярных рекуррентных архитектур.
3.1. Байесовское разреживание рекуррентных нейронных сетей
Рекуррентная нейронная сеть принимает последовательность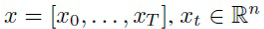 в качестве входа и преобразует ее в последовательность скрытых состояний:
в качестве входа и преобразует ее в последовательность скрытых состояний:
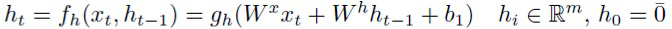 (7)
(7)
По всему описанию принято допущение, что выход РНС зависит только от последнего скрытого состояния:
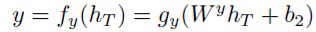 (8)
(8)
Здесь gh и gy - некоторые нелинейные функции. Однако все рассматриваемые далее методы можно применить к более сложным случаям, например, к языковой модели с несколькими выходами для одной входной последовательности (по одному выходу для каждого временного шага).
Для разреживания весов мы применяем SparseVD к РНС. Однако рекуррентные нейронные сети обладают некоторыми особенностями, которые необходимо учитывать при построении данной вероятностной модели.
В соответствии с Molchanov и др. ([18]) используется полностью факторизованное лог-равномерное априорное распределение, а апостериорное распределение аппроксимируется полностью факторизованным нормальным распределением на веса ω={Wx, Wh}:
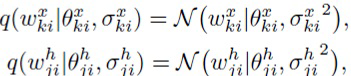 (9)
(9)
где 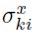 и
и 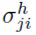 имеют то же самое значение, что и в аддитивной репараметризации (4).
имеют то же самое значение, что и в аддитивной репараметризации (4).
Для обучения этой модели максимизируется аппроксимация вариационной нижней оценки
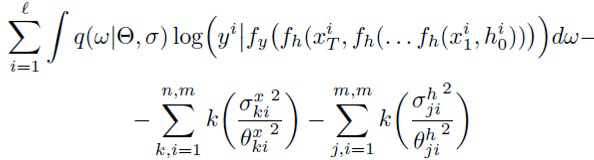 (10)
(10)
по параметрам {Θ, log σ} с использованием стохастических методов оптимизации по минибатчам. При этом рекуррентность в ожидаемом слагаемом логарифма правдоподобия разворачивается как в (7), а KL аппроксимируется с использованием (6). Интеграл в (10) оценивается одним сэмплом 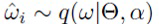 на каждый минибатч. Трюк репараметризации (для несмещенной интегральной оценки) и аддитивная репараметризация (для уменьшения дисперсии градиентов) используются для сэмплирования матриц весов "входной→скрытый" Wx и "скрытый→скрытый" Wh.
на каждый минибатч. Трюк репараметризации (для несмещенной интегральной оценки) и аддитивная репараметризация (для уменьшения дисперсии градиентов) используются для сэмплирования матриц весов "входной→скрытый" Wx и "скрытый→скрытый" Wh.
Трюк локальной репараметризации невозможно применить ни к матрице "скрытый→скрытый" Wh, ни к матрице "входной→скрытый" Wx. Поскольку применение трехмерного шума (две размерности для Wh и размер минибатча) слишком ресурсоемко, генерируется одна матрица шума для всех объектов в минибатче для эффективности:
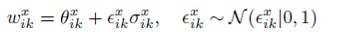 (11)
(11)
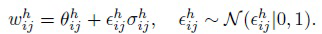 (12)
(12)
Полученный метод работает следующим образом: генерируют матрицы весов "входной→скрытый" и "скрытый→скрытый" (по одной на каждый минибатч), оптимизируют вариационную нижнюю оценку (10) по {Θ, log σ}, и для многих весов получают апостериорное распределение в виде δ-функции в нуле, поскольку KL-дивергенция обеспечивает разреженность. Эти веса можно затем безопасно удалить из модели.
В LSTM рассматривается та же пара априорного и апостериорного распределений для всех матриц "входной→скрытый" и "скрытый→скрытый", и все вычисления остаются такими же. Матрицы шума для соединений "входной→скрытый" и "скрытый→скрытый" генерируются отдельно для каждого гейта i, o, f и информационного потока g.
3.2. Групповое байесовское разреживание LSTM
В (4) имеются два уровня шума: шум на группы весов и шум на отдельные веса. Однако, популярные рекуррентные нейронные сети обычно имеют более сложную структуру с гейтами, которую можно использовать для достижения лучшего уровня сжатия и ускорения. В LSTM имеется внутренняя память ct и три гейта управляют обновлением, стиранием и выдачей информации из этой памяти:
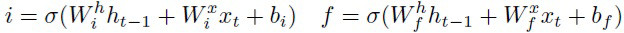 (13)
(13)
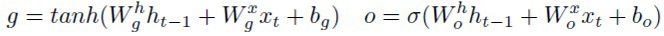 (14)
(14)
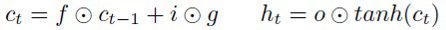 (15)
(15)
Для учета этой структуры с гейтами предлагается ввести промежуточный уровень шума в слой LSTM наряду с шумом на весах и на входных (zx) и скрытых нейронах (zh). В частности, мультипликативный шум zi, zf, z°, zg накладывается на преактивации каждого гейта и информационный поток g. Полученный слой LSTM выглядит следующим образом:
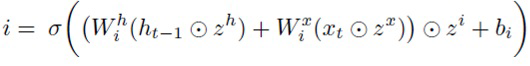 (16)
(16)
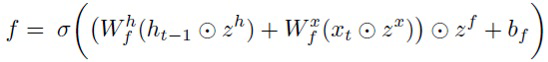 (17)
(17)
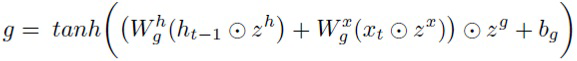 (18)
(18)
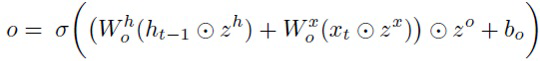 (19)
(19)
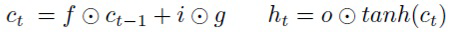 (20)
(20)
Эта модель эквивалентна наложению групповых мультипликативных переменных не только на столбцы весовых матриц (как в (4)), но и на их строки. Например, для матрицы 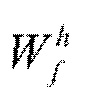 эта параметризация выглядит следующим образом:
эта параметризация выглядит следующим образом:
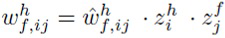
Формулы для остальных семи весовых матриц LSTM получают таким же образом.
Как и в (4), при приближении какой-либо компоненты zx или zh к нулю можно удалить из модели соответствующий нейрон. Но аналогичное свойство также имеет место и для гейтов: при приближении какой-либо компоненты zi, zf, z°, zg к нулю соответствующий гейт или компонента информационного потока становится константной. Это означает, что данный гейт не надо вычислять и проход вперед по LSTM ускоряется.
Кроме того, новый промежуточный уровень шума помогает разреживать входные и скрытые нейроны. Такая трехуровневая иерархия работает следующим образом: шум на отдельные веса позволяет обнулить значения отдельных весов, промежуточный уровень шума на гейты и информационный поток улучшает разреживание промежуточных переменных (гейтов и информационного потока), а последний уровень шума на нейроны помогает разреживать уже нейроны целиком.
В (4) авторы изобретения накладывают стандартное нормальное априорное распределение на отдельные веса. Например, модель для компонент 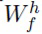 выглядит следующим образом:
выглядит следующим образом:
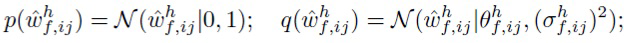 (21)
(21)
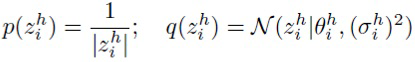 (22)
(22)
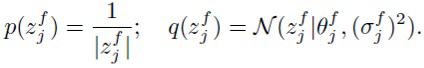 (23)
(23)
Авторы изобретения доказали экспериментально, что применение лог-равномерного априорного распределения вместо стандартного нормального для отдельных весов усиливает разреживание групповых переменных. Поэтому используется та же самая пара априорного и апостериорного распределений, что и в SparseVD для всех переменных.
Для обучения модели используется тот же процесс, что и в SparseVD для РНС, но в дополнение к генерации 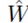 также генерируются мультипликативные групповые переменные.
также генерируются мультипликативные групповые переменные.
4. Байесовское сжатие для обработки естественного языка
В задачах обработки естественного языка большинство весов в РНС часто сосредоточены в первом слое, который связан со словарем, например, в слое представления (embedding layer). Однако для некоторых задач большинство слов не являются необходимыми для точных прогнозов. В предлагаемой модели авторы изобретения вводят мультипликативные веса для слов, чтобы осуществить разреживание словаря (см. подраздел 4.3). Эти мультипликативные веса обнуляются во время обучения и тем самым отфильтровываются соответствующие ненужные слова из модели. Это позволяет еще больше повысить уровень разреживания РНС.
4.1. Обозначения
В остальной части описания изобретения x=[x0,..., xT] является входной последовательностью, y - истинным выходом и 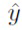 является результатом, предсказанным РНС (y и
является результатом, предсказанным РНС (y и 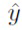 могут быть векторами, последовательностями векторов и т.д.). X, Y обозначает обучающую выборку {(x1, y1), …, (xN, yN)}. Все веса РНС, кроме смещений, обозначаются символом ω, а один вес (элемент любой весовой матрицы) обозначается wij. Следует отметить, что смещения здесь отделяются и обозначаются буквой B, потому что они не разреживаются.
могут быть векторами, последовательностями векторов и т.д.). X, Y обозначает обучающую выборку {(x1, y1), …, (xN, yN)}. Все веса РНС, кроме смещений, обозначаются символом ω, а один вес (элемент любой весовой матрицы) обозначается wij. Следует отметить, что смещения здесь отделяются и обозначаются буквой B, потому что они не разреживаются.
Для определенности, авторы изобретения иллюстрируют модель на примерной архитектуре для задачи моделирования языка, где y=[x1,..., xT]:
● слой представления:  ;
;
● рекуррентный слой: 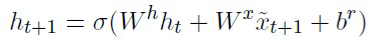 ;
;
● полносвязный слой: 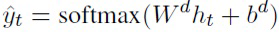 .
.
В этом примере 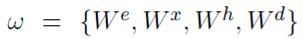 , B={br, bd}. Однако данную модель можно непосредственно применить к любой рекуррентной архитектуре.
, B={br, bd}. Однако данную модель можно непосредственно применить к любой рекуррентной архитектуре.
4.2. Разреживающий вариационный дропаут для РНС
Как отмечалось выше, следуя [4], [18], авторы изобретения накладывают полностью факторизованное лог-равномерное распределение на веса:
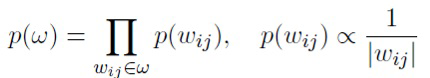 ,
,
и аппроксимируют апостериорное распределение полностью факторизованным нормальным распределением:
 .
.
Задача аппроксимации апостериорного распределения
minθ,σ,B KL(q(ω|θ, σ)||p(ω|X, Y, i)) эквивалентна оптимизации вариационной нижней оценки ([18]):
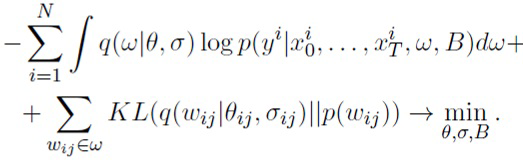 (24)
(24)
Здесь первое слагаемое, специфическая для задачи функция потерь, аппроксимируется с использованием одного сэмпла из q(ω|θ, σ). Второе слагаемое является регуляризатором, который делает апостериорное распределение более похожим на априорное и обеспечивает разреженность. Упомянутый регуляризатор можно с высокой точностью аппроксимировать аналитически
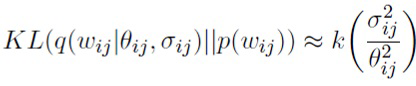 , (25)
, (25)
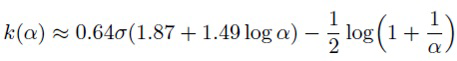 .
.
Чтобы получить несмещенную оценку интеграла, генерацию из апостериорного распределения выполняют с использованием трюка репараметризации [12]:
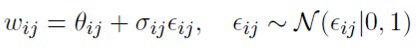 . (26)
. (26)
Важным отличием РНС от сетей прямого распространения является использование одних и тех же весов в различных временных шагах. Таким образом, один и тот же сэмпл весов следует использовать для каждого временного шага t при вычислении вероятности 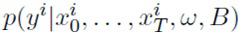 ([6], [7], [5]).
([6], [7], [5]).
Kingma и др. [13], Molchanov и др. [18] также используют трюк локальной репараметризации (ТЛР, LRT), в котором производится сэмплирование преактиваций вместо отдельных весов. Например,
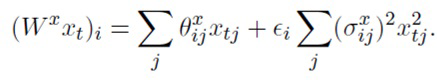 .
.
Связанное сэмплирование весов делает ТЛР неприменимым к весовым матрицам, которые используются более чем в одном временном шаге в РНС.
Для матрицы "скрытый→скрытый" Wh линейная комбинация (Whht) не распределена нормально, так как ht зависит от Wh из предыдущего временного шага. В результате, правило о сумме независимых нормальных распределений с постоянными коэффициентами неприменимо. На практике сеть с ТЛР на весах "скрытый→скрытый" невозможно обучить должным образом.
Для матрицы "входной→скрытый" Wx линейная комбинация (Wxxt) распределена нормально. Однако сэмплирование одной и той же Wx для всех временных шагов не эквивалентно сэмплированию одного и того же шума 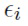 для преактиваций для всех временных шагов. Один и тот же сэмпл Wx соответствует различным сэмплам шума
для преактиваций для всех временных шагов. Один и тот же сэмпл Wx соответствует различным сэмплам шума 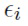 на разных временных шагах из-за разных xt. Следовательно, теоретически ТЛР здесь ннеприменим. На практике сети с ТЛР на весах "входной→скрытый" могут давать похожие результаты, и в некоторых экспериментах они даже сходятся немного быстрее.
на разных временных шагах из-за разных xt. Следовательно, теоретически ТЛР здесь ннеприменим. На практике сети с ТЛР на весах "входной→скрытый" могут давать похожие результаты, и в некоторых экспериментах они даже сходятся немного быстрее.
Поскольку процедура обучения эффективна только с двумерным тензором шума, авторы изобретения предлагают генерировать шум на веса на каждом минибатче, а не на каждом отдельном объекте.
Обобщая вышесказанное, процедура обучения выглядит следующим образом. Для выполнения прохода вперед для минибатча авторы изобретения сначала генерируют все веса ω, следуя (26), а затем применяют РНС как обычно. Затем вычисляются градиенты (24) относительно θ, log σ, B. На этапе тестирования используются средние веса θ [18]. Регуляризатор (25) приводит к приближению большинства компонент θ к нулю, и веса разреживаются. Точнее сказать, удаляются веса с низким отношением сигнал/шум 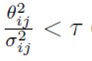 [18].
[18].
4.3. Мультипликативные веса для разреживания словаря
Одним из преимуществ байесовского разреживания является легкое обобщение для разреживания любой группы весов, которое не усложняет процедуру обучения ([4]). Для этого следует ввести общий мультипликативный вес для каждой группы, и удаление этого мультипликативного веса будет означать удаление соответствующей группы. Авторы изобретения используют данный подход для разреживания словаря.
В частности, авторы изобретения вводят мультипликативные вероятностные веса 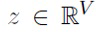 для слов в словаре (здесь V - размер словаря). Проход вперед с z выглядит следующим образом:
для слов в словаре (здесь V - размер словаря). Проход вперед с z выглядит следующим образом:
1. сэмплируют вектор zi из текущей аппроксимации апостериорного распределения для каждой входной последовательности xi из минибатча;
2. умножают каждый элемент xti (закодированный вектором из 0 и 1 с одной 1 - one-hot) из последовательности xi на zi (здесь xi and zi V-размерные);
3. продолжают проход вперед как обычно.
Авторы изобретения работают с z так же, как и с другими весами W: используется лог-равномерное априорное распределение, а апостериорное распределение аппроксимируется с помощью полностью факторизованного нормального распределения, имеющего обучаемое среднее и дисперсию. Однако, поскольку z является одномерным вектором, его можно генерировать отдельно для каждого объекта в минибатче, чтобы уменьшить дисперсию градиентов. После обучения элементы z с низким отношением сигнал/шум обрезаются, и затем соответствующие слова из словаря не используются, а столбцы весов удаляются из представления или весовых матриц "входной→скрытый".
4.4. Эксперименты
Авторы изобретения провели эксперименты с архитектурой LSTM для двух типов задач: классификация текста и моделирование языка. Здесь приводится сравнение трех моделей: основной модели без какой-либо регуляризации, модели SparseVD и модели SparseVD с мультипликативными весами для разреживания словаря (SparseVD-Voc) согласно настоящему изобретению.
Чтобы измерить уровень разреженности этих моделей, рассчитывают степень сжатия отдельных весов как |w|/|w≠0|. Разреживание весов может привести не только к сжатию, но также и к ускорению РНС в результате групповой разреженности. Таким образом, авторы изобретения сообщают количество оставшихся нейронов во всех слоях: входном слое (словарь), слое представления и рекуррентном слое. Чтобы вычислить это число для слоя словаря в SparseVD-Voc, используются введенные переменные zv. Для всех остальных слоев в SparseVD и SparseVD-Voc нейрон отбрасывается, если удаляются все веса, связанные с этим нейроном.
В данном случае сети оптимизируются с использованием [11]. Базовые сети переобучаются для всех анализируемых задач, поэтому авторы изобретения представляют для них результаты с ранним остановом. Для всех разреживаемых весов log σ инициализировался как -3. Веса с отношением сигнал-шум менее τ=0,05 удаляются. Более подробная информация об организации эксперимента представлена в Приложении А.
4.4.1. Классификация текста
Предложенный подход, отвечающий настоящему изобретению, оценивался на двух стандартных наборах данных для классификации текста: набор данных IMDb ([9]) для двухклассовой классификации и набор данных AGNews ([10]) для четырехклассовой классификации. Авторы изобретения выделили 15% и 5% обучающих данных для целей проверки, соответственно. Для обоих наборов данных использовался словарь из 20000 наиболее часто встречающихся слов.
Авторы изобретения использовали сети с одним слоем представления из 300 единиц, одним слоем LSTM из 128/512 скрытых единиц для IMDb/AGNews и, наконец, полносвязным слоем, применявшемся к последнему выходу LSTM. Слой представления инициализировался word2vec ([15])/GloVe ([17]), а модели SparseVD и SparseVD-Voc обучались 800/150 эпох на IMDb/AGNews.
Результаты представлены в Таблице 1. SparseVD приводит к очень высокой степени сжатия без значительного снижения качества. SparseVD-Voc повышает степени сжатия все еще без значительного снижения точности. Такие высокие степени сжатия достигаются, главным образом, благодаря разреживанию словаря: для классификации текстов необходимо прочесть только некоторые важные слова из них. Остающиеся после разреживания слова в предложенных моделях преимущественно являются интерпретируемыми для данной задачи (см. Приложение B со списком остальных слов для IMBb).
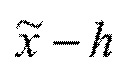
SparseVD
SparceVD-voc
85.1
83.6
1135х
12985х
4611
292
16-17
1-8
SparseVD
SparceVD-voc
88.8
89.2
322х
469х
5727
2444
179-56
127-32
4.4.2. Моделирование языка
Авторы изобретения оценили предложенные модели на задаче моделирования языка на уровне знаков и на уровне слов на корпусе Penn Treebank ([19]) в соответствии с делением корпуса на обучающий/валидационный/тестовый по работе [21]. Этот набор данных имеет словарь из 50 знаков или 10000 слов.
Для решения задач на уровнях знаков/слов авторы изобретения использовали сети с одним слоем LSTM из 1000/256 скрытых единиц и полносвязный слой с активацией softmax для прогнозирования следующего знака или слова. Модели SparseVD и SparseVD-Voc обучались 250/150 эпох на задачах на уровне знаков/на уровне слов.
Результаты представлены в Таблице 2. Для получения этих результатов применяли ТЛР на последнем полносвязном слое. В экспериментах с моделированием языка ТЛР на последнем слое ускорил обучение без ухудшения конечного результата. При этом не были достигнуты такие экстремальные степени сжатия, как в предыдущем эксперименте, однако способность сжимать модели в несколько раз с достижением лучшего качества относительно исходного уровня все еще сохраняется благодаря эффекту регуляризации SparseVD. Входной словарь не разредился в задаче на уровне знаков, потому что имеется всего 50 знаков и все они имеют значение. В задаче на уровне слов было отброшено более половины слов. Однако, поскольку в моделировании языка важны почти все слова, разреживание словаря затрудняет задачу для сети и приводит к снижению качества и общего сжатия (сеть требует более сложной динамики в рекуррентном слое).
верный
bits-per-char
SparseVD
SparceVD-voc
1.472
1.4584
1.429
1.4165
4.2х
3.53х
50
48
431
510
Перплек
сивность
SparseVD
SparceVD-voc
115.0
126.3
109.0
120.6
14.0х
11.1х
9985
4353
153
207
A. Экспериментальная модель
Инициализация для классификации текста. Весовые матрицы скрытый→скрытый Wh инициализируются ортогонально, а все остальные матрицы инициализируются равномерно с использованием метода [22].
Сети обучались с использованием минибатчей размера 128 и скоростью обучения 0,0005.
Инициализация для моделирования языка. Все весовые матрицы сетей инициализировались ортогонально, и все смещения инициализировались нулями. Исходные значения скрытых элементов и элементов памяти LSTM не являются обучаемыми и равны нулю.
Для задачи на уровне знаков сети обучались на неперекрывающихся последовательностях длиной в 100 знаков в минибатчах размером 64 с использованием скорости обучения 0,002 и отсечения градиентов с порогом 1.
Для задачи на уровне слов сети разворачивались на 35 шагов. Конечные скрытые состояния текущего минибатча использовались в качестве исходного скрытого состояния последующего минибатча (последовательные минибатчи последовательно покрывают обучающую выборку). Размер каждого минибатча равен 32. Эти модели обучались с использованием скорости обучения 0,002 и отсечения градиентов с порогом 10.
B. Список оставшихся слов в IMDB
SparseVD с мультипликативными весами сохранил следующие слова в задаче IMDB (отсортированные по нисходящей частоте во всем корпусе):
start, oov, and, to, is, br, in, it, this, was, film, t, you, not, have, It, just, good, very, would, story, if, only, see, even, no, were, my, much, well, bad, will, great, first, most, make, also, could, too, any, then, seen, plot, acting, life, over, off, did, love, best, better, i, If, still, man, some- thing, m, re, thing, years, old, makes, director, nothing, seems, pretty, enough, own, original, world, series, young, us, right, always, isn, least, interesting, bit, both, script, minutes, making, 2, performance, might, far, anything, guy, She, am, away, woman, fun, played, worst, trying, looks, especially, book, DVD, reason, money, actor, shows, job, 1, someone, true, wife, beautiful, left, idea, half, excellent, 3, nice, fan, let, rest, poor, low, try, classic, production, boring, wrong, enjoy, mean, No, instead, awful, stupid, remember, wonderful, often, become, terrible, others, dialogue, perfect, liked, supposed, entertaining, waste, His, problem, Then, worse, definitely, 4, seemed, lives, example, care, loved, Why, tries, guess, genre, history, enjoyed, heart, amazing, starts, town, favorite, car, today, decent, brilliant, horrible, slow, kill, attempt, lack, interest, strong, chance, wouldn, sometimes, except, looked, crap, highly, wonder, annoying, Oh, simple, reality, gore, ridiculous, hilarious, talking, female, episodes, body, saying, running, save, disappointed, 7, 8, OK, word, thriller, Jack, silly, cheap, Oscar, predictable, enjoyable, moving, Un- fortunately, surprised, release, effort, 9, none, dull, bunch, comments, realistic, fantastic, weak, atmosphere, apparently, premise, greatest, believable, lame, poorly, NOT, superb, badly, mess, perfectly, unique, joke, fails, masterpiece, sorry, nudity, flat, Good, dumb, Great, D, wasted, unless, bored, Tony, language, incredible, pointless, avoid, trash, failed, fake, Very, Stewart, awesome, garbage, pathetic, genius, glad, neither, laughable, beautifully, excuse, disappointing, disappointment, outstanding, stunning, noir, lacks, gem, F, redeeming, thin, absurd, Jesus, blame, rubbish, unfunny, Avoid, irritating, dreadful, skip, racist, Highly, MST3K.
В заключение следует отметить, что способ (100) сжатия РНС согласно настоящему изобретению описывается со ссылками на Фиг. 1. Предполагается, что для ввода РНС обеспечивается набор возможных элементов входных последовательностей. Элементами этого набора могут быть слова.
На этапе 110 выполняется разреживание весов РНС.
Это разреживание включает в себя выполнение оптимизации для получения апостериорного распределения весов, которое аппроксимируется вторым распределением. Оптимизация использует априорное распределение весов, являющееся первым распределением. В соответствии с вышесказанным, в качестве первого распределения предпочтительно используется полностью факторизованное лог-равномерное распределение, а в качестве второго распределения предпочтительно используется полностью факторизованное нормальное распределение. Тем не менее, специалисту будет понятно, что, в рассматриваемом контексте могут использоваться другие виды подходящих распределений. Оптимизация включает в себя генерацию весов из аппроксимированного апостериорного распределения. Следует отметить, что каждый сэмпл веса идентичен для любого временного шага в одной входной последовательности.
Разреживание на этапе 110 дополнительно включает в себя идентифицирование весов и/или одной или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога. После этого идентифицированные веса удаляются из РНС, и/или идентифицированные группы весов удаляются из РНС.
Как отмечалось выше, в качестве упомянутого ассоциированного значения предпочтительно используется отношение квадрата среднего к дисперсии, а заданный порог предпочтительно установлен на 0,05. Тем не менее, специалисту будет понятно, что в рассматриваемом контексте могут использоваться другие пороги и значения.
На этапе 120 вводятся первые мультипликативные переменные для элементов входного набора РНС, как было описано выше. Затем, на этапе 120 к первым мультипликативным переменным применяется разреживание, подобное разреживанию на этапе 110. В частности, на этапе 120 выполняется вышеупомянутая оптимизация с использованием упомянутой пары априорного и аппроксимированного апостериорного распределения для первых мультипликативных переменных; после этого идентифицируются первые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и элементы этого набора, ассоциированные с идентифицированными первыми мультипликативными переменными, удаляются из РНС на этапе 120.
На этапе 130 вводятся вторые мультипликативные переменные для входных и скрытых нейронов РНС, как обсуждалось выше, и к этим мультипликативным переменным применяется разреживание, аналогичное разреживанию на этапе 110. В частности, на этапе 130 выполняют вышеупомянутую оптимизацию, используя упомянутую пару априорного и аппроксимированного апостериорного распределений для вторых мультипликативных переменных. Затем, на этапе 130 идентифицируют вторые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше заданного порога, и затем на этапе 130 удаляют из РНС входные и скрытые нейроны РНС, которые ассоциированы с идентифицированными переменными.
В соответствии с вышеприведенным обсуждением, РНС может иметь архитектуру с гейтами, и такая архитектура с гейтами может быть реализована в виде слоя LSTM сети РНС. Тем не менее, здесь следует подчеркнуть, что предлагаемый подход, в принципе, применим к РНС без гейтов.
Если РНС имеет архитектуру с гейтами (например, на основе LSTM), то предложенный способ 100 предпочтительно дополнительно содержит этап 104 (обозначенный пунктирной линией на Фиг. 1).
На этапе 140 вводятся третьи мультипликативные переменные для преактиваций гейтов и информационного потока в слое LSTM сети РНС, как обсуждалось выше, и выполняется разреживание, аналогичное разреживанию на этапе 110, для этих третьих мультипликативных переменных. В частности, на этапе 140 выполняется вышеупомянутая оптимизация с использованием упомянутой пары априорного и аппроксимированного апостериорного распределений для третьих мультипликативных переменных. Затем, на этапе 140 любой гейт делается константным, если ассоциированная с ним третья мультипликативная переменная имеет ассоциированное значение меньше заданного порога. Аналогичным образом, информационный поток делается константным на этапе 140, если ассоциированная с ним третья мультипликативная переменная имеет ассоциированное значение меньше заданного порога.
Как отмечалось выше, предложенный способ можно эффективно применять к задачам классификации текста или моделирования языка. Тем не менее, следует понимать, что он также применим к различным другим задачам, для которых используются рекуррентные нейронные сети, в частности, к машинному переводу и распознаванию речи. В соответствии с вышесказанным, изобретение было протестировано на задачах моделирования языка, где предложенные методы обеспечили двукратное сжатие соответствующей модели с незначительным снижением качества. Следовательно, можно ожидать значительное сжатие и ускорение моделей для других подобных задач.
Кроме того, специалисту будет понятно, что описанные выше способы согласно изобретению могут быть реализованы на практике с помощью обычного программного обеспечения и компьютерных технологий. В частности, на Фиг. 2 показана высокоуровневая блок-схема обычного вычислительного устройства (200), в котором могут быть реализованы аспекты настоящего изобретения. Вычислительное устройство 200 содержит блок 210 обработки данных и блок 220 хранения данных, подключенный к блоку 210 обработки данных. Блок 210 обработки данных обычно содержит один или несколько процессоров (ЦПУ), которые могут быть универсальными или специализированными, выпускаемыми серийно или изготовленными на заказ процессорами. Блок 220 хранения данных обычно содержит различные машиночитаемые носители и/или запоминающие устройства, как энергонезависимые (например, ПЗУ, жесткие диски, флэш-накопители и т.п.), так и энергозависимые (например, различные виды ОЗУ и т.п.).
В контексте настоящего изобретения блок 220 хранения данных содержит машиночитаемые носители данных с записанным на них соответствующим программным обеспечением. Программное обеспечение содержит машиноисполняемые команды, которые при их исполнении блоком 210 обработки данных предписывают ему выполнять способ согласно изобретению. Такое программное обеспечение может быть соответственно разработано и внедрено с использованием известных технологий и сред программирования.
Специалисту будет понятно, что вычислительное устройство 200, задействованное в реализации изобретения, включает в себя также другое известное оборудование, такое как устройства ввода/вывода, интерфейсы связи и т. д., а также базовое программное обеспечение, такое как операционная система, пакеты протоколов, драйверы и т. д., которые могут быть как серийными, так и заказными. Компьютерное устройство 200 может быть выполнено с возможностью связи с другими вычислительными устройствами, инфраструктурами и сетями с помощью известных технологий проводной и/или беспроводной связи.
Следует понимать, что проиллюстрированные варианты осуществления изобретения являются всего лишь предпочтительными, но не единственными возможными примерами изобретения. Напротив, объем изобретения определяется нижеследующей формулой изобретения и эквивалентами. Раскрытие вместе с перечисленными ниже документами включено в данное описание посредством ссылок.
5. Процитированные публикации
[1] Amodei, Dario, Ananthanarayanan, Sundaram, Anubhai, Rishita, and et al. Deep speech 2: End-to-end speech recognition in english and mandarin. In Proceedings of The 33rd International Conference on Machine Learning, 2016.
[2] Wei Wen, Yuxiong He, Samyam Rajbhandari, Minjia Zhang, Wenhan Wang, Fang Liu, Bin Hu, Yiran Chen, and Hai Li. 2018. Learning intrinsic sparse structures within long short-term memory. In International Conference on Learning Representations.
[3] Chan, William, Jaitly, Navdeep, Le, Quoc V., and Vinyals, Oriol. Listen, attend and spell: A neural network for large vocabulary conversational speech recognition. In ICASSP, 2016.
[4] Christos Louizos, Karen Ullrich, Max Welling. Bayesian compression for deep learning. In arXiv preprint arXiv:1705.08665, 2017.
[5] Meire Fortunato, Charles Blundell, and Oriol Vinyals. 2017. Bayesian recurrent neural networks. Computing Research Repository, arXiv:1704.02798.
[6] Gal, Yarin and Ghahramani, Zoubin. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, 2016.
[7] Gal, Yarin and Ghahramani, Zoubin. A theoretically grounded application of dropout in recurrent neural networks. In Advances in Neural Information Processing Systems 29 (NIPS), 2016.
[8] Ha, David, Dai, Andrew, and Le, Quoc V. Hypernetworks. In Proceedings of the International Conference on Learning Representations (ICLR), 2017.
[9] Andrew L. Maas, Raymond E. Daly, Peter T. Pham, Dan Huang, Andrew Y. Ng, and Christopher Potts. 2011. Learning word vectors for sentiment analysis. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies - Volume 1, HLT '11, pp. 142-150, Stroudsburg, PA, USA. Association for Computational Linguistics.
[10] X. Zhang, J. Zhao, and Y. LeCun. 2015. Character-level convolutional networks for text classification. In Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems (NIPS).
[11] Kingma, Diederik P. and Ba, Jimmy. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, 2015.
[12] Kingma, Diederik P. and Welling, Max. Auto-encoding variational bayes. CoRR, abs/1312.6114, 2013.
[13] Kingma, Diederik P., Salimans, Tim, and Welling, Max. Variational dropout and the local reparameterization trick. CoRR, abs/1506.02557, 2015.
[14] Kirill Neklyudov, Dmitry Molchanov, Arsenii Ashukha, Dmitry Vetrov. Structured bayesian pruning via log-normal multiplicative noise. In arXiv preprint arXiv:1705.07283, 2017.
[15] Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26, pp. 3111-3119.
[16] Le, Quoc V., Jaitly, Navdeep, and Hinton, Geoffrey E. A simple way to initialize recurrent networks of rectified linear units. CoRR, abs/1504.00941, 2015.
[17] Jeffrey Pennington, Richard Socher, and Christopher D Manning. 2014. Glove: Global vectors for word representation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, vol. 14, pp. 1532-1543.
[18] Molchanov, Dmitry, Ashukha, Arsenii, and Vetrov, Dmitry. Variational dropout sparsifies deep neural networks. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, 2017.
[19] Mitchell P. Marcus, Mary Ann Marcinkiewicz, and Beatrice Santorini. 1993. Building a large annotated corpus of English: The penn treebank. Comput. Linguist., 19(2):313-330.
[20] Narang, Sharan, Diamos, Gregory F., Sengupta, Shubho, and Elsen, Erich. Exploring sparsity in recurrent neural networks. CoRR, abs/1704.05119, 2017.
[21] T. Mikolov, S. Kombrink, L. Burget, J. Cernocky, and S. Khudanpur. 2011. Extensions of recurrent neural network language model. In 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 5528-5531.
[22] Xavier Glorot and Yoshua Bengio. 2010. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, volume 9 of Proceedings of Machine Learning Research, pp. 249-256, Chia Laguna Resort, Sardinia, Italy. Proceedings of Machine Learning Research.
[23] Ren, Mengye, Kiros, Ryan, and Zemel, Richard S. Exploring models and data for image question answering. In Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems, 2015.
[24] Srivastava, Nitish. Improving neural networks with dropout. PhD thesis, University of Toronto, 2013.
[25] Tjandra, Andros, Sakti, Sakriani, and Nakamura, Satoshi. Compressing recurrent neural network with tensor train. CoRR, abs/1705.08052, 2017.
[26] Wang, Sida and Manning, Christopher. Fast dropout training. In Proceedings of the 30th International Conference on Machine Learning, 2013.
[27] Wu, Yonghui, Schuster, Mike, Chen, Zhifeng, and et al. Google's neural machine translation system: Bridging the gap between human and machine translation. CoRR, abs/1609.08144, 2016.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОТЛАДКИ ОБУЧЕННОЙ РЕКУРРЕНТНОЙ НЕЙРОННОЙ СЕТИ | 2019 |
|
RU2715024C1 |
| АДАПТИВНОЕ УЛУЧШЕНИЕ АУДИО ДЛЯ РАСПОЗНАВАНИЯ МНОГОКАНАЛЬНОЙ РЕЧИ | 2016 |
|
RU2698153C1 |
| СПОСОБ И СИСТЕМА РЕГУЛИРОВАНИЯ ТЕМПЕРАТУРЫ ЛЕЗВИЯ УЛЬТРАЗВУКОВОГО СКАЛЬПЕЛЯ НА ОСНОВЕ МОДЕЛИ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ТЕМПЕРАТУРЫ | 2022 |
|
RU2829310C2 |
| СПОСОБ РАСЧЕТА КРЕДИТНОГО РЕЙТИНГА КЛИЕНТА | 2019 |
|
RU2723448C1 |
| Способ синтеза двумерного изображения сцены, просматриваемой с требуемой точки обзора, и электронное вычислительное устройство для его реализации | 2020 |
|
RU2749749C1 |
| СПОСОБ И УСТРОЙСТВО БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2018 |
|
RU2685767C1 |
| СПОСОБ ПОЛУЧЕНИЯ НИЗКОРАЗМЕРНЫХ ЧИСЛОВЫХ ПРЕДСТАВЛЕНИЙ ПОСЛЕДОВАТЕЛЬНОСТЕЙ СОБЫТИЙ | 2020 |
|
RU2741742C1 |
| АНАЛОГОВАЯ АППАРАТНАЯ РЕАЛИЗАЦИЯ НЕЙРОННЫХ СЕТЕЙ | 2020 |
|
RU2796649C2 |
| ТЕМАТИЧЕСКИЕ МОДЕЛИ С АПРИОРНЫМИ ПАРАМЕТРАМИ ТОНАЛЬНОСТИ НА ОСНОВЕ РАСПРЕДЕЛЕННЫХ ПРЕДСТАВЛЕНИЙ | 2018 |
|
RU2719463C1 |
| РАСПОЗНАВАНИЕ СОБЫТИЙ НА ФОТОГРАФИЯХ С АВТОМАТИЧЕСКИМ ВЫДЕЛЕНИЕМ АЛЬБОМОВ | 2020 |
|
RU2742602C1 |
Изобретение относится к области искусственного интеллекта, и в частности, к рекуррентным нейронным сетям (РНС). Техническим результатом является повышение степени сжатия. Предложен новый метод байесовского разреживания для рекуррентных архитектур с гейтами, в котором учитываются их рекуррентные особенности и механизм с гейтами. В предложенном методе удаляются нейроны из ассоциированной модели и гейты делаются константными, что обеспечивает не только сжатие сети, но и значительное ускорение прохода вперед. На дискриминативных задачах данный метод обеспечивает максимальное сжатие LSTM, так что остается лишь небольшое количество входных и скрытых нейронов при незначительном снижении качества. Такую малую модель легко интерпретировать. 3 н. и 16 з.п. ф-лы, 2 ил., 2 табл.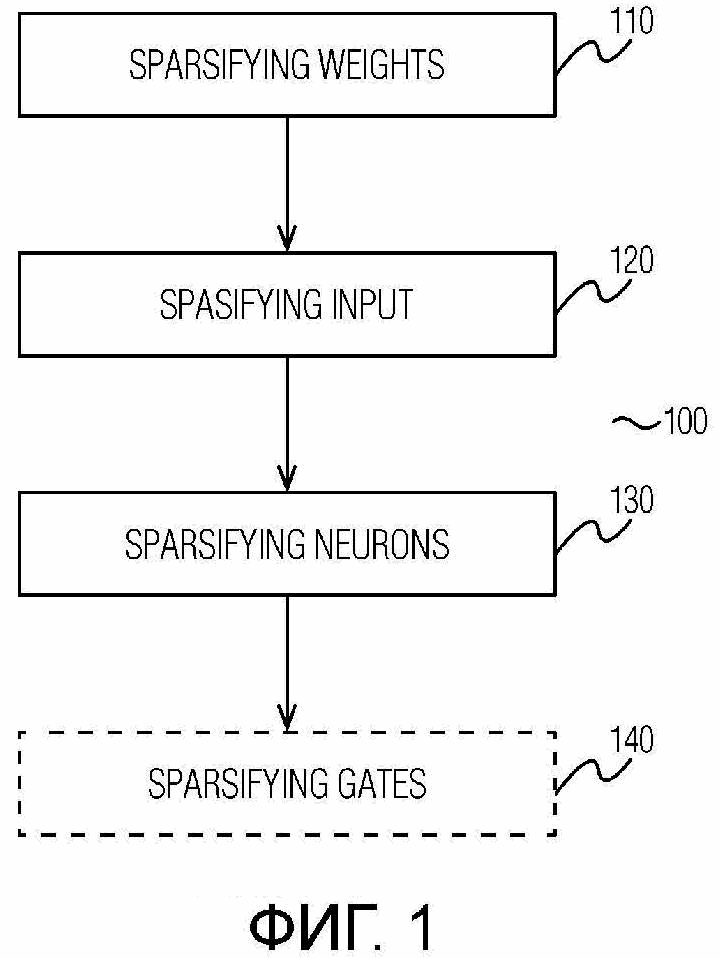
1. Компьютерно-реализуемый способ сжатия рекуррентной нейронной сети (РНС), содержащий этапы, на которых:
выполняют разреживание в отношении весов РНС, причем разреживание содержит этапы, на которых:
i) выполняют оптимизацию для получения апостериорного распределения весов, при этом апостериорное распределение весов аппроксимируется вторым распределением, причем при оптимизации используют априорное распределение весов, представляющее собой первое распределение, и при оптимизации генерируют веса из аппроксимированного апостериорного распределения, и
ii) идентифицируют веса и/или одну или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС идентифицированные веса и/или удаляют из РНС идентифицированные группы весов;
вводят первые мультипликативные переменные для элементов входного набора возможных элементов входных последовательностей РНС;
выполняют разреживание в отношении первых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и на этапе ii) идентифицируют первые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаляют из РНС элементы упомянутой группы, которые ассоциированы с идентифицированными первыми мультипликативными переменными;
вводят вторые мультипликативные переменные для входных и скрытых нейронов РНС; и
выполняют разреживание в отношении вторых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и на этапе ii) идентифицируют вторые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаляют из РНС входные и скрытые нейроны, ассоциированные с идентифицированными вторыми мультипликативными переменными.
2. Способ по п.1, в котором первое распределение является полностью факторизованным лог-равномерным распределением, а второе распределение - полностью факторизованным нормальным распределением.
3. Способ по п.1, в котором каждая выборка веса идентична для любого временного шага в одной входной последовательности.
4. Способ по п.1, в котором РНС имеет архитектуру с гейтами, при этом способ дополнительно содержит этапы, на которых:
вводят третьи мультипликативные переменные для преактиваций гейтов РНС;
выполняют разреживание в отношении третьих мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и на этапе ii) делают гейт константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше упомянутого заданного порога.
5. Способ по п.4, в котором архитектура с гейтами реализована в виде слоя LSTM сети РНС.
6. Способ по п.5, в котором
при введении третьих мультипликативных переменных дополнительно вводят третью мультипликативную переменную для преактивации информационного потока в слое LSTM, и
на этапе ii) дополнительно делают информационный поток константным, если третья мультипликативная переменная, ассоциированная с данным информационным потоком, имеет ассоциированное значение меньше упомянутого заданного порога.
7. Способ по п.1, в котором упомянутое ассоциированное значение представляет собой отношение квадрата среднего к дисперсии.
8. Способ по п.1, в котором упомянутый заданный порог равен 0,05.
9. Способ по п.1, в котором элементами упомянутого набора являются слова, и данный способ применим для классификации текста или моделирования языка, в котором используются упомянутые слова.
10. Устройство для сжатия рекуррентной нейронной сети (РНС) с архитектурой с гейтами, содержащее:
один или более процессоров, и
один или более машиночитаемых носителей данных, на которых хранятся машиноисполняемые команды, исполнение которых одним или более процессорами предписывает одному или более процессорам:
выполнять разреживание в отношении весов РНС, причем разреживание содержит:
i) выполнение оптимизации для получения апостериорного распределения весов, при этом апостериорное распределение весов аппроксимируется полностью факторизованным нормальным распределением, причем при оптимизации используется априорное распределение весов, представляющее собой полностью факторизованное лог-равномерное распределение, и оптимизация содержит генерирование весов из аппроксимированного апостериорного распределения, и
ii) идентифицирование весов и/или одной или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаление из РНС идентифицированных весов и/или удаление из РНС идентифицированных групп весов;
вводить первые мультипликативные переменные для элементов входного набора возможных элементов входных последовательностей РНС;
выполнять разреживание в отношении первых мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и операция ii) содержит идентифицирование первых мультипликативных переменных, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаление из РНС элементов упомянутого набора, которые ассоциированы с идентифицированными первыми мультипликативными переменными;
вводить вторые мультипликативные переменные для входных и скрытых нейронов РНС; и
выполнять разреживание в отношении вторых мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и операция ii) содержит идентифицирование вторых мультипликативных переменных, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаление из РНС входных и скрытых нейронов, ассоциированных с идентифицированными вторыми мультипликативными переменными;
вводить третьи мультипликативные переменные для преактиваций гейтов РНС; и
выполнять разреживание в отношении третьих мультипликативных переменных, причем операция i) содержит выполнение оптимизации с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и в операции ii) гейт делается константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше упомянутого заданного порога.
11. Устройство по п.10, при этом каждая выборка веса идентична для любого временного шага в одной входной последовательности.
12. Устройство по п.10, при этом упомянутое ассоциированное значение представляет собой отношение квадрата среднего к дисперсии.
13. Устройство по п.10, при этом упомянутый заданный порог равен 0,05.
14. Устройство по п.10, в котором архитектура с гейтами реализована в виде слоя LSTM сети РНС.
15. Устройство по п.14, в котором
при введении третьих мультипликативных переменных дополнительно вводится третья мультипликативная переменная для преактивации информационного потока в слое LSTM, и
в операции ii) дополнительно информационный поток делается константным, если третья мультипликативная переменная, ассоциированная с данным информационным потоком, имеет ассоциированное значение меньше упомянутого заданного порогового значения.
16. Устройство по п.10, при этом элементами упомянутого набора являются слова, и РНС применяется для задачи классификации текста или моделирования языка, в которой используются упомянутые слова.
17. Один или более машиночитаемых носителей данных, на которых хранятся машиноисполняемые команды, которые при их исполнении одним или более процессорами вычислительного устройства предписывают одному или более процессорам выполнять операции для сжатия рекуррентной нейронной сети (РНС) с архитектурой с гейтами, которая реализована в виде слоя LSTM сети РНС, причем упомянутые операции содержат этапы, на которых:
выполняют разреживание в отношении весов РНС, содержащее этапы, на которых:
i) выполняют оптимизацию для получения апостериорного распределения весов, при этом апостериорное распределение весов аппроксимируется полностью факторизованным нормальным распределением, причем при оптимизации используется априорное распределение весов, представляющее собой полностью факторизованное лог-равномерное распределение, и оптимизация содержит генерирование весов из аппроксимированного апостериорного распределения, и
ii) идентифицируют веса и/или одну или более групп весов, каждая из которых имеет ассоциированное значение меньше заданного порога, и удаляют из РНС идентифицированные веса и/или удаляют из РНС идентифицированные группы весов;
вводят первые мультипликативные переменные для элементов входного набора возможных элементов входных последовательностей РНС;
выполняют разреживание в отношении первых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для первых мультипликативных переменных, и на этапе ii) идентифицируют первые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаляют из РНС элементы упомянутого набора, которые ассоциированы с идентифицированными первыми мультипликативными переменными;
вводят вторые мультипликативные переменные для входных и скрытых нейронов РНС; и
выполняют разреживание в отношении вторых мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для вторых мультипликативных переменных, и на этапе ii) идентифицируют вторые мультипликативные переменные, каждая из которых имеет ассоциированное значение меньше упомянутого заданного порога, и удаляют из РНС входные и скрытые нейроны, ассоциированные с идентифицированными вторыми мультипликативными переменными;
вводят третьи мультипликативные переменные для преактиваций гейтов и информационного потока в слое LSTM сети РНС; и
выполняют разреживание в отношении третьих мультипликативных переменных, причем на этапе i) выполняют оптимизацию с использованием упомянутого априорного распределения и упомянутого аппроксимированного апостериорного распределения для третьих мультипликативных переменных, и на этапе ii)
делают гейт константным, если третья мультипликативная переменная, ассоциированная с данным гейтом, имеет ассоциированное значение меньше упомянутого заданного порога, и
делают информационный поток константным, если третья мультипликативная переменная, ассоциированная с данным информационным потоком, имеет ассоциированное значение меньше упомянутого заданного порога.
18. Машиночитаемый носитель данных по п.17, при этом
упомянутое ассоциированное значение представляет собой отношение квадрата среднего к дисперсии,
упомянутый заданный порог равен 0,05, и
каждая выборка веса идентична для любого временного шага в одной входной последовательности.
19. Машиночитаемый носитель данных по п.17, при этом элементами упомянутого набора являются слова, причем РНС применяется для задачи классификации текста или моделирования языка, в которой используются упомянутые слова.
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| EP 3179415 A1, 14.06.2017 | |||
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ЛОКАЛЬНОГО ПРАВИЛА СОСТЯЗАТЕЛЬНОГО ОБУЧЕНИЯ, КОТОРОЕ ПРИВОДИТ К РАЗРЕЖЕННОЙ СВЯЗНОСТИ | 2012 |
|
RU2586864C2 |
Авторы
Даты
2019-10-14—Публикация
2018-10-15—Подача