ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к области гидроэнергетики и может быть использовано для контроля комбинаторных зависимостей при проведении испытаний на работающем агрегате без использования специальных средств измерения.
УРОВЕНЬ ТЕХНИКИ
Эффективность использования водноэнергетических ресурсов низконапорными поворотно-лопастными агрегатами зависит от величины открытия направляющего аппарата (НА) и строго соответствующей ей и действующему напору величины утла разворота лопастей рабочего колеса (РК).
Режим работы турбины, величины открытия НА и угла разворота лопастей РК. в котором установлены таким образом, что обеспечивается достижение наивысшего КПД преобразования энергии водотока в механическую мощность, называется комбинаторным. Если задать некоторую величину открытия, то в зависимости от величины напора нетто можно подобрать угол разворота лопастей, при котором режим работы турбины будет комбинаторным. Зависимость утла разворота лопастей РК от величины открытия НА и напора Н нетто называется комбинаторной, если все определенные в соответствии с ней величины углов установки лопастей рабочего колеса гарантируют работу турбины в комбинаторном режиме. Так как напор нетто рассматривается как внешний и не зависящий от величин открытия и угла разворота лопастей фактор, то комбинаторная зависимость задается в виде однопараметрического семейства кривых с параметром «напор нетто», в дальнейшем просто напор. Если обозначить открытие направляющего аппарата как А0 (мм), угол разворота рабочего колеса как β(°) и напор нетто H (м), то комбинаторную зависимость можно записать в виде 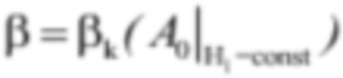 для i=1, 2, …, n, где обычно n=5÷7.
для i=1, 2, …, n, где обычно n=5÷7.
Величина открытия НА, а также угол разворота лопастей РК представляют собой параметры, определяющие положение решеток профилей соответствующих регулирующих органов управления режимом, при этом их изменение производится главными сервомоторами приводов НА и РК, от положения которых эти параметры зависят однозначно. Поэтому режим турбины может характеризоваться не только параметрами, определяемыми кинематикой потока, но и величинами положений сервомоторов приводов регулирующих органов.
Положение главного сервомотора привода НА обозначается Y1, а его относительное положение задается величиной:
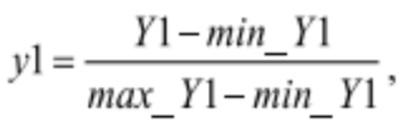
где min_Y1 - положение сервомотора, соответствующее закрытому направляющему аппарату, а max_Y1 - положение сервомотора на верхнем ограничителе его конструктивного хода.
Положение главного сервомотора привода лопастей РК обозначается Y2, а его относительное положение задается величиной:
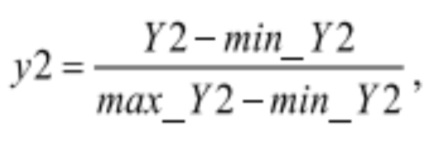
где min_Y2 соответствует минимальному углу разворота лопастей РК, а max_Y2 соответствует максимальному углу разворота лопастей РК.
Для действующего напора используется относительное отклонение его от номинального (расчетного) значения:
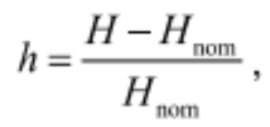
где H - текущее значение напора, а Hnom - значение напора в основном расчетном режиме.
Комбинаторные зависимости могут быть представлены, как в координатах (A0, β), так и в (y1, y2), а в качестве параметра, как правило, используется величина напора нетто. Далее в описании комбинаторные зависимости будут представлены в относительных величинах положений сервомоторов регулирующих органов.
Известен ряд методов идентификации комбинаторных зависимостей. В частности, можно выделить прямые методы определения комбинаторной зависимости в процессе энергетических испытаний турбин, которые включают в себя абсолютный метод и индексный метод определения рабочих характеристик. Абсолютный метод позволяет определить расход в физических единицах и абсолютное значение КПД. Для реализации указанного метода требуется тщательная подготовка, связанная с большими затратами. Проведение испытании абсолютным методом регламентируется ГОСТ 55260.3.2.-2013 Гидроэлектростанции, часть 3-2. Гидротурбины. Методы оценки технического состояния. Гл. 8. п.п. 8.1.1. Индексный или относительный метод определения КПД турбины является одним из самых часто используемых для контроля комбинаторных зависимостей, точнее, их дрейфа во времени с износом турбины. Этот метод базируется на формуле зависимости (формула Винтера-Кеннеди) перепада давлений между пьезометрическими выводами спиральной камеры от расхода. При использовании метода Винтера-Кеннеди расход через турбину определяется по зависимости:
Q=K·(Δd)n,
где K - коэффициент, Δd - измеренный перепад давлений и n - показатель степени.
Метод рекомендован IEC 41-1991-11 и СО 153-34.20.161-2003. и широко используется как в России (контроль деформации эксплуатационных и рабочих характеристик этим методом регламентируется упомянутым выше ГОСТ 55260.3.2 -2013). так и за рубежом в штатных системах измерения расхода. Согласно указанным документам показатель степени я в зависимости от конструкции спиральной камеры турбины варьируется в пределах 0,48÷0,52 и уточняется при тарировании створа абсолютным методом или расчетным путем на основе расчетной эксплуатационной характеристики, а коэффициент K естественным образом варьируется в широких пределах и зависит от мощности, напора и конструкции агрегата. При этом указанными нормативными документами не рекомендуется использовать метод при расходах меньших 50% от номинального, из-за малости измеряемого перепада и неустойчивости потока в режимах малой нагрузки агрегатов.
Характерным для индексного метода идентификации комбинаторных зависимостей является изменение во время эксперимента положения направляющего аппарата, а также зависящих от его положения параметров режима: мощности и расхода в широком диапазоне. Обработка данных в широком диапазоне их изменения позволяют достоверно выделить экстремумы полученных зависимостей и сравнить их с результатами предыдущих исследований.
В настоящее время указанные абсолютный и индексный методы являются основными и практически единственными используемыми для идентификации энергетических характеристик и комбинаторных зависимостей поворотно-лопастных агрегатов. Однако данным методам присущ ряд недостатков:
- большая трудоемкость, особенно в случае абсолютного метода:
- непрогнозируемая изменчивость величин K и n в формулах для вычисления величины расхода по показаниям дифманометров, используемых в методе Винтера-Кеннеди, для агрегатов установленных на одной ГЭС:
- недостоверность измерения индексным методом расходов меньших 50% от номинального:
- аппаратная ненадежность измерения расхода методом Винтера-Кеннеди, связанная с зарастанием проложенных в монолитном железобетоне трубок отбора импульсов давления и невозможностью восстановления их работоспособности;
- необходимость вывода агрегата из эксплуатации приблизительно на двое суток (при применении индексного метода) при идентификации комбинаторной зависимости для одного значения напора:
- затраты времени на проведение испытаний абсолютным методом примерно в 5-7 раз превосходят длительность индексных исследований:
- при изменении в течение опыта напора нетто необходимо по формулам приведения производить коррекцию всех величин: расхода, мощности и приведенной частоты вращения:
- проведение испытаний требует участие квалифицированных специалистов в области исследования гидротурбин.
В повседневной эксплуатации гидроагрегатов снятие полных энергетических характеристик турбин не является первоочередной задачей. Однако контроль комбинаторной зависимости и уверенность, что машина находиться в комбинаторном режиме, т.е. преобразование энергии воды в электрическую энергию осуществляется с максимально возможной эффективностью, будет всегда актуально.
В процессе любого из опытов напор, под которым подразумевается напор нетто, определяемый как разность полных удельных энергий воды на входе и выходе из турбины) является внешним, слабо влияющим, в силу малого изменения в процессе эксперимента, параметром, вычисляемым в конце процедуры нахождения каждой точки комбинаторного режима для привязки ее к некоторому постоянному значению его. Таким образом, далее речь идет только о мощности турбины, коэффициенте полезного действия, точнее его максимальном значении, и расходе турбины. Так как напор нетто, который является мерой разности полных удельных энергий воды, составляющие которой, являющиеся скоростными напорами на входе и выходе из турбины, то последние должны быть учтены в конце эксперимента, так как они являются функциями расхода.
Алгоритмы экстремум-регуляторов теоретически позволяют реализовать процедуру выявления комбинаторного режима турбины при нормальной эксплуатации. Однако присущие эксплуатации гидроагрегата режимы постоянного изменения мощности под воздействием системных регуляторов потоков мощности по линиям электропередачи и собственного регулятора частот вращения вызывают сложные гидродинамические процессы, в частности, сопровождающее каждое движение регулирующих органов явление гидравлического удара и продолжительное формирование потока в проточной части, вызывающее практически непрерывное расхода не оставляют шансов реализовать поисковое движение на фоне непрерывного управления. Очевидна и другая сторона вопроса: отсутствие средств и методов измерения расхода, обеспечивающих необходимую точность для сравнения результатов пошагового изменения взаимного положения регулирующих органов. Тем не менее, методы, базирующиеся на правилах формирования поисковых движений экстремум регуляторов, нашли свое применение в способах, которые сочетают обработку результатов, полученных при выполнении последовательности изменения взаимного положения регулирующих органов по определенным законам. Это методы постоянных мощности или расхода, применение которых не позволяет узнать значение КПД в точке комбинаторного режима, а только указывает, что режим комбинаторный.
Сущность метода постоянной мощности применительно к гидравлическим турбинам кратко изложена в [Киселев Г.С. Определение оптимальной комбинаторной зависимости поворотно-лопастной турбины по изолинии мощности. - Гидротехническое строительство. 1980 г., №2, стр. 38. 39] со ссылкой на монографию [Владиславлев Л.А. Испытания гидромеханического оборудования гидроэлектрических станций. - Москва.: Госэнергоиздат, 1957]. Согласно методу, если принять, что (y1(K), y2(K) представляет собой комбинаторное сочетание положений сервомоторов НА и РК. В окрестности этой точки при отклонении сервомотора НА от этого положения на некоторую величину (Δy1) всегда можно укатать изменение (Δy2) положения сервомотора РК такое, что величина мощности останется постоянной, а расход увеличится, так как режим перестал быть комбинаторным и КПД турбины уменьшился.
Если обозначить:
Мощность турбины 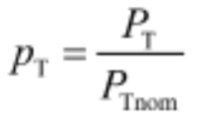
и расход через турбину 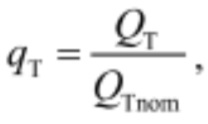 то
то
КПД гидротурбины 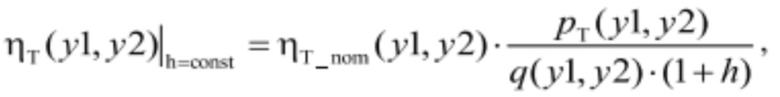
причем
при pT(y1, y2)=const и при 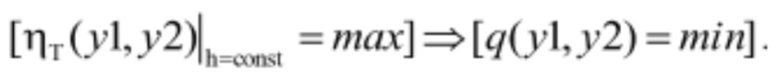
Таким образом, перебрав в окрестности комбинаторного режима несколько сочетаний открытия и угла разворота лопастей, удовлетворяющих условию постоянства мощности и замеряя индексный расход для каждой такой нары, можно указать сочетание, при котором расход будет минимальным, а КПД будет максимальным [Ивахненко А.Г. Техническая кибернетика. Государственное из-во технической литературы УССР. Киев, 1962 г. стр. 96-98]. Такое сочетание и будет комбинаторным. Выполнив указанную последовательность действий для нескольких значений мощности можно выявить комбинаторную зависимость. В этом случае говорят, что комбинаторный режим определяется на изолинии мощности.
В методе постоянного расхода также используется разнонаправленное движение регулирующих органов по изолинии расхода. Комбинаторному режиму соответствует взаимное положение регулирующих органов, при котором мощность турбины будет максимальной.
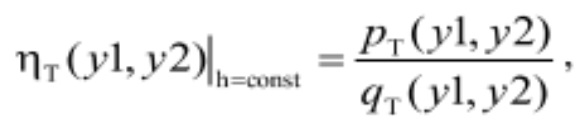
при qT(y1, y2)=const и при 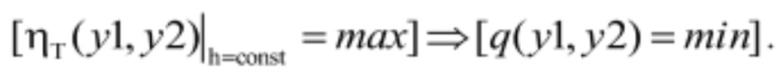
Использование указанного метода постоянного расхода раскрыто в патенте РФ №230255) (опуб. 10.07.2007. F03B 15/00). описывающем способ адаптивной коррекции комбинаторной зависимости поворотно-лопастной гидротурбины.
Следует обратить внимание на разнонаправленность движения регулирующих органов. В обоих случаях отклик на шаг пробного движения заключается в изменении расхода в первом случае и мощности во втором, при переходе от одной пары «открытие-угол разворотам к другой в районе искомого экстремума невелико и оценивается уровнем примерно 0.1-0.2% от их значении в точке комбинаторного режима. Если измерение электрической мощности машины с такой точностью не является чем-то непреодолимым, то измерение перепада давления между двумя точками спиральной камеры с указанной точностью не представляется возможным. В примере применения описанного выше метода идентификации комбинаторной точки на изолинии мощности [Киселев Г.С. Определение оптимальной комбинаторной зависимости поворотно-лопастной турбины но изолинии мощности - Гидротехническое строительство, 1980 г., №2, стр. 38. 39] ошибка в опенке комбинаторного положения главного сервомотора НА при открытиях меньших 40% (y1<0,4) может достигать 13% от его максимального перемещения при этом величина перепада давления при максимальном расходе равна всего 100 мм водяного столба. Кроме того, следует упомянуть о малой надежности аппаратной реализации метода Винтера-Кеннеди и нестабильности его как метода измерения расхода.
Перечисленные выше методы идентификации комбинаторных режимов, основанные на измерении мощности турбины и расхода через нее, обладают существенными недостатками:
- использование абсолютного и индексного методов измерения расхода (недостатки которых перечислены выше) невозможно применить в режиме эксплуатации агрегата, в связи с процедурой перебора большого числа взаимных положений регулирующих органов и изменений мощности и расхода одновременно в широком диапазоне,
- методы локального поиска точек комбинаторных режимов на изолиниях мощности или расхода не используются в связи с низкой точностью и ненадежностью метода измерения мало отличающихся расходов.
Поэтому актуальной задачей является выявление признаков комбинаторного режима, не связанных с определением величины расхода.
В качестве прототипа выбран описанный выше способ определения оптимальной комбинаторной зависимости поворотно-лопастной турбины по изолинии мощности или метод «постоянной мощности» [Киселев Г.С. Определение оптимальной комбинаторной зависимости поворотно-лопастной турбины по изолинии мощности. - Гидротехническое строительство. 1980 г., №2, стр. 38, 39]. Данный способ предполагает итеративный поиск точки комбинаторного режима на изолинии мощности без измерения расхода. Этот способ базируется на необходимом условии экстремума функции двух переменных.
Приращение мощности при перемещении режимной точки по изолинии (pT=const) мощности по определению всегда составляет:
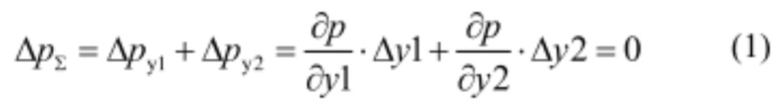
Пусть (y1(K), y2(K)) - точка комбинаторного режима, т.е. КПД турбины в этой точке достигает своего максимума, а значит, в этой точке выполняется и необходимое условие экстремума:
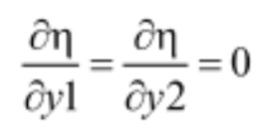
С другой стороны, приращение мощности вдоль изолинии в этой точке может быть подсчитано но формуле:
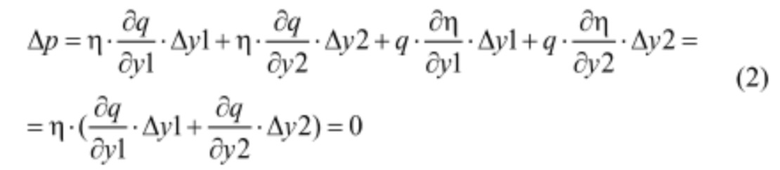
Таким образом, так как η≠0, то из (1) и (2) следует:
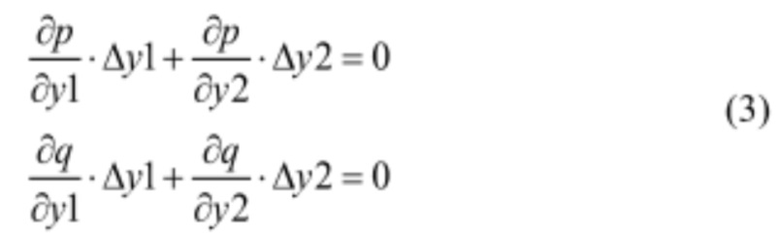
Однородная линейная система (3) имеет отличное от нулевого решение: Δy1≠0, Δу2≠0. Это возможно тогда, и только тогда, когда определитель системы:
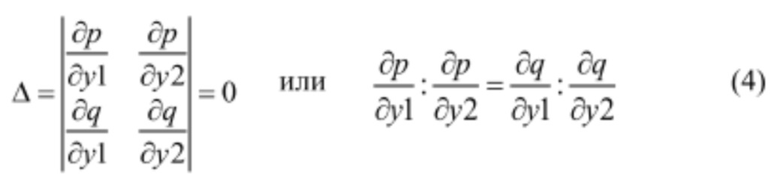
Известный способ заключается в вычислении частных производных мощности и частных производных расхода по перемещениям регулирующих органов в произвольной точке на изолинии мощности. Если в некоторой точке изолинии мощности выполняется (4), то эта точка будет комбинаторной при условии, что на изолинии мощности существует экстремум КПД и он является единственным.
В процессе определения точки комбинаторного режима выбирается уровень мощности, для которого будет экспериментально получены три зависимости:
- зависимость положения сервомотора рабочего колеса от положения сервомотора направляющего аппарата при постоянстве мощности турбины - изолиния мощности:
- зависимость мощности турбины от положения сервомотора направляющего аппарата при постоянстве положения сервомотора лопастей рабочего колеса;
- зависимость мощности турбины от положения сервомотора рабочего колеса при постоянстве положения сервомотора направляющего аппарата.
Согласно способу, соотношения (4) распространяются на все точки изолинии мощности, т.е. отношения величин частных производных от мощности по перемещениям регулирующих органов приравниваются к отношениям частных производных расхода по этим же перемещениям.
Однако, замена частных производных расходной функции по координатам перемещения регулирующих органов частными производными мощности турбины но тем же координатам приводит к неопределенности задачи из-за выполнения равенства (2) для всех принадлежащих изолинии мощности точек «положение сервомотора направляющего аппарата - положение сервомотора рабочего колеса», удовлетворяющих условию определения комбинаторною режима работы турбины. Кроме тою, для проведения испытаний и определения даже одной точки комбинаторного режима требуются значительные затраты времени (три движения: формирование самой изолинии мощности и два пробных для определения частных производных расхода по перемещению сервомоторов НА и РК, а также вывод агрегата из эксплуатации). Необходимость учитывать указанные требования приводит к сложности автоматизации данного способа.
Техническая задача настоящего изобретения заключается в разработке автоматизированного способа идентификации на плоскости «положение сервомотора НА - положение сервомотора РК» координат точки комбинаторного режима на изолинии мощности заданной величины, который отличается быстродействием, экономичностью и однозначностью получаемого результата и может быть выполнен без вывода агрегата из эксплуатации и использования специальных средств измерения.
РАСКРЫТИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Техническим результатом заявленного изобретение является повышение надежности определения координат точки комбинаторного режима при нормальной эксплуатации гидроагрегата.
Данный технический результат достигается применением способа определения координат точки комбинаторной зависимости поворотно-лопастной турбины на изолинии мощности заданной величины, построенной в координатных осях относительного положения сервомоторов приводов регулирующих органов поворотно-лопастной турбины относительно их полного хода, при котором формируют изолинию мощности, соответствующую заданному значению мощности, посредством разнонаправленного поочередного перемещения регулирующих органов поворотно-лопастной турбины. При этом под управлением регулятора мощности изменяют положение одного регулирующего органа таким образом, что выполняется последовательный переход от первого значения мощности к заданному значению мощности, а затем ко второму значению мощности к заданному значению мощности, а затем ко второму значению мощности, а затем изменяют положение другого регулирующего органа таким образом, что осуществляется обратный последовательный переход от второго значения мощности к заданному значению мощности, а затем к первому значению мощности, при этом заданное значение мощности равно полусумме первого и второго значений мощностей, сохраняют значения координат точек, соответствующих первому, второму и заданному значениям мощностей, осуществляют построение трех изолиний мощности, соответствующих первому значению мощности, второму значению мощности и заданному значению мощности на основании сохраненных значений координат точек, соответствующих первому, второму и заданному значениям мощностей соответственно, затем на изолинии мощности, соответствующей заданному значению мощности, выбирают ряд точек, расстояние между которыми в районе интенсивного изменения производной не превышает одного процента от полных перемещений сервомоторов приводов регулирующих органов, и проводят через выбранные точки прямые, параллельные координатным осям, вычисляют длины отрезков, содержащих точку изолинии мощности, соответствующей заданному значению мощности и отсекаемых от упомянутых линии изолиниями мощности, соответствующих первому и второму значениям мощностей, и вычисляют среднеквадратическое значение длин двух полученных отрезков, при этом точка на изолинии мощности, соответствующей заданному значению мощности, в которой вычисленное среднеквадратичное значение будет минимально, принимается за точку комбинаторной зависимости для заданного значения мощности при текущем напоре нетто.
В предлагаемом способе определения координат точки комбинаторной зависимости поворотно-лопастной турбины на изолинии мощности заданной величины аналитические выражения для изолиний мощности могут быть получены путем монотонной сплайновой аппроксимации.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Далее предлагаемое изобретение поясняется более подробно со ссылкой на прилагаемые черт ежи, на которых:
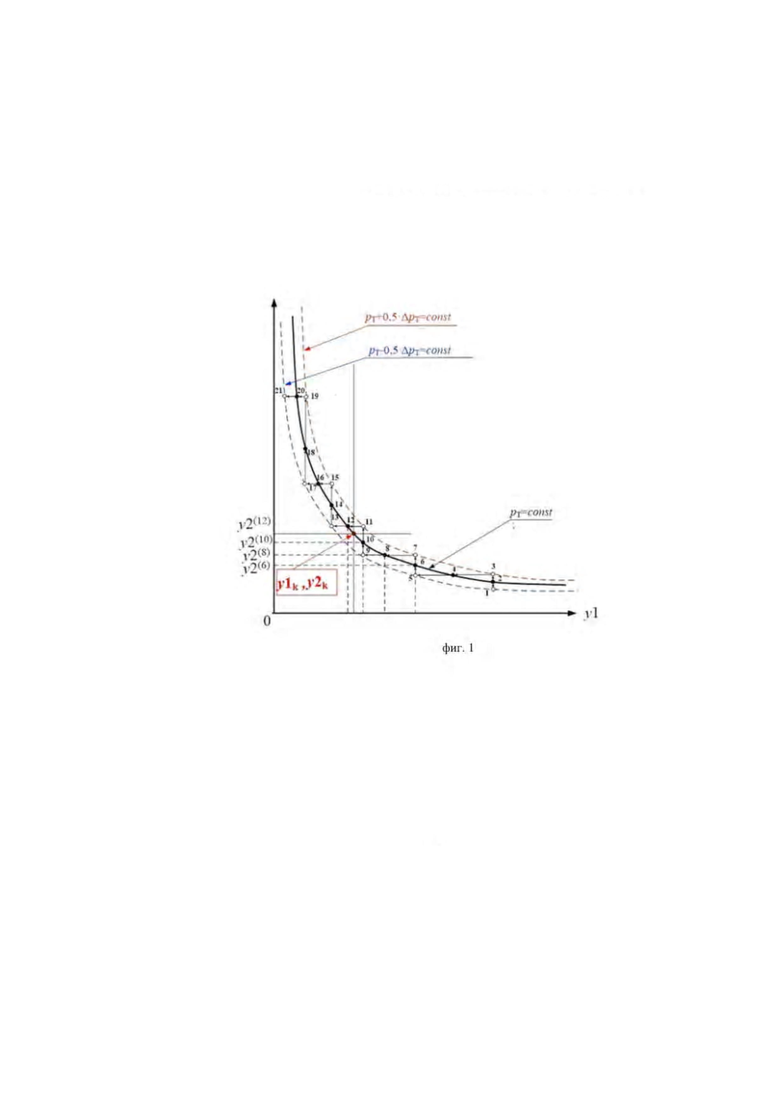
фиг. 1 изображает процесс построения изолиний мощности:
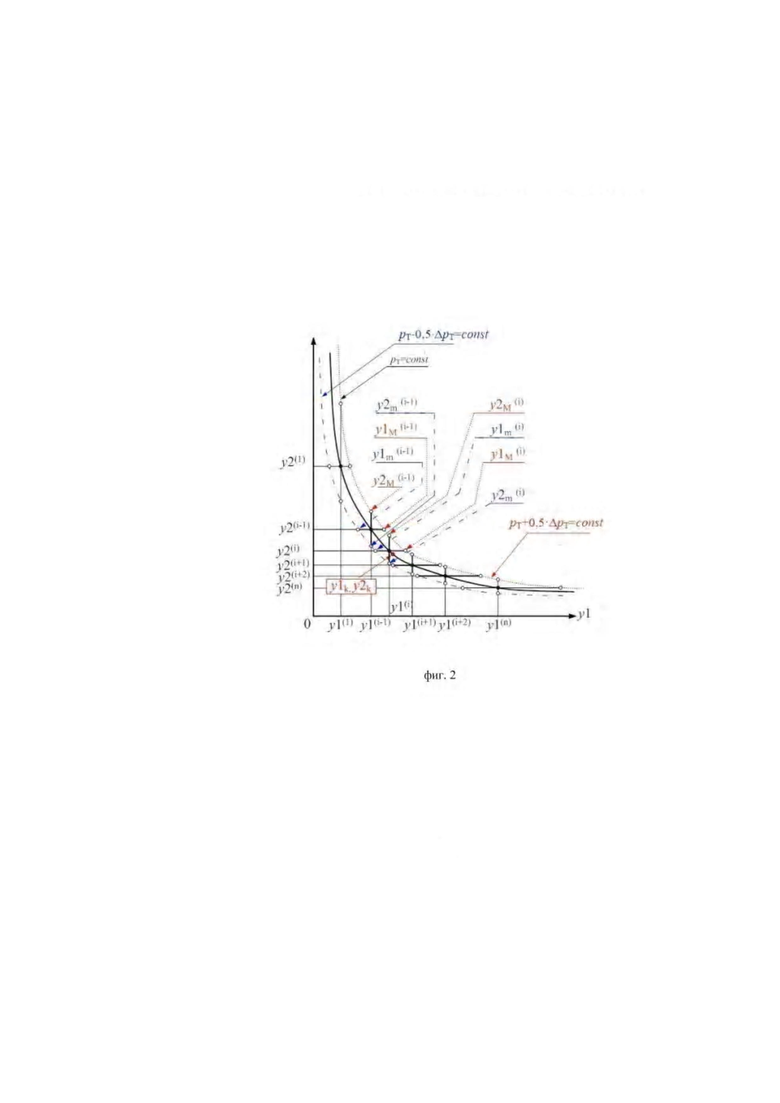
фиг. 2 изображает процесс нахождения точки комбинаторной зависимости на изолиниях мощности но фиг. 1;
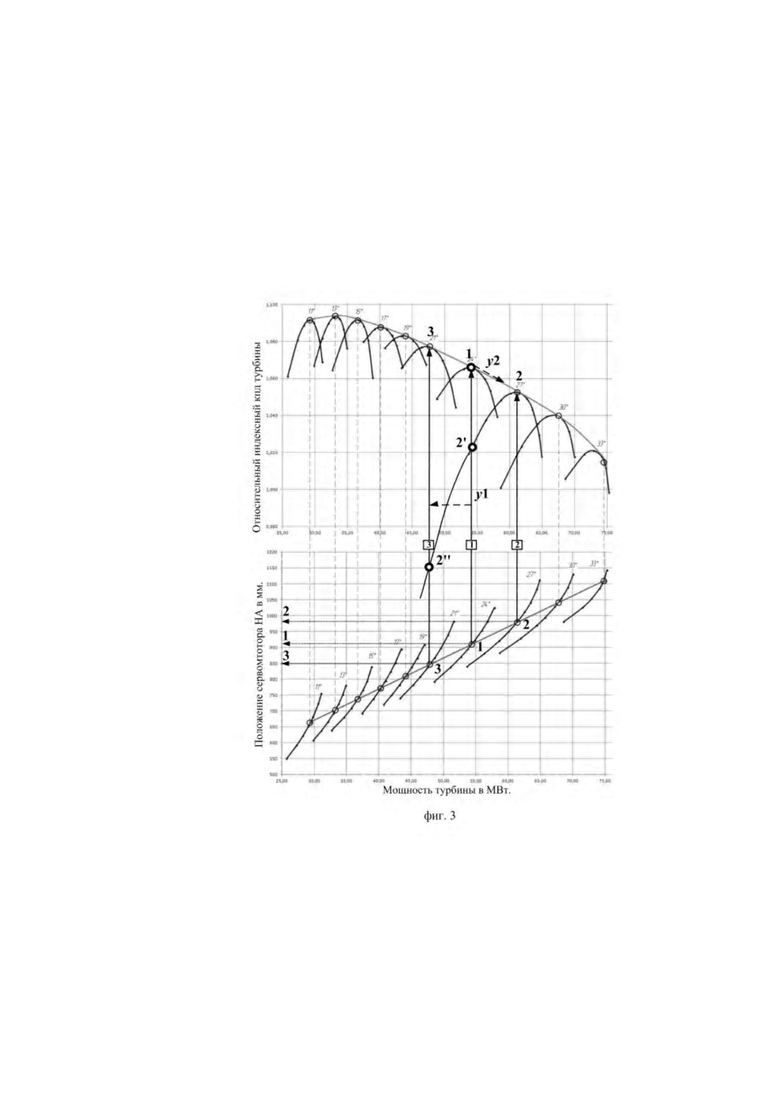
фиг. 3 изображает пропеллерные рабочие характеристики (зависимости КПД и мощности турбины от положения сервомотора НА при фиксированных положениях угла разворота лопастей РК), полученные индексным методом:
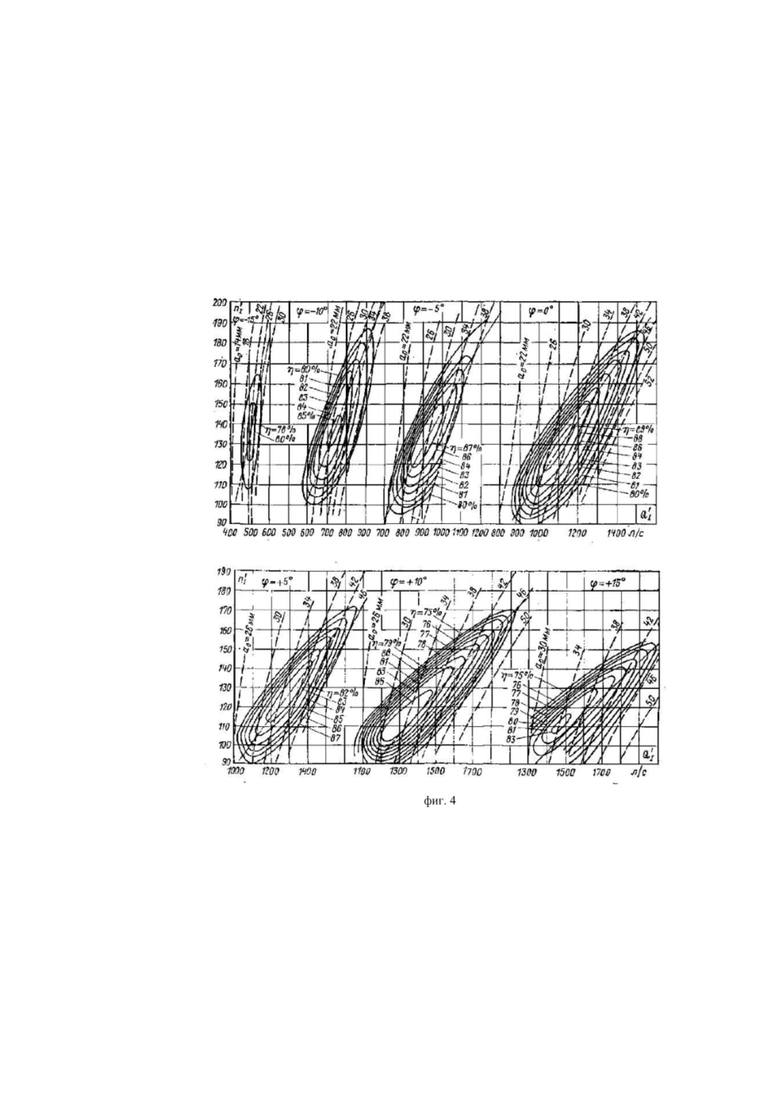
фиг. 4 изображает пропеллерные характеристики, иллюстрирующие, что но мере роста угла разворота лопастей расстояние между линиями равного угла разворота лопастей увеличивается:
фиг. 5 изображает графики комбинаторных зависимостей;
фиг. 6 изображает приведенные к напору 18,09 м зависимости положения y2k сервомотора рабочего колеса от положения y1 сервомотора направляющего аппарата в комбинаторном режиме;
фиг. 7 изображает зависимости мощности, развиваемой гидротурбиной, от положения y1 сервомотора направляющего аппарата.
ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ
Предложенный способ определения координат точки комбинаторной зависимости поворотно-лопастной турбины демонстрируется на фиг. 1-2.
На фиг. 1 показана траектория движения точки (y1, у2), соответствующей положению регулирующих органов в системе координат, в которой абсцисса y1 представляет собой положение сервомотора направляющего аппарата, а ордината y2 представляет собой положение сервомотора рабочею колеса. Согласно способу осуществляют последовательное увеличение мощности турбины от первого значения мощности pT - 0,5·Δp до заданного значения мощности pT и далее до второго значения мощности pT+0,5·Δр за счет увеличения угла разворота лопастей соответствующим изменением положении y2 сервомотора рабочего колеса при постоянной величине открытия и положения у1 сервомотора направляющего аппарата. Затем осуществляют последовательное уменьшение мощности турбины в обратном порядке от второго значения мощности pT+0,5·Δp до заданного значения мощности pT и далее до первого значения мощности pT-0,5·Δp посредством уменьшения величины открытия изменением положения y1 при положении y2, зафиксированном при предыдущем изменении положении y2 сервомотора рабочего колеса. При этом заданное значение мощности равно полусумме первого и второго значений мощностей. Перемещение в обоих направлениях по одним и тем же значениям мощности позволяет обнаружить люфты в механических передачах, преобразующих линейные перемещения сервомоторов в утлы поворота лопаток НА и разворота лопастей РК.
Через каждую из перечисленных групп точек проводится изолиния мощности: (pT=const) - изолиния мощности, соответствующую заданному значению мощности, (pT-0,5·Δp=const) - изолиния мощности, соответствующую первому значению мощности, и (pT+0,5·Δp=const) - изолиния мощности, соответствующую второму значению мощности. Аналитические выражения для изолиний мощности могут быть получены путем кубической монотонной сплайновой аппроксимации.
При этом точки с номерами (1+4·(k-1)) лежат на изолинии мощности, соответствующей первому значению мощности, или миноранте, точки с номерами (2·k) лежат на изолинии мощности, соответствующей заданному значению мощности, или медиане, а точки с номерами (3+4·(k-1)) лежат на изолинии мощности, соответствующей второму значению мощности, или мажоранте, где k=1, 2, 3… - натуральное число. В указанных точках происходит остановка, а их координаты сохраняют.
Далее, как показано на фиг. 2 на изолинии мощности, соответствующей заданному значению мощности выбирают последовательность лежащих на ней точек
(у1(l), у2(l)), …, (y1(i-l), y2(i-1)), (y1(i), y2(i)), (y1(i+1), у2(i+1), (у1(i+2), у2(i+2), …, (y1(n), y2(n)) по возрастанию координаты y1, при этом выбор осуществляют таким образом, что расстояние между указанными точками в районе интенсивного изменения производной не превышает одного процента от полных перемещений сервомоторов приводов регулирующих органов. Указанные точки также могут выбирать по убыванию координаты y1. Количество выбираемых точек определяется требуемой точностью установки регулирующих органов.
Далее проводят через выбранные точки прямые, параллельные координатным осям, при этом для любой из лежащих на изолинии pT точек (y1(i), y2(i)) находят две пары точек на миноранте и мажоранте, которые имеют одинаковые значения координаты (y1=у1(i)), но разные значения y2. Положение сервомотора рабочего колеса, соответствующее положению сервомотора направляющего аппарата (y1=y1(i)) на мажоранте обозначают как 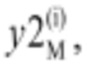 а на миноранте обозначают как
а на миноранте обозначают как 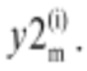 Аналогичным образом обозначают координату положения сервомотора направляющего аппарата, соответствующую положению сервомотора рабочего колеса как y2(i), на мажоранте обозначают как
Аналогичным образом обозначают координату положения сервомотора направляющего аппарата, соответствующую положению сервомотора рабочего колеса как y2(i), на мажоранте обозначают как 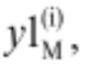 а на миноранте обозначают как
а на миноранте обозначают как 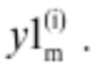
При этом для любой точки, лежащей на изолинии (pT) будут выполняться равенства:
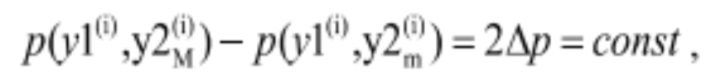
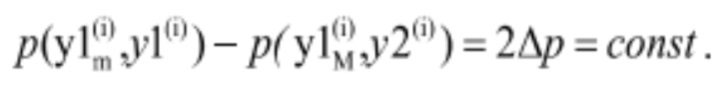
Далее вычисляют длины отрезков, содержащих точку изолинии мощности, соответствующей заданному значению мощности и отсекаемых от упомянутых линий изолиниями мощности, соответствующих первому и второму значениям мощностей, и вычисляют среднеквадратического значение длин двух полученных отрезков, при этом точка на изолинии заданной мощности (pT=const), в которой вычисленное среднеквадратичное значение будет минимально, принимается за точку комбинаторной зависимости для заданного значения мощности при текущем напоре нетто.
Предложенный способ может быть использован в регуляторе частоты вращения и мощности гидротурбины, реализованном на базе программно-технического комплекса, представляющего собой дублированную 32-разрядную вычислительную систему, содержащую периферийные устройства для сбора аналоговой и дискретной информации, управления злектрогидравлическими приводами регулирующих органов и передачи данных о состоянии объекта в соответствующие устройства управления. Однако очевидно, что предлагаемый способ может быть реализован на базе других технических средств, известных в данной области техники.
На фиг. 3 представлены пропеллерные рабочие характеристики, полученные индексным методом и характеризующие зависимости КПД и мощности турбины от положения сервомотора НА при фиксированных положениях утла разворота лопастей РК. На фигуре обозначены три комбинаторных сочетания положений регулирующих органов (1,1]), (2,2) и (3,3), где первая цифра обозначает положение сервомотора НА, а вторая цифра обозначает угол разворота лопастей РК. КПД турбины примерно в равной степени зависит от отклонений открытия НА и величины угла разворота лопастей РК от значений указанных параметров в комбинаторном режиме. Пусть регулирующие органы находятся сначала в положении (1,1), соответствующем комбинаторному режиму работы турбины. Переход из позиции (1,1) в (1,2) в результате изменение угла разворота лопастей с 24° до 27° означает, что лопасти развернуты на угол больший, чем это требуется для комбинаторною режима. Рабочая характеристика, определяемая положением лопастей, изменилась, т.е. КПД турбины будет определяться не кривой, проходящей через точку 1, которая лежит на огибающей рабочих характеристик, а кривой, проходящей через точку 2 той же огибающей. Значение КПД турбины будет определяться пересечением вертикали 1-1 с рабочей характеристикой, соответствующей углу разворота лопастей в 27°, т.е. значением в точке 2'. Далее НА перемещают в положение 3, соответствующее комбинаторному положению лопастей, при этом лопает и останутся в положении 2, следовательно, рабочая характеристика не изменится. Аналогично предыдущему, значение КПД турбины соответствует ординате точки 2'' на оси КПД. На фиг. 3 показаны два разнонаправленных изменения положений регулирующих органов турбины: сначала угла разворота лопастей (показан стрелкой переход координаты у2 из точки 1 в точку 2 по огибающей рабочих характеристик), а потом закрытие сервомотора направляющего аппарата (показан стрелкой, параллельной оси «мощность турбины», из точки 1 в 3). Если первое перемещение приводит к уменьшению КПД приблизительно на 4%. то второе - на 7% по отношению к предыдущему значению.
Введем понятие рассогласования комбинаторной зависимости. Пусть для выбранного уровня мощности лежащая на медиане точка комбинаторного режима имеет координаты (y1k, y2k), а любая другая точка координатной плоскости имеет координаты (y1, у2), при этом для точки комбинаторного режима выполняются условия (y1k≠y1) или ((y2k≠y2) или [(y1k≠y1) и (y2k≠y2)] и sign(y1-y1k)·sign(y2-y2k)≤0, тогда мерой рассогласования комбинаторной зависимости будем называть величину
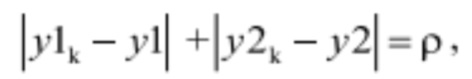
где y1, y1k, y2, y2k больше нуля.
Эта величина определяет меру рассогласования комбинаторной зависимости при разнонаправленном изменении их положений относительно комбинаторной точки. Изолинии постоянной мощности являются подмножеством таких точек но отношению к точке комбинаторного режима для выбранного уровня мощности.
Пусть режимная точка имеет некоторые координаты (y1, у2), принадлежащие линии равной мощности и не являющиеся координатами (y1k, y2k) точки комбинаторного режима, при этом для определенности у1<y1k и y2>y2k, и пусть для определенности производится разнонаправленное изменение положений регулирующих органов δy1<0 и δy2>0 с возвращением режимной точки на изолинию мощности. В этом случае величина рассогласования ρ будет увеличиваться и КПД турбины будет уменьшаться как при изменении положения y1 сервомотора НА, так и при изменении положения y2 сервомотора РК.
Если принять параметры режима комбинаторного режима за базовые, то для любого положения регулирующих органов на линии постоянной мощности турбины ее мощность выражается зависимостью:
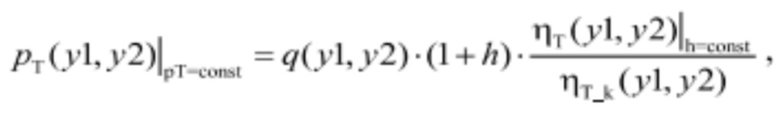
так как линия постоянной мощности предполагает постоянство напора, а величины ηT_k(y1, y2) и (1+h) не зависят от положения регулирующих органов и режима работы турбины, то приведенная выше формула может быть записана в более простом виде:
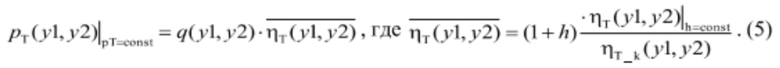
Формула (5) лучше отражает сущность процесса происходящего в турбине: величина расхода характеризует количественную сторону процесса: сколько нужно воды при том КНД (качестве) ее использования, которое определяется данным положением регулирующих органов.
Для изолинии мощности при поочередном перемещении регулирующих органов выполняются условия: либо y1=const, либо y2=const.
Таким образом, в процессе изменения мощности турбины посредством перехода с миноранты на мажоранту и обратно путем изменения положения только одного из регулирующих органов может рассматриваться как функция одной переменной. При этом положение другого регулирующего органа играет роль постоянного параметра.
Пусть, например, положение сервомотора НА изменилось на величину Δy1 и стало равным y1+Δy1, а положение сервомотора РК на Δy2 и стало равным y2+Δy2:
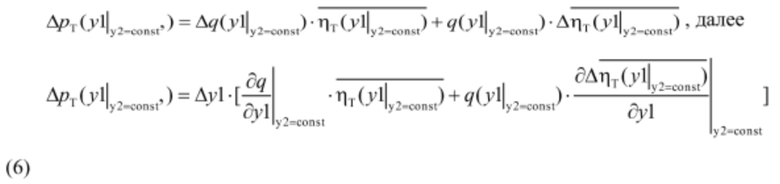
Круговой перестановкой индексов получаем:
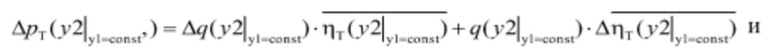
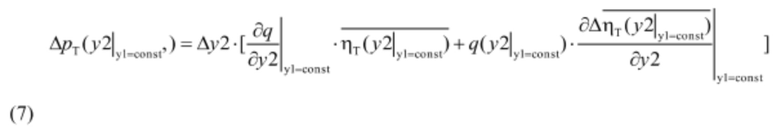
В формулах (6) и (7) производные расхода от перемещения соответствующего регулирующего органа всегда положительны: при перемещении сервомотора НА в сторону увеличения открытия последнего расход всегда растет, точно такая картина наблюдается и при перемещении сервомотора РК в сторону увеличения угла разворота лопастей РК. При выбранном выше направлении увеличения рассогласования комбинаторной зависимости увеличение открытия НА сопровождается уменьшением рассогласования, а КПД турбины увеличивается, т.е. производная КПД по перемещению сервомотора НА является положительной. При перемещении сервомотора РК в сторону увеличения утла разворота величина рассогласования увеличивается, и производная КПД турбины по перемещению сервомотора РК является отрицательной. Таким образом, расставляя знаки сомножителей в формулах (6) и (7) получим:
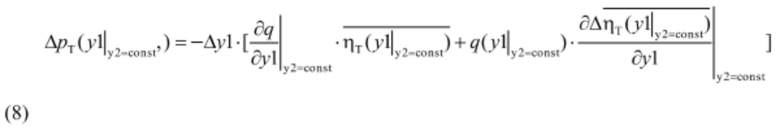
и
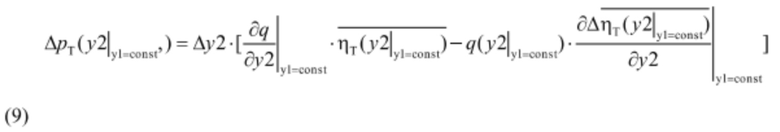
Анализ приведенных формул (8) и (9) позволяет сделать вывод о том, что влияние первого слагаемого, стоящего в квадратных скобках в формулах (8) и (9), по мере увеличения рассогласования комбинаторной зависимости будет уменьшаться из-за быстрого уменьшения 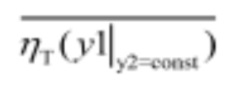 и
и 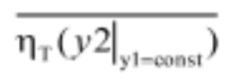 в связи с перераспределением перепада давлений в проточной части турбины в пользу другого регулирующего органа, что неминуемо приведет к увеличению
в связи с перераспределением перепада давлений в проточной части турбины в пользу другого регулирующего органа, что неминуемо приведет к увеличению 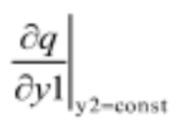 и
и 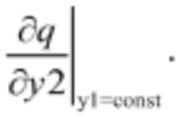 Данный вывод проиллюстрирован на фиг. 4, на которой изображены пропеллерные характеристики, свидетельствующие о том, что по мере роста угла разворота лопастей расстояние между линиями равного угла разворота лопастей увеличивается. Кроме того, можно сделать вывод о том, что второе слагаемое в обеих формулах зависит только от лавинообразно увеличивающейся скорости уменьшения КПД турбины при увеличении рассогласования комбинаторной зависимости и увеличения расхода, вызванного снижением КПД. Следовательно, предложенная методология позволяет определить точку с максимальным КПД, т.е. являющуюся комбинаторной. Действительно, согласно предложенному способу осуществляется построение трех изолиний для значений мощности (pT+0,5·Δp), pT и (pT-0.5·Δp) на плоскости (y1, 0, y2), координаты которой представляют собой положения сервомоторов приводов регулирующих органов поворотно-лопастной турбины лопаток НА и лопастей РК. Вторым фактором, изменяющим соотношение перемещений регулирующих органов в ту же сторону, является необходимость пропуска увеличивающегося расхода при снижении суммарного перепада давлений. Действительно, при закрытии регулирующего органа площадь сечения для пропуска воды уменьшается, и, следовательно, согласно уравнению Бернулли, скорость его должна увеличиваться, а для этого надо затратить больший перепад давления, и на другой регулирующий орган остается меньшая доля общего перепада. Но последний, для поддержания мощности, надо открыть, что сопровождается увеличением расхода и еще большим значением перепада, который будет необходим первому регулирующему органу.
Данный вывод проиллюстрирован на фиг. 4, на которой изображены пропеллерные характеристики, свидетельствующие о том, что по мере роста угла разворота лопастей расстояние между линиями равного угла разворота лопастей увеличивается. Кроме того, можно сделать вывод о том, что второе слагаемое в обеих формулах зависит только от лавинообразно увеличивающейся скорости уменьшения КПД турбины при увеличении рассогласования комбинаторной зависимости и увеличения расхода, вызванного снижением КПД. Следовательно, предложенная методология позволяет определить точку с максимальным КПД, т.е. являющуюся комбинаторной. Действительно, согласно предложенному способу осуществляется построение трех изолиний для значений мощности (pT+0,5·Δp), pT и (pT-0.5·Δp) на плоскости (y1, 0, y2), координаты которой представляют собой положения сервомоторов приводов регулирующих органов поворотно-лопастной турбины лопаток НА и лопастей РК. Вторым фактором, изменяющим соотношение перемещений регулирующих органов в ту же сторону, является необходимость пропуска увеличивающегося расхода при снижении суммарного перепада давлений. Действительно, при закрытии регулирующего органа площадь сечения для пропуска воды уменьшается, и, следовательно, согласно уравнению Бернулли, скорость его должна увеличиваться, а для этого надо затратить больший перепад давления, и на другой регулирующий орган остается меньшая доля общего перепада. Но последний, для поддержания мощности, надо открыть, что сопровождается увеличением расхода и еще большим значением перепада, который будет необходим первому регулирующему органу.
Так как изолиния мощности является совокупностью установившихся режимов, определяемых однозначно тремя величинами: положением сервомотора НА, положением сервомотора РК и действующим напором нетто, то независимо каким образом агрегат был переведен в этот режим, его эксплуатационные параметры: расход, мощность и КПД будут оставаться неизменными. Таким образом, если выполнять формирование изолинии мощности предложенным способом, то остановка в любой из точек установившегося режима и движение в обратном направлении с таким же шагом ΔpT, обеспечит возврат с остановками в точках, являющимися точками остановки в первоначальном движении. При этом процесс формирования другой (правой) ветви изолинии мощности будет зеркальным отражением рассмотренного выше процесса, то есть угол разворота лопастей будет уменьшаться, а открытие направляющего аппарата увеличиваться.
Таким образом, предлагаемый способ позволяет однозначно определять координаты точки комбинаторной зависимости, и. следовательно, повысить надежность определения указанных координат. Кроме того, указанный способ может быть реализован на базе существующих программно-технических комплексов электрогидравлических регуляторов частоты и мощности гидротурбины и не требует применения дополнительных устройств, что обеспечивает простоту реализации указанного способа.
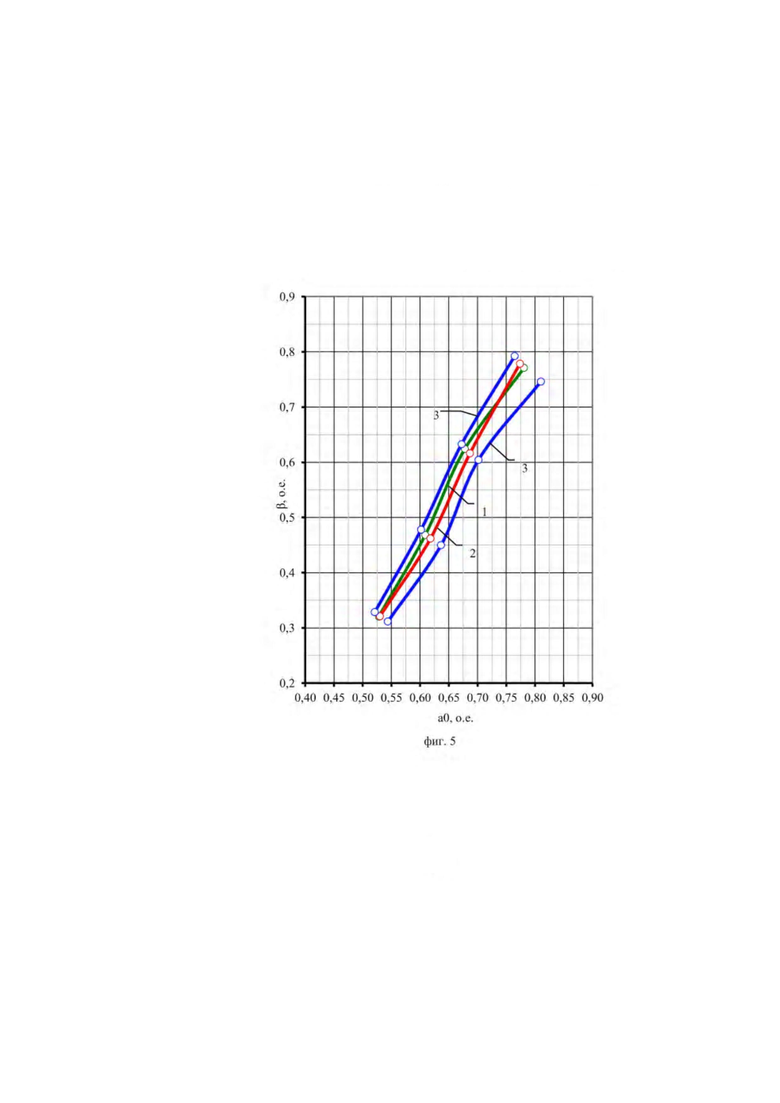
Для проверки предлагаемого способа был проведен вычислительный эксперимент, для которого была разработана цифровая модель турбины, имитирующая расходную и мощностную характеристики в функции от приведенных частоты вращения и напора. Для построения модели использовались частные пропеллерные характеристики турбины Новосибирской ГЭС типа ПЛ30-В-800. Для номинального напора, составляющего 17 м, производились вычисления КНД при разных уровнях мощности, с минимизацией величины расхода вдоль сгенерированных согласно предлагаемому способу изолиний мощности. И большом количестве точек изолиний вычислялся расход и отмечалась точка, в которой расход был минимальным. Данная точка считалась истинной точкой комбинаторного режима. На фиг. 5 показаны результаты вычислительного эксперимента применения предлагаемого способа, представленные в виде графиков комбинаторных зависимостей в координатах, на оси абсцисс которой показывает относительное значение открытия α0 НА, представляющее собой условную единицу, равную разности максимальною и минимальною значений открытия, а ось ординат представляет собой относительное значение угла 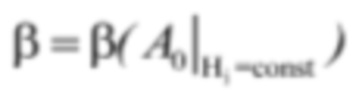 разворота лопастей в условных единицах, представляющих собой разность максимального и минимальною значений угла разворота лопастей. На фиг. 5 представлены следующие кривые: 1 - комбинаторная зависимость, построенная по результатам прямого поиска минимума расхода на линии равной мощности, величина которой равна мощности, взятой из расчетов завода, при том же значении утла разворота, 2 - комбинаторная зависимость, полученная предлагаемым способом постоянной мощности, реализующая критерий минимума расхода (максимальный КНД), 3 - границы зоны размещения комбинаторных зависимостей, отличающихся от комбинаторной зависимости минимума расхода ±0,2% по величине КПД турбины.
разворота лопастей в условных единицах, представляющих собой разность максимального и минимальною значений угла разворота лопастей. На фиг. 5 представлены следующие кривые: 1 - комбинаторная зависимость, построенная по результатам прямого поиска минимума расхода на линии равной мощности, величина которой равна мощности, взятой из расчетов завода, при том же значении утла разворота, 2 - комбинаторная зависимость, полученная предлагаемым способом постоянной мощности, реализующая критерий минимума расхода (максимальный КНД), 3 - границы зоны размещения комбинаторных зависимостей, отличающихся от комбинаторной зависимости минимума расхода ±0,2% по величине КПД турбины.
Предложенный способ определения точки комбинаторной зависимости также был проверен специалистами компании Ракурс в период проведения натурных энергетических испытаний гидроагрегата №6 Новосибирской ГЭС на расчетном напоре, проводимых экспертной организацией ЦКТН. Диапазон измеренного статического напора ГЭС составил 19.3÷19.5 м. В процессе испытаний проводились: проверка алгоритма формирования изолинии мощности и проверка алгоритмов определения комбинаторной точки на изолинии выбранной мощности.
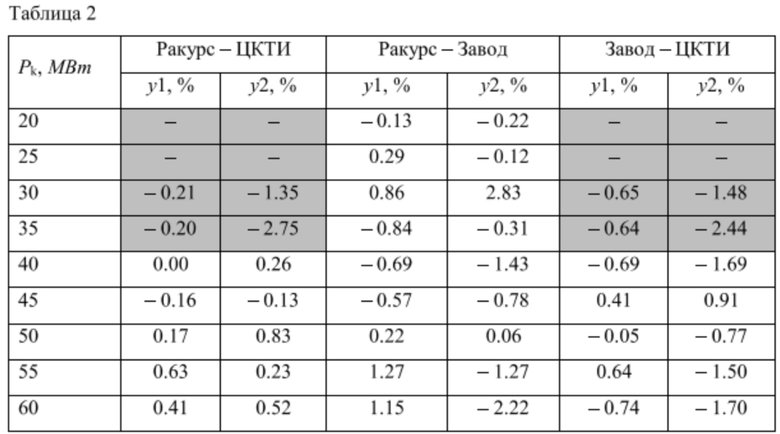
Сравнение комбинаторных зависимостей производилось по величине перемещения сервомоторов НА, взятых для равных мощностей.
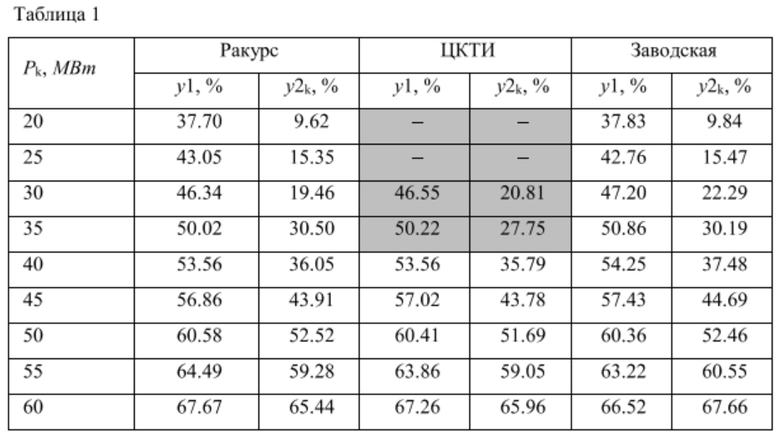
В таблице 1 показаны координаты комбинаторных зависимостей, приведенные к значению напора H=18,09 м. Указанные выше величины мощностей приведены в столбце (Pk, МВт), а соответствующие им величины положений сервомотора НА в столбцах «Ракурс: у1, %», «ЦКТИ: у1, %», «Заводская: у1, %». По полученным таким образом значениям положений сервомоторов НА по графикам, представленным на фиг. 2, были определены положения сервомоторов РК, представленные в столбцах «Ракурс: y2k, %», «ЦКТИ: y2k, %». «Заводская: y2k, %».
В связи с невозможностью точного измерения напора нетто и наличием люфтов в приводе регулирующих органов, сравнение полученных данных с заводскими данными не может считаться полностью корректным. Однако допустимо сравнивать характеры повеления полученных кривых.
В качестве характеристики «Ракурс» используется результат, полученный при движении сервомотора РК на разворот лопастей. ЦКТИ, если судить по программе испытаний, действуют аналогичным образом. Это позволяет снимать характеристику с гарантированно выбранным люфтом, поскольку гидравлическое усилие со стороны лопастей направлено на увеличение угла разворота. Испытания проводились практически параллельно с разницей в несколько часов, поэтому можно считать, что внешние условия для сравнения полученных результатов измерения одинаковы, и, следовательно, полученные результаты, приведенные в таблице), должны быть близки.
В таблице 1 выделены результаты режимов турбины с расходом меньшим пятидесяти процентов от номинальною. Далее в таблице 2 приведены величины отклонений результатов, полученных в эксперименте («Ракурс») от принимаемых за базовые, в качестве которых служат комбинаторные характеристики, даваемые заводом («Завод») и полученные ЦКТИ («ЦКТИ»).
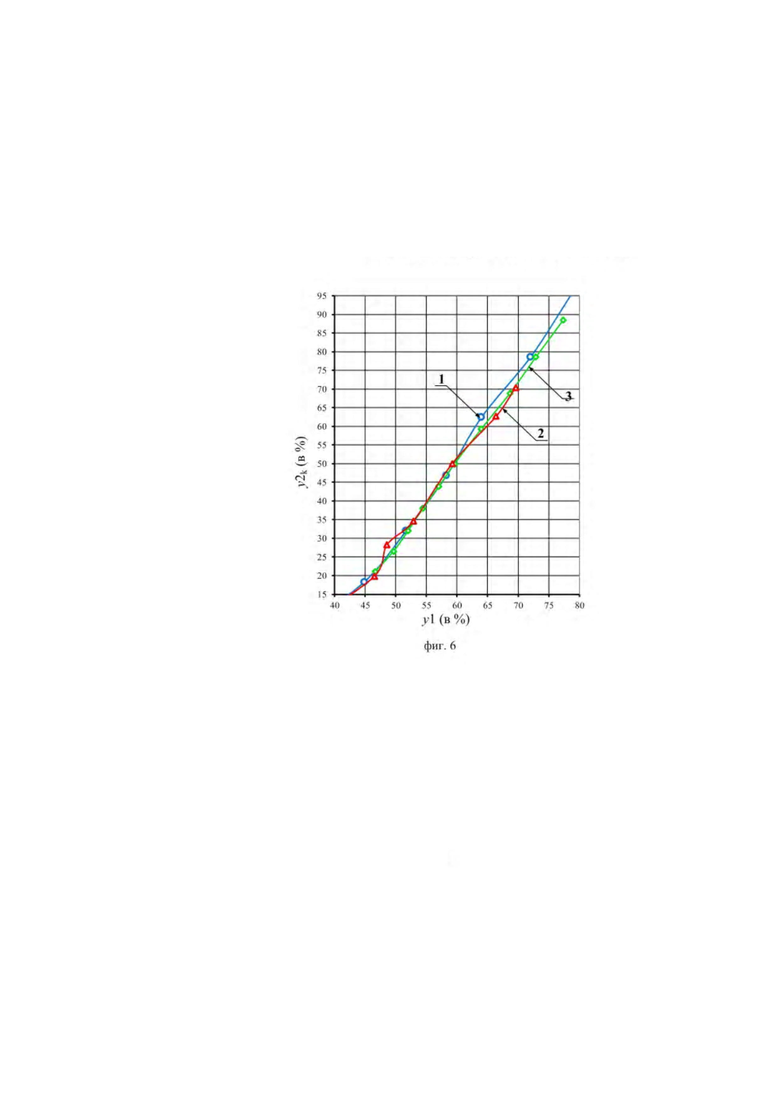
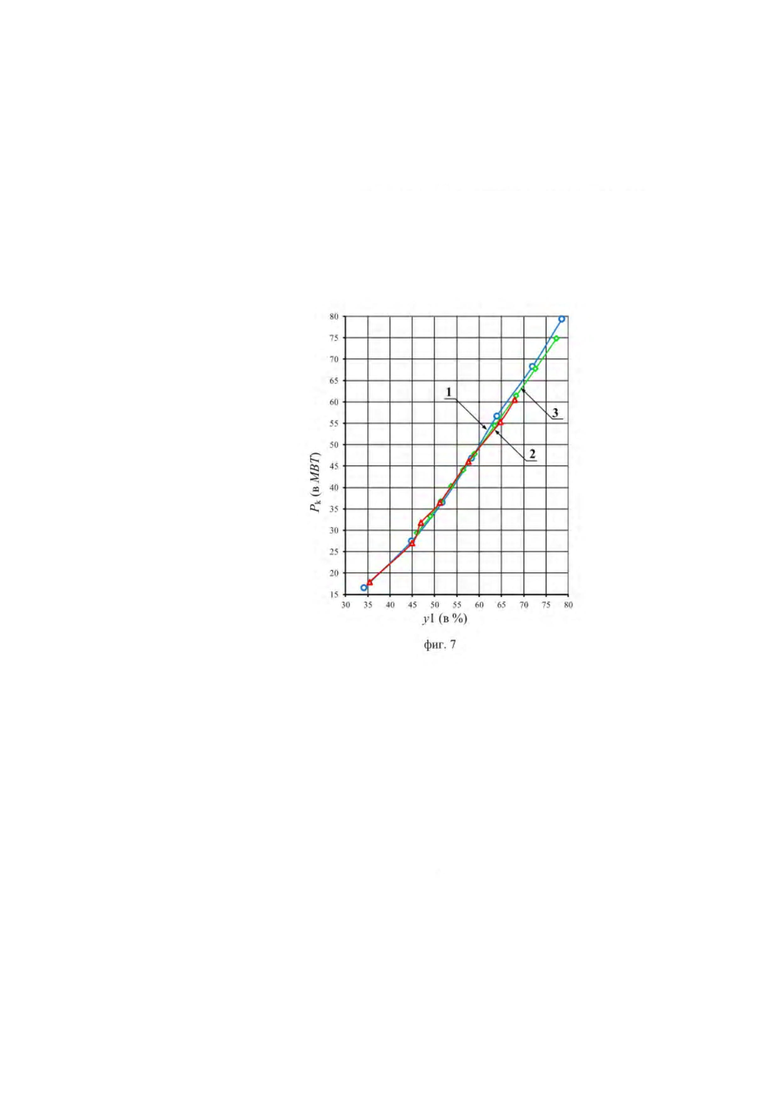
На фиг. 6 и 7 изображены комбинаторные зависимости, построенные по данным, представленным в таблице). На фиг. 6 представлены приведенные к напору 18,09 м зависимости положения y2k сервомотора рабочего колеса от положения y1 сервомотора направляющею аппарата в комбинаторном режиме y2k=ƒy(y1). На фиг. 7 представлены зависимости мощности, развиваемой гидротурбиной, от положения y1 сервомотора направляющего аппарата 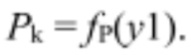 На фиг. 6 и 7 обозначены следующие зависимости: 1 - зависимость, рассчитанная заводом изготовителем и реализуемая программой регулятора в процессе эксплуатации агрегатом, 2 - зависимость, полученная «Ракурсом» в процессе экспериментальной проверки предлагаемого способа, 3 - зависимость, полученная индексным методом ЦКТН.
На фиг. 6 и 7 обозначены следующие зависимости: 1 - зависимость, рассчитанная заводом изготовителем и реализуемая программой регулятора в процессе эксплуатации агрегатом, 2 - зависимость, полученная «Ракурсом» в процессе экспериментальной проверки предлагаемого способа, 3 - зависимость, полученная индексным методом ЦКТН.
(равнение комбинаторных зависимостей производилось с использованием универсальной характеристики турбины следующим образом:
- при нескольких выбранных значениях y1, в которых значения величины y2k имеют значительный разброс, по универсальной или эксплуатационной характеристике определяют расход, например: Q(y1, y2k_1), Q(y1, r2k_2), Q(y1, y2k_3) соответственно для зависимостей 1, 2, 3, показанных на фиг. 8:
- по зависимостям Pk=ƒP(y1) определяют величины мощностей в тех же точках: Pk (y1, y2k_1), Pk (y1, y2k_2), Pk(y1, y2k_3) соответственно для зависимостей 1, 2 и 3, показанных на фиг. 7;
- поскольку напор при снятии и расчете всех трех зависимостей одинаков, то разброс КПД при использовании каждой из комбинаторных зависимостей будет определяться отношениями:
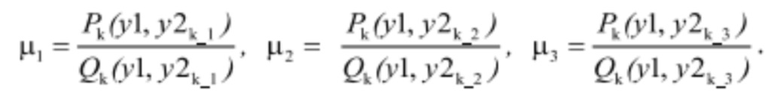
Приняв значение этого отношения для расчетной кривой 1 завода за единицу, и вычислив отношения:
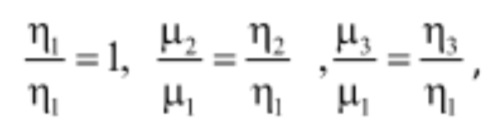
сравнивают результаты расчета с экспериментальными данными, полученными разными методами определения комбинаторных режимов.
И рассмотренном случае при у1=65%:
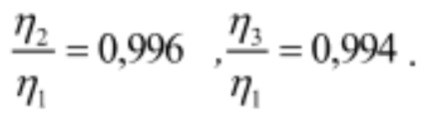
Приведенные данные вычислительных экспериментов для рабочих колес ряда ГЭС позволяют сделать вывод о простоте и эффективности предлагаемого способа.
Изобретение относится к области гидроэнергетики и может быть использовано для контроля комбинаторных зависимостей при проведении испытаний на работающем гидроагрегате. Разработан автоматизированный способ идентификации на плоскости «положение сервомотора направляющего аппарата - положение сервомотора рабочего колеса» координат точки комбинаторного режима на изолинии мощности заданной величины, который отличается однозначностью получаемого результата и может быть выполнен без вывода гидроагрегата из эксплуатации и использования специальных средств измерения. Изобретение направлено на повышение надежности определения координат точки комбинаторного режима при нормальной эксплуатации гидроагрегата. 1 з.п. ф-лы, 7 ил.
1. Способ определения координат точки комбинаторной зависимости поворотно-лопастной турбины на изолинии мощности, построенной в координатных осях положения сервомоторов приводов регулирующих органов поворотно-лопастной турбины относительно их полного хода, при котором формируют изолинию мощности, соответствующую заданному значению мощности, посредством разнонаправленного поочередного перемещения регулирующих органов поворотно-лопастной турбины,
отличающий тем, что
под управлением регулятора мощности изменяют положение одного регулирующего органа таким образом, что выполняется последовательный переход от первого значения мощности к заданному значению мощности, а затем ко второму значению мощности, а затем изменяют положение другого регулирующего органа таким образом, что осуществляется обратный последовательный переход от второго значения мощности к заданному значению мощности, а затем к первому значению мощности, при этом заданное значение мощности равно полусумме первого и второго значений мощностей,
сохраняют значения координат точек, соответствующих первому, второму и заданному значениям мощностей,
осуществляют построение трех изолиний мощности, соответствующих первому значению мощности, второму значению мощности и заданному значению мощности, на основании сохраненных значений координат точек, соответствующих первому, второму и заданному значениям мощностей соответственно,
затем на изолинии мощности, соответствующей заданному значению мощности, выбирают ряд точек, расстояние между которыми в районе интенсивного изменения производной не превышает одного процента от полных перемещений сервомоторов приводов регулирующих органов, и проводят через выбранные точки прямые, параллельные координатным осям, вычисляют длины отрезков, содержащих точку изолинии мощности, соответствующей заданному значению мощности, и отсекаемых от упомянутых линий изолиниями мощности, соответствующих первому и второму значениям мощностей, и вычисляют среднеквадратическое значение длин двух полученных отрезков,
при этом точка на изолинии мощности, соответствующей заданному значению мощности, в которой вычисленное среднеквадратическое значение будет минимально, принимается за точку комбинаторной зависимости для заданного значения мощности при текущем напоре нетто.
2. Способ по п. 1, отличающийся тем, что аналитические выражения для изолиний мощности получают путем монотонной сплайновой аппроксимации.
| Киселев Г.С | |||
| Определение оптимальной комбинаторной зависимости поворотно-лопастной турбины по изолинии мощности, Гидротехническое строительство, Москва, Энергопрогресс, 1980, N2, стр | |||
| Способ сужения чугунных изделий | 1922 |
|
SU38A1 |
| СПОСОБ АДАПТИВНОЙ КОРРЕКЦИИ КОМБИНАТОРНОЙ ЗАВИСИМОСТИ ПОВОРОТНО-ЛОПАСТНОЙ ГИДРОТУРБИНЫ | 2005 |
|
RU2302551C2 |
| Способ и устройство повышения точности управления углом установки лопастей поворотно-лопастной турбины | 2015 |
|
RU2608793C2 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ АКТИВНОЙ МОЩНОСТЬЮ И ЧАСТОТОЙ ГИДРОАГРЕГАТА С ПОВОРОТНО-ЛОПАСТНОЙ ТУРБИНОЙ | 2013 |
|
RU2531068C1 |
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ АКТИВНОЙ МОЩНОСТЬЮ ГИДРОАГРЕГАТА С ПОВОРОТНО-ЛОПАСТНОЙ ТУРБИНОЙ | 2009 |
|
RU2468246C2 |
| ПИПЕРИДИНОВЫЕ СОЕДИНЕНИЯ И ФАРМАЦЕВТИЧЕСКАЯ КОМПОЗИЦИЯ, ОБЛАДАЮЩАЯ АКТИВНОСТЬЮ АНТАГОНИСТА ПЕРИФЕРИЧЕСКОГО ДЕЙСТВИЯ ОПИОИДОВ | 1992 |
|
RU2076863C1 |
Авторы
Даты
2021-02-24—Публикация
2020-07-13—Подача